PreNTT：面向zk-SNARK的数论变换计算并行加速方法

摘 要：简洁非交互式零知识证明（zk-SNARK）由于具备证明验证过程简捷快速的优点，已在加密货币等众多领域得到广泛应用。但其证明生成过程所需计算仍复杂耗时，影响了进一步的应用拓展。针对zk-SNARK证明生成过程中的主要计算瓶颈——数论变换（NTT），提出了一种基于GPU的NTT计算加速方法PreNTT。首先，提出了基于预计算的NTT并行计算方法，利用预计算与旋转因子次幂算法优化，减少NTT并行计算开销，并结合动态预计算，进一步提高NTT计算效率。其次，通过“动态自适应计算核调度”，可以根据NTT输入规模自适应地分配GPU片上资源，提升了大规模NTT任务的计算能效。然后，通过核外整体数据混洗和核内局部数据混洗相结合的方式，避免了访存冲突。最后，使用CUDA多流技术执行数据传输和计算过程，对预计算时间进行了有效隐藏。实验结果表明：基于PreNTT实现的zk-SNARK系统，与目前业界最先进的系统Bellperson相比，NTT模块运行时间获得了全规模最低1.7倍的加速比，最高加速比为9倍。PreNTT能够有效提高NTT算法并行度，降低zk-SNARK运算时间开销。

关键词：简洁非交互式零知识证明；数论变换；GPU；并行计算；加速

中图分类号：TP311;TP309.7 文献标志码：A 文章编号：1001-3695（2024）10-025-3059-09

doi：10.19734/j.issn.1001-3695.2024.03.0054

PreNTT：parallel acceleration method for number theory transformation calculations for zk-SNARK

Ding Dong1a，Li Zhengquan1a，2，Chai Zhilei1b

（1.a.School of Internet of Things Engineering，b.School of Artificial Intelligence & Computer Science，Jiangnan University，Wuxi Jiangsu 214122，China;2.State Key Laboratory of Networking & Switching Technology，Beijing University of Posts & Telecommunications，Beijing 100876，China）

Abstract：Zero-knowledge succinct non-interactive proofs（zk-SNARK）have found extensive applications in various fields，including cryptocurrencies，due to their swift and efficient proof verification process.However，the computational intensity of the proof generation process poses a significant challenge，particularly at the number theoretic transform（NTT）stage.This paper proposed a GPU-based acceleration method for NTT computations，named PreNTT，to address this bottleneck.The method employed precomputation and optimization of twiddle factor powers to reduce the parallel computation overhead in NTT.It also introduced dynamic precomputation to enhance the efficiency of these computations.The algorithm made use of dynamic adaptive kernel scheduling，which allocated GPU resources on-chip according to the NTT input size，thereby boosting the computational efficiency for large-scale tasks.Additionally，the approach combined external global data shuffling with internal local data shuffling to avoid memory access conflicts.The use of CUDA multi-stream technology allowed for effective concealment of precomputation times during data transfer and computation processes.Experimental results indicate that the zk-SNARK system utilizing PreNTT achieves a speed-up ratio ranging from 1.7x to 9x in NTT module running times compared to Bellperson，the industry-leading system.PreNTT effectively increases the parallelism of the NTT algorithm and reduces the computational overhead in zk-SNARK operations.

Key words：zero-knowledge succinct non-interactive argument of knowledge;number theoretic transformation;GPU;parallel computing;acceleration

0 引言

简洁非交互式零知识证明（zero-knowledge succinct non-interactive argument of knowledge，zk-SNARK）是由Micali等人提出的加密协议［1］，它使得一方（证明者）能够向另一方（验证者）证实某个陈述的真实性，而无须透露任何额外信息。作为零知识证明协议（zero-knowledge proofs，ZKP）的一个先进变体，zk-SNARK生成的证明极其简短，通常只有几百字节，仅需毫秒级验证时间。鉴于其卓越的效率和隐私保护特性，zk-SNARK已被广泛应用于多种场景，包括加密货币［2～4］、电子投票系统［5］、可验证的数据库外包服务［6］、可验证的机器学习过程［7，8］、公钥加密方案［9］以及匿名认证系统［10］等。近些年，基于zk-SNARK的实现方案不断涌现［11～14］，其中Groth16方案［14］因其卓越的效率而备受推崇。

尽管zk-SNARK的验证时间短，但其证明构建阶段计算复杂度极高，且实际应用往往需要频繁构建证明，产生高昂的时间成本。随着数据规模和安全性需求的日益增长，实际应用中越发难以承受持续膨胀的计算开销。因此，计算效率已经成为zk-SNARK实现中重要的性能指标。尤其在证明创建过程中，椭圆曲线配对涉及到的数论变换（number theoretic transformation，NTT）及其逆变换（inverse number theoretic transformation，INTT）在多项式模乘操作中占据了大量证明时间［15］。此外，在全同态加密［16～18］和后量子密码学［19］等领域，也存在着诸多对数论变换的使用需求。研究者们提出多种硬件架构的NTT加速方案，包括CPU、FPGA［20］以及GPU。其中GPU由于其编程灵活度高和高指令吞吐量的特点受到更多关注及应用。

Kim等人［21］对NTT与离散傅里叶变换（DFT）的算法特点进行了对比分析，提出了一种NTT特有动态根生成方法，利用动态旋转（OT）技术计算部分旋转因子，降低模乘成本。但这种优化仅限于NTT的后阶段，对全局计算开销的影响有限。当NTT的计算规模较小时，进行的模乘运算数量有限，这使得OT技术在小规模NTT计算中的优化效果并不显著。Naina等人［22］提出对后量子典型算法FrodoKEM、NewHope和Kyber的GPU加速方案，其中对NTT进行了高效实现。在NTT计算过程中，将中间值存储于GPU片上共享内存，减少对全局存储器的读写操作。然而，zk-SNARK的高安全性需求使得蝶形运算规模显著增加，超出GPU共享内存的容量限制。因此，该方法仅在小规模应用中表现优异，面对zk-SNARK中大规模NTT计算时的优化效果不佳。文献［22］提出了进一步加速GPU上NTT内核的方法，使用CIOS形式的蒙哥马利乘法，并采用分段乘法和PTX指令集来提升循环处理的效率，对NTT/INTT操作进行了数据布局和乱序处理的优化。然而，该方法主要专注于内核级别的细粒度优化，忽略了内核调度与任务分配的重要性。这种偏重导致当数据规模变化时，运算性能表现出明显的不稳定性。因此，该方法在应对多尺度计算负载时难以实现稳定的加速效果。

鉴于NTT计算中内存访问的高敏感性及其高计算复杂度，目前的研究领域还未提供一个针对各种规模计算负载的有效的加速策略。因此，本研究借助CPU-GPU异构计算平台，针对zk-SNARK中的NTT，提出一种适应各种规模任务的高效NTT并行加速方案。本文的主要贡献包括：

a）提出并行加速方法PreNTT。NTT计算中，将需重复计算且计算复杂度高的旋转因子部分预先计算，并使用快速幂算法，有效降低NTT任务中的计算开销以及访存开销，并根据输入规模动态调整预计算内容。

b）在GPU中实现PreNTT，并在其基础上实现“动态自适应计算核”。基于输入规模可适应性分配GPU每个线程块及其内部线程的任务，以此保证GPU计算时各线程的负载平衡性，实现对NTT任务的全规模加速。

c）提出一种整体+局部的数据混洗策略，主计算核整体与核内线程块分别进行数据洗牌，减少计算过程中的数据访存冲突，保证数据正确性。利用CUDA流重叠技术掩盖预计算核执行时间，提高整体运算效率。

此外，在CPU-GPU异构系统上实现了上述并行计算方案，并构建了完整的zk-SNARK系统。与目前业界最优的基于GPU的zk-SNARK实现Bellperson［23］相比，本文NTT模块获得全规模最低1.7倍的加速比，最高加速比为9倍。

1 预备知识

1.1 零知识证明

相较于其他零知识证明协议［24，25］，zk-SNARK拥有简洁性和非交互性两个优势。简洁性是指zk-SNARK生成的证明非常简短，即使面对复杂的语句也能够快速验证。zk-SNARK能够为任何可转换为算术电路的语句提供证明，算术电路指一组可以在私密信息上求值的方程。简洁性的实现依赖于使用R1CS（rank-1 constraint system），zk-SNARK通过将计算问题转换为约束系统，包含输入变量、中间变量和输出变量之间的关系约束，将复杂问题描述为数学运算电路，生成的证明仅需验证约束关系的解存在即可，无须包含解的详细值，显著缩短了证明的尺寸。

传统零知识证明协议要求验证者和证明者同时在线，多轮交互通信增加了大量通信开销，大大降低了协议的运行效率。zk-SNARK为实现非交互式证明，由可信三方预先设置一系列与特定约束系统紧密相关的公共参数及验证密钥和证明密钥。证明者根据公共参数和私有输入生成证明，验证者则通过公共参数和验证密钥独立验证证明，无须与证明者交互。

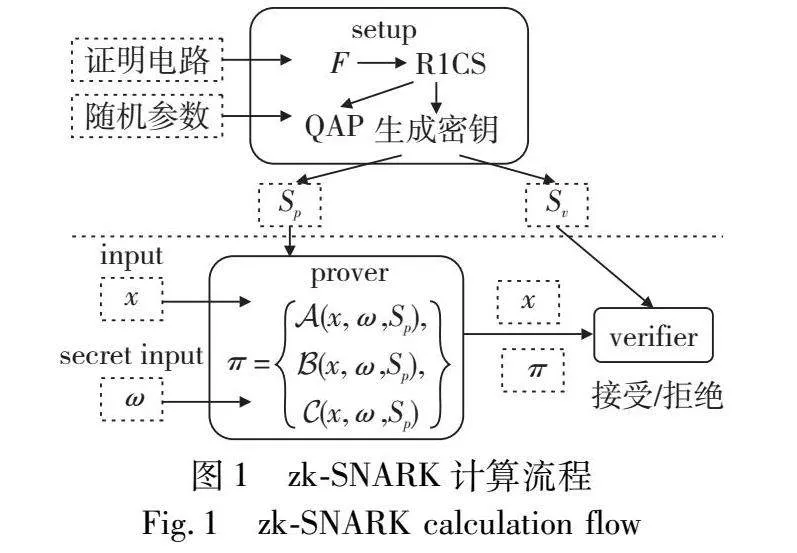
如图1所示，zk-SNARK协议主要分为三个主要步骤：

a）Setup（初始化）：此阶段中生成者（prover）会执行一些预处理操作来设置证明系统，包括选定安全参数、生成公共参数，并根据算术电路构建R1CS。

b）Prove（证明）：证明者根据输入和电路的描述生成证明，表明输入满足电路的规则，并将证明发送给验证方。

c）Verify（验证）：验证者（verifier）使用公共参数、电路描述和证明来验证生成者的声明。验证者仅需执行少量计算即可验证证明的真伪。

Setup阶段主要进行参数设置，包括公共参数和辅助参数。公共参数的生成通常在可信任的设置阶段进行，涉及生成者的验证密钥和承诺密钥等关键参数。辅助参数的生成则可在更高层次的设置过程中进行，包括描述约束系统（R1CS）和约束多项式的系数等。Setup阶段通常具有较高的计算复杂度，但在证明系统中仅需执行一次即可为多个证明提供参数。在prove阶段，证明者使用私有输入和公共参数来生成证明。具体步骤包括将输入映射到约束系统的赋值，使用快速多项式求值方法（如NTT）计算约束多项式的点值形式，并构建证明多项式。证明多项式是一个用于隐藏生成者的私有输入的多项式。生成证明过程需要进行大量的多项式求值操作。这些操作涉及将多项式从系数形式转换为点值形式，并执行多项式乘法和加法。Verify阶段使用时间较短，计算难度较低，本文不再进行赘述。

1.2 数论变换（NTT/INTT）

NTT是一种基于数论的快速傅里叶变换（fast Fourier transform）算法，用于高效完成有限域上的多项式乘法。NTT是在模数为素数p的有限域上进行的变换，其中p通常为2的幂加1，即p=2k+1，k为整数。NTT利用模运算的性质和数论中的同余关系，将多项式乘法转换为在有限域上的点值乘法，从而降低乘法运算的复杂度，式（1）为NTT计算公式。

A=NTT（a）=∑n-1j=0;i=0ajωij（mod p）（1）

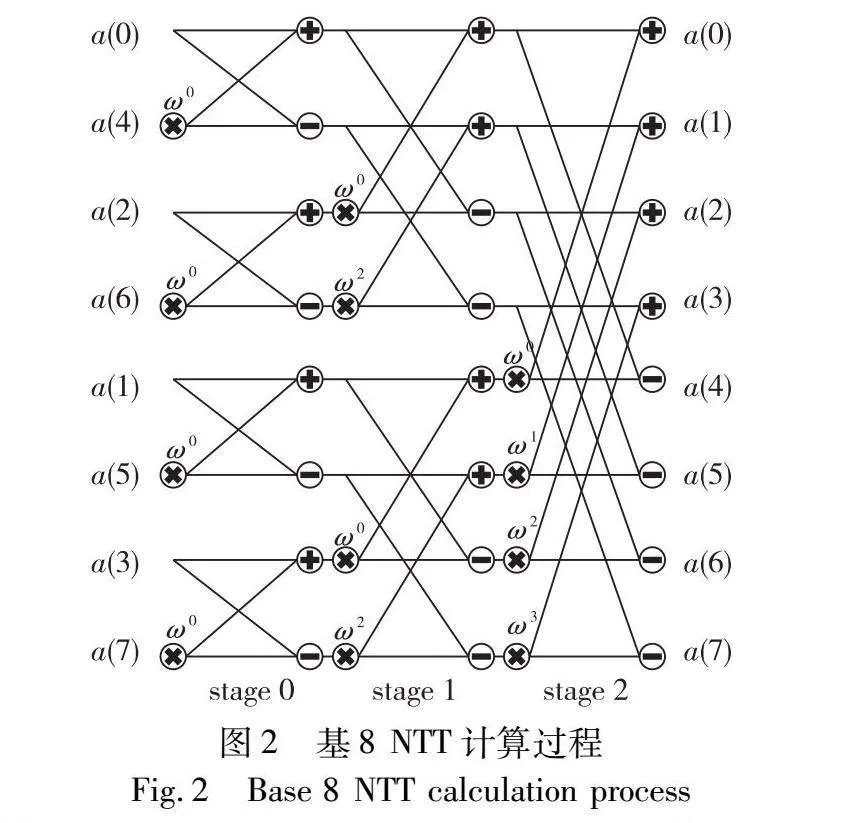
其中：a代表输入数据，一共有n个输入，ω代表旋转因子，每个输入与不同的旋转因子进行乘法运算，并且需要对每个计算结果进行累加才可以得到最终结果。图2展示了规模为8的NTT计算过程。

如算法1所示为目前最流行的NTT迭代算法，其中Fp指有限域。其中以基2蝶形运算为循环底层，通过三层循环实现迭代算法。

算法1 NTT迭代算法

输入：A=（a0，a1，…，an-1）∈Fp；ωn∈Fp。

输出：Y=（y0，y1，…，yn-1）∈Fp。

1Set Y=A

2for i=1 to log2n do //代表蝶形运算轮次

3 ωi=ω（p-1）/2in mod p//旋转因子运算

4 for k=0 to n-1 by 2i do

5 ω=1 mod p

6 for j=0 to 2i-1 do//结合步骤4代表轮内数据运算

7 t=ωyk+j+2i-1 mod p

8 u=yk+j

9 yk+j=（u+t）mod p

10 yk+j+2i-1=（u-1+p） mod p

11 ω=ωωi mod p

12 end for

13 end for

14end for

15return Y

NTT的逆运算只需要将ω替换为逆元，其他的计算顺序和蝶形运算方式不变。完成NTT和INTT后，结果被放大n倍，故需要对INTT的输出序列乘以n的逆元进行归一化处理才能获取最终结果。

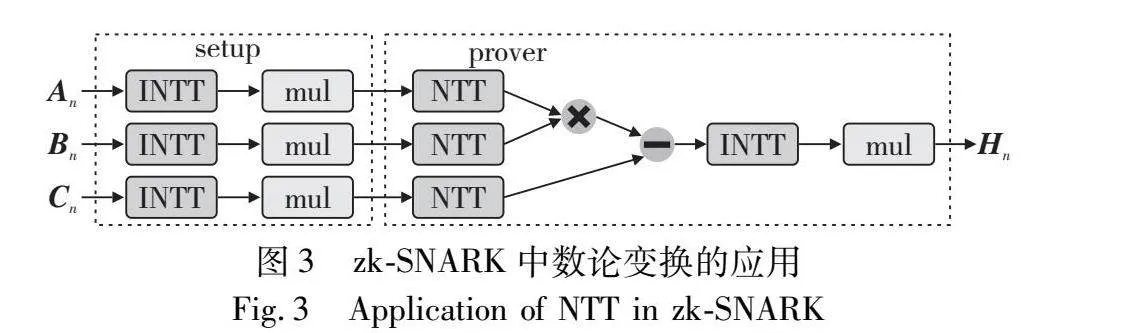
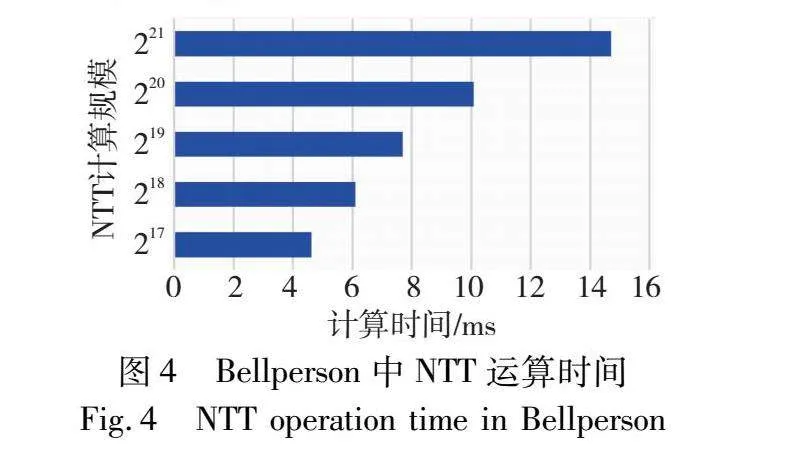
在zk-SNARK最先进的部署Bellperson［23］中，NTT应用主要在两个部分，如图3所示，首先在setup阶段使用INTT实现拉格朗日插值法。特定的约束系统（R1CS）的约束信息一般以一组已知的点的形式给出，使用拉格朗日插值法可将约束信息的点值表示转换为多项式表示。其次在prover阶段使用NTT和INTT组合实现多项式运算。将两个多项式从系数表示转换为点表示再进行运算操作，可以将计算时间复杂度从O（n）降低至O（nlog2n）。图4为Bellperson中不同规模NTT的运算时间。

1.3 现有NTT并行算法

在zk-SNARK实际部署中，NTT的输入规模较大（超过210），根据式（1），NTT运算需要多次蝶形运算，如果直接对NTT任务进行递归处理，需要访问和存储大量数据，会导致访存冲突和内存过载，造成片上资源损耗以及计算效率的降低。因此，需要对NTT算法进行改良以适配高效率并行计算需求。Bellperson是当今最流行的zk-SNARK库，基于Rust语言实现，其使用NTT并行算法将NTT任务分解。

将n个a分为n2×n1的矩阵形式，由式（1）则可推出如下公式：

A［i1+i2n1］=∑n2-1j2=0［（∑n1-1j1=0a［j1n2+j2］ωj1i1n1）ωj2i1n］ωj2i2n2（2）

其中：i1∈［0，n1）;i2∈［0，n2）。

由式（2）可知，原n规模的NTT计算任务被分解为三个部分，第一部分为式（3），第二部分为旋转因子运算，第三部分为式（4）。

∑n1-1j1=0a［j1n2+j2］ωj1i1n1（3）

∑n2-1j2=0a［j1n2+j2］ωj2i2n2（4）

第一部分，将输入矩阵按列展开，共有n2列规模为n1的NTT，这n2个子NTT任务可并行完成。其中n1是n缩小n2倍，n1的大小可根据计算设备的硬件性能自定义。第二部分，当完成n2个规模为n1的子NTT后，需要将每个输出结果分别与ωj2i1n相乘，这些旋转因子的计算开销巨大。最后，根据式（4），对处理过的数据进行转置操作，仍按列展开，每一列为n2规模的NTT，共有n1列数据，对这n1列并行计算即可完成完整规模的NTT计算任务。其具体实现如算法2所示，其中按行按列展开的部分，分配至多线程并行执行。线程内部仍然以基2蝶形运算作为底层操作。

算法2 NTT并行算法

输入：A=a0，a1，…，an2-1an2，an2+1，…，a2n2-1∈Fp，ωn∈Fp。

输出：Y=（y0，y1，…，yn-1）∈Fp。

1Set Y=A

2compute ω（n2*q）n q∈［0，n1）

3 step 1 for i=0 to （n1-1）/2 do //分块并行执行

4 for k=0 to log2n1 do //区分不同轮次，块内并行

5 bit=n1/2k

6 for j=0 to （n1-1）/2 do //结合步骤4进行基2蝶形运算

7 d=j&（bit-1）

8 u=y2j-d

9 t=yu+bit

10 y2j-d=（u+t） mod p

11 yu+bit=（u-t）×ωn2dkn mod p //10，11为基2蝶形运算

12 end for //块内并行结束，需要块内同步数据

13 end for

14end for

15compute ωj2i1n j2∈［0，n2） i1∈［0，n1）

16y=y×ωj2i1n mod p

17transpose Y

18repeat step 1 exchange n2 and n1

19return Y

2 本文方法PreNTT

现有的NTT并行算法通过将n规模的任务分解为多轮较小规模的NTT。其核心思想是通过增加计算任务的数量，从而优化单一计算任务中的计算负载和复杂的内存访问模式。这种方式能够提升每个计算任务的执行效率，并加速整体运算过程。

在实际运用中，该算法将n规模输入分解为方阵时（即设定n2=n1）达到最佳性能，此时并行设备只需实例化一份计算核，且无须进行额外的旋转因子计算。然而，由于现有算法的分解矩阵A的列数是固定的，恰好分解为方阵的情况较为少见。

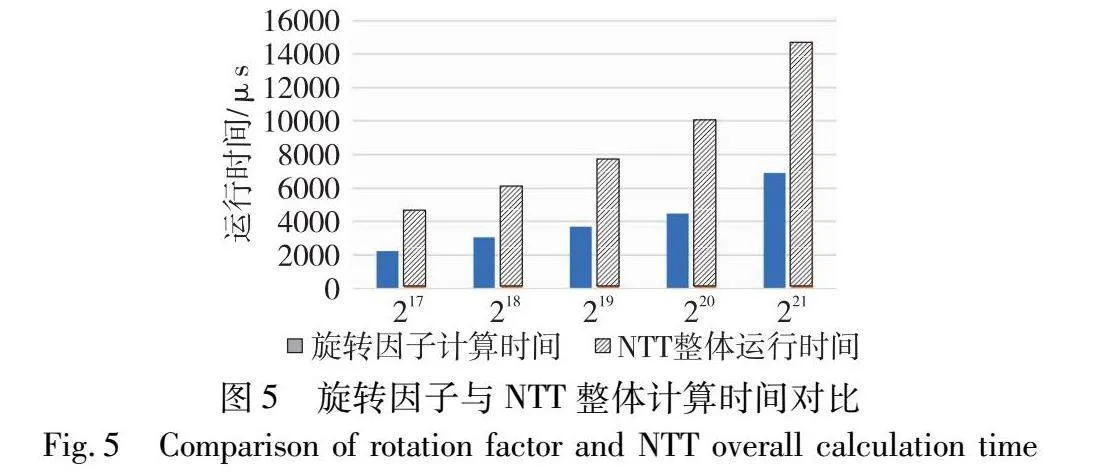
当算法达到最佳性能时，n2=n1=n，以此评估此算法的最小计算成本。首先需要明确的是NTT计算中，计算成本最高的是蒙哥马利模乘［26］，它的代价远超其他在NTT中的常规运算。因此，本文将蒙哥马利模乘的次数作为衡量NTT计算成本的指标。该算法首先将任务分为n1个子任务并行处理，每个子任务进一步分为n1/2个子任务进行蝶形运算，第二层子任务蒙哥马利乘法的次数为T1=log2n1；第二部分计算旋转因子，以最大值ω（n2-1）（n1-1）n计算，此次幂运算涉及的模乘次数为T2=4×log2n1；由于设定n2=n1，第三部分计算成本与第一部分相同，即T3=log2n1。因此总的模乘次数大致为T=6×log2n1，第二部分旋转因子计算占据总计算成本的2/3。图5展示了为旋转因子计算时间与NTT整体运行时间的对比，显而易见，旋转因子计算的开销在总体成本中占据了较大比重。业内许多研究［21，22，27］聚焦于访存优化，缺少有效的旋转因子运算策略。此外，在zk-SNARK的证明生成过程中，需要执行7次NTT/INTT，相应的需要7次旋转因子的计算。值得注意的是，在生成单次证明的过程中，NTT的输入规模及NTT和INTT的原根均保持不变，这意味着每一次NTT/INTT操作中所需的旋转因子也是相同的。因此，如果能够在计算过程开始之前预先计算这些旋转因子，并在后续的每次NTT/INTT操作中重复利用这些预计算结果，就可以显著减少不必要的计算开销。

基于此本文提出了一种基于预计算的NTT并行计算方法，即PreNTT。PreNTT利用二进制快速幂算法预计算NTT中所需的旋转因子，根据输入规模适配不同的分解策略，以保证最佳计算性能。PreNTT只需进行两次旋转因子的预计算便可得到zk-SNARK的证明生成过程中全部NTT计算所需的旋转因子。

在计算旋转因子ωj2i1n时，与算法2将ωi1n和ωj2n分开计算后再相乘的计算方式不同，PreNTT采用二进制快速幂算法优化旋转因子计算。如图6所示，根据j2×i1的二进制值，提取出值为1的位，乘以对应的ω2kn（k为位置坐标）。

此方法所需的蒙哥马利模乘次数为log2n，假设输入规模为n2=n1=n，与NTT并行加速方法中旋转因子幂运算模乘次数4log2n1相比，PreNTT在旋转因子计算上的模乘次数仅为T2=log2n=2log2n1，而总的模乘次数为4log2n1，与现有方法相比，PreNTT的模乘次数加速比为1.5倍。

除了计算成本的优化，PreNTT还在任务分配和负载均衡方面进行了改进。从算法2的分析中，可以明确仅当n2=n1=n时，NTT并行算法中所采纳的分解策略达到最优化。然而在实际应用中，满足此条件显得较为严苛。为此，PreNTT设计了一种动态预计算方法，根据输入规模不同动态规划预计算内容，确保NTT的核心计算部分始终运行在最佳状态。PreNTT对NTT任务进行分解时，分解矩阵A的列数随着输入规模不同自适应变化，即只要输入规模n为2的偶次幂，即可将其分解为方阵以达到并行计算最佳性能。此时，PreNTT在预计算核中只需利用二进制快速幂算法计算旋转因子，主计算核中对其进行索引访问即可。而当输入规模n为2的奇次幂时，为了将主计算核任务分解为方阵，PreNTT提出一种新的预计算策略。

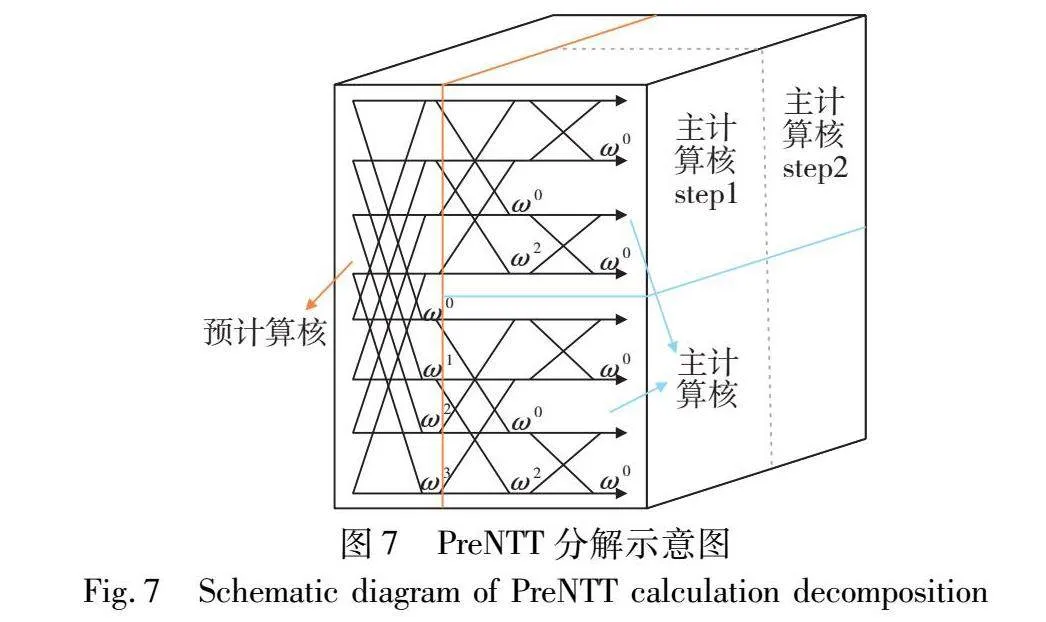
如图7所示，当NTT任务无法分解为方阵时，利用GS蝶形运算［29］，第一轮进行固定步长的蝶形计算操作使得NTT任务得以分解为两个相互独立且无数据依赖关系的子计算任务。

这些子计算任务可视为具有n/2规模的计算实例，按此逻辑继续分解，直到子任务规模nsub=k（k为NTT主计算核规模），将前若干轮蝶形运算与旋转因子合并同时预计算。

当前预计算阶段所获得的旋转因子是不完备的，其原根最高次幂仅至n/2-1。鉴于此，PreNTT提出一种旋转因子补全方法。这种方法利用预计算核中存储的连续次幂的旋转因子，即ωin，i∈［0，n/2）来生成主计算核所需的旋转因子ωin/k，i∈［0，n/k），这里的k代表主计算核的数量。

ωin=ωi/kn/k i∈［0，n/2）（5）

根据式（5），将预计算所得的部分旋转因子与ωn/2n相乘，即可生成缺失的旋转因子。值得注意的是，在预计算核中得到的旋转因子并非每一项都被主计算核所使用，而是按固定步长偏移使用。因此，PreNTT将存储的旋转因子数量减少到原本数量的1/k，从而降低内存占用。

实际部署中，分解策略实施后，最底层蝶形运算的规模实际上减少了一半，较小的运算规模意味着更少的访存次数和较低的计算资源消耗，达到更高的计算效率。例如，在GPU中，这可以有效地避免Bank冲突；而在FPGA中，则有助于减少资源的占用，并提高其他计算任务的并行处理能力。

PreNTT设计一种自适应的动态预计算方法，其将NTT中开销占比较高，且破坏并行计算负载均衡的旋转因子计算提前，使得后续任务更易迁移到并行设备。此外，PreNTT利用更先进的旋转因子算法，减少其计算复杂度，并根据输入规模不同设计不同的任务分解策略，令主计算核的数据结构始终保持方阵状态，达到最佳计算性能。

3 基于GPU的PreNTT实现

3.1 动态自适应计算核的优化实现

在zk-SNARK的计算中，NTT的输入规模总是2的整数次幂，记为2n。n的具体数值对于底层来说无法预测，尽管先前的研究已经取得了一定的进展，但这些方法在处理不同规模输入时的效率并不均衡。当数据规模较小时，对计算核的细粒度优化无法有效提高运行速度；而面对大规模输入时，现有算法往往无法充分利用GPU硬件资源，无法达到最佳性能。为了克服这一局限，本研究基于GPU实现PreNTT，进一步提出“动态自适应计算核”。其自适应调整计算核心，使之可以根据输入规模的不同，灵活选择最合适的计算方案。这种动态优化不仅能够克服传统方法在不同规模输入下的性能波动，还能够在全规模范围内实现加速。通过这种方式，PreNTT的NTT优化核不受输入规模的限制，有效地弥补了现有研究的不足，为zk-SNARK的计算提供了更为高效和稳定的解决方案。

根据PreNTT的设计，其计算核心会根据输入规模动态地进行自适应调整，采用两种不同的计算方案。

当n为偶数时，由于主计算核可直接将计算任务分解为方阵，PreNTT优先处理计算密集型的旋转因子部分，利用GPU的预计算核进行计算并存储。后续步骤中，主计算核仅需执行NTT的蝶形运算部分，而中间所需的旋转因子可通过简单地访问存储系统来获取。

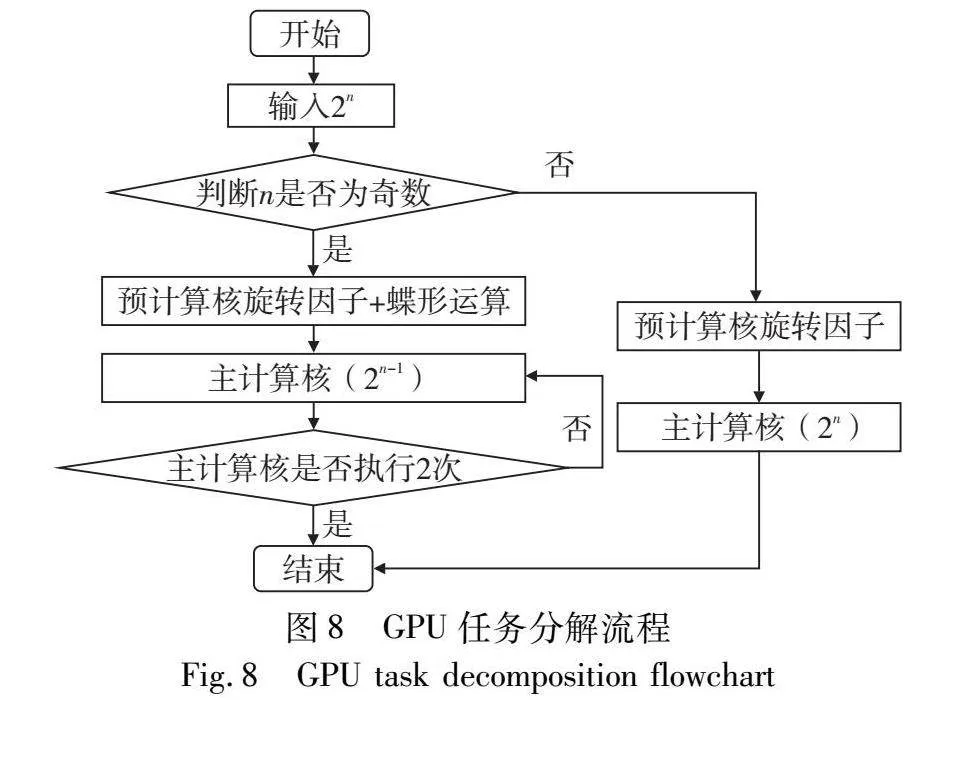
对于n为奇数的情况，问题变得相对复杂。这意味着NTT任务无法将输入数据整理为方阵，直接进行分解将导致需要额外的计算用于蝶形运算所需的旋转因子，从而增加不必要的计算和内存开销。因此，PreNTT采用先前描述的GS分解方法，将第一轮蝶形运算与旋转因子计算合并为一个预计算核心。经过预计算的分解，主计算核的任务被进一步细分为两个子任务，这要求主计算核被连续调用两次，每次所需处理的计算规模为原始任务的一半，此时的计算规模转变为2的偶数次幂，从而可以整理为方阵形式。最后，主计算核心通过旋转因子补全方法获取所需的旋转因子。图8详细展示了PreNTT在GPU上的计算任务分解流程。

值得注意的是，NTT的操作数都是位宽为256位的标量，随着NTT计算规模的扩增，GPU的片上可用共享内存往往不能满足经过两次分解后的子任务的计算需求。以RTX3060为例，其片上共享内存限制了线程块内NTT规模的上限，使其最大仅能达到210，因此，当NTT的总计算规模增至222时，无法将NTT任务分解为二维矩阵进行运算。

当NTT的总计算规模达到或超过222时，简单地对NTT进行两次分解已无法满足性能优化的预期。因此，在部署大规模（超过221）NTT任务至GPU时，本文将计算任务进行三次分解，并专门关注了负载均衡的问题。

设总NTT规模为2n（其中n≥21），线程块内计算规模nb应满足条件：3nb≥n，并取满足此条件的最小值。在此基础上，最后一次计算核的线程块内计算规模定义为n-2nb。这样的设计将NTT计算任务分为三维矩阵，尽可能均衡分配每个维度的数据，确保主计算核中的三个计算任务具有近似的计算量，从而在预计算的旋转因子支持下，实现最佳的性能表现。而在进行三次分解时，由于此输入规模较大，将蝶形运算纳入预计算核会引入大量的内存开销，可能降低CPU与GPU之间的通信效率。因此，在处理大规模（超过221）NTT时统一使用偶数规模分解策略。如果采用片上内存较大GPU或NTT实际计算规模较小，则无须考虑此情况。

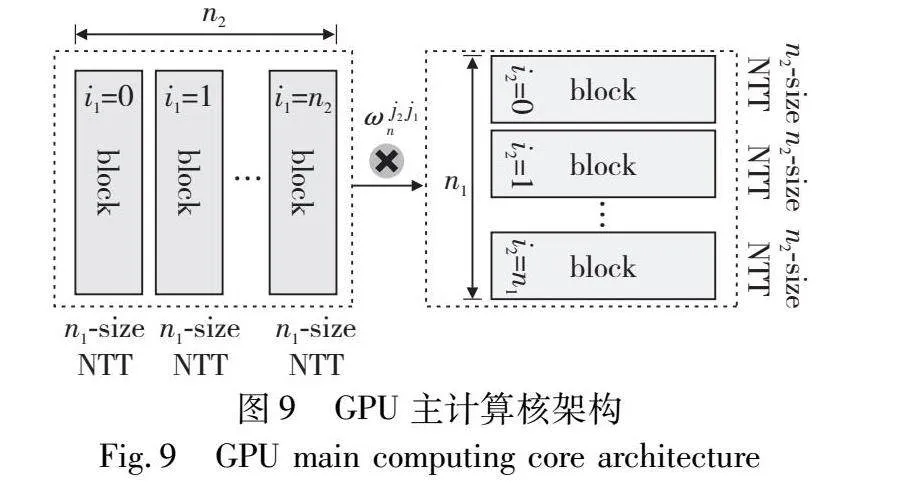
在处理NTT任务时，GPU首先激活预计算核心，NTT任务被逐步分解，主计算核心随后被调用以完成全部计算任务。如图9所示，主计算核将规模为n的NTT分为n1×n2矩阵。主计算过程分为两个独立的计算核心，第一个计算核心划分出n2个线程块（block），每个线程块被分配n1个数据元素，并为其开辟一个大小为n1的共享内存空间。每个block包含n1/2个线程，每个线程负责处理两输入的蝶形运算。在这个阶段，线程块间不存在数据依赖关系，线程块内的线程采用阻塞同步技术来及时更新存储在共享内存中的数据。第二个计算核心遵循类似的逻辑，首先将输入矩阵进行转置，即线程块的数量为n1，每个线程块内含有n2/2个线程，同时，每个线程块内输入数据和其共享内存的大小均设定为n2。

3.2 NTT访存与数据洗牌策略

在NTT的计算过程中，复杂的访存操作是一个不容忽视的挑战。NTT计算本身涉及到大量的数据交互和存取操作，而在实施动态任务分解策略时，这些访存操作变得更为复杂。为了高效处理这些复杂的访存需求，并最大化计算性能，需要对NTT的核内和核外数据访存进行深度优化。

NTT主计算核的细粒度优化策略重点研究了数据洗牌与访存优化技术。为了高效计算，选择使用共享内存和常量内存来存放数据，从而降低对全局内存的依赖和访问频率。尽管全局内存在GPU中提供了充足的全局内存可供所有线程使用，但其较慢的访问速度和频繁的读写操作可能成为性能的制约因子。与此相反，共享内存是设计用来在一个线程块内的各线程间进行数据交换的，它具有更低的延迟和更高的带宽。然而，其容量相对有限，这在大规模计算中可能成为一个限制。考虑到这一点，本文的GPU实现确保每个线程块处理的NTT计算任务规模保持在一定范围内，以确保不超出共享内存的容量。

在PreNTT中，主计算核每个线程块会计算固定规模NTT，并且规模不大，不会超过共享内存的容量限制，故使用共享内存存储单个线程块中蝶形运算的中间数据避免访存冲突，加快读写速度。当为每个线程块分配256规模的NTT计算任务时，首先从全局内存中提取输入数据，然后将其存储在共享内存中，作为蝶形运算的输入。每个线程块将进行8轮蝶形运算。每轮计算的输出结果作为下一轮计算的输入数据，数据通过共享内存交互，有效降速访存延迟，进而提供整体计算性能。

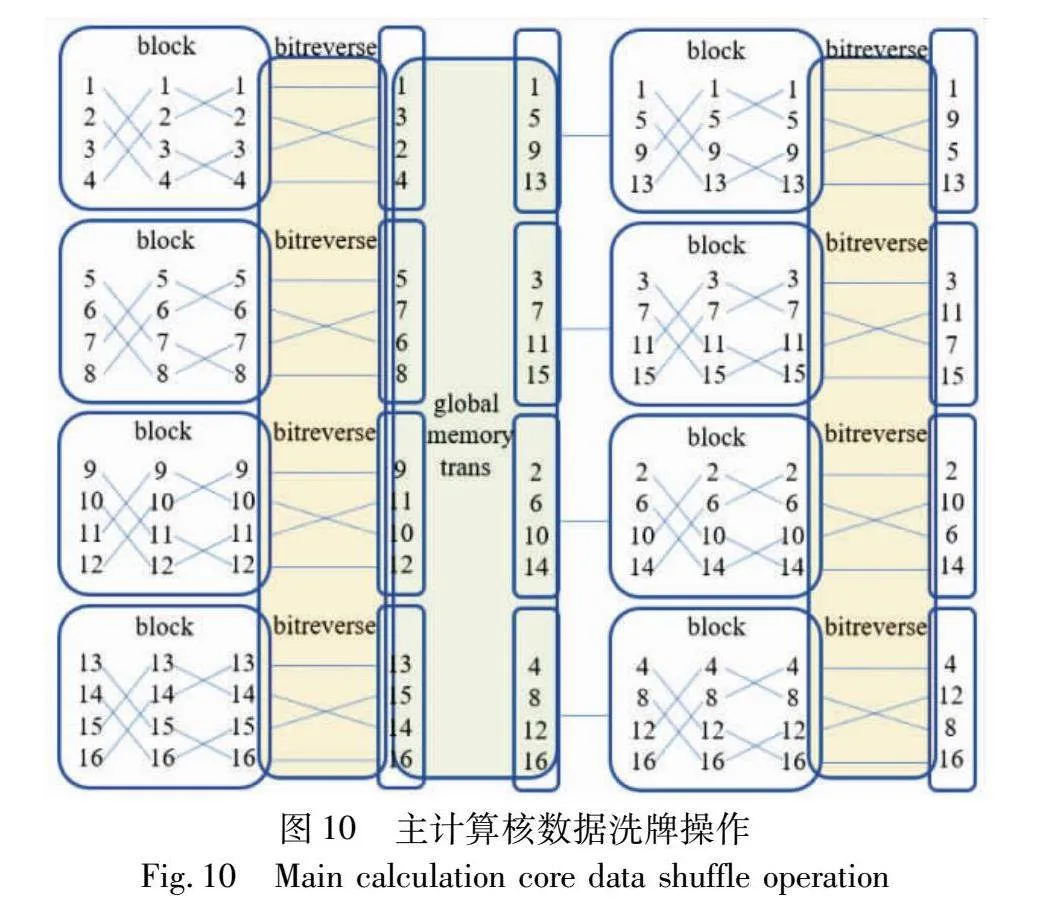
在NTT的蝶形运算过程中，频繁的洗牌操作是一个核心挑战。特别是在GPU上，这种数据洗牌往往导致内存的随机访问，进而触发内存访问的冲突，影响计算性能。核内与线程块内数据洗牌流程如图10所示，线程块内部完成计算后，必须进行一次内部洗牌操作。在NTT任务分配上有固定的规模，位反转操作的输出也相应地固定，PreNTT将位反转操作的数据索引存储在常量内存中，减少多余计算产生的开销。

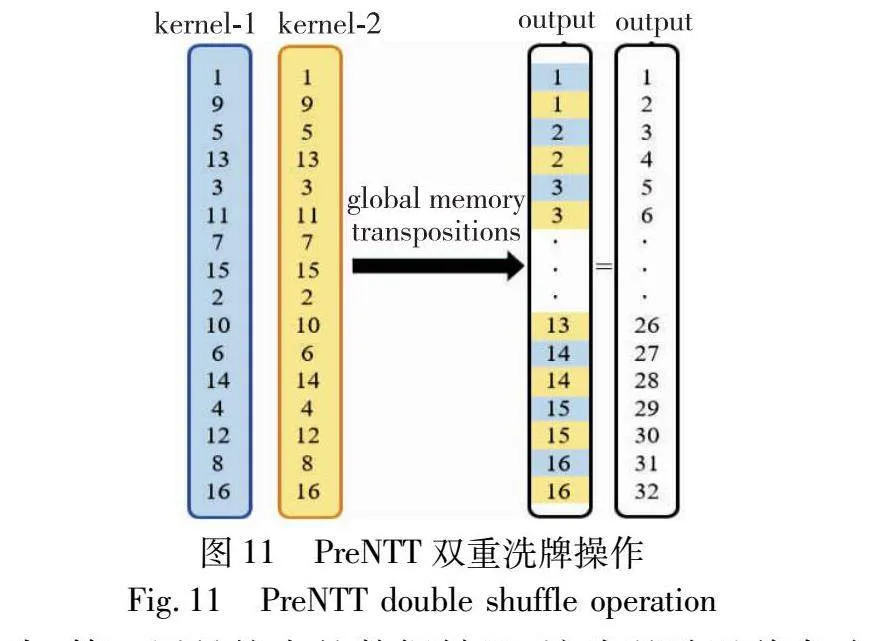
如图11所示，在线程块完成NTT任务之后，需要进行双重的数据洗牌操作。

首先，第一层是核内的数据转置：该步骤涉及将各个线程块的计算结果进行全局转置，从而纠正分解步骤导致的数据错位。接下来，第二层是核外的数据洗牌：在使用GS方法对NTT任务进行预计算分解后，必须将两次子任务的结果进行拼接，这涉及对两个主计算核的数据进行洗牌操作。

在最后一次调用GPU计算核时，GPU同时导入两个主计算核的数据。这些数据随后经过转置和插入处理，通过奇偶索引存储到连续的全局内存区域，主机端从全局内存获得最终的计算输出。

通过利用GPU的共享内存和常量内存资源，结合双重数据洗牌操作，本文不仅减少了对较慢的全局内存的依赖和访问次数，优化了数据在各计算单元间的流动效率，也解决了由PreNTT的任务分解策略引入的数据重组难题，确保了计算过程中的结果正确性。

3.3 CPU-GPU异构系统架构设计

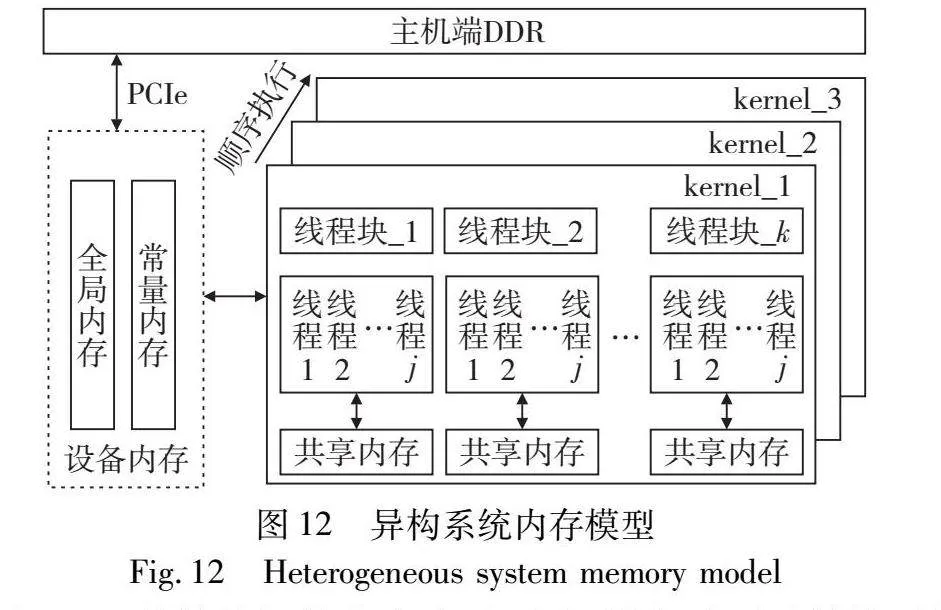
采用上述的PreNTT方法，本文实现了一种用于NTT计算的CPU-GPU异构加速系统，该系统是基于CUDA异构编程框架实现，内存模型如图12所示。

在GPU计算核初始化完毕后，主机端启动预计算核，并通过PCIe将相关参数（输入规模不同，参数内容也不同）传送至设备端的全局内存中。预计算核从全局内存中获取数据，并将每个线程块的数据暂存于块内共享内存，这样可以优化内存访问速度。随后，激活主计算核并直接从设备端的全局内存中获取数据存储于块内共享内存，用于后续的计算任务。所有计算核任务完成后，设备端将最终的计算结果通过PCIe传送回主机端的DDR内存。

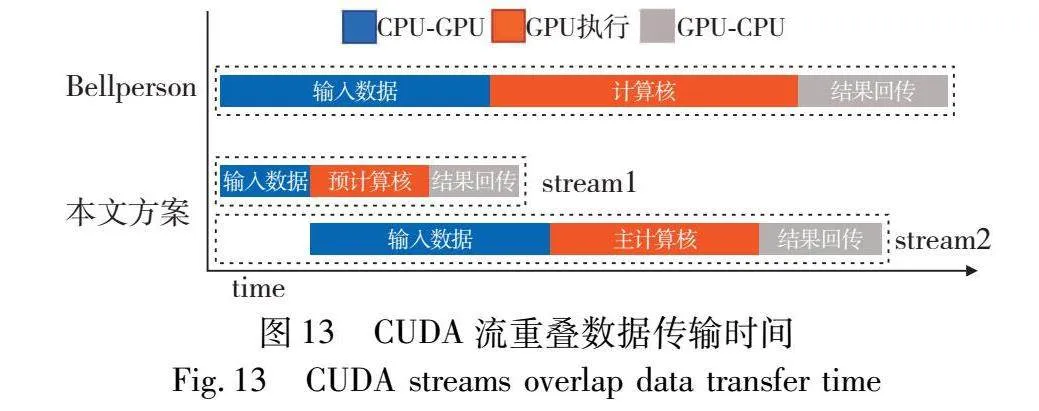
在启动设备端的计算任务前，主机端必须完成若干初始化步骤。在预计算核运行之前，主机端需为其生成旋转因子向量以供内部的快速幂算法使用。当预计算核的任务结束后，主机端需将主计算核所需的全部NTT输入数据映射至设备内存中，由于数据量巨大，其通信开销大于预计算核数据传输与运行时间。PreNTT采用CUDA多流技术，它允许内存传输和计算任务被放置在不同的流中，从而实现异步执行。

如图13所示，当主机端激活预计算核任务时，无须等待预计算完成，可同时进行其他操作，如分配内存空间或映射输入数据。鉴于预计算核的执行时间相对较短，这种方式确保了主机端的数据处理与预计算核的计算任务能够并行执行，掩盖预计算核的计算时间。

4 系统实现与结果评估

4.1 实验平台和环境

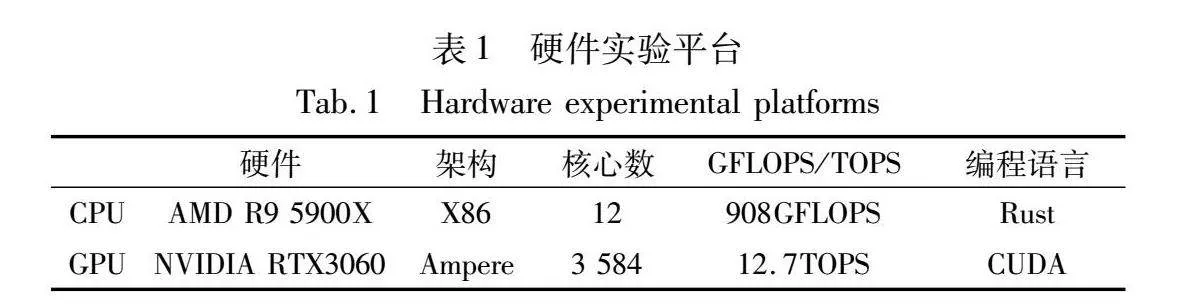
本文的实验是在一台配备3.7 GHz AMD Ryzen 9 5900X处理器（含12个物理核心）、12 GB显存的RTX3060显卡和128 GB DRAM的服务器上进行。该服务器运行Ubuntu 20.04.5操作系统和CUDA 11.8。硬件平台具体数据如表1所示。

4.2 系统实现

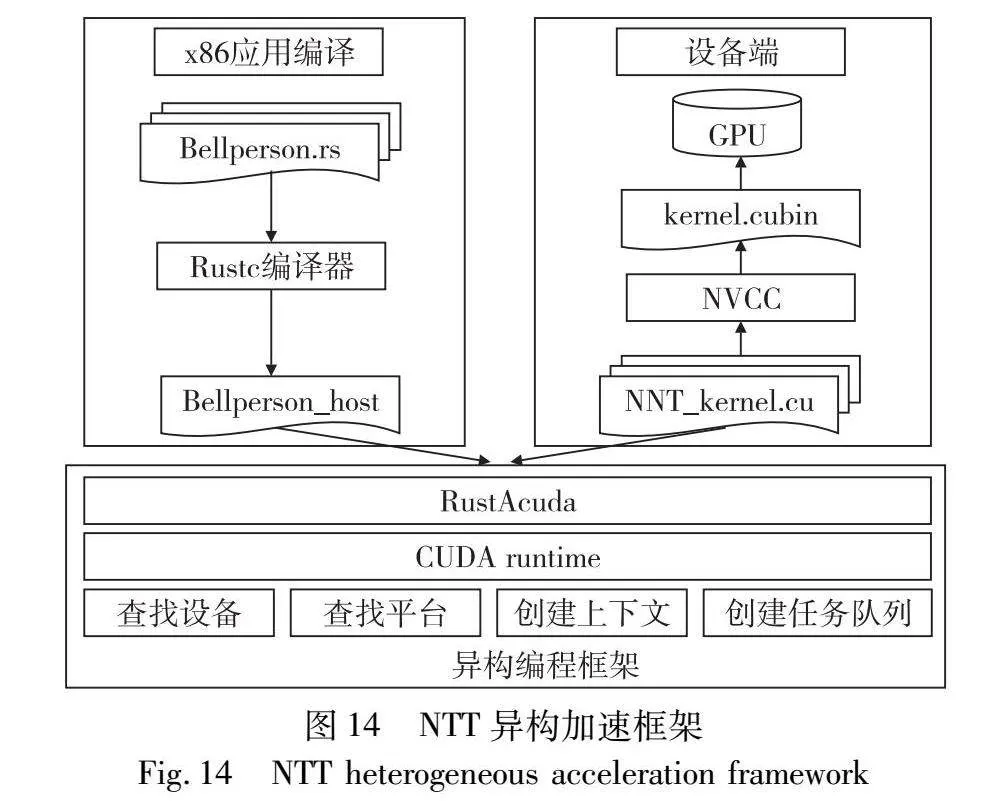
主流的异构编程框架包含CUDA和OpenCL，两者各有优劣。CUDA针对NVIDIA生产的GPU，拥有丰富的生态系统和广泛的开发资源，其中包括核心库、开发工具集以及优化库。相较之下，OpenCL虽有着较强的跨平台能力，能在多种硬件上执行，但由于其相对较小的生态系统，性能优化变得相对困难。考虑到这些因素，本文的系统设计主要包括主机端和设备端两个部分，并借助CUDA异构编程框架来处理主机端与设备端间的数据交互。图14为NTT异构加速框架示意图。

Bellperson是一个基于Rust实现的零知识证明系统库，提供了zk-SNARK证明系统构建所需的工具和库，如电路特性、约束系统和数字抽象。本文核心工作在于对Bellperson的代码重构，考虑到Bellperson使用的CUDA API并不直接支持stream分流，其结构相对复杂，本文选择采用Rust封装的rustAcuda替代原有库，并针对主机端的平台与设备查找、内核创建等功能进行了重新实现。

4.3 结果评估

4.3.1 同类工作对比

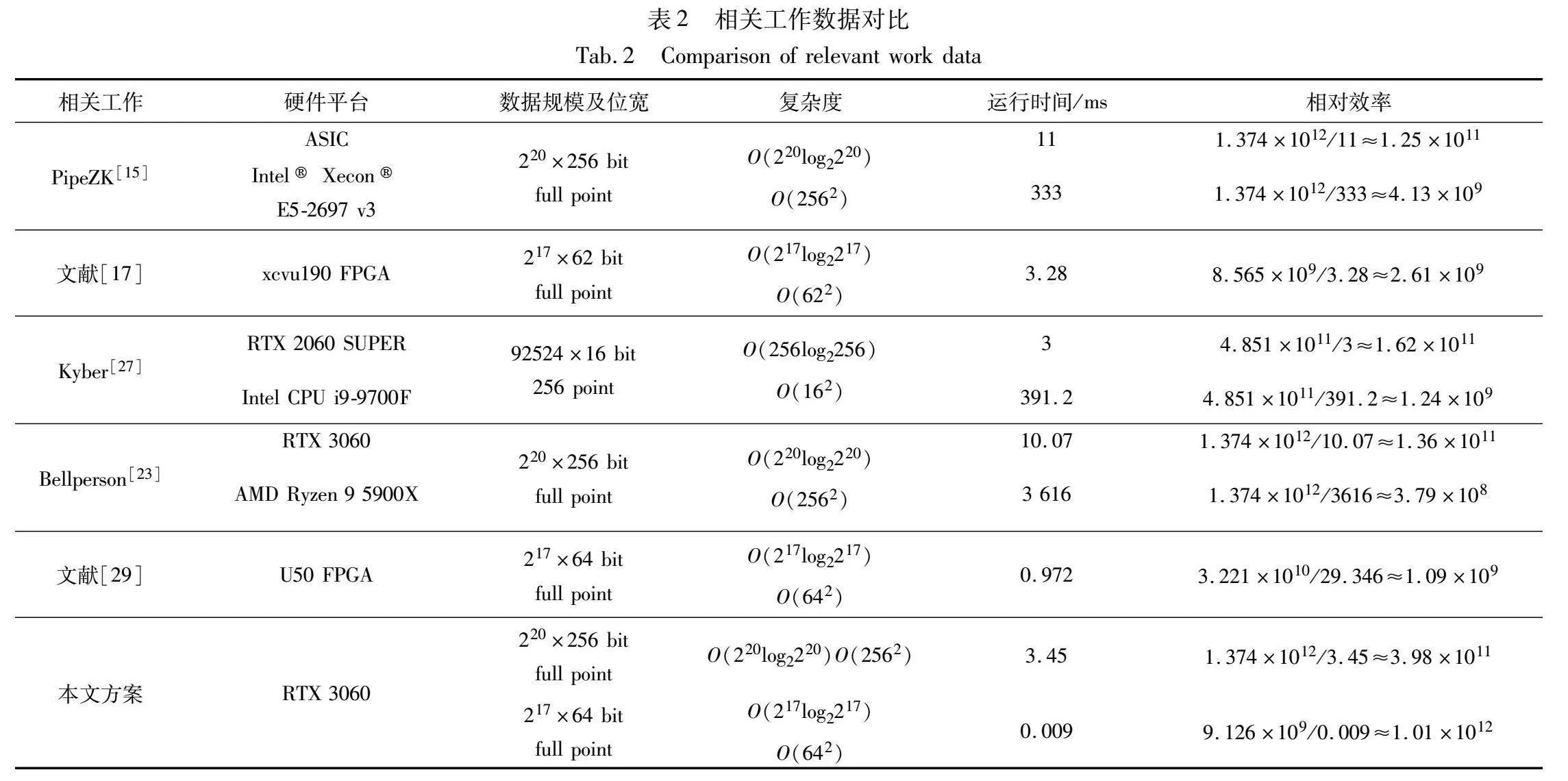
在众多NTT/INTT优化方案中，不同方案使用的硬件平台不同。例如，文献［15］基于ASIC进行实现，而Bellperson［23］则提供了GPU和CPU的实现。此外，不同的应用场景也导致了不同的计算规模和数据位宽，如文献［27］。为了有效地将这些方案与本文的实现进行比较，对部分优化方案进行了计算效率的抽象分析。

NTT/INTT的计算复杂度主要来源于两个方面。首先，蝶形运算中基于蒙哥马利模乘的计算复杂度，可表示为O（Nlog2N），其中N为NTT任务规模;其次，蒙哥马利模乘本身的计算复杂度，该复杂度可表示为O（n2），其中n为数据位宽，以对比不同位宽的实验方案。

总的复杂度可表示为

O（Nlog2N）×O（n2）=N×log2N×n2

相对效率可表示为

N×log2N×n2/NTT runtime

表2展示了本研究与相关工作的计算效率对比。值得注意的是，Kyber的实验是在RTX2060 SUPER平台上执行的。为了确保实验的严谨性，本研究对Kyber的相对效率进行了转换。本文采用TOPS（int32）作为评估GPU计算能力的指标，其中RTX2060 SUPER的TOPS为7.181，而RTX3060的TOPS达到12.7。经过转换后，Kyber的相对效率约为2.86×1011，这是其最佳性能情况。从上述数据分析中，可以清晰地看出，相对于其他相关工作，本研究的方案具有显著的加速效果。

4.3.2 基于PreNTT的Bellperson系统的性能评估

Bellperson主要部署于Zcash和Filecoin等应用代表了当前技术的前沿，其不断根据最新的研究成果和技术进步进行实时更新。这保证了所使用的算法始终处于行业领先水平，使其成为评估新提出策略有效性和先进性的理想对比对象。本文对比的Bellperson版本集成了众多先进NTT加速方案［22，30］，将本文提出的策略与Bellperson对应的NTT算子进行比较，可以准确评估所提策略在当前技术背景下的性能及可行性。

为满足用户对高效交易处理和快速区块确认的需求，实际操作中延迟被视为至关重要的评估指标。本文提出预计算核与主计算核相结合的加速方案，对NTT任务进行分解，实现全规模计算任务的优化。后续部分本文将从预计算核、主计算核与整体加速效果等角度，分别与Bellperson的GPU实现进行详细对比，以验证PreNTT的有效性。

需要强调的是，本文为展现PreNTT的先进性，将对比实验中Bellperson的NTT并行方案进行了改进。Bellperson中对NTT任务分解并不是动态变化的，每次执行运算时，分解矩阵的列数（即线程块的运算量）是固定的，当输入规模增加时，分解之后的任务会存在负载不均衡的问题。在实验中，手动将Bellperson每次的分解矩阵调整到最佳负载情况，即接近方阵的形式。本节展示的Bellperson相关数据为其算法所能展现的最佳性能。

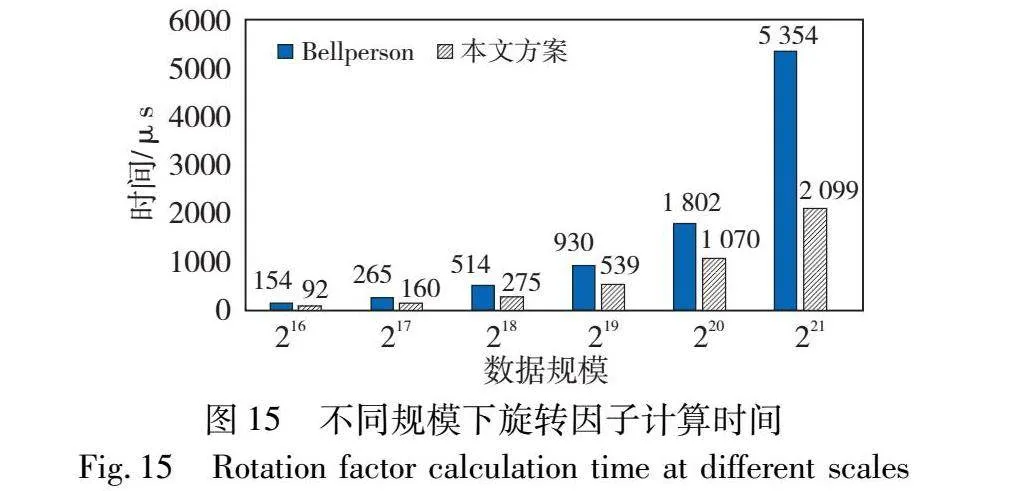
首先，在预计算核部分，通过采用旋转因子的快速幂算法进行了优化。为了明确对比，本文从Bellperson中单独提取了旋转因子的计算开销，与PreNTT预计算中旋转因子的计算时间进行对比。如图15所示，采用快速幂算法来计算旋转因子具有显著的效果。当计算规模为216时已经达到了1.6倍的加速比，随着计算规模的增加，加速效果逐渐显现。在计算规模为221时，加速比进一步提升至2.5倍，这超出了预期的2倍加速比。

GPU中共享内存的可用空间是有限的，当NTT的计算规模扩大到221时，需要进行三次分解以完成全部的计算任务，增加了额外的旋转因子计算开销。这种情况下，使用预计算核来单独处理旋转因子的方法不受NTT任务分解次数的限制，展现出独特的优势。可以预料的是，随着计算规模继续扩大，加速效果将越来越突出。

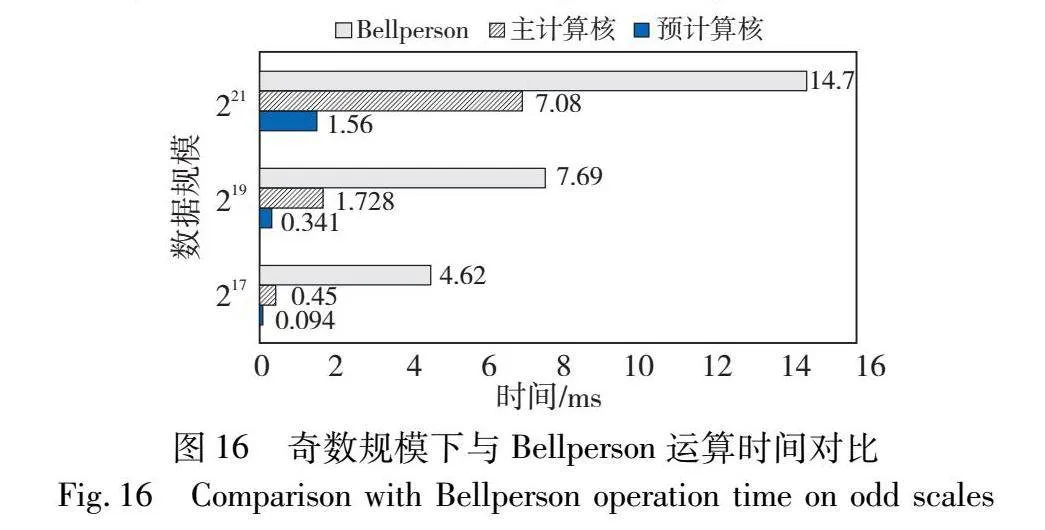
通过结合核内外双重数据混洗策略，本文提出并实现了一个动态自适应的计算框架，无须担心额外的访存冲突和内核调用问题。当规模为2n时，将n的奇偶性作为分类依据，设计了两种预计算策略。系统在执行过程中会依据输入的规模动态选择合适的计算分解方案。当n为奇数时，预计算核执行一轮蝶形运算和部分旋转因子计算。相对应的主计算核会执行对旋转因子的补充计算。图16为n是奇数情况下，预计算模块与主计算模块的运行时间与同规模下Bellperson的对比。

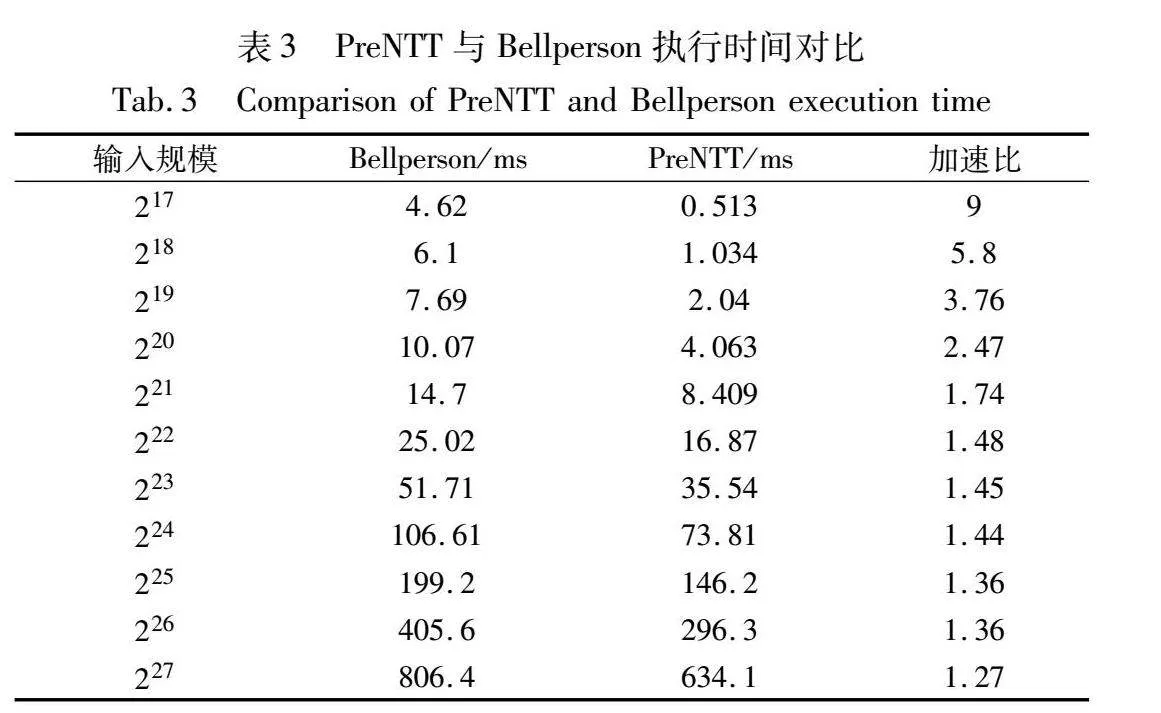
为确保在全规模下提高计算效率，以RTX3060的片上内存作为参考标准，在221或更高的规模下，主计算核采用三维分解策略，预计算核只进行旋转因子计算。值得一提的是，奇数时的分解策略可以将NTT分解为无数据依赖的独立任务，这一特性在多GPU的使用场景中具有重要意义，其应用前景广阔。表3列出了单轮NTT／INTT计算任务中，PreNTT相对于Bellperson的加速比。

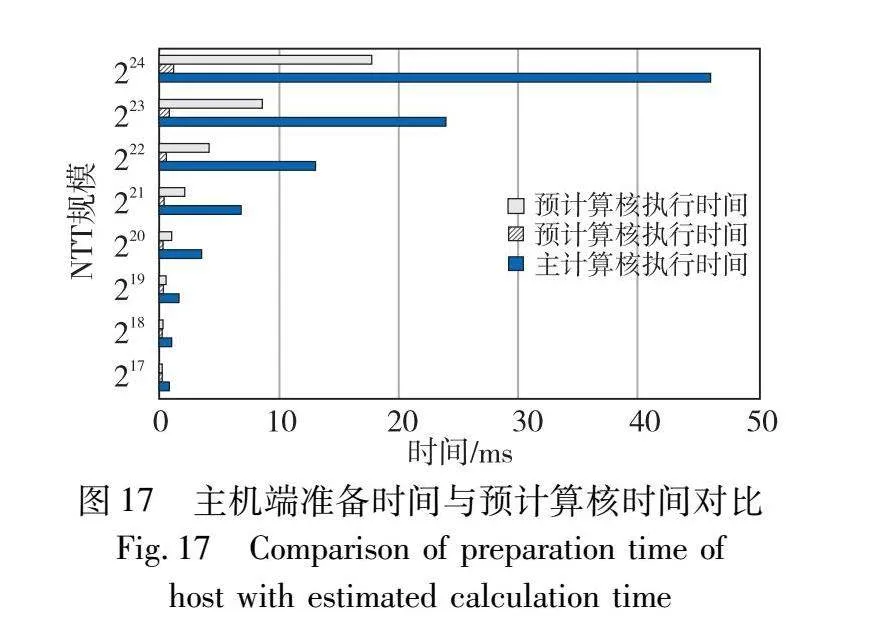
由表3可知，当采用奇偶分解策略时，加速比表现较为显著。但随着任务规模的逐渐扩大，加速比的增幅呈现缓慢的下降趋势。主要原因是在NTT的GPU部署中，性能瓶颈主要集中旋转因子的计算以及全局内存访问和块间通信。本文提出的优化方案效果体现在旋转因子计算和线程内的高效运算上，随着NTT规模的扩大，数据访问和通信的开销逐渐成为影响计算核心整体运行时间的主导因素，导致PreNTT的加速比出现下降趋势。如果能采用具有更大片上内存和带宽的GPU设备，PreNTT有潜力对更大规模的任务实现更高的加速优化。此外，本文采用CUDA多流技术，使得预计算核与主计算核的数据传输与运算能够在两个异步流中并发执行。主机端负责将大量的输入数据映射到GPU内存中，将创建内存空间以及数据传输消耗的时间开销统称为计算核准备时间。如图17所示，主计算核所需的准备时间往往超过预计算核的整体时间。因此，通过CUDA多流重叠的策略，预计算核的执行时间得以与主机端的数据映射时间并行，从而进一步提高了整体的计算效率。

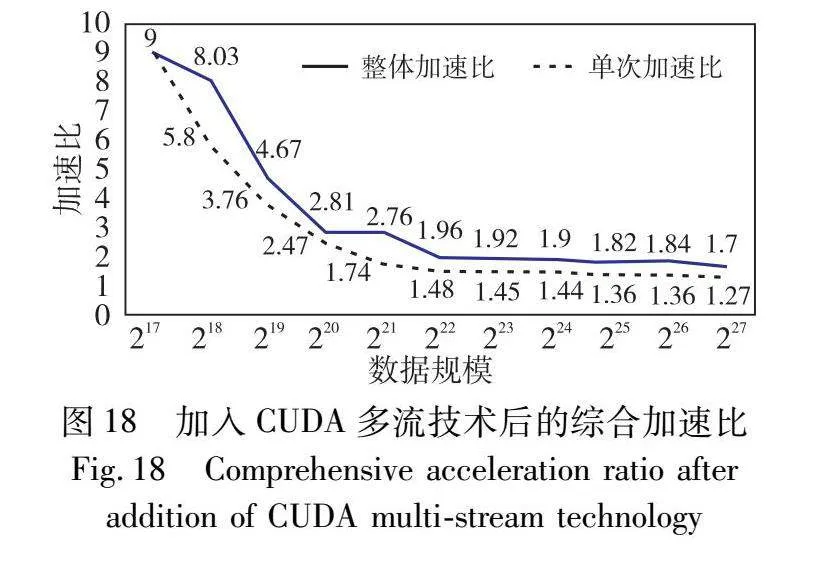
图18展示了采用多流技术掩盖预计算核运行时间之后，NTT整体加速比变化趋势。结果表明，本文NTT并行方案在与Bellperson并行方案的对比下，获得了全模块最低1.7倍的加速比。

5 结束语

本文提出了一种NTT并行加速方法PreNTT，并基于GPU对其进行实现。首先，使用高效的旋转因子预计算方法，结合主计算中自适应的动态分解策略，提出一种高效的NTT并行计算方法PreNTT。其次，在GPU部署PreNTT，采用双层动态任务分解策略，确保各子任务的计算负载平衡，提升计算效率，确保在全数据规模变化下的持续加速能力。在核内实施了双级数据混洗操作，降低了访存冲突的可能性，保证任务分解过程的准确性。最后，利用CUDA流技术，覆盖了预计算核心的时间消耗，进一步提升了加速效果。实验结果显示，与当前最先进的NTT加速方法Bellperson相比，本文方法在计算速度、加速稳定性和拓展性上均有显著提升。在未来的研究中，将继续探索超大规模NTT的优化方法，研究如何利用多设备集群来提高NTT的计算速度，降低其通信复杂性，从而提升zk-SNARK的计算性能。

参考文献：

［1］Benet J，Greco N.Filecoin：a decentralized storage network［R］.［S.l.］：Protocol Labs，2017：1-36.

［2］Miers I，Garman C，Green M，et al.Zerocoin：anonymous distributed e-cash from bitcoin［C］//Proc of IEEE Symposium on Security and Privacy.Piscataway，NJ：IEEE Press，2013：397-411.

［3］柳欣，徐秋亮.改进的支持暂停匿名用户服务的电子现金系统［J］.计算机应用研究，2016，33（10）：3099-3104.（Liu Xin，Xu Qiuliang.Improved support for the suspension of the electronic cash system for anonymous user services［J］.Application Research of Computers，2016，33（10）：3099-3104.）

［4］Sasson E B，Chiesa A，Garman C，et al.Zerocash：decentralized anonymous payments from bitcoin［C］//Proc of IEEE Symposium on Security and Privacy.Piscataway，NJ：IEEE Press，2014：459-474.

［5］刘红，张靖宇，雷梦婷，等.基于区块链的公平和可验证电子投票智能合约［J］.应用科学学报，2023，41（4）：541-562.（Liu Hong，Zhang Jingyu，Lei Mengting，et al.Blockchain-based fair and verifiable electronic voting smart contract［J］.Journal of Applied Sciences，2023，41（4）：541-562.）

［6］Zhang Yupeng，Genkin D，Katz J，et al.vSQL：verifying arbitrary SQL queries over dynamic outsourced databases［C］//Proc of IEEE Symposium on Security and Privacy.Piscataway，NJ：IEEE Press，2017：863-880.

［7］Zhao Lingchen，Wang Qian，Wang Cong，et al.VeriML：enabling inte-grity assurances and fair payments for machine learning as a service［J］.IEEE Trans on Parallel and Distributed Systems，2021，32（10）：2524-2540.

［8］吴昊天，李一凡，崔鸿雁，等.基于零知识证明和区块链的联邦学习激励方案［J］.信息网络安全，2024，24（1）：1-13.（Wu Haotian，Li Yifan，Cui Hongyan，et al.Federated learning incentive scheme based on zero-knowledge proof and blockchain［J］.Netinfo Security，2024，24（1）：1-13.）

［9］景旭，杨少坤.面向联盟链转账隐私保护的+HomElG零知识证明协议［J］.工程科学与技术，2023，55（5）：272-282.（Jing Xu，Yang Shaokun.+HomElG zero-knowledge proof protocol for privacy protection of consortium chain transfers［J］.Advanced Engineering Sciences，2023，55（5）：272-282.）

［10］王后珍，郭岩，张焕国.基于矩阵填充问题的高效零知识身份认证方案［J］.武汉大学学报：理学版，2021，67（2）：111-117.（Wang Houzhen，Guo Yan，Zhang Huanguo.Efficient zero-knowledge identity authentication scheme based on matrix stuffing problem［J］.Journal of Wuhan University：Natural Science，2021，67（2）：111-117.）

［11］Maller M，Bowe S，Kohlweiss M，et al.Sonic：zero-knowledge SNARKs from linear-size universal and updatable structured reference strings［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security.New York：ACM Press，2019：2111-2128.

［12］Byunz B，Fisch B，Szepieniec A.Transparent SNARKs from DARK compilers［C］//Advances in Cryptology-EUROCRYPT 2020：the 39th Annual International Conference on Theory and Applications of Cryptographic Techniques.Berlin：Springer，2020：677-706.

［13］Chiesa A，Hu Y，Maller M，et al.Marlin：preprocessing zkSNARKs with universal and updatable SRS［C］//Advances in Cryptology-EUROCRYPT：the 39th Annual International Conference on Theory and Applications of Cryptographic Techniques.Berlin：Springer International Publishing，2020：738-768.

［14］Groth J.On the size of pairing-based noninteractive arguments［C］//Advances in Cryptology-EUROCRYPT：the 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques.Berlin：Springer，2016：305-326.

［15］Zhang Ye，Wang Shuo，Zhang Xian，et al.Pipezk：accelerating zero-knowledge proof with a pipelined architecture［C］//Proc of ACM/IEEE 48th Annual International Symposium on Computer Architecture.Piscataway，NJ：IEEE Press，2021：416-428.

［16］Haleplidis E，Tsakoulis T，EL-KADY A，et al.Studying OpenCL-based number theoretic transform for heterogeneous platforms［C］//Proc of the 24th Euromicro Conference on Digital System Design.Piscataway，NJ：IEEE Press，2021：339-346.

［17］Kim S，Lee K，Cho W，et al.Hardware architecture of a number theoretic transform for a bootstrappable RNS-based homomorphic encryption scheme［C］//Proc of the 28th IEEE Annual International Symposium on Field-Programmable Custom Computing Machines.Pisca-taway，NJ：IEEE Press，2020：56-64.

［18］周慧凯.同态加密的硬件卸载及其在隐私保护计算中的应用［J］.小型微型计算机系统，2021，42（3）：595-600.（Zhou Huikai.Hardware offloading of homomorphic encryption and its application in privacy-preserving computing［J］.Journal of Chinese Computer Systems，2021，42（3）：595-600.）

［19］Kales D，Ramacher S，Rechberger C，et al.Efficient FPGA implementations of LowMC and picnic［C］//Proc of Cryptographers’Track at RSA Conference.Berlin：Springer，2020：417-441.

［20］Agrawal R，Bu L，Ehret A，et al.Open-source FPGA implementation of post-quantum cryptographic hardware primitives［C］//Proc of the 29th International Conference on Field Programmable Logic and App-lications. Piscataway，NJ：IEEE Press，2019：211-217.

［21］Kim S，Jung W，Park J，et al.Accelerating number theoretic transformations for bootstrappable homomorphic encryption on GPU［C］//Proc of IEEE International Symposium on Work-load Characterization.Piscataway，NJ：IEEE Press，2020：264-275.

［22］Naina G，Arpan J，Kumar C A，et al.PQC acceleration using GPUs：Frodokem，NewHope，and Kyber［J］.IEEE Trans on Parallel and Distributed Systems，2020，32（3）：575-586.

［23］FILECOIN.Bellperson：GPU parallel acceleration for zk-SNARK［EB/OL］.［2020］.https：//github.com/filecoin-project/bellperson.

［24］李龚亮，贺东博，郭兵，等.基于零知识证明的区块链隐私保护算法［J］.华中科技大学学报：自然科学版，2020，48（7）：112-116.（Li Gongliang，He Dongbo，Guo Bin，et al.Blockchain privacy protection algorithm based on zero-knowledge proof［J］.Journal of Huazhong University of Science and Technology：Nature Science，2020，48（7）：112-116.）

［25］Byunz B，Bootle J，Boneh D，et al.Bulletproofs：short proofs for confidential transactions and more［C］//Proc of IEEE Symposium on Security and Privacy.Piscataway，NJ：IEEE Press，2018：315-334.

［26］Montgomery P L.Modular multiplication without trial division［J］.Mathematics of Computation，1985，44（170）：519-521.

［27］Lee W K，Hwang S O.High throughput implementation of post-quantum key encapsulation and decapsulation on GPU for Internet of Things applications［J］.IEEE Trans on Services Computing，2021，15（6）：3275-3288.

［28］Gentleman W M，Sande G.Fast Fourier transforms：for fun and profit［C］//Proc of Fall Joint Computer Conference.New York：ACM Press，1966：563-578.

［29］赵海旭，柴志雷，花鹏程，等.zk-SNARK中数论变换的硬件加速方法研究［J］.计算机科学与探索，2024，18（2）：538-552.（Zhao Haixu，Chai Zhilei，Hua Pengcheng，et al.Research on hardware acceleration method of number theory transformation in zk-SNARK［J］.Journal of Frontiers of Computer Science & Technology，2024，18（2）：538-552.）

［30］Ni Ning，Zhu Yongxin.Enabling zero knowledge proof by accelerating zk-SNARK kernels on GPU［J］.Journal of Parallel and Distributed Computing，2023，173：20-31.