基于Hopf振荡器的Spiking-CPG六足机器人步态运动控制

摘 要：中枢模式发生器（central pattern generator，CPG）在六足机器人的运动步态控制中起着至关重要的作用。为能够更高效、更低能耗地控制六足机器人的步态运动，提出了一种Spiking-CPG（SCPG）神经网络作为六足机器人的仿生控制系统，其结合Hopf振荡器与以时疏的spiking信号传递信息的仿生神经元LIF（leaky integrate-and-fire），采用环型拓扑结构，使用六组各2 000个LIF神经元组成的集合相互连接而成。该SCPG控制系统能够生成六足机器人常见的波动步态、四足步态、三足步态，通过调节相位差参数实现快速、顺滑、稳定的切换运动步态，实时调整所需的频率、振幅，在面对外界干扰时能够在很短的时间内恢复原状，具有很好的鲁棒性。在Webots平台上搭建了一个三维的六足机器人模型，将SCPG的信号输出并经过关节映射函数变换后，来控制六足机器人的运动，验证了所设计六足机器人的运动稳定性和SCPG控制方案的可行性与有效性。最后，在Intel的Loihi芯片上移植了SCPG神经网络控制器，结果表明，其具备高效的执行速度和更低的能耗，在六足机器人的运动控制中具备良好的应用前景。

关键词：六足机器人；运动步态控制；Spiking-CPG；Hopf振荡器；LIF；NEF

中图分类号：TP242.6 文献标志码：A 文章编号：1001-3695（2024）10-024-3053-06

doi：10.19734/j.issn.1001-3695.2024.01.0050

Gait locomotion of hexapod robot based on Spiking-CPG neural system using Hopf oscillator

Luo Shutong1，Song Zigen2

（1.College of Information，Shanghai Ocean University，Shanghai 201306，China;2.School of Aerospace Engineering & Applied Mechanics，Tongji University，Shanghai 200092，China）

Abstract：CPG makes a great contribution to the control of gait motions in hexapod robots.To manage the gait movements of hexapod robots more efficiently and with lower energy consumption，this work introduced a Spiking-CPG（SCPG）neural network as the bionic control system for these robots.The system integrated Hopf oscillators with biologically inspired LIF neurons，which communicated through sparse spiking signals，in a ring topology.It was composed of six groups，each containing 2 000 LIF neurons，interconnected to form the network.This SCPG control system could produce common hexapod robot gaits such as the wave，tetrapod，and tripod gaits.It facilitated rapid，smooth，and stable transitions between motion gaits by adjusting phase difference parameters，and could dynamically adjust the required frequency and amplitude，exhibiting excellent robustness by quickly recovering from external disturbances.It controlled a simple 3D hexapod robot model on the Webots platform.It deve-loped the robot by transforming the SCPG signal output through joint mapping functions，validating the motion stability of the designed hexapod robot and the feasibility and effectiveness of the SCPG control scheme.Finally，it ported the SCPG neural network controller proposed to Intel’s Loihi chip，showing that it has high execution speed and lower energy consumption，indicating a promising prospect for application in the motion control of hexapod robots.

Key words：hexapod robot;motion gait control;Spiking-CPG;Hopf oscillator;LIF;NEF

0 引言

现今机器人在人们的生产生活中不可或缺，其中六足机器人因其运动灵活稳定，对环境的适应性强等特点，在探测、运动控制等领域扮演了重要角色［1］。运动控制是机器人极为重要的一个方向，基于中枢模式发生器的仿生控制方法模拟自然界生物的节律运动，可以在没有来自高层信号和外部反馈量的情况下生成稳定的节律信号，极好地模仿动物的行走方式。文献［2］运用Kuramoto相位振荡器构建四足机器人的CPG网络模型。文献［3］提出一种σ-Hopf振荡器实现机器人步态的瞬时同步。文献［4，5］提出基于延迟耦合的Van der Pol振荡器控制蛇形机器人以多种步态运动。然而为使机器人能够更智能地运动，往往需要搭载高维的传感器收集外界信息，同时需要保证在变化的环境中低延迟、高效地处理信息。传统基于模型的CPG控制策略虽然能产生稳定的节律性输出，其局限在于不擅长处理外界信息从而往往无法适应未知情况［6］。

受生物神经机制的启发，智能信息是通过使用神经细胞的脉冲或峰值来处理的，新一代的神经网络系统模型脉冲神经网络（SNN）已经被提出，其通过结合单个峰值序列的时空信息来相互通信［7，8］。SNN已经成为一种科学而有用的工具，以高效率和低功耗解决应用工程中的问题，例如机器人工程中的应用［9，10］。研究人员也尝试使用以深度学习的方法更智能的控制机器人的行走。文献［11］提出以深度强化学习训练一种分布式控制结构从而使六足机器人更好地学习步态行为。在运行人工神经网络时计算延迟和响应时间往往不能满足实时执行的要求［12］，并且对边缘机器人来说能源资源有限，在实时性有所要求的机器人控制领域中难以忽视梯度、强化学习的计算密集性以及高延迟等问题。

在神经硬件上运行的SNN［13］证明了自己克服这些问题的能力［14］，为了高效率和低功耗解决应用工程中的问题，SNN被用于构建CPG神经网络来控制仿生机器人，这种网络被称为Spiking-CPG（SCPG）网络。SNN由尖峰神经元和互连突触组成，这些突触由可调节的标量权重建模，以神经元单元模拟生物体中的活动，通过结合神经元脉冲序列的时空信息来相互通信以减少能源的消耗。文献［15］提出基于SNN的R-STDP学习算法，以高效地执行机器鱼的目标跟踪任务。文献［16］提出了一种监督多层SNN控制器，使得机器蛇能够实时跟踪目标。得益于SNN信号传输的时疏性，将SCPG加入机器人控制系统中可以降低能耗并快速处理时变的信号，其使用SNN作为上层控制器处理环境信息传递给下层的CPG系统模型控制机器鱼的运动。文献［13］重点关注了神经形态计算在算法和硬件方面的发展以降低计算平台的能源需求。文献［17］在FPGA（现场可编程门阵列）上使用多巴胺神经元组成的CPG模型产生不同的节律模式来模拟二足动物的初级步态。文献［18］使用在集成传感器的树莓派上以SCPG在没有先验知识的情况下学习生成单种三足步态的行走。文献［19］在电路板FPGA上使用SNN复制CPG来实现六足机器人的三种常见步态。文献［20］首次在SpiNNaker硬件板上实现六足机器人步态，但其需要短暂的静止期后才能实现步态的转换。

SCPG网络基于Hopf振荡器模型，使用NEF算法设计了由六组各2 000个LIF神经元群体构成以复制耦合Hopf振荡器的周期性活动来控制六足机器人的步态运动。其能够产生常见的六足步态，可以观测到神经元对应的发放模式，此SCPG网络的优势在于能够通过调节相位差参数实现快速、顺滑、稳定地切换运动步态，并且能够实时调整所需的频率、振幅，在面对外界干扰时能够在很短的时间内恢复原状，具有很好的鲁棒性。本文设计了关节映射函数，在Webots仿真平台上设计简易六足机器人模型加以验证其可行性，并在Intel的Loihi硬件板上移植了SCPG网络，以体现其计算的高效和更低的能耗。

1 SCPG振荡器模型

Hopf振荡器常被用来作为机器人步态的控制系统，其具有参数少、波形稳定的特点，并且参数物理意义明确，很适合振幅、频率的实时调节。为适配六足机器人的控制，单个Hopf并不足够使用，因此需要Hopf之间的耦合项来控制各腿之间的相位。

SCPG网络使用的耦合Hopf数学模型如下：

i=a（R2i-r2i）xi-wyii=a（R2i-r2i）yi-wxiwi=wi+∑iwijri［（xiyi-xjyi）cosi，j-（xixj-yiyj）sini，j］r2i=x2i+y2i（1）

其中：xi，yi为状态变量，即振荡器的输出;a、R、ω为模型参数，能够调整振荡器的动态特性，a值表征振荡器收敛到圆环上的速度，R值是用来表征振幅的，ω值用来表征周期;通过调节i，j任意地改变振子之间的相位差，从而能够实现不同的六足步态。

该网络使用NEF框架来实现该数学模型以搭建SCPG网络，NEF框架将想要拟合的任意维向量解码为神经元活动，并能够再编码回向量空间。NEF中每个神经元群体表示一个标量或向量值，每个神经元有自己编码向量ei，它从神经群体所代表的值的空间（d维的状态空间）映射到神经活动的空间（称为n维的神经元空间）。映射由以下非线性函数定义：

δj（x）=Gj（αjei·x+βj）（2）

其中：x是神经元群体编码的向量值;δj是神经元j的尖峰活动，函数G可以是任何神经元模型的激活函数，包括简单的LIF神经元，或更复杂的生物学详细模型，实验采用LIF神经元模型;αj是随机选择的增益项;βj是随机选取的偏置值。向量x编码后再经过增益以及偏置后的值即为每个神经元的输入电流，电流将会传入神经元也将作为参数传入激活函数G，神经元在电流作用下神经元的膜电位会不断变化，如图1（b）所示。受到电流持续刺激时电压升高，若没有电流输入时电压下降，当达到阈值时便会产生不连续的，时疏的尖峰信号δ，此时膜电压还会被置为0 V。

通过突触后神经元突触处的尖峰接收神经元反应能够生成连续、时变的测量值，由以下公式确定：

aj（x）=∑ihj（t）δj（t-ti（x））（3）

其中：hj（t）是具有时间常数τ的指数衰减的滤波器;为卷积运算;δj（t-ti（x））是神经元j产生的尖峰序列。神经元的尖峰活动如图1（a）所示。图1（b）为第一个神经元的膜电压变化图，由标注有向箭头所示，当达到膜电位阈值时便产生spiking，神经元群体中2 000个神经元的spiking序列共同组成了神经元活动aj（x）。

神经元活动经过解码器的解码求和可以将其变换到向量空间，通过以下公式解码神经元群体的活动：

=∑niaj（x）Dj（4）

其中：n是神经元群体中神经元的数量;Dj是线性解码器;是由神经元群体编码的原始值的估计。线性解码器通过最小二乘法优化到最优解，公式为

‖-x2‖=argmaxDj∫［∑njaj（x）Dj-x］2dx（5）

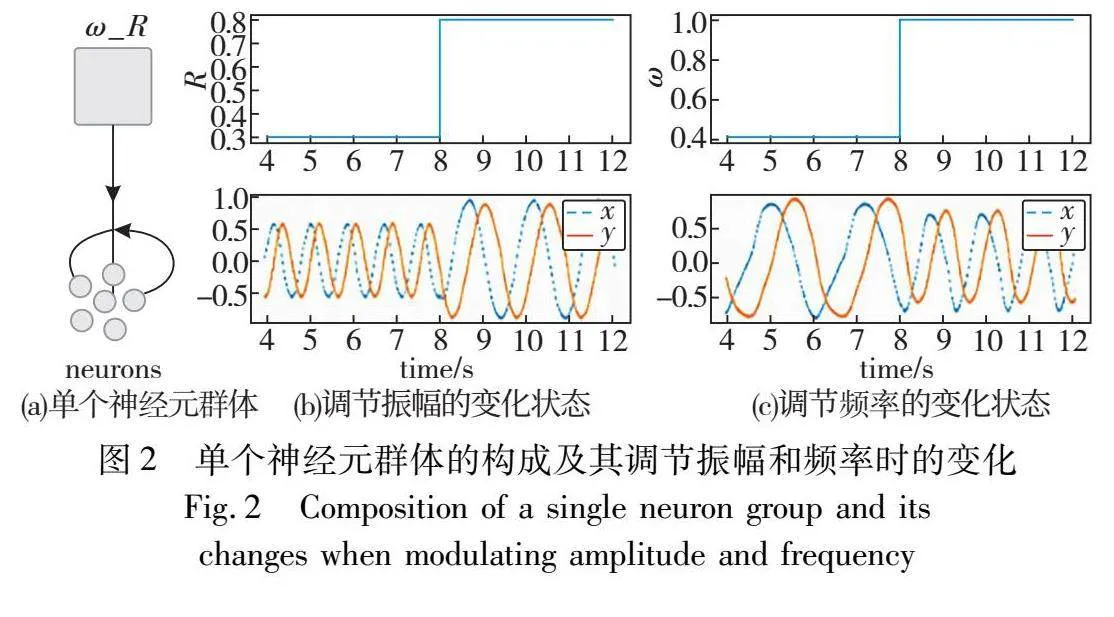
如图2（a）所示，以NEF算法构建单个Hopf振荡中心，将初始值［0.01，0］编码为电流传入神经元群体，各神经元在电流刺激下产生膜电位变化，当膜电位达到发放阈值时产生一次spiking，再将神经元活动解码后所得向量重新作为下一时刻的输入值，不断迭代得到Hopf的输出曲线。此外，如图2（b）（c）所示，得益于SNN快速处理时变信号的能力，通过调节上层控制器参数能够实时改变振荡器输出的振幅和周期，SCPG振子能快速作出反应并得到正确的效果，在外界环境变化时能够快速调整步态的振幅频率以适应环境需要。

2 六足步态实现

2.1 常见仿生六足机器人步态

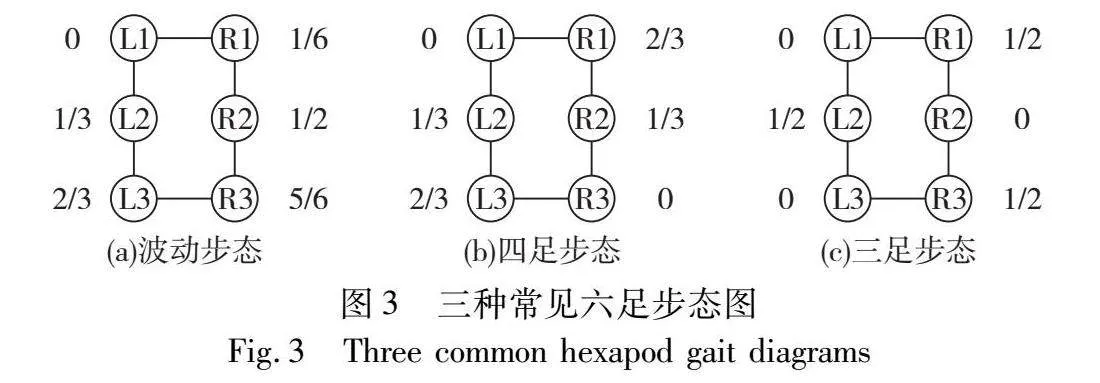
六足机器人有三种常见的运动步态，即三足步态、四足步态、波动步态。以波动步态行走时，六条腿按L1、R1、L2、R2、L3、R3的顺序以60度相位差行进（L1、L2、L3分别为左前、左中、左后腿，R开头为右侧三条腿。字母旁数字为以L1为标准各腿部之间相位差），如图3（a）所示，这种步态于某一时刻只有一条腿摆动也是行进最稳定的步态。在以四足步态行走时，分为（L1，R3）、（L2，R2）、（L3，R1）三组，组间相位为120°，如图3（b）所示。三足步态下六条腿分为（L1、R2、L3）、（R1、L2、R3）两组，同组内的三条腿相位相同，组间相位为180°，如图3（c）所示，三足步态也是运动速度最快的步态。图3中，L1、L2、L3分别为左前、左中、左后腿，R开头为右侧三条腿，字母旁数字为以L1为标准各腿部之间相位差。

2.2 SCPG网络及步态实现

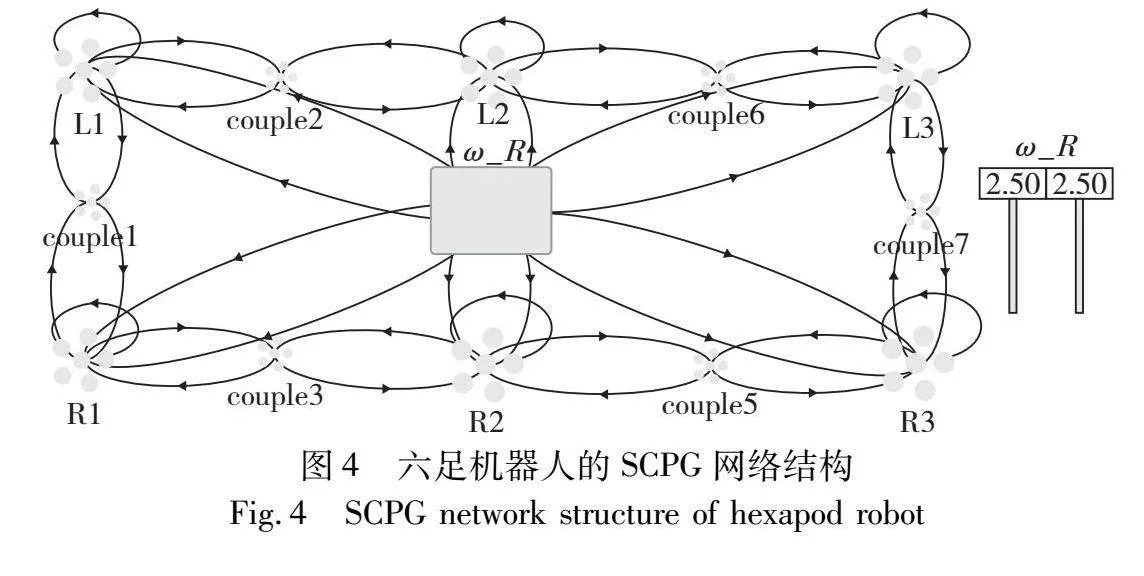
振荡器模型输出信号之间的相位互锁关系，是仿生六足机器人六条腿间能够实现协调运动的关键，常采用环型的耦合网络来实现腿间的相协调的步态输出。整体的六足SCPG模型如图4所示，包括有六个Hopf神经元集合L1～L3、R1～R3，每个集合内包含2 000个LIF神经元，并且引入couple神经元群体实现Hopf振子之间的耦合项以满足腿间相位的需要，而上级控制中心能够控制各Hopf振荡中心的参数以调解振幅和频率适应环境需要。

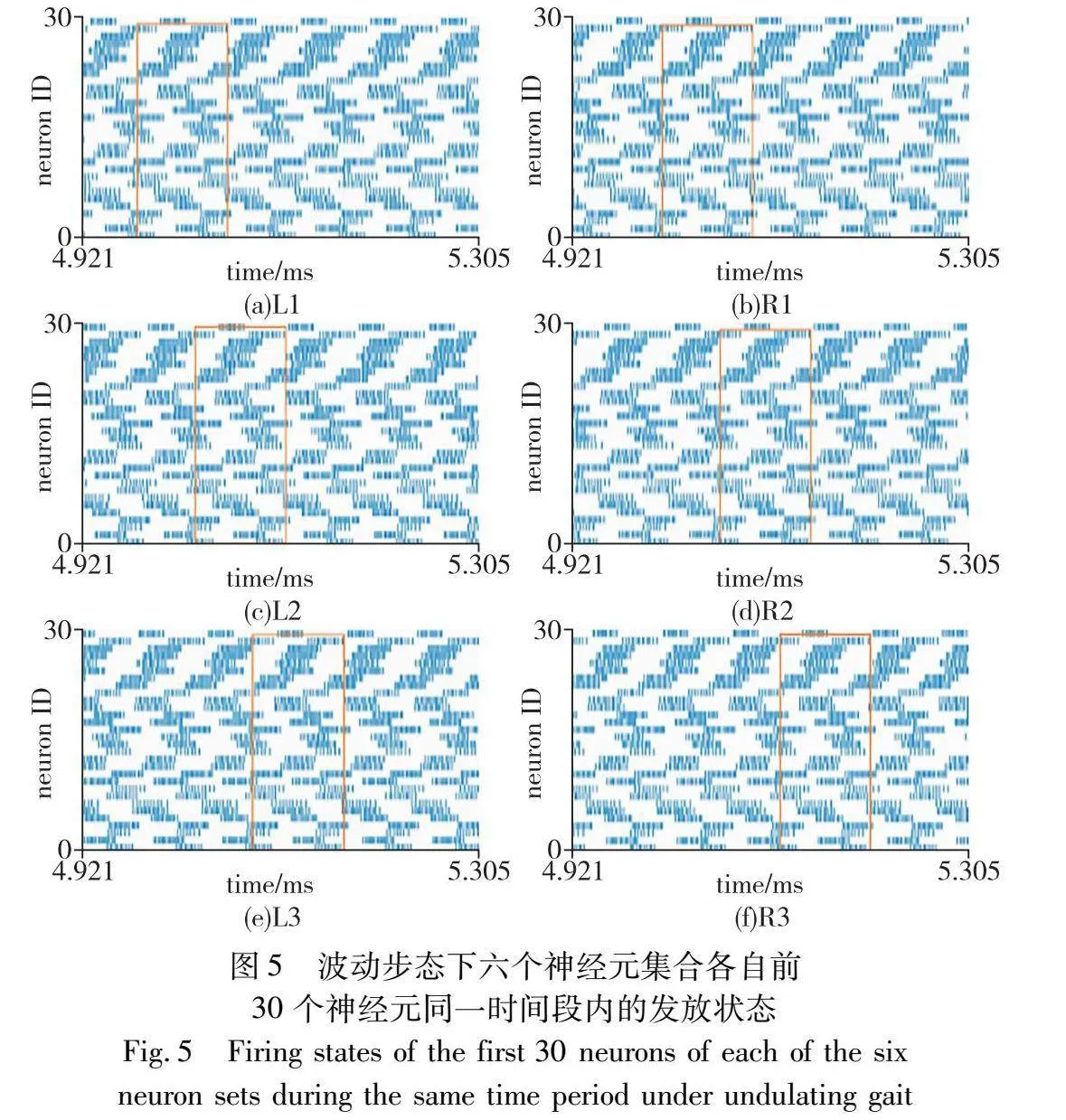
通过调节SCPG网络中振子之间的相位差i，j，以实现SCPG下不同的六足步态。以波动步态为例（图5），纵坐标为神经元集合中的神经元序号，横轴为时间，如第1章所述，初始向量值被编码成仿生神经元间识别的电流信号，不断地刺激并引起神经元发放spiking。图5中每个神经元群体中前30个神经元表达出了波动步态所需的发放模式，橙色矩形框标记了具有恒定相位差的状态（参见电子版）。

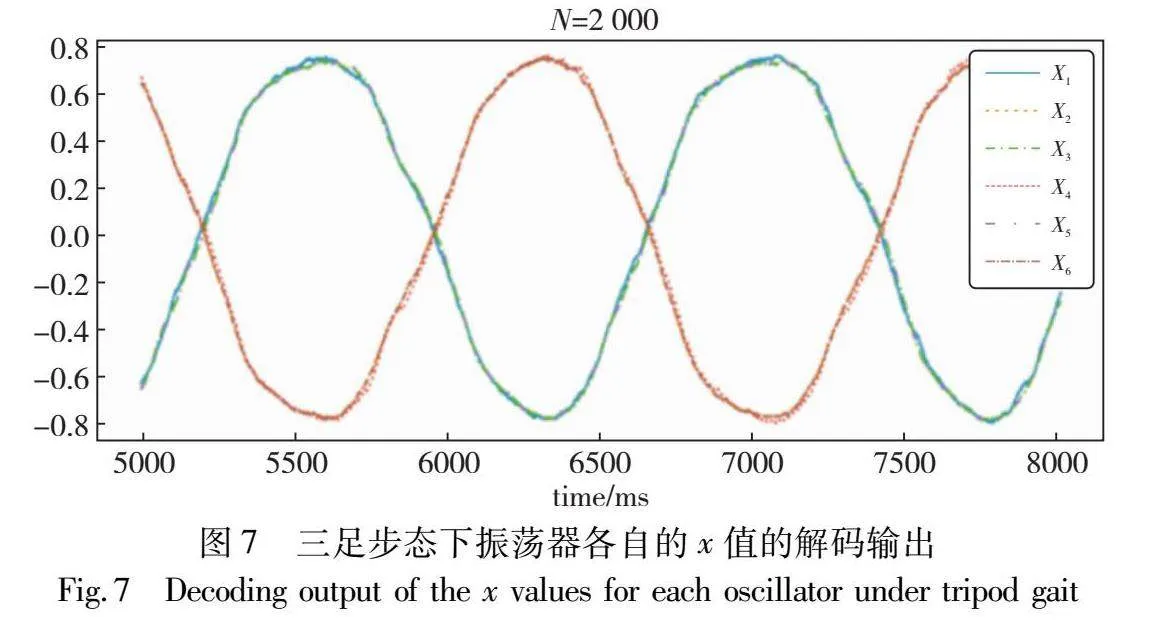
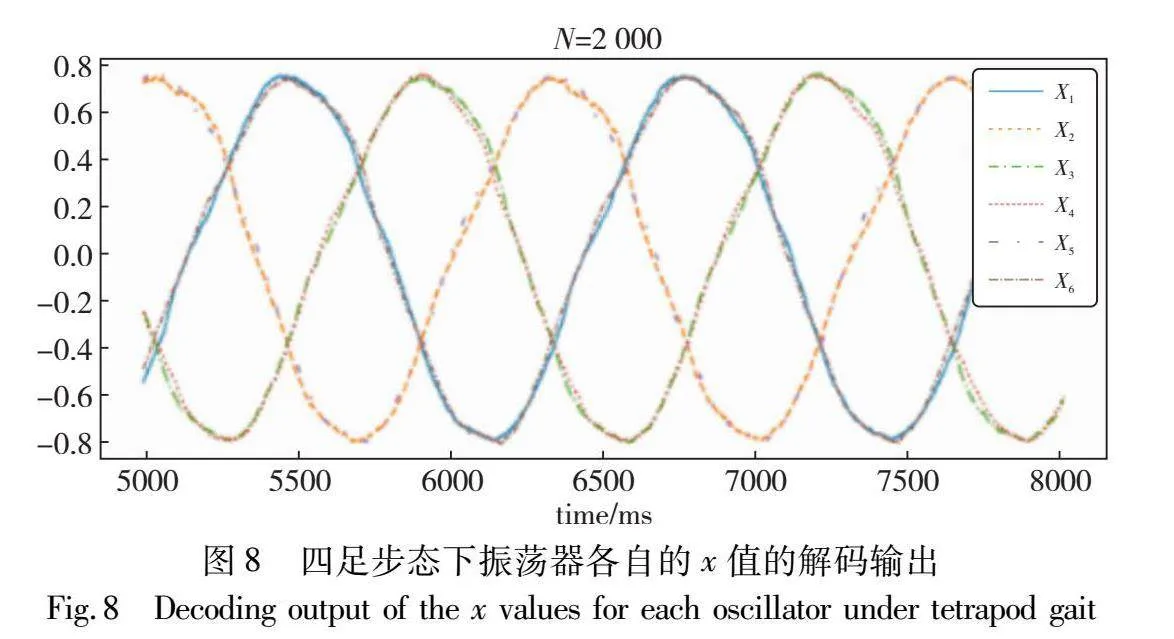
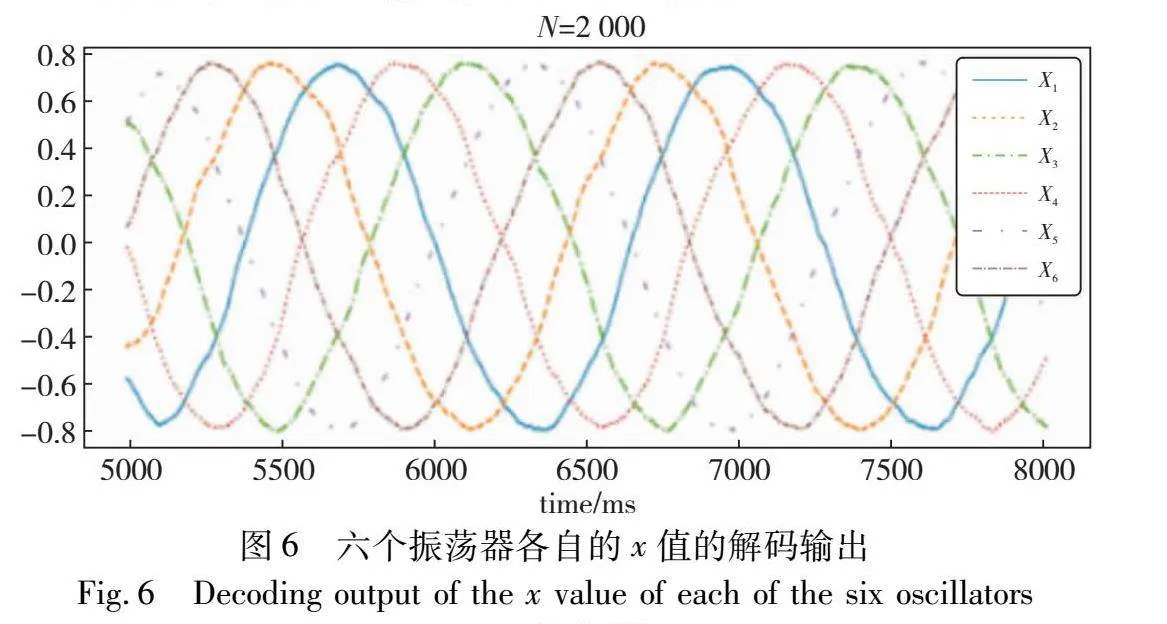
通过式（4）解码神经元的spiking序列后的结果如图6所示。图6中六条曲线分别为六个振荡中心的x值输出信号。图中x1（L1）为深蓝色曲线、x2（R1）为绿色曲线、x3（L2）为橙色曲线、x4（R2）为紫色曲线、x5（L3）为黄色曲线、x6（R3）为浅蓝色曲线，相互间相差六分之一个周期（参见电子版）。对应在步态层面，两组腿间相位差稳定为60°，信号平稳没有波动，与图3（a）中的波动步态相符。

另外的两种步态输出如图7和8所示。

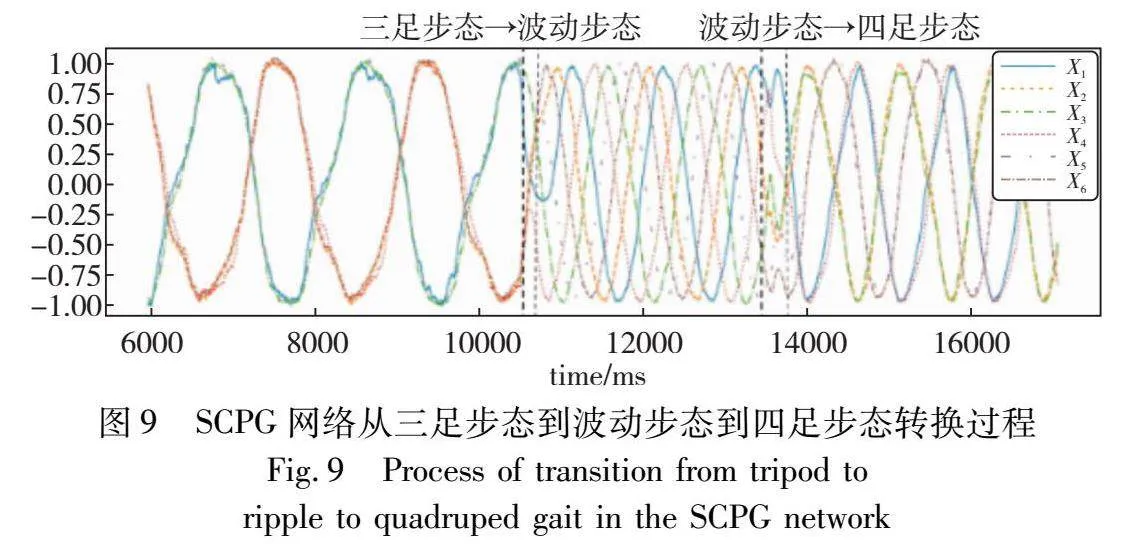
SCPG网络的优良性能使其能够从始至终有着稳定信号输出能力，不需要额外的复杂公式控制，仅仅简单地改变耦合神经元所实现的相位差参数φi，j便能够实现步态的实时切换。图9展示了这三种常见步态的快速切换能力，与文献［21］中使用额外公式进行步态转换相比，本方法中的步态切换只占一个周期的很少一部分，因此更加快速、波动更小。

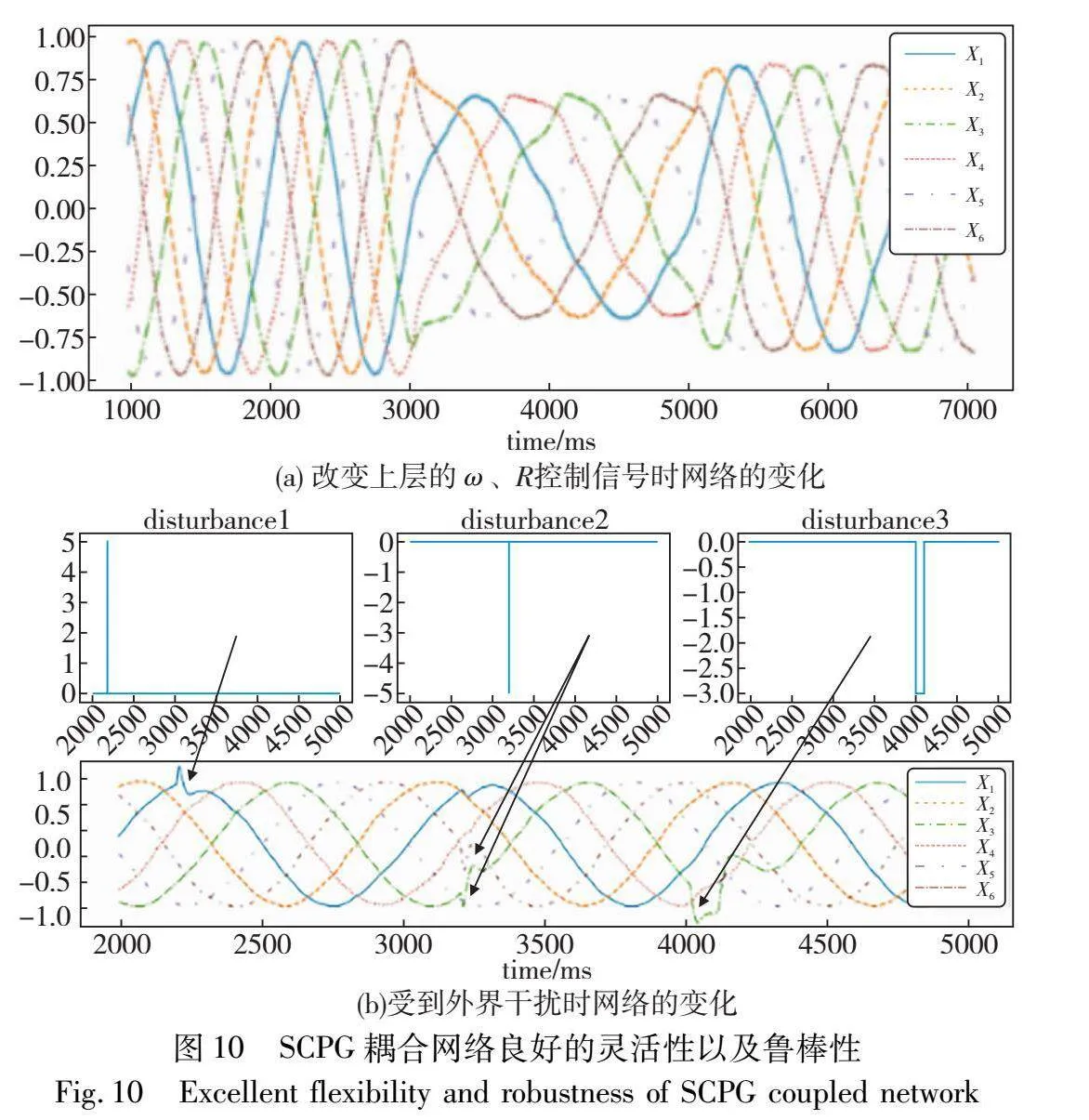
得益于SNN对时变信号的优秀处理能力，该SCPG耦合网络具有很好的灵活性以及鲁棒性。SCPG网络的灵活性如图10（a）所示。在某一时刻改变上层的ω、R控制信号，六组SCPG网络都能同时且快速地作出反应，变换输出信号的振幅和频率以适应环境的需要。

在实际应用中机器人腿部关节极大可能会受到各种阻力妨碍或者是短暂卡顿等情况，该SCPG网络还具有一定的鲁棒性以应对该种情况。图10（b）模拟了这种情况的发生，在某一时刻t1，L1腿部受到外界干扰disturbance1，x1信号产生了短暂的波动，但是在同一时刻其余曲线不受影响，扰动结束过后，该曲线具有在很短时间内恢复原状。在某一时刻t2、x3、x6信号受到外界干扰disturbance2，t3时刻x3信号即便受到长时间的干扰仍然能够在扰动结束之后快速复原。

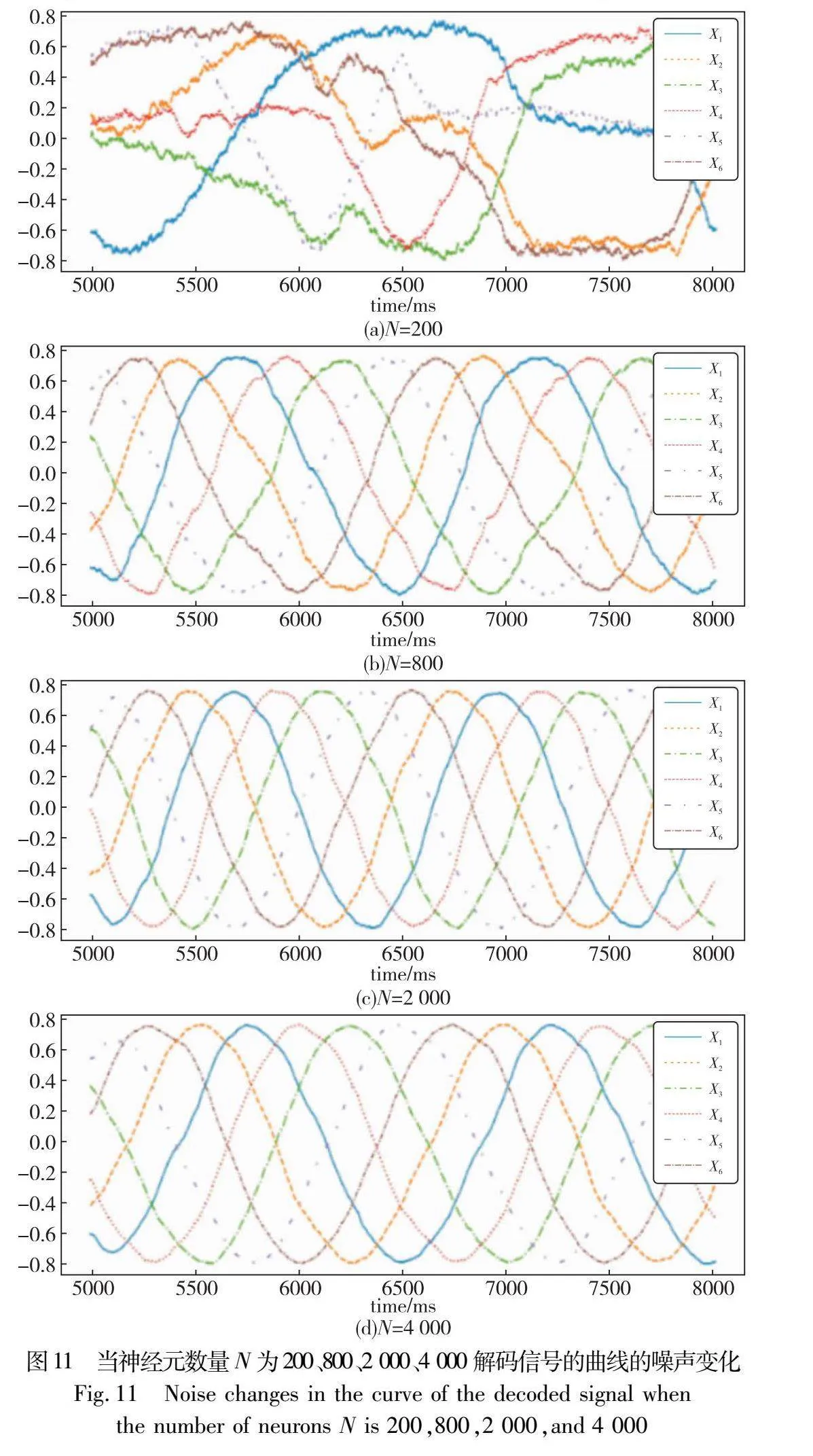
上述实验中一直采用每组SCPG中心由2 000个神经元组成，神经元的数量会对输出信号具有一定的影响。如图11所示，在神经元数量只有200个时，甚至都不能生成完整有序的步态信号。当使用800个神经元时，输出信号已具备一定的顺序但是偶尔会有离本意较远的曲线波动。当神经元数量达到2 000时，输出信号已经足够规整，并且相位的表达也足够完美，而在使用4 000个神经元时曲线的变化已经很微小。实验使用Python环境中模拟的LIF神经元执行，在使用更多的神经元带来更规整输出的同时，部署神经元网络并且优化解码值等过程所需的部署时间增加了一倍有余。需要更多时间成本的同时，更多的神经元也意味着更高的能耗，比起使用个人计算机，在神经元形态硬件比如Intel的Loihi芯片（使用硬件结构搭载SNN所需的仿生神经元模型）上部署SCPG网络无疑带来了成倍的能量减少［14］，这也是设计SCPG网络的初衷之一，因此更需要考虑增加神经元数量带来的能耗增长，并且实际使用中神经元形态硬件的硬件规格，神经元的数量以及突触数量的限制也限制了SCPG网络中神经元数量的使用。

3 六足机器人运动仿真

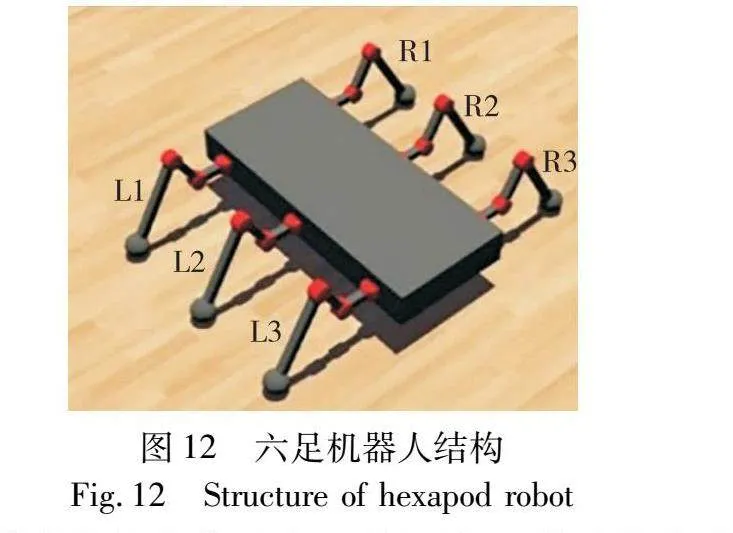
本文设计的六足机器人如图12所示，以蟑螂为基本结构，肢体部分为规整的长方体。共有6条腿部，每一条有三段组成，有三个运动关节控制行走，分别为髋关节、膝关节、踝关节（图中由里到外腿部红色的关节，参见电子版）。每个关节内含有一个舵机，摩擦库仑系数为1，总体质量为5 kg，各关节采用Webots平台默认的PID控制，参数为Kp=20，Ki=3，Kd=2。

由于振荡器的输出信号为无量纲量，不能直接作为控制信号驱动关节舵机，所以采用映射函数的方法对模型的输出进行变换，使其从无量纲量变换为关节旋转角度控制量。SCPG网络输出经过映射函数转换为关节旋转角度数据后传递给机器人各个腿上的电机控制机器人的前向运动。设髋关节、膝关节、踝关节的旋转角度分别为θ1、θ2、θ3，采用的振子输出曲线的映射函数［22］为

θ1=k0xθ2=k1y，y≥0k2y，y<0θ3=k3θ2+β（6）

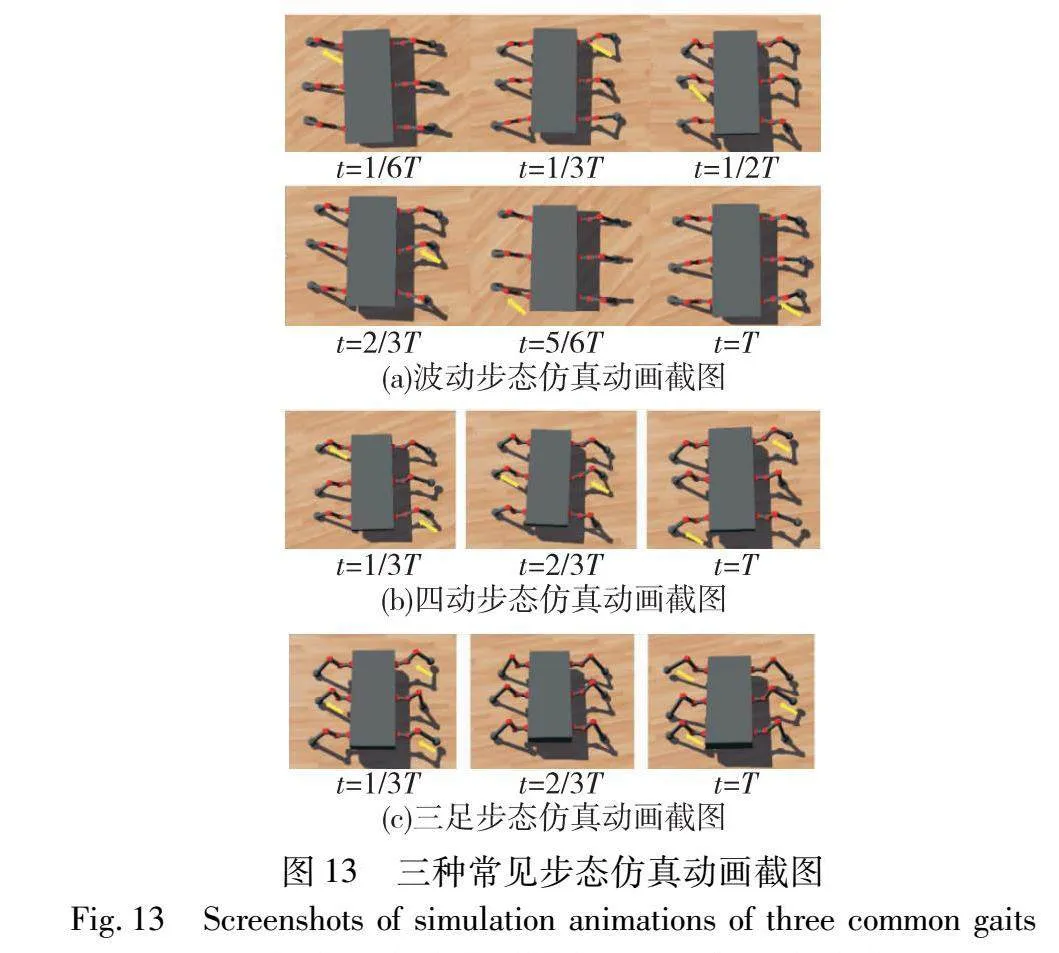
其中：x、y值为L1～R6各神经元集合的信号输出，根据六足机器人动力学模型计算取k0=0.08，k1=0.06，k2=0，k3=-0.13，β=0.2。转换后的关节角度控制变量将传给机器人的相应关节上从而实现六足机器人的行走，在Webots以该六足机器人实现的几种步态模式，仿真结果如图13所示。

图13（a）为波动步态仿真结果，以波动步态向前移动时，五条腿支撑，另一条腿向前摆动，腿部运动相序为L1-R1-L2-R2-L3-R3。Webots中六足机器人运动仿真图像中每六分之一周期箭头指向腿正在向前摆动，与图3（a）所介绍的波动步态运动相序相符合。图13（b）为四足步态仿真结果，机器人的行走速度略慢于三足步态，略快于波动步态，速度和稳定性适中。腿部分为（L1，R3）、（L2，R2）、（L3，R1）三组，每三分之一周期里，两组腿支撑，另一组箭头指向腿向前摆动。图13（c）为三足步态仿真结果三足步态在平坦路面条件下的运动效率最高，但对复杂地形的适应性也较差。腿部分为（L1，R2，L3）和（R1，L2，R3）两组交替摆动。在整个运动过程中一条支撑腿和右边的两条支撑腿一起形成一个稳定的三角形，能很好地保持直线行走。

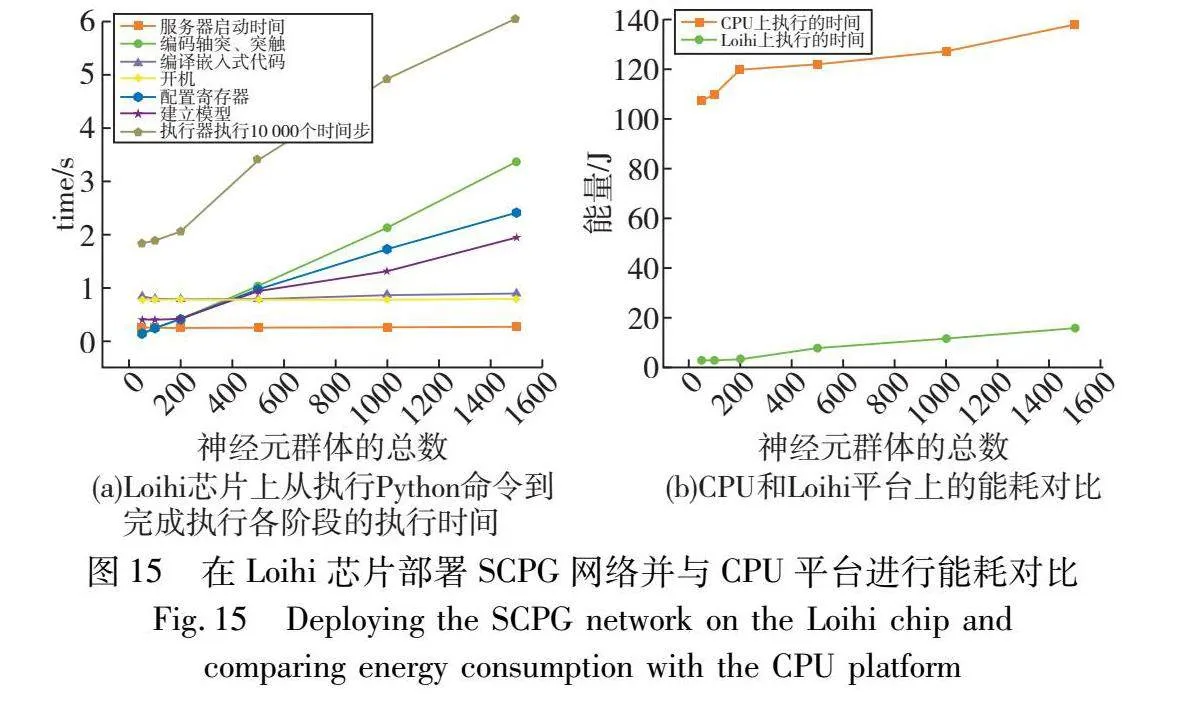
Loihi是英特尔公司开发的一种神经形态硬件板，在一个几平方毫米的小芯片上容纳了超过一百万个硬件神经元，如图14所示。它能够以低功耗且快速运行神经网络程序，这使得机器人即使在要求实时响应的场景中也能有效地执行任务。对于机器人应用来说，实时生成控制信号是非常重要的。最后，将SCPG模型移植到Loihi芯片上，并测试了其所需的运行时间和能耗。

实验在英特尔的云实验室上运行，使用SSH（secure shell）远程连接到载有Loihi硬件的服务器，这意味着启动程序有一个主机服务器的正常启动时间，整体模拟时间为10 s，各环节的所需时间如图15（a）所示。Loihi硬件需要经历一系列初始化过程，包括编译和编码过程，在给主板上电后，还有一段短暂的启动时间、配置寄存器时间，而大部分时间花费在执行10 000个时间步上。在实际任务中，执行时间常常会远远超过10 s，此时初始化操作所占的时间比例会非常小。除此之外，由于芯片初始化和其他I/O操作，总执行时间略大于执行器的执行时间。随着每个神经种群中神经元数量的增加，所需的执行时间也逐渐增加，但仍然只需要秒级别的时间便能够执行10 000个时间步。

能耗是表征Loihi芯片计算优势的一个很好的指标。CPU和Loihi宽带之间能耗的详细比较如图15（b）所示。Loihi提供了一个内置探针，能够便捷地测量能源消耗。CPU平台是指英特尔酷睿i7-11700H@2.5 GHz的个人笔记本电脑。可以观察到，与在CPU上执行SCPG模型相比，Loihi的能耗几乎低了两个数量级。与传统的CPU架构相比，神经形态硬件在执行峰值神经网络时显著降低了能耗，这意味着机器人这种边缘硬件得益于SCPG网络，能够更快速更高效地完成步态运动。

4 结束语

本文使用以时疏的spiking脉冲作为信号传输的LIF神经元搭建了Hopf振荡器以及调整相位所需的耦合神经元群体，构建了一种六足机器人步态控制的SCPG网络。该SCPG网络为常见的环型拓扑结构，使用六组各2 000个LIF神经元组成，能够生成六足机器人常见的波动步态、四足步态、三足步态，并展示了神经元层面模拟生物运动的步态模式。SCPG网络的优势在于能够简单地调节相位差参数而不需要额外的复杂公式参与，快速、顺滑、稳定地实现步态的切换，实时调整所需的频率、振幅，并且SCPG网络能够在部署神经元形态硬件时极大降低能量消耗，这对于机器人所应用的边缘场景有着深远意义。在Webots平台上设计了一款简易六足机器人，将SCPG的输出经过映射函数的转换后控制六足机器人腿关节的运动，结果稳定且符合预期。最后在Intel的Loihi芯片上移植了SCPG网络，实验并验证其高效的执行速度和更低的能耗。

参考文献：

［1］陈斯琴，李思瑶，鲁志刚，等.六足机器人关键技术综述［J］.机电工程技术，2022，51（11）：146-152.（Chen Siqin，Li Siyao，Lu Zhigang，et al.Review on key technology of the hexapod robot［J］.M&E Engineering Technology，2022，51（11）：146-152.）

［2］魏顺祥.基于CPG的四足机器人步态调节与轨迹优化研究［D］.昆明：昆明理工大学，2022.（Wei Shunxiang.Gait adjustment and trajectory optimization of quadruped robot based on CPG［D］.Kunming：Kunming University of Science and Technology，2022.）

［3］Zhu Yaguang，Zhou Shuangjie，Gao Dongxiao，et al.Synchronization of non-linear oscillators for neurobiologically inspired control on a bionic parallel waist of legged robot［J］.Frontiers in Neurorobotics，2019，13：59.

［4］Song Zigen，Xu Jian.Self-/mutual-symmetric rhythms and their coe-xistence in a delayed half-center oscillator of the CPG neural system［J］.Nonlinear Dynamics，2022，108（3）：2595-2609.

［5］Song Zigen，Huang Xiaojun，Xu Jian.Spatiotemporal pattern of periodic rhythms in delayed Van der Pol oscillators for the CPG-based locomotion of snake-like robot［J］.Nonlinear Dynamics，2022，110（4）：3377-3393.

［6］Bing Zhenshan，Cheng Long，Chen Guang，et al.Towards autonomous locomotion：CPG-based control of smooth 3D slithering gait transition of a snake-like robot［J］.Bioinspiration & Biomimetics，2017，12（3）：035001.

［7］Maass W.Networks of spiking neurons：the third generation of neural network models［J］.Neural Network，1997，10（9）：1659-1671.

［8］Maass W.On the relevance of time in neural computation and learning［J］.Theoretical Computer Science，2001，261（1）：157-178.

［9］Strohmer B，Manoonpong P，Larsen L B.Flexible spiking CPGs for online manipulation during hexapod walking［J］.Frontiers in Neurorobotics，2020，14：41.

［10］Bing Z，Meschede C，Rhrbein F，et al.A survey of robotics control based on learning-inspired spiking neural networks［J］.Frontiers in Neurorobotics，2018，12：35.

［11］Heess N，Tb D，Sriram S，et al.Emergence of locomotion behaviors in rich environments［EB/OL］.（2017）.https：//arxiv.org/abs/1707.02286.

［12］Dong Yiping，Wang Yang，Lin Zhen，et al.High performance and low latency mapping for neural network into network on chip architecture［C］//Proc of the 8th IEEE International Conference on ASIC.Pisca-taway，NJ：IEEE Press，2009：891-894.

［13］Roy K，Jaiswal A，Panda P.Towards spike-based machine intelligence with neuromorphic computing［J］.Nature，2019，575（7784）：607-617.

［14］Davies M，Wild A，Orchard G，et al.Advancing neuromorphic computing with Loihi：a survey of results and outlook［J］.Proceedings of the IEEE，2021，109（5）：911-934.

［15］Bing Zhenshan，Jiang Zhuangyi，Cheng Long，et al.End to end lear-ning of a multi-layered SNN based on R-STDP for a target tracking snake-like robot［C］//Proc of IEEE International Conference on Robotics and Automation.Piscataway，NJ：IEEE Press，2019：9645-9651.

［16］Wang Ming，Zhang Yiyang，Yu Junzhi.An SNN-CPG hybrid locomotion control for biomimetic robotic fish［J］.Journal of Intelligent & Robotic Systems，2022，105（2）：45.

［17］匡载波，王江，杨双鸣.多巴胺神经元仿生CPG系统及其FPGA实现［J］.计算机应用研究，2020，37（S1）：169-171.（Kuang Zaibo，Wang Jiang，Yang Shuangming.Dopamine neuron bionic CPG system and its FPGA implementation［J］.Application Research of Computers，2020，37（S1）：169-171.）

［18］Andres E，Horacio R G，Martin C，et al.Design of spiking central pattern generators for multiple locomotion gaits in hexapod robots by Christiansen grammar evolution［J］.Frontiers in Neurorobotics，2016，10：6.

［19］Rostro-Gonzalez H，Cerna-Garcia P A，Trejo-Caballero G，et al.A CPG system based on spiking neurons for hexapod robot locomotion［J］.Neurocomputing，2015，170：47-54.

［20］Gutierrez-Galan D，Dominguez-Morales J P，Perez-Pea F，et al.Neuro-Pod：a real-time neuromorphic spiking CPG applied to robotics［J］.Neurocomputing，2020，381：10-19.

［21］Yu Haitao，Gao Haibo，Ding Liang，et al.Gait generation with smooth transition using CPG-based locomotion control for hexapod walking robot［J］.IEEE Trans on Industrial Electronics，2016，63（9）：5488-5500.

［22］林知微，林翰文，刘宗朋.基于CPG的六足机器人运动步态控制方法［J］.计算机应用研究，2020，37（9）：2749-2753.（Lin Zhiwei，Lin Hanwen，Liu Zongpeng.CPG-based motion gait control method of hexapod robot［J］.Application Research of Computers，2020，37（9）：2749-2753.）