强化学习下浅充浅放充电策略AGV调度研究

摘 要：针对自动化集装箱码头自动导引车（AGV）调度中的充电问题，考虑浅充浅放充电策略构建了混合整数优化模型。该模型以最小化AGV最终完工时间为目标，在考虑AGV电池电量变化以及AGV不同状态耗电差异的约束下，利用AGV空闲时间和一个作业循环结束时间补电，减少AGV充电次数，进而减少总完成时间。模型采用Wolf-PHC强化学习进行求解，并分别与GAMS求解器、Q-learning算法及遗传算法（genetic algorithm，GA）求解结果进行比较，以验证模型的有效性和算法的优越性。算例分析表明在浅充浅放充电策略下AGV利用效率较高，且Wolf-PHC与GA的结合对模型求解效果更佳。

关键词：自动化集装箱码头；自动导引车；浅充浅放充电策略；强化学习；遗传算法

中图分类号：U691.3 文献标志码：A 文章编号：1001-3695（2024）10-022-3038-06

doi：10.19734/j.issn.1001-3695.2024.03.0057

Research on AGV scheduling of shallow charging and shallow discharging charging strategy under reinforcement learning

Zhao Rui，Liang Chengji

（Institute of Logistics Science and Engineering，Shanghai Maritime University，Shanghai 201306，China）

Abstract：For charging problem in AGV scheduling in automated container terminals，this paper constructed a mixed integer optimization model considering the shallow charging and shallow discharging charging strategy.The model aimed to minimize the final completion time of the AGV.Under the constraints of considering the change of AGV battery power and the difference in power consumption in different states of the AGV，the model used the AGV idle time and the end time of a work cycle to make up power，reducing the number of AGV charging times，and thus reducing the total completion time.The model was solved by Wolf-PHC reinforcement learning，and the results were compared with GAMS solver，Q-learning algorithm and genetic algorithm（GA）respectively to verify the effectiveness of the model and superiority of the algorithm.The example analysis shows that AGV utilization efficiency is higher under the shallow charging and shallow discharging charging strategy，and the combination of Wolf-PHC and GA is better for the model solution.

Key words：automated container terminal;automatic guided vehicle（AGV）;shallow charge and shallow discharge charging strategy;reinforcement learning;genetic algorithm

0 引言

自动化集装箱码头始于20世纪90年代初，AGV是自动化集装箱码头的关键组成，承担着水平运输任务。在实际作业中，AGV需要及时充电，否则将影响整个自动化集装箱码头正常作业。因此，在自动化集装箱码头运行过程中AGV充电是一重要环节。为提高自动化集装箱码头AGV的作业效率，使AGV能安全可靠地投入到作业中，自动化集装箱码头AGV调度问题成为了国内外学者的研究热点。Liu等人［1］基于海铁联运集装箱码头新建的U型堆场布局，重点研究了水平运输设备和装卸设备的综合调度，以及AGV的路径规划。Wang等人［2］研究了如何在正常生产和突发故障两种情况下，以总成本最小化为目标，将任务分配给多个AGV。李静等人［3］设计了两阶段的算法，在考虑AGV负载以及冲突情况下，以最小化AGV能量消耗为目标对模型进行求解。梁承姬等人［4］采用多学科变量耦合优化设计的方法对自动化码头AGV调度与AGV配置问题进行研究，并设计遗传算法、粒子群算法和蚁群算法分别进行求解。王鼎新［5］将人工神经网络引入Q-learning算法使AGV可以通过自主学习进行全局优化。初良勇等人［6］提出一种基于DQN的可变调度策略的调度算法，以有效提升AGV利用率。上述文献只是通过不同的模型和算法单独对AGV调度进行研究，没有考虑到AGV为电力驱动，存在电池续航与充电问题，对AGV调度存在一定影响。

在生产实践中发现AGV的充电过程一定程度上影响着自动化集装箱码头作业效率，AGV充电问题引发部分学者的关注。Gao等人［7］考虑动态环境对AGV运行效率的影响，使用编程模型和Q-learning算法生成考虑电池充电的AGV调度计划。Zhan等人［8］提出AGV双极电池充电策略，制定了两阶段的启发式算法，第一阶段AGV根据最近充电站和最小延迟充电站选择，第二阶段考虑到锂离子充电特性，减少了每次充电的持续时间。Nitish等人［9］针对AGV调度问题，考虑AGV电量临界值建立混合整数线性规划模型，提出一种利用自适应大领域搜索算法和线性程序求解的新数学方法。Nitish等人［10］讨论了如何在电池有限的情况下对AGV进行实时调度，以最大限度降低成本。赵涛等人［11］分析了AGV换电过程对调度的影响，考虑换电站数量和换电等待时间建立双层耦合模型，以减少AGV换电时间，提升AGV利用率。石楠路等人［12］构建了考虑换电过程的AGV作业调度混合整数优化模型并通过遗传算法求解。杨其飞等人［13］对AGV充电策略进行优劣性对比，通过遗传算法对分析各充电策略对作业时间的影响，并得出应用机会充电时最佳充电区间。吴洪明等人［14］考虑AGV电池电量约束，在机会充电模式的前提下研究AGV充电过程对作业效率的影响，进而确定AGV最佳充电区间。Xie等人［15］提出一种以离线充电为主在线充电为辅的充电策略，并通过大量仿真实验证明该充电策略的有效性。Ma等人［16］提出了分散式、集中式两种充电站布局及保守充电、渐进充电两种充电策略，并进行了广泛的仿真实验，分析了参数对系统性能的影响。误伟民［17］以厦门自动化码头为研究对象，研究得出充电站的布局、充电管理系统的开发和实施对提高AGV充电过程的安全和效率有极大影响，并提出相关措施和建议。郄佩琦等人［18］为解决因充电桩布局不合理导致充电桩利用率低的问题，考虑区域繁忙度，提出了AGV充电桩选址模型，从而有效提升系统整体效率。朱林等人［19］对AGV换电模式进行创新，设计了AGV分布式浅充浅放循环充电系统，取消了换电环节，提高AGV利用率。唐立辉等人［20］针对我国投产应用的三种AGV换电方式分别从建设成本、作业效率、安全性能及港口建设方面进行了对比研究。

综上所述，针对自动化集装箱码头AGV研究中，大部分文献侧重于AGV调度，忽略了AGV电量约束与充电对调度过程的影响。对于考虑AGV充电的文献中，多数以换电池方式与机会充电方式为背景，且求解方法局限于单一的启发式算法。本文结合自动化码头AGV实际作业情况，针对自动化码头浅充浅放充电策略，建立AGV调度模型，AGV通过空闲时间和每个作业循环与堆场交互时间补电，减少AGV因电量低于充电阈值去充电站的次数从而提高AGV作业效率。模型采用Wolf-PHC强化学习进行求解，并分别与GAMS求解器和GA求解结果进行比较，以验证模型的有效性和算法的优越性。

1 问题描述

1.1 自动化码头AGV充电

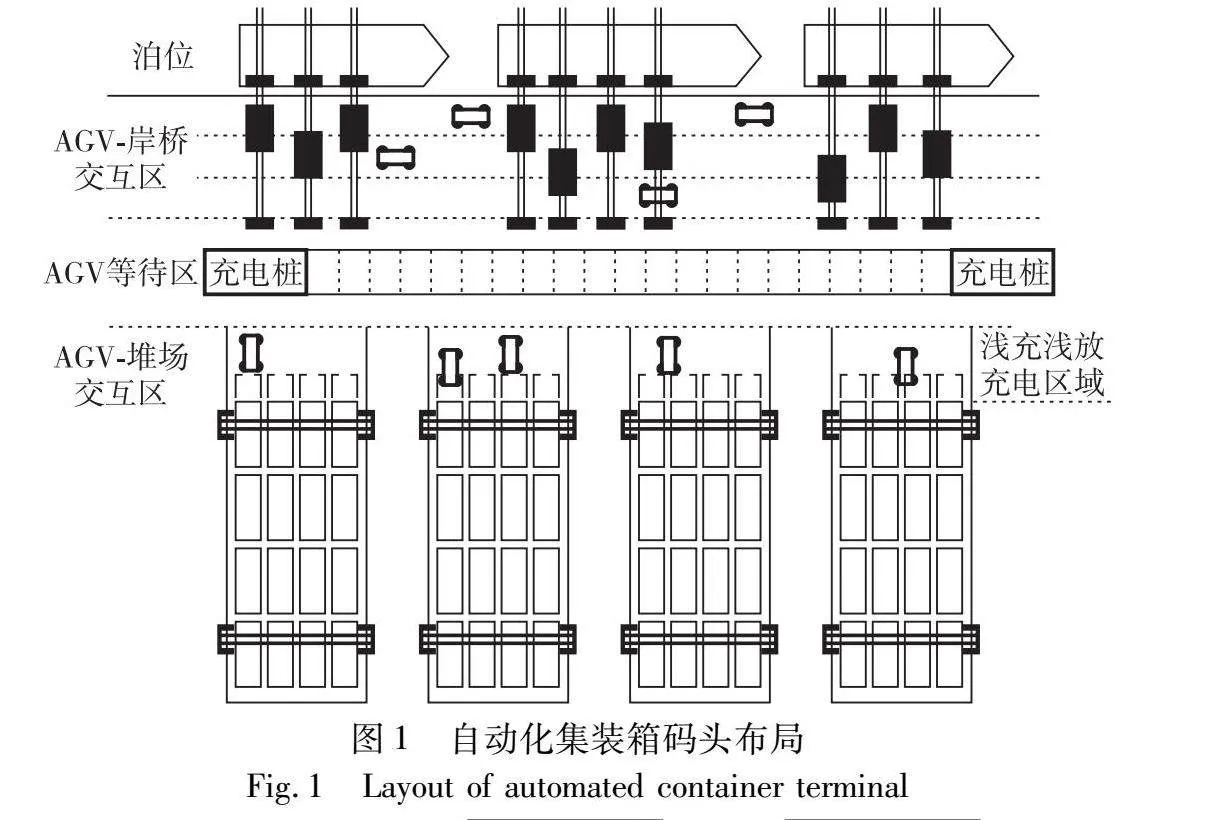
自动化集装箱码头纯电动AGV的充电方式可分为换电池方式、桩式充电和非接触式充电［17］。换电池方式要建设换电站并且配备一定数量的备用电池，不仅费用昂贵还要占用码头专用场地。另外，AGV换电池方式采用满充满放式策略，严重缩短了电池寿命。且AGV换电池操作也占用了作用时间，若出现电池数量不足或换电站故障则会导致码头停产。桩式充电只需要建设一定数量的充电桩，但AGV需要进行较长时间的充电，在作业高峰期导致AGV供应不足，导致AGV利用效率大大降低。非接触式充电可以在车辆行走路线上安装非接触式充电装置，可实现车辆不需停车即可充电。浅充浅放充电策略不需要配备备用电池，而是利用非接触式充电装置，可利用AGV与堆场交互时间进行不停车补电，且浅充浅放充电策略较满充满方式策略一定程度地延缓电池寿命的减少。综上，浅充浅放充电策略解决了传统AGV换电成本高、电池寿命短、具有一定风险隐患等问题，并且可以实现生产与充电同步进行，可达到提升AGV作业效率、有效提高自动化码头整体作业效率、降低码头投资成本的目的。自动化码头布局如图1所示，主要分为泊位、AGV-岸桥交互区、AGV等待区、AGV-堆场交互区。

1.2 AGV浅充浅放充电策略

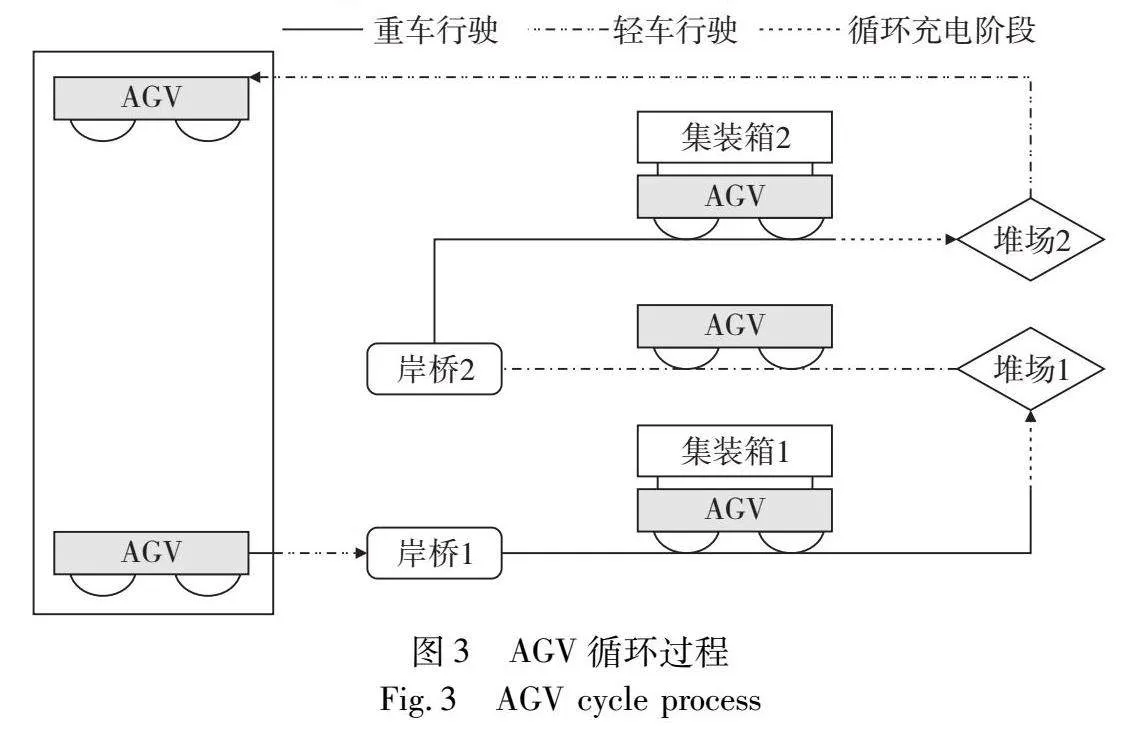
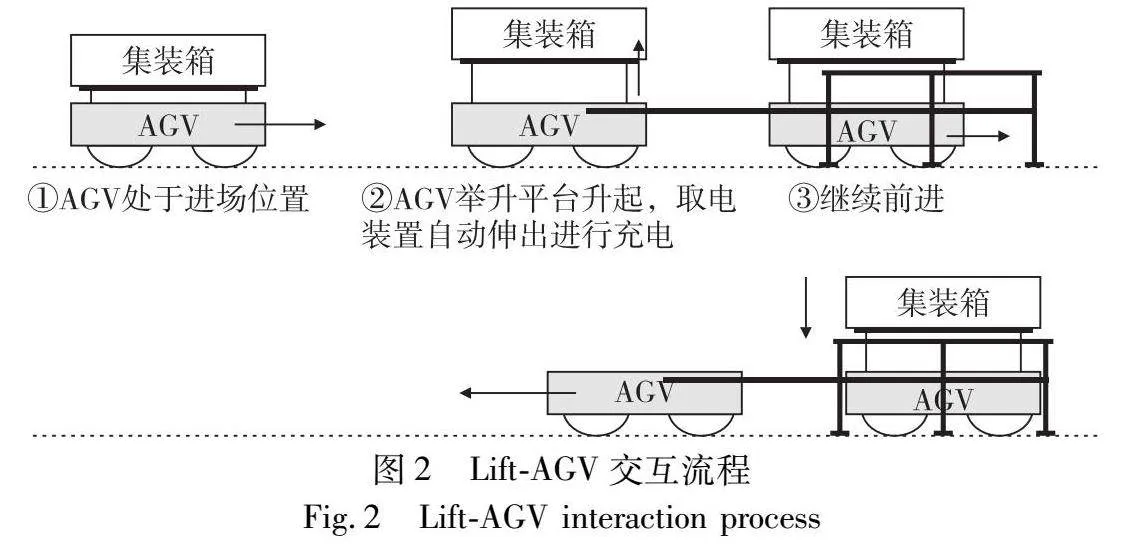
浅充浅放充电策略中，创新AGV交互流程，采用新型Lift-AGV［21］。Lift-AGV装有举升平台如图2所示，AGV作业循环末行驶至堆场交互区利用固定支架完成与轨道吊的交互，全程仅需要一分钟同时进行补电。当AGV剩余极少电量时，行驶至充电桩进行充电至满电。但任务量大时AGV循环放电大于循环充电，易出现电量不足情况，而且AGV电量减少到一定程度一次补电至满时间过长，易造成AGV额外等待时间。本文针对上述状况，考虑AGV有足够的空闲时间到充电桩进行补电的情况，减少AGV电量低于充电阈值补电的次数，充分发挥浅充浅放充电策略的优势，提高AGV作业效率。上文所提“空闲时间”也就是AGV等待所分配任务到达时间，若AGV空闲时间大于其从上一任务卸箱位置到充电桩的时间与充电桩到先任务接箱位置的时间之和，则称AGV有“足够的空闲时间”。如图3所示为AGV循环过程。AGV从岸桥1运输任务1至堆场1，此过程经历循环充电阶段。完成任务1后，判断AGV剩余电量是否低于充电阈值和AGV是否有足够空闲时间。若AGV剩余电量大于充电阈值且没有足够空闲时间，则AGV被指派到岸桥2将集装箱任务2运输至堆场2。完成集装箱任务2后再次进行上述判断，若AGV剩余电量低于充电阈值或有足够空闲时间则去充电站充电，至此一个循环结束。由于AGV电量不同且空车行驶与重车行驶耗电率差异较大，需要区分考虑。

2 模型建立

2.1 模型假设

对所建AGV调度模型需作出如下假设：a）AGV初始电量均为100%；b）不考虑设备故障及碰撞；c）任务到达时间已知；d）不考虑岸桥操作时间；e）不考虑充电排队等待时间。

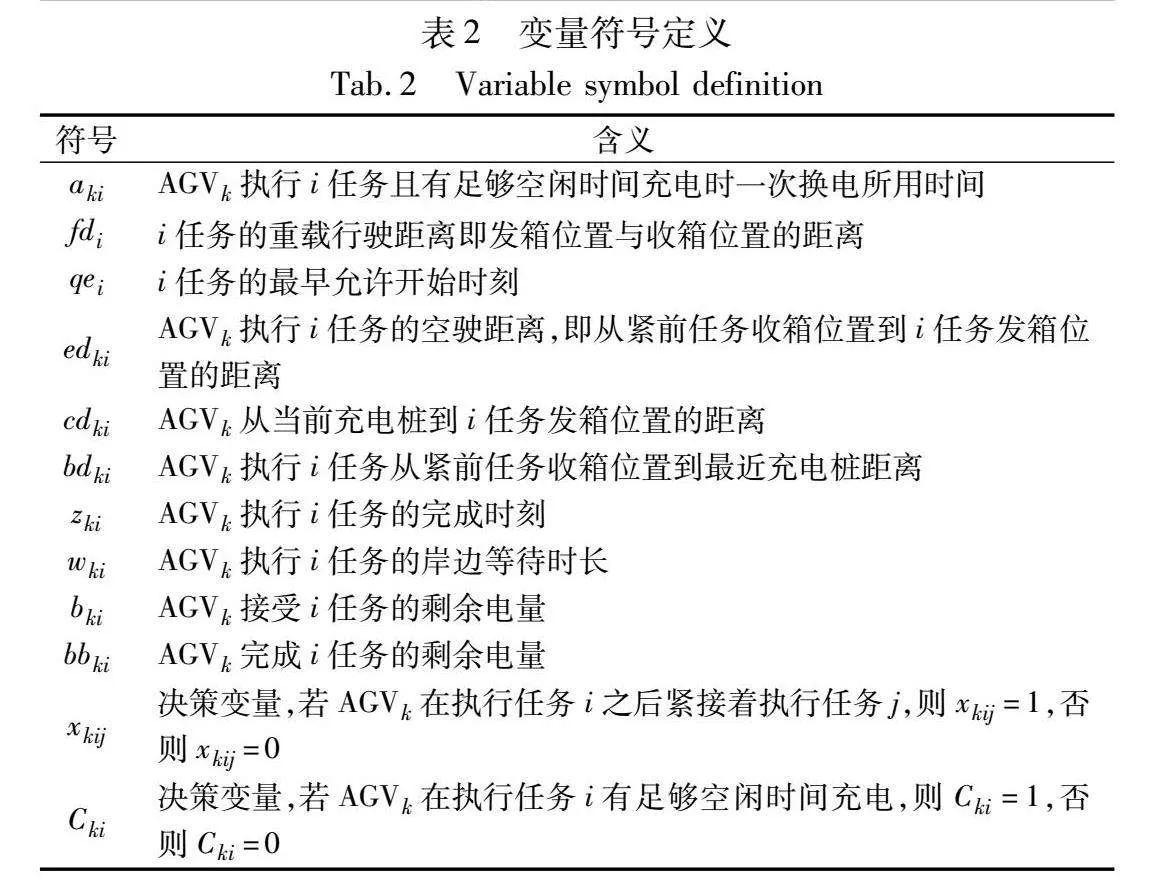
2.2 符号说明

本文所使用符号及说明如表1、2所示。

2.3 AGV调度数学模型

式（1）为目标函数，表示最小化AGV最大完工时间。

Min T（1）

式（2）为最终任务完成时间不小于任意任务的完成时间。

s.t. T≥Zki，k∈K;i∈V（2）

式（3）和（4）表示每台AGV必须完成虚拟开始任务与虚拟结束任务。

∑i∈V0xkij=1 j∈V;k∈K（3）

∑i∈V′0xkij=1 j∈V;k∈K（4）

式（5）和（6）表示每个任务仅有一个紧前和后续任务。

∑k∈K∑i∈Vtxkij=1 j∈V（5）

∑k∈K∑j∈Vtxkij=1 i∈V（6）

式（7）表示中间任务必须运输平衡，即输入等于输出。

∑i∈Vxkih-∑j∈Vxkhj=0 k∈K;h∈Vb∪Vt（7）

式（8）～（10）为等待时间，虚拟任务等待时间为0，换电任务的等待时间由完成上一任务剩余电量和充电桩充电速率决定，普通装卸任务等待时间由到达发箱位置的时间和最早允许作业时间决定。

wki=0k∈K，i∈V0∪V0′WWkik∈K，i∈Vk（8）

WWki=（100-bbkj）/v3+（1-xjik）M k∈K，i∈Vk，j∈V（9）

wkj≥qej-zki-edkj/s1+（xkij-1）M k∈K;j∈Vt;i∈V（10）

式（11）（12）为普通装卸任务与换电任务的完成时间。

zkj≥zki+（1-Ckj）wkj+（1-Ckj）edkj/s1+Ckjbdkj/s1+Ckjcdkj/s1+（1-Ckj）akj+fdkj/s2+（1-xkij）M k∈K;j∈Vt;i∈V（11）

zkj≥zki+wkj+bdkj/s4+cdkj/s4+fdkj/s2+wwkj+（1-xkij）Mk∈K;j∈Vk;i∈V（12）

式（13）为AGV有足够空闲时间充电所用时间。

aki=wki-bdki/s1-cdki/s1 k∈K;i∈Vt（13）

式（14）分别为接受普通装卸任务AGV剩余电量。

bkj≤bbki+M（1-xkij）+Ckj（akjs3-r1bdkj/s1）k∈K;i∈V;j∈Vt（14）

式（15）为接受换电任务时AGV剩余电量不大于充电阈值。

bkj≤MB k∈K;j∈Vb（15）

式（16）（17）为AGV完成正常装卸任务与换电任务时的剩余电量，与式（14）共同描述了AGV利用充浅放充电策略在有足够空闲时间补电前后的电量和利用与堆场交互的时间充电后的电量。

bbki=bki-r1edki/s1-r2fdi/s2+MA k∈K;i∈Vt（16）

bbki=100-r1cdki/s1-r2fdi/s2+MA k∈K;i∈Vb∪V0（17）

式（18）为一台AGV充电次数之和不允许超多最多充电次数n。

∑i∈Vxkij≤n k∈K;j∈Vk（18）

式（19）（20）为变量的约束条件。

xkij∈{0，1}，cki∈{0，1} k∈K;i，j∈V（19）

zki>0，f>0，100≥bbki>0，wki≥0，edki≥0cdki≥0，bdki≥0 k∈K;i∈V（20）

3 基于Wolf-PHC的强化学习算法

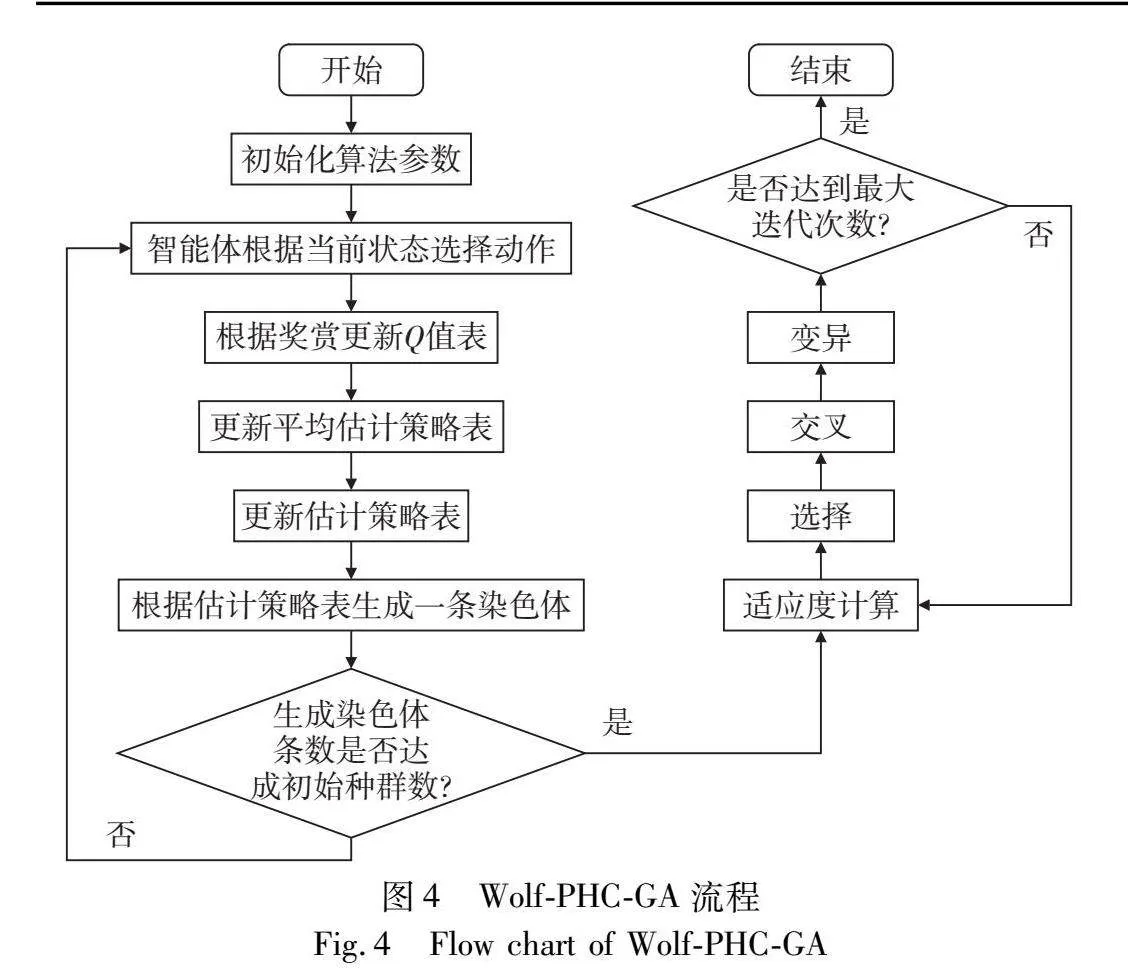
强化学习是一种运用智能体与环境进行“试错”交互，通过实时奖惩值获得反馈，寻找最大累计奖赏值策略的机器学习方法［22］。Wolf-PHC是强化学习中的一种，是win or learn fast规则与policy hill-climbing算法的结合，Wolf指的是当智能体奖赏值较好时缓慢调参，反之加快调参，PHC算法的核心就是通常强化学习思想。强化学习中的很多方法都需要在学习过程中维护Q函数，Wolf-PHC每个智能体只用保存自己的动作来完成学习任务较其他强化学习算法在需存储空间方面有较大的优势。Wolf-PHC具有优秀的自学习和优化能力，可通过不断试错和学习，找到AGV最优的充电时机，使AGV在运行过程中实现能源的高效利用和自主决策。具体而言，Wolf-PHC可以根据AGV的实时状态、任务需求以及充电站距离等情况，动态调整充电调度策略。例如，Wolf-PHC可以有效指导AGV利用空闲时间前往最近的充电桩补电；而当AGV电量低于充电阈值时，Wolf-PHC则可以优化其任务分配，指导AGV到充电桩进行充电至满。综上可知Wolf-PHC与AGV充电调度模型具有较高的关联度，该结合可以实现AGV充电过程的智能调度和优化，进而为自动化集装箱码头系统的高效运行提供有力支持。因GA［23］在求解复杂优化问题中应用广泛，且有较好的鲁棒性。本文将Wolf-PHC与GA进行结合，利用Wolf-PHC生成初始种群带入GA，具体流程如图4所示。

本文将AGV定义为agent，定义动作为集装箱任务编号，状态为不同电量区间AGV行驶的速度。agent之间通过竞争选择集装箱任务后，合作共同寻找到使完成任务总时间最少的策略。浅充浅放循环充电策略中AGV会利用与堆场交互时进行短时间的补电，因此设置AGV去充电桩补电的阈值会很低，也会导致AGV因低于阈值补电的时间会很长。本文考虑浅充浅放循环充电策略的规则，根据最小化完成任务时间构造奖励函数。但Wolf-PHC的目标是累计奖励值最大化，因此奖励函数与完成任务所需时间呈负相关，用式（21）表示。

r（s，a）=-zki（21）

操作步骤如下：

a）输入集装箱任务属性，充电桩-堆场-岸桥距离。初始化种群大小popsize，动作选择概率egreedy，探索迭代次数episode，状态s出现次数C（s），策略效果较差学习率δl，策略效果较好学习率δw，Q值表，πk值表，πk值表。

πk（s，ak）=1/|Ak|，πk（s，ak）=1/|Ak| δl>δw（22）

b）智能体k根据当前的状态s采用ε-贪心策略得到动作ac并执行。

c）观测下一个奖赏值rk和下一个状态s′更新Qk（s，ac），本文设置奖赏值为AGV执行集装箱任务所用时间。

Qk（s，ac）=Qk（s，ac）+α［rk+γmaxQk（s′，a′）-Qk（s，ac）］（23）

d）对于每个ak∈Ak，更新平均估计策略πk（s，ak）。

C（s）=C（s）+1（24）

πk（s，ak）=πk（s，ak）+1/C（s）［πk（s，ak）-πk（s，ak）］（25）

e）根据Qk（s，ac），对每个ak∈Ak更新πk（s，ak）。

πk（s，ak）=πk（s，ak）+Δsa（26）

Δsak=-δsakak≠argmaxa′Q（s，a′）∑a′≠akδsakothers（27）

δsa=min（πk（s，ak），δ/|Ak|-1）（28）

δ=δw∑ak∈Akπk（s，ak）Qk（s，ak）>∑ak∈Akπk（s，ak）Qk（s，ak）δlothers（29）

f）根据πi值表选出每个任务完成时间最短的AGV得出染色体，染色体编码如图5所示。染色体长度由任务数量决定，第i个位置的编码k表示第i个任务由AGVk完成。

g）判断是否达到初始种群数，如果是则输出初始种群，否则执行步骤b）。

h）输入Wolf-PHC生成的初始种群，最大迭代次数generation，交叉概率Pc，变异概率Pm。

i）取调度模型目标函数即在浅充浅放充电策略下最小化AGV最大完工时间的倒数作为适应度函数值，1/T。

j）选择，本文采用轮盘赌选择方法。

k）交叉，本文采用两点交叉法。

l）变异，本文交换变异方法。

m）判断是否到最大迭代次数，如果是则结束迭代，否则执行步骤i）。

4 算例分析

4.1 算例参数设置

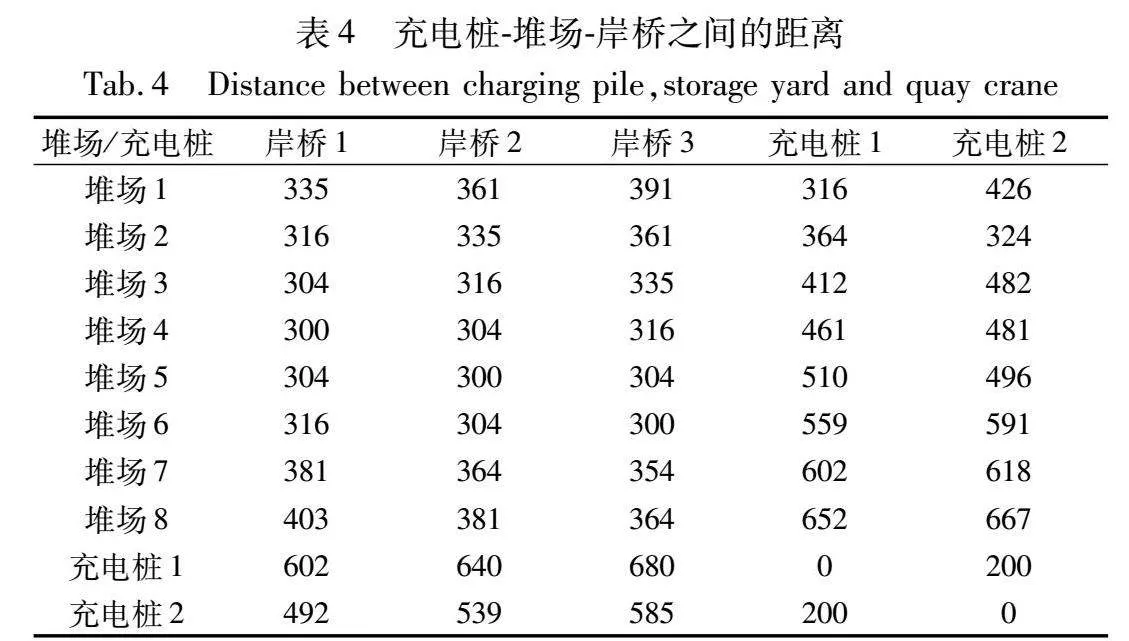
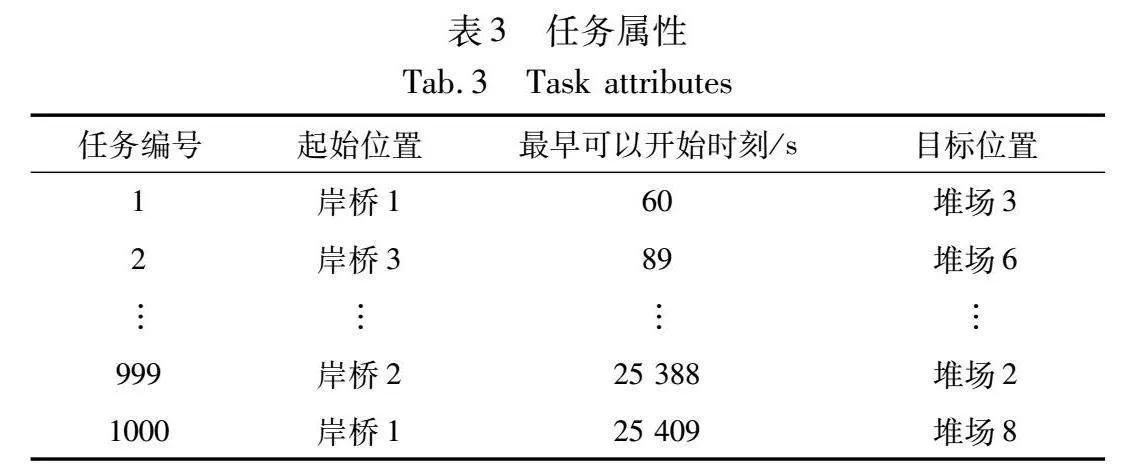
为评估所建立模型的准确性，通过GAMS求解器［24］求解得出模型在具体环境下的精确解，并与Wolf-PHC-GA、强化学习算法中较有代表性的Q-leaning算法［25］及GA所求得最优解进行对比分析，以突出Wolf-PHC与GA结合的有效性及优越性。其中Wolf-PHC-GA、GA、Q-learning均运行10次取平均值作为最终结果。产生1 000个集装箱任务样本，其属性如表3所示。设置初始种群大小popsize=200，动作选择概率egreedy=0.9，探索迭代次数episode=20，策略效果较差学习率δl=0.8，策略效果较好学习率δw=0.4，最大迭代次数generation=200，交叉概率Pc=0.7，变异概率Pm=0.05。充电桩-堆场-岸桥之间的距离如表4所示。令充电阈值（MB）为20%，AGV电量高于充电阈值时空车、重车行驶速度分别为4 m/s、3 m/s，AGV电量低于充电阈值时空车、重车行驶速度分别为2 m/s、1 m/s，AGV空车、重车行驶状态下每米耗电率分别为0.01%、0.02%，设置两个充电桩。

4.2 不同AGV数量下小规模任务结果分析

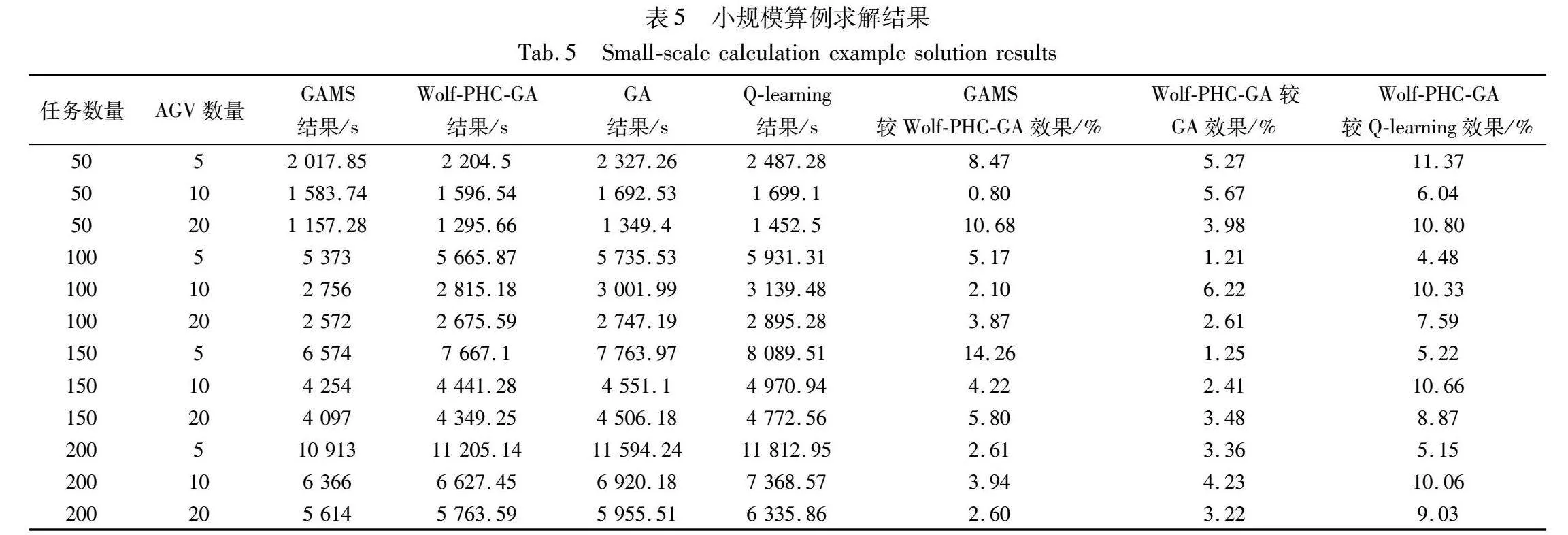
基于以上参数，求解小规模集装箱任务规模及不同AGV数量的完工时间，如表5所示。从表5可以看出，小规模任务下Wolf-PHC-GA结果与GA结果的效果值多数在3%～8%，与Q-learning算法结果的效果值多数在5%～10%，而GAMS求得的精确解结果与Wolf-PHC-GA结果的效果值多数在8%以内。有效说明了Wolf-PHC-GA所求得最优解不仅近似于精确解，还更优于对比算法。

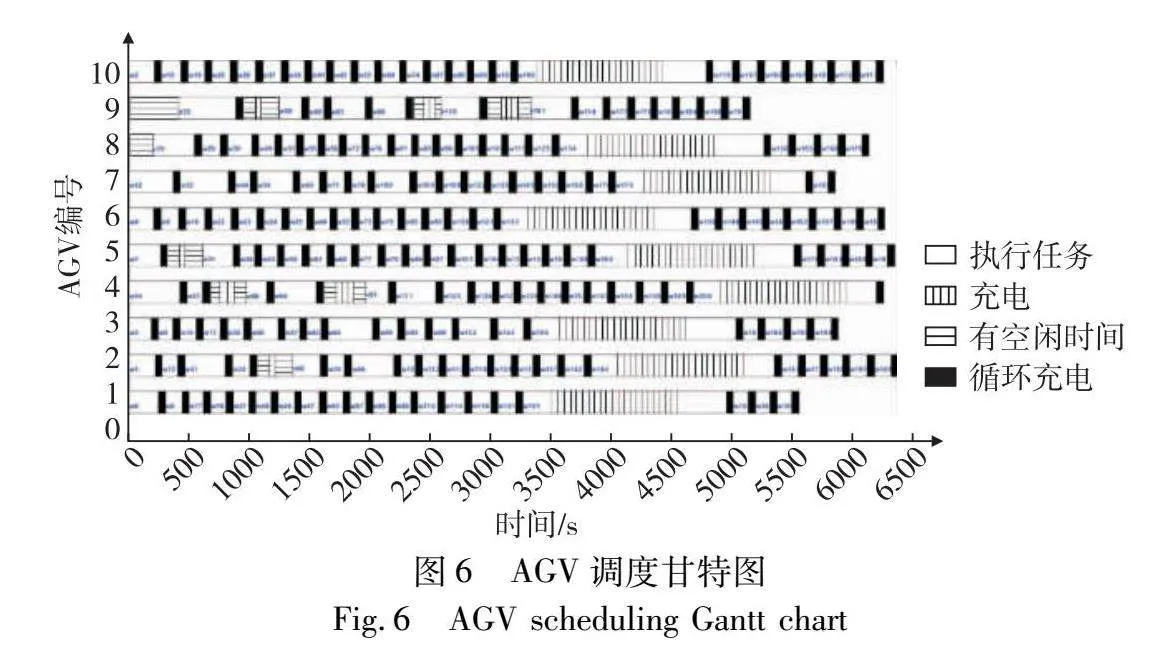
图6为200个集装箱任务10辆AGV调度甘特图。可以看出，在浅充浅放充电策略下AGV可有效利用每个作业循环与堆场交互时间进行补电与在AGV有足够空闲时间进行补电，很大程度上减少了AGV在充电桩补电的次数，从而减少作业时间。

4.3 不同AGV数量下大规模任务结果分析

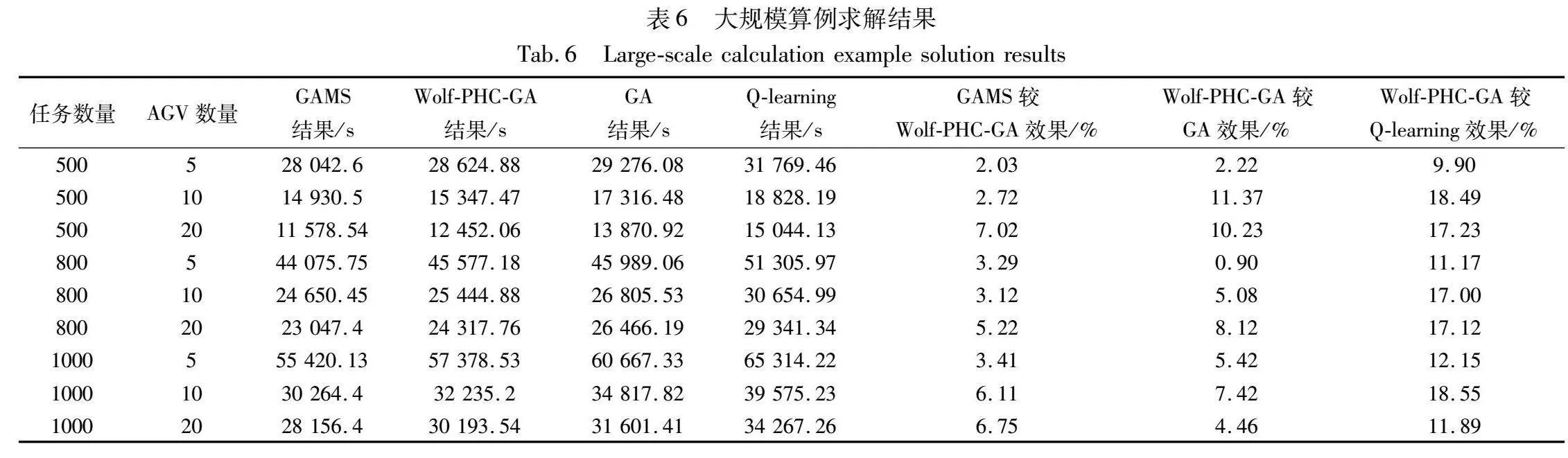
大规模集装箱任务下，不同AGV数量的结果对比如表6所示。总体来看，大规模任务量优化效果比小规模任务量略胜一筹：Wolf-PHC-GA与GA的效果值多数在5%～10%，与Q-learning算法的效果值多数在10%～17%，而GAMS与Wolf-PHC-GA的效果值多数在6%以内。说明Wolf-PHC-GA求解大规模任务效果更佳，更适用于自动化集装箱码头实际运作场景。

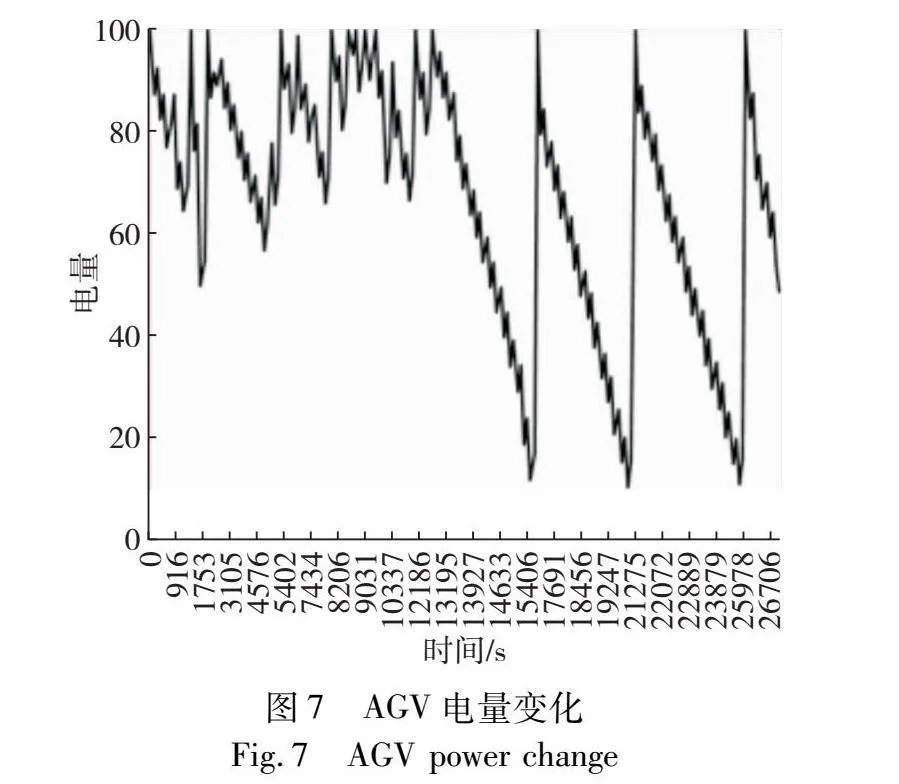
图7为1 000个集装箱任务10辆AGV调度中的一辆AGV电量变化。图中均匀锯齿状下降部分反映了AGV与堆场交互时一分钟补电的情况；在均匀锯齿状下降过程中会有上升的情况，代表AGV有足够空闲时间补电；最后出现三次急剧上升的情况，则代表AGV因电量低于MB到充电桩进行充电至满。

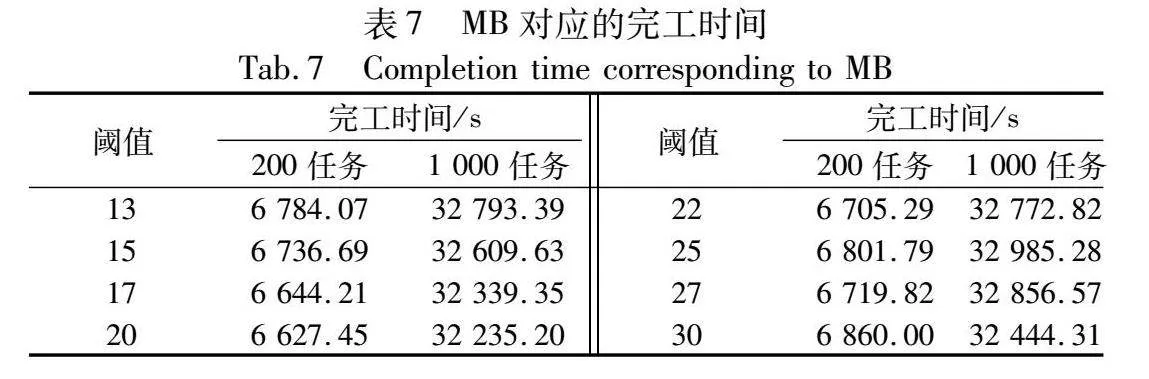
4.4 充电阈值（MB）对结果影响分析

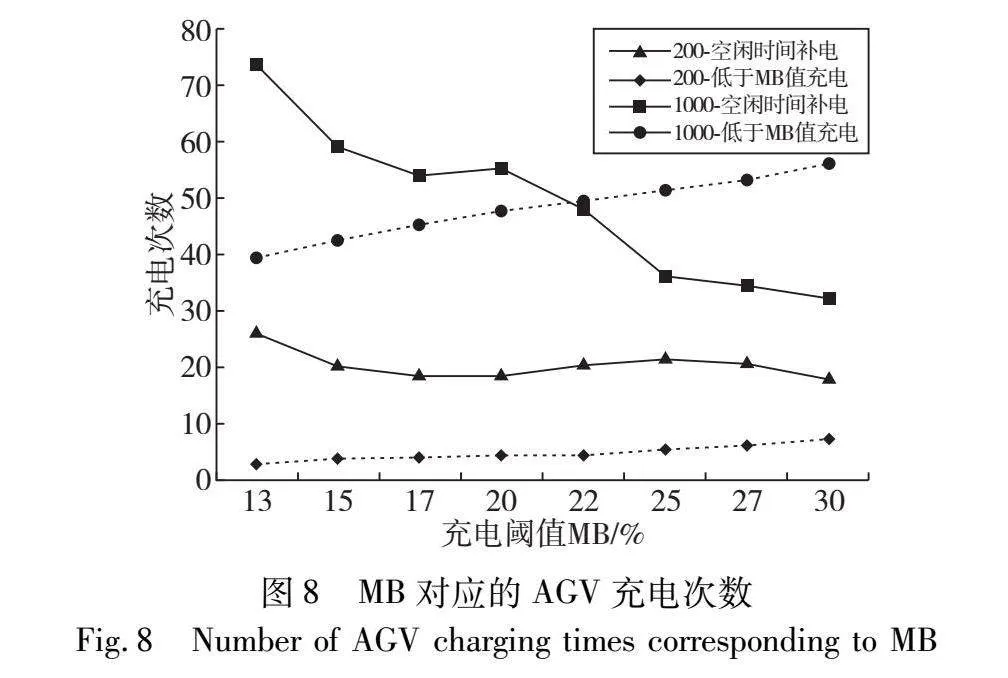
经过上述对比分析可知MB对最终完工时间有较大影响，因此设定MB在13%～30%取值，分别取大小规模任务量10辆AGV进行分析，最终得到的不同MB值对应的完工时间如表7所示，AGV有足够空闲时间补电及低于MB值充电次数如图8所示。可以看出，改变MB值能够影响AGV最终完工时间：当MB值增大，AGV电量低于MB值充电次数程上升趋势，小规模任务量利用空闲时间充电次数浮动在5次以内，大规模任务量效果更明显，利用空闲时间充电次数整体呈下降趋势。当MB值在17%～20%取值时，完工时间较短。因此可见，合理设置MB值，更能发挥浅充浅放充电策略的优势。

4.5 不同学习率比值（δl/δw）对结果的影响分析

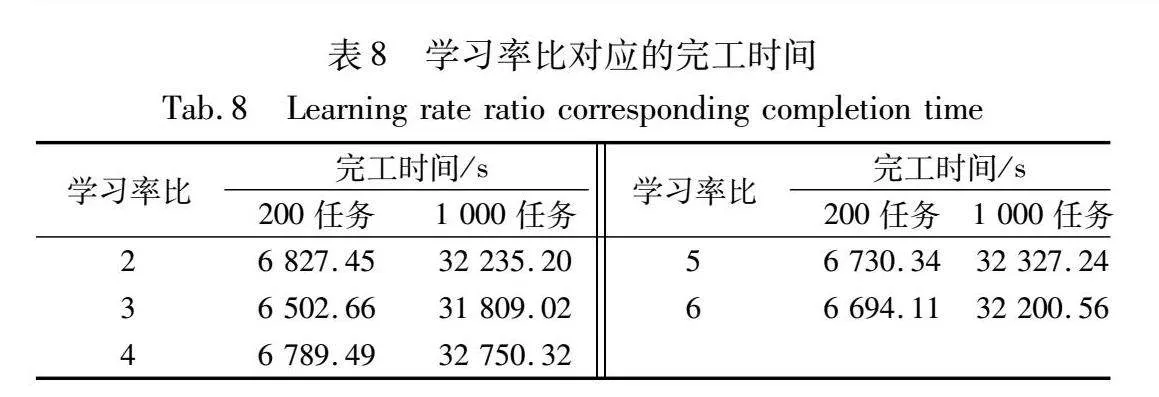
上述结果是在δl=0.8、δw=0.4时计算得出的。改变δl、δw的比值得到如表8所示的结果。从表中可看出，大小规模任务量在不同学习率比的影响下，完工时间变化在0.1～0.3 h。其中δl/δw=3时总完工时间最短，效果最好。

5 结束语

本文在自动化集装箱码头AGV调度过程中考虑了AGV浅充浅放充电策略，区分不同状态下AGV耗电程度，考虑了充电过程对AGV作业效率的影响，建立了AGV调度混合整数优化模型，运用GAMS求解器验证所建立模型的有效性，并与Wolf-PHC-GA、GA、Q-learning算法进行对比求解。在小规模算例下对比分析得出Wolf-PHC-GA求解结果比GA求解结果提升了3%～8%，比Q-learning求解结果提升了5%～10%，说明了Wolf-PHC-GA求解的优越性，并以200个任务10辆AGV为例说明了浅充浅放充电策略可有效减少AGV低于阈值充电的次数，提高AGV利用率。大规模算例下Wolf-PHC-GA求解结果较GA求解结果提升5%～10%，较Q-learning求解结果提升10%～17%，进一步说明Wolf-PHC-GA求解的优越性，并以1 000个任务10辆AGV为例分析AGV在浅充浅放充电策略下电量变化。通过对充电阈值的分析可知，设置充电阈值在17%～20%完工时间较短，有效提升自动化码头工作效率。最后，对Wolf-PHC-GA中重要参数学习率比值进行分析可得，在学习率比值为3时效果最佳。本文所建立混合整数优化模型对于自动化集装箱码头AGV浅充浅放充电问题具有一定指导意义。但是本文未考虑频繁充放电对AGV电池寿命影响，可加深对此方面的研究。同时，可以继续深入研究不同自动化集装箱码头布局、充电桩位置及数量与AGV浅充浅放充电的关系。

参考文献：

［1］Liu Wenqian，Zhu Xiaoning，Wang Li，et al.Multiple equipment scheduling and AGV trajectory generation in U-shaped sea-rail intermodal automated container terminal［J］.Measurement，2023，206：112262.

［2］Wang Xue，Zou Wenqiang，Meng Leilei，et al.Effective metaheuristic and reschedul-eng strategies for the multi-AGV scheduling problem with sudden failure［J］.Expert Systems with Applications，2024，250：123473.

［3］李静，朱小林.集装箱码头上多自动引导车的调度和路径规划［J］.计算机集成制造系统，2022，28（5）：1449-1461.（Li Jing，Zhu Xiaolin.Scheduling and path planning of multiple automatic guided vehicles in container terminals［J］.Computer Integrated Manufacturing Systems，2022，28（5）：1449-1461.）

［4］梁承姬，陈登川.自动化集装箱码头AGV配置与调度耦合问题研究［J］.计算机工程与应用，2020，56（14）：216-225.（Liang Chengji，Chen Dengchuan.Research on coupling problem of AGV configuration and scheduling in automated container terminal［J］.Computer Engineering and Applications，2020，56（14）：216-225.）

［5］王鼎新.基于改进Q-learning算法的AGV路径规划［J］.电子设计工程，2021（4）：7-11.（Wang Dingxin.AGV path planning based on improved Q-learning algorithm［J］.Electronic Design Enginee-ring，2021（4）：7-11.）

［6］初良勇，梁冬.基于DQN的自动化集装箱码头AGV多目标调度优化［J］.哈尔滨工程大学学报，2024（5）：1-9.（Chu Liangyong，Liang Dong.Multi-objective scheduling optimization of AGVs in automated container terminal based on DQN［J］.Journal of Harbin Engineering University，2024（5）：1-9.）

［7］Gao Yinping，Chang Daofang，Chen C H，et al.A digital twin-based decision support approach for AGV scheduling［J］.Engineering Applications of Artificial Intelligence，2024，130：107687.

［8］Zhan Xiangnan，Xu Liyun，Zhang Jian，et al.Study on AGVs battery charging strategy for improving utilization［J］.Procedia CIRP，2019，81（3）：558-563.

［9］Nitish S，Quang-Vinh D，Alp A，et al.A matheuristic for AGV scheduling with battery constraints［J］.European Journal of Operational Research，2022，298（3）：855-873.

［10］Nitish S，Alp A，Quang-Vinh D，et al.Dispatching AGVs with battery constraints using deep reinforcement learning［J］.Computers & Industrial Engineering，2024，187：109678.

［11］赵涛，梁承姬，胡筱渊，等.自动化集装箱码头AGV调度与换电双层模型求解［J］.大连理工大学学报，2021，61（6）：623-633.（Zhao Tao，Liang Chengji，Hu Xiaoyuan，et al.Solution of AGV scheduling and battery exchange two-layer model for automated container terminal［J］.Journal of Dalian University of Technology，2021，61（6）：623-633.）

［12］石楠路，梁承姬.考虑换电过程的自动化码头AGV调度优化［J］.现在制造工程，2019（2）：6-11.（Shi Nanlu，Liang Chengji.Optimization of AGV operation scheduling for automated terminal considering replacement processes［J］.Modern Manufacturing Engineering，2019（2）：6-11.）

［13］杨其飞，兰培真.考虑充电过程的自动化码头AGV调度［J］.集美大学学报：自然科学版，2023，28（2）：142-149.（Yang Qifei，Lan Peizhen.Automated terminal AGV scheduling considering the charging process［J］.Journal of Jimei University：Natural Science，2023，28（2）：142-149.）

［14］吴洪明，邹梦艳.考虑电池电量约束的自动化码头AGV调度［J］.起重运输机械，2021（3）：47-52.（Wu Hongming，Zhou Mengyan.Automated terminal AGV scheduling considering battery power constraints［J］.Hoisting and Conveying Machinery，2021（3）：47-52.）

［15］Xie Danlan，Guo Di，Ji Yuan，et al.Simulation research on optimization of AGV charging strategy for automated terminal［J］.Journal of System Simulation，2020，32（10）：2227-2236.

［16］Ma Ning，Zhou Chenhao，Stephen A.Simulation model and perfor-mance evaluation of battery-powered AGV systems in automated container terminals［J］.Simulation Modelling Practice and Theory，2021，106：102146.

［17］吴伟民.厦门远海自动化码头的充电装置升级改造［J］.电子元器件与信息技术，2023，7（12）：209-212.（Wu Weimin.Charging device upgrade at Xiamen Yuan Hai automated terminal［J］.Electronic Components and Information Technology，2023，7（12）：209-212.）

［18］郄佩琦，陈传军，陈佳梁，等.基于区域繁忙度的AGV充电桩选址研究［J］.制造业自动化，2023，45（8）：214-220.（Qie Peiqi，Chen Chuanjun，Chen Jialiang，et al.Research on AGV charging pile siting based on regional busyness［J］.Manufacturing Automation，2023，45（8）：214-220.）

［19］朱林，王伟，唐立辉，等.自动化集装箱码头AGV分布式浅充浅放循环充电系统［J］.港口装卸，2020（6）：8-13.（Zhu Lin，Wang Wei，Tang Lihui，et al.AGV distributed shallow charging shallow discharge cycle charging system in automated container terminal［J］.Port Operation，2020（6）：8-13.）

［20］唐立辉，张连钢.自动化集装箱码头水平运输系统动力系统及充电方案［J］.水运工程，2020（6）：74-78.（Tang Lihui，Zhang Liangang.Power system and charging scheme of horizontal transportation system of automated container system［J］.Port & Waterway Engineering，2020（6）：74-78.）

［21］王伟，孙秀良，徐哲，等.一种自动化集装箱码头纯电动AGV充电方式［J］.港口装卸，2019，245（2）：1-2.（Wang Wei，Sun Xiuliang，Xu Zhe，et al.Charging mode of pure electric AGV in automated container terminal［J］.Port Operation，2019，245（2）：1-2.）

［22］傅启明.强化学习中离策略算法的分析及研究［D］.苏州：苏州大学，2014.（Fu Qiming.Analysis and research on off-policy algorithms in reinforcement learning［D］.Suzhou：Suzhou University，2014.）

［23］许彭锦，梁承姬.考虑电池包数量的自动化集装箱码头多AGV调度优化［J］.计算机应用研究，2022，39（9）：2653-2659.（Xu Pengjin，Liang Chengji.Research on multi-AGV scheduling optimization of automated container terminal considering number of battery packs［J］.Application Research of Computers，2022，39（9）：2653-2659.）

［24］马书艳.GAMS在复杂系统中的应用研究［J］.科学技术创新，2020（31）：96-97.（Ma Shuyan.Research on the application of GAMS in complex systems［J］.Scientific and Technological Innovation，2020（31）：96-97.）

［25］赵德京，马洪聪，王家曜，等.改进Q学习算法在多智能体强化学习中的应用［J］.自动化与仪器仪表，2022（6）：13-16，22.（Zhao Dejing，Ma Hongcong，Wang Jiayao，et al.Application of improved Q learning algorithm to multi-intelligent body reinforcement learning［J］.Automation & Instrumentation，2022（6）：13-16，22.）