基于改进堆优化算法求解电动汽车并网动态经济调度

摘 要：针对堆优化算法HBO处理含电动汽车的动态经济调度问题时存在收敛慢和精度低等问题，提出一种改进的堆优化算法RDHBO。首先，在RDHBO中引入了最优成员区域搜索和双种群交互策略。前者引导最优成员移动到更有希望的区域，提升了算法的收敛精度和收敛速度；后者充分利用被淘汰的劣势个体，丰富了种群的多样性，避免了算法陷入局部最优。然后，将RDHBO应用于四种充电场景的10机组电动汽车动态经济调度问题。仿真结果表明，与已有的代表性方法相比，RDHBO在产生低燃料成本和稳定性方面具有很强的竞争力。最后，对RDHBO的两种改进策略进行了消融实验，验证了两种改进策略的有效性。

关键词：动态经济调度；电动汽车；堆优化算法；区域搜索；双种群交互

中图分类号：TP18;TM73 文献标志码：A 文章编号：1001-3695（2024）10-021-3032-06

doi：10.19734/j.issn.1001-3695.2024.03.0058

Solving dynamic economic dispatch with electric vehicle based on improved heap-based optimizer algorithm

Chen Xu，Zhang Zhixiang

（School of Electrical & Information Engineering，Jiangsu University，Zhenjiang Jiangsu 212013，China）

Abstract：When dealing with dynamic economic dispatch problems involving electric vehicles（EVDED），HBO suffers from slow convergence and low accuracy.This paper proposed an improved heap-based optimizer algorithm called RDHBO.RDHBO adopted the optimal member region search and dual population interaction strategies.The former guided the optimal members to move to more promising regions，improving the convergence accuracy and convergence speed.The latter made full use of the eliminated inferior individuals，enriching the diversity of the population，avoiding the algorithm falling into the local optimum.It investigated a 10-unit EVDED problem with four charging scenarios.The simulation results show that RDHBO is highly compe-titive in generating low fuel cost and high stability compared with the existing representative methods.Finally，two improved strategies of RDHBO were subjected to ablation experiments，and the results show that combining the two strategies are effective.

Key words：dynamic economic dispatch（CDED）;electric vehicle;heap-based optimizer（HBO）;regional search;dual population interaction

0 引言

经济调度（economic dispatch，ED）是电力系统运行中最重要的优化问题之一［1］。经济调度分为静态经济调度和动态经济调度（DED）。DED是在满足系统物理约束和运行约束的条件下，分配整个调度周期内的机组发电量，使得发电总成本最小。DED问题的运行约束通常包括发电机容量约束、斜坡率约束、功率平衡约束等［2］。

为了求解复杂DED问题，研究人员已经开发了各种优化方法，主要分为传统数学方法和启发式方法。传统数学方法包括线性规划［3］、二次规划［4］等，该类方法只能近似处理具有非凸特征的DED问题，较难得到质量较高的可行解。为了高效地解决DED问题，启发式算法逐渐受到了研究者们的青睐。文献［5］应用鲸鱼优化算法求解DED问题，算法模拟鲸鱼的捕食行为包括包围猎物、发泡网攻击和搜索捕食行为特征。文献［6］提出了一种改进的海洋捕食者算法，并将其应用于求解DED问题。改进的算法中，所有个体之间分享最佳经验，仿真结果表明算法求解精度更高。文献［7］提出了一种基于双学习策略的自适应回溯搜索算法，该算法能够提高解的精度并避免过早收敛。文献［8］提出了一种求解DED问题的自适应混合回溯搜索算法，算法的核心思想是基于当前最优个体设计合适的耦合结构。文献［9］提出了一种基于反重力的模糊引力搜索算法，算法在动态经济调度问题中获得了较好的优化结果。

近年来，随着电动汽车数量的不断增加，大规模电动汽车充电不协调的特性会对电网的安全造成威胁［10］。在实际生活中，EV充电也存在着不确定性。文献［11］研究了一种包含电动汽车的动态经济调度问题，综合考虑了阀点效应、等式约束以及不等式约束。文献［12］提出了多智能体模糊强化学习，满足不同地区、不同用户的可充电电动汽车的能源需求，同时提升能源调度的可靠性。文献［13］应用黑寡妇优化算法，对电动汽车的EPRI、峰值、随机、非峰值等多种充电策略解决调度成本小最小化问题。文献［14］综合考虑电动汽车和风力发电一体化，提出一种新颖的病毒优化算法，在风力发电机组和电动汽车白天和夜间存在的测试系统上，验证了所提方法的有效性。

从已有文献可以看出，开发高效算法来改善动态经济调度问题的求解至关重要。本文讨论的堆优化算法（heap-based optimizer，HBO）是一种十分高效的优化算法［15］。该方法在2020年提出，采用一种新型的树型结构来模拟公司等级结构，较差的个体可以向优秀个体学习，确保迭代效率。此外，相比较其他的新型优化算法，HBO迭代方式是维度更新，不是直接更新个体，这种迭代方式尤其适合动态经济调度问题。HBO已在测试函数和其他工程问题上被证明具有优异性能［16～18］，但是其性能需要进一步挖掘。

本文提出了一种改进算法RDHBO（HBO with region search and dual population interaction）求解含电动汽车的动态经济调度（dynamic economic dispatch with electric vehicles，EVDED）问题，建立了包含充电汽车的动态经济调度EVDED模型，设计了最优成员区域搜索策略和双种群交互策略。

1 含电动汽车的EVDED模型

EVDED模型的主要目标是最小化发电总成本。因此，本文以发电成本最小化为优化目标，同时考虑实际生活中设备运行的各种约束。这些约束主要包括功率平衡约束、发电机容量、爬坡速率限制以及四种充电方案的限制。

1.1 优化目标

动态经济调度通过控制发电机组的电力负荷，确保满足电力需求的同时，使得发电总成本最小化。在实际生产中，多阀流轮机发电机中普遍存在阀门位置误差。考虑阀门位置对成本的影响，目标函数中加入正弦函数，得到如下形式的目标函数：

min Fc=∑Tt=1∑Nu=1au+buPut+cuP2ut+|eusin（fu（Pminu-Put））|（1）

其中：N为发电机个数；T为调度周期内的总时段数；au、bu、cu为燃料成本系数；eu、fu为阀点系数；Pminu表示第u台发电机的最小功率输出；Fc为N台发电机在T时段内的总燃料成本；Fut为t时段内第u台发电机的燃料成本；Put表示第u台发电机t时段的输出功率。

1.2 约束条件

1.2.1 功率平衡约束

对于第t时段（t=1，2，…，T），如果考虑传输损耗的功率平衡约束，可以表示为

∑Nu=1Put=PDt+PLt t=1，2，…，T（2）

其中：PDt为t时段的电力需求；PLt为t时段内的传输损耗，可由式（3）求得。

PLt=∑Nu=1∑Nh=1PutBuhPht+∑Nu=1B0uPut+B00（3）

其中：Buh、B0u、B00为损失系数。如果忽略传输损耗的DED，式（2）可以改写为

∑Nu=1Put=PDt t=1，2，…，T（4）

1.2.2 发电容量限制

对于每台发电机，输出功率受到上下限的限制，分别为

Pminu≤Put≤Pmaxu（5）

其中：Pminu和Pmaxu分别表示第u台发电机的最小和最大输出功率。

1.3 爬坡速率约束

在实际应用中，对于在间隔t内的第u台发电机，每台发电机的实际运行范围都受到相应斜坡速率的限制，以避免对锅炉和燃烧设备施加过大的压力。可以被建模如下：

Pu（t-1）-Put≤DRuPut-Pu（t-1）≤URu（6）

其中：URu表示第u台发电机的爬坡上升限制；DRu表示第u台发电机的爬坡下降限制。

1.4 考虑电动汽车的功率需求

实际生活中，受每个用户出行距离以及出行时间的影响，EV充电时间是不固定的，因此每小时充电效率都有所不同。式（2）可以更改为

∑Nu=1Put=PDt+PDev+PLt t=1，2，…，T（7）

其中：PDev表示第t时段内汽车的电力需求，由式（8）求得。

PDev=PDtotal×Proev（8）

其中：PDtotal表示电力总需求；Proev为表1中t时段内电动汽车充电的概率分布。

1.5 四种电动汽车充电方案

本文采用的四种不同的电动汽车充电场景来自文献［19］，如表1所示，分别包括：a）电力研究院（Electric Power Research Institute，EPRI）提供的充电分布描述；b）OFFPEAK指的是非高峰时段进行充电；c）PEAK指的是高峰时段进行充电；d）STO假设电动汽车充电是随机的。

以上是主流的四种充电场景，考虑多数人群的出行习惯，因此对这四种场景进行研究是合理的。

2 HBO算法改进

2.1 HBO算法

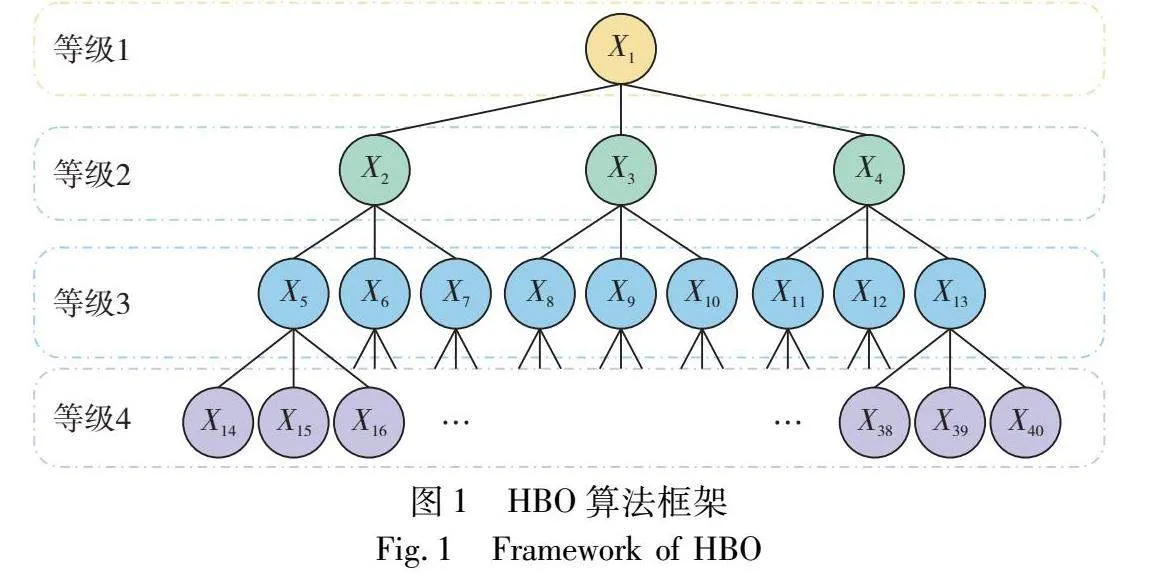
HBO［15］采用了一种三分支的树型结构来模拟公司等级结构。如图1所示。堆节点表示公司成员，每个成员都有且仅有一个直接领导，位于同一等级的成员称之为同事。分支表示成员之间的支配关系。另外，通过计算成员适应度构建并更新堆结构。从图1不难看出，成员X1是整个公司的当前最优成员。HBO涉及成员与直接领导之间的互动，成员与同事之间的互动，以及成员的自我贡献三个方面的互动。

成员与其直接领导之间的互动可以用式（9）表示，每个成员向其领导学习。

Xji（g+1）=Bj+γλj|Bj-Xji（g）|（9）

其中：|*|表示绝对值；g表示当前迭代次数，g∈［1，G］，G表示最大迭代次数；j表示当前处理的维度索引，j∈［1，D］，D为搜索空间的总维度数；i表示当前处理的个体索引，i∈［1，M］，M为成员总数；Xi=（X1i，…，Xji，…，XDi）和B分别表示当前个体和当前个体直接领导的位置；λj可以由式（10）随机生成。

λj=2r-1（10）

其中：r是［0，1］均匀分布的随机数。另外，式（9）中的γ为

γ=|2-t modGCG4C|（11）

C=|G/25|（12）

其中：参数C是一个整数，可以调节算法性能。

此外，成员与同事之间的互动建模如式（13）所示，每个成员通过与其同事比较适应值，决定允许搜索的区域，如下所示。

Xji（g+1）=Sjr+γλj|Sjr-Xji（g）|f（Sr）<f（Xi）Xjr+γλj|Sjr-Xji（g）|f（Sr）≥f（Xi）（13）

其中：Sr表示随机选择的同事；f（Sr）表示同事的适应值；f（Xi）表示当前成员的适应值。员工的自我奉献可以被建模为

Xji（g+1）=Xji（g）（14）

最后，使用式（15）计算累积概率p1、p2和p3后，通过轮盘赌来平衡勘探和开采。

p1=1-t/Tp2=p1+（1-p1）/2p3=p2+（1-p1）/2=1（15）

因此，HBO每个成员的一般更新机制如下：

Xji（g+1）=Xji（g）p≤p1Bj+γλj|Bj-Xji（g）|p1<p≤p2Sjr+γλj|Sjr-Xji（g）|p2<p≤p3&f（Sr）<f（Xi）Xji+γλj|Sjr-Xji（g）|p2<p≤p3&f（Sr）≥f（Xi）（16）

2.2 RDHBO算法

HBO算法具有优异的性能，但是仍存在许多的缺陷。例如，最优成员不参与搜索过程，最优成员会引领整个种群的进化，存在搜索效率慢的问题和成员与其他层的成员之间仅通过动态更新堆实现信息共享，信息交互少，存在多样性不足的问题。本文设计了最优成员区域搜索策略和双种群交互策略。前者引导最优成员移动到更有希望的区域，增强了算法前期的全局开发能力，提升了收敛精度和收敛速度；后者充分利用被淘汰的劣势个体，丰富了种群的多样性，提高了算法后期的局部搜索能力，避免陷入局部最优。

2.2.1 最优成员区域搜索策略

在一个企业中，最优成员的能力对企业的快速发展至关重要。由于HBO特殊的三元树结构，最优成员缺乏自身的更新方程，导致搜索效率较差。所以，本节设计了最优成员区域搜索策略。最优成员区域搜索策略受启发于文献［20］，但文献［20］通过更新较多精英解来探索大规模的搜索空间，需要较多的评价次数。与他们的做法不同，本文仅考虑最优成员。首先，区域搜索的核心思想是成员不再看做一个点，而是看做一个半径为R的区域。如图2（a）所示，实心点X1是最优成员的位置，X2、X3则是次最优成员的位置。X1执行区域搜索策略时，第j维生成公式如下所示。

Xnew，j1=Xj1+N（0，1）×R1if j==v or rand<pXj1otherwise（17）

其中：R1是此时最优成员的搜索半径；j表示最高领导者当前正被扰动的维数，j∈［1，D］；v是一个随机整数，v∈［1，D］；p取值为0.01。图2解释了执行一次区域搜索的过程，红色实线代表最优成员执行区域搜索时的搜索方向，Rnew1表示更新后的搜索半径，Xnew1表示成员的新位置。图2（b）中，最优成员并未找到质量更好的解，意味着其已经处于一个较有希望的区域内。为了避免跳出这个有希望的区域，需要适当减小搜索半径。图2（c）中X1找到了更好的位置Xnew1，这意味着X1正在向更有希望的区域转移，并且为了加快算法的收敛速度需要适当增大搜索半径。搜索半径的更新迭代公式如下：

Rnew1=R1×Kf（X1）<f（Xnew1）R1/Kf（Xnew1）<f（X1）（18）

其中：K是比例因子，取值0.5;f（Xnew1）表示新位置的适应值;f（X1）表示原来的适应值。搜索半径上限约束公式如下：

R1，max=（X1，max-X1，min）10×G-g+1G（19）

其中：X1，max和X1，min分别表示成员X1的上下限。

另外，设计了一个随着迭代次数动态调整的参数φ，φ控制执行区域搜索的次数，计算公式如下：

φ=ceil（5×（g/G））（20）

其中：ceil（*）表示对圆括号内的数值向上取整。

2.2.2 双种群交互策略

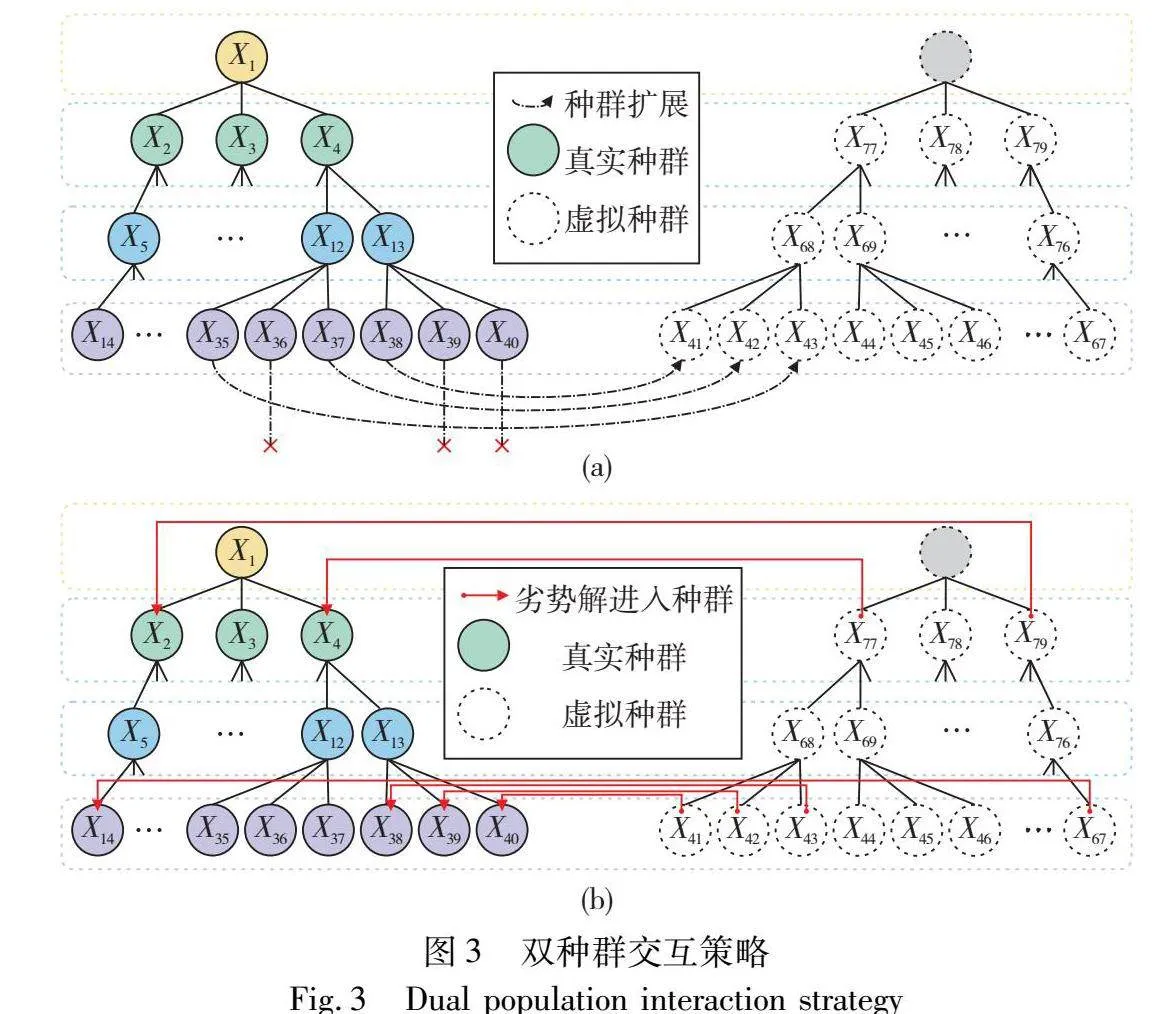
在一个企业中，如果一个成员长时间没有改进，就会失去职场活力，由于HBO独特的树状结构，下属学习的效果会逐渐减弱，这对企业的健康发展是不利的。为了避免这种情况的发生，本节受启发于文献［21］，提出了双种群交互策略，分为公司扩建和成员替换两个模块。

1）公司扩建 公司扩建的核心思想是分析被淘汰的新成员，有机会将其添加到母公司中。为了不影响区域搜索的效果，子公司最大规模设置为（N1-1），成员活力阈值设置为L。

图3（a）可以直观地理解为公司扩建。左边是母公司，右边是子公司，虚线代表劣势成员去向，best_notchange记录最优成员没有更换的次数。在母公司中，如果成员Xi搜索的新成员Xnewi没有更优异，且best_notchange达到阈值L，则Xnewi被放入子公司中。例如，在图3中，成员X39找到的新成员并不优异，但是因为best_notchange未到其阈值L，所以新成员不放入子公司中。X38找到的新成员同样并不优异，但是假设此时best_notchange已经到了阈值，所以将被淘汰的新成员放入子公司的X41位置。后面的X37、X35同理。综上所述，每次都需要分析被淘汰的新成员是否放入子公司中。每一轮迭代都会执行一遍公司扩建，右边子公司几乎所有的成员都会被刷新一遍，子公司的成员规模会逐渐饱和。

2）成员替换 成员替换的核心思想是找出母公司中失去职场活力的成员，并用子公司中的成员替换。通过分析成员的晋升情况来判断成员的职场活力，从而选择出活力最差的成员。图3（b）可以直观地理解为成员替换。红色实线（参见电子版）部分代表子公司成员进入母公司的方向。例如，X41是公司扩建而来，包含了X38的相关信息，X40可以被X41替换。但是这样可以促进彼此之间的信息交互。同样地，子公司和母公司一样保持着等级划分。目的是确保母公司中阶级高的成员被替换时选择到的也是阶级高的成员，可以确保领导能力不会丧失。成员的活力丧失值设计为

dv（Xi）=f（Xi）-f（Xbest）+0.1f（Xworst）-f（Xbest）+0.1×notChangei（21）

其中：常数0.1是为了避免因子为零;notChangei记录成员Xi没有变化的次数。如果dv（Xi）较大，则表示f（Xi）接近f（Xworst），或者成员Xi很长时间没有变化。

基于以上描述，RDHBO算法的详细步骤呈现在算法1中。算法前期，最优成员质量较差且子公司规模并未扩展开，因此前期以最优成员区域搜索为主；算法后期，最优成员基本靠近最优解，且母公司中成员陷入局部最优可能性较大，因此算法后期主要执行双种群策略。

算法1 RDHBO算法

a） 初始化算法参数T、R、K、L、best_notchange、notChangei，母公司规模N1=40，子公司规模N2在0～39。

b）初始化成员适应度，根据适应度构建堆结构，定义全局最优成员为X1。

c）/********最优成员区域搜索***********/

使用式（20）计算区域搜索策略执行次数。

使用式（17）更新X1的位置。

d）如果新成员更优，则替换最优成员，并根据式（18）扩大搜索半径R1；否则，根据式（18）减小搜索半径R1，约束搜索半径。

e）判断区域搜索策略执行次数是否达到最大搜索次数。如果达到最大搜索次数，则跳转步骤f），否则跳转步骤c）。

f）/********基本堆优化算法***********/

令i=40，N2=0

g）找出成员Xi的直接领导并随机挑选一个同事。

使用式（16）更新成员Xi的信息。

h）如果成员Xnewi适应度更好则替换成员Xi，且令notChangei=0，跳转步骤j）；如果成员Xnewi适应度更差，则notChangei=notChangei+1，跳转步骤i）。

i）/********种群扩建***********/

判断best_notchange是否到了阈值L。

如果满足条件，则把劣势新成员放入子公司并且N2=N2+1；不满足条件则不采取措施。

j）成员Xnewi与成员X1适应度进行比较。

如果成员Xnewi适应度好于X1，则best_notchange=0；否则best_notchange=best_notchange+1。

k）更新堆结构，并且notChangei需与Xi绑定。i=i-1，如果i递减到2，则跳转步骤l），否则跳转步骤g）。

l）/********成员替换***********/

根据式（21）计算母公司中39个成员的退化值，并挑选出退化值最大的成员Xworst。

m）条件1：活力值是否达到了阈值K；条件2：替换的那个成员不是最优成员；条件3：子公司中存在对应的成员替换母公司成员。如果满足上述条件，则进行成员替换。

n）令N2=N2-1，判断N2是否缩减到0，如果没有，跳转步骤l）。

o）满足迭代终止则停止运行，否则跳转步骤c）。

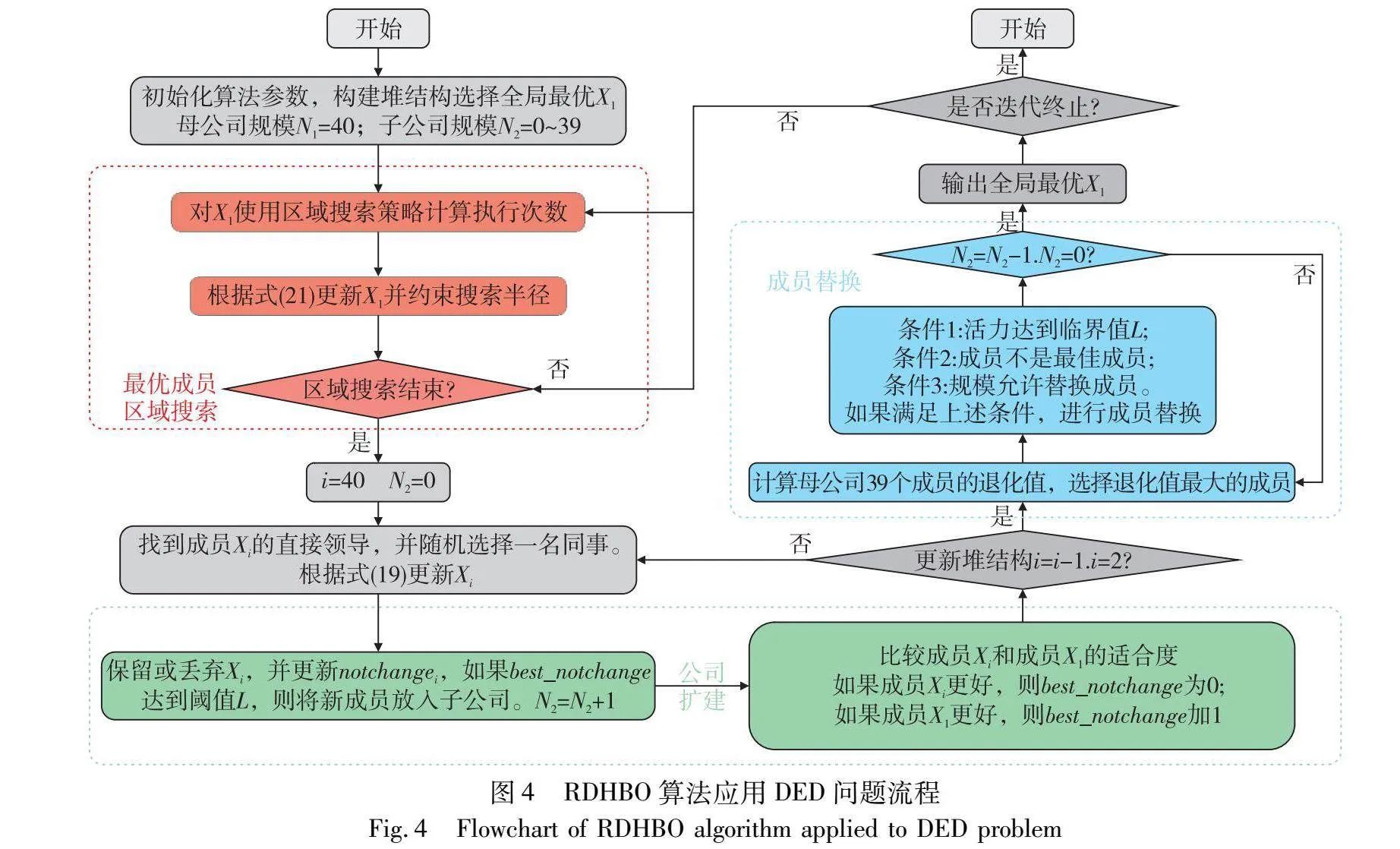
RDHBO算法的应用流程如图4所示。

3 实验验证分析

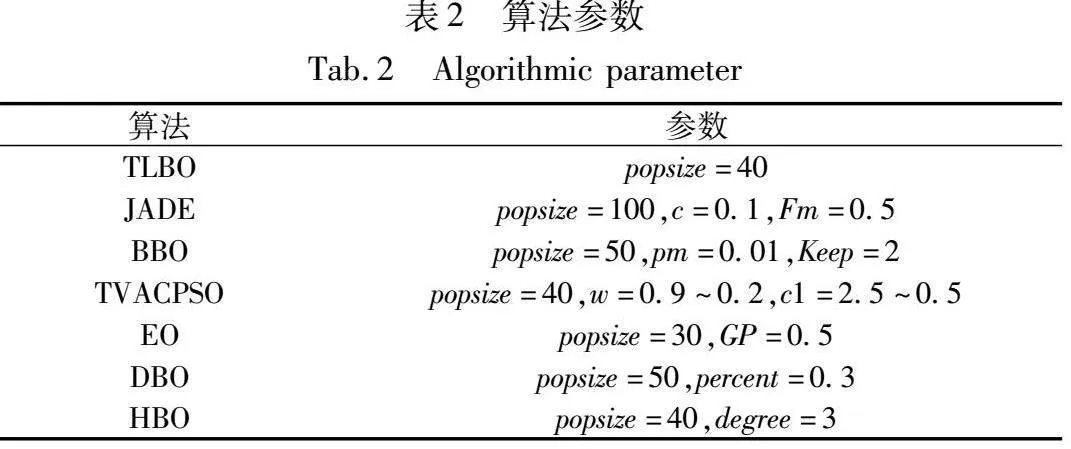
为了验证RDHBO的优越性，本文选取七种算法作为对比算法，分别为HBO、TLBO（teaching-learning-based optimization）［22］、EO（equilibrium optimizer）［23］、DBO（dung beetle optimizer）［24］、TVACPSO（time varying acceleration coefficients particle swarm optimization）［25］、BBO（biogeography-based optimization）［26］、JADE（adaptive differential evolution）［27］。算法的参数设置列于表2。所有算法都在MATLAB 2019a上进行编码。分别独立运行30次，最大函数评价次数maxFES设置为250 000。为了使实验数据更加可靠，使用均值（mean）、执行时间（time）、标准差（Std）、秩检验（sign）等指标。

3.1 考虑四种充电场景的10单元系统

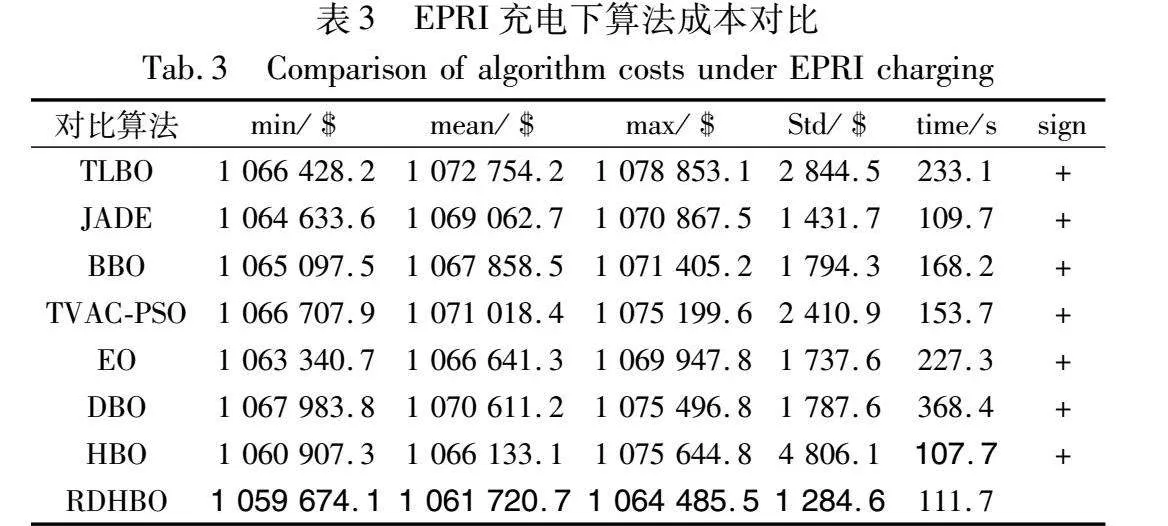
本节研究的调度系统由10个发电机构成，考虑了传输损耗、爬坡约束以及EV。RDHBO与其他算法统计对比如表3所示。表中每种算法最优结果用粗体表示，不难发现：

a）RDHBO在最小、平均和最大成本上都取得了最优异的结果，分别是1 059 674.11 $、1 061 720.47 $和1 064 485.25 $。这表明RDHBO在求解精度方面远远超过其他算法；另外，运行速度最快的HBO求得的成本较RDHBO差了约5 000 $，因此RDHBO执行时间多了几秒是可以接受的。

b）RDHBO的标准偏数值在所有算法中都是最佳的，表明RDHBO很稳定。

c）秩和检验的符号都是“+”，表明RDHBO明显优于其他算法。

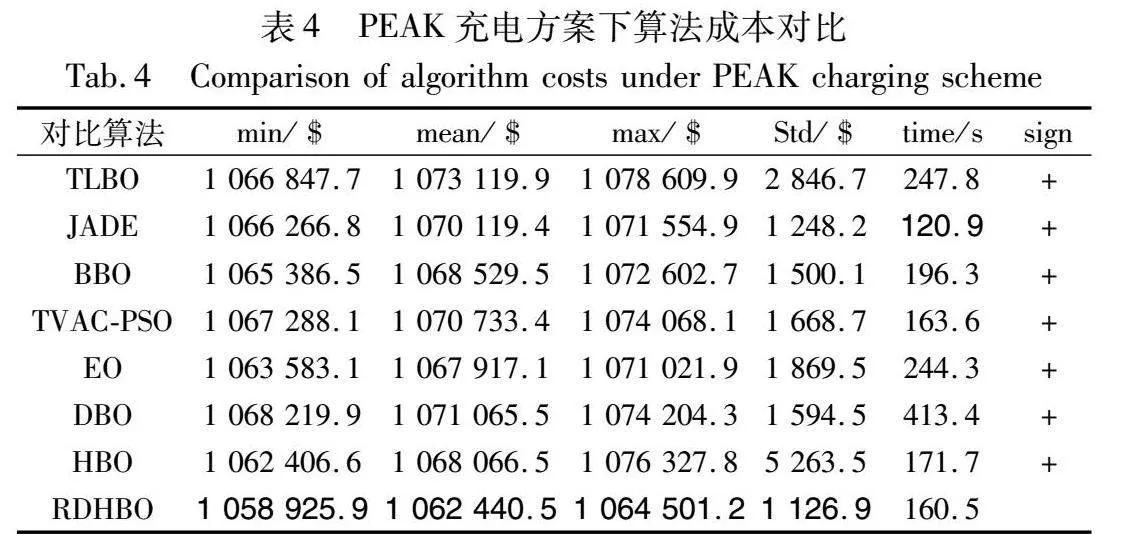
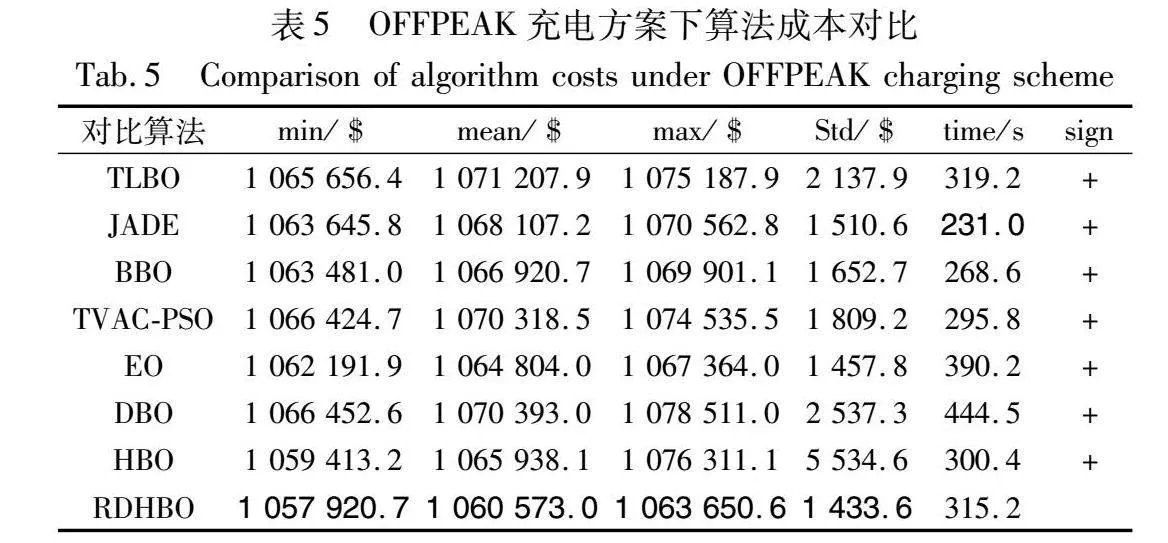
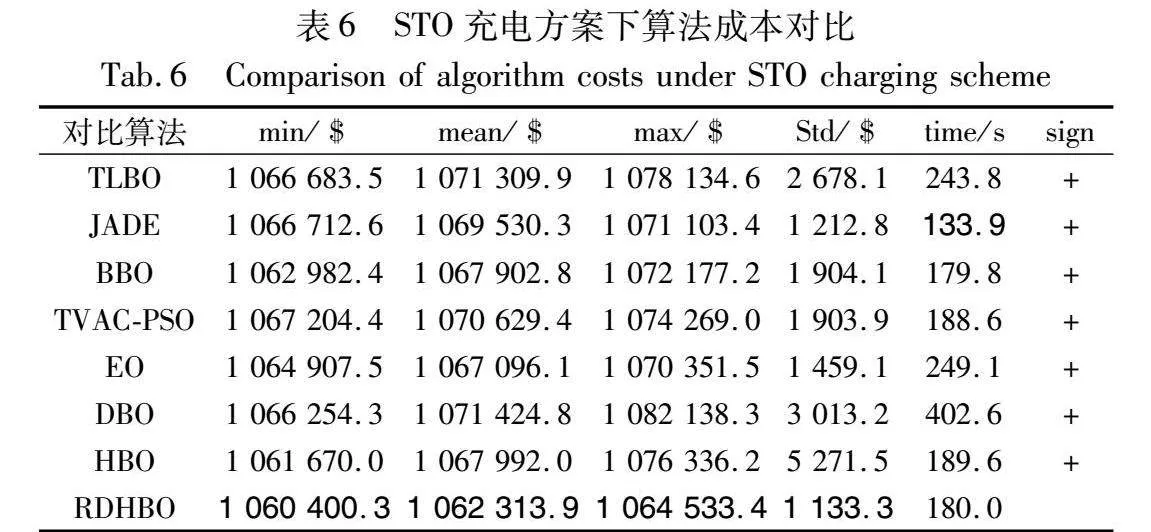
另外三种充电场景下算法对比如表4～6所示。

从表4～6可以发现以下结论：a）RDHBO在这三种场景下的最小值、平均值和最大值都优于其他算法，这表明RDHBO在求解精度方面远远超过其他算法；b）RDHBO在四种充电场景中平均成本分别为是1 061 720.7 $、1 062 440.5 $、1 060 573.0 $和1 062 313.9 $，OFFPEAK下发电成本最低，因此优先选择非高峰状态收费对发电厂收益最佳；c）虽然RDHBO的执行时间略高于其他算法，但差距并不大，观察执行时间最短的算法JADE，其求解精度较RDHBO差了约8 000 $，因此，RDHBO的执行时间在可接受范围内。

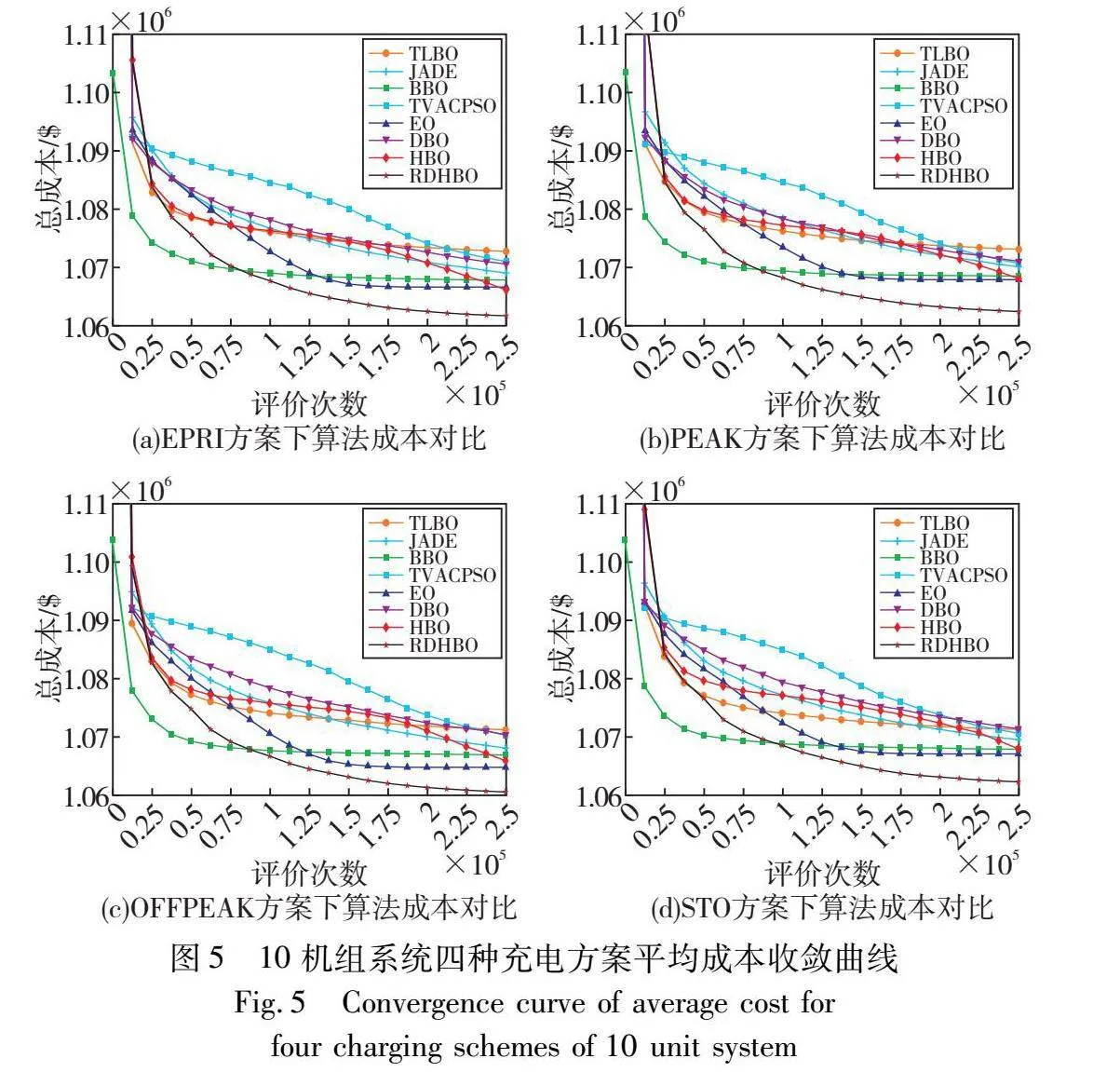
为了更直观地观察RDHBO的性能，算法的平均成本收敛曲线如图5所示。采用形状区分算法，本文算法用五角星表示，原HBO算法用菱形表示。

从图5可以发现，所有算法在250 000次函数评价后均表现出优异的性能，但RDHBO在大约8 000次函数评价后求得的成本就已经超过了所有的算法，可见RDHBO准确性更高。另外，RDHBO最小值达到1.07E5 $时，只花费了十万次评价次数，而其他的经典算法以及最新算法需要花费更多的评价次数才能达到此数值，可见RDHBO具备快速收敛的特性。此外，与HBO相比，RDHBO前期应用最优成员区域搜索，引导最优成员趋向更有希望的区域，可以更快地搜索到最优解，后期应用双种群策略增加多样性，防止成员陷入局部最优，避免浪费评价次数。可见资源利用方面RDHBO更胜一筹。

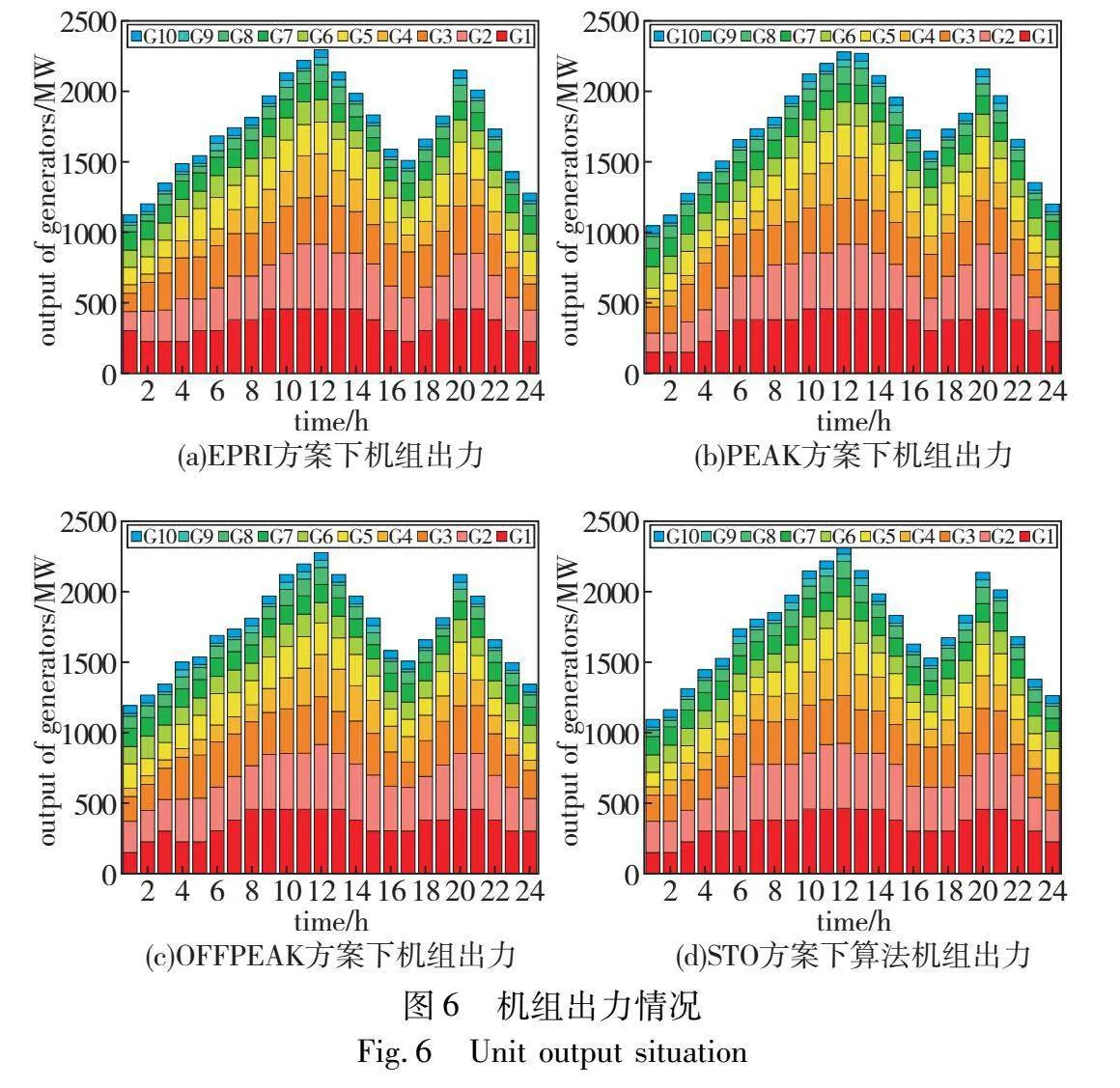
综上所述，RDHBO迭代效率好于其他算法。四种充电方案下机组出力情况如图6所示，颜色区分机组，每一列代表某一小时之内所有的十个机组的发电情况。

3.2 消融实验

为进一步验证最优成员区域搜索策略和双种群交互策略的有效性，本节将RDHBO与三种算法进行对比分析：a）HBO算法：原始堆优化算法；b）RHBO：HBO只采用最优成员区域搜索；c）DHBO：HBO只采用双种群交互策略。

将几种充电方案下不同算法的成本表示在图7中。形状区分算法，颜色区分表示充电场景。分析图7发现，两种策略对HBO的改进都是有效的，并且两个策略分别负责算法前期的全局搜索以及后期的局部搜索，两者互不冲突，将两个策略结合在一起可以相辅相成，发挥出更好的作用。

4 结束语

如今，电动汽车已经成为一种流行的交通工具。然而，随着充电需求的增加，电网的经济调度面临着巨大的挑战。模型考虑了实际情况下电动汽车充电的四种行为，并提出RDHBO算法来解决含电动汽车的EVDED问题。为了克服原HBO算法存在的一些缺陷，本文提出了一种最优成员区域搜索策略，用于更新最优成员，提高了RDHBO的收敛速度。此外，提出双种群交互策略，分析被淘汰的劣势成员，使其有可能在后面的迭代中被添加到种群中，提高了RDHBO的多样性，避免算法陷入局部最优。结果表明，RDHBO在求解精度方面明显优于其他算法。从消融实验可知，本文提出的两种策略对HBO的改进都是有效的。RDHBO可以作为解决含电动汽车的动态经济调度问题的优秀方法。但是算法的性能仍然可以进一步提升。例如，可以改进本文提出的策略，进一步提高HBO的收敛速度和准确性。

参考文献：

［1］陈海东，蒙飞，张越，等.基于生成对抗模仿学习的电力系统动态经济调度［J］.电网技术，2022，46（11）：4373-4380.（Chen Hai-dong，Meng Fei，Zhang Yue，et al.Dynamic economic dispatch of power system based on generative adversarial imitation learning［J］.Power System Technology，2022，46（11）：433-4380.）

［2］Chen Junjie，Li Yan，Peng Guoqiang，et al.Conditional value-at-credibility for random fuzzy wind power in demand response integrated multi-period economic emission dispatch［J］.Applied Energy，2020，261：114337.

［3］Pan Shanshan，Jian Jinbao，Yang Linfeng.A hybrid MILP and IPM approach for dynamic economic dispatch with valve-point effects［J］.International Journal of Electrical Power & Energy Systems，2018，97：290-298.

［4］Mclarty D，Panossian N，Jabbari F，et al.Dynamic economic dispatch using complementary quadratic programming［J］.Energy，2019，166：755-764.

［5］许德刚，王再庆，郭奕欣，等.鲸鱼优化算法研究综述［J］.计算机应用研究，2023，40（2）：328-336.（Xu Degang，Wang Zaiqing，Guo Yixin，et al.Review of whale optimization algorithm［J］.Application Research of Computers，2023，40（2）：328-336.）

［6］Hassan M H，Yousri D，Kamel S，et al.A modified marine predators algorithm for solving single-and multi-objective combined economic emission dispatch problems［J］.Computers & Industrial Enginee-ring，2022，164：107906.

［7］Hu Zhongbo，Dai Caiyun，Su Qinghua.Adaptive backtracking search optimization algorithm with a dual-learning strategy for dynamic economic dispatch with valve-point effects［J］.Energy，2022，248：123558.

［8］Dai Caiyun，Hu Zhongbo，Su Qinghua.An adaptive hybrid backtrac-king search optimization algorithm for dynamic economic dispatch with valve-point effects［J］.Energy，2022，239：122461.

［9］Yu Xianrui，Zhao Qiuhong，Wang Tongyu，et al.An antigravity-based fuzzy gravitational search algorithm for economic dispatch problems［J］.Applied Soft Computing，2023，145：110630.

［10］周筝，龙华，李帅，等.时空需求下的电动汽车充电设施选址优化模型［J］.计算机应用研究，2023，40（9）：2633-2638，2645.（Zhou Zheng，Long Hua，Li Shuai，et al.Optimization model for location of electric vehicle charging station under spatial-temporal demand［J］.Application Research of Computers，2023，40（9）：2633-2638，2645.）

［11］Al-Bahrani L T，Horan B，Seyedmahmoudian M，et al.Dynamic economic emission dispatch with load demand management for the load demand of electric vehicles during crest shaving and valley filling in smart cities environment［J］.Energy，2020，195：116946.

［12］Navin N.A multiagent fuzzy reinforcement learning approach for economic power dispatch considering multiple plug-in electric vehicle loads［J］.Arabian Journal for Science and Engineering，2021，46（3）：1431-1449.

［13］Ahmed I，Rehan M，Basit A，et al.A dynamic optimal scheduling strategy for multi-charging scenarios of plug-in-electric vehicles over a smart grid［J］.IEEE Access，2023，11：28992-29008.

［14］Zou Yuwei，Zhao Junfeng，Ding Diankuan，et al.Solving dynamic economic and emission dispatch in power system integrated electric vehicle and wind turbine using multi-objective virus colony search algorithm［J］.Sustainable Cities and Society，2021，67：102722.

［15］Askari Q，Saeed M，Younas I.Heap-based optimizer inspired by corporate rank hierarchy for global optimization［J］.Expert Systems with Applications，2020，161：113702.

［16］Shaheen A M，El-Sehiemy R A，Elattar E，et al.An amalgamated heap and jellyfish optimizer for economic dispatch in combined heat and power systems including N-1 unit outages［J］.Energy，2022，246：123351.

［17］Zhang Xinming，Wen Shaochen.Heap-based optimizer based on three new updating strategies［J］.Expert Systems with Applications，2022，209：118222.

［18］张贝，闵华松，张新明.强化信息交流的堆优化算法及其机器人路径规划［J］.计算机应用研究，2022，39（10）：2935-2942.（Zhang Bei，Min Huasong，Zhang Xinming.Information interchange streng-thened heap-based optimizer and its application to robot path planning［J］.Application Research of Computers，2022，39（10）：2935-2942.）

［19］Ma Haiping，Yang Zhile，You Pengcheng，et al.Multi-objective biogeo-graphy-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging［J］.Energy，2017，135：101-111.

［20］Jian Junrong，Chen Zonggan，Zhan Zhihui，et al.Region encoding helps evolutionary computation evolve faster：a new solution encoding scheme in particle swarm for large-scale optimization［J］.IEEE Trans on Evolutionary Computation，2021，25（4）：779-793.

［21］Zhang Xin，Zhan Zhihui，Zhang Jun.Adaptive population differential evolution with dual control strategy for large-scale global optimization problems［C］//Proc of IEEE Congress on Evolutionary Computation.Piscataway，NJ：IEEE Press，2020：1-7.

［22］刘三阳，靳安钊.求解约束优化问题的协同进化教与学优化算法［J］.自动化学报，2018，44（9）：1690-1697.（Liu Sanyang，Jin Anzhao.A co-evolutionary teaching-learning-based optimization algorithm for constrained optimization problems［J］.Acta Automatica Sinica，2018，44（9）：1690-1697.）

［23］Faramarzi A，Heidarinejad M，Stephens B，et al.Equilibrium optimizer：a novel optimization algorithm［J］.Knowledge-Based Systems，2020，191：105190.

［24］Xue Jiankai，Shen Bo.Dung beetle optimizer：a new meta-heuristic algorithm for global optimization［J］.The Journal of Supercompu-ting，2023，79（7）：7305-7336.

［25］Ratnaweera A，Halgamuge S K，Watson H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients［J］.IEEE Trans on Evolutionary Computation，2004，8（3）：240-255.

［26］梁远升，陈礼昕，李海锋，等.基于二次变异改进生物地理学优化算法的限流器配置方法［J］.电力系统自动化，2020，44（1）：183-191.（Liang Yuansheng，Chen Lixin，Li Haifeng，et al.Configuration method for fault current limiter based on improved biogeography-based optimization algorithm with second mutation［J］.Automation of Electric Power Systems，2020，44（1）：183-191.）

［27］Zhang Jianqiao，Sanderson A C.JADE：adaptive differential evolution with optional external archive［J］.IEEE Trans on Evolutionary Computation，2009，13（5）：945-958.