基于分区个体排名的非线性种群缩减的人工蜂群算法

摘 要：针对人工蜂群算法（ABC）探索性强而开发性弱，从而导致收敛速度慢的问题，提出了一种基于分区个体排名的非线性种群缩减策略（UPSR-CIR）。首先，该策略设计长尾非线性种群规模缩减函数，在前期保持大种群充分探索，中期快速缩减使得后期保持小种群加强开发，同时为后期分配相对较多计算资源以加速收敛；其次，为确保种群多样性，采用K-means聚类通过间隔一定代数对种群进行动态分区，并以分区为单位进行种群缩减；同时，种群按分区缩减时，按照分区内最优个体在整个种群排名确定删除个体数量，为排名高的潜能分区保留相对较多的计算资源来进一步加强开发。采用22个基准测试函数在ABC及其变体上对UPSR-CIR进行实验对比分析，结果表明UPSR-CIR表现出更高的求解精度、稳定性和收敛速度，同时对于ABC变体具有普适性。最后采用12个经典旅行商问题（TSP）案例进一步验证UPSR-CIR在实际应用问题上的实用性和优越性。

关键词：非线性种群缩减；人工蜂群算法；聚类；排名；旅行商问题

中图分类号：TP18 文献标志码：A 文章编号：1001-3695（2024）10-020-3021-11

doi：10.19734/j.issn.1001-3695.2024.02.0045

Artificial bee colony algorithm with unlinear population size reduction based on cluster individual rank

Zhao Ming，Liu Shanzhi，Song Xiaoyu，Shen Xiaopeng

（School of Computer Science & Engineering，Shenyang Jianzhu University，Shenyang 110168，China）

Abstract：Aiming at the problem that ABC has strong exploration but weak exploitation，which leads to slow convergence speed，this paper proposed an unlinear population size reduction strategy based on cluster individual rank（UPSR-CIR）.Firstly，the strategy designed the long-tail unlinear population size reduction function which maintained a large population to explore fully in the early stage，and reduced the population size rapidly in the middle stage，so as to maintain a small population to strengthen exploitation in the late stage，while allocating relatively more computing resources for the late stage to accelerate convergence.Secondly，to ensure the diversity of the population，it used K-means clustering dynamically to divide the population into clusters every a certain number of generations，and carried out the population size reduction in the unit of cluster.At the same time，when the population size reducing in the unit of cluster，it determined the number of individuals deleted according to the rank of the best individual in the cluster，so as to reserve relatively more computing resources for the potential cluster with higher rank to further strengthen exploitation.This paper used 22 benchmark test functions to compare and analyze the UPSR-CIR on ABC and its variants.The results show that the UPSR-CIR exhibits higher solution accuracy，stability and convergence speed.It is also universally applicable to ABC variants.Finally，this paper also used 12 classical TSP cases to validate the practicality and superiority of the UPSR-CIR strategy on real application problem.

Key words：unlinear population size reduction;artificial bee colony algorithm;clustering;rank;traveling salesman problem

0 引言

人工蜂群算法（ABC）是Karaboga等人［1］提出的一种建立在蜜蜂自组织型和群体智能基础上的优化算法。由于其参数简单、易于求解和性能优异等特点［2］，在解决诸多实际优化问题中被成功应用，如路径规划、负荷调度、系统设计以及工程优化等［3～7］。但是，基本ABC算法也存在不足之处，由于其擅长探索而不擅长开发，往往收敛速度较慢［8］。为了更好地平衡探索和开发，加快它的收敛速度，相关学者对其在初始化策略、种群划分及调节、搜索策略及参数自适应、多策略协同、邻域结构、多维改进以及概率选择等方面进行了大量的改进研究。

文献［9］提出了一种新的初始解生成策略，该策略保存了过去每次实验产生的初始解，并且在每次重新产生初始解时以一定的概率重新使用它们，该策略有效减少了产生初始解所用的函数评估次数。文献［10］在雇佣蜂阶段将整个种群划分为两个不同的子种群，并对不同的子种群采用不同的搜索策略。文献［11］提出了一种调节雇佣蜂和跟随蜂数量的机制，进一步在雇佣蜂阶段和跟随蜂阶段分别采用了两个参数自适应的微分搜索方程。文献［12］考虑了局部最优解、邻域最优解和迭代最优解的优势，提出了一种在雇佣蜂阶段和跟随蜂阶段的临时解搜索策略。文献［7］提出了一种基于邻域搜索的多策略协作，将当前种群和邻域中的最优个体信息分别应用于雇佣蜂和跟随蜂的搜索，在此基础上进一步引入修正率对解的各个维度进行随机扰动。文献［13］引入最大熵上位计算连续函数的维交互，以指导雇佣蜂和跟随蜂搜索方程的适应选择。文献［14］引入了一种维度内存机制实现多维更新。文献［15］在跟随蜂阶段采用一种定制的双型精英引导开发机制，通过一种新的轮盘赌选择概率计算范式来调节有希望的精英蜜源的开发强度。文献［6］使用贝叶斯估计的概率计算方式代替原来的选择概率计算方式。从以上相关研究可以看出，对于影响ABC性能的组成要素上，相关学者都已经进行了大量改进研究，但对于种群规模这一算法核心参数的调节尚未见到系统研究。而近年来，其他群体智能优化算法尤其是差分进化算法（differential evolution algorithm，DE）的研究学者发现，算法初期需要大规模种群覆盖整个搜索空间，后期需要缩小种群规模来节约计算资源，加强后期开发能力［16］。与此同时为了避免陷入局部最优，需要在搜索过程中保持种群多样性［16］。因而关于种群的规模和调节方面，有了一些研究成果。为了提高收敛速度和优化效果，文献［17］针对SHADE算法提出了线性种群规模缩减的L-SHADE算法，每代种群个体按照适应度由大到小排序，以线性规律缩减排序靠后的适应度小的个体，实验结果表明L-SHADE明显优于SHADE。为了提升Self-adaptive DE算法的优化效果，文献［18］提出了种群折半缩减的dynNP-DE，当算法迭代到一定次数时，把相对优秀的个体放入前一半，把后一半的个体删除，实验结果发现该算法在高维问题上表现得非常好。为了保护pr-DE算法的种群多样性，文献［19］将K-means聚类法应用于pr-DE算法进而提出了Dapr-DE算法，在种群中随机选择一些核心向量，其余个体距离哪个核心向量近就将该个体划分给那个核心向量从而形成聚类，然后根据聚类情况计算熵值来调整每个聚类的大小，实验表明K-means有助于在种群缩减过程中防止种群多样性的大量丢失。

本文在以上相关研究的基础上，根据ABC善于探索而不善于开发的特点对其进行种群规模缩减策略的深入研究。首先，根据大种群有利于探索而小种群有利于开发的理论，受sigmoid函数启发，提出了长尾非线性种群规模缩减函数，前期利用大种群确保全面探索解空间，中期快速进行种群缩减以便后期充分利用小种群进行开发以加速收敛，同时为了充分弥补ABC开发不足这一缺点，利用长尾效应为后期小种群分配更多计算资源;其次，由于种群规模缩减会导致多样性损失从而求解容易陷入局部最优，利用K-means聚类算法对种群进行分区，在种群规模缩减时以分区为单位进行个体移除，相对于以整个种群为单位该方法能够通过确保分区对解空间的覆盖来保护多样性;最后，在确定分区移除个体数量时应考虑为更具潜能的分区保留更多开发可能，为最优个体在种群中排名较高的分区保留相对于其他分区较多的个体以实现保留相对较多的计算资源分配。

1 基本ABC

ABC模拟蜂群的智能觅食行为，包括雇佣蜂、跟随蜂和侦查蜂［20］三种蜜蜂。雇佣蜂主要承担蜂群的觅食工作，它们会在原食物源的附近寻找更好的食物源，并通过摆尾舞与跟随蜂分享食物源的质量等信息；每只跟随蜂则会通过雇佣蜂所提供的信息，选择一个特定的食物源进行进一步开发；当某个食物源连续若干代没有得到改进时，该食物源对应的雇佣蜂就会变为侦查蜂，并随机寻找新的食物源。基本ABC包括初始化阶段、雇佣蜂阶段、跟随蜂阶段和侦查蜂阶段四个阶段。在初始化阶段，创建包括SN个解的初始种群P，对应食物源的初始位置，其中SN表示食物源的数量。在搜索空间上，每个初始解x0i=（x0i，1，x0i，2，…，x0i，D）均采用式（1）随机产生。

x0i，j=xL，j+rand（0，1）×（xU，j-xL，j）（1）

其中：i=1，2，…，SN，j=1，2，…，D，D表示搜索空间的维数；xL，j和xU，j分别是第j维的下界和上界;rand（0，1）表示［0，1］的随机实数。食物源的质量对应优化问题解的适应度，适应度越大，对应解的质量就越好。食物源的适应度值采用式（2）进行计算。

fiti=11+fiif fi≥01+|fi|otherwise（2）

其中：fiti和fi是食物源xi的适应度值和目标函数值。

初始化阶段之后，ABC变成了雇佣蜂阶段、跟随蜂阶段和侦查蜂阶段的循环，直到满足终止条件为止。在雇佣蜂阶段，食物源与雇佣蜂为一一对应的关系，即一个食物源对应一个雇佣蜂。每只雇佣蜂都保留了它之前搜索过程中的最优解，并且在保留的最优解的邻域搜索候选解。如果搜索到的新解适应度值不低于原来保留的解，原来的解就会被新的解所取代；否则，原来的解就会被保留下来。对食物源xi产生候选食物源vi时，雇佣蜂使用的搜索方程为

vGi，j=xGi，j+i，j×（xGi，j-xGk，j）（3）

其中：G表示代数；k从{1，2，…，SN}当中随机选择并且k≠i，j从{1，2，…，D}当中随机选择；i，j是［-1，1］的随机实数。当雇佣蜂完成搜索过程，就会与跟随蜂分享食物源的质量信息和位置。在跟随蜂阶段，每只跟随蜂会根据食物源对应的选择概率以轮盘赌的方式随机选择一个食物源，共有SN只跟随蜂，食物源选择概率的计算方法如式（4）所示。

pi=fiti∑SNj=1fitj（4）

其中：pi为食物源xi的选择概率，显然食物源的适应度值越大，选择概率就越大。在跟随蜂选择一个食物源后，采用式（3）产生一个候选食物源，并采用与雇佣蜂一样的方式进行贪婪选择。当所有跟随蜂完成搜索过程时，如果一个食物源的质量没有在预定的循环次数（limit）内得到改善，该食物源对应的雇佣蜂就会变成侦查蜂并采用式（1）随机寻找新的食物源取代原来的食物源。最后，当算法循环达到最大函数评估次数（MAX_NFE）时，算法终止循环并输出搜索到的最优解信息。

2 基于分区个体排名的非线性种群缩减

2.1 动机

由于大种群有利于探索小种群且有利于开发［16］，受到sigmoid非线性函数的启发，设计ABC的非线性种群规模缩减函数，在前期保持大种群以实现对解空间全局进行充分探索，中期种群规模快速非线性缩减，后期保持小种群以便更加充分利用计算资源加强开发。同时，考虑到ABC开发能力差导致收敛速度慢这一弱点，适当为后期的小种群搜索分配更多的计算资源，进而形成了长尾非线性种群规模缩减函数，从而更好地平衡ABC的探索与开发能力。

在缩减的过程中如何尽可能维持多样性以避免陷入局部最优，这是种群缩减应考虑并必须解决的核心问题，也是算法能否找到全局最优的一个核心影响因素。在确定了整个种群的规模缩减策略后，利用K-means聚类通过间隔一定代数对种群进行动态分区，同时以分区为单位进行种群缩减，通过确保分区覆盖更好地保护种群多样性以确保全局探索性。在种群按分区缩减时，还应考虑各分区进化潜能的区别，对更有希望的区域应保留相对较多的个体，因而对分区按照其范围内最优个体在整个种群的排名确定删除个体数量，从而为更有潜质的分区保留相对较多的计算资源以便加大对其的开发。

2.2 非线性种群缩减策略（UPSR）

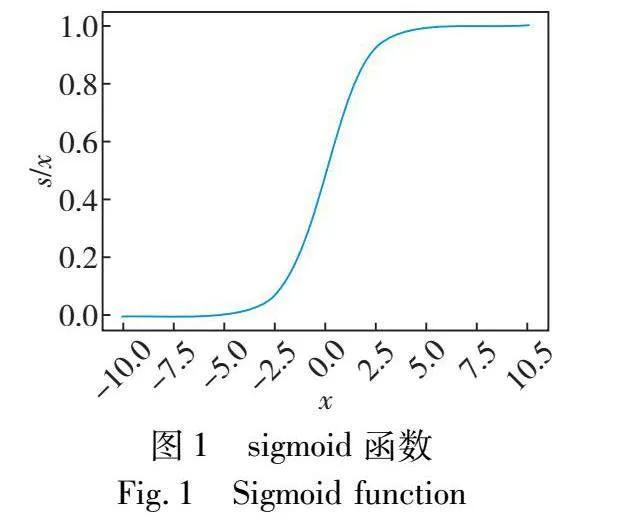
原始sigmoid函数图像为非线性单调递增，如式（5）所示，原图像如图1所示。

S（x）=11+e-x（5）

显然，sigmoid函数无法直接应用于ABC的非线性单调递减的种群缩减，因此将函数进行一系列对称、平移以及缩放，最终变形如式（6）所示。

SNG=SNmin+（SNmax-SNmin）×（11+e20×NFEGMAXNFE-10）（6）

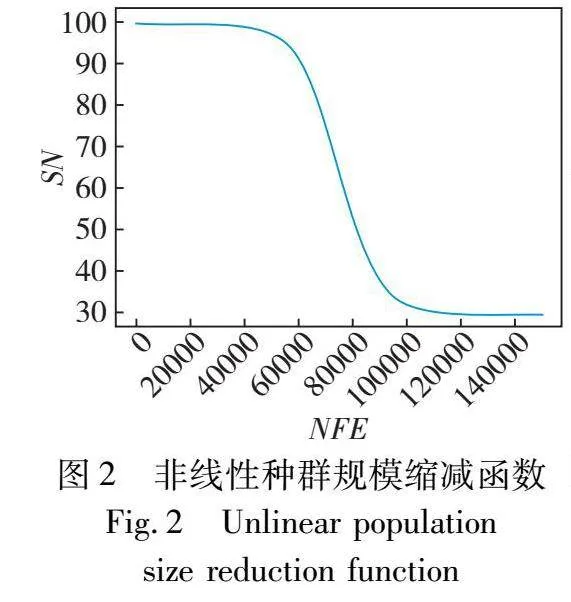
其中：SNG代表G代雇佣蜂和跟随蜂的种群规模;SNmin和SNmax分别代表种群规模的下限和上限;NFEG表示G代前已耗用函数评估次数。种群规模随着搜索过程变化的图像如图2所示（以SNmin=30，SNmax=100，MAX_NFE=150000为例）。根据图2不难发现，算法前期、中期和后期使用的计算资源大体相同，前期保持大种群充分探索，中期快速进行缩减，后期保持小种群加强开发从而加速收敛。考虑到ABC本身探索性强而开发性弱，进一步对三个阶段的计算资源分配进行调整，适当缩短前期并扩大后期，以便让算法更加侧重于后期开发来加快收敛，因而将缩减函数由式（6）调整为式（7），种群规模随着搜索过程变化的图像如图3所示。

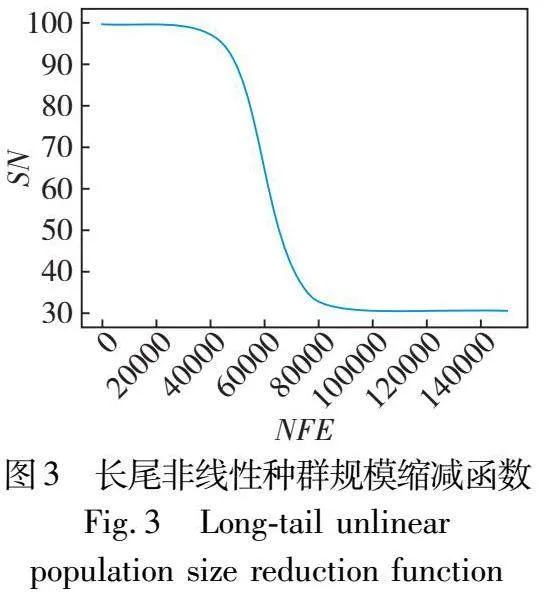
SNG=SNmin+（SNmax-SNmin）×11+e25×NFEGMAX_NFE-10（7）

对式（7）进行深入分析，SN初始为SNmax（此时NFE为0），在NFEG/MAX_NFE为1/4时，SN为0.98SNmax+0.02SNmin（由SNmin+0.98（SNmax-SNmin）计算得），与SNmax差距微小，也就是在搜索前期种群规模基本维持在最大规模；随着搜索继续，NFEG/MAX_NFE持续增长，种群规模开始快速下降，在NFEG/MAX_NFE为1/2时，SN为0.08SNmax+0.92SNmin（由SNmin+0.08（SNmax-SNmin）计算得），非常接近于SNmin，实现了搜索的中期种群规模的快速缩减；而后直至搜索结束，种群规模维持在SNmin，表明搜索阶段的后期种群规模最小。可见，这三个阶段NFE即计算资源的分配比例为1∶1∶2（由1/4∶（1/2-1/4）∶（1-1/2）计算得），也就是为后期分配计算资源达到整体的一半，对种群规模的调节控制实现了长尾效应。

2.3 基于分区个体排名的移除（CIR）

通过聚类可以将当前种群中相似的个体聚集成分区，不同的分区可以代表解空间的不同区域。在种群缩减时从不同的区域删除个体，相对于从整个种群中进行个体删除，能够更好地保留种群对解空间的覆盖。因此，每间隔c代采用K-means基于欧氏距离对种群进行聚类，动态反映种群分区情况。在确定种群缩减数量后，基于每个分区最优个体在整个种群中的排名确定各分区删除个体数量，使得最优个体排名靠前的分区相对保留较多个体，以保留较多计算资源从而保证对潜能区域的开发。

基于欧氏距离的K-means算法具体步骤如下：

a）随机选取K个互不相同的个体作为聚类中心;

b）计算所有个体到这K个个体的欧氏距离;

c）找到每个个体距离最近的聚类中心，并将该个体划分给距离最近的聚类中心形成类簇。

每代通过式（7）确定本代种群规模后，采用式（8）确定本代每个分区的个体缩减数量。

deleteSNGk=（SNG-1-SNG）×rank（bestGk）/∑Kk=1rank（bestGk）（8）

其中：deleteSNGk表示第k个分区的个体缩减数量（k=1，…，K）；SNG-1-SNG表示G代种群缩减数量；rank（bestGk）表示G代种群中第k个分区的最优个体在整个种群当中按照适应度从大到小的排名。从式（8）可以看出，某个分区的最优个体在整个种群中的排名越高，表示该分区存在全局最优的可能性就越大，就越需要对其加强开发，因而为其缩减较少的个体以保留相对较多的计算资源。在确定每个分区的个体缩减数量后，以轮盘赌选择的方式选择分区个体进行删除，既有利于保护种群多样性，同时倾向于删除没有潜力的个体。

2.4 时间复杂度分析

将融入UPSR和CIR的ABC与基本ABC在各搜索阶段对比进行时间复杂度分析。

a）初始化阶段。对种群的初始化，ABC-UPSR+CIR与ABC相同，时间复杂度为O（SN×D）；对食物源的适应度值的计算，ABC-UPSR+CIR与基本ABC相同，时间复杂度为O（SN×D）；ABC-UPSR+CIR初始种群进行K-means聚类，时间复杂度为O（SN×K）。

b）人工蜂搜索阶段。ABC-UPSR+CIR在每间隔c代对种群进行K-means聚类，时间复杂度为O（SN×K）；ABC-UPSR+CIR算法在每代计算本代种群规模，时间复杂度为O（1）；ABC-UPSR+CIR算法计算每个聚类最优个体在整个种群中的排名，时间复杂度为O（SN+SN×K），即O（SN×K）；ABC-UPSR+CIR计算每个聚类缩减个体数量，时间复杂度为O（K）；ABC-UPSR+CIR对每个聚类按照适应度轮盘赌删除个体，时间复杂度为O（SN）。此后的雇佣蜂搜索和跟随蜂搜索，ABC-UPSR+CIR与ABC相同，时间复杂度分别为O（SN）。

c）侦查蜂搜索阶段。ABC-UPSR+CIR与ABC相同，时间复杂度为O（SN）。

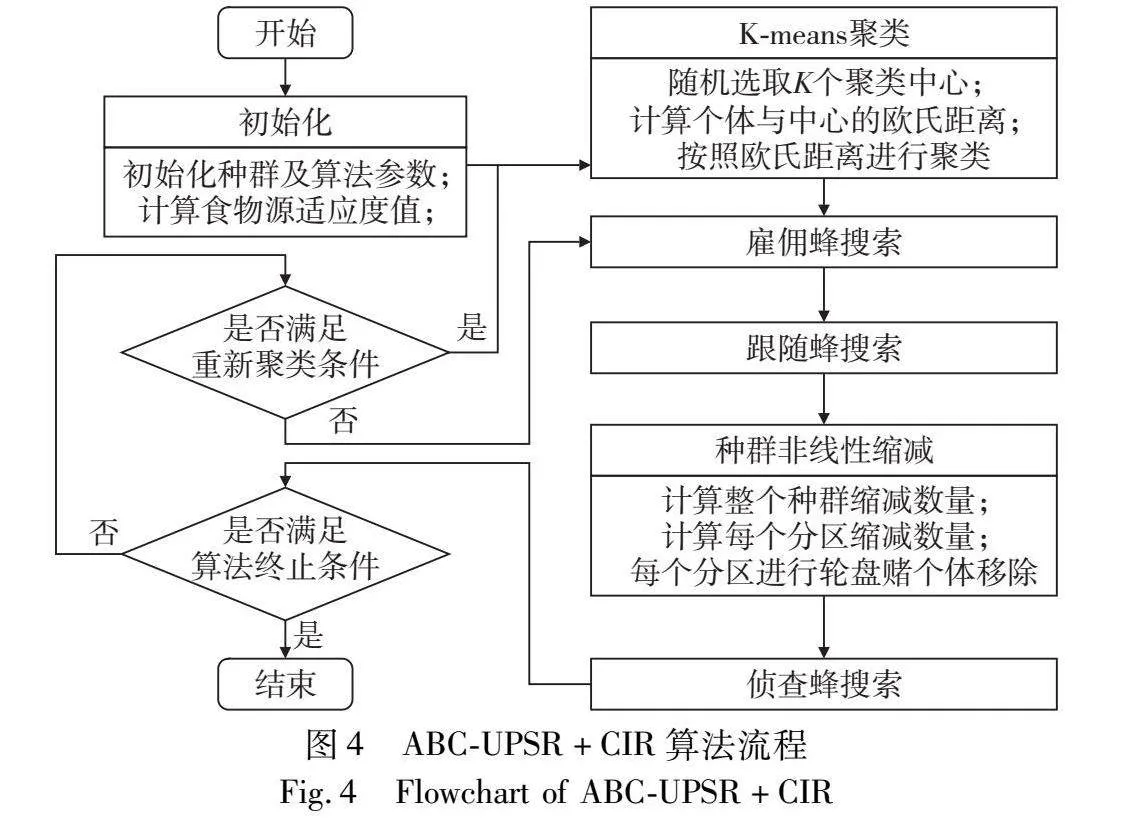
通过以上分析可以看出，ABC-UPSR+CIR与ABC相比较，整个算法在各阶段额外增加的时间复杂度量级分别为O（SN×K）、O（1）、O（K）和O（SN），由于K的建议取值为D/10，所以ABC-UPSR+CIR的时间复杂度最大量级仍为O（SN×D），与ABC相同。整个ABC-UPSR+CIR的流程如图4所示。

3 实验设计

本文主要进行六个实验：实验1验证非线性种群缩减策略（UPSR）以及基于分区个体排名的个体移除策略（CIR）对于ABC的有效性，将其与线性种群缩减策略（LPSR）和折半种群缩减策略（dynNP）进行对比分析，并分别采用多次运行求解结果的均值和标准差评价求解精度和稳定性，进一步绘制收敛图评价收敛性；实验2验证两者对其他ABC变种算法的普适性，将它们分别融入两个近年来性能良好的ABC变体ARABC［21］、DFSABC_elite［22］和DAABC［23］，分别采用多次运行求解结果均值和标准差对比分析原算法与新算法的求解精度和稳定性；实验3验证参数K-means聚类数量K对ABC性能的影响，分别对其设置不同的初值后，采用多次运行求解结果均值和标准差来分析它对算法求解精度和稳定性的影响，并给出建议设置；实验4分析融入UPSR和CIR两个策略后的ABC在种群多样性方面的特性，基于种群熵［19］指标对求解各阶段种群的多样性进行计算，并将其与基本ABC对比；实验5分析融入UPSR和CIR的ABC在不同阶段的寻优能力，输出前期大种群探索阶段、中期种群快速缩减阶段及后期小规模开发阶段算法多次运行的求解结果均值与标准差，并将其与基本ABC对比分析性能变化；实验6采用应用问题对UPSR和CIR进行进一步有效性验证，对比分析ABC和融入两个策略的改进ABC在求解经典TSP时的求解精度和稳定性，分别采用多次运行求解得到的平均NqaKQQQS6AY0b8cnz/CzbQ==路径长度、最优路径长度、最差路径长度和偏差率作为评价标准，并进一步绘制对应点坐标路径图进行直观对比。

实验1～5使用的测试集为DFSABC_elite所提出的测试集［22］，共包含了22个测试函数，基准函数如表1所示。其中，f1-f6和f8为连续单峰函数，f7是非连续阶跃函数，f9为噪声函数。f10为Rosenbrock函数（维数D≤3时为单峰函数，维数D>3时为多峰函数），f11～f22为多峰函数，并且它们的局部最优点随着问题规模的增加呈指数增加。实验3使用的测试集为不同规模的经典TSP实例，共包含12个，城市数最少为14，最多为150，分别为burma14、bayg29、oliver30、att48、eil51、eil76、pr76、st70、gr96、eil101、ch130和ch150。实验平台采用英特尔酷睿i5-7300HQ CPU，基准速度为2.50 GHz，使用Windows 10操作系统，编程语言为C++，编译器为CodeBlocks GNU GCC。

3.1 有效性检验

3.1.1 均值和标准差

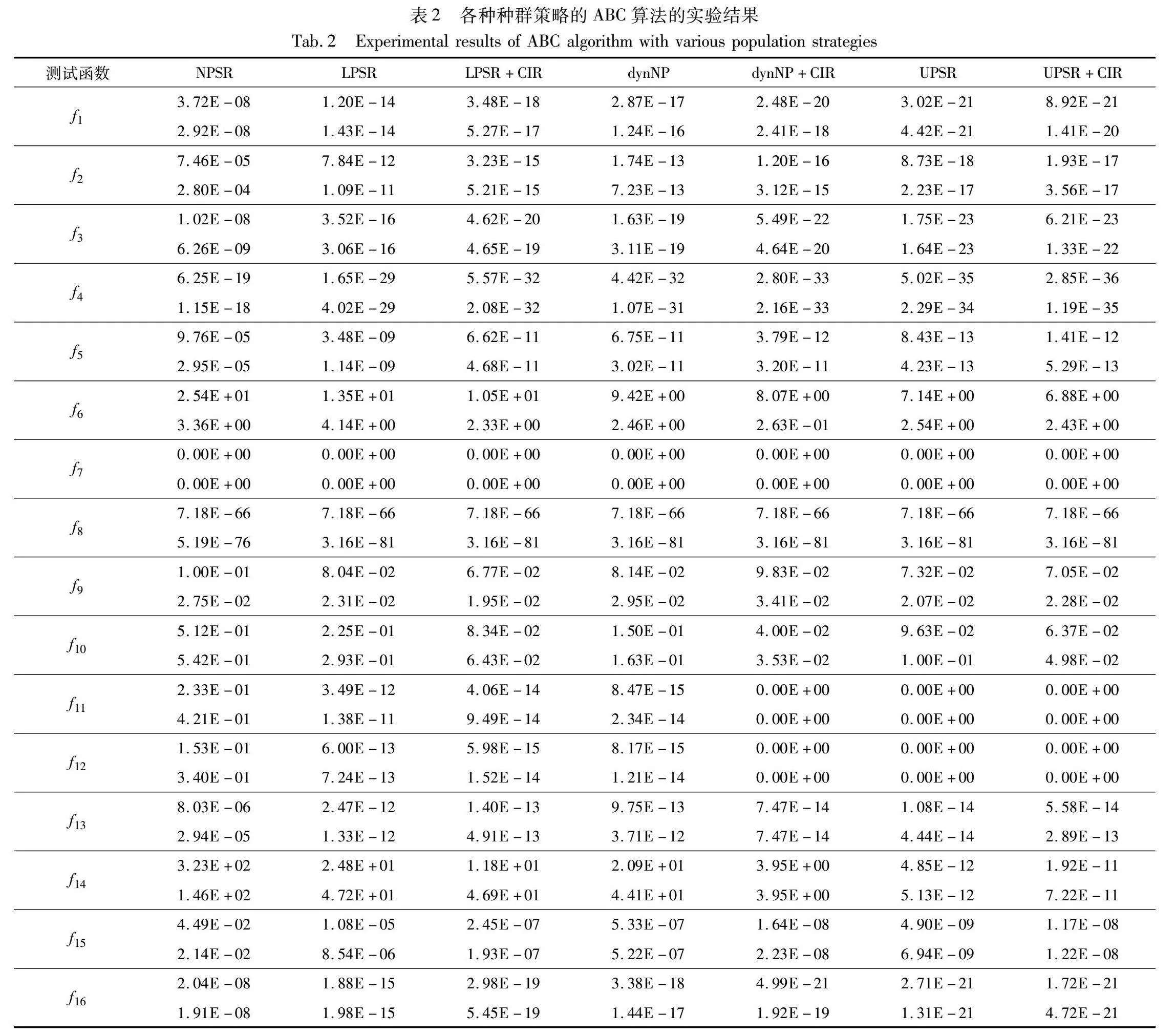
本实验使用了均值和标准差两个评价指标，均值越小，说明算法的求解精度越高；标准差越小，说明算法的稳定性越好。实验参数设置如下：D=30，MAX_NFE=5000×D，SNmax=3×D，SNmin=D，limit=200，K=D/10，聚类间隔代数c=100，运行次数runtime=30。实验结果如表2所示，表中从左至右依次为无种群缩减的ABC（NPSR）、种群规模线性缩减的ABC（LPSR）、基于分区个体排名进行移除的种群规模线性缩减的ABC（LPSR+CIR）、种群规模折半缩减的ABC（dynNP）、基于分区个体排名进行移除的种群规模折半缩减的ABC（dynNP+CIR）、种群规模非线性缩减的ABC（UPSR）、基于分区个体排名进行移除的种群规模非线性缩减的ABC（UPSR+CIR）。

由表2可以看出，NPSR、LPSR、LPSR+CIR、dynNP、dynNP+CIR、UPSR和UPSR+CIR分别在1、2、3、2、6、13和10个函数上取得了最优。并且由表2可以看出，UPSR与UPSR+CIR在其他不是表现最佳的函数上与最佳结果相比数量级相同或仅仅相差一个数量级，说明性能差异不大。从以上结果及分析可以看出，相对于无种群缩减的ABC，分别加入线性缩减策略、折半缩减策略和非线性缩减策略后，在22个函数上的求解均值及标准差全部减小，说明这三种种群缩减策略都能够显著提高ABC的求解精度和稳定性。为了进一步精确对比各种缩减策略以及它们融入CIR后的性能差异，依据表2中的数据进行两两相关的Wilcoxon秩和检验，结果如表3所示。

从表3可以看出，对于线性缩减策略和折半缩减策略，非线性缩减策略的求解性能显著优越（p_value远小于0.05）。加入CIR策略后，线性缩减策略和折半缩减策略的求解性能进一步显著提升（p_value远小于0.05）。与加入CIR策略的线性缩减和折半缩减对比，加入CIR的非线性缩减策略的性能具有显著优越性（p_value远小于0.05）。

3.1.2 收敛图

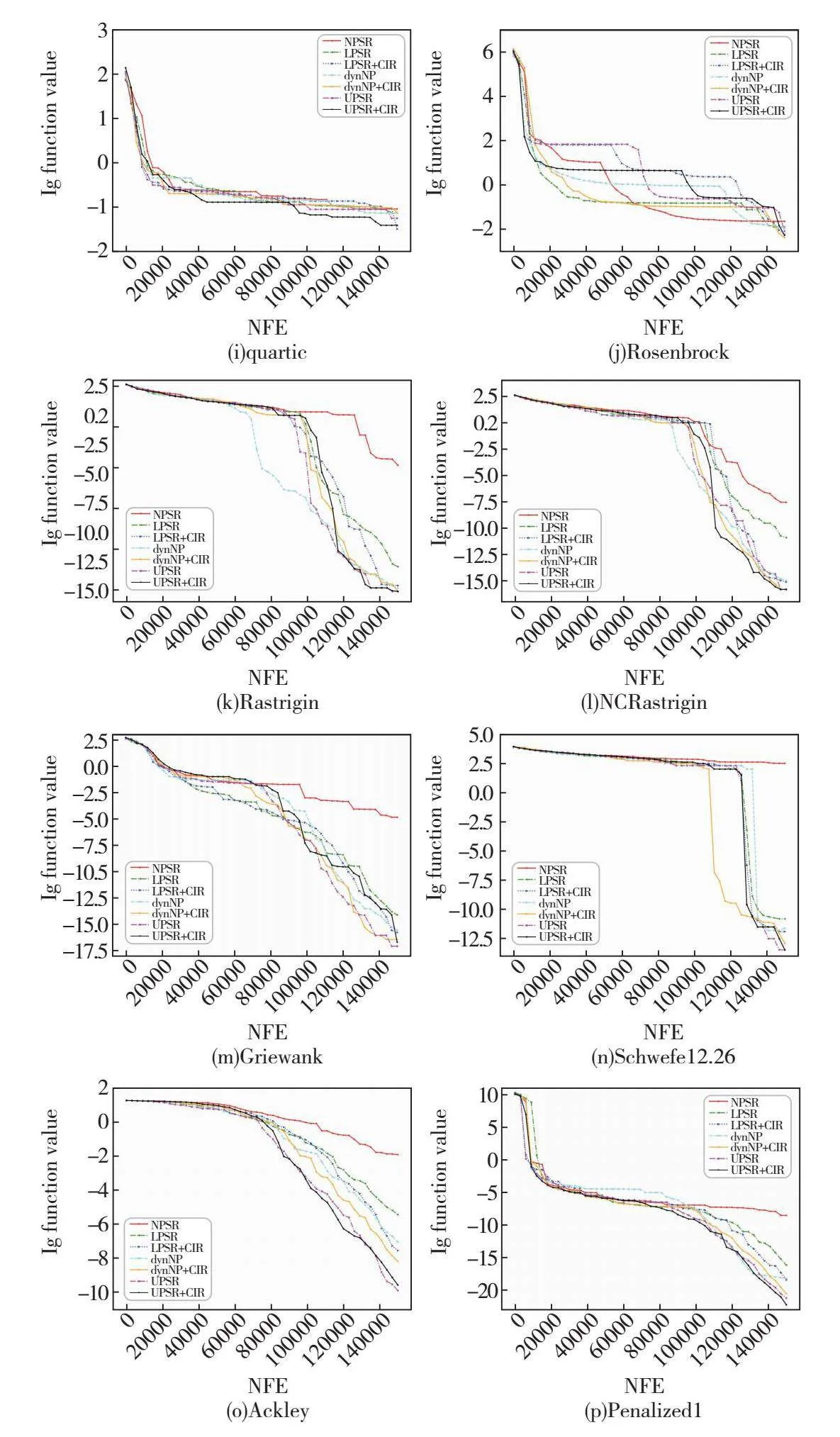
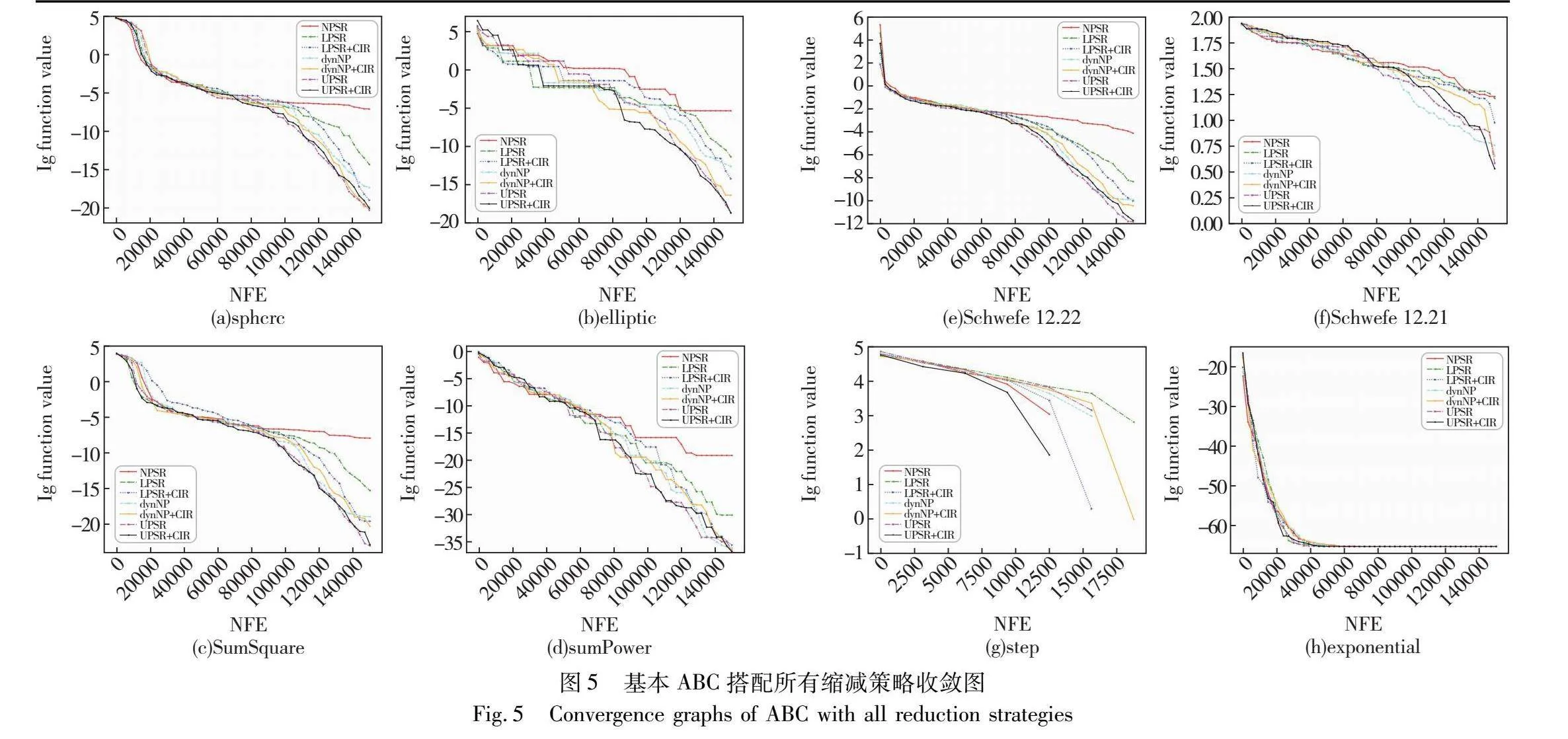
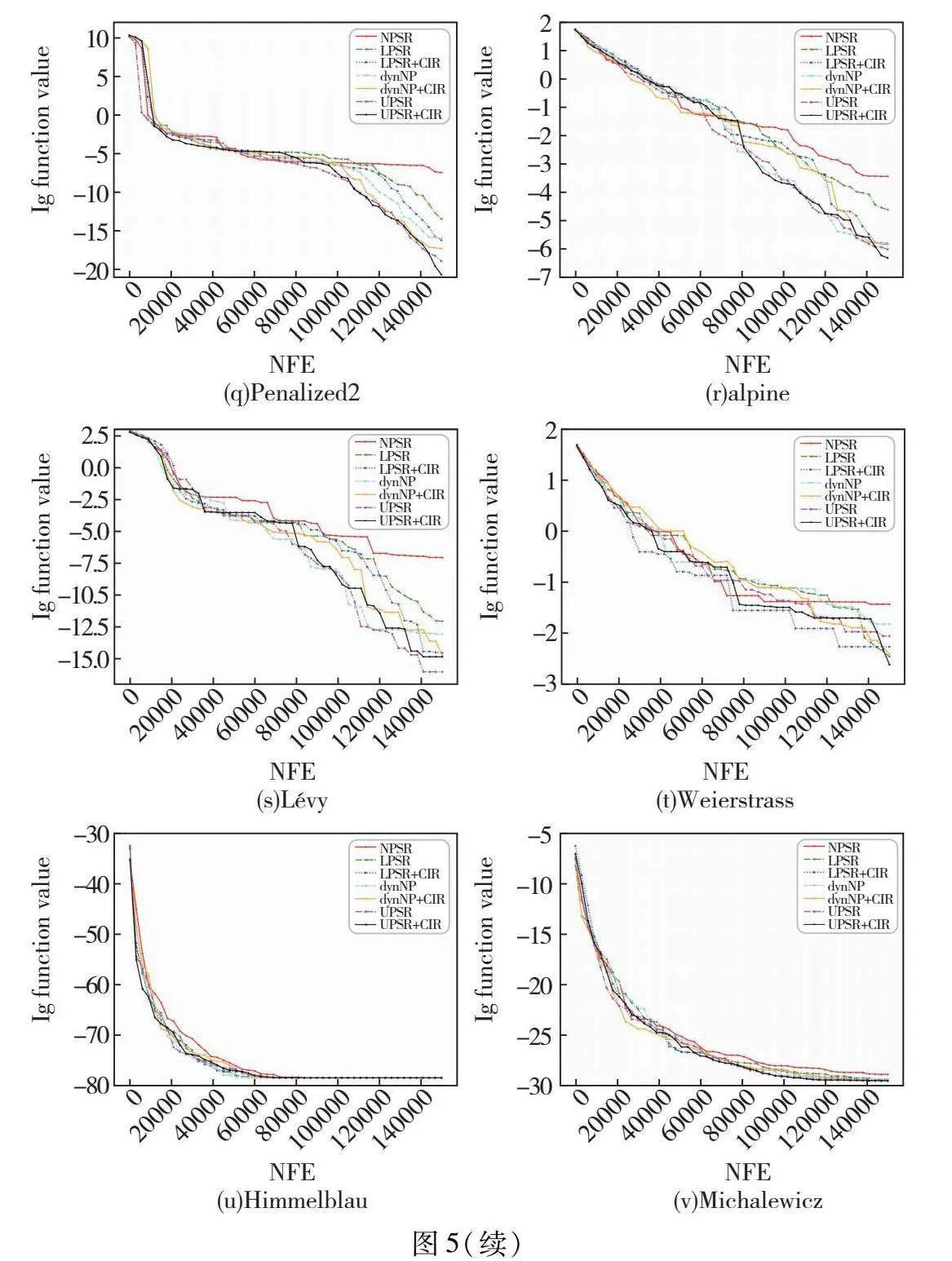
绘制ABC融入各种种群策略后在每个函数上的收敛图，如图5所示，其中横轴为函数评估次数，纵轴为目标函数值的对数。从图5可以看出，UPSR与UPSR+CIR策略在绝大多数测试函数上的收敛速度均快于其他种群缩减策略。并且值得注意的是，在收敛速度上尤其是在算法后期收敛速度上，UPSR与UPSR+CIR策略都表现得十分优秀，明显优于其他现有种群缩减策略。这也再次说明了非线性种群缩减策略与基于分区个体排名的非线性种群缩减策略可以更好地平衡ABC的探索与开发能力，同时证明了它们在搜索后期对种群多样性有更好的保护作用。

3.2 适应性检验

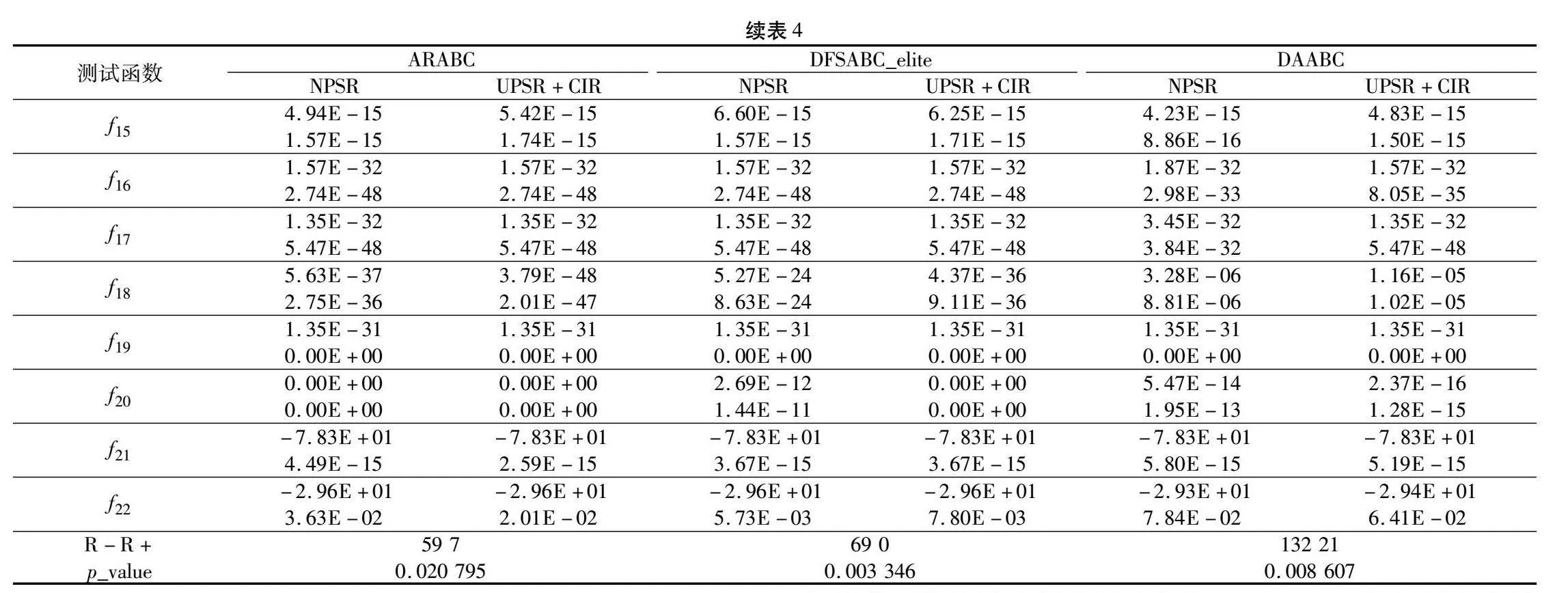
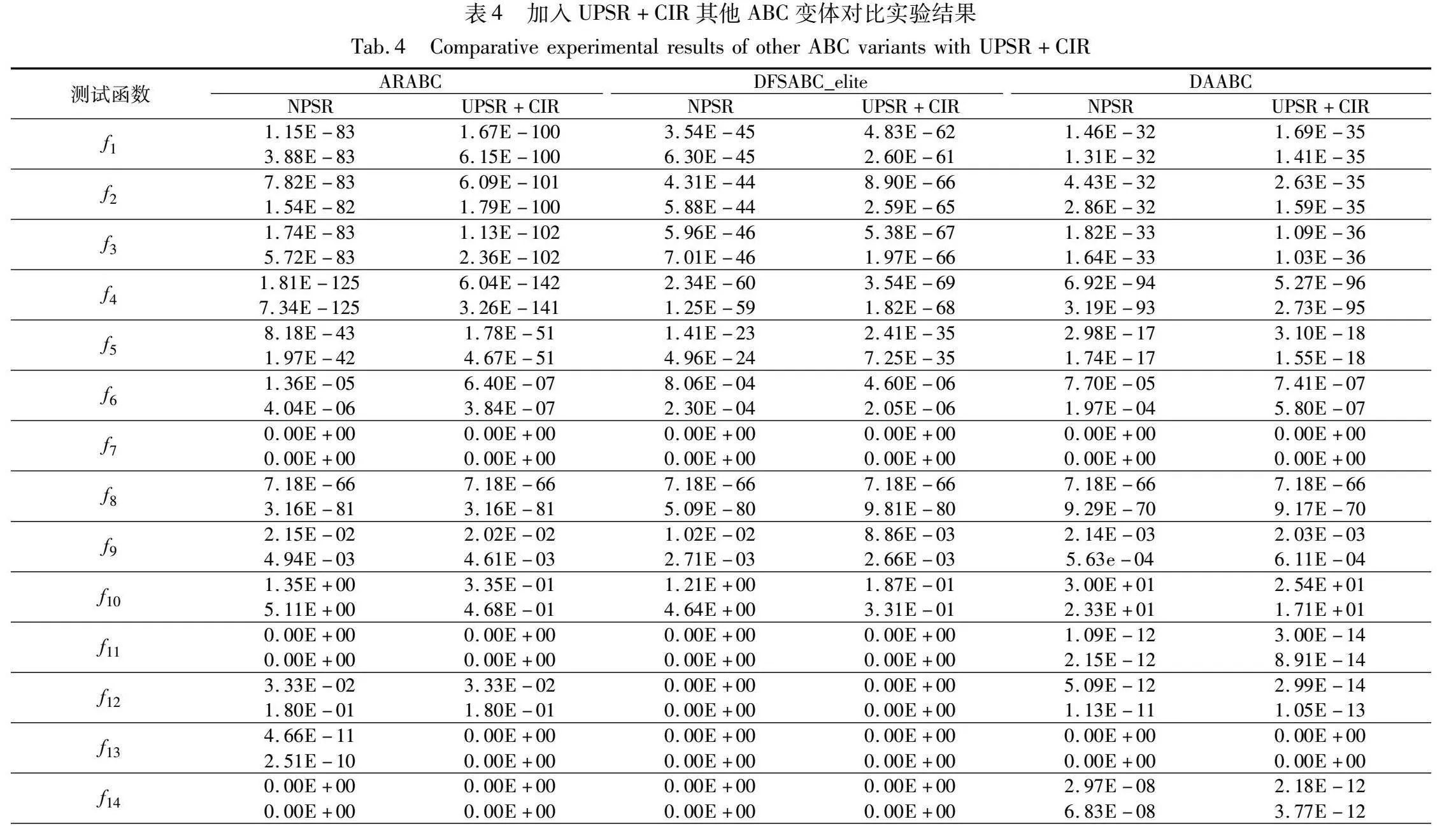
实验公共参数设置与2.6节相同，ARABC、DFSABC_elite和DAABC三个算法的其他参数设置源于其提出文献，实验结果如表4所示，表4最后一行为Wilcoxon秩和检验结果。从表4可以看出，融入UPSR和CIR的ARABC、DFSABC_elite和DAABC与原算法对比，性能显著提升（p_value远小于0.05），说明本文提出的两个策略对于其他ABC变体具有普适性。

3.3 参数敏感性分析

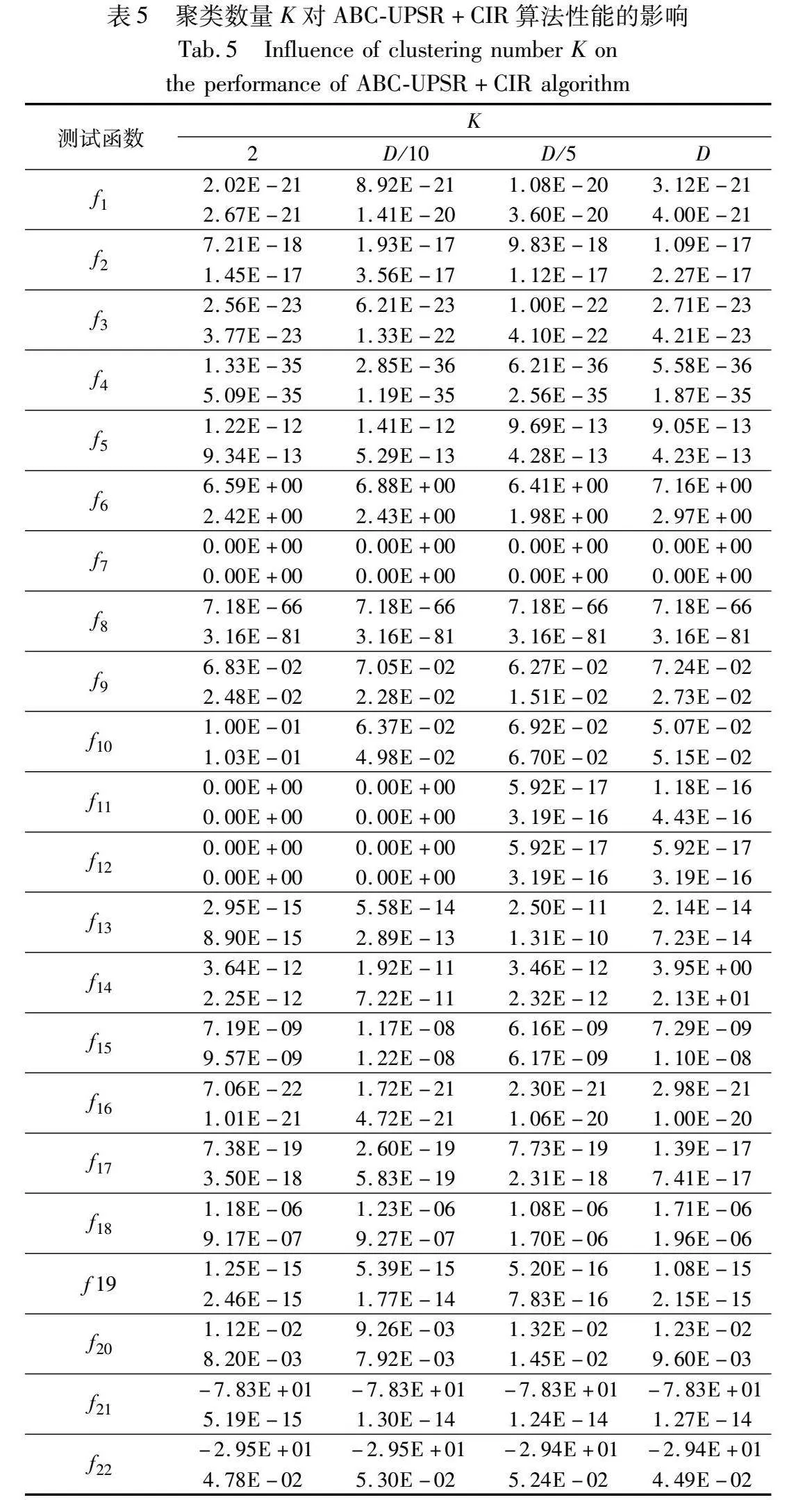
为了验证本文引入参数K-means聚类数量K对ABC-UPSR+CIR性能的影响，分别设置K为2、D/10、D/5和D进行实验，其他参数设置同2.6节，实验结果如表5所示。

从表5可以看出，当K增大到D/5后，对f11和f12的求解性能显著下降，没有求得全局最优值；K为D/10时，虽然表现最优的函数数量为8，小于K为2时的12，但表现不是最优的函数求解结果与K为2时差距不大。考虑到随着问题维数D的增加，算法应适度随之增加聚类个数以便以较多的分区覆盖搜索空间，因此本文建议K的取值为D/10。

3.4 种群多样性分析

种群熵是衡量算法种群多样性的一个重要指标，计算熵H的方法如下［19］：设当前种群有NP个个体，算法进化过程中迄今得到的最优个体和最差个体的适应度值分别为fmax，和fmin。

a）解空间表示。εmin=（1-δ）×fmin，εmax=（1+δ）×fmax，δ=0.1，则解空间S可以用［εmin，εmax］表示，区间长度λ=εmax-εmin。

b）解空间分割。把区间［εmin，εmax］分成M（M=NP）个小区间［εmin+λ（i-1）/M，εmax+λ（i-1）/M］，统计每一区间的个体数Ni（i=1，2，…，M）。

c）计算个体出现在第i个区间的概率pi。

pi=Mi/M（9）

d）种群熵值计算。

H=-∑Mi=1pilnpi（10）

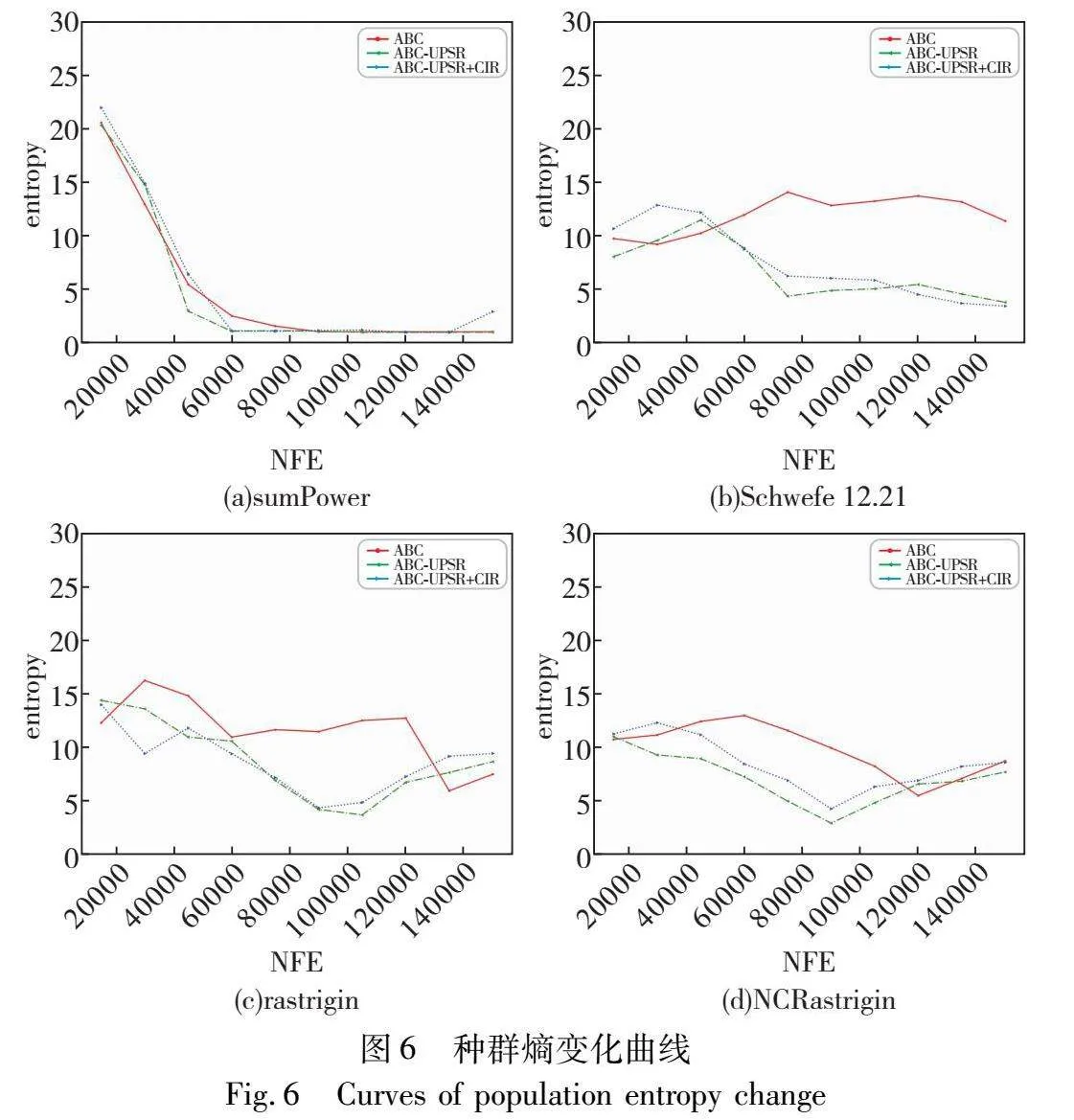
种群熵越大说明种群多样性越大，算法越倾向于探索；种群熵越小说明种群多样性越小，算法越倾向于收敛和开发。本文从22个函数中选出具有代表性的函数，其中包括2个单峰函数和2个多峰函数，以500×D次函数评价为间隔，绘制种群熵随之变化的曲线，如图6所示。可以看出，种群熵随着函数评价次数的增加整体上呈现下降趋势，说明种群随着搜索的进行，不断地收敛；ABC-UPSR与ABC-UPSR+CIR由于种群规模缩减损失一部分多样性，尤其在搜索的中后期随着种群规模的快速下降，多样性不如种群规模不变的ABC，但总体损失不大；此外，ABC-UPSR+CIR的种群熵明显略高于ABC-UPSR，这说明基于聚类的CIR策略在移除个体时更好地保护了种群多样性。

3.5 阶段寻优能力分析

为了验证具有UPSR+CIR策略的ABC能够在搜索各阶段表现出更好的寻优能力，在实验1的基础上，

分别输出NFE为37 500、75 000以及110 000时（分别对应前期大种群探索阶段结束、中期种群快速缩减阶段结束以及后期小规模开发阶段中间），ABC和ABC-UPSR+CIR求解每个测试函数获得的均值和标准差，结果如表6所示。从表6可以看出，相比于ABC，ABC-UPSR+CIR的求解精度和稳定性，在所有的22个函数上无论在前期、中期和后期均表现更优，充分说明了UPSR+CIR策略在各阶段都能表现出更好的寻优能力。

3.6 TSP应用问题检验

3.6.1 TSP描述

TSP（traveling salesperson problem）是一个经典的组合优化问题，通常用来描述如下情境：假设有一个旅行推销员，他需要访问一系列城市，并最终回到出发城市，保证每个城市都会被访问并且仅被访问一次，同时确保总行程最短［24］，形式化描述如下：

a）城市集合。有一个包含n个城市的集合，通常用C={1，2，…，j，…，n}表示，j代表城市编号。

b）距离或成本。对于任意两个城市——城市i和j（i≠j），都有一个与之相关的非负距离或成本d（i，j），

这个距离可以代表两个城市之间的实际距离、时间、费用等等，该属性具有对称性，即d（i，j）=d（j，i）。

c）目标。旅行推销员的目标是找到一条从出发城市出发，访问每个城市一次，然后返回出发城市的路径，使得路径的总距离或成本最小，这个路径就被称为TSP的解。

TSP被认为是NP难问题，目前没有已知的多项式时间算法可以解决所有实例。对于小规模问题，可以使用精确方法（如穷举法或分支定界法）找到最优解；

对于大规模问题，通常需要使用智能优化算法来寻找近似最优解。TSP在物流规划、电路设计、DNA测序、旅游路线规划等很多领域具有重要应用价值。

3.6.2 求解TSP的ABC算法

1）解的编码 假设某个TSP实例中有n个城市，那么n对应的就是解的维数（D=n），因此每个解每一维都由从1到n的数字组成，每个数字代表了城市的编号。根据TSP的性质可知，任何一个解的任意两维对应的城市编号不可以相同，表示将每个城市访问且仅访问一次，并最终回到起点。因此，解的编码由式（11）表示。

Xi={Xi，0，Xi，1，…，Xi，j，…，Xi，u，…，Xi，n-1}Xi，j∈{1，2，…，n}Xi，j≠Xi，uj，u∈{0，1，…，n-1}，j≠u（11）

其中：Xi代表一个n维解，包含了n个互不相同的城市编号序列。

2）初始化阶段 初始化的过程本质上就是生成随机解的过程，随机生成SNmax个互不相同解，本文将初始种群大小设置为3×n，以便覆盖整个搜索空间。

每个初始解中的每个城市编号均以随机选择的方式生成，假设一个初始解中随机选择的第一个城市编号为i，那么这个初始解中第二个城市编号就从{1，2，…，i-1，i+1，…，n}当中随机选择一个城市编号j，第三个城市编号就从{1，2，…，i-1，i+1，…，j-1，j+1，…，n}当中随机选择，以此类推，直到所有的城市编号都被选择一次。

值得注意的是，城市的数量n越大，初始解的数量也越大。如果某个TSP有n个城市，那么就有（n-1）！/2个解［25］。因此，3×n个解当中存在相同解的概率可以由式（12）计算。

P=C23n1（（n-1）！/2）2（12）

由式（12）不难看出，仅当n=10时，概率P值约为千万分之一。当n取更大值时，P值会更加接近0。因此在大多数TSP实例中，不必考虑初始解重复的可能性问题。

3）适应度函数计算 在TSP中，解的路径长度与它的目标函数值相对应。一个合法的解序列就是一个旅行商需要依次经过的城市序列。在计算了某个解对应的路径长度后，计算适应度的方法与基本ABC相同。解的路径长度越长，它的函数值就越大，适应度值就越小，质量就越差。

4）雇佣蜂阶段 本文在解决TSP时，雇佣蜂所使用的搜索方程与基本ABC相同。需要特别说明的是，在使用式（3）生成vGi，j以后，需要对vGi，j进行解的合法性检查与校正，避免其存在不符合约束条件的情况。vGi，j中共包含了n个元素，可能存在的不合理情况以及处理方式如下：

a）若vGi，j为负值，仅需对其取绝对值进行校正即可。此外，若vGi，j为非整型数值，则对其向下取整即可。

b）若vGi，j超过最大城市编号，那么肯定存在至少一个城市编号在vGi当中没有出现，因此从中随机选择并替换vGi，j即可。

c）若vGi，j=vGi，u（j≠u），即存在重复的城市编号，这与TSP中每个城市访问且仅访问一次产生了矛盾。显然如果一个城市编号重复出现两次，则至少存在一个城市编号未出现，因此找到没有出现城市编号来随机替换即可。

5）跟随蜂阶段 跟随蜂所采用的搜索方程与雇佣蜂相同，并采用与雇佣蜂相同的合法性检查和校正方法。本文中跟随蜂选择食物源的方法与基本ABC相同，即轮盘赌选择方式。

6）侦查蜂阶段 侦查蜂也是在某个解（即路径）连续limit次没有得到更新时，如果这个解不是当前全局最优解就抛弃这个解，并且随机产生新的可行解进行替换。

7）种群缩减与个体移除 将UPSR-CIR融入基本ABC应用于优化TSP，并且与无种群缩减策略的ABC进行实验对比，UPSR-CIR策略的详细过程在之前已经有详细介绍，本小节恕不赘述。

3.6.3 实验结果与对比分析

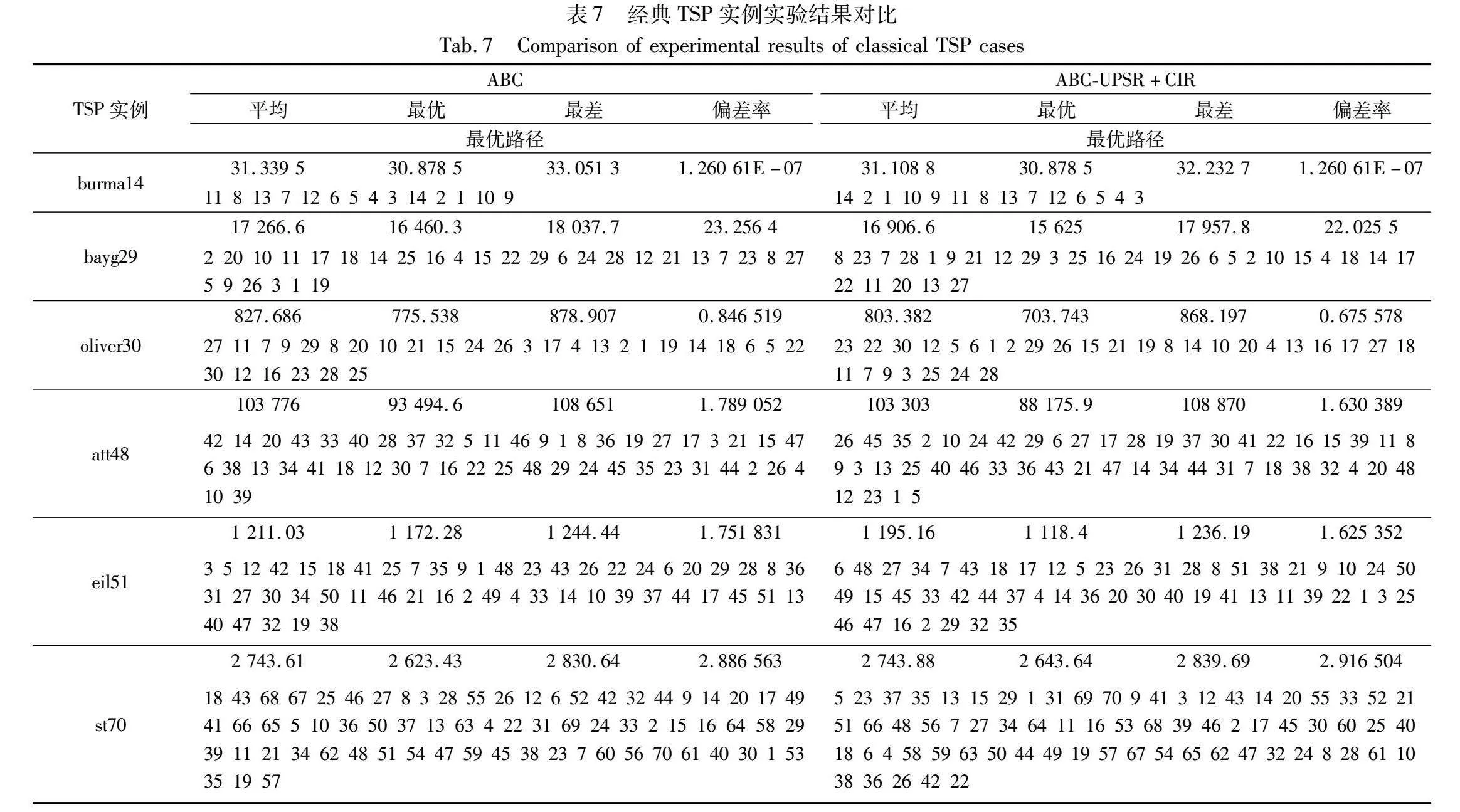
将求解TSP的基本ABC和融入UPSR-CIR的ABC分别在12个经典TSP实例上进行实验验证分析，并对比两者多次求解获得的平均路径长度、最优路径长度、最差路径长度以及偏差率，并且给出每个算法求得的最优路径。其中，路径长度反映了求解的质量，偏差率反映了解之间的离散程度；路径长度越小说明解的质量越高，偏差率越小说明算法的稳定性越好。偏差率的计算方法如式（13）所示。

偏差率=（求解每个实例获得的最优路径长度-该实例已知最优路径长度）该实例已知最优路径长度×100%（13）

本实验中MAX_NFE设置为10000×D，其余实验参数设置与4.2节相同。实验结果如表7所示。对表7中的实验结果进行汇总，列出每个算法在平均路径长度、最优路径长度、最差路径长度以及偏差率表现最好的TSP实例，结果如表8所示。

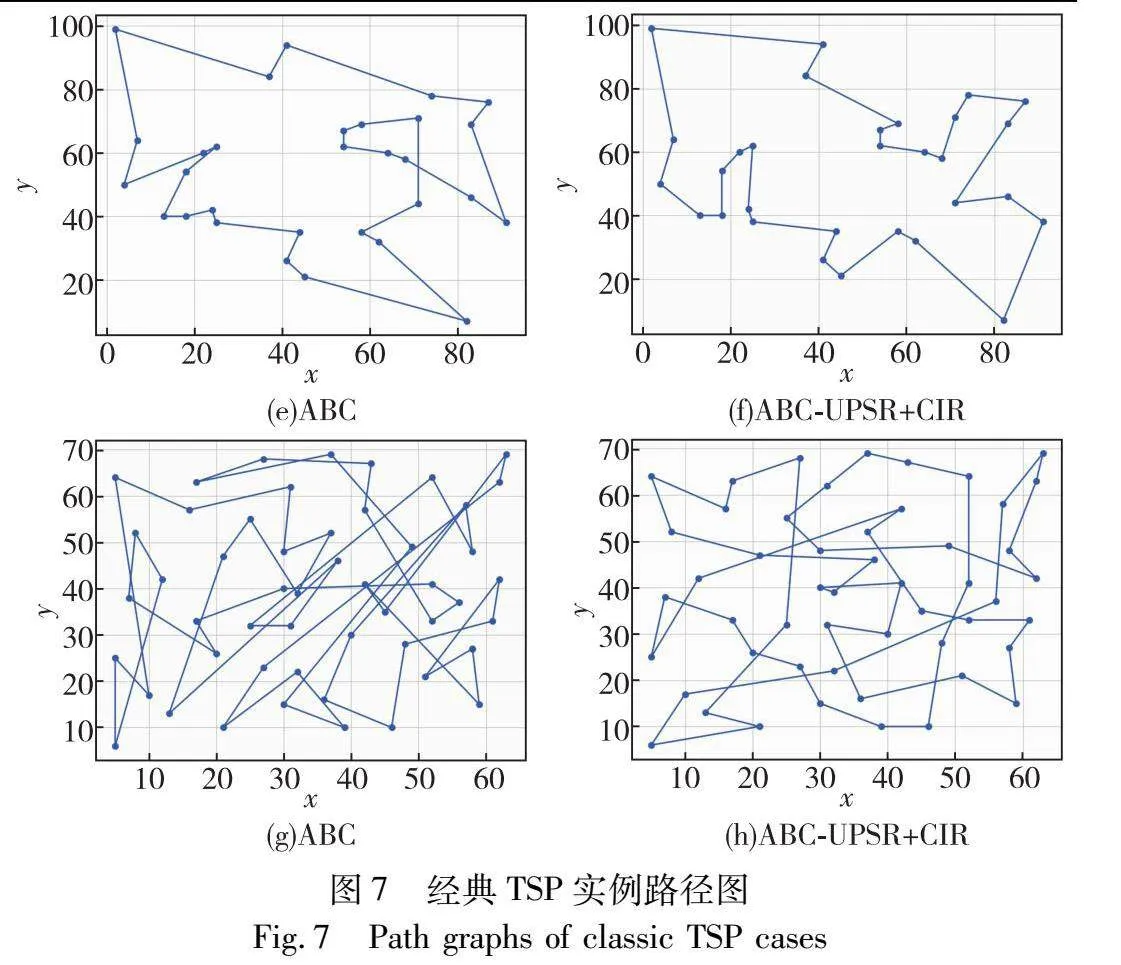
由表8可以看出，融入UPSR-CIR的ABC在平均路径长度、最优路径长度、最差路径长度以及偏差率上均在大多数实例上优于基本ABC，可见本文UPSR-CIR策略的有效性以及在实际应用问题上的适用性。

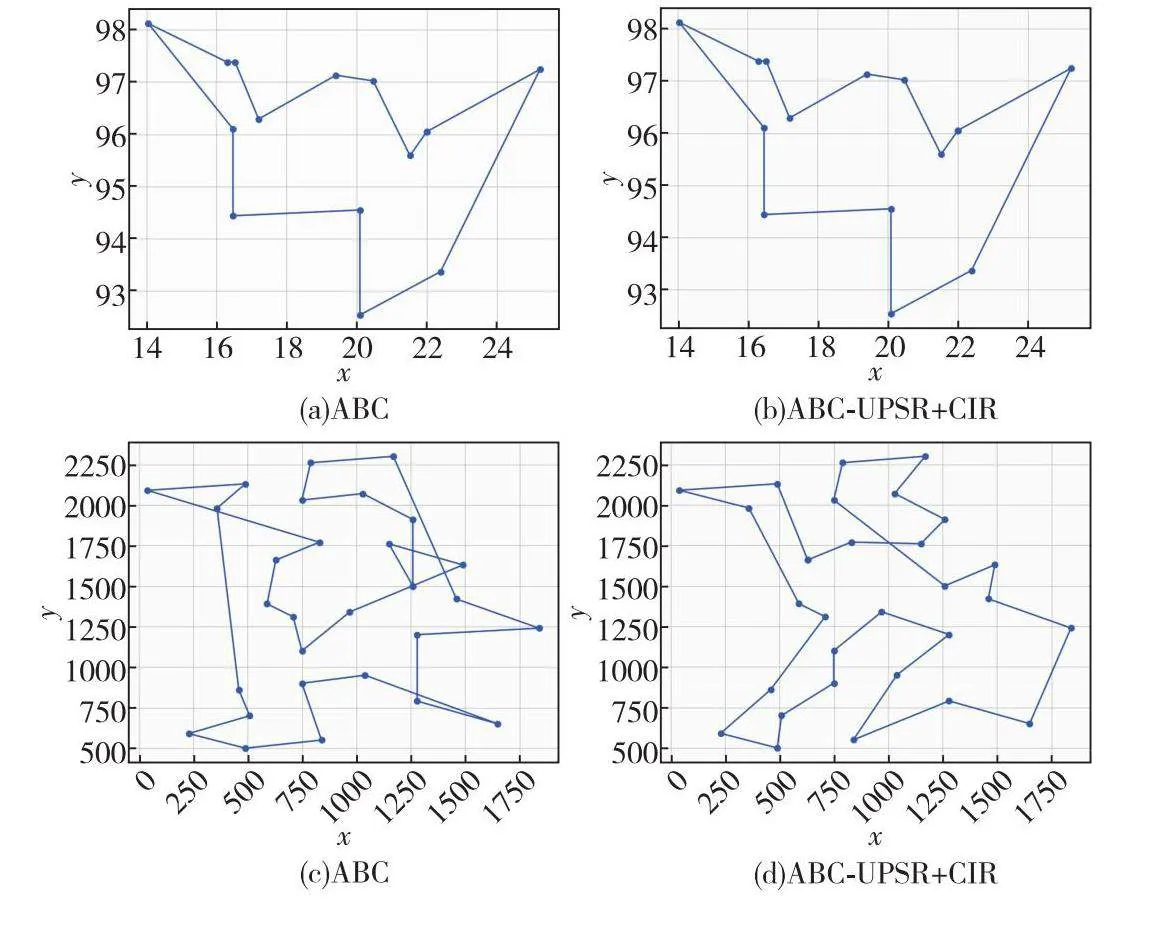
进一步选择burma14、bayg29、oliver30、eil51实例绘制路径图，且将实例中坐标位置按照一定比例进行缩放，便于观察对比，结果如图7所示。

从图7可以看出，加入UPSR-CIR策略的ABC在求解经典TSP实例时表现出明显的优势，其求得的路径图比基本ABC更优。这是由于UPSR-CIR策略充分利用了大种群的探索优势以及小种群的开发优势，保护了种群多样性进而更好地平衡了探索与开发能力，避免了计算资源的不必要浪费。

4 结束语

为了平衡ABC的探索性和开发性，提高它的收敛速度，本文利用大种群有利于探索而小种群有利于开发的原理，设计了非线性种群缩减策略UPSR；为了在保持种群多样性的同时进一步增加开发性，通过K-means动态分区确保对搜索空间的覆盖，同时根据分区个体排名确定分区移除个体数量，形成了基于分区个体排名的个体移除策略CIR。

在22个基准测试函数上的对比分析实验结果表明，相对于其他种群缩减策略，UPSR-CIR在ABC上表现出更好的求解质量、更强的稳定性和更快的收敛速度；对于ARABC、DFSABC_elite和DAABC三个ABC变体，UPSR-CIR性能的优越性表现出了普适性；而后对聚类数量做了参数敏感性分析并且证明了本文选择的聚类数量的合理性；并且在算法不同阶段通过实验证明了UPSR-CIR策略的优越性；最后，在12个TSP经典实例上的实验结果进一步表明UPSR-CIR策略具有实际应用价值。

在后续研究中，在差分进化等其他智能优化算法上进一步验证分析UPSR-CIR策略的适用性，并在多目标以及离散多约束等工程优化问题方面进一步拓展其实际应用领域。

参考文献：

［1］Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：artificial bee colony（ABC）algorithm［J］.Journal of Global Optimization，2007，39（3）：459-471.

［2］Etminaniesfahani A，Gu H，Salehipour A.ABFIA：a hybrid algorithm based on artificial bee colony and Fibonacci indicator algorithm［J］.Journal of Computation Science，2022，61：101651.

［3］Cui Yibing，Hu Wei，Rahmani A.A reinforcement learning based artificial bee colony algorithm with application in robot path planning［J］.Expert Systems with Application，2022，203：117389.

［4］Ni Xinrui，Hu Wei，Fan Qiaochu，et al.A Q-learning based multi-strategy integrated artificial bee colony algorithm with application in unmanned vehicle path planning［J］.Expert Systems with Application，2024，236：121303.

［5］Sutar M，Jadhav H T.A modified artificial bee colony algorithm based on a non-dominated sorting genetic approach for combined economic-emission load dispatch problem［J］.Applied Soft Computing，2023，144：110433.

［6］Wang Chunfeng，Shang Pengpeng，Shen Peiping.An improved artificial bee colony algorithm based on Bayesian estimation［J］.Complex & Intelligent Systems，2022，8（6）：4971-4991.

［7］Li Xing，Zhang Shaoping，Yang Le，et al.Neighborhood-search-based enhanced multi-strategy collaborative artificial bee colony algorithm for constrained engineering optimization［J］.Soft Computing：A Fusion of Foundations，Methodologies and Applications，2023，27（19）：13991-14017.

［8］Ye Tingyu，Wang Wenjun，Wang Hui，et al.Artificial bee colony algorithm with efficient search strategy based on random neighborhood structure［J］.Knowledge-Based Systems，2022，241：108306.

［9］Gao Hao，Fu Zheng，Pun C M，et al.An efficient artificial bee colony algorithm with an improved linkage identification method［J］.IEEE Trans on Cybernetics，2020，52（6）：4400-4414.

［10］Xu Minyang，Wang Wenjun，Wang Hui，et al.Multipopulation artificial bee colony algorithm based on a modified probability selection model［J］.Concurrency and Computation：Practice and Experience，2021，33（13）：e6216.

［11］Cui Yibing，Hu Wei，Ahmed R.Improved artificial bee colony algorithm with dynamic population composition for optimization problems［J］.Nonlinear Dynamics，2022，107（1）：743-760.

［12］Thirugnanasambandam K，Rajeswari M，Bhattacharyya D，et al.Direc-ted artificial bee colony algorithm with revamped search strategy to solve global numerical optimization problems［J］.Automated Software Engineering，2022，29（1）：13.

［13］Zhao Fuqing，Wang Zhenyu，Wang Ling，et al.An exploratory landscape analysis driven artificial bee colony algorithm with maximum entropic epistasis［J］.Applied Soft Computing，2023，137：110139.

［14］Naser C，Miri M，Rashki M.An adaptive artificial neural network for reliability analyses of complex engineering systems［J］.Applied Soft Computing，2023，132：109866.

［15］Yu Haibo，Kang Yaxin，Kang Li，et al.Bi-preference linkage-driven artificial bee colony algorithm with multi-operator fusion［J］.Complex & Intelligent Systems，2023，9（6）：6729-6751.

［16］朱武.基于种群自适应策略的差分演化算法及其应用研究［D］.上海：东华大学，2013.（Zhu Wu.Research on differential evolution algorithm based on population adaptive strategy and its applications［D］.Shanghai：Donghua University，2013.）

［17］Tanabe R，Fukunaga A S.Improving the search performance of shade using linear population size reduction［C］//Proc of IEEE Congress on Evolutionary Computation.Piscataway，NJ：IEEE Press，2014：1658-1665.

［18］Brest J，Mauec M S.Population size reduction for the differential evolution algorithm［J］.Applied Intelligence，2007，29：228-247.

［19］单天羽，管煜旸.基于种群多样性的可变种群缩减差分进化算法［J］.计算机科学，2018，45（Z2）：160-166.（Shan Tianyu，Guan Yuyang.Differential evolution algorithm with adaptive population size reduction based on population diversity［J］.Computer Science，2018，45（Z2）：160-166.）

［20］李瑞，徐华，杨金峰，等.改进近邻人工蜂群算法求解柔性作业车间调度问题［J］.计算机应用研究，2024，41（2）：438-443.（Li Rui，Xu Hua，Yang Jinfeng，et al.Improved algorithm of near-neighbor artificial bee colony for flexible job-shop scheduling［J］.Application Research of Computers，2024，41（2）：438-443.）

［21］Cui Laizhong，Li Genghui，Wang Xizhao，et al.A ranking-based adaptive artificial bee colony algorithm for global numerical optimization［J］.Information Sciences，2017，417：169-185.

［22］Cui Laizhong，Li Genghui，Lin Qiuzhen，et al.A novel artificial bee colony algorithm with depth-first search framework and elite-guided search equation［J］.Information Sciences，2016，367-368：1012-1044.

［23］赵明，焦剑如，宋晓宇，等.维适应人工蜂群算法的研究［J］.小型微型计算机系统，2024，45（3）：562-569.（Zhao Ming，Jiao Jianru，Song Xiaoning，et al.Research on improved adaptive artificial bee colony algorithm［J］.Journal of Chinese Computer Systems，2024，45（3）：562-569.）

［24］禹博文，游晓明，刘升.引入动态分化和邻域诱导机制的双蚁群优化算法［J］.计算机应用研究，2023，40（10）：3000-3006.（Yu Bowen，You Xiaoming，Liu Sheng.Dual-ant colony optimization algorithm with dynamic differentiation and neighborhood induction mechanism［J］.Application Research of Computers，2023，40（10）：3000-3006.）

［25］陈峰.人工蜂群算法及其应用研究［D］.广州：华南理工大学，2014.（Chen Feng.Research on artificial bee colony algorithm and its applications［D］.Guangzhou：South China University of Technology，2014.）