基于TSACO及动态避障策略的无人机路径规划

摘 要：为了提高无人机路径规划中的避障效率，首先针对全局规划，提出一种改进蚁群算法TSACO（turning-sensitive ant colony optimization）。该算法利用A算法进行非均匀分配初始信息素，通过在概率函数中引入转向启发函数，以及采用精英蚂蚁系统等方法，来提高算法的收敛速度，减少路径的转角次数。其次，针对局部规划提出一种改进速度障碍算法，加入了无人机动力学方程，考虑障碍物自适应碰撞半径和紧急碰撞锥，以及最优速度选择法等，来改善无人机局部避障的实时性与安全性。仿真实验表明，该算法相较于其他算法，在路径长度、转向次数及动态避障等方面，均具有更好的有效性。

关键词：无人机；路径规划；蚁群算法；速度障碍法

中图分类号：V279 文献标志码：A 文章编号：1001-3695（2024）10-019-3015-06

doi：10.19734/j.issn.1001-3695.2024.01.0028

UAV path planning based on TSACO and dynamic obstacle avoidance strategy

Jiang Nan，Xu Haiqin，Xing Haoxiang

（College of Information Science & Technology，Donghua University，Shanghai 201620，China）

Abstract：This paper proposed an improved ant colony optimization named TSACO and an enhanced velocity obstacle（VO）to solve the UAV path planning problem.The TSACO incorporated non-uniform initial pheromone distribution，a turning heuristic function，and an elite ant system to improve the convergence speed and reduce the number of path corners during global planning.The enhanced VO integrated the UAV’s dynamic equation，adaptive collision radius and emergency collision cone，along with an optimal velocity selection approach to increase real-time and safe local obstacle avoidance during local planning.Simulation experiments demonstrate that the proposed algorithms have better effectiveness in terms of path length，number of turns，and dynamic obstacle avoidance compared to other algorithms.

Key words：unmanned aerial vehicle（UAV）;path planning;ant colony optimization;velocity obstacle

0 引言

近年来，无人机（UAV）因为其体积小、运动速度快、成本低、配置灵活等优点被广泛运用于搜索巡逻［1］、侦察监视［2］、电力巡检［3］、农林植保［4］等军事和民用领域，而无人机路径规划是该领域的一个热门研究方向，其主要由全局规划和局部规划两部分组成［5］。无人机在全局路径规划中根据环境信息避开静态障碍物，再在局部规划中通过传感器等装置获取即时信息避开动态障碍物，实现完整的路径规划［6］。当前对于全局路径规划的研究方法可分为两大类：a）传统搜索算法如A算法、D算法和图搜索法等;b）智能优化算法如粒子群算法、蚁群算法、模拟退火算法等［7］。常见的局部规划算法有动态窗口法、速度障碍法、人工势场法等［8］。

蚁群算法在全局路径规划中运用十分广泛［9，10］，其正反馈并行机制具有良好的鲁棒性及较强的全局搜索能力，且易与其他算法相融合，但也存在收敛速度慢、易陷入局部最优、早熟收敛等问题。目前已有许多学者针对蚁群算法存在的不足进行相应的改进。王晓燕等人［11］采用人工势场法计算初始路径与下一节点之间距离综合构造启发信息，避免算法陷入局部最优；Wang等人［12］在蚁群系统基础上运用精英蚂蚁和最大最小蚁群算法改善算法收敛速度；申铉京等人［13］采用双向蚁群算法，减小了蚁群算法的计算规模，改善最优解与收敛速度。但上述算法普遍存在搜索范围较小、转向次数较多等问题。

速度障碍法（VO）是一种局部避障算法，主要思想是在避障过程中考虑无人机和障碍物的速度，以确定无人机能够安全通过的速度空间，但其存在避障速度和避障时间难以选择等问题。众多学者已对其提出了一些改进方案，许文瑶等人［14］将动态障碍物在速度空间中的运动不确定性转换为位置的不确定性，改善了算法的安全性；Ueda等人［15］对碰撞锥划分不同的碰撞概率区域来选择速度，改善了路径的抖动和转弯角度过大的问题；杨秀霞等人［16］提出基于时间的速度障碍法，为无人机提供了更大范围的可选避障速度向量范围，改善了避障的实时性。但上述算法存在避障时间过早，未考虑无人机运动学方程等问题。

本文在前人研究的基础上，针对全局规划提出改进蚁群算法TSACO。该算法先通过A算法改进初始信息素，后在蚁群算法的概率函数和目标函数中加入转向策略和转角代价，并运用精英转角蚂蚁等方法以改善规划路径的转角数与长度；针对局部规划提出一种结合动力学的速度障碍法，考虑障碍物自适应碰撞半径和紧急碰撞锥来优化避障时机，加入最优避障速度选择策略，兼顾速度连续性与避障有效性。通过对两者的有效结合进行仿真实验，模拟无人机路径规划和运动过程，仿真验证了改进算法的优越性以及无人机在运动中的局部避障效果。

1 问题描述

为解决无人机路径规划问题，本文将实际环境简化为二维环境，并运用栅格法建模，在该环境中，存在动态障碍物和静态障碍物，其中动态障碍物可能会在规划过程中发生移动。路径规划的起点设定为环境中的第一个栅格，终点为最后一个栅格。全局路径规划旨在找到起点到终点的一条最优路径，而局部路径规划则负责在这条全局路径的基础上进行微调，以应对环境中的障碍物和动态变化。为了简化问题，本文作出以下合理的假设：a）全局规划中将无人机视为质点，忽略动力学特性；b）局部规划中忽略传感器误差和响应延迟。

1.1 环境建模

本文采用栅格法来进行环境建模，将环境划分成Nx×Ny个等面积的方块作为栅格。建立二维直角坐标系时，对栅格依次进行编号为1，2，…，Nx×Ny，其中第i个栅格的位置坐标（xi，yi）与序号的映射关系如下：

xi=a×［Nx-0.5］ mod（i，Nx）=0a×［mod（i，Nx）-0.5］ 其他yi=a×［Ny+0.5-ceil（i/Nx）］（1）

其中：a为栅格的边长；i为栅格序号；ceil为向上取整函数；mod为取余函数。

1.2 无人机动力学模型与控制

局部规划问题中，将动态避障算法与无人机动态特性相结合能更好地验证避障算法的有效性和实用性。本文使用四旋翼无人机的动力学模型，其主要可分为位置动力学模型与姿态动力学模型，将两者联立即可得到无人机飞行控制刚体模型［17］，如式（2）所示。

=1m（cossinθcosψ+sinsinψ）×U=1m（cossinθsinψ-sinsinψ）×U=1m（coscosθ）×U-g=1Ixx［Ux+（Iyy-Izz）+JrΩ］=1Iyy［Uy+（Izz-Ixx）-JrΩ］=1Izz［Uz+（Ixx-Iyy）］（2）

其中：m表示无人机的质量；、θ和ψ分别代表无人机机体坐标系和大地坐标系X、Y、Z轴之间的旋转角度；、和表示无人机在大地坐标系下沿X、Y、Z轴的加速度；U表示作用在无人机上的总升力；Ux、Uy和Uz分别表示作用在无人机三个坐标轴上的力矩大小；g表示重力加速度；Ixx、Iyy和Izz是无人机对各旋转轴的转动惯量；Jr表示无人机电机和螺旋桨的总转动惯量；Ω=ω1-ω2+ω3-ω4，其中ω1，ω2，ω3，ω4分别代表无人机四个电机的转速。

对应动力学方程需要进行姿态控制和位置控制，位置控制分为悬停控制和轨迹跟踪控制。在姿态控制器方面，本文基于模型预测生成无人机的参考姿态角速度并通过PD控制来调整无人机的姿态角速度，实现期望的姿态控制。在悬停控制器中，运用PD控制器来计算无人机的位置误差和速度误差，并产生一个控制输入，以调整无人机的位置和速度，使其保持在指定的悬停位置。对于轨迹跟踪控制，LQR（linaer quadratic regulator）控制器根据改进VO算法规划节点结合无人机的动力学模型和环境信息生成最优轨迹，再通过线性二次调节来计算最优控制器，以实现能量最小化和轨迹控制。最后使用PD控制器通过实时轨迹信息和期望轨迹的误差来计算无人机的姿态角速度和推力，使其跟踪期望轨迹。

2 算法原理

本章针对全局规划和局部规划分别采用TSACO和改进VO算法，以找到一条能兼顾路径长度、转角次数并能合理动态避障的路径。在本章后续内容中，将先后介绍两种方法的算法流程与改进内容。

2.1 TSACO算法描述

2.1.1 改进初始信息素

在传统蚁群算法中，各节点之间的初始信息素都为同一常数值S，这使得蚁群算法初期寻路有很大的盲目性，算法效率较低，故文献［18］在原始信息素基础上，按照式（3）增加A所得路径节点间的信息素浓度，其余路径浓度仍保持S值不变。

τ（R）=QS（3）

其中：R为运用A算法所得的路径；Q为正实数。

2.1.2 改进启发函数

传统蚁群算法中，启发函数仅考虑当前节点到下一待选节点欧氏距离，并未考虑其与终点之间的关系，这样会带来蚁群搜索过程中的盲目性，易陷入局部最优、收敛速度过慢等问题，故本文修改启发函数如式（4）所示。

ηij=1μdij+σdje（4）

其中：dje为下一节点到终点的欧氏距离；μ和σ是常数，可按需求改变。

无人机实际飞行中，大量的转弯会导致路径轨迹不平滑，能量消耗过多。因此为了限制转弯次数，减少能量消耗，本文将在转移概率中引入转角启发函数：

=e-g×θ（5）

其中：g是自适应参数，根据迭代次数的不同自适应改变，本文设定为［0，1］即在迭代前期设定为0，当达到总迭代数的20%时设定为1；θ为待选节点和当前节点连线与当前节点和前一节点连线的夹角。则改进后的蚁群转移概率如式（6）所示。

pkij（t）=［τij（t）］α×［ηij（t）］β×∑s∈allowedk［τis（t）］α×［ηis（t）］β×j∈allowedk0jallowedk（6）

其中：pkij（t）为t时刻蚂蚁k从节点i处移动到下一个节点j的概率；τij（t）为t时刻从节点i到j路径上的信息素浓度。

2.1.3 精英蚂蚁体系

传统精英蚂蚁方法会针对路径最短的蚂蚁所走路径进行信息素的更新，增大其所带有的信息素浓度，让后续蚂蚁更多地选择较优的路径，以增强正反馈效果，因本文加入了转角策略，故在传统精英蚂蚁基础上加入精英转角蚂蚁与精英转向蚂蚁，以增强最优路径的转角特性。相应的信息素修改如式（7）所示。

Δτij=∑mk=1Δτk，ij+ePΔτbP，ij+eTΔτbT，ij+eθΔτbθ，ij（7）

其中：eP、eT和eθ分别为最短路径、总最小转角次数、总最小转角角度的精英蚂蚁影响权重；而ΔτbP，ij、ΔτbT，ij和Δτbθ，ij由式（8）～（10）给出。

ΔτbP，ij=1/LbP（i，j）∈TbP0其他（8）

ΔτbT，ij=1/LbT（i，j）∈TbT0其他（9）

Δτbθ，ij=1/Lbθ（i，j）∈Tbθ0其他（10）

其中：TbP、TbT和Tbθ分别为一次迭代中路径最短、总转角次数最小和总转角角度最小的路径；LbP、LbT和Lbθ为其对应的路径长度值。

2.2 改进VO算法

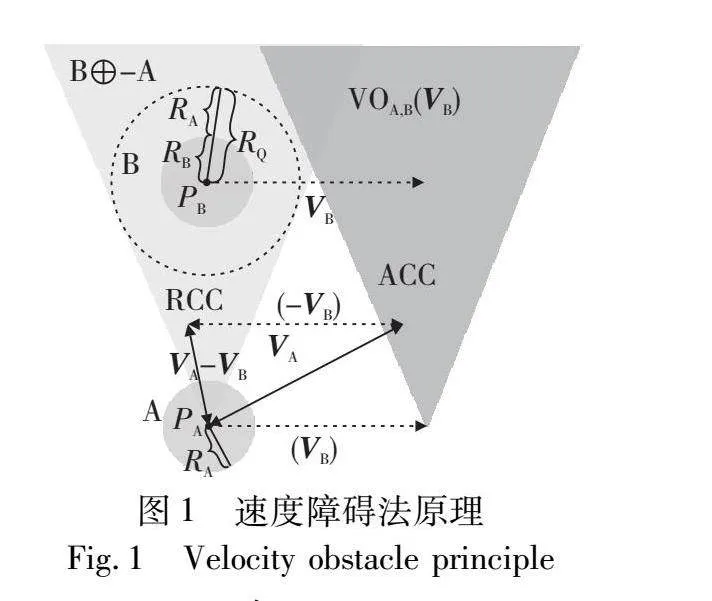
VO算法是一种广泛运用于智能体避障的算法，具有简单直观、能够实时避障等优点，其最早由意大利学者Fiorini［19］在1998年提出。VO算法基本原理如图1所示，无人机的位置、半径和速度分别为PA、RA、VA，障碍物的位置、半径和速度分别为PB、RB、VB。一般在VO中，将无人机简化为粒子，将障碍物的威胁区半径扩大至RQ=RA+RB，过无人机位置对威胁区作两条切线，则其形成的锥形区域为相对碰撞锥（RCC），将相对碰撞面积沿障碍物B的速度移动，可得到绝对碰撞锥（ACC）。如果无人机速度VA与障碍物速度VB的相对速度VAB（VA-VB）在相对碰撞锥或VA在绝对碰撞锥内，则在未来一段时间内，无人机将与障碍物发生碰撞。在这种情况下，需要选择新的速度矢量，以避开动态障碍物。绝对碰撞区域定义为

VOA，B（VB）={VA|λ（PA，VA-VB）∩（B⊕-A）≠}（11）

λ（P，V）={P+Δt×V|Δt≥0}（12）

其中：Δt为时间间隔;⊕为闵可夫斯基和;B⊕-A为相对速度障碍区域。如图1所示，此时无人机速度矢量的终点落在ACC以内，说明一段时间后，无人机将与障碍物发生碰撞;反之则不会。

2.2.1 障碍物不确定性分析

当无人机检测到障碍物时，使用VO算法计算碰撞锥，若速度落在绝对碰撞区域内，则认为无人机将与障碍物发生碰撞，可通过选择碰撞锥范围外的速度来避开障碍物；若速度刚好落在碰撞锥的边缘，则无人机避障过程所需的时间最短，且其与障碍物相切，如果此时障碍物的速度突然发生变化，或者传感器的检测精度受到限制，检测延迟等情况出现时，就有可能发生碰撞；若速度远离碰撞锥，无人机虽然可以与障碍物保持一定的安全距离，但避障时间会变长，会降低避障的实时性［20］。故本文在VO算法计算碰撞锥的过程中，为障碍物添加不确定性半径，设定了自适应系数使不确定性半径随着无人机与障碍物的距离，以及无人机速度的改变而变化，以同时兼顾安全性与实时性。自适应不确定半径r定义为

r=d×（ΔRB+RA）（13）

其中：ΔRB为最大不确定半径，具体取值如式（14）所示；RA为无人机半径，作安全距离裕度；d为自适应系数具体取值如式（15）所示。

ΔRB=Δt×V2B（t）+（VB（t）+ΔVB）2-2×VB（t）×（VB（t）+ΔVB）×cos（ΔθB）（14）

d=e10-ζ10<ζ≤201ζ≤100其他（15）

其中：Δt为无人机最小决策时间间隔；VB（t）为t时刻障碍物的速率；ΔVB为障碍物最大速率变化估计量；ΔθB为障碍物最大方向变化估计量；ζ=|nAB|2/（nAB·VAB）为预测碰撞时间系数，nAB为无人机与障碍物的相对位置向量，VAB为无人机和障碍物的相对速度。故本文障碍物膨胀圆半径为RQ+r。

2.2.2 紧迫碰nu52wDx61L8me35Zq9cqX3ia51kyes622DJkyHZmwO0=撞锥

VO算法中碰撞锥是针对障碍物的速度做线性模拟得出的，故当距离无人机较远的障碍物做非线性运动时，这样的估计就会出现偏差，容易使无人机造成误避障的操作；此外在障碍物较多时，距离较远处的障碍物在一定时间内都不会存在威胁，远近障碍物同时考虑可能会导致避障困难［19］。故本文定义紧迫碰撞锥VOh：

VOh={VA|VA∈VO，‖VAB‖>dm/Th}（16）

其中：Th为紧迫时间，表征了无人机避障的时间条件；dm为障碍物和无人机之间的相对距离；VO为绝对碰撞锥；VOh表示了在Th时间之内无人机和障碍物会发生碰撞的速度集合区域，具体区域如图2所示。

2.2.3 最优避障速度选择

在传统VO算法中，避障速度一般选取与指向目标点速度向量差模值最小的速度向量［14］，这样的选取方式会造成避障结束后速度方向的突变，虽在理论算法中影响不大，但在真实的无人机跟踪中因为动力学约束，将很难跟踪该轨迹，可能导致无人机运动失衡的情况。故本文设置了避障速度选择的目标函数：

D（VA（t））=ωV‖VA，pref-VA（t）‖+ωc‖VA（t）-VA（t-1）‖（17）

其中：ωV是考虑趋向目标的权重;ωc是考虑速度变化量的权重；VA，pref=VAmaxPg-PA‖Pg-PA‖表示无人机相对目标点的速度矢量，其中Pg为目标点坐标，VAmax为无人机速度最大值。此外，为了避免无人机间避障的速度选择冲突，本文设定无人机优先向右侧避让。

2.3 算法融合与分析

2.3.1 TSACO评价函数

鉴于TSACO考虑了路径长度、转角次数和总转角角度。为了更好地体现三者的改善效果，本文以A算法的路径数据作为衡量标准，定义了如式（18）所示的评价函数G。

G=a1LALLLA，ALL+a2TALLTA，ALL+a3θALLθA，ALL（18）

其中：LALL、TALL、θALL分别为仿真算法所得路径的总长度、总转向次数与总转角度；LA，ALL、TA，ALL、θA，ALL则分别为A算法所得仿真路径的总长度、总转向次数与总转角度；a1、a2和a3为权重，满足a1+a2+a3=1。

2.3.2 融合算法流程

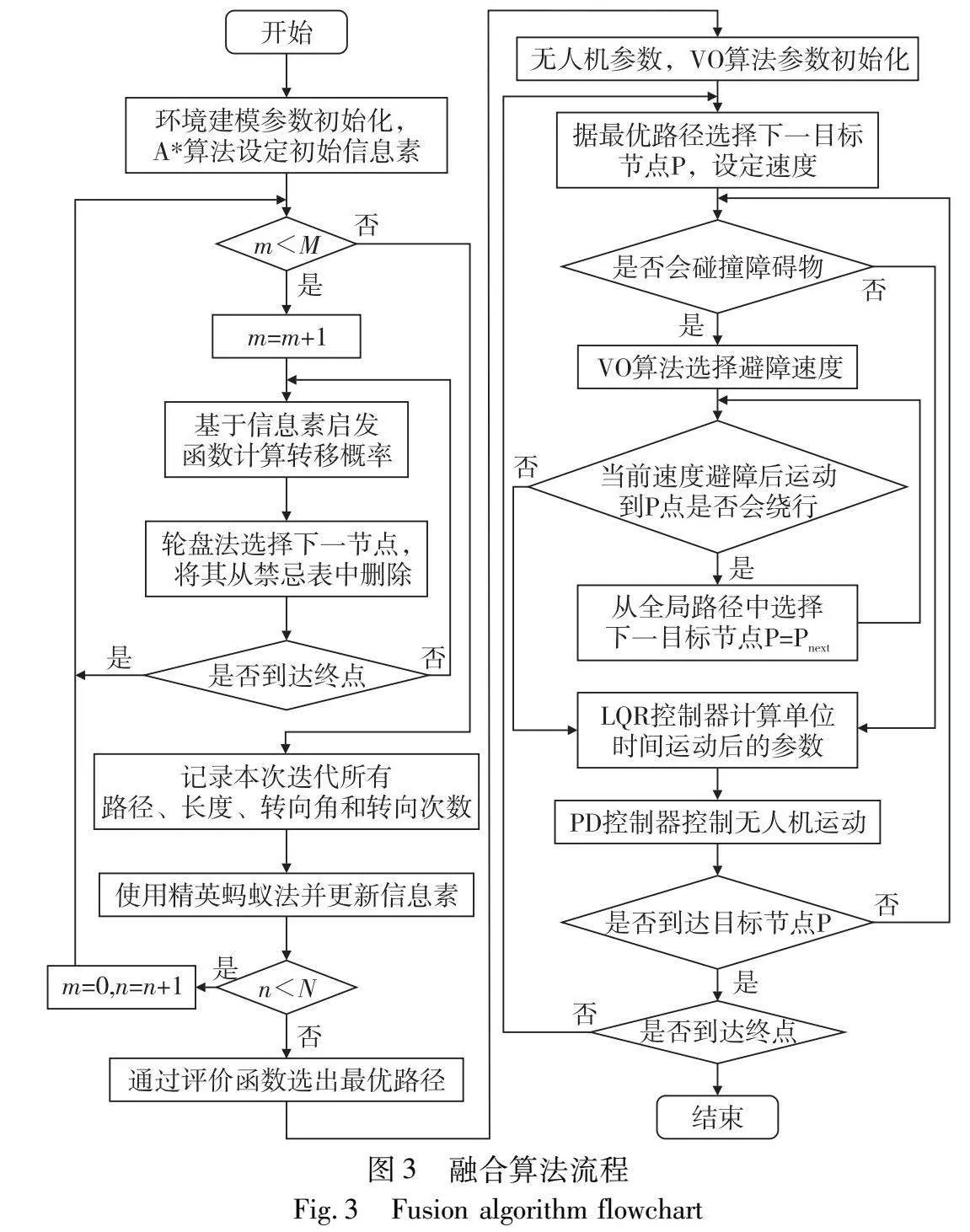
本文融合算法实现流程如图3所示。

2.3.3 算法复杂度分析

算法复杂度可分为时间复杂度与空间复杂度，设参数：iter为迭代次数，M为蚂蚁数目，n是问题规模，N为障碍物的数量。则TSACO算法和改进VO算法的时间复杂度分别为式（19）和（20），空间复杂度分别为式（21）和（22）。

T1=O（iter×M×n2）（19）

T2=O（N2）（20）

S1=O（n2）（21）

S2=O（N）（22）

由式（19）～（22）可知，本文算法与传统算法的运算复杂度一致，改进方法对传统算法的性能和逻辑结构产生积极影响，同时对整体复杂度的增加可忽略。

3 仿真实验与结果分析

本章通过仿真实验来验证前述提出的TSACO和改进VO算法在无人机路径规划问题中的可行性和有效性，仿真实验工具为MATLAB 2019a，运行环境为Windows 10，Intel i7-8750H CPU 2.20 GHz，16 GB。实验主要分为两个部分：a）将TSACO算法与现有算法，包括文献［21］（IACO，融合回退机制Xfj+1H8Brez8nTWsxOxpmnIpW/Riq3nAN8EfeP39XXY=与转角策略），文献［22］（EACO，融合航路选择权重和转向启发函数），传统蚁群算法（ACO）相比较，并按2.3.1节所述的评价函数进行评估；b）基于改进VO算法，设计包含多个动态障碍物的环境作为测试案例，对其动态避障特性进行仿真实验。

3.1 TSACO实验分析

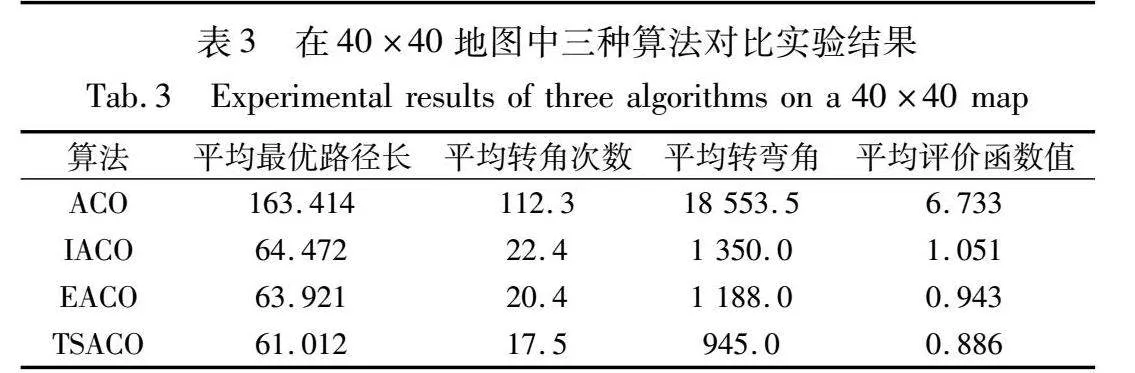
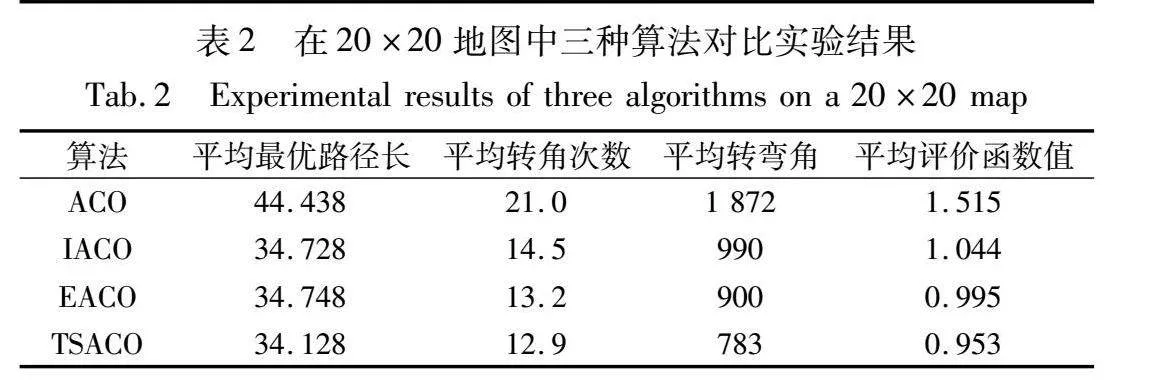
为检验TSACO的寻优性能，本文分别在20×20和40×40的栅格环境下对ACO、IACO、EACO与TSACO进行仿真对比，分别进行10次独立实验，评价函数的参数设定为a1=0.5，a2=0.3，a3=0.2，实验参数如表1所示，具体路径参数对比如表2、3所示，其中40×40的寻优结果如图4所示。

从表2、3和图4可看出，在两种环境中，TSACO在参数相同的情况下，相较于ACO、IACO和EACO搜索到了更短的全局最优路径，且平均转角和平均转向次数相较于其他两种算法也更小。在40×40的栅格环境中，TSACO、IACO、EACO和ACO得到的最短路径长度分别为61.012、64.472、63.921和163.414，平均转角次数分别为17.5、22.4、20.4和112.3，平均转弯角分别为945.0、1 350.0、1 188.0和18 553.5，TSACO相较于IACO、EACO和ACO得到的路径长度分别缩短了5.4%、4.6%和62.6%，平均转角次数减少了21.9%、14.2%和84.4%，平均转弯角减少了30.0%、20.5%和94.9%。然而，相较于文献算法，TSACO的收敛速度略慢，这是为了获得更优的路径，TSACO在蚁群的初始迭代过程中未加入转角启发函数，而是在迭代次数达到总数的20%后才引入。这样的设计可以避免过早地收敛于转角较优但路径长度较长的局部最优路径，因此需要更长的时间来搜索路径，但这种策略能使TSACO最终收敛到评价函数值更优的路径，且在全局规划对实时性要求不高的情况下，略低的收敛速度对算法的整体影响并不显著。

3.2 多动态障碍物环境中的避障实验

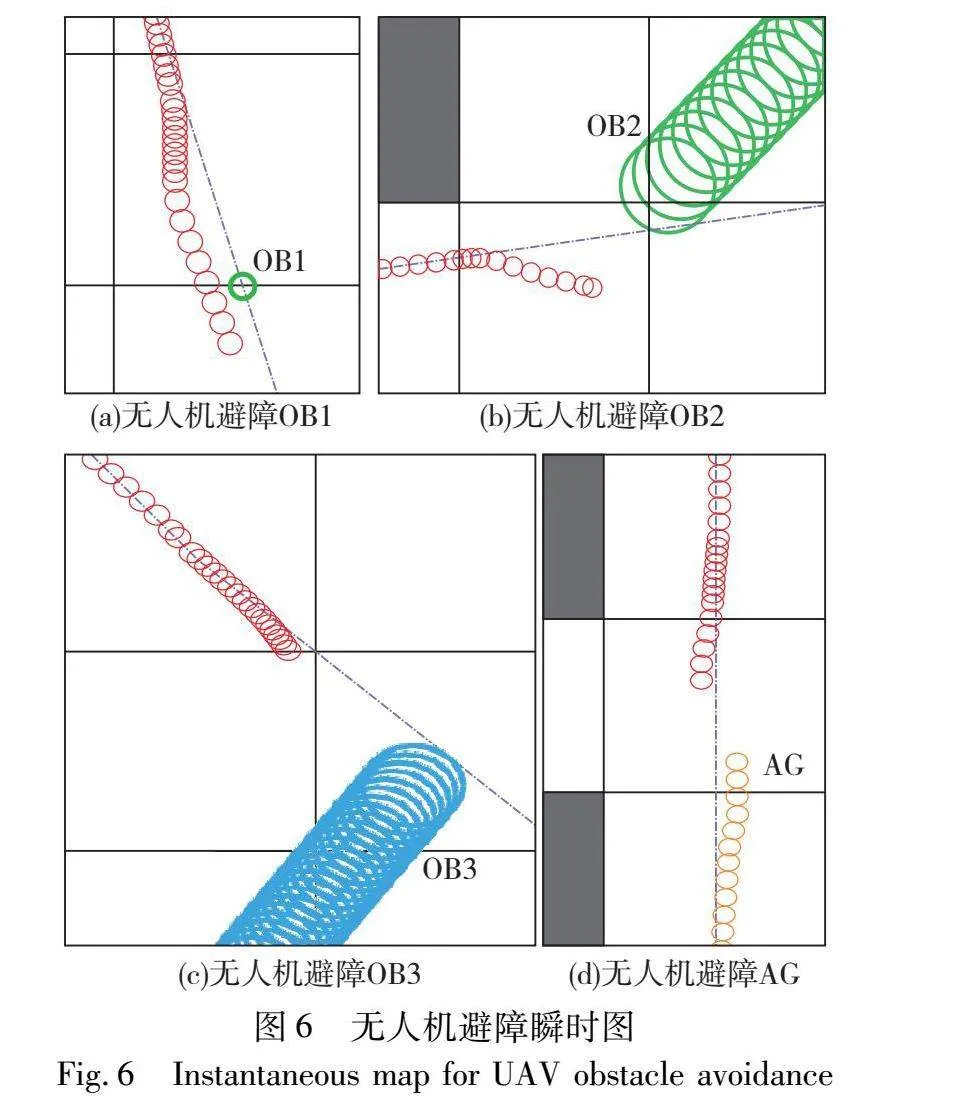
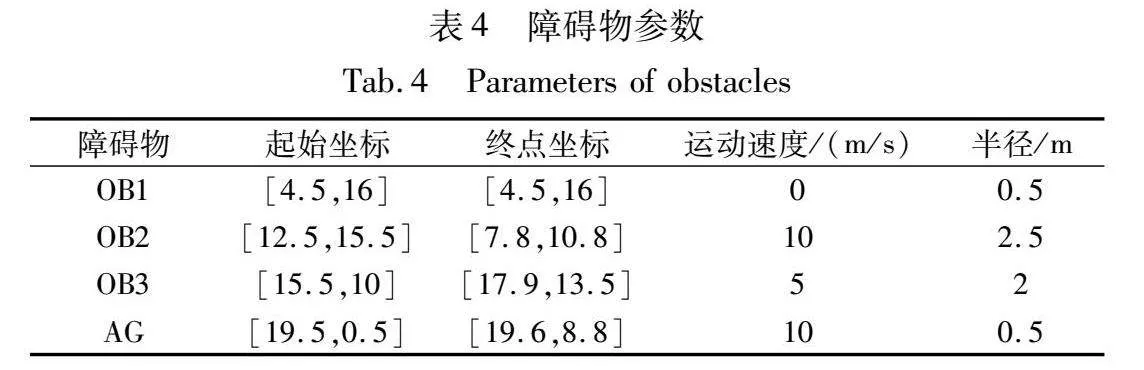
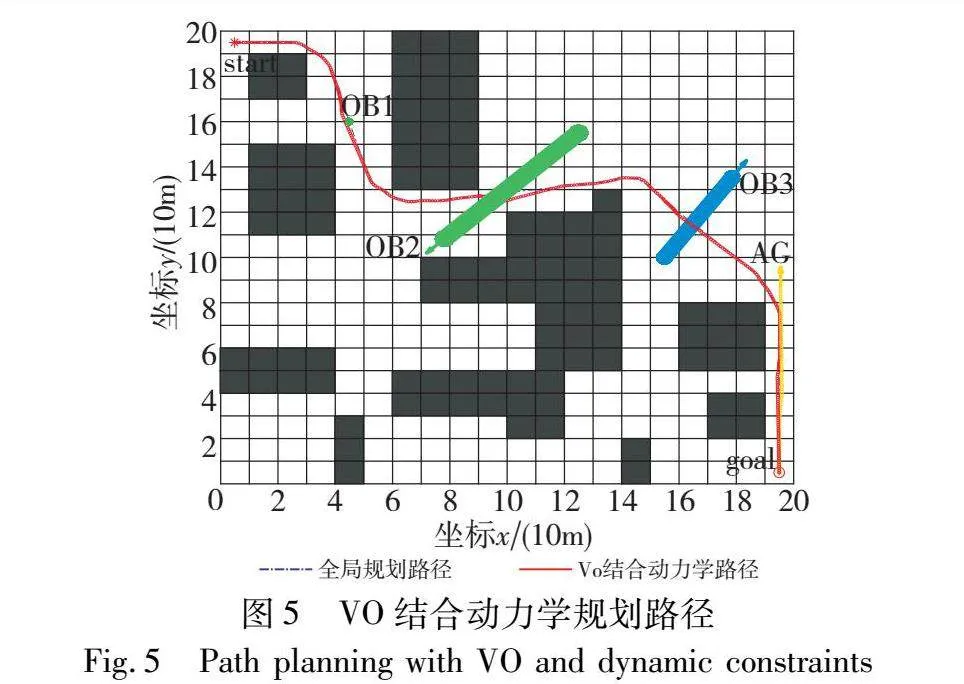
本文结合无人机动力学模型的改进VO算法，在20×20的栅格环境下进行仿真实验，障碍物的参数信息如表4所示，其中无人机最大速度设定为10 m/s，半径为0.5 m，对环境信息进行采样的时间周期为0.1 s。局部避障效果如图5、6所示，无人机控制参数反馈如图7所示。

图5中，蓝色点画线为参考线（部分被红色圈线覆盖），是使用TSACO规划的全局路径；红色圈所构成的路径为无人机的运动轨迹；OB1为做局部规划时出现的静态障碍物；OB2和OB3分别为与无人机运动方向夹角呈钝角和锐角的匀速动态障碍物；AG为同样运用VO算法和无人机相向而行的智能体，箭头分别为各个动态障碍物的运动方向。从图5可以看出无人机在遇到障碍物前会沿着全局规划路径前进，而当判断前方出现障碍物时便启用改进VO算法，根据碰撞锥和最优速度选择原则选定速度来避开障碍物。值得注意的是在发现障碍物后无人机都会进行减速（圈更密集），而在传统VO算法避障时无人机则会不减速直接转向，这是因为加入了无人机动力学方程后，无人机的运动速度不能像理想算法那样突变，故会更加保守地选择改变速度来避开障碍物。图6为无人机动态避障的瞬时图，从图中可更清晰地看出无人机在检测到障碍物后先减速，再改变速度方向避障的过程（红色圈部分）。此外，因本文设定无人机优先向右侧避障，故图6（a）～（d）中无人机均按全局规划路线的右侧方向分别避开障碍物。在本次避障实验中，共进行了43次避障变速操作，平均解算时间为0.024 4 s，最大解算时间0.034 1 s，均在单次采样周期0.1 s以内。

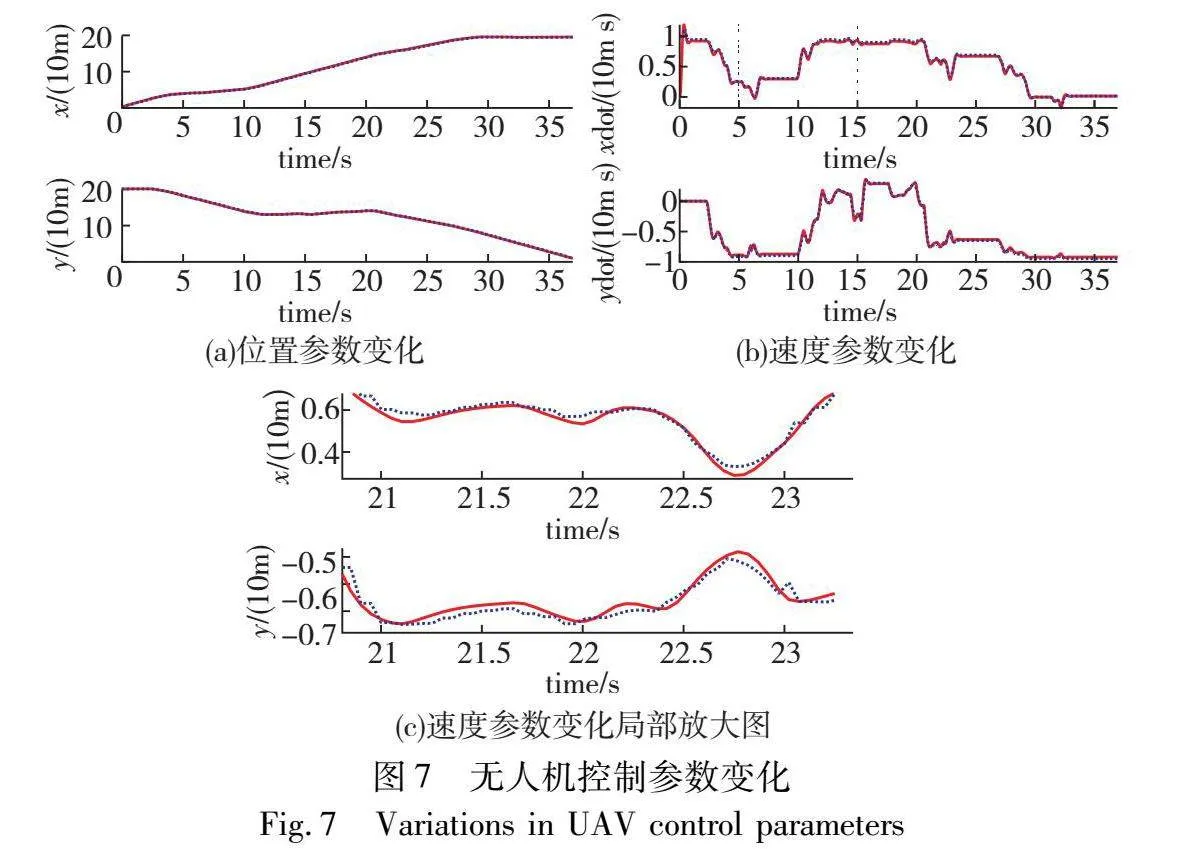
图7（a）为无人机运动过程中横纵坐标的变化曲线；图7（b）为横纵方向上的速度分量变化曲线；蓝色虚线为LQR控制器所生成的期望轨迹参数；而红色曲线为PD控制的跟踪轨迹参数。从图7可以看出跟踪轨迹的参数几乎和期望轨迹参数一致，可见控制效果较好，但在起步阶段因为VO算法设定的初始速度为10 m/s，所以跟踪轨迹在速度参数方面有一段0～10 m/s的起步阶段。如图7（c）所示，跟踪轨迹相较期望轨迹更为平滑，这是由于LQR控制器使用线性化的系统模型计算最优控制输入，无法准确地描述无人机系统的非线性特性，而在跟踪轨迹中通过PD控制平衡了系统响应速度和稳定性，更好地适应无人机系统的非线性特性。

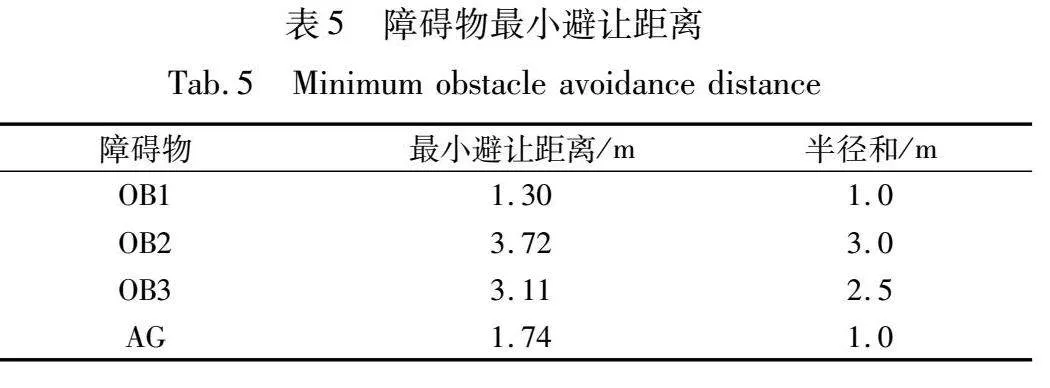
为了更直观地验证改进VO算法的避障特性，本文计算了仿真过程中无人机与各障碍物的最小避让距离（实时距离的最小值），如表5所示，其中半径和为无人机半径与障碍物半径的代数和。

从表5可看出，使用改进VO算法进行避障时，无人机能够在避开障碍物时保留足够的空间。具体而言，对于障碍物OB1、OB2、OB3和AG，无人机分别保留了0.3 m、0.72 m、0.61 m和0.74 m的安全裕度。需要注意的是OB1最小避让距离相对较小，这是因为OB1是静止的障碍物，其速度为0，无人机无须保留较大的避障距离，故2.2.1节中的不确定半径计算结果较小，使得避让距离的裕度较小，提高了避障效率。

4 结束语

本文从全局和局部两方面完整地进行了无人机路径规划研究。在全局规划方面，以传统蚁群算法为基础，利用A非均匀分配初始信息素，解决初始搜索效率低的问题；在概率函数中对启发函数进行改进，使路径减少转向，搜索时更有目标性；采用精英蚂蚁系统加快收敛速度。通过仿真比较验证了TSACO的优越性。在局部避障规划方面，在传统VO算法基础上，加入障碍物自适应不确定半径，增加了避障时的安全性；将碰撞锥改为紧急碰撞锥，避免过早避障；加入速度选择函数，保证所选速度兼顾目标性与连续性。最后在仿真实验中，加入无人机动力学模型，验证了所用算法在模拟环境中都能有效地避开动态障碍物。在今后的研究工作中，会侧重于三维环境和真实环境下的无人机路径规划研究。

参考文献：

［1］Lee K S，Ovinis M，Nagarajan T，et al.Autonomous patrol and surveillance system using unmanned aerial vehicles［C］//Proc of the 15th International Conference on Environment and Electrical Engineering.2015：1291-1297.

［2］杜云，贾慧敏，邵士凯，等.面向多目标侦察任务的无人机航线规划［J］.控制与决策，2021，36（5）：1191-1198.（Du Yun，Jia Huimin，Shao Shikai，et al.UAV trajectory planning for multi-target reconnaissance missions［J］.Control and Decision，2021，36（5）：1191-1198.）

［3］郭英萃，靳慧斌.基于稳定风场下的无人机电力巡检路径规划研究［J］.综合运输，2023，45（3）：110-117.（Guo Yingcui，Jin Hui-bin.Path planning of UAV electric power inspection based on stable wind field［J］.China Transportation Review，2023，45（3）：110-117.）

［4］王东.山地果园植保无人机自适应导航关键技术研究［D］.杨凌：西北农林科技大学，2019.（Wang Dong.Key technologies of adaptive navigation for plant protection UAV in mountain orchard［D］.Yangling：Northwest A&F University，2019.）

［5］王中玉，曾国辉，黄勃.基于改进双向A的移动机器人路径规划算法［J］.传感器与微系统，2020，39（11）：141-143，147.（Wang Zhongyu，Zeng Guohui，Huang Bo.Mobile robot path planning algorithm based on improved bidirectional A［J］.Transducer and Microsystem Technologies，2020，39（11）：141-143，147.）

［6］冯建新，解爽，郭冠麟，等.POMDP-APF：一种基于POMDP模型的APF无人机路径规划策略［J］.计算机应用研究，2023，40（7）：2124-2129，2145.（Feng Jianxin，Xie Shuang，Guo Guanlin，et al.POMDP-APF：UAV path planning strategy of APF based on POMDP model［J］.Application Research of Computers，2023，40（7）：2124-2129，2145.）

［7］赵畅，刘允刚，陈琳，等.面向元启发式算法的多无人机路径规划现状与展望［J］.控制与决策，2022，37（5）：1102-1115.（Zhao Chang，Liu Yungang，Chen Lin，et al.Research and development trend of multi-UAV path planning based on metaheuristic algorithm［J］.Control and Decision，2022，37（5）：1102-1115.）

［8］张艳菊，吴俊，程锦倩，等.多搬运任务下考虑碰撞避免的AGV路径规划［J］.计算机应用研究，2023，41（5）：1-9.（Zhang Yanju，Wu Jun，Cheng Jinqian，et al.AGV path planning considering collision avoidance of multiple handling tasks［J］.Application Research of Computers，2023，41（5）：1-9.）

［9］Dorigo M，Maniezzo V，Colorni A.ANT system：optimization by a colony of cooperating agents［J］.IEEE Trans on Systems，Man，and Cybernetics：Systems，1996，26（1）：29-41.

［10］Dorigo M，Gambardella L M.Ant colony system：a cooperative learning approach to the traveling salesman problem［J］.IEEE Trans on Evolutionary Computation，1997，1（1）：53-66

［11］王晓燕，杨乐，张宇，等.基于改进势场蚁群算法的机器人路径规划［J］.控制与决策，2018，33（10）：1775-1781.（Wang Xiaoyan，Yang Le，Zhang Yu，et al.Robot path planning based on improved ant colony algorithm with potential field heuristic［J］.Control and Decision，2018，33（10）：1775-1781.）

［12］Wang Qingyi，Sun Yongkui，Tang Qichao，et al.A dual-robot cooperative welding path planning algorithm based on improved ant colony optimization［J］.IFAC-Papers Online，2022，55（8）：7-12.

［13］申铉京，施英杰，黄永平XZ8KAlzi5Nv9rbso0gKdsw==，等.基于双向蚁群算法的路径规划研究［J］.哈尔滨工程大学学报，2023，44（5）：865-875.（Shen Xuanjing，Shi Yingjie，Huang Yongping，et al.Path planning optimization using the bidirectional ant colony algorithm［J］.Journal of Harbin Engineering University，2023，44（5）：865-875.）

［14］许文瑶，贺继林.基于改进速度障碍法的水下机器人动态避障［J］.电光与控制，2021，28（12）：86-90.（Xu Wenyao，He Jilin.Dynamic obstacle avoidance for ROV based on improved velocity obstacle method［J］.Electronics Optics & Control，2021，28（12）：86-90.）

［15］Ueda Y，Motoi N.Local path planning based on velocity obstacle considering collision probability and kinematic constraint for mobile robot［C］//Proc of the 48th Annual Conference of the IEEE In dustrila Electronics Society.Piscataway，NJ：IEEE Press，2022：1-6.

［16］杨秀霞，华伟，孟启源.基于有限时间速度障碍法的UAV避障研究［J］.弹箭与制导学报，2018，38（5）：19-22，26.（Yang Xiuxia，Hua Wei，Meng Qiyuan.Study on UAV obstacle avoidance based on finite time velocity obstruction method［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2018，38（5）：19-22，26.）

［17］Michael N，Mellinger D，Lindsey Q，et al.The GRASP multiple micro-UAV testbed［J］.IEEE Robotics & Automation Magazine，2010，17（3）：56-65.

［18］赵倩楠，黄宜庆.融合A蚁群和动态窗口法的机器人路径规划［J］.电子测量与仪器学报，2023，37（2）：28-38.（Zhao Qiannan，Huang Yiqing.Robot path planning based on A ant colony and dynamic window algorithm［J］.Journal of Electronic Measurement and Instrumentation，2023，37（2）：28-38.）

［19］Fiorini P.Motion planning in dynamic environments using velocity obstacles［J］.The International Journal of Robotics Research，1998，7（17）：760-772.

［20］Fu Jun，Lyu Teng，Li Bao.Underwater submarine path planning based on artificial potential field ant colony algorithm and velocity obstacle method［J］.Sensors，2022，22（10）：3652.

［21］Song Baoye，Miao Huimin，Xu Lin.Path planning for coal mine robot via improved ant colony optimization algorithm［J］.Systems Science & Control Engineering，2021，9（1）：283-289.

［22］吴剑，江泽军，朱效洲，等.基于改进蚁群算法的隐身无人机快速突防航路规划技术［J］.电光与控制，2023，30（12）：18-23.（Wu Jian，Jiang Zejun，Zhu Xiaozhou，et al.Rapid penetration path planning of stealth UAVs based on improved ant colony optimization［J］.Electronics Optics & Control，2023，30（12）：18-23.）