基于统计推理的不一致数据清洗方法

摘 要：不一致数据修复是数据清洗领域的一个重要研究方向，现有方法大多是基于完整性约束规则的，采用最小代价原则进行修复，然而，代价最小的修复方案通常是不正确的，导致现有修复方法的准确率较低。针对现有方法准确率较低的问题，提出了一种基于统计推理的不一致数据清洗方法BayesOUR，兼顾修复的代价与质量，提高修复准确性。BayesOUR主要分为三个阶段：首先根据完整性约束规则进行错误检测；然后利用贝叶斯网络推理所有可能的一致性修复方案概率；最后选择概率最大的修复方案进行数据清洗。真实数据上的实验结果表明，该方法与目前领先的方法相比，能够显著提高不一致数据修复的准确性。

关键词：不一致数据；贝叶斯网络；统计推理

中图分类号：TP301 文献标志码：A 文章编号：1001-3695（2024）10-015-2987-06

doi：10.19734/j.issn.1001-3695.2024.02.0055

Cleaning inconsistent data based on statistical inference

Zhang Anzhen1，2，Hu Shengji2，Xia Xiufeng2

（1.Shenyang Institute of Computing Technology，Chinese Academy of Sciences，Shenyang 110168，China;2.School of Computer Science，Shenyang Aerospace University，Shenyang 110136，China）

Abstract：Inconsistent data repair is an important research direction in the field of data repair.Most of the existing methods are based on integrity constraint rules and use the principle of minimum cost for repair.However，the repair scheme with the minimum cost is usually incorrect，which leads to the low accuracy rate of the existing repair methods.To address the problem of low accuracy of existing methods，this paper proposed an inconsistent data repair method based on statistical inference BayesOUR，to balance the cost and quality of repair and improve the repair accuracy.It mainly divided BayesOUR into three phases.Firstly，it performed error detection based on the integrity constraint rule，and then utilized Bayesian network to reason about the probability of all the possible consistent repair schemes.Finally，it selected the repair scheme with the largest probabGKv+QZu+Td7KJLWmUnZiFA==ility for data repair.Experimental results on real data show that the method in this paper can significantly improve the accuracy of inconsistent data repair compared with the current leading methods.

Key words：inconsistent data;Bayesian network;probabilistic inference

0 引言

数据清洗（data cleaning）是数据预处理过程中的一个重要步骤，旨在识别和纠正数据中的错误、缺失、重复或者不一致之类的问题。数据清洗有助于提高数据的质量、准确性和可用性，使其更适合分析和挖掘。随着大数据时代的到来，数据质量问题也随之而来，严重影响了生产生活的方方面面，数据清洗变得越发重要。

本文主要研究数据不一致问题的数据清洗［1］，现有的数据清洗方法一是为了尽可能减少对原始数据的改动，通常遵循最小化修复代价原则，将对数据改动最少的修复方案作为最优修复；二是单纯地统计数据整体出现的频率估计概率，将概率最大的修复方案作为最优修复方案。然而，这些方法仅仅考虑了整体的修复代价或者修复概率，没有考虑整体上的修复质量，导致修复的准确率较低。

为此，本文提出了一种基于统计推理的不一致数据清洗方法BayesOUR，该方法利用贝叶斯网络上的数据结构，考虑其相关属性之间的概率信息，进行概率的统计推理来计算每种修复方案的正确性概率，选择概率最大的修复方案作为最优修复方案，进而提高了修复准确性。具体过程如下：首先，利用完整性约束规则进行不一致检测，识别不一致元组以及可能出错的属性；其次，对每个出错元组，计算其所有可能的一致性修复方案；最后，利用贝叶斯网络建模属性之间的关联关系，并在此基础上设计高效的统计推理方法，计算每种修复方案的正确概率并从中选择概率最大的作为最优方案。

综上所述，本文的主要贡献如下：

a）提出一种高效的启发式错误检测方法，可以有效减小不一致元组规模，提高修复效率。

b）提出了正确性概率模型来量化修复方案质量，并提出一种高效的统计推理方法计算每种修复方案的正确性概率。

c）通过大量实验评估，验证本文方法在真实世界数据集上的有效性和高效性。

1 相关工作

目前，数据清洗领域的研究工作主要分为基于完整性约束规则的以及规则与概率相结合的两大类［2～6］。基于完整性约束规则的方法通常采用最小化修复代价原则，选择对数据改动最小的方案进行数据修复［7～12］。例如，文献［13～16］提出了多种启发式修复方法来提高修复准确性；文献［17］提出了迭代式修复框架DEC，利用联合概率分布修复数据错误；文献［18］提出了“统计失真”定义修复后的数据分布与理想数据分布之间的距离；文献［19］提出了基于最大似然估计的错误修复框架SCARE；文献［20］设计了增量式数据清洗框架ActiveClean；文献［21］提出了基于信念传播和关系依赖网络的迭代修复框架ERACER。这类方法忽视了数据之间的关联关系，导致修复准确性不高。

为了提高修复准确率，Prokoshyna等人［22］最早将概率与规则相结合，提出了概率扰动最小的修复方案求解方法。随后，文献［23，24］提出了基于马尔可夫逻辑网络与拒绝约束规则的混合式数据清洗框架。Rekatsinas等人［25］提出了将完整性约束、知识库、统计学等多种修复方法相结合的HoloClean系统。由于满足约束规则的方法不止一个，Yu等人［26］提出选取概率较大的几种修复方案提交给用户，让用户从中选择真实值，然后根据反馈结果更新概率计算模型。Mahdavi等人［27］同样提出结合统计学习、完整性约束以及概率推理的Raha系统来进行错误数据修复。这些方法在一定程度上提高了修复准确率，然而还未达到实际应用场景对数据质量的要求。

2 预备知识以及问题定义

本章首先介绍函数依赖与数据修复背景知识，其次给出基于统计推理的不一致数据清洗方法的问题定义，最后介绍基于统计推理的数据修复方法。值得一提的是，本文只考虑由拼写错误、替换错误等引发的数据不一致问题，其他类型的错误（如缺失值、重复值等）不在本文研究范围内。

2.1 函数依赖和数据修复

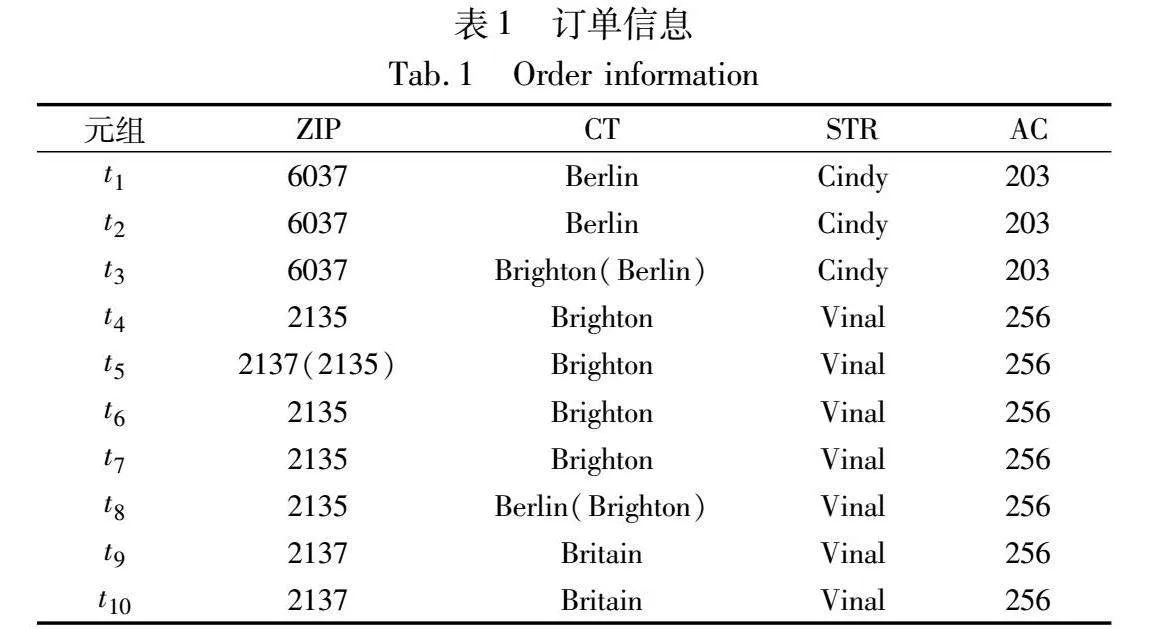
函数依赖（functional dependency，FD）是数据清洗领域中经常使用的一种完整性约束规则，可以简洁有效地表达属性之间的关联关系。为了讨论方便，本文也采用函数依赖作为完整性约束规则。值得一提的是，本文方法可以通过一些扩展应用于其他类型的完整性约束规则。下面，首先介绍本文用到的一个真实数据集。表1展示了部分订单信息表（ZIP表示邮政编码，CT表示城市，STR表示街道，AC表示区编码），其中标红的数据表示错误，括号中的是其真实值。

定义1 函数依赖。给定一个关系模式R，X和A是R上属性集，I是R上的实例。R中FD：X→A，表示X中的属性取值能够唯一地确定A中的属性取值。更正式地说，令ti［A］表示ti元组在A属性中的取值，FD：X→A对于所有元组对ti，tj∈I成立的充要条件如下：如果对所有B∈X，ti［B］=tj［B］，则ti［A］=tj［A］。称X为FD的左部属性（left hand side，LHS），A为右部属性（right hand side，RHS）。

定义2 属性字典。给定关系实例I及FD集合Σ，Ic是I上的干净数据，若存在Σ中任意FD：X→A，那该FD对应的属性字典为Ic上X属性和A属性的所有取值集合。

例1 假设表1上的FD为ZIP→CT（即邮政编码能够唯一确定城市名称）。对应的属性字典为{（6037，Berlin），（2135，Brighton），（2137，Britain）}。

定义3 不一致元组。给定关系实例I及FD集合Σ，对于I中任意元组ti，若存在Σ中任意FD：X→A以及元组tj，j≠i，使得ti［X］=tj［X］，但ti［A］=tj［A］，则ti是不一致元组；反之，ti是一致元组。

例2 假设表1上的FD为ZIP→CT。对于t1元组，由于存在t3元组使得t1［ZIP］=t3［ZIP］，但t1［CT］≠t3［CT］，所以t1是不一致元组。

定义4 不一致数据集。给定数据集实例D及FD集合Σ，若I中所有元组都是一致元组，则D是一致的，记作D|=Σ;否则，D不一致，记作D|≠Σ。

例3 表1中元组t1、t2和元组t3是不一致的，可以通过修改t1、t2或者修改t3解决不一致问题，形成一致数据集。由此看出，表中存在指数多个一致数据集，即，经过错误检测后，会得到多种修复方案，为了兼顾数据修复的质量与数量，通过统计推理的方法得到最优的修复方案。

2.2 问题定义

给定关系实例I及一组FD集合Σ，Iu是I的一个更新集合，对于Iu中的元组t的最大概率修复方案J为

J=argmax{∏t∈Iup（tui）：tui∈Ut，Σ}（1）

其中：Ut，Σ表示t的所有一致性修复方案集合；tui为更新后的元组t，概率为p（ti），p（ti）∈［0，1］。

3 数据修复框架BayesOUR

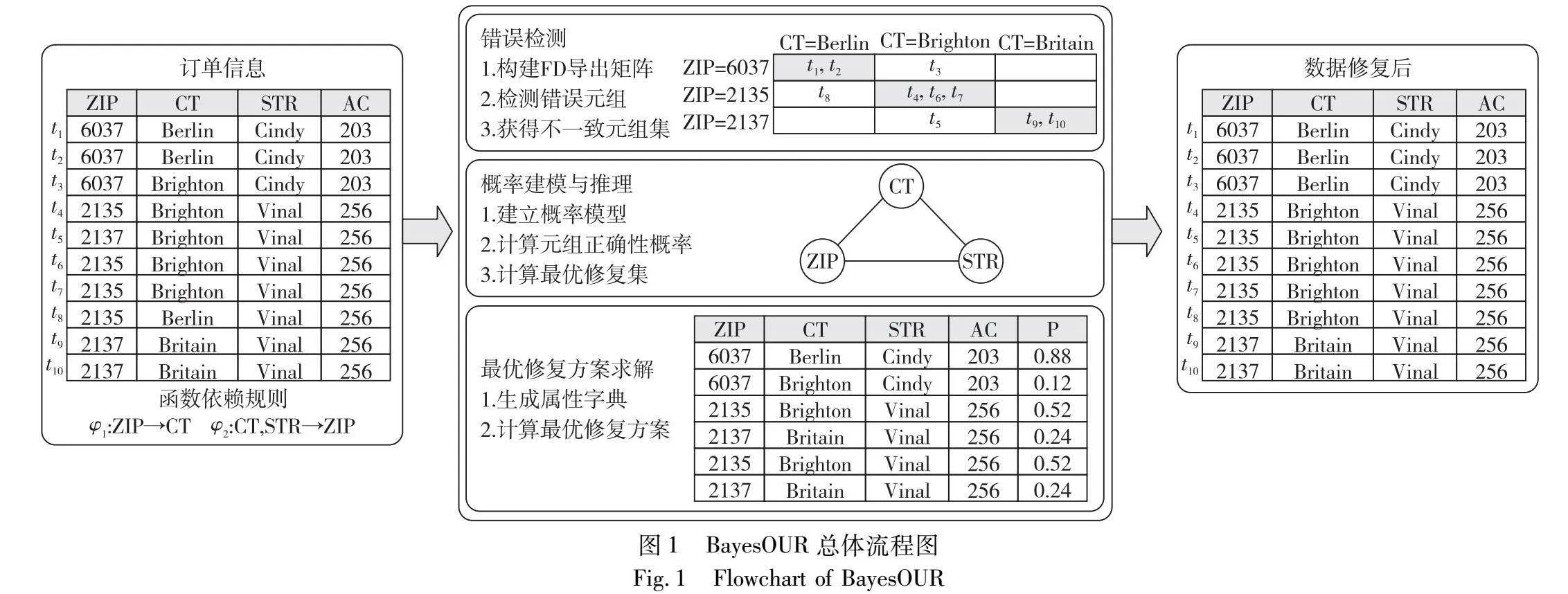
基于统计推理的不一致数据清洗方法BayesOUR的总体流程如图1所示，输入是关系实例I以及FD集合Σ，输出是修复后的数据元组集合，BayesOUR框架主要包括三个阶段：错误检测、概率建模以及最优修复方案求解。错误检测阶段利用FD导出矩阵进行错误检测，将数据分成错误元组和正确元组；概率计算阶段对修复方案正确性概率进行建模并给出一种高效的概率推理方法；修复阶段计算所有一致性修复方案，并从中选择概率最大的作为最终的修复方案。

3.1 错误检测

本节介绍错误检测阶段的具体过程，并且给出FD导出矩阵的定义以及检测流程。

定义5 FD导出矩阵。给定实例I及FD：X→A，若I中元组在X属性集合上有m种可能取值x1，x2，…，xm，在A属性上有n种可能的取值a1，a2，…，an，将I中元组按X与A的取值划分到m×n的导出矩阵Mφ中。矩阵的行表示按X划分的分组，第i行代表X=xi分组，每个分组按照A属性值划分为不同单元格，位于第j列的格子称为A=aj单元格，Mφ反映了I中元组在X属性和A属性上的取值分布情况。

例4 假设表1中数据按照FD：ZIP→CT，按照ZIP和CT取值划分得到FD导出矩阵Mφ，结果如图2所示。根据FD语义可知，ZIP值可以确定唯一的CT值，因此FD导出矩阵的每个分组中应有且仅有一个单元格非空。

错误检测阶段遵循少数服从多数的原则，将每个分组中规模最大的单元格中的元组标记为正确元组，其余单元格内的元组标记为错误元组。例如，图2中对于ZIP=6037分组，CT=Brighton单元格中的元组数量大于其他分组中的数量，因此将该单元格内的元组t1和t2标记为正确，t3标记为错误。

算法1 FD导出矩阵错误检测算法

输入：实例I以及函数依赖集合Σ。

输出：不一致数据修复元组集合U。

1 for i←1 to|Σ|do

2 根据给定函数依赖Σ以及数据构建FD导出矩阵Mφ

3 计算每个分组|X=xi|内所有单元格的大小

4 for X=xi∈Mφi do

5 if |X=xi|分组的任一单元格内元组数量最大

6 将该单元格内的元组标记为正确

7 else

8 将该单元格内的元组标记为错误

9 将标记错误的元组放入更新数据修复集U

FD导出矩阵的错误检测算法如算法1所示。算法的输入是关系实例I和FD集合Σ，输出是不一致数据修复集合U。算法首先对Σ中的每条函数依赖φi构建FD导出矩阵Mφ，并计算每个分组内单元格的大小，然后检测Mφ中的分组，并将其中错误元组进行标记（行1～3）;其次，遍历FD导出矩阵Mφi，若分组内某个单元格内元组数量最大，确定该单元格内元组是正确的，将不在正确单元格内的元组标记为错误（行4～8）;最后，将标记的元组加入U中（行9）。

定理1 FD导出矩阵错误检测算法的时间复杂度为O（|Σ|N）。

证明 算法1遍历函数依赖规则共进行|Σ|次循环，每次循环遍历FD导出矩阵中的元组并标记错误，实例I中共有N个元组，因此，总时间开销为O（|Σ|N）。

3.2 概率建模与推理

本节给出修复方案正确性概率模型，并给出一种基于马尔可夫毯的概率推理方法，可以有效提高推理效率。

对于错误元组t∈U和FD ：X→A，错误可能出现在FD的左部属性X或者右部属性A，在没有进一步分析的情况下，无法确定错误发生的具体位置。因此，将X中的属性和A中的属性都添加到查询集合Q中，该查询集合表示可能发生错误的噪声属性，称其他属性E=A-Q为证据属性，它代表干净的属性（本文仅考虑不一致性错误）。因此，错误元组t可以分为两部分：噪声部分t［Q］和干净部分t［E］。本文目标是使用干净的属性值来预测修改后错误元组的噪声属性的概率。

设t［E］=t［E1，E2，…，EL］且t［Q］=t［Q1，Q2，…，QL］，SE=DOM（E1）×DOM（E2）×…×DOM（EL）表示证据属性的空间，SQ=DOM（Q1）×DOM（Q2）×…×DOM（QK）表示t的查询属性的空间。假设根据SQ×SE上的概率分布P（Q，E）随机生成元组。本文将t修改后的元组tui正确概率建模为给定证据属性值的查询属性值的条件概率，即P（Q=tui［Q］|E=tui［E］）（简称P（tui［Q］|tui［E］））。根据贝叶斯理论，得到

p（tui）=P（tui［Q］|tui［E］）=P（tui［Q］，tui［E］）P（tui［E］）（2）

例5 以错误元组t3为例。由于t3违反了FD：ZIP→CT，在其查询集合中添加噪声属性ZIP和CT，即Q={ZIP，CT}，而其他属性添加到证据属性中，即E={AC，STR}。在给定E的情况下，依据属性字典元组t3的一致性修复方案共有两种，两种修复方案的正确概率分别为p（tu13）=P（ZIP=6037，CT=Berlin|STR=Cindy，AC=203）和p（tu23）=P（ZIP=6037，CT=Brighton|STR=Cindy，AC=203）。

为了推断正确的概率，本文使用了一个广泛的概率图模型——贝叶斯网络，它提供了一种简洁地描述属性的概率分布的方法（图3）。根据贝叶斯网络中的局部马尔可夫性质，网络中所有变量的联合分布都可以因式分解为以其父变量为条件的单个密度函数的乘积。给定A=Q∪E上的贝叶斯网络，式（2）中的P（tui［Q］，tui［E］）可以用以下方程式来近似。

P（tui［Q］，tui［E］）=∏Ki=1P（tui［Qi］|parent（Qi））∏Lj=1P（t［Ei］|parent（Ei））（3）

其中：父节点parent（Qi）和parent（Ei）分别表示Qi和Ej的父节点集。由于所有属性的值都是已知的，所以P（tui［Qi］|parent（Qi））和P（tui［Ej］|parent（Ej））是贝叶斯网络中的条件概率表（CPT）中的常量。

式（2）中的P（tui［E］）是证据属性的边际分布，可以通过边际化查询属性上的联合分布来计算，如式（4）所示。类似于先前的分析，对于Q={Q1，Q2，…，Qk}中的每个Q，可以根据CPT有效地确定P（q，tui［E］）。

P（tui［E］）=∑q∈SQP（q，tui［E］）（4）

事实上，Qi的分布取决于其马尔可夫毯子中属性的联合分布。因此，本文提出在马尔可夫毯子的基础上对Qi进行剪枝。具体地说，设MB（Q）表示Q的马尔可夫毯，且MB（Q）=MB（Q1）∩MB（Q2）∩…∩MB（QK）是所有查询变量的马尔可夫毯的交集。然后使用MB（Q）中的证据属性来剪枝Q，即只考虑与E∩MB（Q）的值在数据集中至少出现一次的查询属性值。贝叶斯网络结构以及条件概率表如图3所示。

例6 以元组t3为例，当t3修复为tu13时，其正确性概率计算过程如下：P（tu13［Q］，tu13［E］）=P（ZIP=6037|CT=Berlin）·P（CT=Berlin|AC=203）·P（STR=Cindy|CT=Berlin，ZIP=6037）·P（AC=203）=0.5×0.67×1×0.33=0.111，对应的MB（Q）={STR}。原始数据中STR=Cindy，则ZIP和CT的组合可以是{6037，Berlin}或者{6037，Brighton}。因此，P（tu13［E］）=P（ZIP=6037，CT=Berlin，STR=Cindy，AC=203）+P（ZIP=6037，CT=Brighton，STR=Cindy，AC=203）=0.1105+0.0154=0.1259，则p（tu13）=P（tu13［Q］，tu13［E］）/P（tu13［E］）=0.88。

3.3 最优修复方案求解

通过概率建模和推理检测出错误元组，根据FD规则为错误元组建立属性字典，其中包含了错误属性在e9DVJSLY/gDjqjrqWbJVuGNVt7QSjogsbgz2knQ+q84=干净数据（标记为正确的元组）中的所有取值情况。给定证据属性下，将属性字典中的属性取值赋给错误元组对应的属性，从而得到错误元组所有可能的一致性修复方案。针对所有一致性修复方案，利用式（2）计算每种一致性修复方案的正确性概率，并选择其中概率最高的修复方案作为错误元组的最终修复方案。

例7 依据属性字典并计算一致性修复方案的正确性概率如图4所示。在给定E={STR，AC}时，t3仅有一种修复方案，选择概率为0.88的一致性修复方案。同理，t5和t8选择概率为0.52的一致性修复方案。通过对比表1中的真实值可以发现，BayesOUR的修复结果都是正确的。

4 实验

在本章中，本文在不同的数据集上将BayesOUR和最先进的方法HoloClean进行对比，此外，还对不同的错误率以及错误类型进行分析。

4.1 实验设置

BayesOUR以及对比方法HoloClean均采用Python实现，实验运行环境配置为IntelCoreTMi7-7700HQ CPU @ 2.80 GHz处理器，8 GB内存，运行Windows 10操作系统。

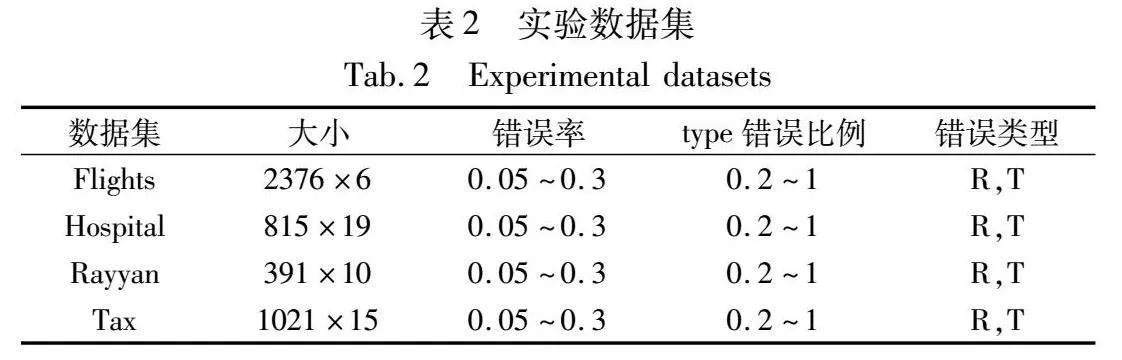
本文在三个真实世界的数据集和一个生成的数据集上进行了实验，这些数据集大多用于测试数据清理工作。表2中给出了数据集、大小、错误率以及错误类型。

Flights是一个真实世界的数据集，该数据集包含网络上不同数据源报告的航班起飞和到达时间的信息。本文使用四个函数依赖来确保每个航班都有唯一的预计和实际的出发和到达时间。

Hospital是一个真实世界的数据集，该数据集是多篇数据清理论文中使用的基准数据集，其拥有高达十五个函数依赖并且具有多属性列决定一个属性列，通过Hospital数据集来确定BayesOUR具有处理多数量以及多属性的函数依赖的数据集性能。

Rayyan是一个真实世界的数据集，该数据是关于文章的相关信息，里面数据的重复率极低。

Tax是一个合成数据集，该数据集来自于BART存储库的综合数据集，获取其中的一部分用于测试BayesOUR对合成数据集的清理性能。

分别给这些数据集注入5%、10%、15%、20%、25%和30%的替换错误和拼写错误，并且控制拼写错误比例为20%、40%、60%、80%、100%，来检测BayesOUR对于两种不同错误造成数据不一致的修复性能。

1）对比方法 本文与先进的数据修复方法HoloClean以及通用数据清理平台NADEEF进行数据修复的实验对比，并评估BayesOUR的性能。

HoloClean是最先进的基于机器学习的数据清理系统，具有完整性约束、外部数据和统计分析。它将现有的依赖于完整性约束或外部数据的定性数据修复方法与利用输入数据的统计属性的定量数据修复方法统一结合起来。

NADEEF是一个规则违规检测系统，允许用户指定多种类型的规则来检测数据错误。

2）评估方法 本实验采用准确率、召回率和F1-score来评估这些方法在错误检测以及修复的有效性。F1-score被定义为

F1=2×Precision×RecallPrecision+Recall（5）

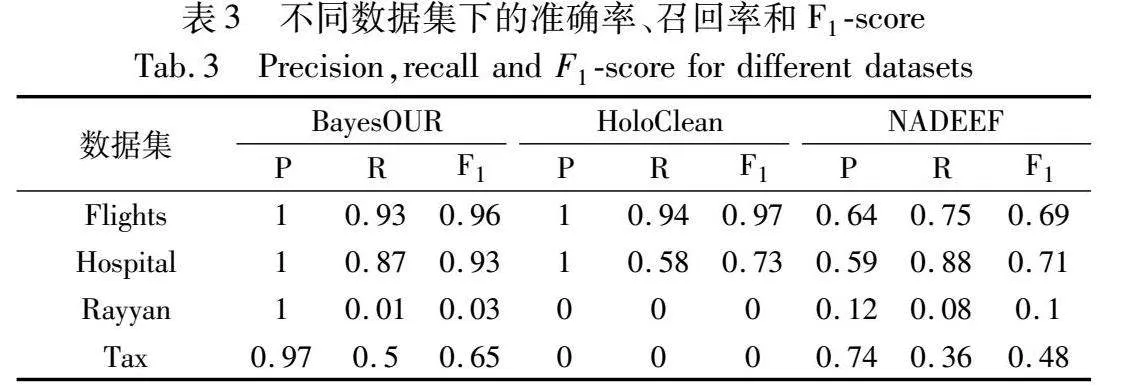
表3是四个数据集在错误率为0.2，type错误比例为0.5情况下，BayesOUR、HoloClean和NADEEF运行后的准确率、召回率和F1-score。从表中可以看出，BayesOUR在不一致数据集（替换错误和拼写错误）上面，相比于其他方法拥有更高的准确率、召回率以及F1-score。

4.2 实验分析

为了证明BayesOUR对不一致数据具有很好的修复结果，本文分别对Flights、Hospital、Rayyan和Tax数据集进行不同错误率以及错误类型比例的注错，来测试错误率以及错误类型对BayesOUR性能的影响。通过大量实验结果分析表明了BayesOUR对于不同错误率和错误类型的数据集都具有良好的修复结果，能够准确修复大部分错误数据。

4.2.1 错误率分析

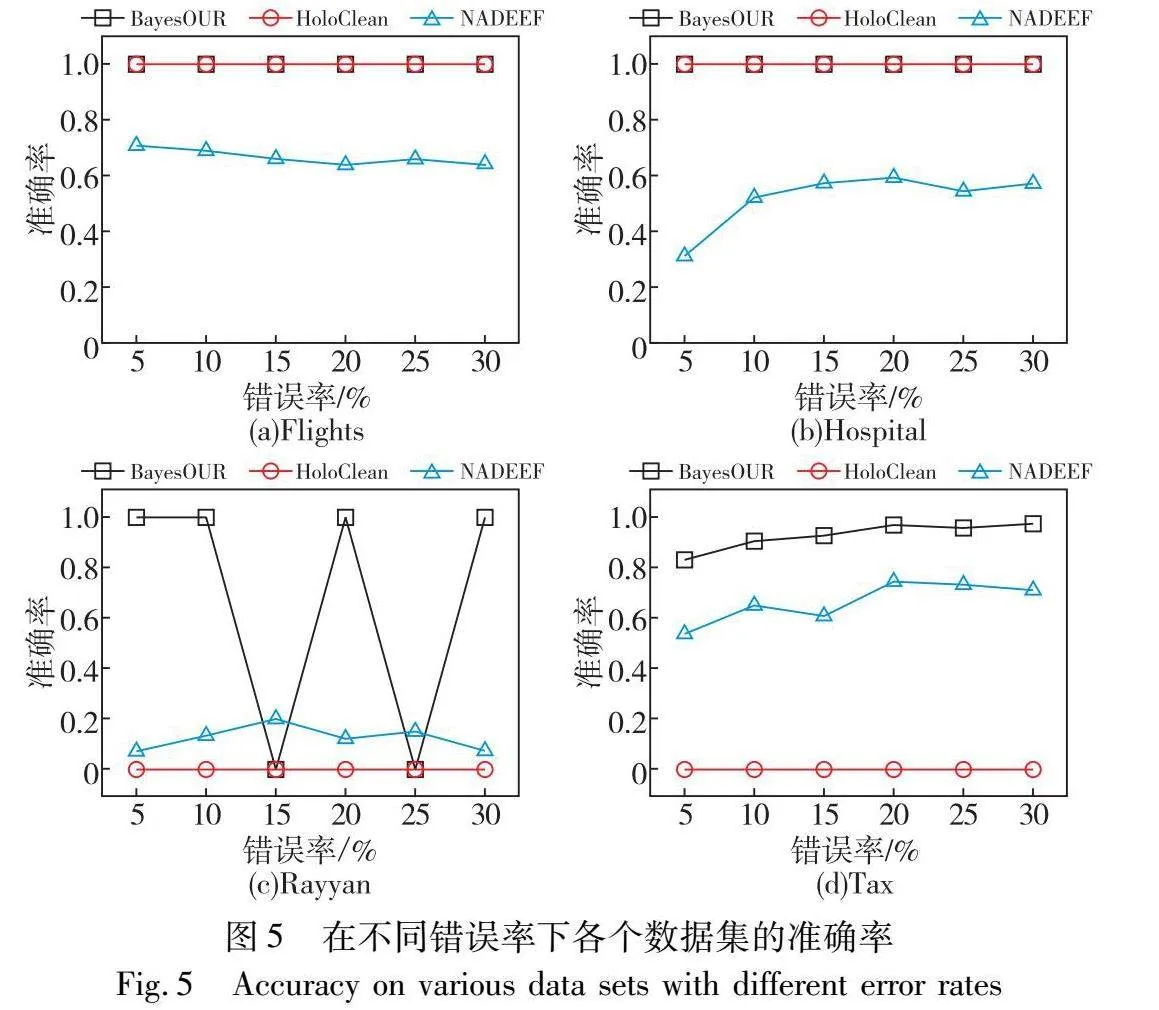
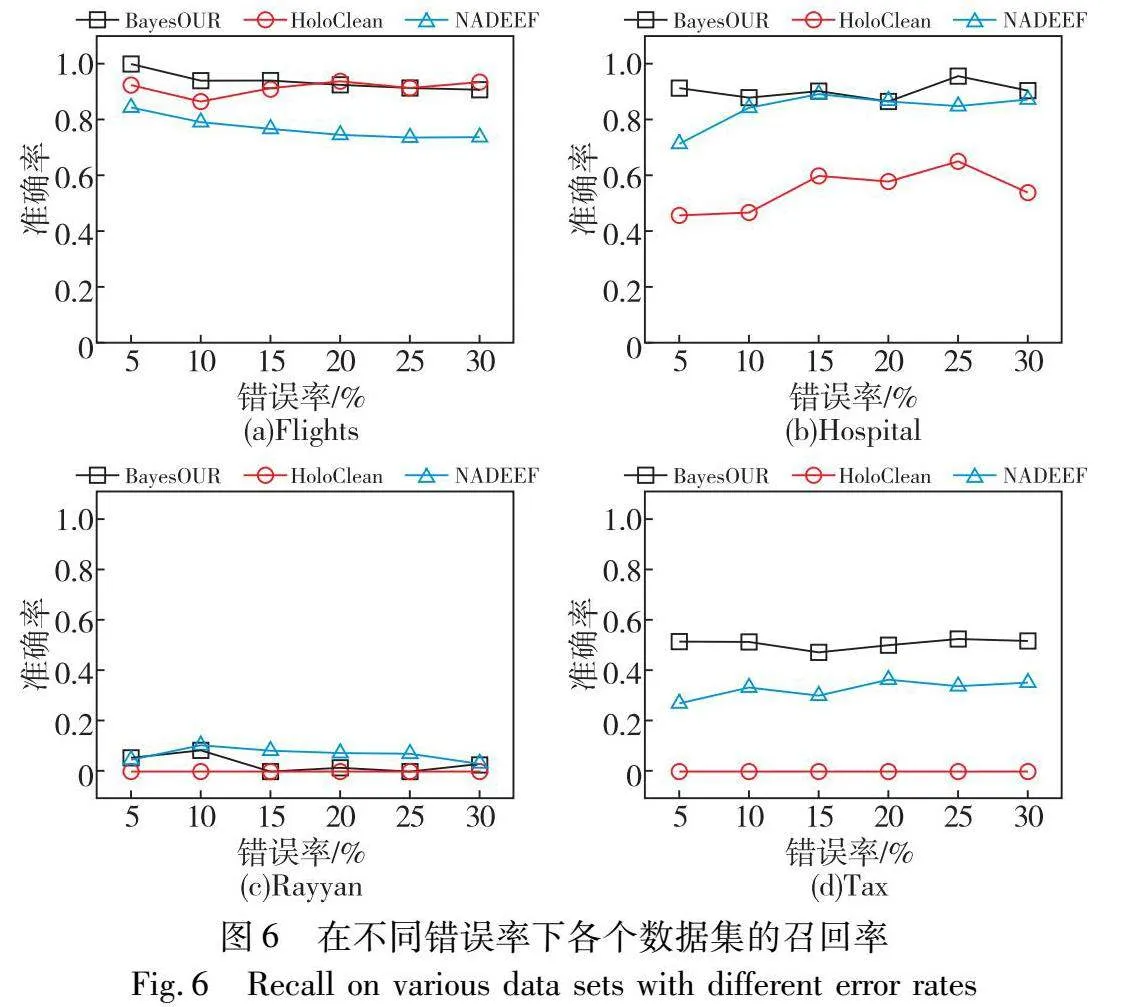
为了考察错误率对BayesOUR的影响，在错误率为5%～30%的不同数据集上运行BayesOUR、HoloClean和NADEEF，分别得到准确率、召回率以及F1-score实验结果，如图5～7所示。

在准确率方面，随着错误率的不断增加，BayesOUR在四种数据集上的实验结果均优于HoloClean和NADEEF，这表明了BayesOUR的基于统计推理的算法能够准确建立数据的正确概率并识别出错误数据。NADEEF在四种数据集上的准确率不高，因为它是根据FD规则去识别错误，并没有结合概率。HoloClean在Rayyan数据集上表现不佳是因为数据集中数据重复率很低，在注入错误后仍具有数据唯一性，无法利用概率信息检测到错误数据，在Tax数据集上表现不佳是因为该数据集由BART自动生成的，生成的数据中有很多数据符合不一致错误，使得其无法识别其中的错误。

在召回率方面，随着错误率的不断增加，BayesOUR在四种数据集上均有良好的数值，表明了其能够识别出数据集中大量的错误数据，这得益于其将规则与概率相结合以及依据数据在贝叶斯网络中的相关性来建立概率模型进行统计推理。HoloClean表现不佳是因为其将整个数据集划分为噪声和干净的部分，使用误差检测方法选取的干净值来学习统计模型以推断每个噪声值的概率。随着误码率的增加，噪声部分和干净部分之间的统计差异增大，导致其无法识别大部分错误。NADEEF仅靠FD规则来识别数据中的错误是不行的，尤其是在数据错误较多时，会把正确数据识别成错误数据。

在F1-score方面，通过图中数据分析可以知道，BayesOUR的实验效果均优于其他两种方法，对于Rayyan这种重复率极低的数据集，BayesOUR只能识别出少量错误，其他两种方法同样很难识别出这种数据集中的错误。而在人工合成数据集Tax上，BayesOUR虽然表现不如Flights和Hospital数据集上的效果好，但是F1-score也高于HoloClean和NADEEF。

4.2.2 错误类型分析

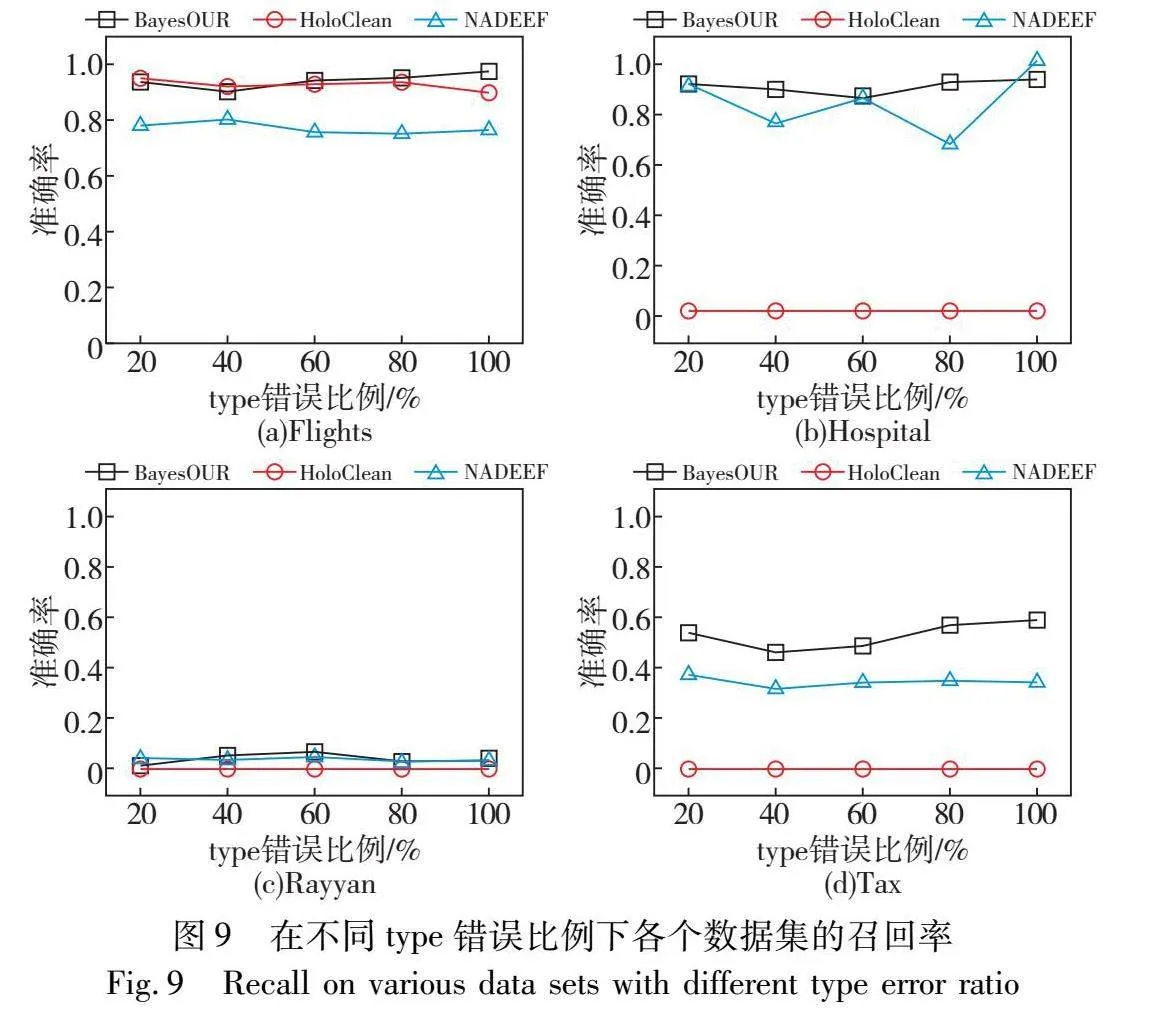
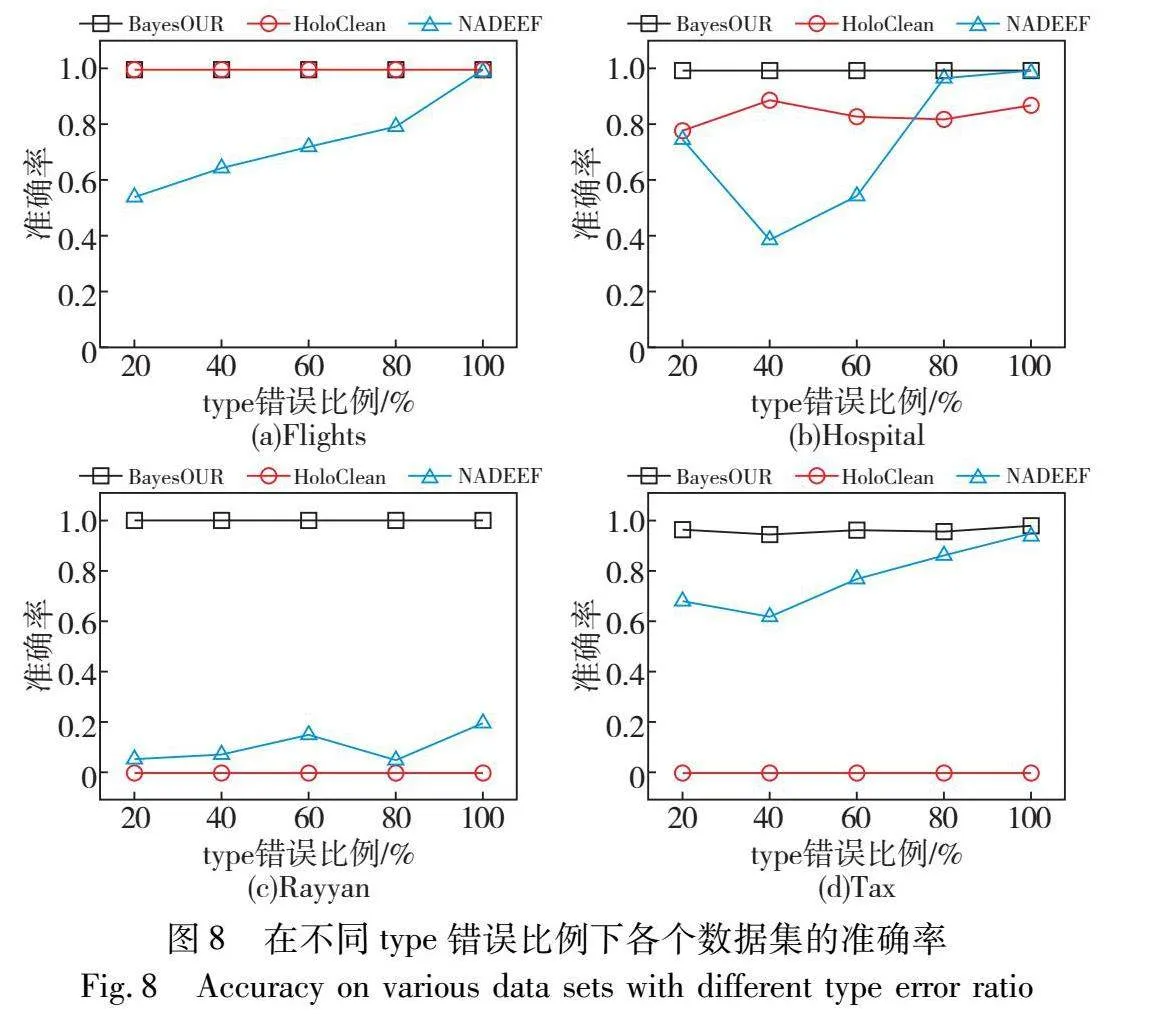
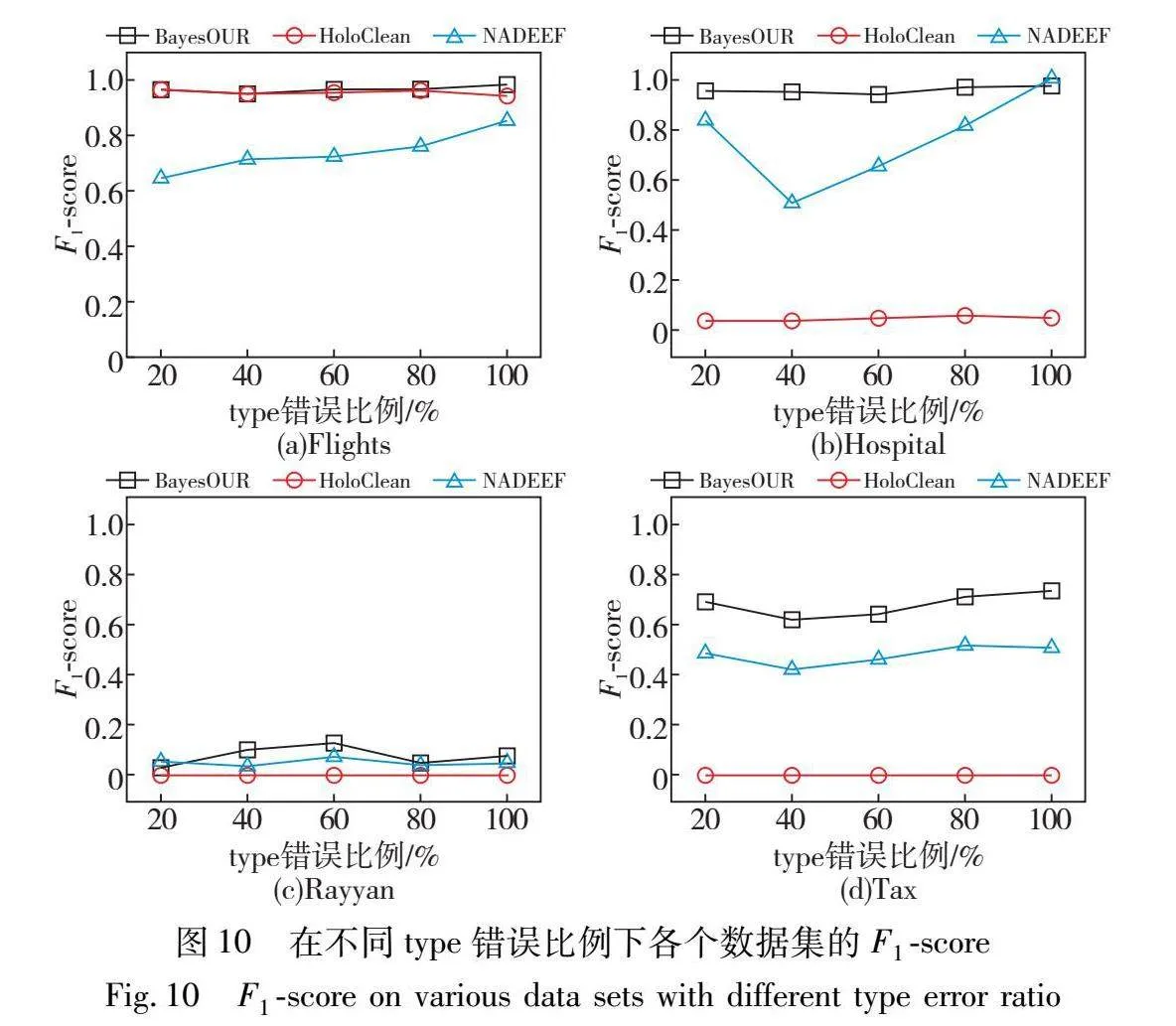
为了考察不同错误类型（替换错误和拼写错误）对BayesOUR性能的影响，在type错误比例为20%～100%的数据集上运行BayesOUR、HoloClean和NADEEF，得到准确率、召回率以及F1-score结果，如图8～10所示。

通过分析图8的实验信息可以发现，错误类型对BayesOUR的准确率并无影响，仅存在微乎其微的波动，而HoloClean和NADEEF的准确率却有较大的影响。造成这种情况的原因是HoloClean和NADEEF对于替换错误的识别能力很弱，当替换错误过多时，会造成局部错误数据数量大于正确数据数量，进而使得其将正确数据识别为错误数据。

通过分析图9的实验信息可以发现，BayesOUR在高度的准确率情况下能够识别出数据集中大部分错误，而HoloClean和NADEEF仅能够识别出数据集中的个别错误或者错误识别正确数据，同样证明了不同的错误类型对其有一定的影响。

通过分析图10的实验信息可以发现，不同错误类型的数据集下，BayesOUR都具有比HoloClean和NADEEF更高的F1-score，充分体现了数据中的不同错误类型并不会影响BayesOUR的数据清洗性能。

5 结束语

本文研究了不一致数据修复问题，提出了基于统计推理的不一致数据清洗方法。该方法通过FD导出矩阵进行数据错误检测，并利用贝叶斯网络进行概率推理建立概率模型，计算元组的正确性概率。最后，通过对错误元组数据建立属性字典以及计算所有一致性修复方案的概率确定最终的修复方案。通过真实数据以及生成数据上的实验结果验证了提出方法的准确性优于现有的修复方法。然而，在重复率较低的数据上，修复性能可能会受到影响。未来的研究将致力于解决这些挑战。

参考文献：

［1］徐耀丽，李战怀，陈群，等.基于可能世界模型的关系数据不一致性的修复［J］.软件学报，2016，27（7）：1685-1699. （Xu Yaoli，Li Zhanhuai，Chen Qun，et al.Repairing inconsistent relational data based on possible world model［J］.Journal of Software，2016，27（7）：1685-1699.）

［2］Bertossi L，Kolahi S，Lakshmanan L V S.Data cleaning and query answering with matching dependencies and matching functions［C］//Proc of the 14th International Conference on Database Theory.New York：ACM Press，2011：268-279.

［3］Chu Xu，Ilyas I F，Papotti P.Holistic data cleaning：putting violations into context［C］//Proc of the 29th IEEE International Conference on Data Engineering.Piscataway，NJ：IEEE Press，2013：458-469.

［4］张安珍，司佳宇，梁天宇，等.规则与概率相结合的不一致数据子集修复方法［J］.软件学报，2024，35（9）：4448-4468. （Zhang Anzhen，Si Jiayu，Liang Tianyu，et al.Subset repair method combining rules and probabilities for inconsistent data［J］.Journal of Software，2024，35（9）：4448-4468.

［5］Livshits E，Kimelfeld B，Roy S.Computing optimal repairs for functional dependencies［J］.ACM Trans on Database Systems，2020，45（1）：1-46.

［6］Sun Yu，Song Shaoxu.From minimum change to maximum density：on S-Repair under integrity constraints［C］//Proc of the 37th IEEE International Conference on Data Engineering.Piscataway，NJ：IEEE Press，2021：1943-1948.

［7］Chomicki J，Marcinkowski J.Minimal-change integrity maintenance using tuple deletions［J］.Information and Computation，2005，197（1-2）：90-121.

［8］Afrati F N，Kolaitis P G.Repair checking in inconsistent databases：algorithms and complexity［C］//Proc of the 12th International Confe-rence on Database Theory.New York：ACM Press，2009：31-41.

［9］Arenas M，Bertossi L，Chomicki J，et al.Scalar aggregation in inconsistent databases［J］.Theoretical Computer Science，2003，296（3）：405-434.

［10］Lopatenko A，Bravo L.Efficient approximation algorithms for repairing inconsistent databases［C］//Proc of the 23rd IEEE International Conference on Data Engineering.Piscataway，NJ：IEEE Press，2007：216-225.

［11］Kolahi S，Lakshmanan L V S.On approximating optimum repairs for functional dependency violations［C］//Proc of the 12th International Conference on Database Theory.New York：ACM Press，2009：53-62.

［12］Bohannon P，Fan Wenfei，Flaster M，et al.A cost-based model and effective heuristic for repairing constraints by value modification［C］//Proc of ACM SIGMOD International Conference on Management of Data.New York：ACM Press，2005：143-154.

［13］Dallachiesa M，Ebaid A，Eldawy A，et al.NADEEF：a commodity data cleaning system［C］//Proc of ACM SIGMOD International Conference on Management of Data.New York：ACM Press，2013：541-552.

［14］Khayyat Z，Ilyas I F，Jindal A，et al.BigDansing：a system for big data cleansing［C］//Proc of ACM SIGMOD International Conference on Management of Data.New York：ACM Press，2015：1215-1230.

［15］Abedjan Z，Akcora C G，Ouzzani M，et al.Temporal rules discovery for Web data cleaning［J］.Proceedings of the VLDB Endowment，2015，9（4）：336-347.

［16］Geerts F，Mecca G，Papotti P，et al.The LLUNATIC data-cleaning framework［J］.Proceedings of the VLDB Endowment，2013，6（9）：625-636.

［17］Berti-équille L，Dasu T，Srivastava D.Discovery of complex glitch patterns：a novel approach to quantitative data cleaning［C］//Proc of the 27th IEEE International Conference on Data Engineering.Piscataway，NJ：IEEE Press，2011：733-744.

［18］Dasu T，Loh J M.Statistical distortion：consequences of data cleaning［J］.Proceedings of the VLDB Endowment，2012，5（11）：1674-1683.

［19］Yakout M，Berti-Equille L，Elmagarmid A K.Don’t be SCAREd：use SCalable automatic REpairing with maximal likelihood and bounded changes［C］//Proc of ACM SIGMOD International Conference on Management of Data.New York：ACM Press，2013：553-564.

［20］Krishnan S，Wang Jiannan，Wu E，et al.Active-Clean：interactive data cleaning for statistical modeling［J］.Proceedings of the VLDB Endowment，2016，9（12）：948-959.

［21］Mayfield C，Neville J，Prabhakar S.ERACER：a database approach for statistical inference and data cleaning［C］//Proc of ACM SIGMOD International Conference on Management of data.New York：ACM Press，2010：75-86.

［22］Prokoshyna N，Szlichta J，Chiang F，et al.Combining quantitative and logical data cleaning［J］.Proceedings of the VLDB Endowment，2015，9（4）：300-311.

［23］Ge Congcong，Gao Yunjun，Miao Xiaoye，et al.A hybrid data cleaning framework using Markov logic networks［J］.IEEE Trans on Know-ledge and Data Engineering，2022，34（5）：2048-2062.

［24］Ge Congcong，Gao Yunjun，Miao Xiaoye，et al.IHCS：an integrated hybrid cleaning system［J］.Proceedings of the VLDB Endowment，2019，12（12）：1874-1877.

［25］Rekatsinas T，Chu Xu，Ilyas I F，et al.HoloClean：holistic data repairs with probabilistic inference［EB/OL］.（2017-02-02）.https：//arxiv.org/abs/1702.00820.

［26］Yu Zhuoran，Chu Xu.PIClean：a probabilistic and interactive data cleaning system［C］//Proc of International Conference on Management of Data.New York：ACM Press，2019：2021-2024.

［27］Mahdavi M，Abedjan Z，Fernandez R C，et al.Raha：a configuration-free error detection system［C］//Proc of International Conference on Management of Data.New York：ACM Press，2019：865-882.