基于属性隐私的统计查询定价模型

摘 要：现有统计查询定价模型没有考虑查询结果揭露数据集敏感属性的问题，难以通过相应地补偿数据提供方激励共享，对此提出一种基于属性隐私的定价模型。首先，基于提出的宽松近似Wasserstein机制（RAWM）计算查询敏感度，直接计算输出分布对距离的宽松上界以提高效率；然后，以约束属性隐私损失为前提，根据查询敏感度、噪声方差、补偿参数对数据提供方进行补偿；最后，在补偿之上运用成本加成法设计了多个无套利定价函数，可以针对单补偿成本和多边际成本等场景定价。实验结果表明，查询敏感度的计算时间从线性复杂度降低到了常数复杂度，在一亿数据量下仅有0.52%的效用代价；定价模型能够提供细粒度补偿以激励共享；设计的定价函数满足无套利性。

关键词：数据定价；数据共享；属性隐私；河豚鱼隐私；无套利

中图分类号：TP301 文献标志码：A 文章编号：1001-3695（2024）10-014-2978-09

doi：10.19734/j.issn.1001-3695.2024.02.0044

Pricing statistical query based on attribute privacy

Fang Jiahao， Guo Bing

（College of Computer Science， Sichuan University， Chengdu 610065， China）

Abstract：Current statistical query pricing models have not considered the problem that query results reveal sensitive attri-butes of datasets， making it difficult to incentivize sharing by compensating data providers accordingly. Therefore， this paper proposed a pricing model based on attribute privacy. Firstly， the model calculated query sensitivity based on the relaxed approximation Wasserstein mechanism （RAWM） proposed， improving efficiency by directly calculate the relaxed upper bound of output distribution pairs. Then， with bounding privacy loss， the model compensated data providers based on query sensitivity， noise variance and compensation parameters. Finally， by using cost-plus pricing on compensation， this paper designed several arbitrage-free pricing functions， which could be used in scenarios such as single compensation costs and multiple marginal costs. The experiment results show that the running time of calculating query sensitivity is reduced from linear complexity to constant complexity， with a utility cost of only 0.52% when data volume is 100 million. The pricing model provides fine-grained compensation to incentivize sharing. Pricing functions satisfy arbitrage freeness.

Key words：data pricing; data sharing; attribute privacy; pufferfish privacy; arbitrage freeness

0 引言

数据共享是数字经济的关键环节。如何让社会各方积累的数据流通起来，打破数据孤岛并盘活数据，是当今急需研究和解决的问题［1］。目前，国内外已经出现了如贵阳大数据交易所［2］、DAWEX［3］等数据交易中心和平台。查询交易市场可以避免直接交易原始数据［4］。统计查询服务是最基本的数据服务形式，如直方图查询、数据立方查询等［5～7］。

数据定价是解决数据共享难题的重要基础。数据质量是定价的重要参考因素。陈思莹等人［8］综合考虑了准确性、完整性、时效性、一致性四个数据质量维度，设计了定价函数。文献［9］认为现有研究忽略了数据信息价值评估，用香农熵和非噪声比设计了信息质量指标指导定价。这些基于数据质量的方法，都没有考虑到数据共享对数据敏感属性的揭露问题。

基于模型贡献衡量的定价也是重要的定价思路。刘珂［10］在预测任务中基于Shapley值将特定预测结果与平均预测结果之差作为定价依据。Wang等人［11］设计了考虑训练数据贡献顺序的联邦Shapley值以对训练数据估值。Xu等人［12］将模型参数分布的信息熵减小量作为数据贡献衡量和定价参考。基于模型贡献衡量的定价适用于明确的数据应用场景，能够保证合作多方公平利益分配，不适合本文中应用场景不明确的统计查询。

此外，也有基于博弈论和拍卖理论设计定价机制的方法。卢玉等人［13］设计了考虑底价的数据密封拍卖机制对数据进行定价。涂辉招等人［14］设计了带有平台利润约束的Stackelberg博弈机制以提升数据市场多方效用。Wang等人［15］将众包数据蕴涵的个性化位置隐私作为激励双边拍卖定价的参考。Li等人［16］在基于Stackelberg博弈的数据定价机制中平衡了隐私和公平。然而这些方法对于存在敏感属性顾虑的场景难以指导卖家出价，导致多方博弈定价结果无法对卖家实现效用最大化。

数据安全和隐私是数据共享中的重要问题，巫朝霞等人［17］ 强调了医疗数据共享的安全性和隐私性。基于隐私补偿的定价是数据定价的重要思路之一。Li等人［18］提出了由统计查询和噪声量共同确定价格的个人数据查询市场，但是要求个人数据之间相互独立，针对数据间存在关联的情况，Niu等人［6］通过在补偿函数中引入一个表征数据关联度的量实现了更准确的补偿和定价。Shen等人［19］基于差分隐私框架设计了个人数据银行的查询服务定价方法。Cai等人［20］通过量化属性相关性实现更精准的高维个人数据定价。然而，这些方法只考虑了对个人隐私损失的补偿，只适用于个人数据，没有考虑针对更广泛的属性隐私损失对数据提供方进行补偿和激励。

近年来，越来越多的研究提到一种新的隐私问题，即使是在数据集上提供非原始数据的数据服务，如统计查询和机器学习服务，也会揭露数据集的全局属性，这些全局属性蕴涵着商业秘密、安全秘密、知识产权等敏感信息［21］。例如，互联网视频公司共享观看数据统计查询，会揭露其流量水平和盈利状况［22］；铁路局提供某地区物理车辆的开行记录统计查询，会揭露车辆投用和维护状态比例，导致战时后勤运输能力等敏感信息被推断；语音识别软件公司提供语音识别服务，攻击者可以通过观察特殊样本输出，反向推断训练集的特殊口音样本比例，进而挖掘该公司模型领先市场的秘诀［23］。形式化描述敏感属性保护问题的隐私理论框架被相应提出。针对差分隐私（DP）［24］只能衡量个人隐私保护问题的不足，Kifer等人［25］对DP进行推广，提出了可以描述更多隐私保护场景的河豚鱼隐私定义。Zhang等人［26］针对敏感属性保护问题，基于河豚鱼隐私提出了属性隐私定义，将数据集统计特性和背后的分布参数作为需要保护的对象。然而，上述隐私定义只描述了敏感属性保护问题，没有解决揭露敏感属性的数据定价问题。

隐私定义只能从理论上描述隐私保护问题，而随机化机制是保护隐私的具体方法。Song等人［27］以满足河豚鱼隐私要求为目标提出了通用但计算难的Wasserstein机制（WM）。Zhang等人［26］提出了满足属性隐私要求的马尔可夫毯机制（MQM）。Chen等人［28］以河豚鱼隐私为基础针对敏感属性保护问题定义提出了近似Wasserstein机制（AWM）和期望机制（EVM）。然而这些随机化机制无法同时保证高效用和高效率，高效的EVM和MQM存在缺乏合理性或低效用的问题，而高效用的WM和AWM存在低效率或无法精确计算的问题，因此基于这些随机化机制设计定价方法都存在缺陷。

针对上面提到的问题，本文提出一种基于属性隐私的统计查询定价模型。首先，提出满足属性隐私要求的随机化机制RAWM，并基于RAWM计算查询敏感度，在计算分布距离时直接高效计算宽松上界；然后，综合查询敏感度、噪声方差、补偿参数设计了补偿函数；最后，给出了设计无套利定价函数的方法，在补偿之上使用成本加成法针对多个场景设计了无套利定价函数。

本文的主要工作如下：

a）首次考虑了包含敏感属性揭露问题的数据统计查询定价问题，提出了相应的补偿方法和定价方法。

b）首次提出了随机化机制RAWM，并基于RAWM计算RAWD敏感度作为查询敏感度，以极小效用代价提高了效率。

c）在真实数据集上对本文定价模型进行了实验。实验结果表明：在一亿数据量下，本文的查询敏感度算法仅以0.52%的效用代价将计算时间从线性复杂度降低到了常数复杂度；模型能够提供细粒度补偿以激励共享；套利攻击均未成功，验证了定价函数的无套利性。

1 相关技术基础

1.1 属性隐私

属性隐私［26］是用于保护数据集敏感属性的严格隐私定义。属性隐私是河豚鱼隐私的一个实例，而河豚鱼隐私是差分隐私的一个推广［25］。河豚鱼隐私由三个部分组成：一个数据提供方想要保护的潜在秘密集合S，一个数据提供方希望他人无法判别的秘密对集合SP=S×S，以及一类代表了攻击方对数据D生成方式的可能信念的分布集合Θ。通过对河豚鱼隐私定义的三个部分进行实例化，就可以得到属性隐私定义。

定义1 （，δ）-属性隐私［26］。让（Dj1，…，Djm）， j∈［n］表示一条从一组随机变量X=（Xj1，…，Xjm）中独立同分布采样得到的m维记录，其中n是数据集记录数，Xi描述了Di服从的边缘分布。从每个随机变量Xi选取出一个分布参数i，i进一步被看做是随机变量Φi的一个实现，其中Φi的取值范围表示为Ψi。全体Φi构成m维随机变量Φ=（Φ1，…，Φm），属性间的关联由Φ服从的联合分布描述，其中Φ∈AC，AC表示可能的m维随机变量的集合。SC［m］表示数据集D敏感属性列的下标集合。给定下面的三元组（S，SP，Θ）：

a）秘密集合：S={sia：=1［Φ i=a］：a∈ΨiS，ΨiSΨi，i∈SC} 。

b）秘密对集合：SP={（sia，sib）∈S×S，i∈SC}。

c） 数据分布集合：

Θ是D所有可能数据分布θ的集合。对于每一个可能的m维随机变量Φ∈AC，Θ中都有一个对应的数据分布θΦ∈Θ代表着D总体服从的分布。

一个随机化机制Euclid Math OneMAp被称为是满足（，δ）-属性隐私的，当其对于任意（sa，sb）∈SP，任意θ∈Θ，都满足

P（Euclid Math OneMAp（D）=O|sa，θ）≤exp（）·P（Euclid Math OneMAp（D）=O|sb，θ）+δ

其中：是隐私预算；δ是近似概率。

为了方便表示秘密集合S和秘密对集合SP专属于敏感属性下标i∈SC的子集，本文接下来用Si表示S专属于i的子集：Si={sia：=1［Φ i=a］：a∈ΨiS，ΨiSΨi}，用SPi表示SP专属于i的子集：SPi={（sia，sib）∈Si×Si}。

1.2 近似Wasserstein机制

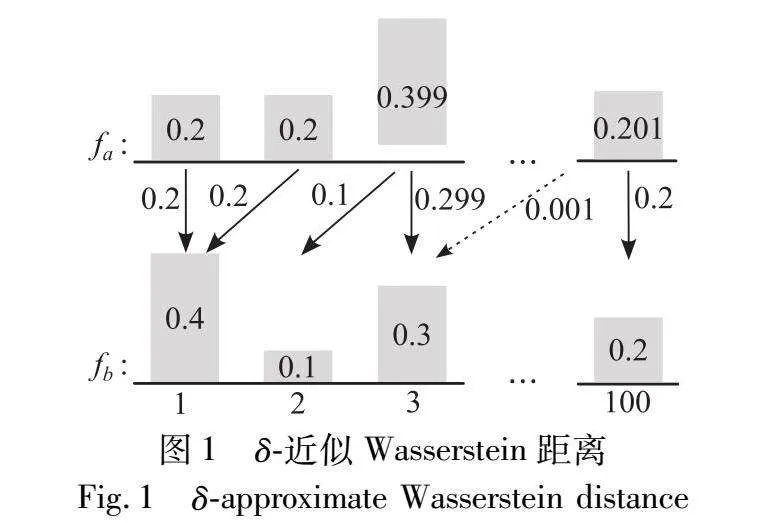
WM是第一个可以满足河豚鱼隐私定义的通用随机化机制，需要计算查询输出分布对fa、 fb的∞-Wasserstein距离，计算过程可以看作寻找使得概率最大转移代价最小的联合分布［27］。但是当fa、 fb的支撑集范围很大，却只由极少概率质量决定最大转移代价，WM计算的∞-Wasserstein距离便会偏大，导致添加过多的拉普拉斯噪声，查询效用过差。对此，相较于WM，近似Wasserstein机制（AWM）［28］在计算∞-Wasserstein距离时忽略联合分布支撑集上至多δ概率质量，以规避极小部分概率质量的影响，只需要添加适量的噪声即可实现河豚鱼隐私保证。AWM计算出来的距离被称为δ-近似Wasserstein距离，严格定义如下：

定义2 δ-近似Wasserstein距离［28］。让fa、 fb表示一对定义在Euclid ExtraaBp上的概率分布，Γ（fa， fb）表示所有以fa、 fb为边缘分布的联合分布集合。对于一个联合分布γ∈Γ（fa， fb），让Rsupp（γ）表示一个概率值不低于1－δ的支撑集子集，则fa、 fb之间的δ-近似Wasserstein距离被定义为

Wδ（fa， fb）=infγ∈Γ（fa，fb），Rsupp（γ）max（t，s）∈R|t－s|

如图1所示，对于图中两个分布，∞-Wasserstein距离为97，而忽略掉概率转移中代价为97的0.001质量后，剩下部分的最坏转移代价仅为1，也就是说δ-近似Wasserstein距离为1，意味着WM添加的噪声是AWM所添加噪声的97倍。AWM虽然无法计算δ-近似Wasserstein距离的精确解析解，但提供了一种忽略联合分布支撑集子集上少量概率的近似计算思路。

AWM遍历河豚鱼隐私框架中所有秘密对（sa，sb）∈SP和数据分布θ∈Θ的组合，计算每一个组合条件下数据分布对的δ-近似Wasserstein距离，找出最大值，并结合隐私预算对查询结果添加一个拉普拉斯噪声，满足河豚鱼隐私要求。用Lap（λ）表示一个位置参数为0，尺度参数为λ的拉普拉斯分布。用fa、 fb分别表示F（X）|sa，θ和F（X）|sb，θ服从的分布。

定理1 近似Wasserstein机制：

Euclid Math OneMAp（D）=F（D）+Lapsup（sa，sb）∈SP，θ∈ΘWδ（fa， fb））（1）

满足（，δ）-河豚鱼隐私［28］。

1.3 无套利性

在定价理论中，定价函数的无套利性是一个重要的性质，尤其是对于数据定价［5］。因为与许多传统商品不同的是，以统计查询为代表的数据服务具有更加丰富的多样性，更容易发生套利现象，被买家恶意利用。套利现象描述的是这样一种行为：一个狡猾的买家想要购买查询A，同时他也注意到他也可以通过购买B和C并组合查询结果得到A的结果。如果B和C的价格之和低于A的价格，那么该买家一定会选择购买B和C，而不会购买A。一个合理的定价函数应该是无套利的，以避免发生套利行为。用符号Q=（F，v）表示一个统计查询服务，其中v为拉普拉斯噪声方差。潜在的套利关系可以由查询确定性关系的符号Euclid ExtraaAp表示，例如在上面的例子中，假设服务的噪声方差都为0.1，通过组合查询B和C的结果，可以在不购买A的前提下推断出查询A的结果，则该关系可以表示为{（B，0.1），（C，0.1）}Euclid ExtraaAp（A，0.1）。

定义3 查询确定性［6，18］。查询确定性是定义在一个查询服务多重集合Q={Q1，…，Qt}={（F1，v1），…，（Ft，vt）}和一个统计查询服务Q=（F，v）之间的一种关系。Q确定Q，用符号表示为QEuclid ExtraaApQ，并且该关系需要满足以下性质：

a）加性，{（F1，v1），…，（Ft，vt）}Euclid ExtraaAp（∑tk=1Fk，∑tk=1vk）；

b）标量乘性，c∈Euclid ExtraaBp，（F，v）Euclid ExtraaAp（cF，c2v）；

c）松弛性，v≥v′，（F，v′）Euclid ExtraaAp（F，v）；

d）传递性，若Q1Euclid ExtraaApQ1，…，QtEuclid ExtraaApQt且{Q1，…，Qt}Euclid ExtraaApQ，

则∪tk=1QkEuclid ExtraaApQ。

查询确定性还有一种更加凝练的表述方式：{（F1，v1），…，

（Ft，vt）}Euclid ExtraaAp（F，v），当且仅当存在c1，…，ct使得

c1F1+…+ctFt=F和c21v1+…+c2tvt≤v成立。基于查询确定性的表述，可以对无套利性进行严格定义，用符号π（Q）表示查询服务Q的价格。

定义4 无套利性［6，18］。一个定价函数π（·）被称作是无套利的，或者说满足无套利性的，如果对t≥1，只要有{Q1，…，Qt}Euclid ExtraaApQ，那么就有π（Q）≤∑tk=1π（Qk）。

2 定价模型

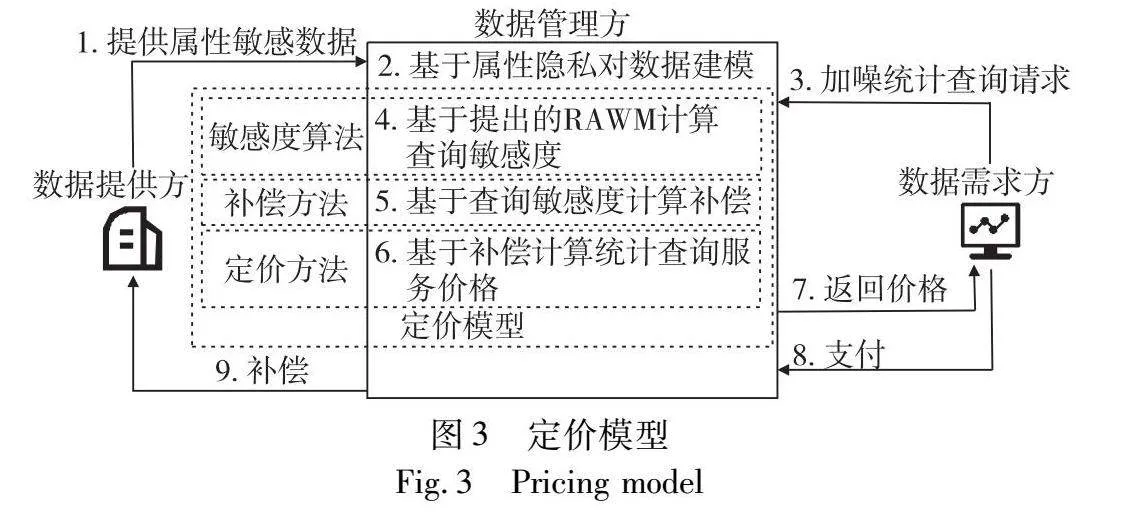
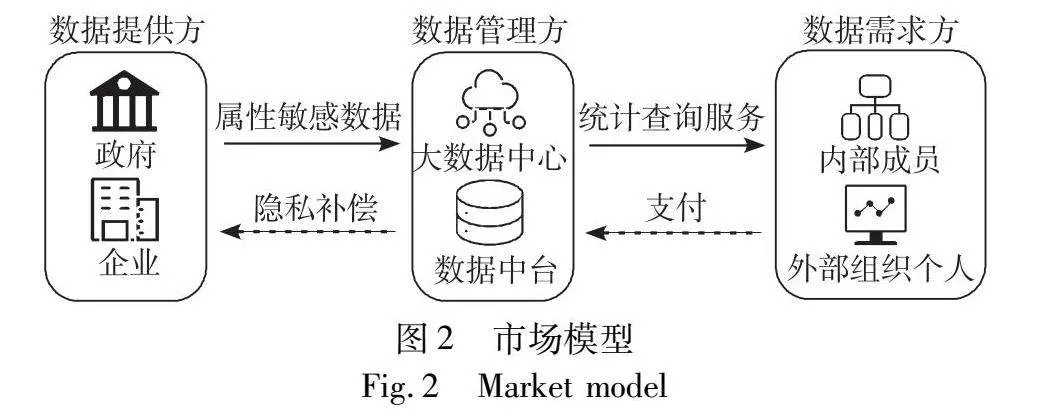
本文定价模型所面向的市场模型为中心化数据市场模型，或者说为中心化数据共享模型。如图2所示，市场中有数据提供方、数据管理方和数据需求方三类角色。数据提供方为拥有属性敏感数据集的组织，如企业和政府等。数据管理方为一个可信的第三方管理者或组织内部的数据部门，例如不同政府部门的数据交由大数据中心进行汇聚和托管，企业内部每个部门将数据交由负责开发数据中台的数据部门进行统一管理。数据需求方可以是对统计查询有需求的外部个人或组织，或者是公司内部各部门、集团内部各方。

如图3所示，在该中心化数据市场模型基础上，数据提供方使用本文定价模型，定价模型包含查询敏感度算法、补偿方法和定价方法三个部分。在查询敏感度算法中，数据管理方基于本文RAWM，高效地计算RAWD敏感度作为查询敏感度。在补偿方法中，数据管理方以约束属性隐私损失为依据，根据查询敏感度等因素，对数据提供方进行补偿；在定价方法中，数据管理方基于补偿进行成本加成，针对多种场景使用不同的无套利定价函数对统计查询定价。

2.1 模型假设

对于一个特定的数据提供方，其数据集表示为D=［D1，…，Dm］，Di表示数据集在完成特征预处理后的第i列。原始数据集中的每一列可以通过特征编码或特征离散化分解为多列。预处理后的数据集有m列，SC［m］表示敏感属性列的下标集合。数据集有n行，每行记录（Dj1，…，Djm）， j∈［n］都是独立同分布的。数据管理方在获取到数据集D后对数据分布进行学习，使用属性隐私框架进行建模，并根据数据提供方的要求在D上对外提供统计查询服务，记查询函数为F。为了控制查询结果对敏感属性的揭露程度，数据管理方在查询结果中加入方差为v的随机噪声。因此，查询服务Q可以表示为二元组Q=（F，v），添加噪声所用的随机化机制表示为Euclid Math OneMAp。由于属性隐私定义中包含一个近似概率参数δ，数据市场的各方还约定δ为一个确定的微小值（如δ=0.001）。数据管理方最终返回给数据需求方的查询结果为Euclid Math OneMAp（D）而不是F（D）。相应地，数据管理方对数据需求方收取一定的费用，查询服务的价格表示为π（Q）=π（F，v）。此外，因为查询服务揭露了数据提供方希望保护的敏感属性，数据管理方还需要给予数据提供方ρ（Q）=ρ（F，v）的补偿。

数据管理方在使用属性隐私框架进行建模时，需要作一定的假设，因为在没有假设的前提下就使用隐私定义会导致几乎零效用的查询服务［25］。所作的假设代表了攻击者对数据生成方式的信念。既然对数据分布作非常全面的假设非常不实用，数据管理方合理地约束攻击者对数据分布的不确定性，每个数据列上的不确定性体现为无法确定该列分布参数的取值。对于数值列，不确定性体现在分布均值参数上（如正态分布的μ参数）；对于布尔值列，不确定性体现在伯努利分布的p参数上。在对数据集作了如上的假设后，数据管理方进行建模。此外，数据管理方和数据需求方掌握的数据集知识不对等，因为数据集D对数据管理方是可见的，所以查询结果对数据管理方表现为F（D）。然而，数据集由于不可见性而对数据需求方表现为X，查询结果也相应地对数据需求方表现为F（X）。

数据管理方向数据需求方提供了多种统计查询，如直方图查询、数据立方查询和均值查询。所有的统计查询最终都可以归为求平均和求和两类。例如，比例查询可以看作对服从伯努利分布的数据作了平均查询，计数查询可以看作对服从伯努利分布的数据作了求和查询，直方图查询可以看作一组计数查询查询结果组成的向量。类似地，各种复合的统计查询最终都可以分解成最基本的求平均或求和查询。因此，本文接下来只讨论求平均和求和两种基本的统计查询。两种查询的表达式不同，但是都可以使用中心极限定理求出查询输出的近似正态分布，使Xi，i∈［m］表示进行统计查询的数据列随机变量，用μ和σ2表示Xi的期望和方差，即E（Xi）=μ和Var（Xi）=σ2。那么，求平均查询可以表示为F（X）=1n∑nj=1Xji～N（μ，σ2n），而求和查询可以表示为F（X）=∑nj=1Xji～N（nμ，nσ2）。

2.2 查询敏感度算法

查询敏感度是一个反映统计查询和数据敏感属性关联程度的量，查询敏感度越大，代表该查询对敏感属性的揭露程度越高。严格的查询敏感度定义应该以满足属性隐私要求的随机化机制为依据：对于越敏感的查询，该随机化对其添加的噪声越大，说明可以从噪声大小中诱导出一个用于反映敏感程度的量，进而定义查询敏感度。例如，WM计算的最大∞-Wasserstein距离，AWM计算的最大δ-近似Wasserstein距离，这些量与噪声尺度参数呈正比，可以用于定义查询敏感度。然而计算∞-Wasserstein距离或δ-近似Wasserstein距离的时间复杂度是O（n），多数情况下数据量n较大。这意味着虽然可以基于WM或AWM定义查询敏感度，但是会导致敏感度计算成本过高。

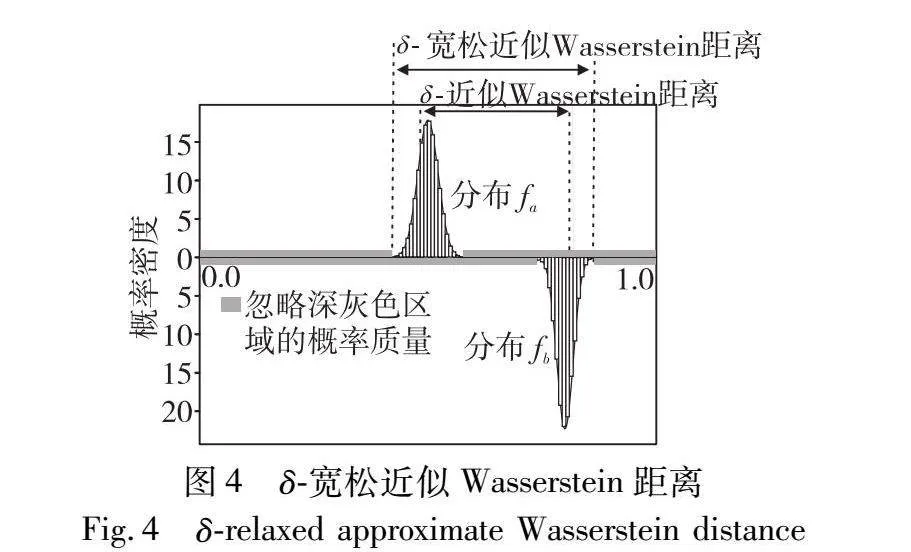
对此，本节结合统计查询输出分布的近似正态特征，提出能够满足（，δ）-属性隐私的宽松近似Wasserstein机制（RAWM），并基于RAWM提出RAWD敏感度算法，将RAWD敏感度作为查询敏感度，为后续补偿与定价奠定基础。RAWM需要计算查询输出分布对的δ-宽松近似Wasserstein距离（δ-RAWD），下面结合统计查询输出分布对的近似正态特点，正式定义δ-RAWD。

定义5 δ-宽松近似Wasserstein距离（δ-RAWD）。对于统计查询F，给定（sia，sib）∈SP和θ∈Θ，用fa～N（μa，σ2a）和fb～N（μb，σ2b）分别表示F（X）|sia，θ和F（X）|sib，θ近似服从的正态分布。给定近似概率δ，用ppf表示标准正态分布的百分点函数（percent point function， 累积分布函数的逆函数），记d=ppf（1-δ/4），则fa与fb之间的δ-宽松近似Wasserstein距离定义为

Wδ（fa，fb）=|μa－μb|+dσa+dσb（2）

如图4所示，给定两个正态分布fa、 fb，计算δ-RAWD相当于先忽略掉每个正态分布左右支撑集上的各δ/4概率质量，也即忽略掉每个正态分布的δ/2概率质量，fa剩下的支撑集子集为R′a=［μa－dσa，μa+dσa］，fb剩下的支撑集子集为R′b=［μb－dσb，μb+dσb］，由正态分布性质可得P（faR′a）=δ/2和P（fbR′b）=δ/2。根据布尔不等式，任意以fa、 fb为边缘分布的联合分布γ都满足P（γR′a×R′b）≤δ，这相当于忽略了fa、 fb之间至多δ的概率质量映射。δ-RAWD直接选定一个次优联合分布γ′，但是不计算γ′所代表概率质量转移过程的距离，而是计算R′a、R′b边界的最大距离|μa－μb|+dσa+dσb，作为最大转移距离的一个宽松上界，避免了时间复杂度为O（n）的∞-Wasserstein距离计算。δ-RAWD以此解决了数据量大时∞-Wasserstein距离或δ-近似Wasserstein距离计算成本高的问题。

对于每个敏感属性下标i∈SC，RAWM遍历所有秘密对（sia，sib）∈SP和数据分布θ∈Θ的组合，计算每一个组合条件下数据分布对fa、 fb的δ-RAWD，找出最大值，并结合隐私预算对查询结果添加一个拉普拉斯噪声。

定理2 宽松近似Wasserstein机制（RAWM）：

Euclid Math OneMAp（D）=F（D）+Lapmaxi∈SCsup（sia，sib）∈SPi，θ∈ΘWδ（fa，fb）（3）

满足（，δ）-属性隐私。

证明 考虑任意敏感属性下标i∈SA，任意秘密对（sia，sib）∈SP和数据分布θ∈Θ，用fa～N（μa，σ2a）和fb～N（μb，σ2b）分别表示F（X）|sia，θ和F（X）|sib，θ近似服从的正态分布，记W=maxi∈SAsup（sia，sib）∈SPi，θ∈ΘWδ（fa， fb）。

记d=ppf（1-δ/4）。RAWM对fa选取支撑集子集R′a=［μa－dσa，μa+dσa］，对fb选取支撑集子集R′b=［μb－dσb，μb+dσb］，根据正态分布的性质可以得到P（faR′a）=δ/2和P（fbR′b）=δ/2。记R′=R′a×R′b，结合定义5中Wδ（fa，fb）的表达式有

sup（t，s）∈R′|t－s|≤

|μa－μb|+dσa+dσb=Wδ（fa，fb）≤

maxi∈SAsup（siyZbPEuWrnqWX4h7RY/1b0Q==a，sib）∈SPi，θ∈ΘWδ（fa，fb）=W（4）

任意选取一个联合分布γ′∈Γ（fa，fb），根据布尔不等式有P（γR′a×R′b）≤δ，即

（t，s）R′γ′（t，s）dtds≤δ（5）

接着，对于任意满足P（Euclid Math OneMAp（X）∈O）≥δ的ORange（Euclid Math OneMAp），有

P（Euclid Math OneMAp（X）∈O|sia，θ）=P（F（X）+Z∈O|sia，θ）=

∫t P（F（X）=t|sia，θ）P（Z+t∈O）dt=

∫t ∫s γ′（t，s）P（Z+t∈O）dsdt=

（t，s）∈Rγ′（t，s）P（Z+t∈O）dsdt+（t，s）Rγ′（t，s）P（Z+t∈O）dsdt（6）

由差分隐私的拉普拉斯机制可得，当所添加噪声Z=Lap（W/ε），对于任意满足|t－s|≤W的（t，s）∈R′有

P（Z+t∈O）≤exp（）P（Z+s∈O）（7）

然后，对于式（6）中的两项进行约束，对于第一项，结合式（4）和（7），有

（t，s）∈Rγ′（t，s）P（Z+t∈O）dsdt≤

exp（）（t，s）∈Rγ′（t，s）P（Z+s∈O）dtds（8）

对于第二项，结合式（5），有

（t，s）Rγ（t，s）P（Z+t∈O）dsdt≤

（t，s）Rγ（t，s）dsdt≤δ（9）

最后，将式（8）（9）代入到式（6），有

P（Euclid Math OneMAp（X）∈O|sia，θ）≤

exp（）（t，s）∈Rγ′（t，s）P（Z+s∈O）dtds+δ=

exp（）∫s P（F（X）=s|sib，θ）P（Z+s∈O）ds+δ=

exp（）P（F（X）+Z∈O|sib，θ）+δ=

exp（）P（Euclid Math OneMAp（X）∈O|sib，θ）+δ（10）

证毕。

定理2证明了RAWM是满足属性隐私要求的，因此可以基于RAWM定义RAWD敏感度，本文定价模型将其作为查询敏感度。下面对RAWD敏感度进行正式定义。

定义6 RAWD敏感度。对于敏感属性下标i∈SC和查询函数F，给定θ∈Θ和（sia，sib）∈SPi，用fa和fb分别表示F（X）|sia，θ和F（X）|sib，θ近似服从的正态分布。给定近似概率δ，则查询F在下标为i的敏感属性上的RAWD敏感度为

Wδi（F）=sup（sia，sib）∈SPi，θ∈ΘWδ（fa，fb）（11）

RAWD敏感度相当于在全部专属于敏感属性下标i∈SC的组合条件下，其中的最大δ-RAWD，表示查询F在该敏感属性上的敏感程度。算法1给出了计算RAWD敏感度的具体步骤：对于目标属性下标为k的统计查询F，算法遍历所有属于i的秘密对（sia，sib）∈SPi和数据分布θ∈Θ，在每一个迭代中，首先计算目标列Xk的条件期望和条件方差，然后根据F的类型和表达式（已在2.1节中分析）确定F（Xk）的条件期望和条件方差，得到近似正态的查询输出分布对fa、 fb，最后计算fa、 fb之间的δ-RAWD，如果是已计算的最大值就保存下来。遍历结束后，返回找到的最大δ-RAWD。

算法1 RAWD敏感度

输入：数据量n；敏感属性下标i∈SC；目标属性下标为k的统计查询F；属性隐私框架（S，SP，Θ）；近似概率δ。

输出：RAWD敏感度Wδi（F）。

1 maxDist←0.0;

2 for all （sia，sib）∈SPi，θ∈Θ： // 遍历所有条件组合

3 // 计算目标列的条件期望和条件方差

4 μka←E（Xk|Φi=a）;σ2ka←Var（Xk|Φi=a）;

5 μkb←E（Xk|Φi=b）;σ2kb←Var（Xk|Φi=b）;

6 // 根据查询类型和查询表达式得到输出分布对

7 if F属于求平均类查询：

8 μa←μka;σ2a←σ2ka/n;σ2a←σ2ka/n;σ2b←σ2kb/n

9 else if F属于求平均类查询：

10 μa←nμka;σ2a←nσ2ka;μb←nμkb;σ2b←nσ2kb;

11 fa←N（μa，σ2a）;fb←N（μb，σ2b）;

12 // 计算最大的δ-RAWD并保存

13 dist←Wδ（fa，fb）;

14 if dist>maxDist：

15 maxDist←dist;

16 return maxDist

接下来分析算法1的时间复杂度。记（sia，sib）∈SPi和θ∈Θ的组合数量为，由于算法13行计算δ-RAWD的时间复杂度为O（1），所以算法1的时间复杂度为O（），与数据量无关。如果基于WM或AWM，将算法13行处替换为计算∞-Wasserstein距离或计算δ-近似Wasserstein距离，那么整个算法的时间复杂度就会变为与数据量相关的O（n）。因此，相较于基于WM或AWM的敏感度算法，本文的RAWD敏感度算法更高效。

2.3 补偿方法

数据提供方因为敏感属性被揭露而期望得到补偿，揭露的程度由2.2节计算的查询敏感度和噪声方差共同决定。查询敏感度越高，说明统计查询与敏感属性的关联越强。噪声方差越大，说明查询结果被扰动的程度越高，敏感属性被保护得更好。由此可以得出，当敏感度越高，或者当噪声方差越小，加噪统计查询结果对敏感属性的揭露程度越高。因此，对数据提供方的补偿应该与查询敏感度呈正相关，而和噪声方差呈负相关，以实现更好的激励效果。

接下来从属性隐私框架的角度，给出一个使用查询敏感度和噪声方差计算的属性隐私损失上界，作为后续设计补偿函数的理论依据。

定义7 δ-属性隐私损失。对于每个i∈SC，随机化机制Euclid Math OneMAp在敏感属性i上造成的δ-属性隐私损失定义为

εδi（Euclid Math OneMAp）=sup（sia，sib）∈SPi，θ∈Θ，ORange（Euclid Math OneMAp）logP（Euclid Math OneMAp（X）∈O|sia，θ）－δP（Euclid Math OneMAp（X）∈O|sib，θ）（12）

其中：输出集合O满足P（Euclid Math OneMAp（X）∈O|sia，θ）≥δ。

定理3 给定统计查询F，噪声方差v，敏感属性下标i∈SC。对于随机化机制Euclid Math OneMAp（X）=F（X）+Lap（v/2），定义7中Euclid Math OneMAp在i上造成的δ-属性隐私损失被上界Wδi（F）/v/2约束：

δi（Euclid Math OneMAp）≤Wδi（F）v/2（13）

证明 从属性隐私框架（S，SP，Θ）中，从秘密集合S和秘密对集合S中选取属于i的子集，生成属性隐私框架（Si，SPi，Θ）。给定一个隐私预算，由定理2和定义6可得，按如下方式对查询结果F（X）添加噪声：

F（X）+LapWδi（F）（14）

可以满足（，δ）-属性隐私，即对于任意秘密对（sa，sb）∈SP，任意数据分布θ∈Θ，都满足

P（Euclid Math OneMAp（D）=O|sa，θ）≤exp（），P（Euclid Math OneMAp（D）=O|sb，θ）+δ（15）

当不给定，而是给定方差v时，由拉普拉斯分布性质可得

=Wδi（F）v/2（16）

将式（10）代入式（9），不等式变换后可得

P（Euclid Math OneMAp（D）=O|sa，θ）－δP（Euclid Math OneMAp（D）=O|sb，θ）≤expWδi（F）v/2（17）

式（10）对于任意（sia，sib）∈SPi和θ∈Θ都满足，因此与结论等价。

证毕。

定理3给出了属性隐私损失上界Wδi（F）/v/2，该量与查询敏感度正相关，与噪声方差负相关，符合本节开头的分析，是一个能够表征统计查询服务对敏感属性揭露程度的量，后面将基于该量设计补偿函数。除了查询敏感度和噪声方差两个因素以外，不同的敏感属性的重要程度也不同，有的敏感属性对数据提供方而言非常重要，而有的不太重要。对此，补偿函数还需要引入可以由数据提供方根据需要自由设置的补偿参数，以在不同重要程度的敏感属性上取得不同的补偿。

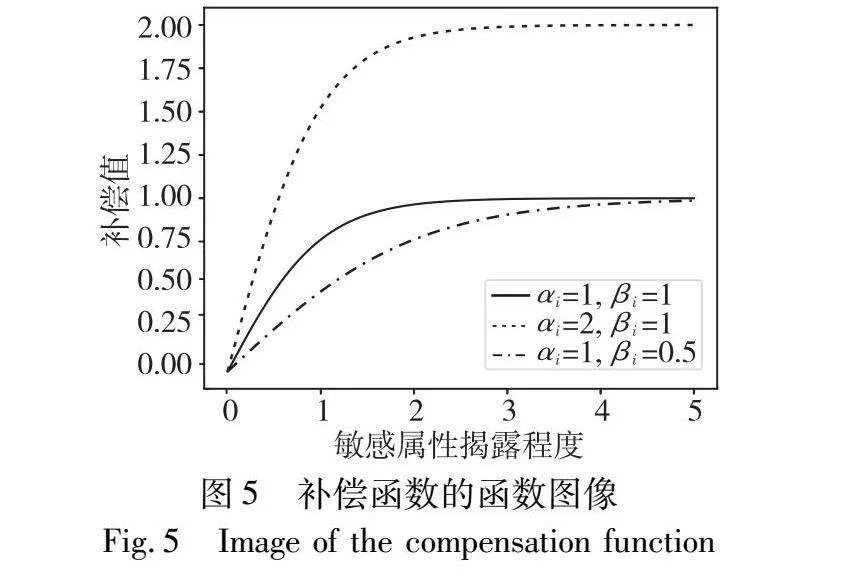
数据提供方为数据集中的每个敏感属性i∈SC设置两个补偿参数αi、βi。当一个统计查询服务Q=（F，v）请求到来时，数据提供方因Q而在敏感属性i上应得的补偿ρi（Q）为

ρi（Q）=αitanh（βiWδi（F）v/2）（18）

数据管理方对于每个敏感属性i∈SC，都按式（18）计算应得补偿，然后对每个敏感属性上的应得补偿求和，得到总补偿值ρ（Q），在该服务完成交易后，数据管理方就要按照该约定补偿值，对数据提供方进行补偿。总补偿值ρ（Q）公式为

ρ（Q）=∑i∈SCρi（Q）（19）

补偿ρi（Q）的表达式中使用了一个tanh函数，是为了对补偿值进行约束，确保补偿函数的有界性。如果不进行约束，那么当方差v为零时，会计算出无穷大的补偿值，即使限制v不为零，当v接近零时，也会计算出非常大的补偿值，这些结果是不合理的。另外，ρi（Q）的表达式使用了两个补偿参数αi和βi，这两个补偿参数都反映了敏感属性的重要程度，但具体作用不同：αi越大，数据提供方在敏感属性i上应得的补偿上限越大；βi越大，应得补偿随揭露程度提高而接近上限值αi的速率就越大。图5展示了在不同补偿参数组合下，补偿函数ρi（Q）的图像，其中横轴为表征揭露程度的量Wδi（F）/v/2。

2.4 定价方法

2.3节描述了如何对数据提供方进行补偿，以激励数据提供方共享数据。每经历一次统计查询服务，就要对数据提供方进行一次补偿，因此该补偿是统计查询服务的边际成本之一。本文定价模型需要确保数据管理方在边际成本之外可以获得一定的收益，以对数据管理方同样形成一定激励。定价除了保证收益外，还必须满足1.3节中介绍的无套利性。

接下来，本节对统计查询服务的无套利性质进行更细致的分析，证明几个用于构造无套利定价函数的命题，然后针对多个可能的场景，应用这些命题设计出不同的无套利定价函数。

考察一个在数据集X上计算的复杂统计函数F，根据2.1节中的假设，F可以被分解成最基本的求平均查询和求和查询。于是在X上的所有最基本最小的查询可以看作是一个向量组（F′1，…，F′T），T>0，F可以表示为F=w1F′1+…+wTF′T形式的线性组合，其中wk∈Euclid ExtraaBp。换句话说，这个基本向量组在Euclid ExtraaBp上张成了一个向量空间V=span（F′1，…，F′T），F可以看作是V中的一个向量。例如，在医院病例数据集上查询A疾病或B疾病的比例，相当于查询A疾病比例加上B疾病比例，这里的“A疾病比例”和“B疾病比例”就是最基本最小的查询，是基本向量组里的2个向量。在数学中有一类名为半范数的函数，它们的性质与无套利定价函数所需要满足的性质相近。一个定义在V上的半范数是满足下列条件的实值函数g：V→Euclid ExtraaBp。

a）次可加性：g（F1+F2）≤g（F1）+g（F2），F1，F2∈V；

b）正齐次性：g（cF）=|c|g（F），F∈V和c∈Euclid ExtraaBp；

c）非负性：g（F）≥0，F∈V。

定理4 定义6中的RAWD敏感度Wδi（F）是一个定义在统计查询向量空间V上的半范数。

证明 要证明Wδi（F）是一个半范数，需要分别证明非负性，正齐次性，次可加性。

对于非负性，明显可以由定义6中Wδi（F）的表达式得到。

对于正齐次性作以下表示：对任意（sia，sib）∈SP和θ∈Θ，用N（μa，σ2a）、N（μb，σ2b）、N（cμa，c2σ2a）、N（cμb，c2σ2b）分别表示F（X）|sia，θ、F（X）|sib，θ、cF（X）|sia，θ、cF（X）|sib，θ近似服从的正态分布。那么正齐次性可由期望和方差的性质推出：

Wδi（cF）=sup（sia，sib）∈SPi，θ∈Θ{|cμa－cμb|+d|c|σa+d|c|σb}=

|c|×sup（sia，sib）∈SP，θ∈Θ{|μa－μb|+dσa+dσb}=

|c|×Wδi（F）（20）

对于次可加性作以下表示：对任意（sia，sib）∈SP和θ∈Θ，用N（μ1a，σ21a）、N（μ1b，σ21b）、N（μ2a，σ22a）、N（μ2b，σ22b）、N（μ1a+μ2a，σ21a+σ22a）、N（μ1b+μ2b，σ21b+σ22b）分别表示F1（X）|sia，θ、F1（X）|sib，θ、F2（X）|sia，θ、F2（X）|sib，θ、F1（X）+F2（X）|sia，θ、F1（X）+F2（X）|sib，θ近似服从的正态分布，可进行如下推导：

Wδi（F1+F2）=

sup（sia，sib）∈SP，θ∈Θ{|（μ1a+μ2a）－（μ1b+μ2b）|+dσ21a+σ22a+

dσ21b+σ22b}=sup（sia，sib）∈SP，θ∈Θ{|μ1a－μ1b+μ2a－μ2b|+dσ21a+σ22a+

dσ21b+σ22b}≤

sup（sia，sib）∈SP，θ∈Θ{|μ1a－μ1b|+|μ2a－μ2b|+dσ1a+dσ2a+

dσ1b+dσ2b}≤sup（sia，sib）∈SP，θ∈Θ{|μ1a－μ1b|+dσ1a+dσ1b}+

sup（sia，sib）∈SP，θ∈Θ{|μ2a－μ2b|+dσ2a+dσ2b}=

Wδi（F1）+Wδi（F2）（21）

其中：第一个等式由统计查询函数的可加性得到；第二个等式由期望和方差的性质得到；第一个不等式由绝对值和平方根的次可加性得到，第二个不等式由上确界（sup）的性质得到。

证毕。

定理5 如果g是一个半范数，那么定价函数g2（F）/v满足无套利性。

证明 根据定义3描述的查询确定性，下面的查询确定性关系成立：{（F1，v1），…，（Ft，vt）}Euclid ExtraaAp（F，v），当且仅当存在c1，…，ct使得c1F1+…+ctFt=F和c21v1+…+c2tvt≤v。对于一个查询确定性关系{（F1，v1），…，（Ft，vt）}Euclid ExtraaAp（F，v），可推出

∑tk=1π（Fk，vk）=∑kg2（Fk）vk=（∑kg2（Fk）vk）（∑kc2kvk）∑kc2kvk≥

（∑k|ck|g（Fk））2∑kc2kvk=（∑kg（ckFk））2∑kc2kvk≥

g2（F）v=π（F，v）（22）

其中：第一个不等式由柯西不等式得到，第二个不等式由半范数性质得到。

证毕。

定理4证明了本文RAWD敏感度是一个半范数，可以用于设计无套利定价函数。定理5给出了无套利定价函数的一个最简单的形式g2（F）/v。接下来，定理6将展示如何利用满足非递减性和次可加性的函数合成更多无套利定价函数。然后，通过应用定理6，推论1将给出一些真实满足非递减性和次可加性的函数。对于任意x，y∈Euclid ExtraaBpt，函数h：（Euclid ExtraaBp+）t→Euclid ExtraaBp+满足非递减性，如果x≤y蕴涵h（x）≤h（y）；h满足次可加性，如果h（x+y）≤h（x）+h（y）。

定理6 给定一系列无套利定价函数π1，…πs，s≥1。让h：（Euclid ExtraaBp+）t→Euclid ExtraaBp+表示一个满足非递减性和次可加性的函数，那么使用h合成的定价函数π（Q）=h（π1（Q），…，πs（Q））也是无套利的。

证明 考虑查询确定性关系{Q1，…，Qt}→Q，其中t≥1，可以推出

π（Q）=h（π1（Q），…，πs（Q））≤h（∑tk=1π1（Qk），…，∑tk=1πs（Qk））≤

∑tk=1h（π1（Qk），…，πs（Qk））=∑tk=1π（Qk）（23）

其中：第一个不等式由π1，…，πs的无套利性和h的非递减性得到，第二个不等式由h的次可加性得到。

证毕。

推论1 给定一系列无套利定价函数π1，…，πt，t≥1。那么下面列出的定价函数也是无套利的。

a）线性组合：c1π1（Q）+…+ctπt（Q），c1，…，ct≥0；

b）幂函数：πc1（Q），0<c≤1；

c）有界函数：tanh（π1（Q）），sigmoid（π1（Q）），arctan（π1（Q）），π1（Q）π21（Q）+1。

证明 可以验证上面列出的函数都满足非递减性和次可加性。根据定理6，可以推出上述结论。证毕。

本文定价模型采用成本加成定价法，因为补偿是边际成本之一，所以定价函数需要依赖2.3节中的补偿函数ρ（Q）。定理7证明了补偿函数ρ（Q）满足无套利性，可以用于设计更多无套利定价函数。

定理7 补偿函数：

ρ（Q）=∑i∈SCαitanhβiWδi（F）v/2（24）

满足无套利性。

证明 根据定理4和5，可得到（Wδi（F））2/v满足无套利性。然后，根据推论1，可以按顺序依次证明下列定价函数满足无套利性：

Wδi（F）v/2 （使用线性组合和幂函数）

tanhβiWδi（F）v/2 （使用线性组合和tanh函数）

∑i∈SCαitanhβiWδi（F）v/2 （使用线性组合）（25）

下面针对几个不同的现实场景，应用本节给出的几个命题设计无套利定价函数。首先考虑一个最基本的场景，统计查询结果是一维的，并且补偿是唯一的边际成本因素，那么可以在补偿ρ（Q）之上乘以一个不小于1的系数来确保收益。用η表示一个非负的收益率，那么该场景下的定价函数为

π（Q）=（1+η）ρ（Q）=

（1+η）∑i∈SCαitanhβiWδi（F）v/2（26）

由推论1和定理7，该定价函数相当于在无套利的补偿函数上复合了线性组合函数，所以也满足无套利性。

接着考虑查询结果多维的场景，例如数据需求方请求的是一个完整的直方图查询，直方图内包括了多个取值的计数，该直方图查询可以表示为一个查询包F={F1，…，Ft}，该次统计查询服务可以看作t个基本统计查询服务的集合Q={（F1，v），…，（Ft，v）}，那么此时的边际成本就是t个基本服务的补偿之和，该场景下的定价函数为

π（Q）=（1+η）∑tk=1ρ（Fk，v）=

（1+η）∑tk=1∑i∈SCαitanhβiWδi（Fk）v/2（27）

由推论1和定理7，该定价函数也相当于在无套利的补偿函数上复合了线性组合函数，所以也满足无套利性。

然后，考虑补偿是唯一边际成本，但有其他统计查询价值因素（如精确度、一致性等）的场景，用∑sk=1wkfactork（Q）表示加权综合了其他价值因素的无套利定价函数，用c∈（0，1］表示幂函数参数（幂函数用于价格折扣），该场景下定价函数为

π（Q）=（1+η）ρ（Q）+（∑sk=1wkfactork（Q））c（28）

由推论1和定理7，该定价函数相当于在无套利定价函数上进一步复合幂函数和线性组合函数，所以也满足无套利性。

最后，考虑有多个边际成本因素的场景，将其他满足无套利性的边际成本函数表示为cost1（Q），…，costs（Q），该场景下定价函数为

π（Q）=（1+η）（ρ（Q）+∑sk=1costk（Q））（29）

由推论1和定理7，该定价函数相当于在无套利定价函数上多次复合了线性组合函数，所以也满足无套利性。现实中更常见的一种情况是，数据管理方根据生产中每一次查询的平均消耗，设置一个固定边际成本，该情况是上述多边际成本场景的特殊场景，即只有一个取值固定的cost1（Q）。固定取值成本函数是无套利的，因此定价函数也是无套利的。

3 实验结果与分析

a）实验环境。定价模型的实现代码使用Python 3.8.13编写，其中计算敏感度的部分使用Java 8编写。所有的实验都运行在一台拥有2.8 GHz Intel CoreTM i7-7700HQ处理器和16 GB内存的物理机上。

b）数据集和分布建模。实验采用真实的UCI公开数据集Adult［29］。该数据集包含了来自不同国家的48 842条人口普查数据，拥有年龄、婚姻状态和是否高收入等数据列。实验假设二值型和种类型数据列上的属性是服从伯努利分布的，而数值型数据列上的属性服从连续分布（如正态分布）。接着，实验使用一个多元正态分布对这些分布的均值参数关联进行建模。为了学习该多元正态分布，将数据集按照不同的国家划分成多个子集，求出每个子集的均值参数，然后将每个子集作为一个样本对多元正态分布进行估计。在该前提下，算法1复杂度中的取值为1。

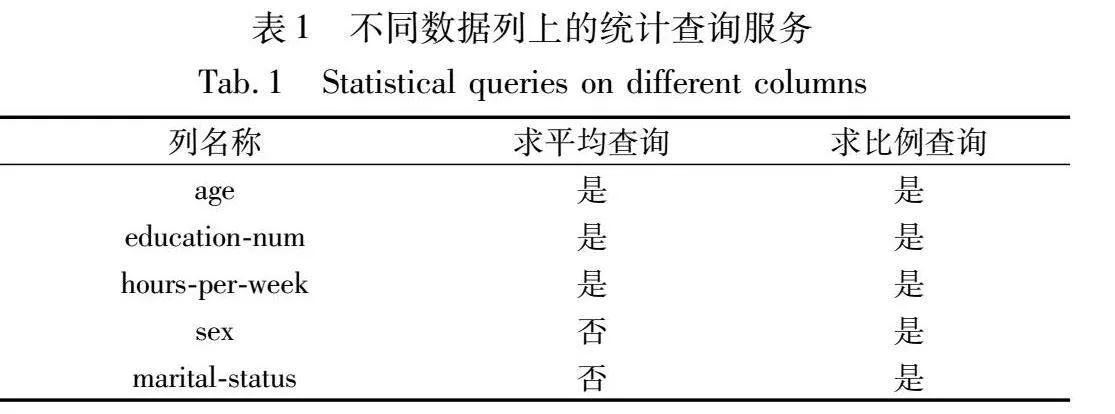
c）查询服务和属性设置。数据市场各方约定近似概率为δ=0.001。数据提供方设置了两个敏感属性：一是收入超过50 k的人口比例，二是在民营企业工作的人口比例。数据管理方提供数据提供方允许的各类统计查询。表1列出了不同数据列上提供的基本统计查询类型，在其之上有更多衍生的统计查询，不在表格中一一列出。

3.1 效率与效用平衡

本节评估在2.2节中基于RAWM计算的RAWD敏感度，从效率和效用两个角度评估。效率即计算时间，而效用是随机化机制向查询中添加噪声后的查询准确程度，在随机化机制满足隐私框架要求的前提下，随机化机制的效用越高，说明添加噪声的大小对查询敏感程度衡量得越紧，效果更好，也意味着基于该随机化机制计算的查询敏感度效果更好。评估效用采用的指标是1－F（X）－Euclid Math OneMAp（X）F（X）+Euclid Math OneMAp（X）［6］，其中，F（X）表示真实查询结果，Euclid Math OneMAp（X）表示经随机化机制扰动后的查询结果。

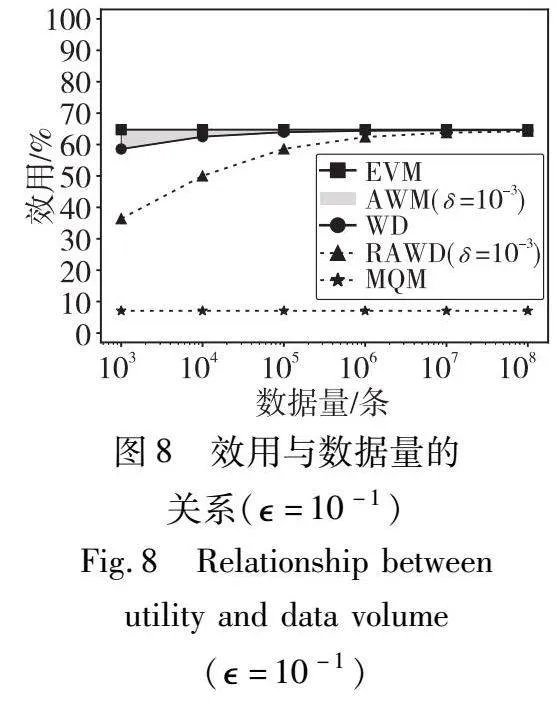
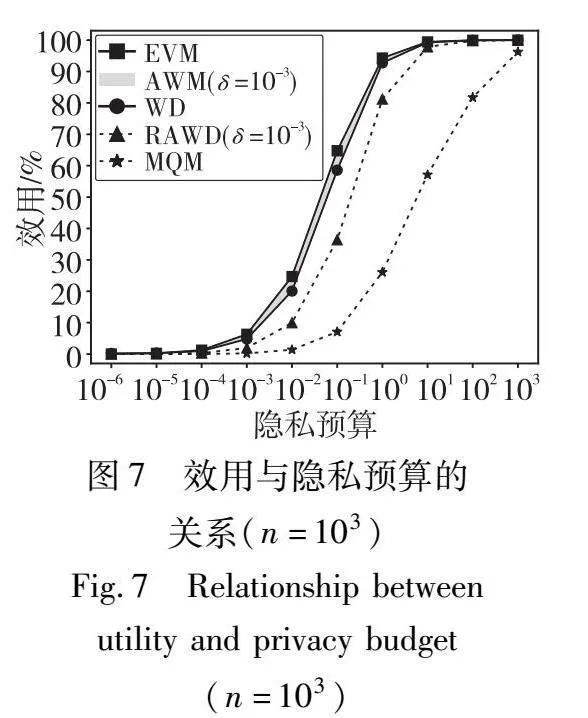
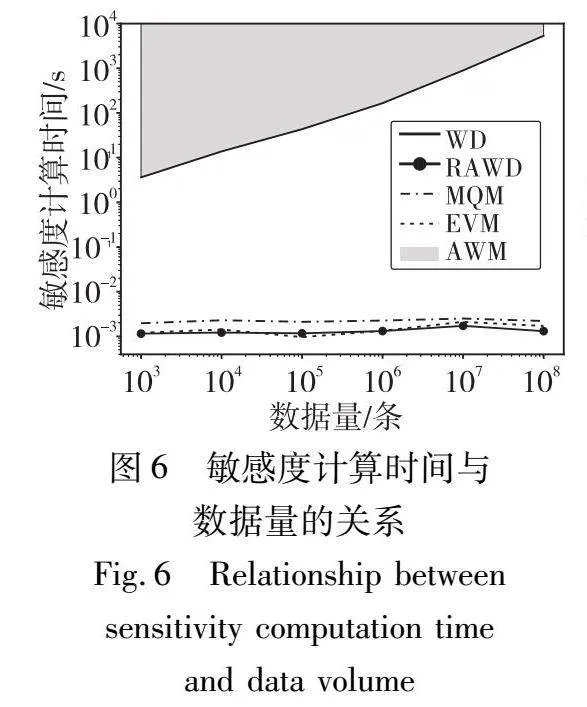
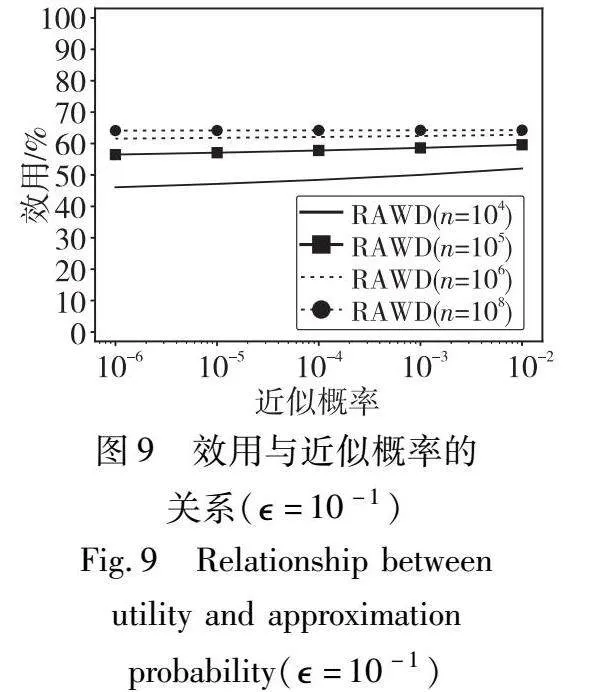
实验对比的方法有AWM［28］、WM［27］、EVM［28］、MQM［26］。其中主要对比的方法是AWM，相较于AWM，RAWM（RAWD敏感度）计算时间大大减少，但是添加了更多的噪声，因此会使查询服务的效用略有下降，也就是说RAWD敏感度会比基于AWM的敏感度效果略差。实验在不同的参数配置下模拟了约1 500 000个查询服务，记录下每个服务效用和定价时间，绘制结果与各参数之间的关系图并观察。在参数中，数据量n范围为{103，104，105，106，107，108}，隐私预算范围为{10－6，10－5，10－4，10－3，10－2，10－1，100，101，102，103}，近似概率δ范围为{10－6，10－5，10－4，10－3，10－2}。AWM计算定义2中的δ-近似Wasserstein距离意味着需要找到最优的联合分布γ和支撑集子集R组合，但是，目前没有可用的解析解或算法能寻找出该最优组合［28］。虽然AWM难以准确计算，但是其计算时间不低于WM，其效用在EVM和WM之间［28］。因此，实验计算WM和EVM作为AWM的时间和效用边界，并在图6中将WM的时间作为AWM的时间下界，在图7、8中用一片区域表示AWM的效用范围，使用最坏情况下的效用差距（即AWM效用上界和RAWM效用的差距）作为本文RAWM的效用代价。图6展示了敏感度计算时间与数据量n之间的关系。图7展示了当n=103时效用与隐私预算之间的关系。图8展示了当=10－1时效用与数据量n之间的关系。图9展示了当=10－1时效用与近似概率δ之间的关系。

从图6可以得出，相较于基于AWM或WM的方法，本文RAWD敏感度将时间复杂度从Ω（n）降低到了O（1）。基于EVM的方法也是O（1）复杂度，但是EVM无法满足属性隐私要求，缺乏合理性。基于MQM的也是O（1）复杂度。

从图7可以观察到，当n=103时，在=10－1处，不同方法的效用差距是最明显的，实验中当n取其他值时，同样也是在=10－1处差距最大（由于篇幅限制不全部展示）。因此，图8和9都在固定=10－1的基础上对比效用。图7的=10－1处对应了图8的n=103处。

从图8可以得出，MQM效用太低，RAWD效用低于EVM、AWM、WM三个方法。然而随着数据量n变大， EVM、AWM、WM三个方法与RAWD之间的效用差距越来越小，特别地，当n=108时，RAWD和AWM的效用差距不超过0.52%。说明在大数据量下，RAWD也能取得很好的效用。

从图9可以得出，RAWD的效用会随着近似概率δ的增加而略微增加，影响不大，因此本文定价模型对δ取固定值。

综上，EVM缺乏合理性，MQM时间复杂度也为O（1）但效用过差，因此都不如本文的RAWD敏感度。对于AWM和WM，RAWD效用略差但大大减小了计算时间，因为多数情况下数据量n是一个比较大的值，所以本文RAWD敏感度将定价模型中查询敏感度的计算时间复杂度从Ω（n）降低到了O（1），仅仅付出了很低的效用代价。

3.2 细粒度补偿

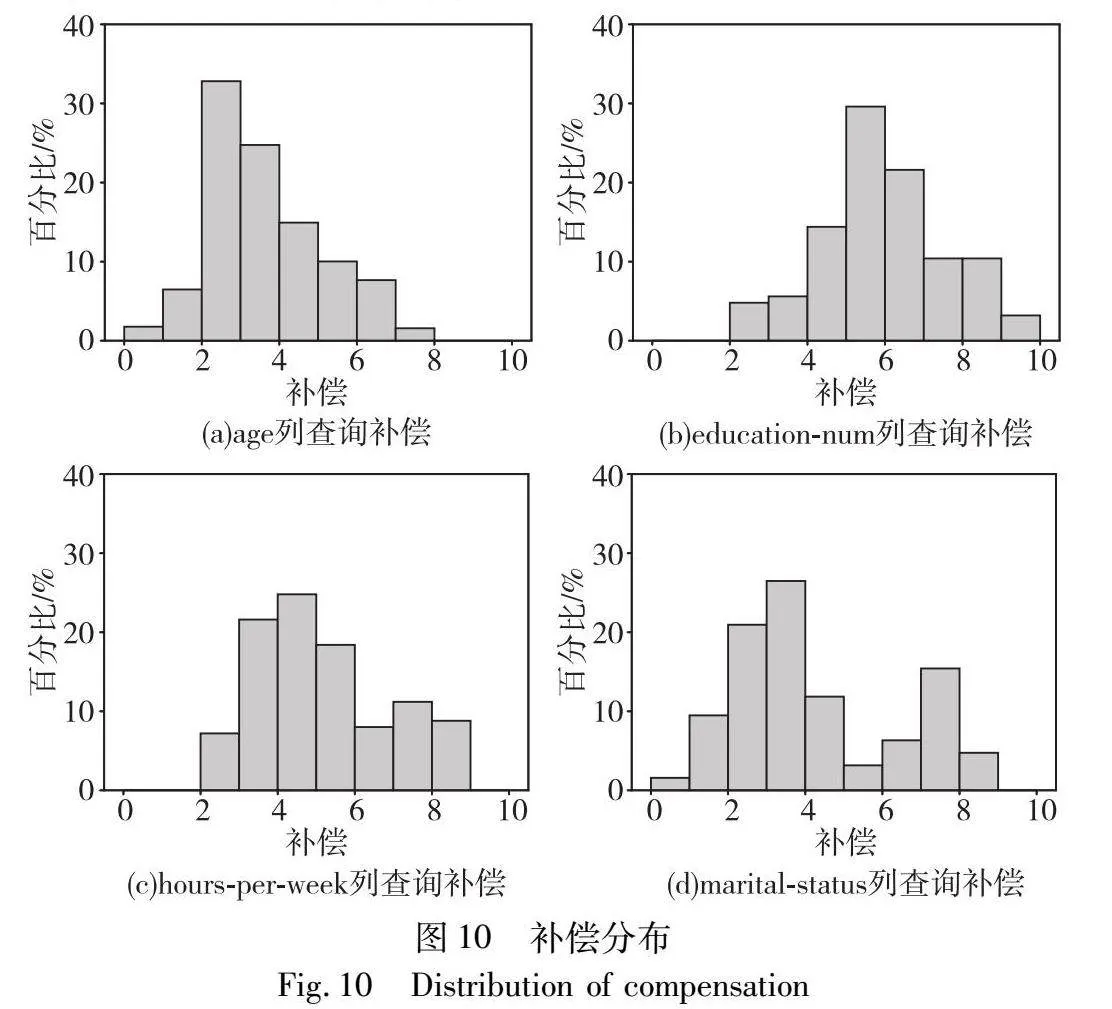
本节评估在2.3节中设计的补偿函数。评估方式为在一个数据列上模拟同方差的多个服务，观察补偿值分布是否分散，是否能够区分不同服务对敏感属性的不同揭露程度。选取的数据列包括age、education-num、hours-per-week、marital-status。服务方差统一为0.01。两个敏感属性的补偿参数都为αi=5，βi=1，所以补偿的取值范围为［0，10］。在不同数据列上模拟统计查询服务的补偿分布如图10所示。

观察图10可以发现，在每个数据列上模拟统计查询服务的补偿分布在区间的不同部分中，可以区分一个数据列上统计查询服务对敏感属性的不同揭露程度，并且不同数据列上的总体补偿水平也有不同，例如education-num列上的补偿比age列上的补偿总体要高，这是因为education-num列和敏感属性（收入超过50 k的人口比例，在民营企业工作的人口比例）之间的关联更大，相应地，education-num列上的查询比age列上的查询对敏感属性揭露程度更高。以上分析说明，本文设计的补偿函数能够对数据提供方进行细粒度补偿，合理反映统计查询服务对敏感属性的揭露程度，形成更好的激励效果。

3.3 无套利性

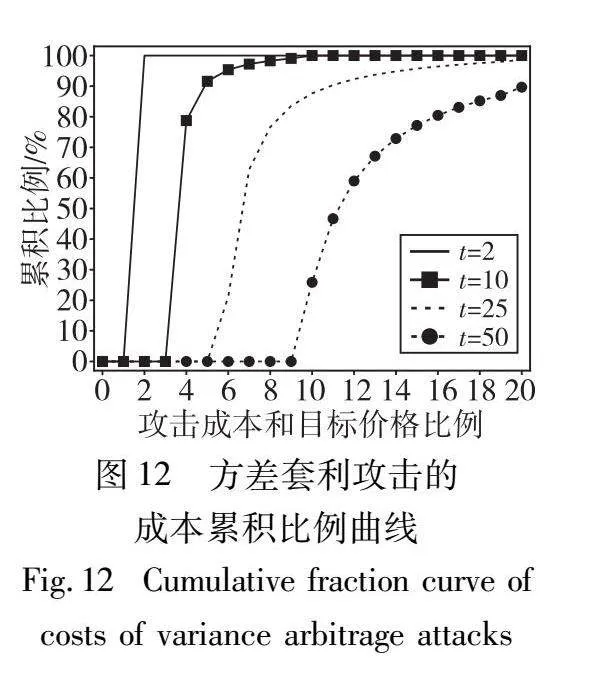
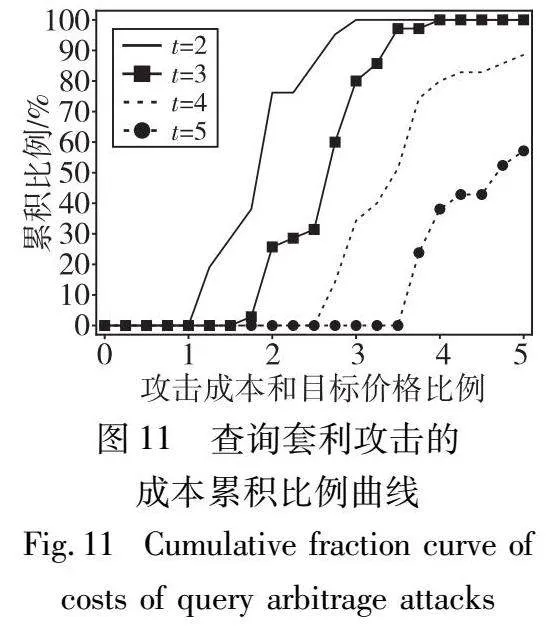
本节评估在2.4节中设计的无套利定价函数。评估无套利性使用的指标为套利攻击成本∑tk=1π（Qk）和目标查询价格π（Q）的累积比例［6］。当攻击成本和目标价格的比率小于1时，称为一次成功的套利攻击。累积比例曲线上的一个点代表攻击成本和目标价格比例小于该点的套利攻击比例，也就是说，累积比例曲线在点1处的值代表了成功套利攻击的比例。实验模拟了两种套利攻击，分别为查询攻击和套利攻击。查询套利攻击可表示为{（F1，v/t），…，（Ft，v/t）}Euclid ExtraaAp（F，v）；方差套利攻击可表示为{（F，tv）1，…，（F，tv）t}Euclid ExtraaAp（F，v）。实验模拟了约40 000次套利攻击，查询套利攻击的参数t取值范围为{2，3，4，5}，方差套利攻击的参数t取值范围为{2，10，25，50}。图11展示了查询套利攻击的累积比例曲线。图12展示了方差套利攻击的累积比例曲线。

观察图11、12可以发现，累积比例曲线在成本比例为1时都为0%。这说明没有任何攻击的成本比例小于1，所有的套利攻击都没有成功，验证了定价函数的无套利性。此外，随着参数t的增加，累积比例曲线呈现右移的趋势，这与直觉一致，因为参数t也代表了套利攻击的查询个数，查询个数更多会导致攻击成本比例更高。

4 结束语

本文针对现有统计查询定价模型没有考虑查询结果揭露数据集敏感属性的问题，提出了基于属性隐私的统计查询定价模型。模型提出了RAWM，基于RAWM提出RAWD敏感度作为查询敏感度，可以在常数时间复杂度内计算，使用查询敏感度、噪声方差、补偿参数综合地计算补偿，针对多个场景，在补偿之上使用成本加成定价法设计了多个无套利定价函数。在公开数据集上进行了实验，实验结果表明，模型中的查询敏感度算法很好地实现了效用和效率的平衡，模型能够提供细粒度补偿以更好地激励共享，模型设计的定价函数满足无套利性。

但是，本文定价模型仍有不足。例如只能对统计查询服务进行定价，无法衡量机器学习服务对数据集敏感属性的揭露；只能将数据集的分布参数视为敏感属性，没有考虑当敏感属性是数据集的复杂特征表达式时该如何定价。

参考文献：

［1］江东， 袁野， 张小伟， 等. 数据定价与交易研究综述［J］. 软件学报， 2023， 34（3）： 1396-1424. （Jiang Dong， Yuan Ye， Zhang Xiao-wei，et al. A survey on data pricing and trading research［J］. Journal of Software， 2023， 34（3）： 1396-1424.）

［2］DAWEX. Global big data exchange［EB/OL］. （2024-04-03）. https：//www.gzdex.com.cn/.

［3］DAWEX. Sell， buy and share data［EB/OL］. （2024-04-03）. https：//www. dawex.com/en/.

［4］Zhang Mengxiao， Beltrán F， Liu Jiamou. A survey of data pricing for data marketplaces［J］. IEEE Trans on Big Data， 2023， 9（4）： 1038-1056.

［5］Koutris P， Upadhyaya P， Balazinska M，et al. query-based data pricing［J］. Journal of the ACM， 2015， 62（5）： 1-44.

［6］Niu Chaoyue， Zheng Zhenzhe， Wu Fan，et al. ERATO： trading noisy aggregate statistics over private correlated data［J］. IEEE Trans on Knowledge & Data Engineering， 2021， 33（3）： 975-990.

［7］He Zaobo， Cai Zhipeng. Trading aggregate statistics over private Internet of Things data［J］. IEEE Trans on Computers， 2024， 73（2）： 394-407.

［8］陈思莹， 张丹， 丁小欧， 等. 基于数据质量的公平数据定价［J］. 大数据， 2024， 10（2）： 54-67. （Chen Siying， Zhang Dan， Ding Xiaoou，et al. Fair data pricing based on data quality［J］. Big Data Research， 2024， 10（2）： 54-67.）

［9］Yu Mingkai， Wang Jianxiao， Yan Jie，et al. Pricing information in smart grids： a quality-based data valuation paradigm［J］. IEEE Trans on Smart Grid， 2022， 13（5）： 3735-3747.

［10］刘珂. 基于Shapley值的冷链物流检测信息特征组合定价研究［D］. 重庆： 重庆邮电大学， 2022. （Liu Ke. Shapley value-based pricing for feature combination of detection information in cold chain logistics［D］. Chongqing： Chongqing University of Posts and Telecommunications， 2022.）

［11］Wang Tianhao， Rausch J， Zhang Ce，et al. A principled approach to data valuation for federated learning［M］// Yang Qiang， Fan Lixin， Yu Han. Federated learning： privacy and incentive. Cham： Springer International Publishing， 2020： 153-167.

［12］Xu Anran， Zheng Zhenzhe， Li Qinya，et al. VAP： online data valuation and pricing for machine learning models in mobile health［J］. IEEE Trans on Mobile Computing， 2024， 23（5）： 5966-5983.

［13］卢玉， 王静宇， 刘立新， 等. 拍卖机制驱动的数据激励共享方案［J］. 计算机科学与探索，2024，18（8）：2203-2220. （Lu Yu， Wang Jingyu， Liu Lixin，et al. Auction mechanism driven data incentive sharing solution［J］. Journal of Frontiers of Computer Science and Technology， 2024，18（8）：2203-2220.）

［14］涂辉招， 刘建泉， 遇泽洋， 等. 基于改进型Stackelberg博弈的自动驾驶测试数据定价模型［J］. 同济大学学报： 自然科学版， 2023， 51（11）： 1735-1744. （Tu Huizhao， Liu Jianquan， Yu Ze-yang，et al. Pricing model of autonomous vehicle testing data based on evolved Stackelberg game［J］. Journal of Tongji University： Natural Science， 2023， 51（11）： 1735-1744.）

［15］Wang Jiandong， Liu Hao， Dong Xuewen，et al. Personalized location privacy trading in double auction for mobile crowdsensing［J］. IEEE Internet of Things Journal， 2022， 10（10）： 8971-8983.

［16］Li Chuang， He Aoli， Wen Yanhua，et al. Optimal trading mechanism based on differential privacy protection and Stackelberg game in big data market［J］. IEEE Trans on Services Computing， 2023， 16（5）： 3550-3563.

［17］巫朝霞， 唐靖蕾， 苗志伟. 云环境下支持多授权机构的医疗数据安全共享方案［J］. 计算机应用研究， 2023， 40（12）： 3800-3804. （Wu Chaoxia， Tang Jinglei， Miao Zhiwei. Medical data secure sharing scheme supporting multi-authority in cloud environment［J］. Application Research of Computers， 2023， 40（12）： 3800-3804.）

［18］Li Chao， Li D Y， Miklau G，et al. A theory of pricing private data［J］. Communications of the ACM， 2017， 60（12）： 79-86.

［19］Shen Yuncheng， Guo Bing， Shen Yan，et al. Personal big data pricing method based on differential privacy［J］. Computers & Security， 2022， 113： 102529.

［20］Cai Hui， Yang Yuanyuan， Fan Weibei，et al. Towards correlated data trading for high-dimensional private data［J］. IEEE Trans on Parallel and Distributed Systems， 2023， 34（3）： 1047-1059.

［21］董恺， 蒋驰昊， 李想， 等. 基于代理训练集的属性推理攻击防御方法［J］. 计算机学报， 2024， 47（4）： 907-923. （Dong Kai， Jiang Chihao， Li Xiang，et al. Defending against property inference attacks based on agent training datasets［J］. Chinese Journal of Compu-ters， 2024， 47（4）： 907-923.）

［22］Manousis A， Shah H， Milner H，et al. The shape of view： an alert system for video viewership anomalies［C］// Proc of the 21st ACM Internet Measurement Conference. New York： ACM Press， 2021： 245-260.

［23］Ateniese G， Mancini L V， Spognardi A，et al. Hacking smart machines with smarter ones： how to extract meaningful data from machine learning classifiers［J］. International Journal of Security and Networks， 2015， 10（3）： 137-150.

［24］Dwork C， Roth A. The algorithmic foundations of differential privacy［J］. Foundations and Trends in Theoretical Computer Science， 2014， 9（3-4）： 211-407.

［25］Kifer D， Machanavajjhala A. Pufferfish： a framework for mathematical privacy definitions［J］. ACM Trans on Database Systems， 2014， 39（1）： 1-36.

［26］Zhang Wanrong， Ohrimenko O， Cummings R. Attribute privacy： framework and mechanisms［C］// Proc of ACM Conference on Fairness， Accountability， and Transparency. New York： ACM Press， 2022： 757-766.

［27］Song Shuang， Wang Yizhen， Chaudhuri K. Pufferfish privacy mechanisms for correlated data［C］// Proc of ACM International Conference on Management of Data. New York： ACM Press， 2017： 1291-1306.

［28］Chen M， Ohrimenko O. Protecting global properties of datasets with distribution privacy mechanisms［C］// Proc of the 26th International Conference on Artificial Intelligence and Statistics. ［S.l.］： PMLR， 2023： 7472-7491.

［29］Becker B， Kohavi R. Adult［DB/OL］. （1996-04-30）. https：//archive.ics.uci.edu/dataset/2/adult.