基于统计显著性检验的高效用项集挖掘算法

摘 要：针对传统高效用项集挖掘算法在具有不同类型标签事务中报告假阳性高效用项集的问题，提出两个基于统计显著性检验的高效用项集挖掘算法——FHUI和PHUI算法。这两个算法首先找到所有待检验高效用项集并依据项集长度进行分组；然后，FHUI算法根据项集自身的频率分布生成零分布，PHUI算法根据事务内置换策略或事务间置换策略构造置换事务集合来生成零分布。最后，FHUI和PHUI算法从零分布中计算出p值并运用错误发现率剔除假阳性高效用项集。基准事务集合实验结果显示FHUI和PHUI算法能够剔除大量的假阳性高效用项集，在后续分类任务中取得了更高的正确率；仿真事务集合实验结果显示FHUI和PHUI算法报告的项集中假阳性高效用项集数量占比低于4.8%且平均效用高于39 000。实验结果证明，在具有不同类型的标签事务中，FHUI和PHUI算法报告的统计显著高效用项集可靠性和实用性更强。

关键词：数据挖掘；高效用项集挖掘；统计显著性检验；Fisher检验；置换检验

中图分类号：TP391 文献标志码：A 文章编号：1001-3695（2024）10-013-2970-08

doi：10.19734/j.issn.1001-3695.2024.01.0027

Mining high utility itemsets based on statistical significance testing

Wu Jun， Wei Dandan， Ouyang Aijia， Wang Ya

（School of Information Engineering， Zunyi Normal University， Zunyi Guizhou 563000， China）

Abstract：Aiming at the problem of traditional high utility itemset mining algorithms reporting false positive high utility itemsets in transactions with class labels， this paper proposed two high utility itemset mining algorithms called FHUI and PHUI. The FHUI and PHUI firstly found all the candidates and grouped them by length. Then， the FHUI established null distributions with the frequency distributions， while the PHUI established null distributions by the permutation strategy within or between transactions. Finally， the FHUI and PHUI calculated the p values from the null distributions and exploited the false discovery rate to eliminate the false positive high utility itemsets. The experiments on the benchmark data sets show that the FHUI and PHUI can eliminate a large number of false positive itemsets， which allows them to achieve higher accuracy rates in the classification tasks. The experiments on synthetic data sets reveal that the proportions of false positive itemsets reported by FHUI and PHUI are lower than 4.8% and the average utility values are higher than 39 000. Experimental results prove that the statistically significant high utility itemsets reported by the FHUI and PHUI are more reliable and practical in transactions with class labels.

Key words：data mining; high utility itemset mining; statistical significance testing; Fisher testing; permutation testing

0 引言

发现数据中有趣和实用的项集是数据挖掘中一个重要的研究领域。在该领域中，频繁项集挖掘是研究最为全面的任务［1］。但实际应用中发现报告的大部分频繁项集都不具备有趣性和实用性。例如，在超市购买记录中，虽然{牛奶，面包}项集通常出现的频率很高，但其不具备有趣性和实用性，因为该项集提供的信息是一种普遍的消费行为。导致上述现象的原因是频繁项集挖掘任务设定每个项具有相同的权重。

为了发现真正有趣且实用的项集，频繁项集挖掘任务被拓展成高效用项集挖掘任务［2］。高效用项集挖掘任务通过赋予项独立的外部效用和内部效用使得每个项具有不同的权重。至今，高效用项集被广泛运用到不同问题中提供重要的数据特征［3］。由于项集的效用值不具备反单调性，高效用项集挖掘任务相较于频繁项集挖掘任务更具有挑战性。自高效用项集挖掘任务提出以来，研究人员陆续设计出一些有效的挖掘算法［4～7］。这些算法的不同之处在于搜索方法、事务表示形式、检索策略、效用计算方式等方面。按照算法流程可以将现有的算法分为两阶段算法和一阶段算法［8］。两阶段算法的核心思路是首先生成高效用项集的候选项集，然后计算候选项集的效用并筛除不满足效用阈值的项集。该类算法的代表有Two-Phase算法［9］、 HUI-PR算法［10］、HUIM-BDE算法［11］等。两阶段算法中生成并存储不满足效用阈值的候选项集浪费了计算和存储资源。为了避免资源浪费，一些算法跳过候选项集生成步骤直接计算每个项集的效用并判断其是否满足效用阈值，即一阶段算法。一阶段算法的代表是FHM算法［12］、HUIM-SU算法［13］、MLHMiner算法［14］等。以上这些算法均为完全高效用项集挖掘算法，具有相同的输入和输出，只在运行时间、内存占用和可拓展性等性能方面存在差别。

在具有类型标签的事务中，项集发现任务的主要研究方向是找到能够揭示不同类型事务差别特征的项集［15］。相关挖掘算法已被广泛应用于不同领域的问题研究中，例如在医学中探索不同癌症之间的症状差别［16］，在教育学中发现不同学生群体的学习和心理状态差别［17］，在市场营销学中揭示不同顾客群体的消费行为差别［18］。当传统高效用项集挖掘算法应用于具有类型标签的事务时，虽然能够报告大量满足效用阈值约束的高效用项集，但其中大部分高效用项集表达的信息并不能正确体现事务的特征差别，即存在大量随机产生的假阳性高效用项集。基于假阳性高效用项集提供的虚假特征作出的决策大概率会导致失败的结果，因此找到结果中的假阳性高效用项集并将其剔除是至关重要的。

分析发现，传统算法报告大量假阳性高效用项集的原因是这些算法无法识别项集在不同类型事务中的效用分布。统计显著性检验是评估统计度量分布是否具有显著性的有效方法［19］。目前，统计显著性检验被广泛应用于许多数据挖掘任务中筛除假阳性结果，达到了提升挖掘结果可靠性的目的，例如社群发现任务［20］、对比序列模式挖掘任务［21］等。在高效用项集挖掘任务中，目前只存在少量基于统计显著性检验的高效用项集挖掘算法，例如HUSP算法［22］。因此，使用统计显著性检验剔除假阳性高效用项集还需要投入大量的研究。

立足于上述分析，本文提出两种基于不同类型统计显著性检验的高效用项集挖掘算法：FHUI（Fisher testing-based high utility itemsets mining）和PHUI（permutation testing-based high utility itemsets mining）算法。该算法首先使用基于垂直事务结构的ULB-Miner算法［23］找到原始事务集合中的待检验高效用项集并根据项集长度分组。接着，针对每组，FHUI算法使用Fisher检验［24］根据高效用项集在不同类型事务集合中的频率分布生成零分布；而PHUI算法使用置换检验［15］构造置换事务集合并从中找到随机效用差生成零分布。其中，PHUI算法设计了两种置换策略：事务内置换策略和事务间置换策略。最后，FHUI和PHUI算法从各自的零分布中计算出待检验高效用项集的统计显著性p值，并使用错误发现率（false discovery rate， FDR）控制结果中的假阳性高效用项集数量。基准事务集合和仿真事务集合中的实验结果证明FHUI和PHUI算法能够成功剔除一定数量的假阳性高效用项集，从而达到更高的分类任务正确率和平均效用，因此根据FHUI和PHUI算法报告的高效用项集作出的后续决策可靠性和实用性更强。此外，合理量化文献［16～18］实例应用中事务的内部效用和外部效用后，FHUI和PHUI算法能够直接应用于对应问题的研究中。

1 基本概念

1.1 高效用项集

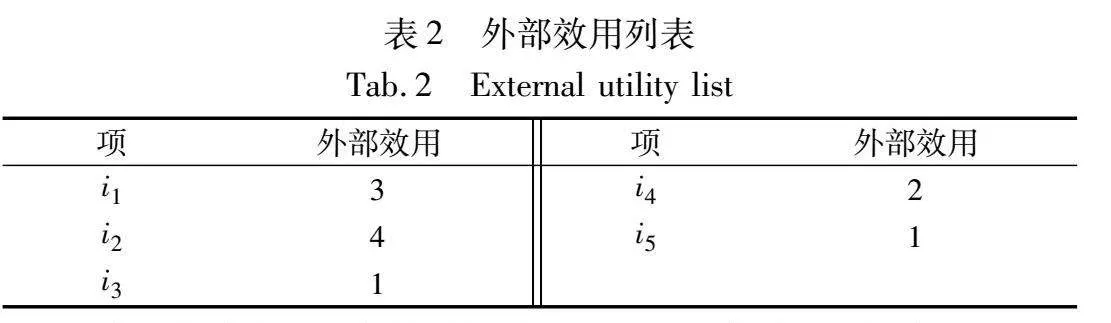
假设I={i1，i2，…，i|I|}表示项的集合，其中| |表示集合大小。每一个项ij都被分配了一个正整数eu（ij），表示其外部效用。项的集合X被称为项集，即XI。假设D={d1，d2，…，d|D|}表示一个事务集合，其中每一条dv由若干个项和一个类型标签cq构成。项ij在dv中的内部效用被定义为一个正整数iu（ij， dv）。以超市消费记录事务为例，顾客的一次购物记录可以看作是一条事务，每个商品的利润可以量化为项的外部效用，每个商品购买的数量可以量化为项的内部效用。X在D中的支持度指的是D中包含X的事务数量，即sup（X， D）=|{dv|Xdv∧dv∈D}|。为了阐明基本概念，表1展示了一个事务集合的样例，其中每个项的外部效用如表2所示。

项ij在事务dv中的效用由u（ij， dv）表示，定义为

u（ij，dv）=eu（ij）×iu（ij，dv）（1）

例如，表1中i2在d1中的效用u（i2， d1）=4×3=12。

项集X在事务dv中的效用由u（X， dv）表示，定义为

u（X，dv）=∑ij∈Xu（ij，dv）（2）

例如，假设X={i2， i3}，表1中u（X， d3） =4×4+1×2=18。

项集X在事务集合D中的效用由u（X， D）表示，定义为

u（X，D）=∑dv∈Du（X，dv）（3）

例如，同样假设X={i2， i3}，表1中u（X， D）= u（X， d3）+u（X， d6）=18+10=28。

如果X在D中的u（X， D）不小于效用阈值αuti，那么X被称作高效用项集。例如，如果 αuti=25，那么表1中{i2， i3}为高效用项集。高效用项集挖掘任务的目标是找到事务集合D中所有效用不低于αuti的项集。

1.2 统计显著性检验

面向具有类型标签的事务时，由于传统高效用项集挖掘算法无法捕获高效用项集在不同类型事务集合中的效用分布，结果中会存在一定数量随机产生的假阳性高效用项集。统计显著性检验是剔除假阳性高效用项集的有效策略，其标准步骤是：首先，建立与任务匹配的零假设；其次，收集与零假设一致的证据值并使用这些证据值生成零分布；最后，从零分布中计算出待检验目标的统计显著性并作出是否拒绝零假设的决定。结合高效用项集挖掘任务，建立的零假设为待检验高效用项集在不同类型的事务集合中的效用分布是随机产生的。证据值的收集与零分布的生成见2.1和2.2节具体的描述。

在统计显著性检验中，待检验高效用项集的统计显著性通常由p值量化，其定义是在零假设为真的前提下，发现一个比待检验高效用项集更极端的项集概率，其中极端主要体现在证据值上。高效用项集挖掘算法通常会报告大量项集，该情况能够使用多重假设检验控制整体待检验结果中假阳性高效用项集的数量。在多重假设检验中，FDR是使用最为频繁的约束度量之一，其定义为在所有报告的结果中假阳性结果占比的期望值。后续提出的FHUI和PHUI算法将使用FDR控制待检验高效用项集中假阳性高效用项集的数量。

2 挖掘算法

2.1 FHUI算法

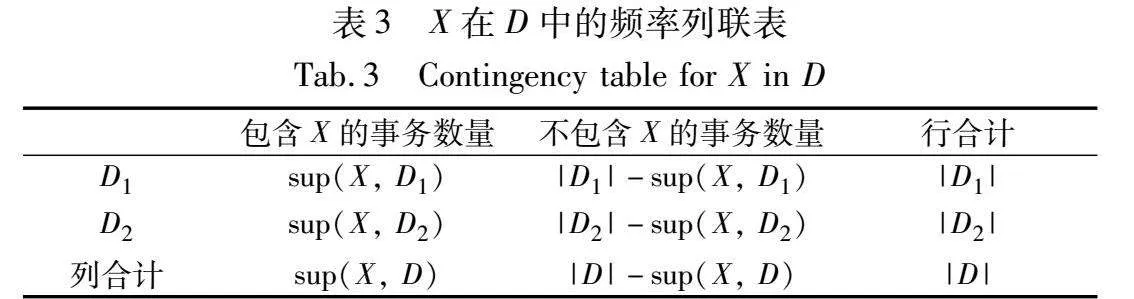
FHUI算法的核心思路是先使用待检验高效用项集在不同类型事务中的频率分布刻画效用分布，再使用Fisher检验将该频率分布作为项集的零分布并从中计算出p值。具体而言，设类型标签集合C={c1，c2}，根据C可以将D划分成D=D1∪D2，其中D1中事务的类型标签均为c1，D2中事务的类型标签均为c2。待检验高效用项集X在D中的频率列联表如表3所示。

根据表3中X的频率分布，可以得出X的sup（X， D1）服从超几何分布，即

h（sup（X，D1）|X）=|D1|sup（X，D1）|D2|sup（X，D2）|D|sup（X，D）（4）

根据Fisher检验［24］，可以将式（4）作为待检验高效用项集的零分布并从中计算出项集的p值，其中p值中的极端项集被定义为X在D1中频率分布大于等于sup（X， D1）的情况。p值计算公式为

p1（X，D）=∑wj=1h（sup（X，D1）+j|X）（5）

其中：w=min{sup（X， D2）， |D1|－sup（X， D1）}。式（5）中包含了大量的二项式计算，导致计算开销较高。为了快速计算出待检验高效用项集的p值，参考了文献［25］中的近似上界方法加速p值计算，即

b（X，D）=sup（X，D2）（|D1|－sup（X，D1））（sup（X，D1）+1）（|D2|－sup（X，D2）+1）（6）

p1（X，D）≈h（sup（X，D1）|X）1－b（X，D）w+11－b（X，D）（7）

通过式（7）计算出所有待检验高效用项集的p值后， FHUI算法使用BH方法［19］约束FDR达到控制假阳性高效用项集数量的目的。BH方法计算公式如下：

BH（Rk，αsig）={X|p1（X，D）≤gX×αsig|Rk|∧X∈Rk}（8）

其中：Rk表示k长度待检验高效用项集的集合；αsig表示统计显著水平；gX表示X在Rk中根据p值从小到大排序的索引值。详细的FHUI算法流程见算法1。

算法1 FHUI 算法

输入：事务集合D；效用阈值αuti；统计显著水平αsig。

输出：统计显著高效用项集集合S。

a） R ← ULB_Miner （D， αuti）

b） R1， R2， …， Rmax_len （R） ← len_group（R）

c） L ← fac_buffer（D）

d） for k=1 to max_len （R） do

e） for each X in Rk do

f） X.w ← min{sup（X， D2）， |D1|－sup（X， D1）}

g） X.b ← b（X， D）

h） X.p ← p1（X， D， L）

i） end for

j） sort（Rk）

k） S ← S∪BH（Rk， αsig）

l） end for

m） return S

FHUI算法流程的说明如下：

a）使用ULB-Miner算法［23］找到所有待检验高效用项集，并使用len_group（）方法依据项集长度分组（步骤a）b）），分组检验的目的是为了避免项集长度的影响。利用fac_buffer（）方法构建阶乘缓存加速后续二项式的计算（步骤c））。

b）针对各组中每个待检验高效用项集X，先计算出其频率分布上界X.w，再依据式（6）和（7）计算出X的p值（步骤d）～i））。

c）使用sort（）方法将每组中待检验高效用项集依据p值从小到大进行排序，再使用BH（）方法找到统计显著高效用项集并放入集合S中（步骤j）～l））。最后，返回保存了所有统计显著高效用项集的集合S（步骤m））。

FHUI算法的时间复杂度主要由四部分构成：待检验高效用项集挖掘、阶乘缓存建立、零分布与p值计算以及假阳性结果剔除。根据文献［23］可知，ULB-Miner算法的时间复杂度是O（e2log e），其中e表示平均效用列表长度；阶乘缓存建立的时间复杂度为O（|D|）；每个项集生成零分布并从中计算p值是通过式（4）（6）（7）完成的，这三个公式的时间复杂度均为O（1），因此所有待检验高效用项集零分布与p值计算的时间复杂度为O（|R|）；使用BH方法约束FDR剔除假阳性结果的时间复杂度为O（|R|log|R|+|R|））。综上，FHUI算法的时间复杂度为O（e2log e+|D|+|R|+|R|log|R|+|R|）），合并化简后的结果为O（e2log e+ |D|+|R|log|R|）。

2.2 PHUI算法

PHUI算法的核心思路是使用置换检验构造置换事务集合，利用从中收集的随机效用差生成零分布并计算出项集的p值。效用差的定义为

udif（X，D）=abs（u（X，D1）－u（X，D2））（9）

其中：abs（）表示取绝对值。为了模拟随机效用差的分布，PHUI算法在零假设约束下设计了两种不同的置换策略构造置换事务集合，即事务内置换策略和事务间置换策略。

事务内置换策略通过随机置换每条事务的内部效用构造置换事务集合。具体而言，针对每一条事务，首先生成项的随机置换序列，然后根据该序列置换项的内部效用。例如，假设原始事务集合如图1（a）所示，对于d1，生成的项的随机置换序列是d1：{i4，i7，i5，i1，i3}。根据该序列，将i1的内部效用置换给i4，将i3的内部效用置换给i7，依此类推，直到完成所有内部效用的置换。假设余下事务的随机置换序列为d2：{i4，i5，i2}、d3：{i7，i3，i6，i4}、d4：{i6，i4，i1}、d5：{i6，i4，i2，i1}。根据事务内置换策略，最终构造的置换事务集合D如图1（b）所示。

事务间置换策略通过置换事务之间的类型标签、项及其内部效用构造置换事务集合。详细步骤如下：

a）选择一个［1， min_tran（D）］的随机整数z，其中min_tran（）返回D中最短的事务长度；并为每条事务随机标记z个项的位置，将这些位置信息存入集合G中。

b）生成一个事务编号的随机置换序列，根据该序列首先置换每条事务的类型标签，然后置换每条事务在G中标记位置对应的项及其内部效用。置换后事务若存在相同的项，则进行内部效用合并。

举个例子，给定D如图1（a）所示，从中可知min_tran（D）=3。假设z=2，G={d1：{2，5}， d2：{1，2}， d3：{3，4}， d4：{1，3}， d5： {2，3}}，生成的事务编号随机置换序列为{d4，d1，d5，d2，d3}。根据该序列，先将d1的类型标签置换给d4，再将d1中{2，5}位置的项及其内部效用置换到d4的{1，3}位置；先将d2的类型标签置换给d1，再将d2中{1，2}位置的项及其内部效用置换给d1的{2，5}位置，置换后存在相同的项i4，故将其内部效用合并得到（i4，5）；如此迭代，直至完成随机置换序列所有的置换，最终构造的置换事务集合D如图1（c）所示。

使用事务内或事务间置换策略构造一定数量的置换事务集合后，PHUI算法从这些集合中收集待检验高效用项集的随机效用差为不同长度的项集生成置换检验零分布Nk。随后，再通过式（10）计算出待检验高效用项集p值：

p2（X，D，Nk）=|{j|udif（X，D）≤j∧j∈Nk}||Nk|（10）

计算出所有待检验高效用项集的p值后，PHUI算法同样使用BH方法约束FDR，即使用式（8）控制假阳性高效用项集的数量。详细的PHUI算法流程见算法2～4。其中，算法2流程的说明如下：

a）使用ULB-Miner算法［23］找到所有待检验高效用项集，并使用len_group（）方法分组。此外，将每组保存随机效用差的集合Nk初始化为空集（步骤a）～c））。

b）执行t次相同的置换策略生成置换事务集合，即采用基于事务内置换策略的per_trans（）方法或采用基于事务间置换策略的per_trans（）方法。在每一次置换过程中，首先使用per_trans（）方法构造置换事务集合D；接着使用uti_update（）方法更新待检验高效用项集在D中的随机效用差；最后使用uti_extract（）方法提取各长度项集的随机效用差并放入Nk中（步骤d）～j））。执行完t次置换后，Nk中保存的随机效用差构成k长度待检验高效用项集的零分布。

c）根据式（10）计算出每组中所有待检验高效用项集的p值后，使用sort（）和BH（）方法找到统计显著高效用项集并放入集合S中（步骤k）～q））。最后，返回保存了所有统计显著高效用项集的集合S（步骤r））。

算法2 PHUI 算法

输入：事务集合D；效用阈值αuti；统计显著水平αsig；置换次数t。

输出：统计显著高效用项集集合S。

a） R ← ULB_Miner （D， αuti）

b） R1， R2， …， Rmax_len （R） ← len_group（R）

c） N1， N2， …， Nmax_len（R）←

d） for j=1 to t do

e） D ← per_trans（D）

f） R← uti_update（D， R）

g） for k=1 to max_len （R） do

h） Nk ← Nk∪ uti_extract（R， k）

i） end for

j） end for

k） for k=1 to max_len （R） do

l） for each X in Rk do

m） X.p ← p2（X， D， Nk）

n） end for

o） sort（Rk）

p） S ← S∪BH（Rk， αsig）

q） end for

r） return S

算法3描述了基于事务内置换策略的per_trans（）方法。针对每条事务d，先使用ran_items（）方法生成一个项的随机置换序列M，再使用in_permute（）方法根据M置换每个项的内部效用便得到了一条置换事务d。最后，返回包含所有d的置换事务集合D。

算法3 基于事务内置换策略的per_trans（）方法

输入：原始事务集合D。

输出：置换事务集合D。

a） D←

b） for each d in D do

c） M ← ran_items（d）

d） d← in_permute（M）

e） D← D∪ d

f） end for

g） return D

算法4描述了基于事务间置换策略的per_trans（）方法。首先，使用ran_number（）生成一个［1， min_trans（D）］之间的随机整数z，并使用ran_positions（）为每条事务标记z个项的随机位置存入G中；接着，使用ran_tids（）方法生成一个事务编号的随机置换序列F；然后，针对每条事务d，先使用lab_ permute（）方法根据F置换类型标签得到d1，再根据F和G置换d1中标记位置对应的项及其内部效用得到一条置换事务d2；最后，返回包含所有d2的置换事务集合D。

算法4 基于事务间置换策略的per_trans（）方法

输入：原始事务集合D。

输出：置换事务集合D。

a） D← ， G ←

b） z ← ran_number（1， min_trans（D））

c） for each d in D do

d） G ← G∪ran_positions（d， z）

e） end for

f） F ← ran_tids（D）

g） for each d in D do

h） d1 ← lab_ permute（F）

i） d2← bet_permute（d1， F， G）

j） D← D∪ d2

k） end for

l） return D

PHUI算法的时间复杂度主要由四部分构成：待检验高效用项集挖掘、置换检验零分布生成、p值计算以及假阳性结果剔除。其中，待检验高效用项集挖掘和假阳性结果剔除这两部分与FHUI算法采用了相同的步骤，因此其时间复杂度也相同，分别为O（e2log e）和O（|R|log|R|+|R|）。每个项集的p值能够通过置换检验零分布直接计算得出，因此所有待检验高效用项集p值计算的时间复杂度是O（|R|）。

由于算法3和4使用了不同的置换策略构造置换事务集合D，从而其生成置换检验零分布的时间复杂度也不相同。具体而言，事务内置换策略通过置换每条事务的内部效用生成置换事务集合，其时间复杂度为O（|D|a），其中a表示d中包含的项的数量。事务间置换策略通过置换事务之间的类型标签、项及其内部效用构造置换事务集合，其时间复杂度为O（|D|（z+a））。生成D后，两种策略使用同样的方式更新和提取随机效用差，其时间复杂度为O（|R|）。因此，经过t次事务内置换策略生成置换检验零分布的时间复杂度为O（t（|D|a+|R|））；经过t次事务间置换策略生成置换检验零分布的时间复杂度为O（t（|D|（z+a）+|R|））。

综上，基于事务内置换策略的PHUI算法的时间复杂度是O（e2log e+t（|D|a+|R|）+|R|+|R|log|R|+|R|），合并化简后的结果为O（e2log e+t|D|a+|R|（log|R|+t））；基于事务间置换策略的PHUI算法的时间复杂度是O（e2log e+t（|D|（z+a）+|R|）+|R|+|R|log|R|+|R|），合并化简后的结果为O（e2log e+t|D|（z+a）+|R|（log|R|+t））。

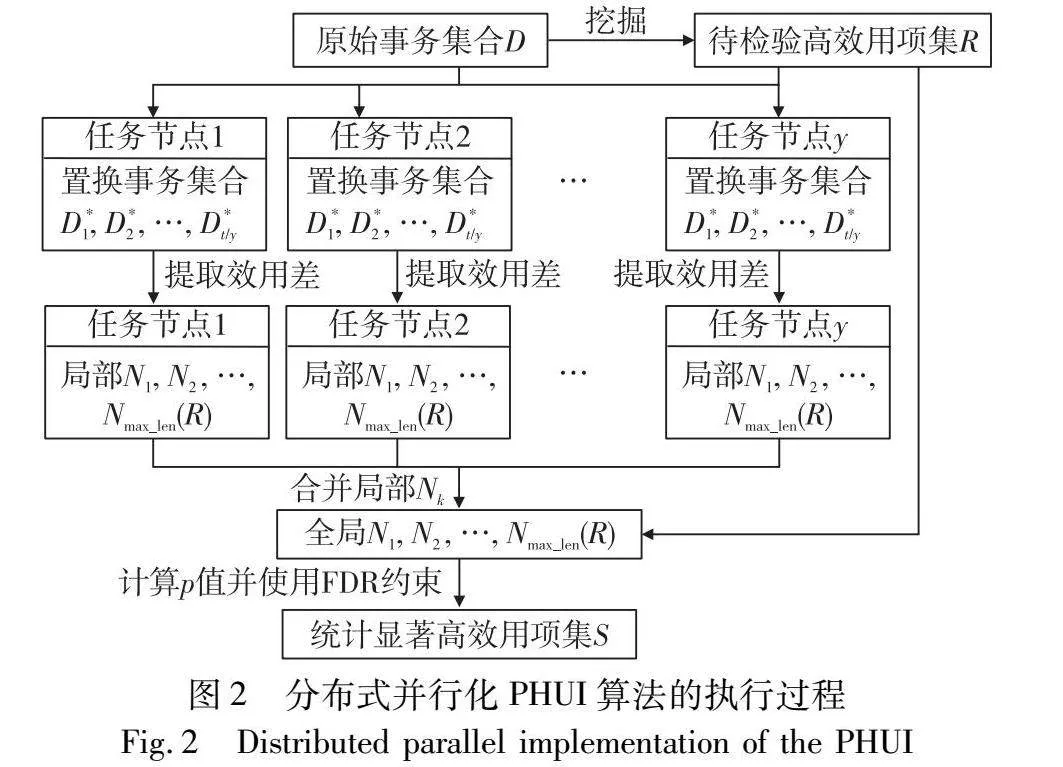
PHUI算法执行过程中需要构造t次置换事务集合，导致计算开销较大。为了提升算法的实用性，分析发现每个置换事务集合的构造和处理是相互独立的，该情况能够使用分布式并行化技术减少置换事务集合构造和处理的时间。具体而言，假设有y个并行任务节点，每个任务节点执行完t/y次PHUI算法的步骤e）～i）后，将所有节点返回的局部Nk进行合并就能得到各个长度待检验高效用项集的全局Nk。分布式并行化的PHUI算法流程如图2所示。

3 实验结果与分析

3.1 实验对比算法

为了分析与验证FHUI和PHUI算法挖掘高效用项集的能力，在基准事务集合和仿真事务集合上实施了大量对比实验。对比算法为HUIM-SU算法［13］、EHNL算法［26］ 和HUSP算法［22］。HUIM-SU算法设计了简化的效用列表结构快速计算项集的效用；EHNL算法在效用阈值约束的基础上额外使用了长度约束筛除部分冗余高效用项集。这两个对比算法均为基于效用阈值约束的算法，未采用任何假阳性高效用项集处理或预防策略。HUSP算法是基于统计显著性检验的算法，使用了LAMP方法计算项集的统计显著性。为了便于实验对比，将原始HUSP算法使用的错误率判断族约束更改为FDR约束。此外，为了区分PHUI算法使用不同的置换策略，PHUI-w算法表示使用了事务内置换策略，PHUI-b算法表示使用了事务间置换策略。

3.2 实验基本设置

在众多分布式并行化计算框架中，Spark框架内存计算效率高、MLlib库丰富，使得其更加适用于迭代运算较多的数据挖掘任务，目前许多传统模式发现算法使用Spark框架完成了特定模式的分布式并行挖掘［1］，因此提出的PHUI算法同样采用Spark框架实现置换事务集合生成和计算的分布式并行化。所有算法均使用Java语言实现，且所有实验均运行在3台计算机组成的集群上，每台配置为3.60 GHz（12核）CPU和64 GB内存。

在置换检验中，需要构造一定数量的置换事务集合生成零分布，数量越多，生成的零分布越准确，但相应的计算开销也越大，通常1 000是置换检验中常用的数量设置［15］。对于αsig而言，阈值设置得越低，假阳性结果的数量会减少，但同时非假阳性结果的数量也会大量减少，因此需要在两种结果中进行相应平衡，0.05是大部分统计显著性检验中常用的αsig阈值［19］。

3.3 实验数据信息

3.3.1 基准事务集合信息

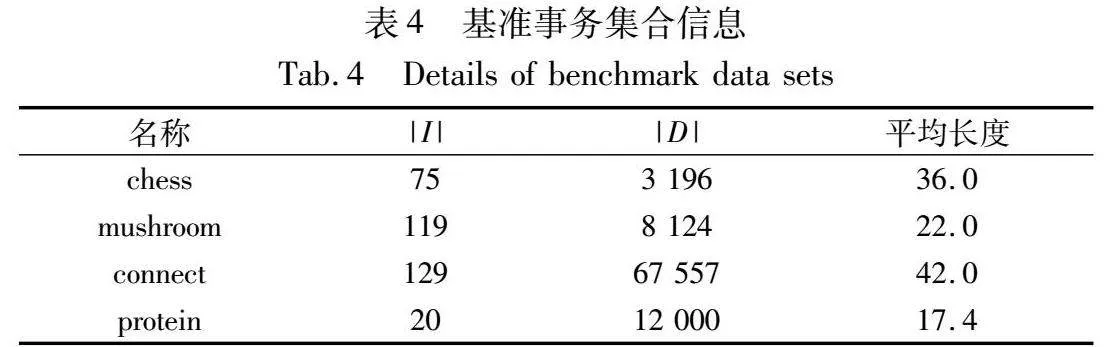
实验采用了高效用项集挖掘任务中广泛使用的4个基准事务集合：chess［27］、mushroom［27］、connect［27］、protein［8］，详细信息如表4所示。其中，connect集合含有3种类型标签，为了便于呈现实验结果，将“loss”和“draw”对应的事务进行了合并。

3.3.2 仿真事务集合信息

基准事务集合中缺少高效用项集的真假信息，于是实验构造了仿真事务集合。内部效用、外部效用和频率分布是影响高效用项集效用分布的重要因素。根据这三个因素，分别构造了三种不同类型的仿真事务集合，具体步骤为：

a）假设Ifal={i1，i2，…，i60}表示构成随机项集的字母表集合；Itru={i61，i62，…，i74}表示构成真实植入项集的字母表集合；C= {c1，c2}表示类型标签集合。

b）分配一个［1，10］的随机整数给Ifal中每一个项ifal作为该项的外部效用，即eu（ifal） ∈［1，10］。

c）将Ifal中的项分为20组，每组包含3个项。为了构造一条事务dsyn，从每组中随机抽取一个项ifal，并为每个抽取的项分配一个［1，10］的整数作为内部效用，即iu（ifal， dsyn） ∈［1，10］。

d）重复执行上一步骤直至构造4 000条事务。将c1分配给前2 000条事务构成D1，c2分配给后2 000条事务构成D2，计算4 000条事务的总效用utotal。

e） 使用Itru中不同的项构造5个1长度、3个2长度、1个3长度的高效用项集。选择f-1、f-2或f-3步骤中的其中一种方式进行全部植入，并保证每个植入项集的效用在［0.01 utotal， 0.02 utotal］。

f-1）内部效用主导植入方式：植入项集中每个项itru的eu（itru） ∈［1，10］，iu（itru， dsyn） ∈［20，30］，D1和D2的频率分布在1.5∶1至3∶1之间。

f-2）外部效用主导植入方式：植入项集中每个项itru的eu（itru） ∈［20，30］，iu（itru， dsyn） ∈［1，10］，D1和D2的频率分布在1.5∶1至3∶1之间。

f-3）频率分布主导植入方式：植入项集中每个项itru的eu（itru） ∈［1，10］，iu（itru， dsyn） ∈［1，10］，D1和D2的频率分布在3∶1至6∶1之间。

实验结果中，如果报告的一个高效用项集只包含Ifal中的项，那么该项集被认定为假阳性高效用项集，因为这样的项集没有包含任何真实信息。此外，为了避免偶然性，分别使用内部效用主导、外部效用主导和频率分布主导的植入方式独立构造10个仿真事务集合。

3.4 基准事务集合实验

3.4.1 报告的高效用项集数量

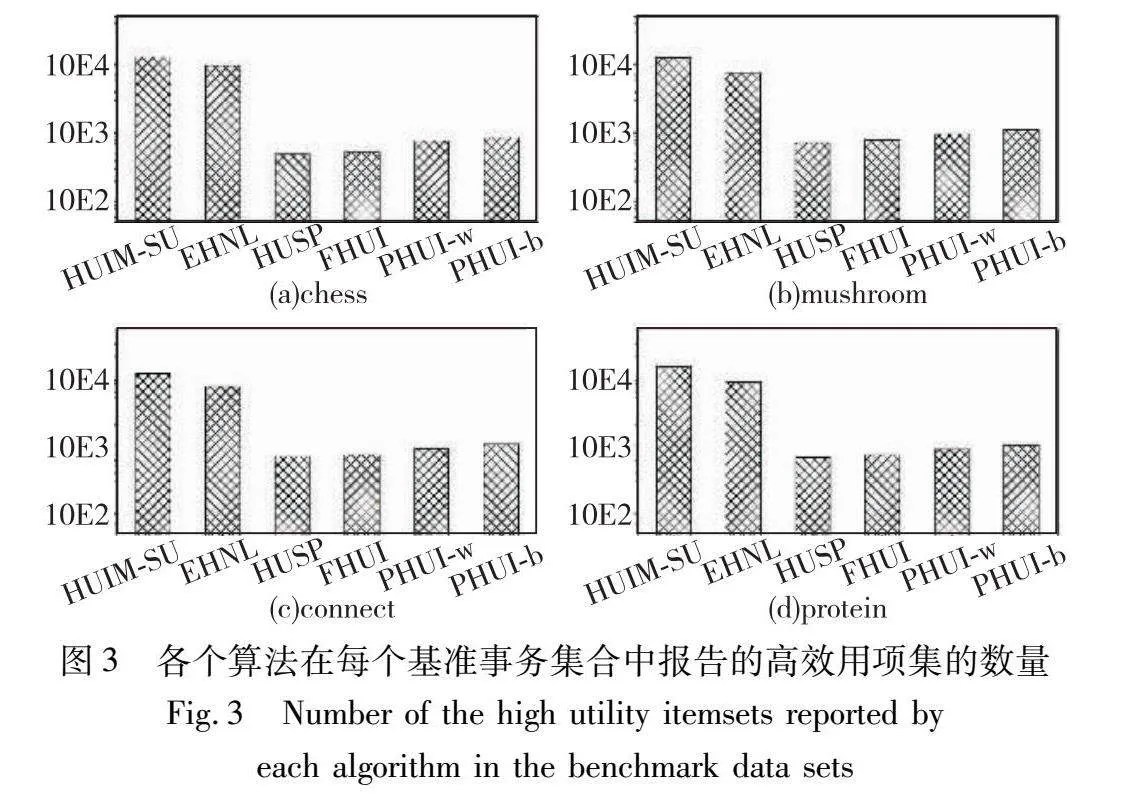
为了比较各个算法挖掘高效用项集的能力，实验比较了各个算法在每个基准事务集合中相同αuti参数下报告的高效用项集数量，其中chess集合的αuti=5.2×105，mushroom集合的αuti=2.5×105，connect集合的αuti=1.4×107，protein集合的αuti=3.4×105。各个算法报告的高效用项集数量如图3所示，从中可以看出，报告的高效用项集数量关系为：HUIM-SU>EHNL>>PHUI-b>PHUI-w>FHUI>HUSP。

造成上述结果的原因是HUIM-SU和EHNL算法是基于效用阈值约束的算法，而HUSP、FHUI、PHUI-w和PHUI-b算法是基于统计显著性检验的算法。基于效用阈值约束的算法只要项集满足αuti阈值就会被报告；而基于统计显著性检验的算法不仅运用了效用阈值约束项集，还在其基础上引入统计显著性检验评估项集的效用分布可靠性。因此基于效用阈值约束的算法报告的结果中存在大量没有正确表达不同类型事务差别特征的项集，从而其报告的项集数量远远大于基于统计显著性检验的算法。此外，大量的高效用项集还会给后续任务带来验证困难、抽样选择、合并表示等额外的问题。

进一步分析，在基于效用阈值约束的算法中，EHNL算法使用了项集长度约束筛除较长的冗余高效用项集，使得其项集数量相较于HUIM-SU算法更少。在基于统计显著性检验的算法中，各个算法使用不同的检验方法计算p值，使得报告的统计显著高效用项集数量也不相同，但整体数量差距并不巨大。由于不确定其中假阳性高效用项集和非假阳性高效用项集的数量，从而无法单从整体数量上对比各个算法挖掘能力的优劣。

YRuH10HvBUDCHOLRA2IQZOLxDBMqfFsCwnm4sSn428I=3.4.2 分类任务正确率

基准事务集合缺少高效用项集的真假信息，为了验证各个算法报告的高效用项集的可靠性，接下来的实验将使用算法报告的高效用项集作为事务的特征进行后续分类任务。具体而言，如果一条事务包含某个高效用项集，则将该项集对应的特征置1，反之则置0。该实验有效性的理论依据是在具有类型标签的事务中报告的高效用项集应当体现不同类型事务的特征差别，否则类型标签毫无意义［6］。为了减少分类器自身的影响，实验采用了朴素贝叶斯和随机森林两种不同类型的分类器。

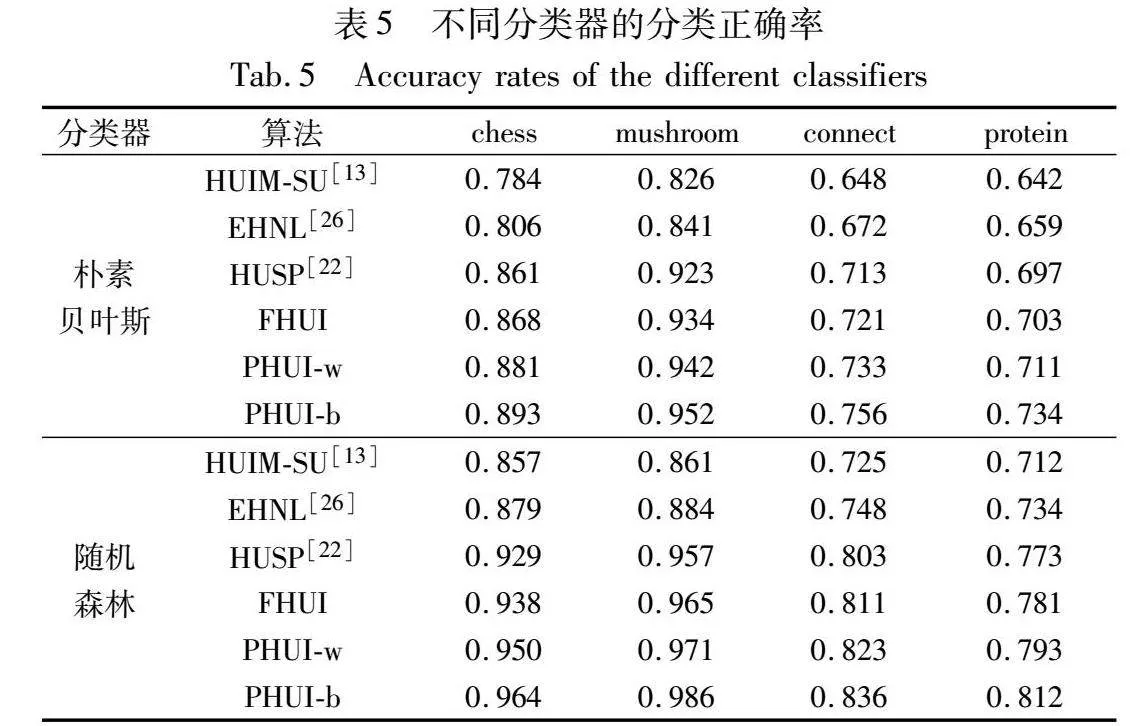
两种分类器在各个基准事务集合中的分类正确率如表5所示，从中可以获知HUIM-SU和EHNL算法构造特征的分类正确率明显低于HUSP、FHUI、PHUI-w和PHUI-b算法。此外，基于统计显著性检验算法构造特征分类正确率的高低关系为HUSP＜FHUI＜PHUI-w＜PHUI-b。

在该实验结果中，导致HUIM-SU和EHNL算法构造特征的分类正确率低于HUSP、FHUI、PHUI-w和PHUI-b算法的主要原因是基于阈值约束的算法中未考虑高效用项集的效用分布，导致其大量的构造特征源自于错误表达事务差别特征的假阳性高效用项集；反之，基于统计显著性检验的算法使用不同检验方法剔除了一定数量的假阳性高效用项集，因而其构造特征对应的统计显著性高效用项集正确体现了不同类型事务的差别特征。进一步分析，对于分类器而言，其根本目的是拟合训练数据的同时实现测试数据的良好泛化。由于假阳性高效用项集对应的特征无法体现不同类型事务的差别，所以其本质上是与分类任务无关的特征［6］，这些无关特征的加入造成了输入数据本身的偏差，从而严重影响了分类器的泛化能力。此外，基于阈值约束的算法构造特征的维度远大于基于统计显著性检验的算法，且大量特征是任务无关特征，导致同类型事务在其相应的特征空间中变得更加稀疏，进一步增加了分类任务的难度。

在基于统计显著性检验的算法中，HUSP 和FHUI算法构造特征的分类正确率低于PHUI-w和PHUI-b算法，其中的原因是HUSP 和FHUI算法均使用项集的频率分布间接刻画效用分布，而PHUI-w和PHUI-b算法使用随机效用差直接刻画效用分布。因此HUSP 和FHUI算法构造特征主要源自频率分布呈现显著差别的高效用项集，未考虑效用分布与频率分布不一致的高效用项集提供的差别特征。

进一步而言，HUSP 算法构造特征的分类正确率低于FHUI算法，这是因为HUSP算法未进行分组检验，导致误判了少量非假阳性高效用项集；PHUI-w算法构造特征的分类正确率低于PHUI-b算法，其原因是事务内置换策略固定了项集的频率分布，事务间置换策略未固定项集的频率分布，导致PHUI-w算法遗漏了效用分布主要体现在频率分布差别的项集提供的特征。

3.5 仿真事务集合实验

3.5.1 报告的高效用项集情况

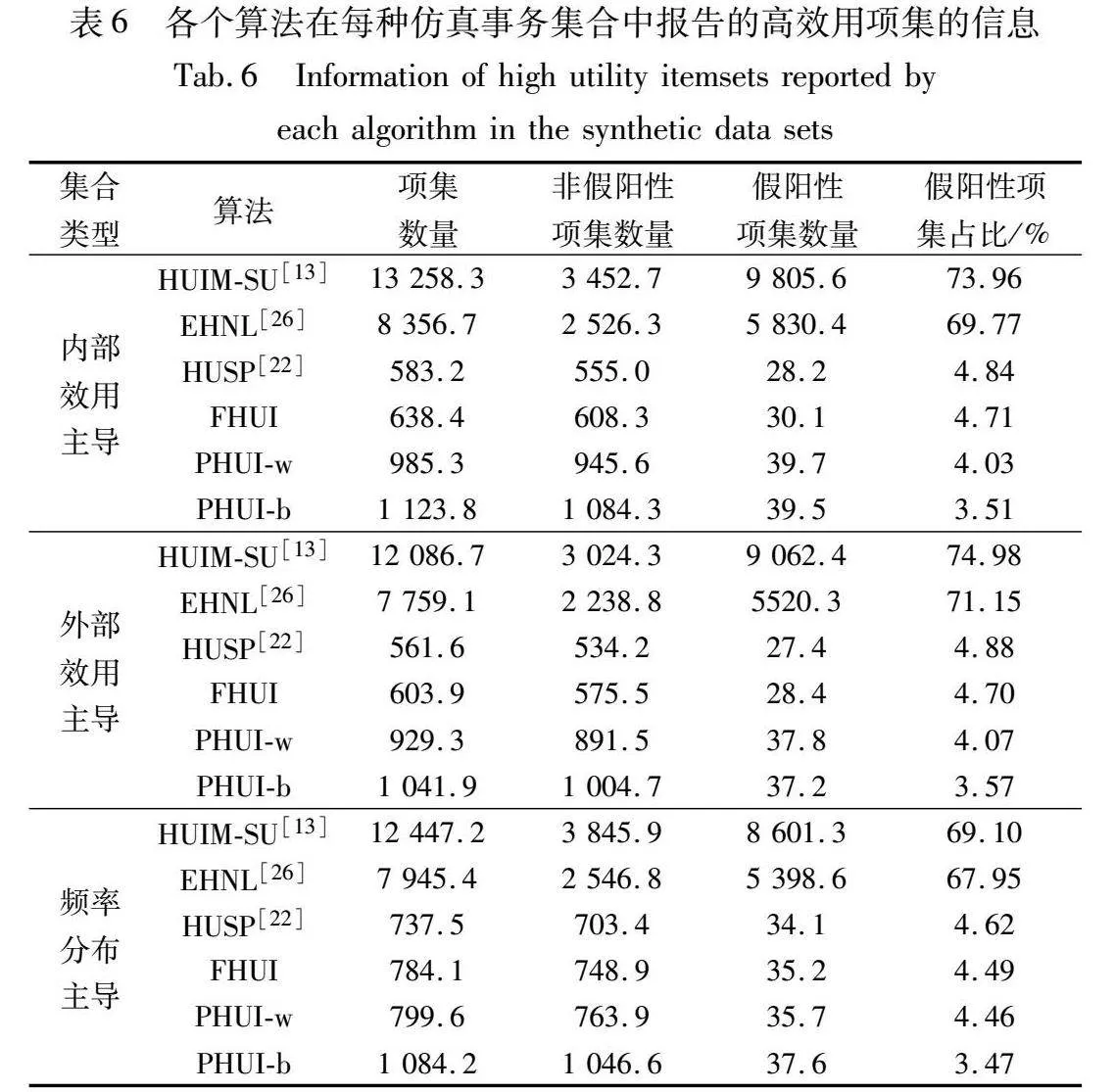
假阳性高效用项集提供的错误差别特征会误导后续任务的决策，例如3.4.2节中的分类任务等。为了直观比较各个算法报告结果中高效用项集的具体情况，在三种不同类型仿真事务集合中运行了各个算法，其中αuti=3.0×104。

各个算法在三种仿真事务集合中报告的高效用项集信息如表6所示，其中每个结果取自于10个相同类型仿真事务集合的平均值。从表6中可以获知，HUIM-SU和EHNL算法在三种不同类型的仿真事务集合中均报告了大量的假阳性高效用项集，其数量占比达到了67%以上；相反地，HUSP、FHUI、PHUI-w和PHUI-b算法报告的结果中假阳性高效用项集的数量占比均小于4.9%。该结果验证了基于统计显著性检验的算法能够有效剔除结果中大量的假阳性高效用项集，保留的项集可靠性更强。此外，提出的FHUI、PHUI-w和PHUI-b算法报告的结果中假阳性高效用项集的数量占比低于HUSP算法。

对于内部效用主导和外部效用主导的仿真事务集合，各个算法呈现的实验结果基本一致。其原因是虽然两种不同类型仿真事务集合植入项集的内部效用和外部效用不相同，但其u（ij， dv）和频率分布基本一致，从而不会对算法挖掘结果造成显著影响。在这两种仿真事务集合中，存在大量仅由Ifal中的项随机构成的项集，且这些项集的效用恰好满足αuti阈值，即假阳性高效用项集。由于基于阈值约束的算法缺失随机项集识别能力，导致其结果中假阳性高效用项集占比很高；相反地，基于统计显著性检验的算法能够根据效用分布识别随机项集并将其剔除，从而其结果中假阳性高效用项集占比较低。

进一步分析，HUSP 和FHUI算法在这两种仿真事务集合中报告的非假阳性项集数量显著低于PHUI-w和PHUI-b算法，从而使结果中假阳性项集占比略高。造成该结果的原因是HUSP 和FHUI算法基于频率分布计算p值，当植入项集的频率分布接近1.5∶1时，这两个算法会将植入项集及其部分子项集或超项集判断为假阳性高效用项集；而PHUI-w和PHUI-b算法直接通过随机效用差计算p值，对于上述项集的误判概率较小。此外，由于HUSP算法未实施分组检验，干扰了FDR约束截断阈值的计算，导致其非假阳性项集数量和假阳性项集占比劣于HUSP算法。PHUI-b算法的非假阳性项集数量和假阳性项集占比优于PHUI-w算法，这是因为PHUI-w算法使用的事务内置换策略是有条件的假设检验，即固定了项集的频率分布，该条件会使得项集计算的p值相较于真实p值偏大［21］，从而导致FDR约束剔除的非假阳性项集数量增多。值得注意的是，不能单纯地从假阳性项集数量判断基于假设检验算法的性能，因为在FDR约束下随着非假阳性项集数量的增加，假阳性项集数量必然也会增加。

在频率分布主导的仿真事务集合中，上述结果的差异分析同样适用。进一步纵向比较，HUIM-SU和EHNL算法的性能略微优于其在效用主导的仿真事务集合，原因是随着植入项集频率分布的增加，其子项集或者超项集更容易达到αuti阈值。同样地，HUSP 和FHUI算法的性能也要优于其在效用主导的仿真事务集合中的表现，这是因为频率分布主导的仿真事务集合植入项集的最低频率分布为3∶1，频率分布的增加降低了这两个算法对植入项集的子项集或超项集的误判率。相反，PHUI-w算法在该仿真事务集合中的性能表现不及其余两种类型的仿真事务集合，其中的原因是PHUI-w算法固定了项集的频率分布，当项集频率分布增大时，该变化无法直接反馈到效用分布的变化上。PHUI-b算法使用的事务间置换策略是无条件检验，能够识别植入项集频率分布变化对效用分布的影响，因此其性能表现与其余两种类型的仿真事务集合一致。

3.5.2 平均效用

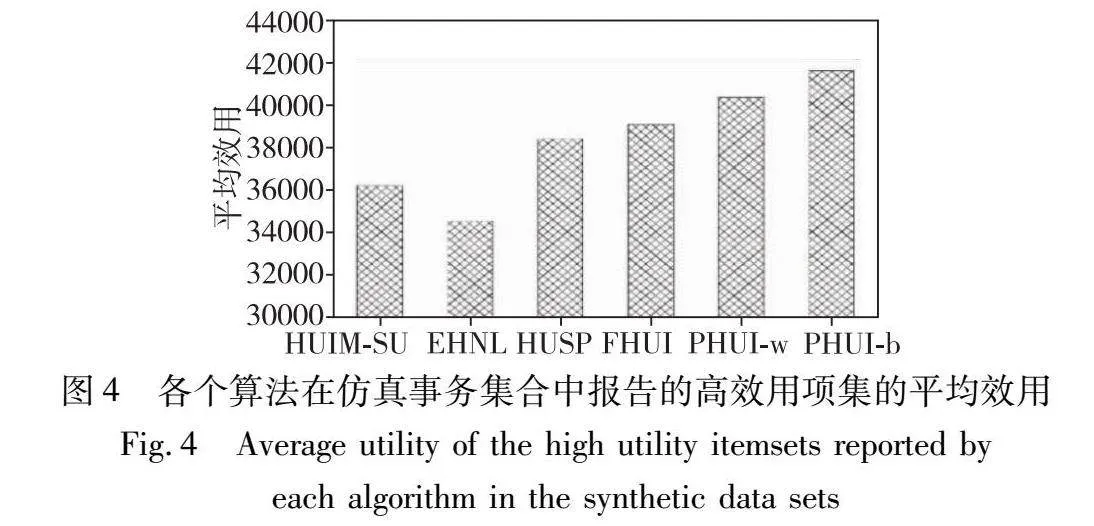
算法报告的高效用项集平均效用越高，表明其报告的高效用项集的实用性越强。举例而言，在市场消费应用中，项集的效用越高意味着对应商品的利润越高；在疾病基因分析中，项集的效用越高意味着对应基因与疾病的关联性越高。为了比较各个算法报告项集的实用性，实验统计了各个算法在30个仿真事务集合中报告的高效用项集的平均效用，详细情况如图4所示。从中可以看出，各个算法平均效用的高低关系为：EHNL＜HUIM-SU＜HUSP＜FHUI＜PHUI-w＜PHUI-b。

HUIM-SU和EHNL算法报告项集的平均效用低于基于统计显著性检验的算法，其原因是这两个算法报告结果中随机产生的大部分假阳性高效用项集的效用仅仅略高于αuti阈值，而大部分统计显著高效用项集的效用明显超过αuti阈值。由于EHNL算法剔除的长度较长的高效用项集表现出了较高的效用，导致其平均效用低于HUIM-SU算法。

进一步比较，HUSP和FHUI算法报告项集的平均效用低于PHUI-w和PHUI-b算法，这是因为这两个算法误判的低频率分布植入项集及其超项集u（ij， dv）更高，容易表现出更高的效用。此外，由于PHUI-w算法计算p值偏大，而错误剔除的非假阳性项集也表现出了较高的效用，从而其报告项集的平均效用不及PHUI-b算法。综上，PHUI-b算法报告的高效用项集实用性更强。

3.5.3 运行时间

运行时间是算法可用性的一个度量指标，不同的后续任务场景会对算法运行时间有不同的要求。例如有的后续任务需要快速找到事务集合中的高效用项集；有的后续任务需要在一个可接受的时间范围内找到事务集合中可靠性更强的高效用项集。为了比较各个算法在运行时间方面的可用性，实验记录了各个算法在不同αuti参数下三种仿真事务集合中的平均运行时间，具体的αuti参数以及实验结果如图5所示。图5中各个算法在相同αuti参数下运行时间的长短关系为：HUIM-SU＜EHNL＜FHUI＜HUSP＜PHUI-w＜PHUI-b。

基于阈值约束的算法运行时间明显短于基于统计显著性检验的算法，其原因是基于统计显著性检验的算法均为后处理算法，即先使用基于阈值约束的算法挖掘出待检验高效用项集，然后再对它们进行统计显著性检验，因此基于阈值约束的算法相当于基于统计显著性检验的算法的第一个步骤。虽然HUIM-SU和EHNL算法运行时间短，但其报告的大量假阳性高效用项集可靠性和实用性都较低。

在基于统计显著性检验算法中，HUSP和FHUI算法通过待检验项集的频率分布直接计算生成零分布，而PHUI-w和PHUI-b算法通过构造置换事务集合，并从中提取效用差生成零分布，从2.1和2.2节的时间复杂度分析可知，计算生成零分布的计算开销远远小于从置换事务集合中提取效用差生成零分布的计算开销，因此FHUI和HUSP算法的运行时间明显短于PHUI-w和PHUI-b算法。进一步讨论，虽然HUSP和FHUI算法采用了相同的检验策略，但FHUI算法对二项式的计算进行了优化加速处理，促使FHUI算法运行时间快于HUSP算法；此外，PHUI-w算法使用的事务内置换策略不需要进行事务之间项的置换，从而不涉及大量项的交换操作，因此其运行时间快于PHUI-b算法。

在硬件要求方面，FHUI和HUSP算法不依赖计算机集群实施分布式并行化计算，从而其对硬件配置的要求相较于PHUI-w和PHUI-b算法更低。进一步而言，当缺少计算机集群设备支持时，PHUI-w和PHUI-b算法的运行时间将会进一步增加；反之，当集群设配资源更为充足时，PHUI-w和PHUI-b算法的运行时间将会进一步减少。综上，就运行时间和硬件要求而言，FHUI和HUSP算法的可用性更强。

3.6 实验结果综合分析

上述实验结果表明，面向具有不同类型标签的事务集合时，虽然传统基于阈值约束的挖掘算法运行时间较快，但其无法识别高效用项集在不同类型事务中的效用分布，从而导致结果中存在大量随机产生的假阳性高效用项集。这些假阳性高效用项集严重误导了分类决策并且表现出较低的平均效用，因此传统基于阈值约束的算法在此类事务数据应用中报告的高效用项集可靠性和实用性较低。

在基于统计显著性检验的算法中，PHUI-w和PHUI-b算法在分类正确率、非假阳性项集数量、假阳性项集占比、项集平均效用方面优于HUSP和FHUI算法，但在运行时间和硬件要求方面劣于HUSP和FHUI算法；此外，FHUI算法在上述各度量上均略优于HUSP算法。因此，当缺少硬件设备实施分布式并行化计算或者后续任务需要快速找到统计显著高效用项集时，更宜采用FHUI算法挖掘高效用项集。当具备硬件支持或者后续任务对高效用项集的数量和可靠性要求较高时，更宜采用PHUI-w和PHUI-b算法。进一步讨论，上述情景中若事务数量较大时，PHUI-w算法更具备实用性，因为此时PHUI-b算法中项交换的计算开销非常巨大；反之，则PHUI-b算法性能更强。

4 结束语

为了剔除随机产生的假阳性高效用项集，提出了两个基于不同类型统计显著性检验的高效用项集挖掘算法——FHUI和PHUI算法。FHUI算法基于Fisher检验生成零分布，PHUI算法基于置换检验生成零分布。此外，PHUI算法还设计了两种置换策略。基准和仿真事务集合中实验结果表明，FHUI和PHUI算法成功剔除了结果中一定数量的假阳性高效用项集，从而报告的统计显著高效用项集更加可靠和实用。对比而言，FHUI算法运行时间更短且硬件要求更低，PHUI算法分类正确率更高且假阳性高效用项集数量占比更低。在后续研究中，会尝试把FHUI算法融入到待检验高效用项集挖掘过程中，也会尝试在不实际构造置换事务集合的情况下直接计算PHUI算法的零分布，达到进一步降低FHUI和PHUI算法运行时间的目的。同时，后续研究也会针对结果中提供了相同信息的冗余高效用项集设计筛除算法。

参考文献：

［1］Kumar S， Mohbey K K. A review on big data based parallel and distributed approaches of pattern mining ［J］. Journal of King Saud University： Computer and Information Sciences， 2022， 34（5）： 1639-1662.

［2］Tung N T， Nguyen L T， Nguyen T D D，et al. Efficient mining of cross-level high-utility itemsets in taxonomy quantitative databases ［J］. Information Sciences， 2022， 587： 41-62.

［3］张春砚， 韩萌， 孙蕊， 等. 高效用模式挖掘关键技术综述 ［J］. 计算机应用研究， 2021， 38（2）： 330-340. （Zhang Chunyan， Han Meng， Sun Rui，et al. Survey of key technologies for high utility patterns mining ［J］. Application Research of Computers， 2021， 38（2）： 330-340.）

［4］单芝慧， 韩萌， 韩强. 动态数据上的高效用模式挖掘综述 ［J］. 计算机应用， 2022， 42（1）： 94-108. （Shan Zhihui， Han Meng， Han Qiang. Survey of high utility pattern mining on dynamic data ［J］. Journal of Computer Applications， 2022， 42（1）： 94-108.）

［5］孙蕊， 韩萌， 张春砚， 等. 精简高效用模式挖掘综述 ［J］. 计算机应用研究， 2021， 38（4）： 975-981. （Sun Rui， Han Meng， Zhang Chunyan，et al. Survey of algorithms for concise high utility pattern mining ［J］. Application Research of Computers， 2021， 38（4）： 975-981.）

［6］Almoqbily R S， Rauf A， Quradaa F H. A survey of correlated high utility pattern mining ［J］. IEEE Access，2021，9： 42786-42800.

［7］Luna J M， Kiran R U， Fournier V P，et al. Efficient mining of top-k high utility itemsets through genetic algorithms ［J］. Information Sciences， 2023， 624： 529-553.

［8］Kumar R， Singh K. A survey on soft computing-based high-utility itemsets mining ［J］. Soft Computing， 2022， 26（13）： 6347-6392.

［9］Gan Wensheng， Lin Chunwei， Fournier V P，et al. A survey of utility-oriented pattern mining ［J］. IEEE Trans on Knowledge and Data Engineering， 2019， 33（4）： 1306-1327.

［10］Wu Mingtai， Lin Chunwei， Tamrakar A. High-utility itemset mining with effective pruning strategies ［J］. ACM Trans on Knowledge Discovery from Data， 2019， 13（6）： 1-22.

［11］Krishna G J， Ravi V. High utility itemset mining using binary diffe-rential evolution： an application to customer segmentation ［J］. Expert Systems with Applications， 2021， 181： 115122.

［12］Kumar R， Singh K. High utility itemsets mining from transactional databases： a survey ［J］. Applied Intelligence， 2023， 53（22）： 27655-27703.

［13］Cheng Zhaihe， Fang Wei， Shen Wei，et al. An efficient utility-list based high-utility itemset mining algorithm ［J］. Applied Intelligence， 2023， 53（6）： 6992-7006.

［14］Tung N T， Nguyen L T T， Nguyen T D，et al. An efficient method for mining multi-level high utility itemsets ［J］. Applied Intelligence， 2022， 52（5）： 5475-5496.

［15］Tonon A， Vandin F. Permutation strategies for mining significant sequential patterns ［C］// Proc of the 21st IEEE International Confe-rence on Data Mining. Piscataway， NJ： IEEE Press， 2019： 1330-1335.

［16］Trasierras A M， Luna J M， Ventura S. A contrast set mining based approach for cancer subtype analysis ［J］. Artificial Intelligence in Medicine， 2023， 143： 102590.

［17］Kong Jie， Han Jiaxin， Ding Junping，et al. Analysis of students’learning and psychological features by contrast frequent patterns mi-ning on academic performance ［J］. Neural Computing and Applications， 2020， 32（1）： 205-211.

［18］Loyola-Gonzlez O， Medina-Pérez M A， Choo K K R. A review of supervised classification based on contrast patterns： applications， trends， and challenges ［J］. Journal of Grid Computing， 2020， 18： 797-845.

［19］Jenkins S， Walzer-Goldfeld S， Riondato M. SPEck： mining statistically significant sequential patterns efficiently with exact sampling ［J］. Data Mining and Knowledge Discovery， 2022， 36（4）： 1575-1599.

［20］He Zengyou， Chen Wenfang， Wei Xiaoqi，et al. Mining statistically significant communities from weighted networks ［J］. IEEE Trans on Knowledge and Data Engineering， 2022， 35（6）： 6073-6084.

［21］Pellegrina L， Riondato M， Vandin F. SPuManTE： significant pattern mining with unconditional testing ［C］// Proc of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM press， 2019： 1528-1538.

［22］Tang Huijun， Qian Jiangbo， Liu Yangguang，et al. Mining statistically significant patterns with high utility ［J］. International Journal of Computational Intelligence Systems， 2022， 15（1）： 88-107.

［23］Duong Q H， Fournier-Viger P， Ramampiaro H，et al. Efficient high utility itemset mining using buffered utility-lists ［J］. Applied Intelligence， 2018， 48（3）： 1859-1877.

［24］Zhao Guolong， Yang Huiyu， Yang Junxia，et al. A data-based adjustment for fisher exact test ［J］. European Journal of Statistics， 2021， 1： 74-107.

［25］Hamalainen W. New upper bounds for tight and fast approximation of Fisher’s exact test in dependency rule mining ［J］. Computational Statistics and Data Analysis， 2016， 93（2）： 469-482.

［26］Singh K， Kumar A， Singh S S，et al. EHNL： an efficient algorithm for mining high utility itemsets with negative utility value and length constraints ［J］. Information Sciences， 2019， 484： 44-70.

［27］Fournier-Viger P， Gomariz A， Gueniche T，et al. SPMF： a Java open-source pattern mining library ［J］. Journal of Machine Lear-ning Research， 2014， 15（1）： 3389-3393.