应对显著变化的动态社区检测方法

摘 要：现实中的网络总是不断变化，网络形态和连接关系也在随着时间推移而不断演变，在动态网络中发现社区的变化一直是个重要课题。当这种变化较为显著时，将导致社区检测算法难以有效利用前一个网络快照中有价值的信息，从而导致下一个时间步的负迁移。为解决算法无法较好适应网络突变问题，提出了一个基于遗传进化思想和高阶知识转移策略的动态社区检测算法。首先利用相邻快照的邻接矩阵相似度确定使用一阶或高阶信息，然后利用蛛网模型进行种群初始化，再通过非支配排序遗传算法NSGA-Ⅱ迭代出位于Pareto前沿的多目标最优解，并设计了新的基因交叉方式以提高种群多样性。最后通过在多个真实数据集及模拟数据集上的实验结果表明，与现有算法相比，该算法在发生网络剧变时能获得时间平滑性更高的社区检测结果，同时也能保持良好的社区模块化程度。

关键词：显著变化；动态网络；高阶信息；社区检测

中图分类号：TP301.6 文献标志码：A 文章编号：1001-3695（2024）10-012-2962-08

doi：10.19734/j.issn.1001-3695.2024.01.0024

Dynamic community detection method for coping with significant changes

Liu Ao， Zhang Junjie， Wang Huan， Zhang Qingming

（School of Computer Science & Technology， Southwest University of Science & Technology， Mianyang Sichuan 621000， China）

Abstract：In real-world networks， the structure and connections are constantly evolving over time. Detecting community changes within dynamic networks has always been an important research topic. When such changes are significant， it leads to difficulty for community detection algorithms to effectively utilize valuable information from the previous network snapshot， resulting in negative transfer in the next time step. To address the issue of poor algorithm adaptability to network mutations， this paper proposed a dynamic community detection algorithm based on genetic evolution ideas and higher-order knowledge transfer strategies. Firstly， it used the adjacency matrix similarity of adjacent snapshots to determine the use of first-order or higher-order information. Then， it employed the spider Web model for population initialization， followed by the non-dominated sorting genetic algorithm NSGA-Ⅱ to iteratively obtain multi-objective optimal solutions on the Pareto front. It designed a novel gene crossover method to enhance population diversity. Finally， experimental results on multiple real and simulated datasets demonstrate that， compared to existing algorithms， the proposed method achieves higher temporal smoothness in community detection results during network upheavals while maintaining a good community modularity level.

Key words：significant changes; dynamic networks; higher-order information; community detection

0 引言

动态社区检测（dynamic community detect，DCD）对于挖掘现实世界网络中的复杂关系变化起着至关重要的作用，是事件检测、趋势分析和用户行为分析的重要工具。在交通网络［1］、金融网络［2］、社交网络［3，4］和生物网络［5］等许多领域中表示动态社区的图都被广泛运用。例如在医疗保健领域，社区检测算法可以帮助人们理解和预测疾病的传播，以及对医疗资源的优化配置，为医疗决策提供有力的数据支持。此外，通过药物处方网络，可以发现可能的药物滥用或欺诈行为；在营销和广告领域，公司可以利用动态社区检测来根据用户不断变化的偏好和行为量身定制他们的策略，从而增强客户参与度和品牌忠诚度；在城市规划和交通管理中，也可以通过社区检测算法挖掘的信息优化交通流量和缓解拥堵。许多方法也被提出用于发现和研究社区结构，如量子行走［6］、谱聚类［7］、深度学习［8］以及非负矩阵分解［9］。由于动态社区检测要求在网络演化过程中持续地调整社区结构，并且需要考虑社区的模块化结构及其连续性等因素，所以DCD问题是NP难的。多数工作采用进化算法（EAs）有效解决此问题，EAs也已成为了其中一个主要的解决方案［10，11］。Li等人［12］就将具有时间平滑性的社区检测模式构建为多目标问题，提出了两种适用于社区的邻域融合策略：邻域多样性策略和邻域集群策略。除此之外，Yin等人［13］提出了一种高效有效的多目标方法，即 DYN-MODPSO，并分别修改和增强了传统的进化聚类框架和粒子群算法。

多数动态社区检测算法都引入了时间平滑性［14～16］的概念，旨在揭示网络中的潜在模式、趋势和周期性变化，为更深入的社区分析提供基础。然而，在网络存在严重波动时，社区的急剧变化可能使得算法难以追踪其长期演化趋势，对社区结构变化的细粒度理解也将受到挑战。对于多数常用的动态社区检测算法，在算法进行之前，通常都有一个假设：从一个时间步到下一个时间步的变化是比较平缓的。当事实与这一假设相互背离时，这些算法的性能往往会下降。其有两点启发：一方面，现有的动态社区检测算法不能较好地适应社区结构在相邻时间步间发生显著变化的情况，从而使前一个社区检测结果给后续的检测任务带来负迁移；另一方面，利用先前时间步的社区信息来提高动态社区检测算法性能是可行的。

本文通过实验确认了动态网络中发生突变情况的存在，所提出的方法将根据不同时间步的变化程度使用一阶或者高阶信息进行社区检测。主要工作如下：a）面向具有显著变化的动态社区检测问题，提出了一个动态社区检测算法HOGA；b）设计了一个新的目标函数，利用高阶信息转移策略CV-HOCV保留先前社区划分的优势，从而减少网络巨大变化带来的负迁移；c）在利用非支配排序遗传算法NSGA-Ⅱ［17］进行迭代计算时，通过优化后的交叉和变异方式使获得的子代种群更具多样性，提高了算法迭代效率。

1 相关工作

多数基于进化的动态社区检测算法都将动态社区检测问题建模为多目标优化问题（MOP）。在动态社区检测领域，解决此类问题的普遍方法是将非支配个体进行排序后进行迭代择优，例如基于非支配排序的多目标进化算法（NSGA）［18］。这些基于进化聚类的方法在计算机领域也引起了越来越多的兴趣［19］。本文方法便是以多目标优化为基础，同时结合了间接迁移学习的策略对动态网络进行社区划分。因此，本章回顾了迁移学习在解决动态多目标问题方面的研究，并对目前的动态社区检测算法进行了综述。

1.1 基于多目标的迁移学习

迁移学习作为一种强大的技术工具，旨在通过在源领域上学到的知识来改善目标领域上的学习性能。在求解基于迁移学习的动态多目标问题（DMOPs）方面，研究领域近年来呈现出蓬勃的发展态势。例如文献［20］介绍了进化转移优化（ETO）方法，这是一种将EA求解器与跨相关领域的知识学习和转移相结合的范例。Jiang等人［21］提出了一种动态多目标进化算法（EA）框架，集成迁移学习和基于种群的EA，重用过去的经验生成有效的初始种群池，以加速进化过程。但由于迁移过程中存在低质量的个体，传统的迁移学习难以得到实质性的改进。为了克服负迁移的影响，文献［22］提出了一种非平衡迁移学习方法KT-DMOEA，通过调整解的权值并利用膝点来权衡不同目标的最佳解。Liu等人［23］提出了一种迁移学习算法，该算法保留了对足够历史信息的预测方法，修改种群预测策略提供的解，以构建新环境下的初始种群并进行优化。Li等人［24］提出了两种新颖的操作来帮助解决DMOPs，当环境发生变化时，使用基于聚类的选择（CBS）和基于聚类的迁移（CBT）来指导知识转移。Jiang等人［25］提出了一种基于个体迁移的动态多目标进化算法，该算法从历史最优解中筛选出一些优秀个体，以避免负迁移。还有一些方法旨在克服线性相关实例的低准确率和训练样本不足的障碍，例如Xu等人［19］提出了一种基于增量支持向量机的动态多目标进化算法，将动态多目标优化问题视为一个在线学习过程，用历史最优解更新并支持向量机，而不会丢弃早期的解信息。考虑到动态多目标优化问题在决策空间和目标空间中可能发生的变化，Zhou等人［26］提出了一种多视图预测的进化搜索算法，该算法在再现Hilbert空间中使用核化的自编码模型来获得多视图预测。文献［27］则提出了一种通过扩展编码进化搜索的方式来提高种群优秀个体的预测质量。文献［28］实现了一种快速动态多目标进化算法，该算法使用记忆机制来保留过去的最佳个体，并使用流形转移学习技术来预测演化中的最优个体。传统迁移学习方法的有效性通常依赖于源领域和目标领域之间的相似性，而在动态社区检测中，社区结构可能随时间发生显著变化，导致源领域和目标领域之间的差异增加，使得迁移学习方法性能下降。

1.2 动态社区检测方法

研究社区的核心问题是确定社区，而网络成员的频繁变化是动态网络中社区结构的重要特征，近年来已经提出了多种算法用于动态社区检测。李辉等人［29］描述了已经提出的几种动态网络社区检测方法。在动态网络中检测社区的方法普遍为将网络视为基于时间戳的快照，并且直接在每个快照的网络上使用静态算法［30］。然而，重复使用静态算法在计算上的成本非常高，特别是当快照的数量非常多时。另一种方式则是利用网络聚类多样性的特征来检测社区。受进化聚类框架的启发，Folino等人提出了动态多目标遗传算法（DYNMOGA）［10］来检测动态网络中的群落结构章。第一个目标是使当前时间步的模块度最大化，第二个目标是使当前时间步的社团结构与前一个时间步的社团结构之间的差异最小化。本文也是选取这两个目标进行优化。之后，Zeng等人［31］引入了共识社区的概念，以使DYNMOGA更好地达到这两个目标。通过这种方式，他们引导动态社区检测朝着关注前一个时间步的社区结构方向发展。Niu等人［32］采用标签传播方法初始化社区，限制遗传算法突变过程的条件，进一步提高了检测效率和有效性。Liu等人［16］发现经典算子无法避免节点经常与其大多数邻居互连等缺陷，设计了一种与经典遗传算子相结合的迁移算子来寻找群落间的联系。为克服社区检测纠错和基于模块化的社区检测存在NP难等问题，Yin等人［13］提出了一种多目标粒子群优化方法来处理动态社区检测问题。Qu等人［33］提出了一种基于进化的动态社区检测方法，解决节点嵌入过程中的数据稀疏性问题，充分考虑了历史结构信息，提高了动态社区检测的准确性和稳定性。

尽管在发现动态社区方面已经作出了巨大的努力，但仍然存在着一些问题尚未解决。具体而言，大多数算法都假定相邻时间步的社区结构不会突然发生剧烈变化，例如在非增量社区检测算法中忽略了这种网络突变，从而没有将时间平滑性融入到社区检测问题中；而在增量社区检测算法中，应对社区急剧变化的方法则是在网络变化超过一定阈值的时间步上重新运行一次静态社区检测算法，但丢失了先前时间步社区中有价值的信息。为探究网络突变对社区检测算法性能的影响，并使算法适应更复杂的网络环境，本文提出基于间接迁移学习和进化算法的动态社区检测算法HOGA。

2 动态社区检测算法HOGA

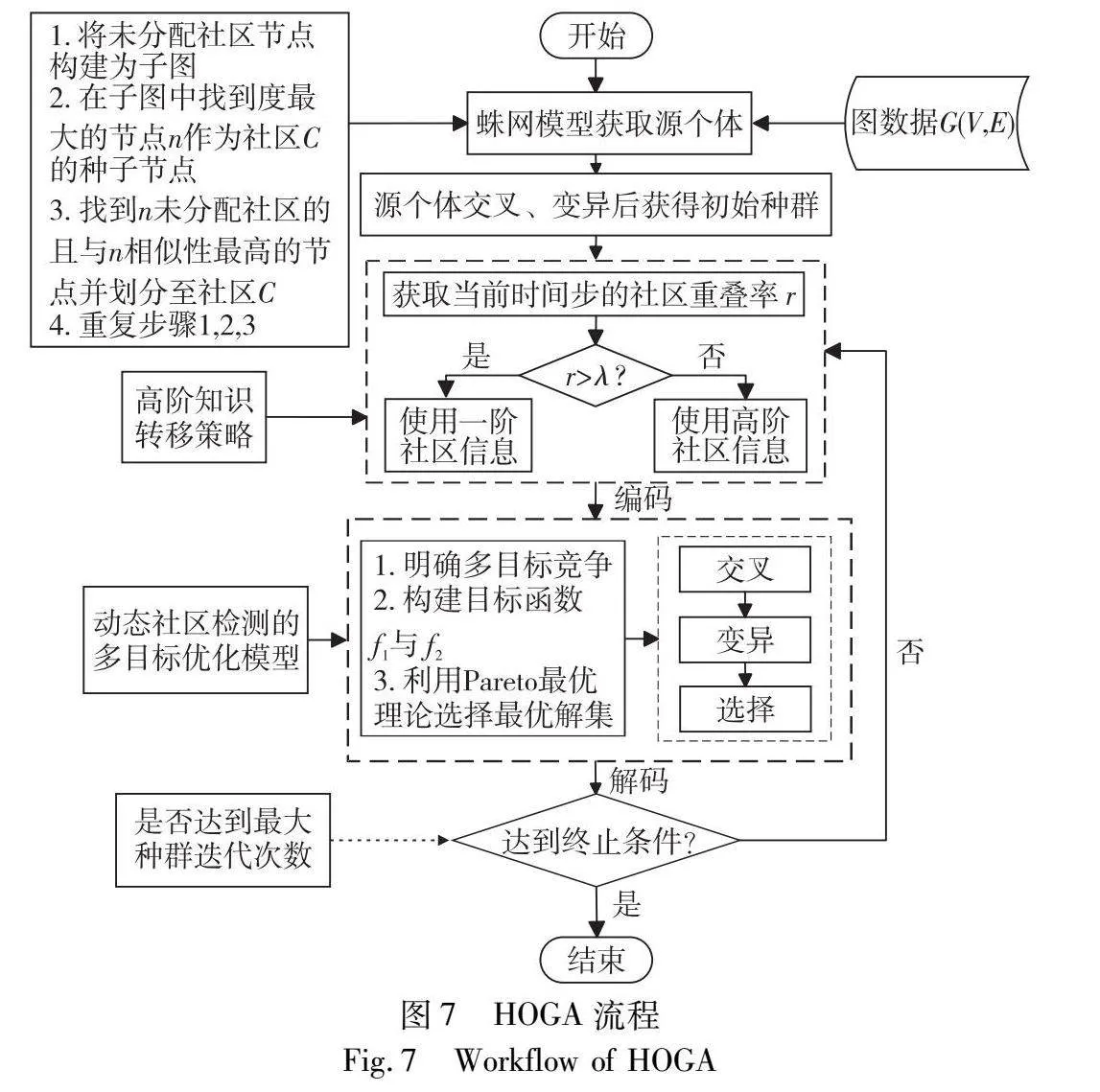
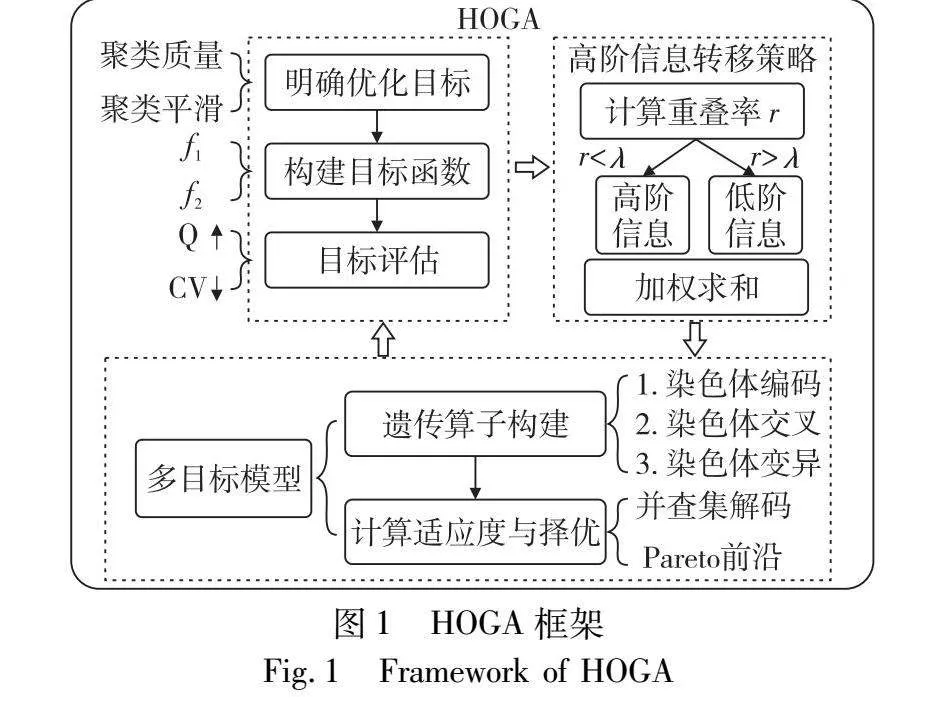
本文算法将高阶信息转移策略应用于动态社区问题的多目标模型中，方法框架如图1所示。

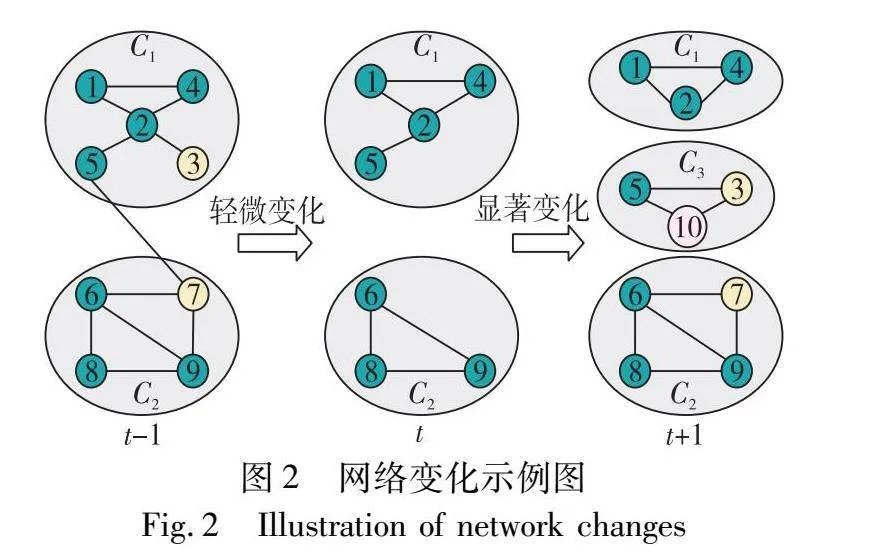
通常，静态网络被建模为图G=（V，E），其中V为节点集合，E为边的集合。动态网络则是序列G={G1，G2，…，GT}，其中Gt是节点和节点之间的连接在t时刻的快照（snaphot）或时间步（timestep），t={1，2，…，T}是一个有限的时间序列集合，T表示该动态网络所含的网络快照数量。Gt和Gt-1的区别在于删除了一些节点和边，或者新增了一些节点和边。动态网络变化如图2所示。其中包括两种情况：a）社区发生轻微变化；b）社区发生显著变化。目前大多数方法都考虑到网络的轻微变化，如图2快照t-1至t，仅有节点3和节点7脱离了原本所在社区。而本文方法主要应对网络发生显著变化的场景，如图2快照t至t+1所示。其中社区C1中的节点5脱离该社区，并且与节点3、节点10组成了新的社区C3；此外，社区C2中的成员7又重新加入了该社区；这种相邻时间步社区出现的较大变动可能引发负迁移，从而导致算法的性能下降和聚类平滑性降低。

2.1 新的目标函数

在优化动态社区检测过程中，需要同时考虑聚类质量和聚类平滑性，因此本文采用的两个目标函数分别为模块度Q［34］和衡量社区变化度的CV，并进行双指标优化。模块度被广泛认为是评价社区结构质量的标准，模块化程度高时社区内连接紧密，不同社区节点间连接密度稀疏。其定义如下：

Q=∑ks=1［lsm－（ds2m）2］（1）

其中：ls为社区Cs内的边数；ds为Cs中节点的度数之和；m为网络Gt中的总边数。社区内节点度数占比越高，模块度值越接近1，表示社区内连接越紧密，社区间区分度越高，聚类质量也越高；而模块度值越接近0，聚类质量越低。

在文献［10］中使用NMI来检测社区，可以通过前一个快照的社区标签计算得到。当给定两组社区A={A1，A2，…，Ai}和社区B={B1，B2，…，Bj}，C为两个社区的混淆矩阵，并且C中i行j列的元素Cji表示同时存在于社区Ai（AiA）和社区Bj（BjB）的节点数。其中NMI的定义如下：

NMI（A，B）=－2∑CAi=1 ∑CBj=1Cjilog（CjiN/Ci.C.j）∑CAi=1Ci.log（Ci./N）+∑CBj=1C.jlog（C.j/N）（2）

其中：CA（CB）是A（B）中的社区数量；Ci.表示混淆矩阵C的第i行元素之和；C.j表示混淆矩阵C的第j列元素之和。NMI在社区集合A和B完全相同时取到最大值1，当这两个社区集合完全不同时，取到最小值0。因此，NMI（CRt，CRt－1）越高，相邻两个时间步的社区结构越为相似，社区结构随时间的平滑性也越高。为充分利用高阶社区信息，本文设计了新的目标函数CV，其定义如下：

CV=1－∑Ck∈CcomSameNum（Ctk，Ct－1k）×1N（3）

其中：SameNum（Ctk，Ct－1k）为社区Ck在两个相邻快照t和t－1上的公共节点数；Ccom为这两个快照中具有公共节点的社区集合；N是公共社区总数。CV的取值为0～1，SameNum（Ctk，Ct－1k）越小则相邻社区相似性越小，CV的值将越接近1，因此社区变化越大；其值越接近0，则表示相邻快照的社区较为接近，社区变化也较小，因此CV可以用于衡量动态社区的变化程度。本文则主要通过降低相邻时间步之间社区变化即CV来提高社区平滑性。

2.2 高阶信息转移策略CV-HOCV

本文算法结合间接迁移学习的思想，使用改进后的高阶知识转移策略［35］适应网络社区的显著变化。当r≥λ时，将使用一阶社区信息，即利用前一个时间步的社区划分结果辅助当前时间步的社区检测，其中r为重叠率，λ为网络变化阈值；而当r<λ时，相邻时间步社区可能发生结构突变，如果使用一阶知识将发生负迁移，因此使用高阶社区信息，计算当前快照Gt与之前所有快照之间的CV，再根据权重ω将它们相加作为HOCV，由此可以充分利用社区划分的先验知识并连接相邻社区。权重ω由相似性矩阵决定，将在3.3节中对其进行详细阐述。一阶知识与高阶知识的定义如下：

a）一阶信息：仅考虑当前时间步t与前一个时间步t－1的社区结构差异。此时目标函数HOCV值为

HOCV=CV（CRt，CRt－1）（4）

b）高阶信息：考虑当前时间步t与多个先前时间步的社区结构差异。此时HOCV值为

HOCV=∑ω（i）×CV（CRi，CRt） i=1，2，…，t－1（5）

其中：ω（i）为时间步i（i=1，2，…，t－1）的权重，且∑ω（i）=1。

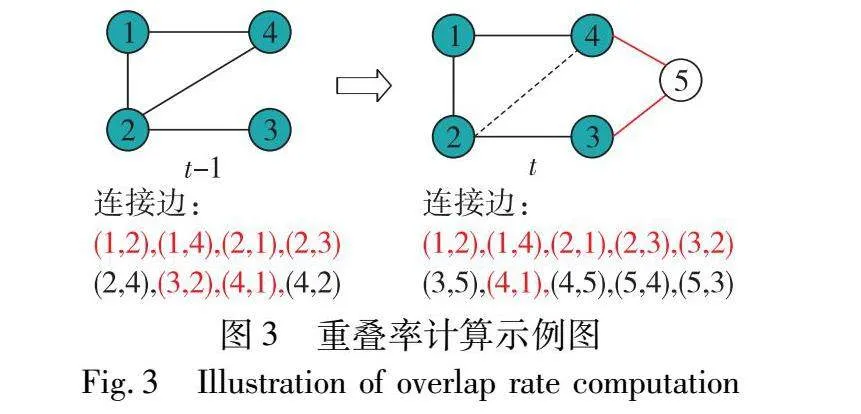
本文使用连续两个时间步的邻接矩阵来计算时间步t与其前一个时间步t-1的邻接矩阵重叠比率。计算公式如下：ratio=SameNum/n。其中SameNum是两个连续时间步的公共边数，n则是时间步t的总边数，重叠率计算的示例如图3所示。快照t总共有10条边，两个时间步的公共边为{（1，2），（1，4），（2，1），（2，3），（3，2），（4，1）}。因此SameNum=6，n=10，故此示例的重叠率r=0.6。

2.3 染色体编码

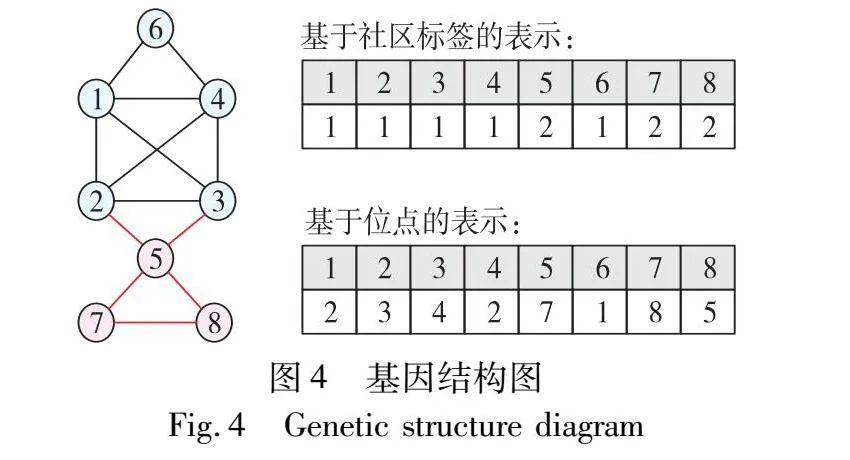
社区的基因编码方式有基于社区标签的表示和基于位点的表示两种类型。在基于社区标签的表示中，种群由N个个体X={X1，X2，…，XT}组成，每个个体包含n个基因{g1，g2，…，gn}，其中T为动态网络的时间步数，n为节点数。若k为群落数，则gi的取值是{1，2，…，k}，为标识节点i的所属社区标签。而在基于位点的表示中，每个基因的表示即gi的取值是{1，2，…，n}，其被定义为节点i所属社区内的相邻节点标签，此时一个基因表示为社区内一对节点的连接。如图4所示，节点1、2、3、4、6属于一个社区，节点5、7、8属于另一个社区。因此，在基于社区标签的表示中，基因1、2、3、4、6的标签为1，基因5、7、8的标签为2。在基于位点的表示中，基因1的标签为2、3、4、6或8，表示在同一个社区中随机选择一个邻节点作为基因1的最终标签。由于节点2和节点5不在同一个社区，所以基因2和基因5不会互相作为标签。基于位点的一个明显优势是，簇的数量可以由个体中所包含的联通分量数量自动确定，并通过解码［35］步骤获得对应的社区结构，而无须以完整社区结构参与迭代过程，从而减少计算量。因此，本文算法采用基于位点的邻接表示作为基因编码方式。

2.4 交叉与变异

遗传算法（genetic algorithm）作为一种模拟自然选择和遗传机制的优化算法，被广泛应用于解决复杂问题和优化搜索空间。其灵感来源于生物学中的进化过程，通过模拟基因的遗传、交叉和突变等操作，逐步演化出更优秀的个体，从而实现对问题的全局搜索和优化。本文使用非支配排序算法NSGA-Ⅱ对种群个体进行迭代，具体过程包括种群初始化、生成子代种群（基因交叉、基因变异）、基因选择。

初始化是遗传算法中引入个体多样性的关键步骤，为遗传算法的进化提供起始点。首先需要初始化个体容量为popsize的父代种群。普遍的做法是通过从图中随机选择一个邻居来对个体的基因进行初始化，每一对基因（i，gi）表示社区内的一组连接。

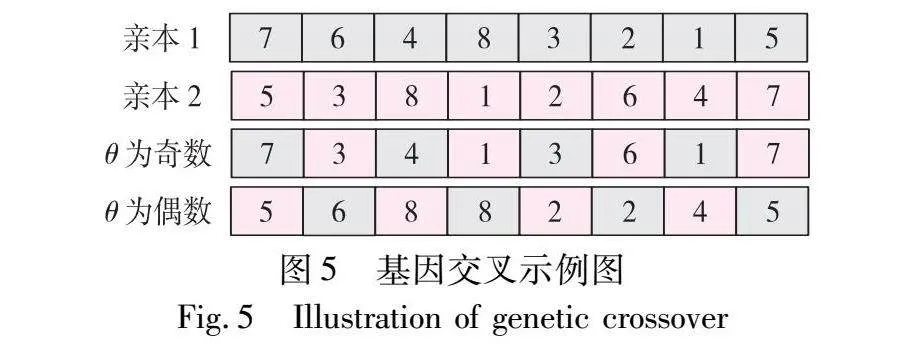
基因交叉通过组合不同个体的优势基因，产生具有更好适应性的子代基因，推动种群向全局最优进化。此过程需选择两个个体作为双亲，并通过随机自然数θ的奇偶性决定基因的交叉方式。当θ为奇数时，选择亲本1的奇数位基因和亲本2的偶数位基因构建子代基因；当θ为偶数时，则选择亲本1的偶数位基因和亲本2的奇数位基因对子代基因进行构建。交叉过程的一个示例如图5所示。

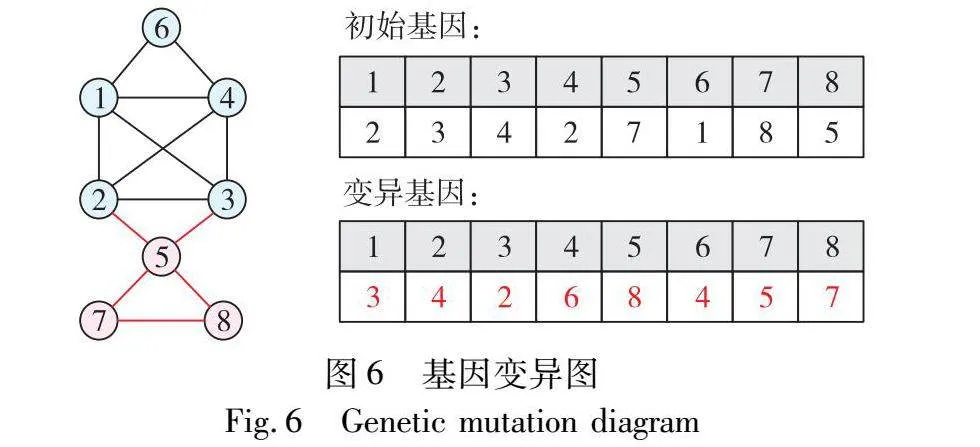
基因突变对于随机性的引入以及保持种群多样性具有重要意义。该步骤选择节点i对应的等位基因gi进行随机突变。图6给出了一个基因突变的示例。基于位点表示的基因初始构成为{2，3，4，2，7，1，8，5}。节点1的同社区邻节点为{2，3，4，6}，随机选择相同社区内节点1的邻节点3，作为等位基因1突变后的标签。执行完整突变过程后，该基因的构成变为{3，4，2，6，8，4，5，7}。需要注意的是，突变范围限定为同一社区的邻居节点，确保变异后的基因仍保持其合理性。

选择过程目的在于从当前种群中挑选优秀个体，构建下一代精英种群。首先需要为每个个体分配一个非支配等级，并按照该等级对种群中的个体进行排序，再将亲代和子代中等级靠前的个体进行择优选取，构成一个新的种群。在此种群中，个体再通过交叉和突变产生新的子代种群。

2.5 总体流程

HOGA算法首先通过蛛网模型生成每个快照的初始种群，再对初始种群进行进化迭代，获得更高质量的子代种群，最终获得多目标最优的社区结构，其流程如图7所示。

给定一个动态网络G={G1，G2，…，GT}，在种群初始化步骤，普遍的做法是仅通过对当前时间步网络Gt（1≤t≤T）中每个节点进行随机初始化，随机选取节点的邻居节点标签作为其基因标签，得到其初始种群。本文则采用蛛网模型［36］进行社区检测以获取源个体，再根据此源个体创建一个个体容量为n=|Vt|的随机初始总体，Vt为当前时间步的节点数量。这是为了避免过于随机，导致初始种群中存在多数低质量个体而陷入局部最优，提高初始种群质量和迭代效率。初始种群再经过交叉和变异过程生成新种群，接着计算出种群中个体与前一个网络快照的重叠率r，当r≥λ时，使用一阶信息进行当前快照的社区划分，当r<λ时则应充分利用高阶社区信息。对于每一代种群个体，进行个体解码以生成快照t的社区，计算出第一个目标值Q，以及利用选取的一阶或高阶信息计算出第二个目标值HOCV，通过这两个目标值作为适应度，并与父代个体一同根据帕累托支配度对种群中个体进行无支配排序，通过精英策略［35］选择出优异个体（等级靠前）进行下一次的种群迭代，直到达到最大迭代次数。每次迭代结束，HOGA返回一组解，每个解都反映了对两个目标值的不同权衡。需要注意的是，t=1时的网络快照不能使用先前的任何社区信息，而t=2时只有一阶信息能够利用，当t≥3时才能使用高阶社区信息。本文最终选取第二目标值HOCV最高的社区作为最终结果，以最小化社区结构波动。算法1描述了HOGA的详细过程。

算法1 动态社区检测算法HOGA

输入：图序列G={G1，G2，…，GT};时间步数T;时间步t的权重ωt（1≤t≤T）;网络变化阈值λ。

输出：社区检测结果C={C1，C2，…，CT}。

a） 通过仅优化模块度即式（1）后获得首个时间步的社区。

b） 遍历剩余时间步的网络结构，利用蛛网模型得到当前时间步的源个体s。

c） 源个体s交叉与变异后生成随机初始种群n=|Vt|。

d） 计算该时间步与上一个时间步的重叠率r。

e） 通过重叠率r与网络阈值λ确定一阶或高阶社区信息用于计算第二目标函数值。

f） 对初始种群进行交叉、变异获得子代种群。

g） 子代种群进行解码后获得社区结构，分别计算两个目标函数值，并进行非支配排序。

h） 通过精英策略选择出优秀个体并置于前沿集front中。

i） 达到终止条件则返回front，否则转步骤f）。

其伪代码如下：

Initialize the clustering CR1={C11，C12，…，C1k} of the network N1 by optimizing Eq（2）.

for t=2 to T

compute overlap ratio r;

if（r≥λ） then

HOCV=CV（CRt，CRt-1）;

else

HOCV=∑ω（i）*CV（CRi，CRt），i=1，2，…，t-1;

end if

create a random population of individuals with the number n=|Vt|;

while（Termination criteria not met） do

Get a new offspring population through crossover and mutation operations

Decode each individual to generate the partitioning CRt={Ct1，Ct2，…，Ctk}

Combine the parents and offspring into a new pool

Assign a rank for each individual by non-domination rank

Put the individual with lower level into front

end while

return front

end for

2.6 时间复杂度

首先重叠率计算的时间复杂度可表示为O（n2T），其中T代表时间步数。由文献［17］可知，NSGA-Ⅱ算法的时间复杂度为O（gp logph－1），其中g为种群代数，p为种群个体总数，h为目标函数个数。由于HOGA优化了两个目标，其非支配排序的时间复杂度为O（gp log p）。HOGA计算复杂度主要由三个部分组成：个体的解码、模块度的计算和NMI计算。解码步骤时间复杂度为O（n log n）；模块度计算需要考虑每个节点的邻居，因此其复杂度为O（m），其中m为边的数量。对于归一化互信息的计算，由文献［10］可知其时间复杂度为O（n），n表示节点的数量。因此HOGA总体复杂度为O（gp log p）×O（n log n+m）。

3 实验及结果分析

为验证本文算法的有效性，选取四种同为演化聚类的动态社区检测算法与本文算法进行对比实验，包括FaceNet［37］、DYNMOGA［10］、L-DMGA［32］和HoKT［35］算法。其中FaceNet是一种概率生成模型，通过当前网络拓扑结构和历史社团结构给出的先验分布来估计当前的社团结构；而DYNMOGA、L-DMGA、HoKT与本文算法相同，均采用遗传算法来优化其目标函数。实验的硬件环境为：英特尔Core i7-7700HQ @ 2.80 GHz 四核，8 GB内存，Windows 10操作系统，算法采用Python语言实现。

3.1 数据集

本文使用表1中的六个数据集对所提算法进行验证，其中highschool_2011、highschool_2012、primary_school以及workplace_contacts为四个真实网络数据集，来源于https：//networkrepository.com/asn.php；并且另外新增了两个模拟数据集作为网络变化程度不同时的参考，其中synx_muw=0.1与synx_muw=0.5为LFR算法生成的人工数据集，分别表示相邻时间步之间有0.1和0.5的概率产生新边，来源于https：//snap.stanford.edu/data。

3.2 评估指标

除2.1节提到的模块度Q和NMI（CRt，CRt－1）作为聚类质量和聚类平滑性的衡量指标外，本文还采用NMI（CRt，CRtreal）和F1-score两个指标来评价社区检测的性能。其中NMI（CRt，CRtreal）是社区检测结果与真实社区的吻合度，CRtreal为时间步t的真实社区标签，计算方式与式（2）相同。F1-score是分类问题的度量，是准确率和召回率的调和平均值。F1-score的定义如下：

F1-score=2×TP（TP+FN）（TP+FP）（6）

其中：TP为预测正确的标签数；FN为实际情况下预测为负但为正的标签数；FP为实际情况下预测为正但为负的标签数。

3.3 参数设置

在对HOGA算法的实验中，由于种群大小（pop_size）设置为100～200时算法已经能够收敛到较优解的范围，足以在解空间中进行有效的搜索，而超过200时算法收敛时间比100成倍增长。为了能够在不大幅牺牲搜索空间的同时缩短收敛时间，最终将pop_size设置为100。同时由于考虑的社区信息最高阶数超过3时，最优解集误差均可控制在10%左右，说明3阶信息已经能够较好地联系相邻时间步的社区。为减少计算量最终确定使用的社区信息最高阶数为3，并且各阶信息的权重ω将根据不同数据集的最佳实验结果进行调整。除此之外，实验发现基因变异概率（MP）超过0.5时，算法收敛速度将比MP<0.5时慢两倍左右，且迭代优化程度不高。因此为了平衡种群多样性与收敛速度，最终将MP设置为0.4，在提高算法探索搜索空间能力的同时保持较合适的收敛速度。所述参数值均为基准值，数据集不同时，参数也将根据最优实验结果依据基准值进行相应调整。

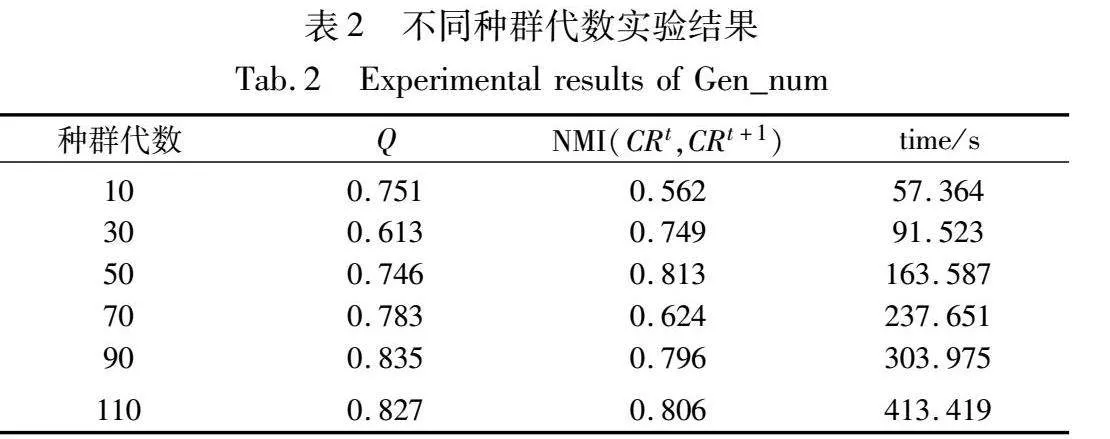
在synx_muw=0.1数据集中，不同种群代数（Gen_num）设置的实验结果如表2所示。其中Q和NMI（CRt，CRt+1）分别表示平均模块度和相邻时间步社区的平均归一化互信息，time为收敛耗时。能够看出在种群代数为50时，相较于其他设置能够使Q和NMI（CRt，CRt+1）值保持在较高水准的同时，收敛时间也相对较短。

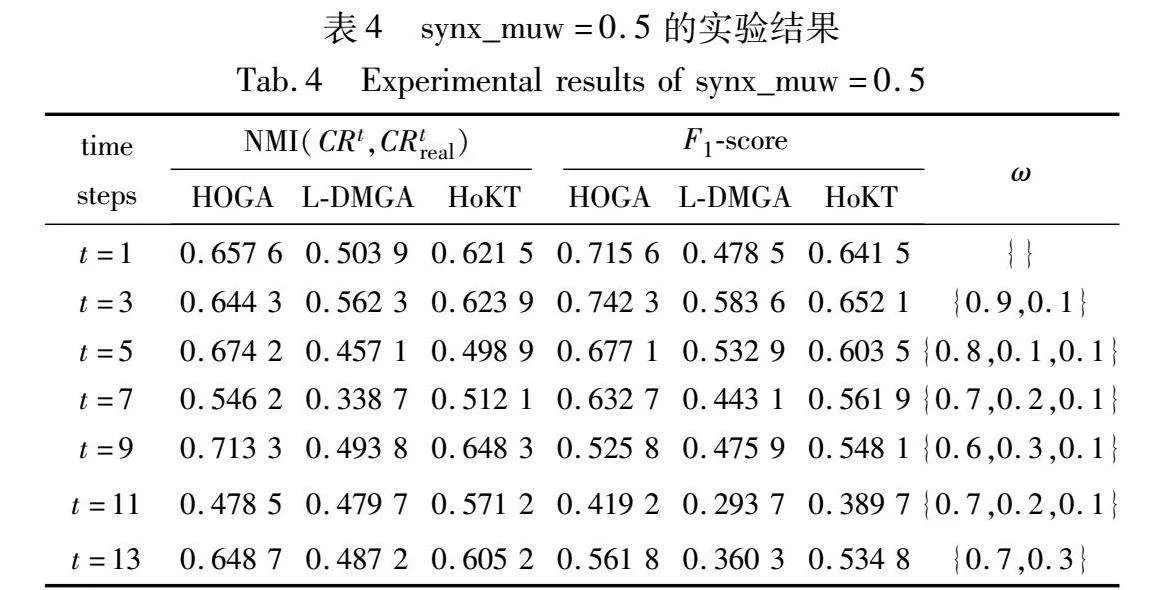
为了更好地比较HOGA在网络社区结构波动较小以及网络波动较大的算法性能，选取配置方案在synx_muw=0.1的模拟数据集上的实验结果，如表3所示，在synx_muw=0.5的模拟数据集上的实验结果，如表4所示。结果表明，HOGA在网络波动较小时能保持良好的性能，而随着社区变化程度增大，相较于另外两种算法，其优势体现也越明显。

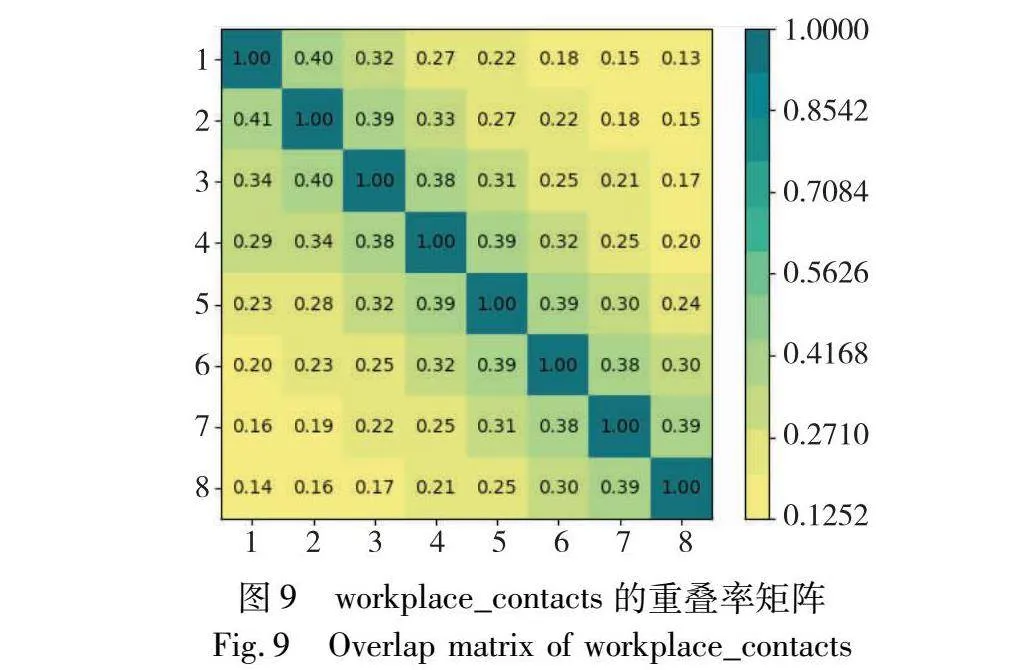
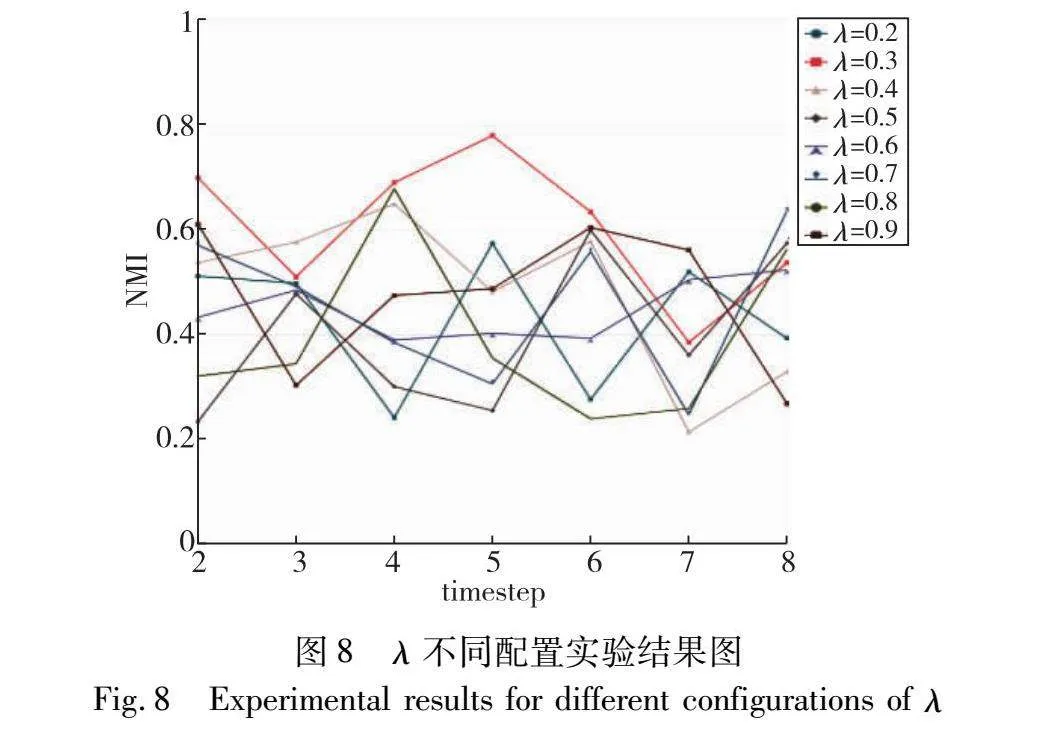
网络变化阈值λ通过NMI与数据集的重叠率矩阵确定。在真实数据集上设置不同的λ={0.2，0.3，0.4，0.5，0.6，0.7，0.8}，并运行HOGA算法，结果如图8所示。图9则给出了数据集workplace_contacts的重叠率矩阵。

图8中λ=0.3时的NMI即红色曲线（见电子版），几乎在每个时间步上都优于其他曲线，并且由于图8的重叠率矩阵中网络相似度在［0.2，0.4］左右，所以本实验的网络变化阈值选择λ=0.3。由此在λ=0.2、0.3、0.4时才可以选用不同阶的社区信息，对不同相似度的网络采取不同的社区划分策略。此外，由于考虑过早的时间步社区信息对于当前网络快照的社区划分意义不大，所以本文主要对二阶和三阶社区进行利用。

3.4 实验结果

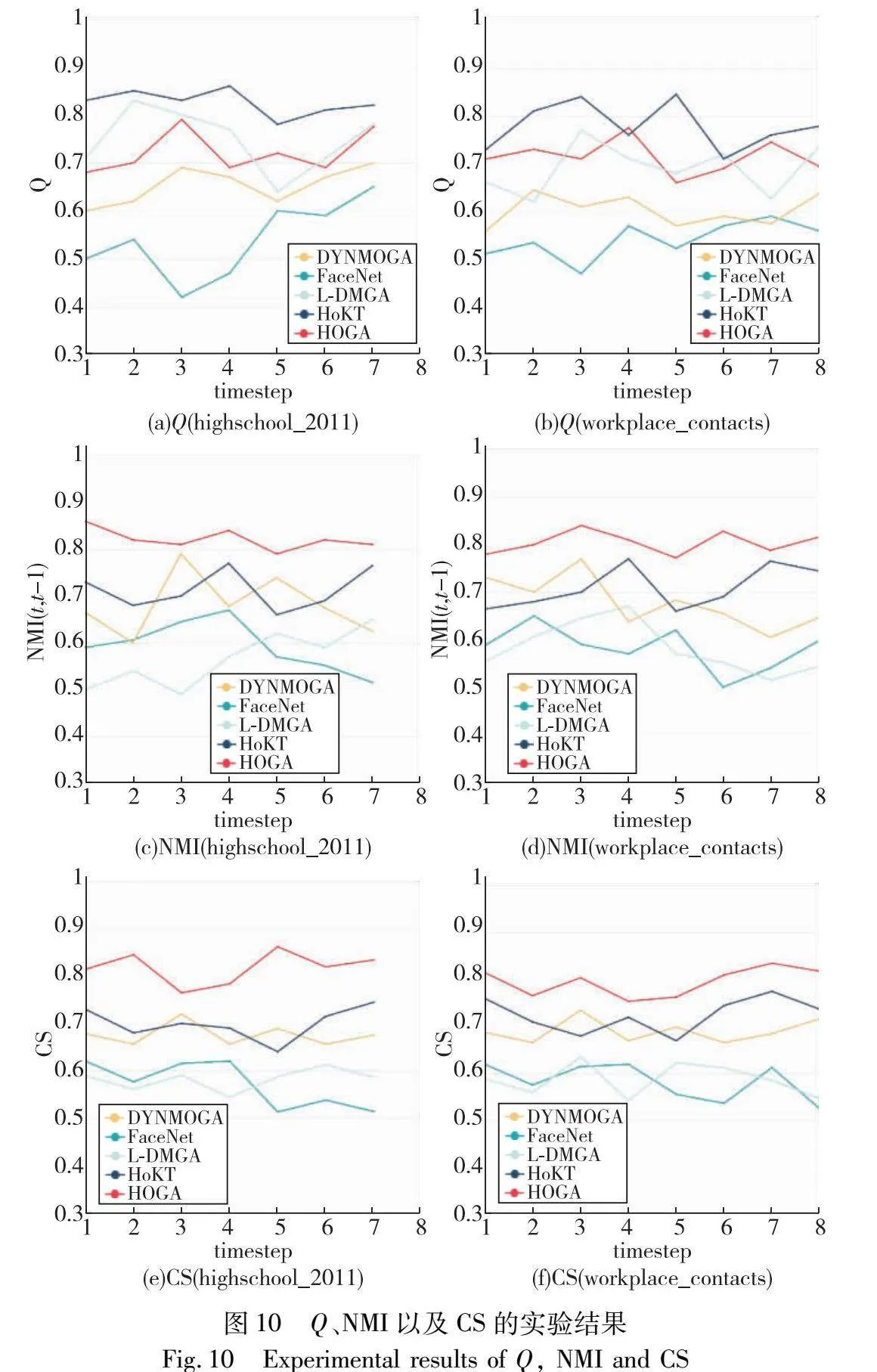
图10为本文算法与所选取的四种社区检测算法在数据集highschool_2011和workplace_contacts中的模块度Q、每个时间步与前一个时间步的社区结构归一化互信息NMI（t，t-1）以及社区结构稳定性CS（community stability）的实验结果。2.1节中，使用CV（community volatility）衡量社区变化，为了方便对图表的观察，采用与其互补的变量CS=1－CV对社区结构的稳定性进行表示。对比图显示出HOGA能够将聚类质量保持在一个较好水平的同时，找到具有最佳聚类平滑性的社区划分方案。虽然HOGA的模块度Q不是四个算法中最优的，但是能够在损失相对较少模块度后，获取到最高的NMI。这四个数据集相邻快照的网络社区大多都发生了显著变化，即本文算法能够在网络发生显著变化时最大化社区稳定性与平滑性，并且能够平衡聚类质量和聚类平滑性这两个社区检测目标。HOGA在维持社区稳定性方面具有更好的性能，这是因为利用的社区划分信息越多，算法也能保留更多先前社区划分的优势。

由于本文算法所使用的优化函数是以减少相邻时间步的社区变化为目标，所以划分出的社区整体变化更小，在对相邻时间步进行分析时避免因为社区变化过于杂乱而影响对于网络结构演变的研究。图11所示为HoKT算法与本文算法在数据集highschool_2012上的部分社区划分结果，在社区划分完成后均使用Fruchterman-Reingold算法对网络结构进行布局。从（a）中可以看出，HoKT算法检测出的社区中单个节点社区迁移较多，社区间的成员流动较为复杂。而从（b）中能够观察到7个红色边框（见电子版）标注的节点经历了社区变动，同时值得注意的是，节点53所在社区有一半的成员移动到了节点81所在的社区。因此本文算法更加利于分析动态网络中社区整体的演变过程与社区之间的关系。

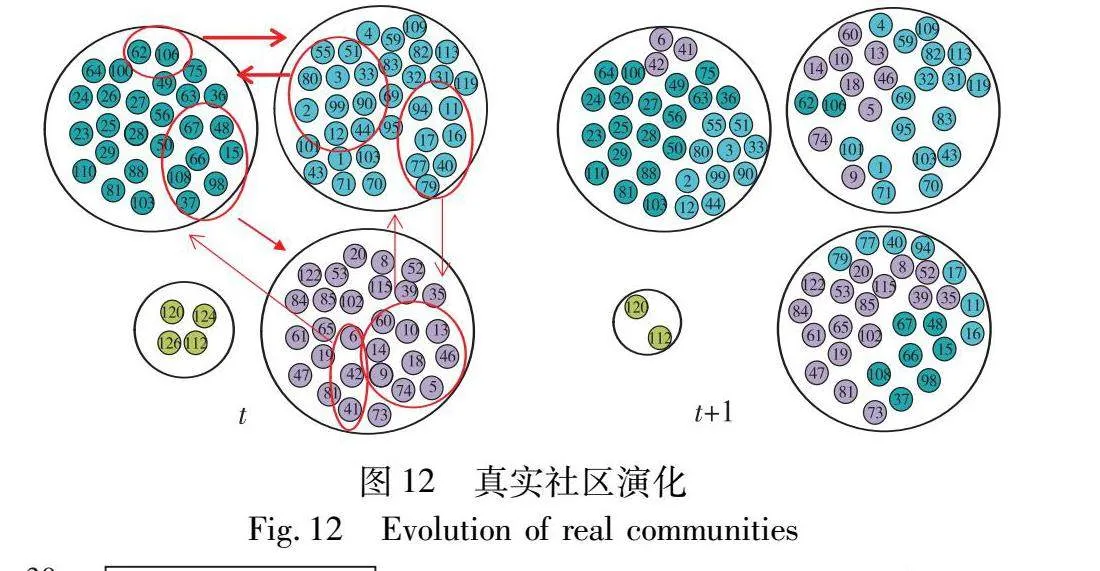
通过HOGA进行社区划分后，真实数据集highschool_2011中由高中学生以及老师关系网络构成的真实社区（选取主要社区）演变过程如图12所示。能够明显观察到三个社区间存在明显的成员流动，因此能够分析出这三个班级可能在这段时间内进行了班级人员调整，例如根据成绩分班或者文理分科后调整班级。同时节点124与126离开了原社区，说明这两个节点所代表的任课老师可能被调整到了其他任课岗位或是办理了离职，该社区也发生了收缩。

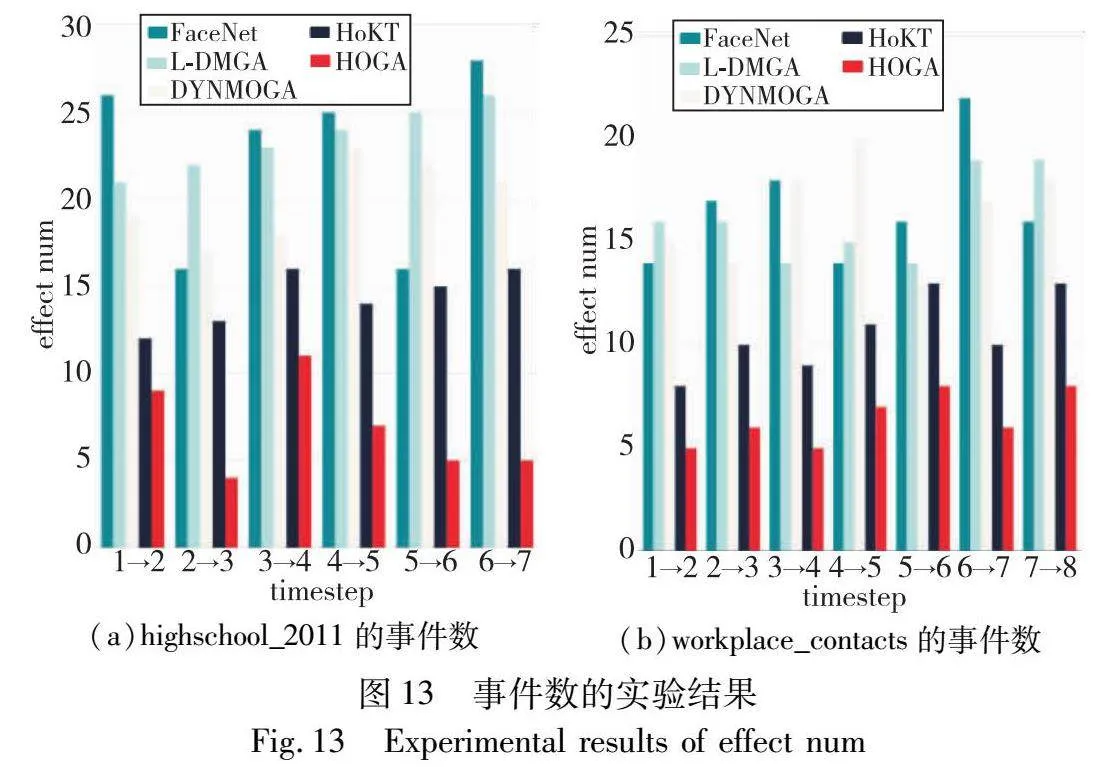
由于算法降低了CV，社区演化事件也会随之减少。图13为五个不同社区检测算法在四个真实数据集上的社区演化事件数。这些事件包括社区的扩张、收缩、合并以及分裂等。由图可知，在社区演化过程中，HOGA算法检测出的社区具有更高的稳定性和一致性。具体而言，HOGA算法在每个时间步上划分出的社区相对于前一个时间步都具有更少的社区变化事件。这意味着在社区的演化过程中，HOGA算法所形成的社区结构更加稳定，变化也更为平滑。

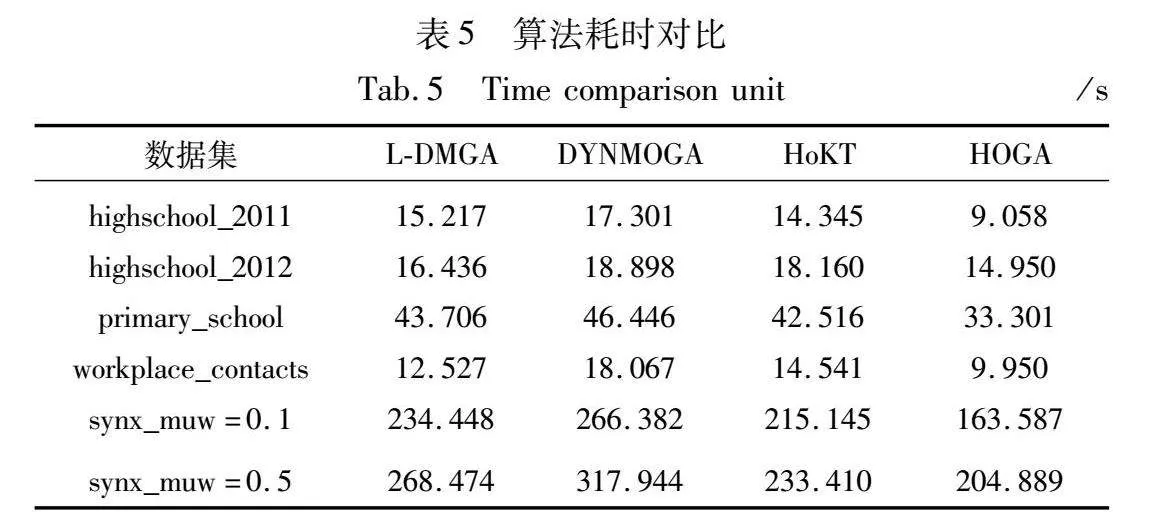
为对算法效率进行公平比较，选取三个基于遗传算法的动态社区检测算法与本文算法进行对比。由于算法未使用随机初始化，而是通过蛛网模型生成质量更高的父代种群，与本文的变异方法共同提高了子代种群多样性，所以能够在不影响算法性能的同时减少种群代数，进而提高算法效率。表5为各算法在不同数据集上的运行时间。可以看出在小规模数据集上，本文算法HOGA略快于其他算法，并且随着数据集规模增大，HOGA所用时间短的优势也能更为明显。

4 结束语

对于突变的处理在许多领域都是至关重要的，本文主要面向相邻时间步发生显著变化的动态网络，基于进化算法以及高阶信息转移策略设计了一个动态社区检测算法HOGA，并设计了新的目标函数HOCV，通过非支配排序遗传算法求解出同时具备较高聚类质量和聚类平滑性的社区划分方案。

实验结果表明，HOGA在网络发生微小变化时能保持良好的性能，而在相邻网络快照社区发生剧烈变化的情况下，对于社区稳定性和平滑性的改善更为明显，检JD2Qu3kRKTbGDcp6GlUHexwiXaEH0yXycDvta8GAvq8=测到的社区演变事件也更少。但该算法也存在一些缺陷，例如在参数设置方面无法做到自适应，这也为之后的研究提供了一种可能的方向。

在未来的工作中，其不仅用于解决当前的社区检测问题，而且要面向更多发生显著变化的场景。例如将高阶信息传递的概念迁移到动态网络布局中，构建多目标模型，对发生巨大变化的网络进行布局，保留先前布局方案的优势并应用到下一个任务中。因此还需不断地探索更好的分析交互方式，同时提供一些动态可视化技术以及一定的交互，方便用户理解和挖掘动态数据背后有价值的信息。

参考文献：

［1］蒋云， 杨文东. 改进Louvain算法的多层航线网络社区划分 ［J］. 北京交通大学学报， 2022， 46（2）： 89-97. （Jiang Yun， Yang Wendong. Community detection of multi-layer air transport network with improved Louvain algorithm ［J］. Journal of Beijing Jiaotong University， 2022， 46（2）： 89-97.）

［2］欧阳资生， 杨希特， 黄颖. 嵌入网络舆情指数的中国金融机构系统性风险传染效应研究 ［J］. 中国管理科学， 2022， 30（4）： 1-12. （Ouyang Zisheng， Yang Xite， Huang Ying. Research on the systemic risk contagion effect of Chinese financial institutions embedded with social media sentiment index ［J］. Chinese Journal of Mana-gement Science， 2022， 30（4）： 1-12.）

［3］沈力峰， 王建波， 杜占玮，等. 基于社团结构和活跃性驱动的双层网络传播动力学 ［J］. 物理学报， 2023， 72（6）： 356-364. （Shen Lifeng， Wang Jianbo， Du Zhanwei，et al. Dynamic propagation in dual-layer networks driven by community structure and activity ［J］. Acta Physica Sinica， 2023， 72（6）： 356-364.）

［4］严玉为， 蒋沅， 杨松青，等. 基于时间序列的网络失效模型 ［J］. 物理学报， 2022， 71（8）： 331-339. （Yan Yuwei， Jiang Yuan， Yang Songqing，et al. Time series-based model for network failures ［J］. Acta Physica Sinica， 2022， 71（8）： 331-339.）

［5］Redekar S S， Varma S L. A survey on community detection methods and its application in biological network ［C］// Proc of International Conference on Applied Artificial Intelligence and Computing. Piscata-way， NJ： IEEE Press， 2022： 1030-1037.

［6］梁文， 闫飞， 陈柏圳. 两阶段量子行走算法在社区检测中的应用 ［J］. 计算机应用研究， 2023， 40（8）： 2329-2333. （Liang Wen， Yan Fei， Chen Bozhen. Two-stage quantum walk algorithm with application to community detection ［J］. Application Research of Computers， 2023， 40（8）： 2329-2333.）

［7］Peng Yong， Huang Wenna， Kong Wanzeng，et al. JGSED： an end-to-end spectral clustering model for joint graph construction， spectral embedding and discretization ［J］. IEEE Trans on Emerging To-pics in Computational Intelligence， 2023， 7（6）： 1687-1701.

［8］Su Xing， Xue Shan， Liu Fanzhen，et al. A comprehensive survey on community detection with deep learning ［J］. IEEE Trans on Neural Networks and Learning Systems， 2024， 35（4）： 4682-4702.

［9］Wang Xilu， Jin Yaochu， Schmitt S，et al. Transfer learning for Gaus-sian process assisted evolutionary bi-objective optimization for objectives with different evaluation times ［C］// Proc of Genetic and Evolutionary Computation Conference. New York：ACM Press， 2020： 587-594.

［10］Li Tianyi， Chen Lu， Jensen C S，et al. Evolutionary clustering of moving objects ［C］// Proc of the 38th IEEE International Conference on Data Engineering. Piscataway， NJ： IEEE Press， 2022： 2399-2411.

［11］Nordahl C， Boeva V， Grahn H，et al. EvolveCluster： an evolutionary clustering algorithm for streaming data ［J］. Evolving Systems， 2022， 13（4）： 603-623.

［12］Li Weimin， Zhou Xiaokang， Yang Chao，et al. Multi-objective optimization algorithm based on characteristics fusion of dynamic social networks for community discovery ［J］. Information Fusion， 2022， 79： 110-123.

［13］Yin Ying， Zhao Yuhai， Li He，et al. Multi-objective evolutionary clustering for large-scale dynamic community detection ［J］. Information Sciences， 2021， 549： 269-287.

［14］Keriven N. Not too little， not too much： a theoretical analysis of graph （over） smoothing ［J］. Advances in Neural Information Processing Systems， 2022， 35： 2268-2281.

［15］Yuan Limengzi， Zhu Qifeng， Zheng Yuchen，et al. Temporal smoothness framework： analyzing and exploring evolutionary transition behavior in dynamic networks ［C］// Proc of the 33rd IEEE International Conference on Tools with Artificial Intelligence. Piscataway， NJ： IEEE Press， 2021： 1206-1210.

［16］Liu Fanzhen， Wu Jia， Xue Shan，et al. Detecting the evolving community structure in dynamic social networks ［J］. World Wide Web， 2020， 23： 715-733.

［17］Deb K， Pratap A， Agarwal S，et al. A fast and elitist multiobjective genetic algorithm： NSGA-Ⅱ ［J］. IEEE Trans on Evolutionary Computation， 2002， 6（2）： 182-197.

［18］Srinivas N， Deb K. Muiltiobjective optimization using nondominated sorting in genetic algorithms ［J］. Evolutionary Computation， 1994， 2（3）： 221-248.

［19］Xu Dejun， Jiang Min， Hu Weizhen，et al. An online prediction approach based on incremental support vector machine for dynamic multiobjective optimization ［J］. IEEE Trans on Evolutionary Computation， 2021， 26（4）： 690-703.

［20］Tan K C， Feng Liang， Jiang Min. Evolutionary transfer optimization： a new frontier in evolutionary computation research ［J］. IEEE Computational Intelligence Magazine， 2021， 16（1）： 22-33.

［21］Jiang Min， Huang Zhongqiang， Qiu Liming，et al. Transfer learning-based dynamic multiobjective optimization algorithms ［J］. IEEE Trans on Evolutionary Computation， 2017， 22（4）： 501-514.

［22］Jiang Min， Wang Zhenzhong， Hong Haokai，et al. Knee point-based imbalanced transfer learning for dynamic multiobjective optimization ［J］. IEEE Trans on Evolutionary Computation， 2020， 25（1）： 117-129.

［23］Liu Zhening， Wang Handing. Improved population prediction strategy for dynamic multi-objective optimization algorithms using transfer learning ［C］// Proc of IEEE Congress on Evolutionary Computation. Piscataway， NJ： IEEE Press，2021： 103-110.

［24］Li Jianqiang， Sun Tao， Lin Qiuzhen，et al. Reducing negative transfer learning via clustering for dynamic multiobjective optimization ［J］. IEEE Trans on Evolutionary Computation， 2022， 26（5）： 1102-1116.

［25］Jiang Min， Wang Zhenzhong， Guo Shihui，et al. Individual-based transfer learning for dynamic multiobjective optimization ［J］. IEEE Trans on Cybernetics， 2020， 51（10）： 4968-4981.

［26］Zhou Wei， Feng Liang， Tan K C，et al. Evolutionary search with multiview prediction for dynamic multiobjective optimization ［J］. IEEE Trans on Evolutionary Computation， 2021， 26（5）： 911-925.

［27］Ma Xiaoke， Dong Di. Evolutionary nonnegative matrix factorization algorithms for community detection in dynamic networks ［J］. IEEE Trans on Knowledge and Data Engineering， 2017， 29（5）： 1045-1058.

［28］Jiang Min， Wang Zhenzhong， Qiu Liming，et al. A fast dynamic evolutionary multiobjective algorithm via manifold transfer learning ［J］. IEEE Trans on Cybernetics， 2020， 51（7）： 3417-3428.

［29］李辉， 陈福才， 张建朋，等. 复杂网络中的社团发现算法综述 ［J］. 计算机应用研究， 2021， 38（6）： 1611-1618. （Li Hui， Chen Fucai， Zhang Jianpeng，et al. Survey of community detection algorithms in complex networks ［J］. Application Research of Compu-ters， 2021， 38（6）： 1611-1618.）

［30］lhan N， üdücüG. Predicting community evolution based on time series modeling ［C］// Proc of IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. Piscataway， NJ： IEEE Press，2015： 1509-1516.

［31］Zeng Xiangxiang， Wang Wen， Chen Cong，et al. A consensus community-based particle swarm optimization for dynamic community detection ［J］. IEEE Trans on cybernetics， 2019， 50（6）： 2502-2513.

［32］Niu Xinzheng， Si Weiyu， Wu C Q. A label-based evolutionary computing approach to dynamic community detection ［J］. Computer Communications， 2017， 108： 110-122.

［33］Qu Song， Du Yuqing， Zhu Mu，et al. Dynamic community detection based on evolutionary DeepWalk ［J］. Applied Sciences， 2022， 12（22）： 11464.

［34］Costa A R. Towards modularity optimization using reinforcement learning to community detection in dynamic social networks ［EB/OL］. （2021-11-25）.https：//api.semanticscholar.org/CorpusID：244729709.

［35］Ma Huixin， Wu Kai， Wang Handing，et al. Higher-order knowledge transfer for dynamic community detection with great changes ［J］. IEEE Trans on Evolutionary Computation， 2024， 28（1）： 90-104.

［36］Yang Haijuan， Cheng Jianjun， Su Xing，et al. A spiderweb model for community detection in dynamic networks ［J］. Applied Intelligence， 2021， 51： 5157-5188.

［37］Lin Yuru， Chi Yun， Zhu Shenghuo，et al. Analyzing communities and their evolutions in dynamic social networks ［J］. ACM Trans on Knowledge Discovery from Data， 2009， 3（2）： 1-31.