基于时空位置关注图神经网络的交通流预测方法
2024-10-14何婷周艳秋辛春花







摘 要:针对现有交通流预测方法存在难以构建空间和时间依赖关系的问题,提出了新的利用时空位置注意力的图神经网络(ST-PAGNN)方法。首先,该图神经网络中包含有位置关注机制,由此能够更好地对城市道路网络中交通节点的空间依赖关系进行有效捕捉;然后,利用带有trend adaptive Transformer (Trendformer)的门控递归神经网络来捕捉交通流序列在时间维度上的局部和全局信息;最后,利用改进的网格搜索优化方法对模型的引入参数进行优化,并以较高的时间效率获得全局最优解。实验结果表明,在数据集PEMS-BAY中,预测步长分别为15 min,30 min,60 min时,ST-PAGNN的评价指标RMSE、MAE和MAPE分别为1.37,2.57,2.67%,1.55,3.64,3.37%,1.97,4.37,4.43%;在数据集METR-LA中,预测步长分别为15 min,30 min,60 min时,ST-PAGNN的评价指标RMSE、MAE和MAPE分别为2.73,5.16,7.13%,2.99,5.97,7.86%,3.53,7.16,9.96%。结论表明,ST-PAGNN在不同粒度下的评价指标中均高于现有模型,从而说明了ST-PAGNN在解决交通预测问题方面的有效性和优越性。
关键词:ST-PAGNN;交通流预测;深度学习;图卷积神经网络;门控循环单元;Trendformer
中图分类号:TP391 文献标志码:A 文章编号:1001-3695(2024)10-008-2932-07
doi:10.19734/j.issn.1001-3695.2024.01.0026
Traffic flow prediction method based on spatial temporal positionattention graph neural network
He Ting, Zhou Yanqiu, Xin Chunhua
(Dept. of Computer Technology & Information Management, Inner Mongolia Agricultural University, Baotou Nei Mongol 010010, China)
Abstract:To address the challenge of constructing spatial and temporal dependencies in existing traffic flow prediction me-thods, this paper proposed a new method called spatial temporal position attention graph neural network (ST-PAGNN), which utilized spatiotemporal location attention. Firstly, the graph neural network contained a location attention mechanism, which could better capture the spatial dependence of traffic nodes in the urban road network. Then, it used a gated recurrent neural network with trend adaptive transformer (Trendformer) to capture the local and global information of the traffic flow sequence in the time dimension. Finally, it used the improved grid search optimization method to optimize the introduced para-meters of the model, obtaining the global optimal solution with high time efficiency. The experimental results show that in the dataset PEMS-BAY, the evaluation indexes RMSE, MAE and MAPE of the ST-PAGNN method are 1.37, 2.57, 2.67%, 1.55, 3.64, 3.37%, 1.97, 4.37 and 4.43%, respectively, when the prediction step size is 15 min, 30 min and 60 min, respectively. In the dataset METR-LA, when the prediction step size is 15 min, 30 min and 60 min, the evaluation indexes RMSE, MAE and MAPE of the ST-PAGNN method are 2.73, 5.16, 7.13%, 2.99, 5.97, 7.86%, 3.53, 7.16 and 9.96%, respectively. The results show that the proposed ST-PAGNN method is higher than the existing models in the evaluation indexes under different granularities, which illustrates the effectiveness and superiority of ST-PAGNN in solving traffic prediction problems.
Key words:ST-PAGNN; traffic flow forecasting; deep learning; GCN; GRU; Trendformer
0 引言
随着城市化进程的加速和人口的不断增长,交通拥堵问题在人们的日常生活中也越来越严重[1]。准确地预测未来短期内的交通流是解决交通拥堵问题的关键。最近几年,交通流预测领域开始普遍应用大数据以及深度学习技术,在此影响下获得了更加有效的问题解决方案[2]。
大数据技术已经成为现代社会不可或缺的组成部分[3]。在交通领域,大数据来源于各类传感器、移动设备、交通监控系统以及社交媒体等多种渠道,提供了大量的交通信息。这些数据的分析和挖掘,通过准确地捕捉交通流的特征和模式,可以为短时交通流预测提供有力支持[4]。作为机器学习技术领域的最新研究和应用成果,深度学习由于自身所具有的模式识别能力非常强,特征学习能力也比较突出等特点,所以能够被深入应用到交通流预测当中。
目前,对于短期交通流预测的研究主要分为经典统计方法、机器学习方法和深度学习方法三类[5]。经典统计方法模型较为简单,因此计算方便,速度较快,但是这些方法对于平稳数据的预测效果较好,对于非线性和复杂的交通流数据表现较差。基于机器学习的方法利用了回归和分类算法进行建模和预测,能够实现较好的预测效果,但在大量数据和特征维度较高的情况下,仍然存在性能瓶颈。随着深度学习技术的兴起,基于深度学习的方法在交通流预测领域取得了显著的突破,其强大的非线性建模能力使得预测准确性大幅提高[6]。
为了弥补机器学习相关方法的不足,现存的深度学习方法,大多是通过设计和完善神经网络来捕捉交通流信息的时间和空间依赖性。例如,循环卷积神经网络 RNN 通过二维时空矩阵将时空交通状态转换为描述交通流时空关系的图像,增强了时空的关联性。RNN的变体[7]长短期记忆网络LSTM解决了RNN梯度消失的问题,提高了时空依赖性。Fu等人[8]提出将门控循环单元(GRU)递归神经网络(NN)结合LSTM方法来捕获时空依赖性模型表现良好。以上方法通常适用于规则的欧几里德结构的数据[9],例如图像、网格等。但是用于收集交通流信息的检测器的分布属于非欧几里德结构,因此这些方法在交通流预测的准确性上存在局限性。为此,Liu等人[10]提出基于图卷积网络(GCN)的模型用来提取交通流的领域信息和社区信息,加快了图卷积神经网络的发展。在图卷积神经网络中,层次交叉的交通路线被建模成图结构,图中交通连接的地方称为图结构中的节点,边权值叫做节点欧氏距离。为了捕获交通数据的时间和空间的依赖性,时间图卷积网络(T-GCN)、图卷积网络和门控循环单元相结合[11~13],用图卷积学习拓扑结构以捕捉空间依赖性,同时用门控递归单元学习交通数据变化以捕获数据的时间依赖性。相较于之前没有采用GCN的方法,这些方法虽然在模型的预测精度上有了一定的提升,但是仍然存在一些问题:a)采用的是定义好的不变的图结构[14],不能动态地反映出节点之间的影响关系;b)无法很好地捕捉交通情况,以上方法使用共享模型参数,而对于特征的交通数据情况,无法捕捉到细粒度的特征表示,例如交通路段封闭;c)不能同时有效地捕捉交通流数据的时空依赖性,从而导致其在预测准确率上面存在局限性[15]。
由于现存方法不能有效解决空间和时间方面依赖关系,针对上述问题,本文设计了一个融合空间-时间依赖和位置注意力图神经网络的交通流预测方法(spatial temporal position attention graph neural network, ST-PAGNN)。
本文的主要贡献如下:
a)为了捕捉道路之间的空间关系,引入添加位置注意力机制的图神经网络模型,从而更加有效地聚集来自相邻道路的交通流信息。
b)利用改进的网格搜索优化方法对模型的引入参数进行优化,并以较高的时间效率获得全局最优解,可以保证整合后模型的普适性。
c)通过GCN学习拓扑来捕获空间依赖性,将LSTM[15]网络嵌入到GCN增加网络时间记忆功能来捕获时间特征,增强长序列处理的能力。
d)通过结合GRU和Trendformer来捕捉局部和全局的时间依赖性,获取交通流的动态趋势,增强模型对特殊事件发生的鲁棒性。
e)提出了新的ST-PAGNN框架进行交通流的预测,特别用于对具有复杂拓扑和时间依赖性的系列数据进行建模。在真实的数据集上验证了ST-PAGNN的可行性和优势,特别是对于以分钟为单位的短时交通速度预测。实验表明,提出的模型明显优于其他几种先进的方法。
1 相关工作
在交通流预测领域,基于传统机器学习和深度学习的方法已经取得了一定的研究成果[16]。基于短时交通流预测问题的深入研究和分析需要,本文在对交通流预测方法进行阐释时,主要基于传统机器学习和深度学习两个维度进行。
1.1 基于传统的机器学习的交通流预测方法
基于传统的机器学习方法通常依赖于手动选取的特征提取,通过构建和训练机器学习模型来预测交通流量[17]。这些方法主要基于统计模型、回归模型和决策树等,它们在交通流量预测中具有一定的可靠性和可解释性。
常见的基于传统的机器学习的方法包括:回归模型如线性回归和非线性回归;决策树算法如CART、随机森林和支持向量机(SVM)等。Toan等人[18]提出了一种使用支持向量机进行短期交通流预测的有效方法,与基线方法(包括历史平均值、基于当前时间和双指数平滑预测因子)进行比较。为了证明 SVM 的效率和准确性,在新加坡泛岛高速公路的一段路上使用了一个月的时间序列交通流量数据来训练和测试模型。结果表明,在大多数预测区间和各种交通条件下,在30 min的滚动水平线上,SVM的性能显著优于基线方法。Miao等人[19]提出了一种多任务贝叶斯增强的对抗时空网络MBA-STNet来学习特定任务的特征和共享特征。结果表明,MBA-STNet优于目前先进的方法。这些方法能够利用历史交通数据和其他影响因素,构建模型来预测交通流量。Peng等人[20]提出了ARIMA-SVM组合预测模型用于预测城市短期交通流量。首先,利用ARIMA和SVM预测城市短期交通流量;然后,利用更新的动态权重加权融合方法预测城市交通流量,得到ARIMA-SVM组合预测模型,并将结果与单独的ARIMA和SVM进行比较。实证结果表明,ARIMA-SVM组合模型能够更准确地预测城市的短期交通流量。然而,这类方法对于特征提取的依赖性较强,需要人工选取合适的特征,并且在处理非线性和高维数据方面的能力有限。
1.2 基于深度学习的交通流预测方法
最近几年,研究领域开始越来越关注基于深度学习的交通流预测方法。深度学习方法通过构建多层神经网络,可以自动学习交通流的特征和模式,并将其应用于交通流量的预测。相对于传统的机器学习方法,深度学习具有更强的非线性建模和特征学习能力[21]。
在日常的研究中,循环神经网络(RNN)是应用最为普遍的基于深度学习的方法,但是除此之外,由此衍生出来的门控循环单元网络以及卷积神经网络(CNN)等也比较常见。文献[22]提出了一种名为M-B-LSTM的混合深度学习网络模型来对短期交通流进行预测。该模型包括数据映射层、统计分布和深度双向长短期记忆网络(DBLSTM)。通过这些组件,M-B-LSTM能够有效地处理交通流数据存在的分布不平衡、过拟合和不确定性问题,从而准确预测未来一段时间内的交通流状态。此外,经过充分的对比实验,结果表明,与现有方法相比,所提模型在解决不确定性和过拟合问题方面具有更好的能力。Zheng等人[23]提出了一种基于深度学习的模型,该模型使用混合和多层架构来自动提取交通流数据的固有特征。首先,为了对空间和短期时间特征进行有效的提取,最好的方法就是进行基于注意力的Conv-LSTM模块的开发,而这又必须要建立在卷积神经网络和长短期记忆(LSTM)网络基础之上;科学合理制定注意力机制,在自动对各个权重进行有效分配的基础之上,能够有效对各个时间流序列的不同重要程度进行界定。其次,基于对长期时间特征进行深入研究的需要,构建了全新的双向LSTM(Bi-LSTM)模块,据此来对每日和每周的周期性特征进行提取,由此能够更好地对交通流从前向和后向的发展变化情况进行捕捉。最后,通过大量的实验结果表明,与其他现有方法相比,所提结合注意力转换和Bi-LSTM的模型具有更好的预测性能。Han等人[24]提出了一个名为LST-GCN的模型。利用LSTM(长短期记忆)网络优化GCN(图卷积网络)参数来模拟交通流预测中存在的时空相关性。具体来说,本文通过GCN学习拓扑来捕获空间相关性,通过将LSTM网络嵌入GCN的训练过程中来捕获时间相关性。该方法改进了原有时空交通流预测中循环神经网络和图神经网络相结合的传统方法,能够更好地捕捉交通流中存在的时空特征。在PEMS数据集上进行的大量实验证明了与其他最新方法相比,该方法更有效。 Liu等人[25]提出一种基于GCN和LSTM网络的深度学习网络。该模型是使用绵阳市的本地交通数据进行训练和测试的。在引入新的深度学习网络后,本文还建立了一种基于时间相关性选择相关道路链接作为模型输入的数据缩减方法。最后,将所提算法与其他常用方法进行对比,在常规的5 min预测测试中可以获得更好的结果。同时,GCN-LSTM模型的性能可以通过多步预测,在5~125 min的不同时间内保持,比其他模型要好得多。这些方法能够通过多层次的网络结构,捕捉交通流的时序特征和空间关系,提高交通流量预测的准确性。深度学习方法还可以通过端到端的训练过程,自动进行特征学习和模型优化,减少对人工特征工程的依赖。
基于上述分析可知,尽管现有的交通流预测方法取得了优异的表现,但是当前利用注意力机制捕获动态空间依赖的模型只使用了车速信息,忽视了其他的一些信息,也没有利用全局的时间依赖。并且大多数的研究工作在空间和时间依赖性的建模上有一定的局限性,难以充分挖掘潜藏在复杂交通网络中的内在模式,难以实现精准的交通流预测。因此,提出了基于ST-PAGNN的交通流预测方法。
2 基于ST-PAGNN的交通流预测方法
时空图神经网络框架如图1所示,由三个主要部分组成:a)空间图神经网络(S-GNN)层,用于捕捉道路之间的空间关系;b)GRU层,用于捕捉序列中的时间关系(或局部时间依赖性);c)改进的Transformer层,用于直接捕捉序列中的长程时间依赖性(或全局时间依赖性)。需要注意的是,S-GNN层用于模拟节点之间的空间关系,并且同时应用于GRU单元的输入和隐藏表示,如图1所示。GRU层[26]和改进的Transformer层[27]都用于独立地捕捉每个节点的时间相关性,分别从不同的角度进行捕捉。接下来,首先讨论利用S-GNN来建模空间依赖性,然后介绍如何利用GRU层和Transformer层来捕捉时间依赖性。在介绍完这些组件之后,将对整个框架进行简要总结。
2.1 空间依赖性建模
交通网络G对道路之间的关系进行了编码。交通网络中的道路如果彼此之间连接在一起,那么其存在相似属性的几率也就越大。如果属于间距较近的两条路,那么其中任意一条路上出现的交通状况都可能会影响到对方。所以,有必要借助于图神经网络模型(graph neural networks model)[28]来对其空间进行捕捉,通过网络转换和传播信息。给定网络上Xin∈Euclid ExtraaBpN×din的输入信息,可生成输出Xout∈Euclid ExtraaBpN×dout如下:
Xout=σ(D-1/2AD-1/2XinW)(1)
其中:σ为非线性激活函数,采用ReLU(·);A=A+IN是细化邻接矩阵;IN是N维标识矩阵;D是细化度矩阵Dii=∑jAij;W是要学习的参数。式(1)中的运算总结如下:
Xout=fg(A,Xin)(2)
上述都是以网络信息为载体的工作,而处于道路上传感器间的地理临近性又是形成网络信息的基本前提。但是,道路间实际上可能会存在更为复杂的影响。比如,车辆密度、道路状况等因素也都可能会对交通流量产生重大影响。所以,式(1)在具体进行聚合的过程当中,要避免在某个中心点对相近节点的信息进行平均聚合。本文尝试采用全新的位置表示来对各个节点的这些因素进行捕捉。如果用vi来表示各节点,那么对应地采用pi来表示该点对周围点的信息进行聚合之后的结果,任意两个节点之间的相互作用关系计算如式(3)所示。
R[i, j]=exp(Φ(score(pi,pj)))∑Nk=1exp(Φ(score(pi,pk)))(3)
其中:Φ表示非线性映射函数,用来对节点间的得分进行变换;score()是一个用点积建模的关系得分函数。
score(pi,pj)=pTipj(4)
除此之外,借助于掩码来稀疏化处理关系矩阵R,从而使计算变得更加简便:
mask(R)=Rij if Aij > 0
0 otherwise(5)
然后,就可以对新学习的关系矩阵mask(R)进行GCN运算:
Xout=σ(D-1/2RRD-1/2RXinW(l))(6)
其中:R=mask(R)+IN;DR是R的度矩阵。式(7)为式(6)的简写,以捕捉空间关系:
Xout=fa(A,Xin)(7)
2.2 时间依赖性建模
基于对时间依赖性进行捕捉的需要,本文在对序列信息进行处理时借助了门控递归单元[26]。各个时间步分别有对应的一个隐藏表示被保留,以便对下个时间步的信息流进行控制,同时当前时间步也是以此作为输出。在所有的节点上都独立应用了GRU运算,但是彼此之间能够共享GRU参数。为了在对序列进行处理时能够将空间关系纳入其中,借助于式(7)中修改后的GCN来对GRU的输入和隐藏表示进行运算。具体而言,将Xt和上一步的隐藏表示Ht-1输入到t也就是时间步骤当中,将修正的GCN运算应用其中:
Xt=fa(A,Xt)Ht-1=fa(A,Ht-1)
(8)
那么,对于时间步长为t的每个节点 vi,GRU 的运行情况 可以表示如下:
zt=σz(WzXt[i,:]+UzHt-1[i,:]+bz)
rt=σr(WrXt[i,:]+UrHt-1[i,:]+br)
Ht[i,:]=tanh(WhXt[i,:]+Uh(rt⊙UhHt-1[i,:])+bh)
Ht[i,:]=(1-zt)Ht-1[i,:]+zt⊙Ht[i,:]
(9)
其中:元素相乘用⊙表示;Wz和Uz代表更新门的权重矩阵;Wr和Ur代表重置门的权重矩阵;Wh,Uh代表候选隐藏状态的权重矩阵;Ht[i,:]具有双重角色,为及时输出结果,同时也作为输入存在于下一时间步中。
GRU的主要作用在于对局部时间信息进行捕捉。但是,在现实当中,时间信息除了具有顺序相关之外还存在其他相关性。所以,在预测交通速度过程当中必须要做好对全局时间信息的捕捉。因此,在GRU层之后,采用了Trendformer来直接捕捉全局相关性。对于节点vi,将GRU的输出序列(H1[i,:],…,HT[i,:])作为转换器的输入。
Trendformer由一个自适应趋势模块、一个时空编码器、一个时空解码器和一个输出模块组成。时空编码器的主要构成部分为时间编码器和空间编码器,且两者并行存在。对于后者而言,又可以细分为串行存在的时间编码器和空间编码器。时间编码器和时间解码器对序列进行多头关注,以提取时间相关性。空间编码器和空间解码器对传感器图进行多头关注,以提取空间相关性。将时间编码器和空间编码器的输出进行融合,以获得编码输出。自适应趋势模块根据编码输出确定可向解码器传输多少趋势信息,并控制预测输出在趋势周围的波动强度。然后,编码器和自适应趋势模块的输出被送入时空解码器。时空解码器之后是一个输出模块,用于产生多步预测输出,并最终输出Hviout∈Euclid ExtraaBpT×d。Trendformer的网络结构如图2所示。
2.3 预测层
在经过Trendformer之后,将输入数据设定为{Hviout|∈vi∈V},借助于多层前馈网络以便更好地对交通流未来的变化情况进行预测。
训练时必须要按照三部分来拆分历史数据y,得到的为ytrain、ytest以及yvalid,分别对应的内容为训练、测试以及验证。然后,通过滑动,在训练数据ytrain上能够得到窗口,其长度为T+T′,由此能够得到相应的训练序列。其中输入为前T个元素,而基本事实则是剩下的T′元素。最后,将损失设定为平均绝对误差,可以表示如下:
L=∑|ytrain|-T′t=1d(f(Yt+1,…,Yt+T),(Yt+T+1,…,Yt+T+T′))(10)
其中:
d(f(Yt+1,…,Yt+T),(Yt+T+1,…,Yt+T+T′))=
∑T′i=1‖Y^t+T+i-Yt+T+i‖(11)
(Y^t+T+1,…,Y^t+T+T′)=f(Yt+1,…,Yt+T)(12)
其中: f()是预测模型,通过式(10)的最小化损失函数完成训练。
2.4 参数优化策略
参数的选择对模型的性能起着至关重要的作用。所提模型利用C和Gamma的独立特性,通过分布式资源并行执行网格搜索来缩短模型搜索时间。
a)对数据集进行数据清理和归一化。根据时间延迟t和嵌入维度m重构相空间后,作为模型训练和测试输入。
b)初始化模型参数,并将训练集分为两部分,第一部分训练集用于GRU训练数据,第二部分子集用于预测。
c)将第二部分子集的预测值和实际值拼接后作为元学习器的训练数据。
d)初始化Trendformer的C和Gamma参数范围和步骤,通过多线程网格搜索找到最优模型,并在交叉验证后返回最优参数组合。
e)根据最优参数重建集成模型,并调用该模型对测试数据进行预测。
3 实验
3.1 实验环境和数据集
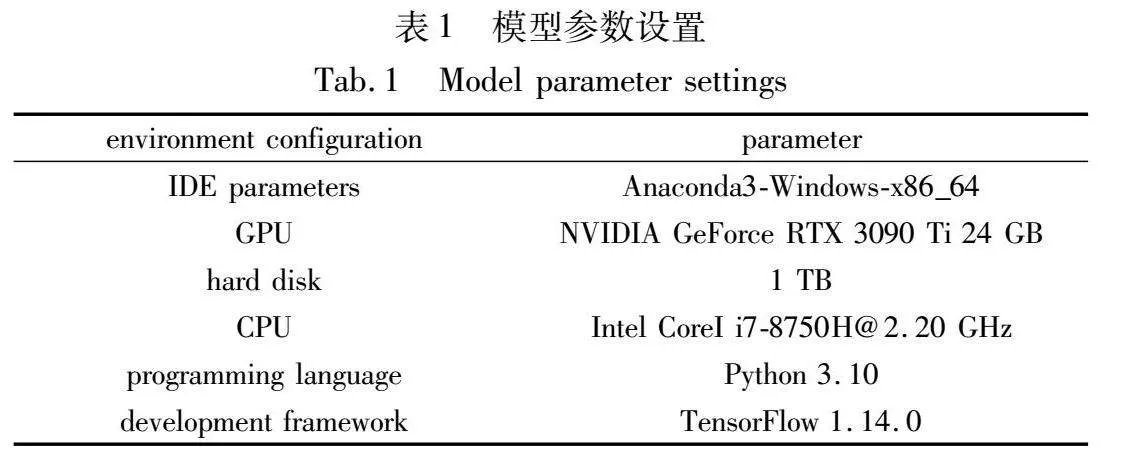
实验环境配置参数如表1所示。每个模型的实验结果均为十次实验结果的平均值。
实验中采用前12个节点进行预测,分别预测未来15 min、30 min、60 min的交通流速[29]。在本次实验中,将模型训练的迭代次数(epoch)设置为100,批量大小(batch size)设置为64,同时优化器(optimizer)选择了AdamW,损失函数(loss function)使用的是MAE指标。实验中的学习率为动态学习率[30],如式(1)所示。
newepochlr=startlr×[epochstepsize](13)
其中:newepochlr代表对应迭代次数的学习率;startlr代表模型训练时的初始学习率;为每次更新学习率的乘法因子;[]为向下取整运算;stepsize为更新学习率的步长。初始学习率startlr设置为0.001,乘法因子设置为0.999,更新步长stepsize设置为10。这里的初始学习率startlr、乘法因子以及更新步长stepsize均是根据文献[30]来进行设置的,同时也通过采用控制变量法进行对比实验,验证了这些参数的设置能够使得模型取得最好的结果。此外,这些参数被设置后,再次通过使用控制变量法进行实验,然后选取对比实验中结果最佳状态下的批量大小。
在两个真实世界的流量数据集上进行了实验,简要介绍如下:
a)METR-LA。该数据为从洛杉矶县的高速公路上的检测器上收集的交通速度[31]数据。每5 min记录一次每个节点的交通速度,本文使用的数据的时间跨度为2020年3月1日至2020年6月30日,时间为4个月。时间片总数为34 272个。
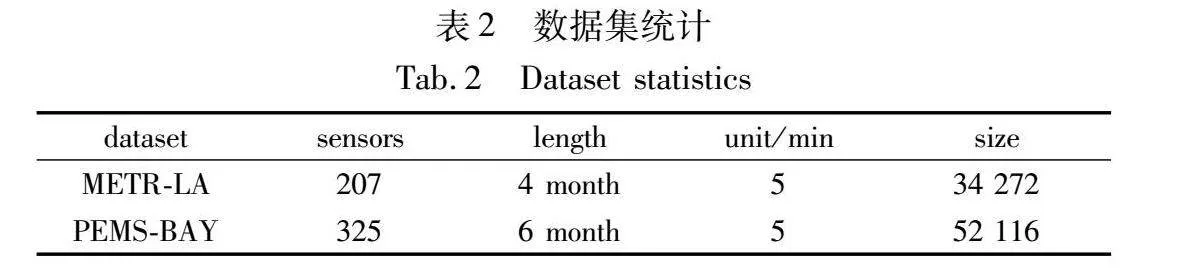
b)PEMS-BAY。该数据集来自加州交通部(Caltrans)的性能测量系统(PeMS)[32]。本文使用的数据来自湾区的325个传感器,时间跨度为2020年1月1日至2020年5月31日,为期6个月。同样该数据每5 min被记录一次,包含了52 116个时间切片。表2展示了两个数据集的关键信息。
3.2 评估指标
为了能够确保最终的实验结果更加具有客观性,在选取性能指标上主要包括平均绝对误差(mean absolute error, MAE)、平均绝对误差百分比(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)三部分。
评价指标计算公式如式(14)~(16)所示。
MAE=1n∑ni=1|yi-i|(14)
RMSE=1n∑ni=1(yi-i)2(15)
MAPE=1n∑ni=1yi-iyi×100%(16)
其中:yi代表实际的客流量数据;i代表预测的客流量数据;n为样本数量。上述评估指标的值越小,说明模型得到的交通流预测效果越好。
3.3 模型性能比较
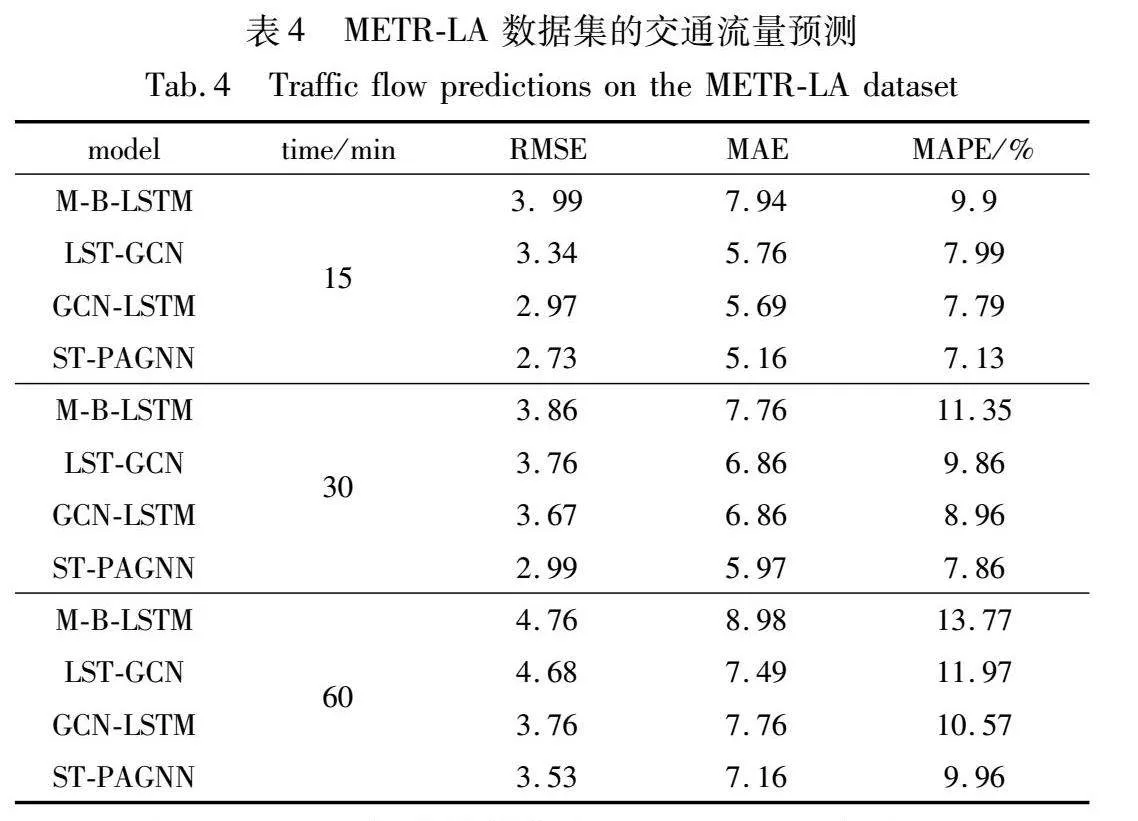
为了验证该模型的优越性,设计了一组比较实验。其中,比较模型包括M-B-LSTM[22]、LST-GCN[24]和GCN-LSTM[25]。
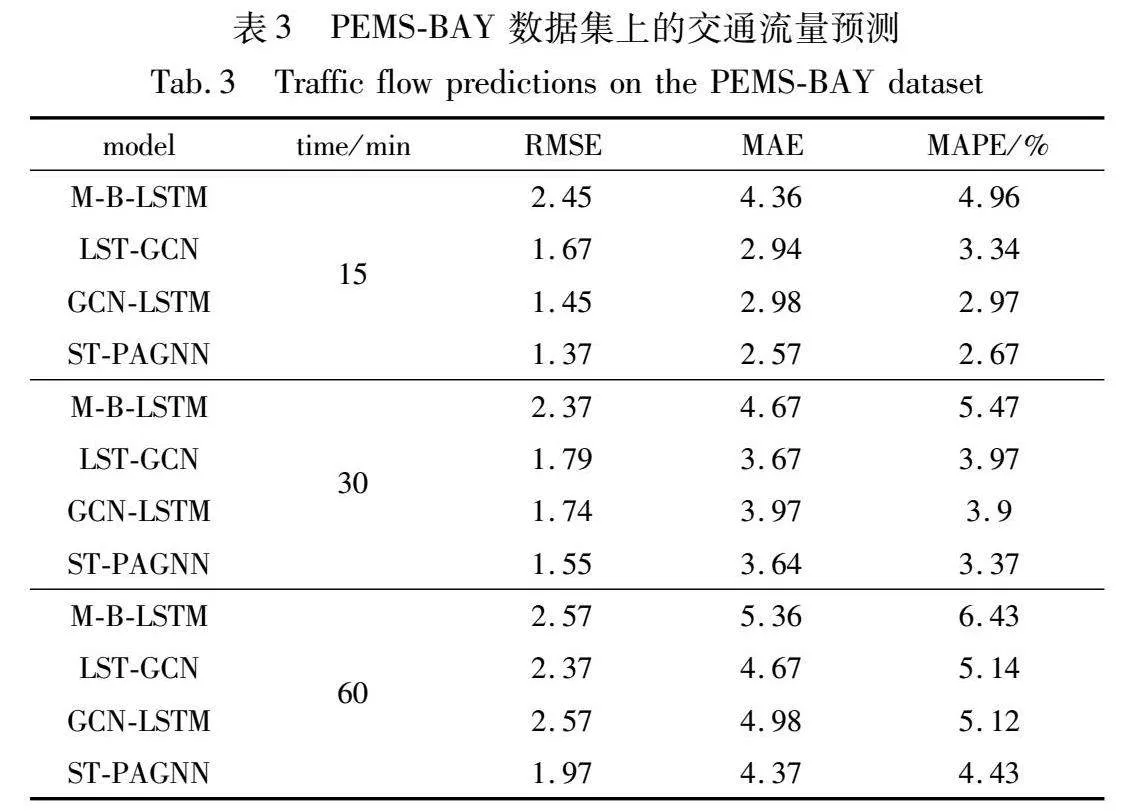
表3、4分别显示了在数据集PEMS-BAY和METR-LA下的预测结果。本文对提前15 min、30 min和60 min的预测结果进行了平均,并突出显示了每种设置下的最佳结果。
由表3、4可知,实验数据集为PEMS-BAY时,在15 min预测步长下,基线模型中表现最好的是GCN-LSTM,相较于该模型,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.08、0.41和0.3百分点;在30 min预测步长下,基线模型中整体上表现较好的是GCN-LSTM,相较于该模型,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.19、0.33和0.53百分点;在60 min预测步长下,基线模型中整体上表现较好的是LST-GCN,相较于该模型,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.40、0.30和0.71百分点。实验数据集为METR-LA时,在15 min、30 min以及60 min预测步长时,基线模型中GCN-LSTM均表现较好。在15 min预测步长下,相较于GCN-LSTM,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.24、0.53和0.66百分点;在30 min预测步长下,相较于GCN-LSTM,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.68、0.89和1.10百分点;在60 min预测步长下,相较于GCN-LSTM,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.23、0.60和0.61百分点。实验结果表明,ST-PAGNN在所有情况下均表现良好,展现出模型良好的表现能力。
3.4 交通流预测的性能分析
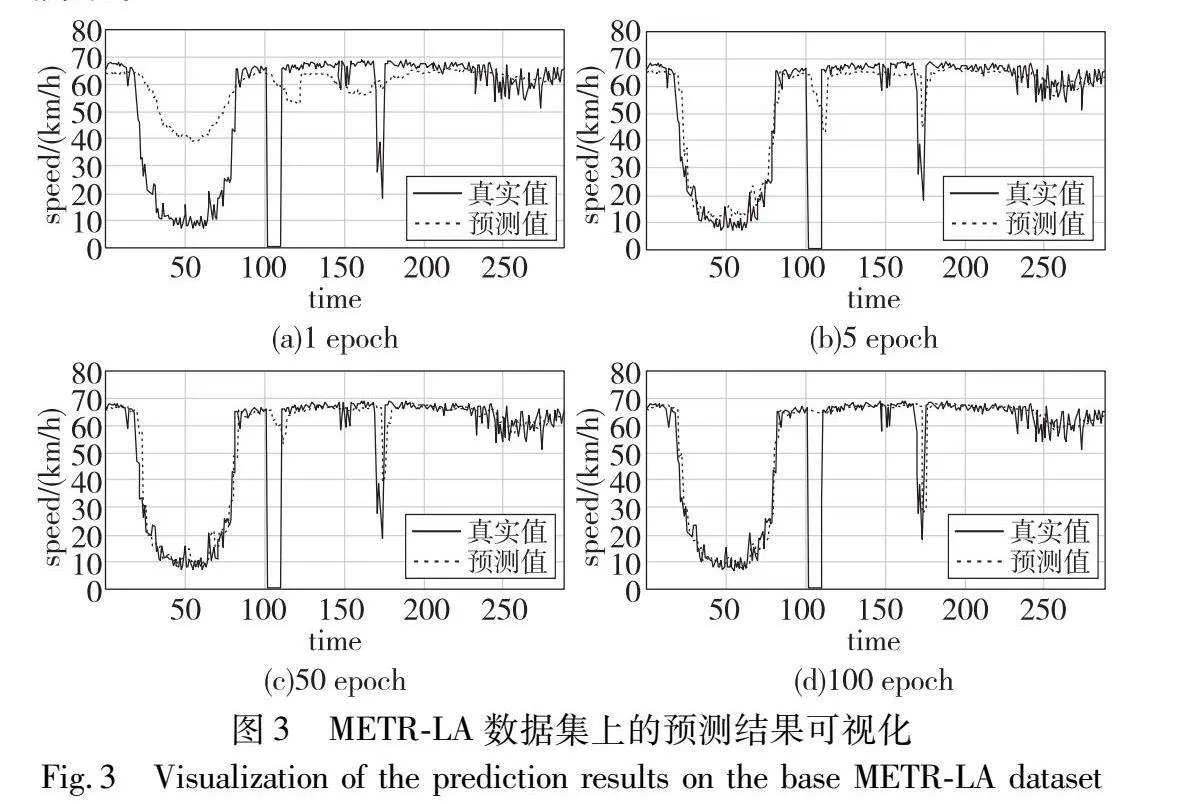
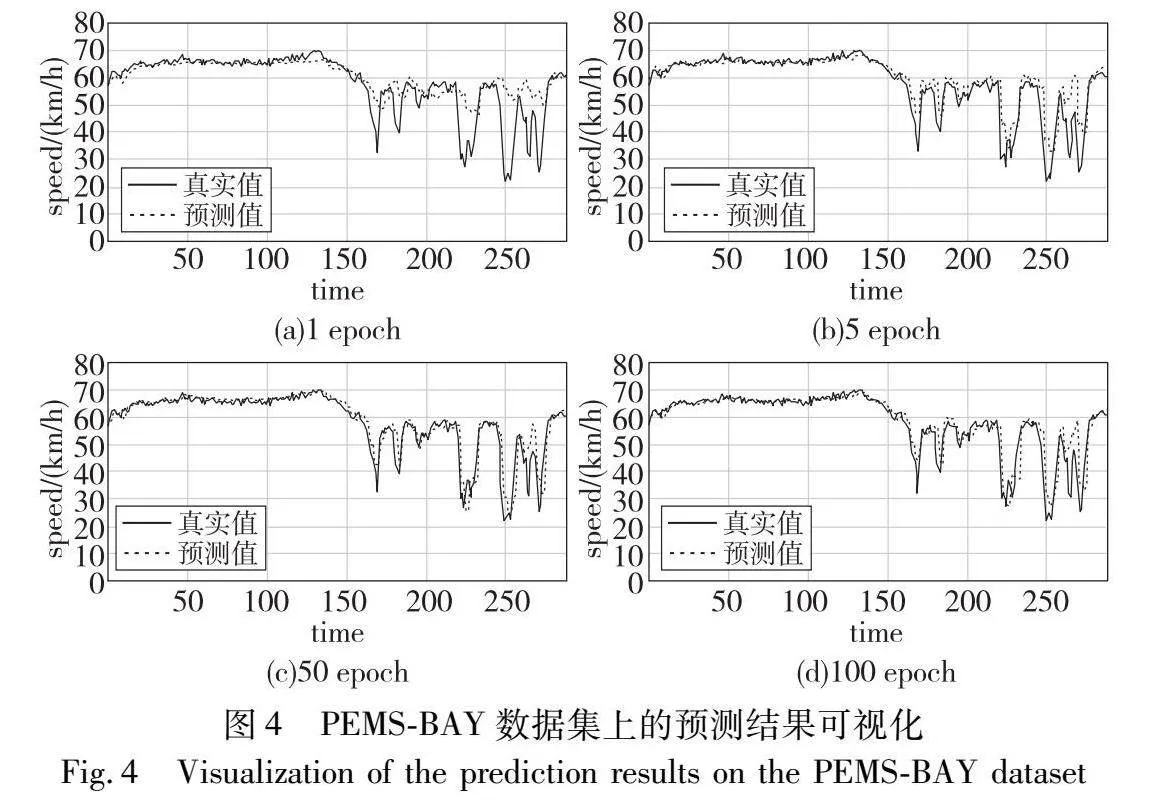
为了展示所提模型处理复杂交通情况的能力,在两个真实数据集上进行案例研究。从每个数据集分别随机选择一个交通传感器节点,时间间隔设置为5 min,利用ST-PAGNN获得交通流预测值,并将其与每个时间段的真实值进行对比,在METR-LA和PEMS-BAY数据集上得到的可视化结果如图3、4所示。
图3中,提出模型在早期训练阶段(1个epoch)表现不佳,经过5个训练epoch后,该模型整体上表现良好,但仍然不能很好地适应一些突变情况,如175个时间间隔附近。幸运的是,当执行50个epoch后,该模型的预测能力被继续提升,且在100个epoch后几乎可以完美地接近真实值。值得注意的是,该传感器在第100个时间间隔附近存在一些缺失值(图中显示的数值为零)。经过100个训练epoch后,提出模型能够通过合理的预测来有效弥合这些缺失值的差距。
图4中,对于从PEMS-BAY采样的节点,真实值的曲线非常复杂,尤其是在末端。同样,提出的模型能够快速学习以获得接近真实值的预测结果,表明该模型可以有效地处理复杂的交通流量预测问题。
3.5 空间依赖性建模分析
为了验证引入位置注意力机制的合理性,ST-PAGNN分别与引入无位置注意力的模型和未引入注意力的模型进行实验对比,实验数据集为METR-LA,如表5所示。
实验结果表明,引入位置注意力的ST-PAGNN使得模型在RMSE、MAE和MAPE指标上均有所降低,例如,在15 min预测步长下,相较于引入无位置注意力机制的模型,ST-PAGNN在RMSE、MAE和MAPE指标分别降低了0.15、0.43和0.67百分点。引入位置注意力机制的ST-PAGNN可以更好地捕捉城市道路网络中交通节点的空间依赖关系,从而使得交通流预测效果得以提升。
3.6 时间依赖性建模分析
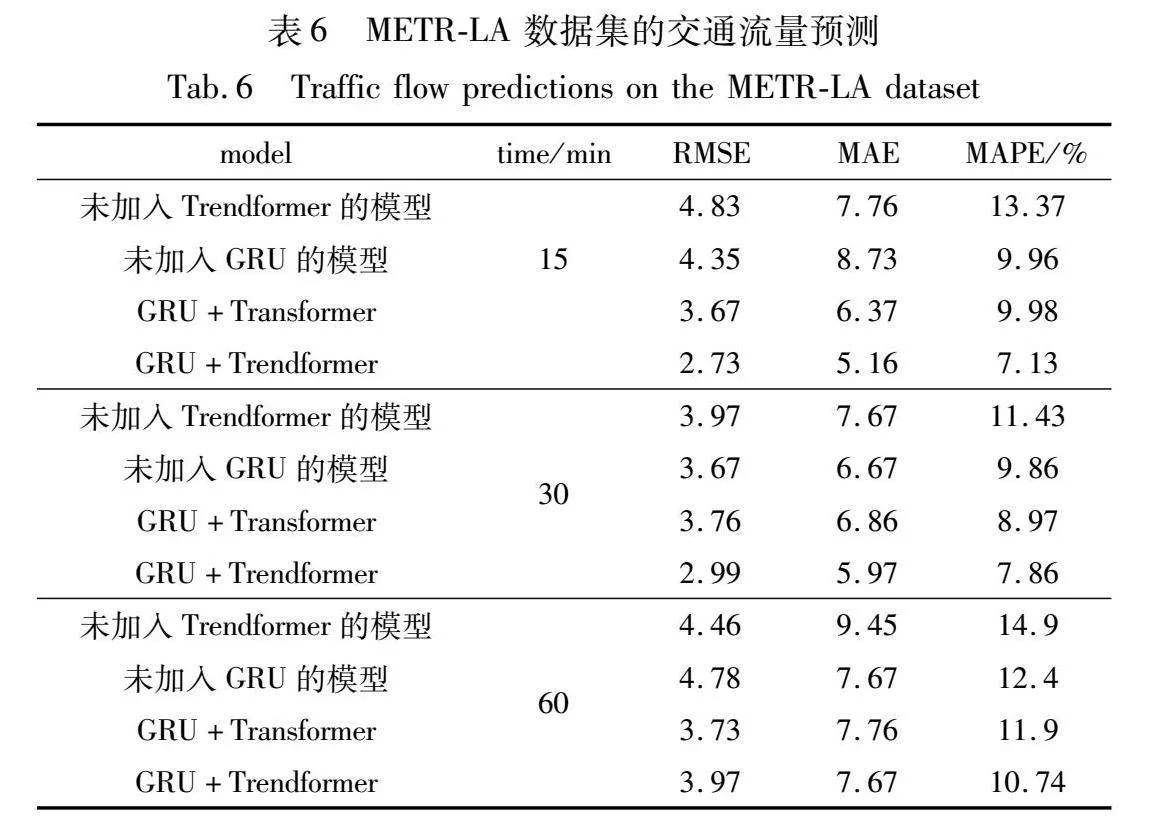
为了验证GRU+Trendformer构建的合理性,ST-PAGNN分别与未加入Trendformer、未加入GRU和GRU+Transformer进行实验对比,实验数据集为METR-LA,如表6所示。
实验结果表明,引入位置注意力机制的GRU+Trendformer使得模型在RMSE、MAE和MAPE指标上均有所降低,例如,在15 min预测步长下,相较于对比模型中表现较好的GRU+Transformer而言,引入位置注意力机制的GRU+Trendformer在RMSE、MAE和MAPE指标方面分别降低了0.94、1.21和2.85百分点。GRU层能够捕捉时间依赖,Trendformer层可以捕捉长期时间依赖,引入带有Trendformer层的门控递归神经网络的ST-PAGNN可以更好地捕捉交通流序列在时间维度上的局部和全局信息,从而使得交通流预测效果得以提升。
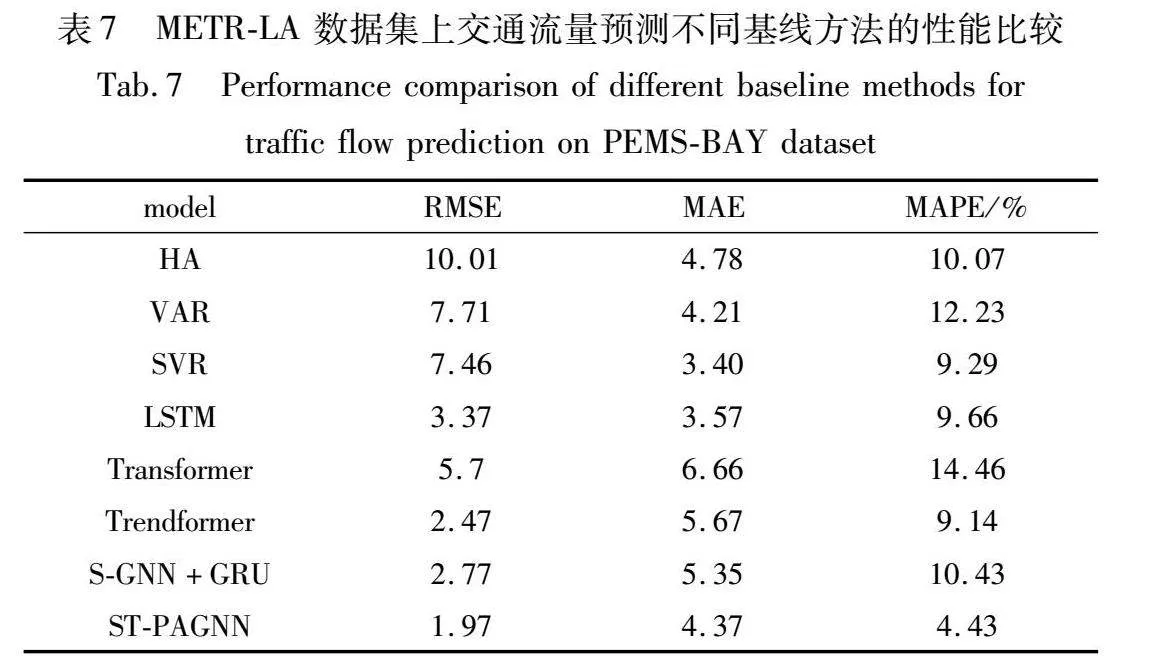
为了测试不同基线和模型的整体性能,本文测试了Trendformer在RMSE、MAE和MAPE三种指标上的精度,表7为各模型在PEMS-BAY数据集上对60 min时间步长的预测结果。LSTM相对比VAR和SVR等传统的机器学习算法,取得了良好的效果,这说明LSTM给本文的模型提供了时空相关性。与改进的Trendformer相对比,Transformer在RMSE、MAE和MAPE三个指标上,分别下降了2.11%,2.99%和1.59%,这说明Trendformer相比Transformer能够提供时空自适应学习以更好地捕获数据的时空相关性。另外对ST-PAGNN各个组成部分进行消融实验,对于S-GNN+GRN和Trendformer而言,ST-PAGNN在RMSE、MAE和MAPE指标上降低了0.80,0.98,6百分点和0.50,1.30和4.71百分点。当结合三种算法的时候,三个指标的误差都有所下降。这验证了Trendformer能够很好地捕捉交通数据的时空相关性,同时在交流预测任务中具有普遍的实用性和有效性。
4 结束语
虽然目前已有一些关于预测未来交通流量的研究,但其中大多数研究在建立空间和时间依赖关系模型方面存在一定的局限性。因此,提出了一种新的时空图神经网络框架来解决交通流预测问题。通过实验验证了所提方法的有效性。通过以上分析和描述,可以得出以下结论:a)如果图神经网络带有位置注意力机制,那么据此能够对城市道路网络中交通节点的空间依赖关系进行捕捉;b)利用带有转换层的门控递归神经网络可以捕捉交通流序列在时间维度上的局部和全局信息。这有效证明了所提框架在解决交通预测问题方面的有效性和优越性。
然而,交通网络与其他类型的网络在结构和动态特性上存在许多差异。因此,直接将该模型应用于其他网络结构或应用场景是不够严谨的。为了更好地理解和利用这种时空模型,未来将在进一步分析不同网络的特征和动态的基础上,尝试将其优势应用于对社交网络的分析和预测任务中。
参考文献:
[1]周楚昊, 林培群. 基于多通道Transformer的交通量预测方法[J]. 计算机应用研究, 2023, 40(2): 435-439. (Zhou Chuhao, Lin Peiqun. Traffic flow prediction method based on multi-channel Transformer[J]. Application Research of Computers, 2023, 40(2): 435-439.)
[2]Li Mengzhang, Zhu Zhanxing. Spatial-temporal fusion graph neural networks for traffic flow forecasting[C]// Proc of AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2021: 4189-4196.
[3]刘卫明, 罗全成, 毛伊敏, 等. 基于Spark和AMPSO的并行深度卷积神经网络优化算法[J]. 计算机应用研究, 2023, 40(10): 2957-2966. (Liu Weiming, Luo Quancheng, Mao Yimin,et al. Pa-rallel deep convolutional neural network optimization algorithm based on Spark and AMPSO[J]. Application Research of Computers, 2023, 40(10): 2957-2966.)
[4]Wang Haoxiang, Smys S. Big data analysis and perturbation using data mining algorithm[J]. Journal of Soft Computing Paradigm, 2021, 3(1): 19-28.
[5]刘起东, 刘超越, 邱紫鑫, 等. 基于时间感知Transformer的交通流预测方法[J]. 计算机科学, 2023, 50(11): 88-96. (Liu Qidong, Liu Chaoyue, Qiu Zixin,et al. Time-aware Transformer for traffic flow forecasting [J]. Computer Science, 2023, 50(11): 88-96.)
[6]Shu Wanneng, Cai Ken, Xiong N N. A short-term traffic flow prediction model based on an improved gate recurrent unit neural network[J]. IEEE Trans on Intelligent Transportation Systems, 2021, 23(9): 16654-16665.
[7]Ma Xiaolei, Dai Zhuang, He Zhengbing,et al. Learning traffic as ima-ges: a deep convolutional neural network for large-scale transportation network speed prediction[J]. Sensors, 2017, 17(4): 818.
[8]Fu Rui, Zhang Zuo, Li Li. Using LSTM and GRU neural network methods for traffic flow prediction[C]// Proc of the 31st Youth Academic Annual Conference of Chinese Association of Automation. Piscataway, NJ: IEEE Press, 2016: 324-328.
[9]Li Chensheng, Qin Xiaowei, Xu Xiaodong,et al. Scalable graph convolutional networks with fast localized spectral filter for directed graphs[J]. IEEE Access, 2020, 8: 105634-105644.
[10]Liu Yanbei, Wang Qi, Wang Xiao,et al. Community enhanced graph convolutional networks[J]. Pattern Recognition Letters, 2020, 138: 462-468.
[11]Yu Bing, Yin Haoteng, Zhu Zhanxing. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting[C]// Proc of the 27th International Joint Conference on Artificial Intelligence. [S.l.]: International Joint Conferences on Artificial Intelligence Organization, 2017: 3634-3640.
[12]Guo Shengnan, Lin Youfang, Feng Ning,et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[C]// Proc of the 33rd AAAI Conference on Artificial Intelligence and the 31st Innovative Applications of Artificial Intelligence Confe-rence and the 9th AAAI Symposium on Educational Advances in Artificial Intelligence. Palo Alto, CA: AAAI Press, 2019: 922-929.
[13]Zhao Ling, Song Yujiao, Zhang Chao,et al. T-GCN: a temporal graph convolutional network for traffic prediction [J]. IEEE Trans on Intelligent Transportation Systems, 2020, 21(9): 3848-3858.
[14]Seo Y, Defferrard M, Vandergheynst P,et al. Structured sequence modeling with graph convolutional recurrent networks[M]// Cheng Long, Leung A C S, Ozawa S. Neural Information Processing. Cham: Springer International Publishing, 2018: 362-373.
[15]Wang Yunbo, Long Mingsheng, Wang Jianmin,et al. PredRNN: recurrent neural networks for predictive learning using spatiotemporal LSTMs[C]// Proc of the 31st International Conference on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2017: 879-888.
[16]倪庆剑, 彭文强, 张志政, 等. 基于信息增强传输的时空图神经网络交通流预测[J]. 计算机研究与发展, 2022, 59(2): 282-293. (Ni Qingjian, Peng Wenqiang, Zhang Zhizheng,et al. Spatial-temporal graph neural network for traffic flow prediction based on information enhanced transmission[J]. Journal of Computer Research and Development, 2022, 59(2): 282-293.)
[17]Li Cong, Xu Pei. Application on traffic flow prediction of machine learning in intelligent transportation[J]. Neural Computing and Applications, 2021, 33(2): 613-624.
[18]Toan T D, Truong V H. Support vector machine for short-term traffic flow prediction and improvement of its model training using nearest neighbor approach[J]. Transportation Research Record, 2021, 2675(4): 362-373.
[19]Hao Miao, Shen Jiaxing, Cao Jiannong,et al. MBA-STNet: Bayes-enhanced discriminative multi-task learning for flow prediction[J]. IEEE Trans on Knowledge and Data Engineering, 2023, 35(7): 7164-7177.
[20]Peng Jiaxin, Xu Yongneng, Wu Menghui. Short-term traffic flow forecast based on ARIMA-SVM combined model[M]// Wang Wuhong, Wu Jianping, Jiang Xiaobei,et al. Green Transportation and Low Carbon Mobility Safety. International Conference on Green Intelligent Transportation System and Safety. Singapore: Springer Nature Singapore, 2021: 287-300.
[21]Kashyap A A, Raviraj S, Devarakonda A,et al. Traffic flow prediction models–a review of deep learning techniques[J]. Cogent Engineering, 2022, 9(1): 2010510.
[22]Qu Zhaowei, Li Haitao, Li Zhihui,et al. Short-term traffic flow forecasting method with M-B-LSTM hybrid network[J]. IEEE Trans on Intelligent Transportation Systems, 2020, 23(1): 225-235.
[23]Zheng Haifeng, Lin Feng, Feng Xinxin,et al. A hybrid deep learning model with attention-based conv-LSTM networks for short-term traffic flow prediction[J]. IEEE Trans on Intelligent Transportation Systems, 2020, 22(11): 6910-6920.
[24]Han Xu, Gong Shicai. LST-GCN: long short-term memory embedded graph convolution network for traffic flow forecasting[J]. Electro-nics, 2022, 11(14): 2230.
[25]Liu Daoguang, Hui Shen, Li Li,et al. A method for short-term traffic flow forecasting based on GCN-LSTM[C]// Proc of International Conference on Computer Vision, Image and Deep Learning. Pisca-taway, NJ: IEEE Press, 2020: 364-368.
[26]Chauhan N S, Kumar N. Traffic flow forecasting using attention enabled Bi-LSTM and GRU hybrid model[C]// Proc of International Conference on Neural Information Processing. Singapore: Springer Nature Singapore, 2022: 505-517.
[27]Huang Lei, Zhu Feng, Li Zhiheng. Trendformer: trend adaptive transformer for traffic flow prediction[C]// Proc of the 5th International Conference on Data Science and Information Technology. Piscataway, NJ: IEEE Press, 2022: 1-6.
[28]Wang Chunzhi, Wang Lu, Wei Siwei,et al. STN-GCN: spatial and temporal normalization graph convolutional neural networks for traffic flow forecasting[J]. Electronics, 2023, 12(14): 3158.
[29]贺文武, 裴博彧, 毛国君, 等. 基于轻量时空图卷积模型的路网交通流预测[J]. 铁道科学与工程学报, 2022, 19(9): 2552-2562. (He Wenwu, Pei Boyu, Mao Guojun,et al. Traffic flow forecasting based on lightweight spatial-temporal graph convolution networks model[J]. Journal of Railway Science & Engineering, 2022, 19(9): 2552-2562.)
[30]Smith L N. Cyclical learning rates for training neural networks [C]// Proc of IEEE Winter Conference on Applications of Computer Vision. Piscataway, NJ: IEEE Press, 2017: 464-472.
[31]Yuan Lilian, Fang Weilin, Xiao Hongbo,et al. Short-term traffic flow prediction by graph deep learning with spatial temporal modeling[C]// Proc of the 2nd International Conference on Electronic Information Technology and Smart Agriculture. Piscataway, NJ: IEEE Press, 2022: 172-177.
[32]Wang Luxuan, Bai Lei, Li Ziyue,et al. Correlated time series self-supervised representation learning via spatiotemporal bootstrapping[C]// Proc of the 19th International Conference on Automation Science and Engineering. Piscataway, NJ: IEEE Press, 2023: 1-7.
[33]Bai Lei, Yao Lina, Li Can,et al. Adaptive graph convolutional recurrent network for traffic forecasting[C]// Proc of the 34th International Conference on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2020: 17804-17815.
