AGCFN:基于图神经网络多层网络社团检测模型

摘 要：基于图神经网络的多层网络社团检测方法面临以下两个挑战。一是如何有效利用多层网络的节点内容信息，二是如何有效利用多层网络的层间关系。因此，提出多层网络社团检测模型AGCFN（autoencoder-enhanced graph convolutional fusion network）。首先通过自编码器独立提取每个网络层的节点内容信息，通过传递算子将提取到的节点内容信息传递给图自编码器进行当前网络层节点内容信息与拓扑结构信息的融合，从而得到当前网络层每个节点的表示，这种方法充分利用了网络的节点内容信息与拓扑结构信息。对于得到的节点表示，通过模块度最大化模块和图解码器对其进行优化。其次，通过多层信息融合模块将每个网络层提取到的节点表示进行融合，得到每个节点的综合表示。最后，通过自训练机制训练模型并得到社团检测结果。与6个模型在三个数据集上进行对比，ACC与NMI评价指标有所提升，验证了AGCFN的有效性。

关键词：多层网络；社团检测；图神经网络；自编码器；自监督学习

中图分类号：TP301.6 文献标志码：A 文章编号：1001-3695（2024）10-007-2926-06

doi：10.19734/j.issn.1001-3695.2024.03.0056

AGCFN： multiplex network community detection model based on graph neural network

Chen Long1a， Zhang Zhenyu1b， Li Xiaoming2， Bai Hongpeng3

（1. a.College of Software， b.College of Information Science & Engineering， Xinjiang University， rümqi 830000， China; 2.College of International Business， Zhejiang Yuexiu University， Shaoxing Zhejiang 312000， China; 3.College of Intelligence & Computing， Tianjin University， Tianjin 300000， China）

Abstract：Multiplex network community detection methods based on graph neural network face two main challenges. Firstly， how to effectively utilize the node content information of multiplex network; and secondly， how to effectively utilize the interlayer relationships in multiplex networks. Therefore， this paper proposed the multiplex network community detection model AGCFN. Firstly， the autoencoder independently extracted the node content information of each network layer and passed the extracted node content information to the graph autoencoder for fusing the node content information of the current network layer with the topology information through the transfer operator to obtain the representation of each node of the current network layer， which made full use of the node content information of the network and the topology information of the network. The modularity maximization module and graph decoder optimized the obtained node representation. Secondly， the multilayer information fusion module fused the node representations extracted from each network layer to obtain a comprehensive representation of each node. Finally， the model under went training， and it achieved community detection results through a self-training mechanism. Comparison with six models on three datasets demonstrate improvements in both ACC and NMI evaluation metrics， thereby va-lidating the effectiveness of AGCFN.

Key words：multiplex network; community detection; graph neural network; autoencoder; self-supervised learning

0 引言

现实生活中许多复杂的系统都可以抽象成一个网络，如社交网络［1］、学术合作网络［2］、商品推荐网络［3］等。网络的一个显著特征就是它们的社团结构。社团检测研究目标是将网络划分成为不同的社团结构，同一个社团中的节点具有相似的特征或功能。当前有许多社团检测方法被提出，但它们大多数仅适用于单层网络［4，5］。然而实际上，很多网络通常由多个层次组成，每一个层次都反映了网络中不同类型的关系［6］。比如，在引文网络中，两篇论文的连接可以是不同类型的，如两篇论文因为同一个作者而连接，或两篇论文因为引用关系而连接［2］。在电影网络中，两个电影可以因为有共同的演员相连，也可以因为是共同的导演相连。这两个网络都可以分成两个层次，在两个层次中，节点是相同的，而节点之间的边是不同的。

许多文献提出了不同的社团检测方法，如文献［7，8］，这些方法通过将多层网络合并为一个单层网络，然后使用单层网络社团检测方法来发现社团结构。然而这类方法忽略了多层网络的层间关系。比如在引文网络的引用层中，仅知道论文的引用关系不能很好地将它们进行社团划分，但是如果这些论文在另一个层次中有通过作者相连接，则确定这些论文的主题就会变得容易，因为作者的研究方向通常是确定的。因此，为了克服这个问题，文献［10～12］进行了新的研究，将多层网络层间关系进行提取，然而这类方法没有利用网络中丰富的节点内容信息。以引文网络为例，如果利用论文中的关键词，则对它们进行社团划分也会变得容易［2］。文献［2，12］利用了节点内容信息来进行多层网络社团检测，并取得了一定的成果。然而，受到图卷积网络层数的限制，这些方法在提取节点内容信息并将其与网络拓扑结构信息融合方面存在一些不足之处。换言之，这些方法未能充分发挥网络节点内容信息和拓扑结构信息的潜在优势。因此，本文提出了一种能够同时考虑多层网络层间信息和节点内容信息的无监督多层网络社团检测模型AGCFN（autoencoder-enhanced graph convolutional fusion network）。

1 相关研究

目前主流多层网络社团检测方法集中于基于展平的方法、直接方法和基于聚合的方法［13］。

基于展平的方法的核心思想是采用基于权重的方式将多层网络转换为单层网络的形式，然后在上面使用基于单层网络的社团检测方法来发现社团结构。文献［7］将多层网络展平为一个单层网络，然后利用标签传播算法进行社团检测，具体来说，它们使用一种新的目标函数和基于约束标签传播的优化策略来自动识别社团。文献［8］提出了一种改进的粒子竞争模型，通过引入本地化度量，使模型可以正确确定社团数量。同时，该模型通过构建一个扩展邻接矩阵来表示多层网络，能够很好地进行社团检测工作。基于展平的方法简单直观，易于理解和实现，常常能够使用单层网络社团检测方法的成果。然而这种方法忽略了不同层次的信息差异，可能导致对多层网络中复杂关系的损失，不适用于包含丰富层次信息的网络。

基于聚合的方法从多层网络的每一个单一的层中提取信息，然后将其聚合成综合的节点特征，以此来进行多层网络的社团检测工作。这类方法的核心思想是将多个网络层上的信息进行整合，从而获得更优的社团结构［9，10，12］。如文献［9］提出一种用于多层网络社团检测的图卷积融合模型GCFM，通过设计一个多尺度融合网络，融合节点在不同层和不同尺度上的编码来学习节点嵌入表示。文献［12］提出了一种基于图神经网络的多层网络社团检测模型 MGCAE，首先引入互信息来对不同层的节点进行局部表示和全局表示，以此探索不同网络层之间的关系。其次通过结合伯努利-泊松损失和模块化最大化损失来共同优化原始邻接矩阵的重建，最终得到更好的节点嵌入表示。

直接方法指的是直接在多层网络上进行社团检测的方法，这种方法同时对每个网络层进行特征提取，从而检测出社团结构。如文献［14］将模块度指标进行扩展，提出了新的模块度指标QM，用于代替原本的模块度最大化指标，使其可以适应多层网络社团检测。

上述方法对于多层网络社团检测都有推动作用，然而也存在着一些问题，如利用多层网络的节点内容信息不充分、不能充分融合多层网络层间信息等。

通过分析上述方法，本文提出了AGCFN模型。首先通过在多层网络的每一层构建深度自编码器模块与图自编码器模块MGCAE，获得网络中每个节点在每个网络层的表示，使模型有效学习网络的节点内容信息与拓扑结构信息；其次，通过模块度最大化模块对每个节点的表示进行优化，同时，MGCAE解码器部分对提取到的节点表示进行重构，使其恢复到每个网络层的邻接矩阵的形式，对于获取的每个网络层的节点的表示，通过多层信息融合模块MIF进行融合，得到每个节点的综合表示；最后，通过自监督模块将各个模块统一在一个框架中，完成无须标签信息的多层网络社团检测任务。

2 基于图神经网络的多层网络社团检测模型

2.1 问题定义

假定一个多层网络G={G1，G2，…，GM}，其中Gm=（V，Em，X）。V={vi}i=1，…，N为具有N个节点的网络的节点集合。Em={（vi，vj）|1≤i，j≤N，i≠j}为多层网络第m个网络层的边集。X=［x1，x2，…，xN］为G的属性，其中xi为vi的属性。A={A1，A2，…，AM}为网络邻接矩阵的集合，Am=Euclid ExtraaBpN×N表示网络第m层的邻接矩阵。其中Amij=1表示节点vi与vj之间存在边，否则Amij=0。

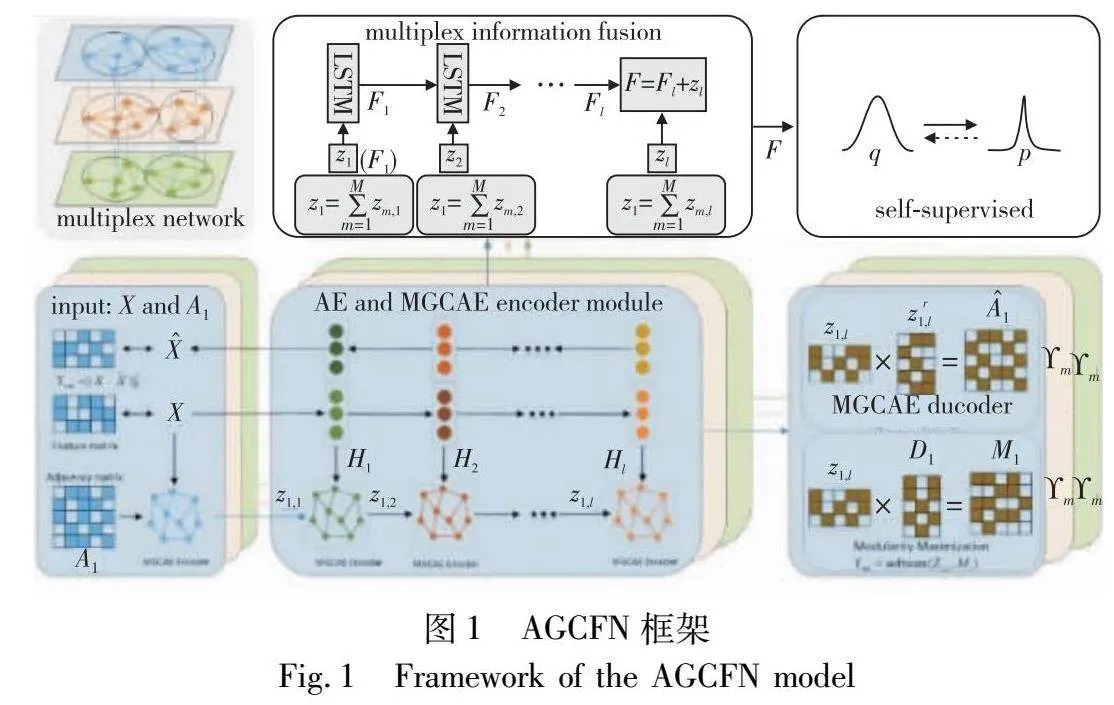
2.2 模型框架

本文模型AGCFN的框架如图1所示。模型主要包含自编码器模块、多层图卷积自编码器模块、模块度最大化模块、多层信息融合模块和自监督模块。

2.2.1 多层自编码器模块

虽然普通的图卷积网络可以自动融合节点内容信息与拓扑结构信息，但是这种融合仅仅将节点内容信息直接输入到图卷积网络中与拓扑结构进行卷积，可能会使模型忽略节点内容信息中的细节部分，并且会使得图卷积层数不能加深，容易出现过拟合问题。换言之，其对节点内容信息与拓扑结构信息利用不够充分。为了充分利用节点内容信息，使用自编码器对每个网络层的节点内容信息进行提取。为了降低算法的复杂性，本文使用线性结构的自编码器［15］。

在多层网络中，节点的内容信息是一致的，而每一层的拓扑结构信息不同，因此对于每一个网络层，本文都设置了自编码器模块用来提取内容信息，而后通过传递算子传递给对应的MGCAE层进行卷积操作。

假设多层网络具有M个网络层，每一个网络层具有L个层次结构的自编码器，则对于第m个网络层的第l层自编码器提取到的内容信息，可由下式得到：

H（）m=（W（）m，eH（－1）m+b（）m，e）（1）

其中：表示激活函数；W（）m，e和b（）m，e分别表示编码器部分第层的权重矩阵和偏置。特别地，对于原始输入，使用网络的节点内容信息X。与编码器对应的是解码部分，公式如下：

H（）m=（W（）m，dH（－1）m+b（）m，d）（2）

其中：W（）m，d和b（）m，d分别表示解码器部分第层的权重矩阵和偏置。第m个网络层解码器部分的输出H（L）m=X^是对原始节点内容信息的重构，因此可以得到如下目标函数：

m，res=‖X－X^‖2F（3）

其中：‖·‖F表示矩阵的弗罗贝尼乌斯范数。因为多层网络共有M个层，因此，关于节点内容信息重构的总损失为

res=∑Mm=1m，res（4）

通过优化该目标函数，可以使算法学习到更加优质的节点内容信息。

2.2.2 多层图卷积自编码器模块

自编码器能够有效学习多层网络的节点内容信息，但是却不能利用网络的拓扑结构信息。经典的图卷积网络在利用两种信息上具有优势，然而为了缓解图卷积层不能加深导致模型提取不到更好的节点表示的问题，本节提出多层图卷积自编码器模块MGCAE，通过传递算子将不同尺度自编码器提取到的节点内容信息传递给对应的图自编码器层，以完成对多层网络每个网络层的节点内容信息与拓扑结构信息的聚合操作，使得模型可以捕捉到更加丰富的全局信息。

对于多层网络第m个网络层，MGCAE的编码器第l层学习到的表示Z（）m可以通过下式得到：

Z（）m=（D－12mAmD－12mZ（－1）mW（－1）m）（5）

其中：表示激活函数；D－12mAmD－12m表示关于第m个网络层的邻接矩阵的规范化拉普拉斯矩阵；Am=Am+I表示第m个网络层的邻接矩阵加单位矩阵。为了将自编码器学习到的对应层的节点内容信息也考虑进来，从而增强MGCAE的学习能力，使用传递算子将Z（－1）m和H（－1）m结合在一起。结合后的新的表示为

Z（－1）m=（1－ε）Z（－1）m+εH（－1）m（6）

其中：ε为平衡参数，其值设置为0.5。通过这种传递方法，将自编码器与MGCAE逐层连接在一起。本文使用Z（－1）m作为第m个网络层的MGCAE编码器的第层的输入，生成的表示Z（）m如下：

Z（）m=（D－12mAmD－12mZ（－1）mW（－1）m）（7）

特别地，对于每个网络层的MGCAE的第一层的输入，使用节点内容信息和当前网络层的邻接矩阵。

在MGCAE的解码器部分，使用如下公式对得到的中间表示Z（）m进行重构，使其恢复成邻接矩阵的形式：

A^m=sigmod（Z（L）m（Z（L）m）T）（8）

其中：A^m表示重构的第m层的邻接矩阵。对于每个网络层的重构损失，使用交叉熵损失函数：

m，adj=－1N∑Ni=1 ∑Nj=1［Am（ij）log（A^m（ij））+

（1－Am（ij））log（1－A^m（ij））］（9）

根据式（9），每个网络层的MGCAE关于邻接矩阵重构总损失为

adj=∑Mm=1m，adj（10）

2.2.3 多层信息融合模块

对于多层网络的每个网络层，本文设计了自编码器模块与图自编码器模块进行网络节点内容信息与拓扑结构信息的融合，进而得到节点表示，并且自编码器与图自编码器都是多尺度的，这样就会得到每个节点在每个网络层不同尺度的表示。又因为每个网络层的邻接矩阵都代表了不同的连接类型，所以每个网络层得到的不同尺度的节点中间表示都是非常重要的。

为了将这些不同层不同尺度的中间表示进行融合，本文提出了一个多层信息融合模块MIF。具体来说，对于一个具有M个网络层的多层网络，因为没有先验信息决定每个网络层的重要程度，本文认为每个网络层提取到的信息同等重要，所以每个网络层的MGCAE的第层提取到的信息使用如下公式将它们进行融合：

Z（）=∑Mm=1Z（）m（11）

受到LSTM网络的启发，在得到了当前尺度的Z（）后，可以使用LSTM单元来整合不同尺度的F（），这样做的好处是可以全面学习不同尺度的中间表示。此外，只有一个单元的LSTM结构还具有简单高效的优势。首先，将第一层的LSTM输入设置为

F（1）=Z（1）（12）

其中：Z（1）为初始维度的表示。接下来，对于第l个维度的节点表示，将多尺度节点表示Z（－1）和F（－1）结合起来。使用如下公式进行计算：

F（）=LSTMCell（F（－1）+Z（－1））（13）

其中：LSTMCell表示的是LSTM单元。算法通过 LSTM 单元可以学到不同尺度特征之间的复杂关系，进而更好地融合这些信息。门控机制有助于模型选择性地关注和保留重要的多尺度信息，避免梯度消失或爆炸的问题，同时提供更强大的建模能力。

对于MIF最后一层的计算，直接将Z（）和F（）进行加和操作。

F=F（）+Z（）（14）

2.2.4 模块度最大化模块

在多层网络社团检测模型中，模块度是衡量社团结构的一个关键指标［16］，它衡量了网络中节点的社团归属度与随机网络的差异程度。模块度的最大化意味着将节点分配到不同的社团中，使得网络的内部连接密集，社团之间的连接稀疏，从而达到社团结构的优化目标。

为了优化模型学习到的网络节点嵌入表示，本文设计了一个多层模块度最大化模块，即为每个网络层都使用模块度最大化方法以确保节点嵌入保留了网络的社团结构。具体而言，在每个网络层都对图解码器部分重构的邻接矩阵计算模块度，以达到优化节点表示的目的。模块度定义如下：

Q=14m∑ni， j（Aij－didj2m）（HiHTj）（15）

其中：di和dj表示节点vi和vj的度。通过定义模块度矩阵B=［Bij］n×n，令Bij=Aij－didj2m，则有

Q=14m∑ni，j（Bij）（HiHTj）（16）

进一步化简可以得到

m，Mod=Tr（HTmBmHm）（17）

其中：Tr（·）表示矩阵的迹且Tr（HTH）=N。H表示节点的社团归属度矩阵，它的每一行都可以看做是节点对应的嵌入表示。接下来将H进行归一化，这样的好处是可以在保留网络社团结构的情况下得到更好的节点嵌入表示［17］。

由于与节点数量相比，社团的数量是非常少的，这种情况下如果以实际社团的个数作为嵌入维度，那么不足以学习到丰富的节点表示。因此，设计一个可学习的全连接层［4］。多层网络第m个网络层的模块度最大化模块损失可以表示为

m，Mod=Tr（HTmBmHm）（18）

其中：Hm=softmax（Z（）mC（）m）。最终关于模块度最大化模块总损失为

Mod=∑Mm=1Tr（HTmBmHm）（19）

2.2.5 自监督模块

通过多层信息融合模块，可以得到关于多层网络中每个节点的最终表示，这个表示融合了每个网络层的层内信息、层间信息和节点的内容信息。为了适应无标签的任务，使用自监督模块来进一步处理节点表示，并使用KL散度计算损失，用以指导算法自动更新。

首先，使用K-means算法寻找社团中心。确定社团中心后，对于第i个样本和第j个社团，本文使用Student’S-T［18］分布来计算函数分布，公式如下：

qij=（1+‖fi－μj‖2/α）－α+12∑j′（1+‖fi－μj‖2）－α+12（20）

其中： fi表示节点最终表示F（L）的第i行；μj表示由自编码器通过K-means方法得到的社团中心；α表示的是带宽参数，本文设置α的值为1。为了提高检测出社团的内聚性，使得最终表F在空间中的相似性更接近其所属的社团中心，将Q进一步计算，得到分布P。计算公式如下：

pij=q2ij/kj∑j′q2ij′/kj′（21）

其中：kj=∑iqij。得到分布P后，使用KL散度来衡量P与Q之间的差距：

KL=KL（P‖Q）=∑i ∑jpijlogpijqij（22）

进一步将计算的所有损失进行统一，得到了算法的损失函数：

=res+adj－λMod+ηKL（23）

其中：λ和η为超参数。本文最终以分布Q来进行社团检测，因为它包含了多层网络的综合信息。对于样本i，分配给社团j的计算公式为

gi=arg maxj qij（24）

其中：qij由式（20）得到。

2.2.6 复杂度分析

AGCFN模型的复杂度主要取决于多层网络的层数和MGCAE的层数。假设多层网络的层数为M，MGCAE模块深度为L，输入数据的维度为d，网络节点个数为N。自编码器模块的时间复杂度为O（Nd1d2…dL－1dLdLdL－1…d2d1），即O（Nd21d22…d2L）。MGCAE模块编码器的时间复杂度与邻接矩阵的边数|ε|呈线性关系，为O（|ε|d1d2…dL），解码器的时间复杂度取决于网络中节点的数量，为O（N）。模块度最大化模块的时间复杂度为O（N2）。对于多层信息融合模块，使用的LSTM单元的时间复杂度也为O（Nd21d22…d2L）。自监督机制的时间复杂度为O（NM+Nlog N）。综上所述，AGCFN的总时间复杂度为O（2Nd21d22…d2L+|ε|d1d2…dL+N2+NM+Nlog N）。

3 实验结果与分析

3.1 数据集

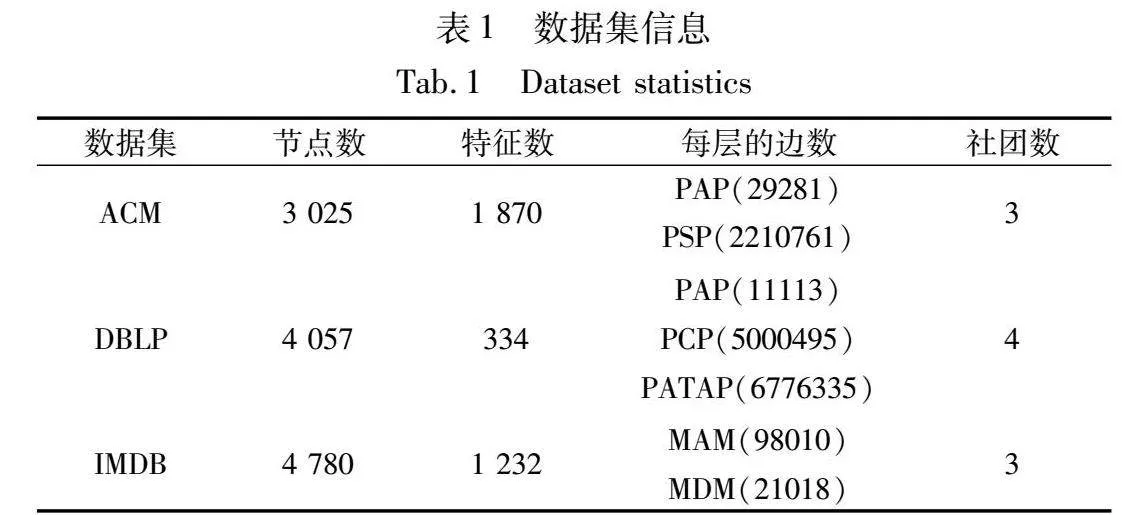
本文选取ACM、DBLP、IMDP三个数据集进行实验。数据集的具体细节如表1所示。

ACM和DBLP数据集是引文网络数据集，ACM数据集具有两个层次，第一层中节点的连接关系为同一作者，第二层的连接关系为相同主题。它的目标是将论文分为数据库、无线通信和数据挖掘三个社团。DBLP数据集的网络有三个层次，在三层网络中，节点之间的连接关系分别为同一作者、同一会议和作者所属团队。它的目标是将论文分为DM、AI、CV和NLP四个社团。IMDB数据集是一个关于电影网络的数据集，它具有两个层次，分别是通过相同导演相连接和通过相同演员连接。它的任务是将电影分为动作、喜剧和戏剧三个社团。

3.2 对比模型与评估指标

为了验证AGCFN的性能，实验将AGCFN与其他6个先进算法进行比较。GCFM［9］通过使用图卷积网络提取节点表示，而后将节点表示融合进行社团检测。MGCAE［12］通过对多层网络的节点拓扑结构信息进行增强，使用基于互信息的方式提取特征进行社团检测。GEAM［10］通过构建层对比学习模块，从每个网络层的局部和全局图视图对节点和图嵌入进行编码，并提出一种自关注自适应融合机制，通过多层融合学习节点表示的综合版本。GAE-avg［19］为GAE模型在多层网络社团检测的扩展。以上几种方法为基于聚合的方法。PMNE［20］是直接方法，在每个网络层上直接进行社团检测。PwMC［21］为展平方法，是一种参数加权的多层网络社团检测方法。

对于社团检测结果的评价指标，使用准确性度量（ACC）、归一化互信息（NMI）这两个广泛使用的指标。ACC是衡量模型在社团检测任务中预测结果与真实结果之间匹配程度的指标。它的高低直接反映了算法在检测社团结构时的准确性和可靠性。NMI是衡量两个分布之间相似度的指标，用于评估模型划分的社团结构与真实社团结构之间的一致性程度。其取值为0～1，其结果越大表示检测出的社团越贴近真实情况。

3.3 参数设置

本实验配置为Windows 10操作系统，CPU型号为AMD EPYC 7542 32-Core Processor，内存204.8 GB，GPU类型为3090-24G。实验使用Python 3.8开发环境。

实验设置AGCFN的迭代次数为50轮，学习率为0000 1。对于AGCFN的自编码器部分，进行20轮的预训练。自编码器模块的维度设置为d－500－500－2000－30，MGCAE模块的维度与自编码器维度相同并将权重参数设置为0.5。

3.4 结果分析

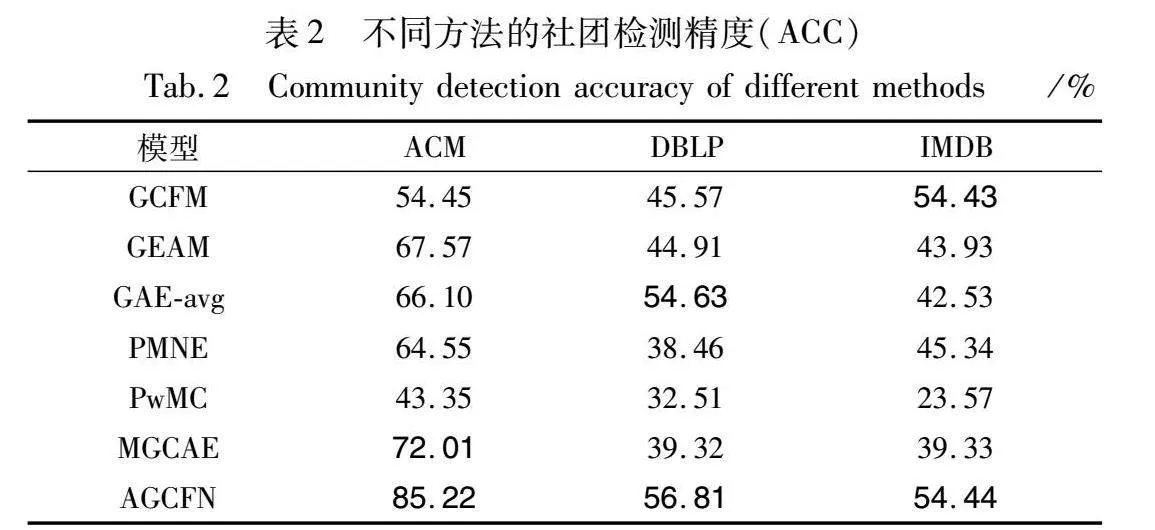
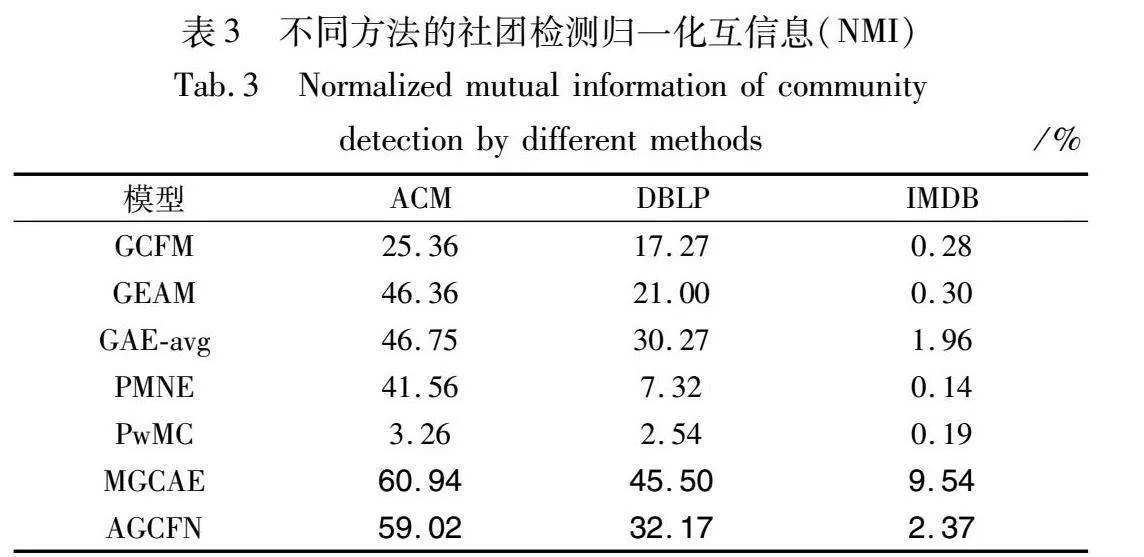
因为部分方法用到了K-means方法，所以会有实验误差，为了防止极端情况发生，将这些方法运行10次，取10次结果的平均值作为最终结果进行评价。表2和3展示了结果，其中最佳结果的前两名使用加粗字体标识。

从表2可以得出结论：在三个数据集的实验结果上，对于ACC评价指标，AGCFN优于所有其他方法；AGCFN具有很好的聚类性能，进行社团检测时准确度很高；自编码器学习到的节点内容信息成功传递给MGCAE模块进行两种信息的融合，并且多层信息融合模块也得到了更优的节点综合表示。自监督模块成功地进行了反向传播，使得模型表现出优势。

通过表3可以得出：对于NMI评价指标，相较于除MGCAE方法外的最好方法，分别提高了12.27%，1.90%，041%。但是AGCFN表现次于MGCAE，这是因为AGCFN的各个模块注重学习网络中节点的嵌入表示并将其进行整合，这个过程会提高节点嵌入的准确性，但在计算社团检测结果与真实社团匹配一致性程度上，MGCAE通过引入超图的计算，选取每个网络层的前k个最大连通子图对拓扑结构信息进行了加强，所以其NMI指标高于AGCFN。本文算法没有引入超图的原因是计算超图会使时间复杂度很高，影响算法的效率。

此外，值得注意的是，在IMDB数据集上，所有的方法在NMI指标上表现都不是很好。这是因为IMDB网络中的节点之间的关联信息比较分散，不具有很高的置信度。但是AGCFN依然能够取得第二名的效果，说明聚合层间关系和考虑节点内容信息有助于社团检测工作。

3.5 消融分析

为了探究AGCFN模型中各个模块的有效性，本节设计了消融实验。具体来说，本次实验设计了三个变体，分别为AGCFN-NAE 、AGCFN-FC 和AGCFN-NM 。AGCFN-NAE在AGCFN的基础上，将AE自编码器去除，不使用其独立提取节点内容信息，用来探究节点内容信息对多层网络社团检测的影响。AGCFN-FC是为了探究多层网络融合模块的作用，本变体将其进行替换，不使用LSTM单元，只使用普通的全连接网络［9］。AGCFN-NM则是将模块度最大化模块去除，用来探究模块度最大化模块对模型的影响。

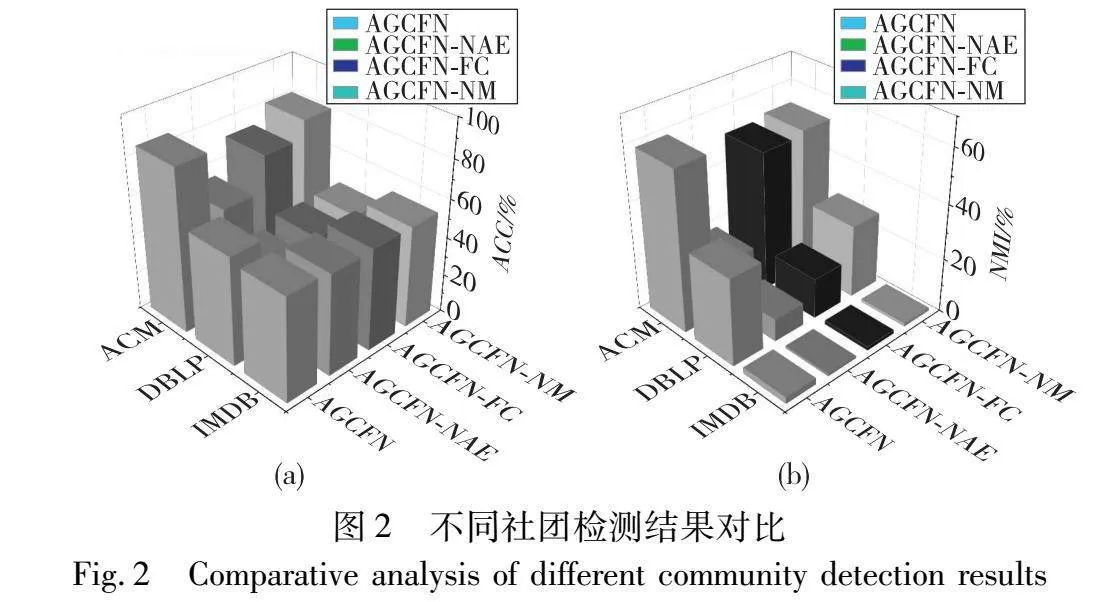
对于每种变体，同样使用ACC和NMI作为评价指标，使用三个数据集进行实验，实验结果如图2所示。

图2中，图（a）表示不同变体社团检测的精度，图（b）为不同变体社团检测的归一化互信息，从中可以看出：在几种变体中，AGCFN-NAE表现与其他几种变体以及AGCFN相比性能最差。这说明了自编码器模块对模型的贡献很大。自编码器能够有效学习多层网络的节点内容信息，并通过传递算子传递给MGCAE模块，这样可以使模型有效学习多层网络每一层的节点表示。AGCFN-FC的表现说明了本研究提出的多层融合模块的重要性。将多层网络每一个网络层学习到的节点表示整合出来，并使用LSTM单元进行传播与学习，能够成功融合不同尺度的节点表示，最终得到一个优质的节点综合表示。AGCFN-NM变体则体现出了模块度最大化模块的作用，表明模块度最大化模块有利于模型进行社团检测工作。

3.6 运行时间与收敛性分析

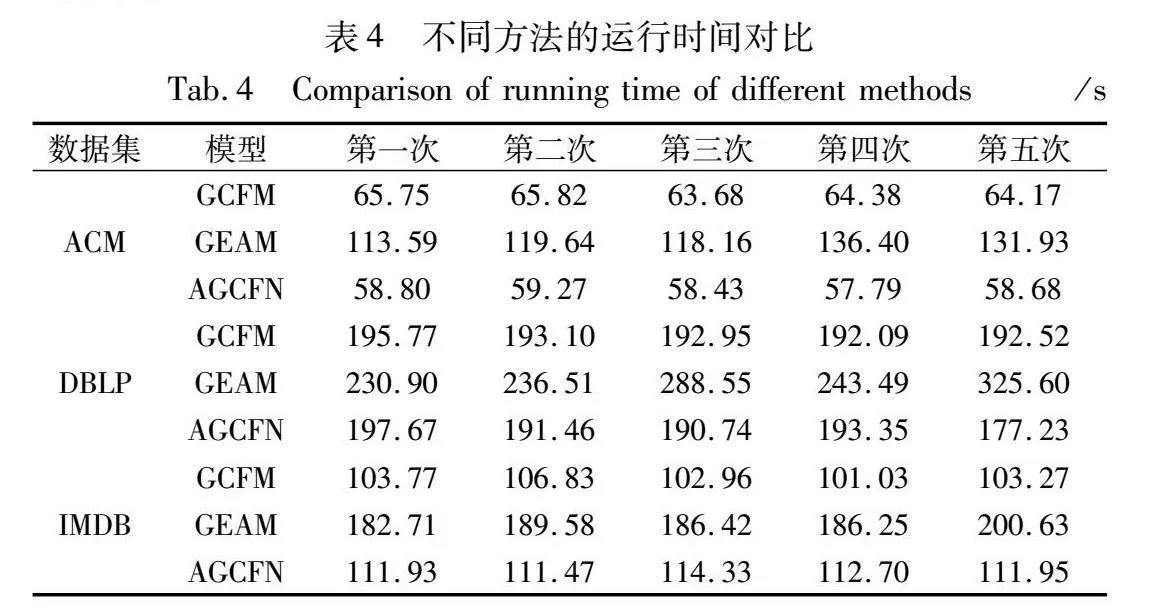
本节通过在三个数据集上进行实验来对AGCFN算法的运行时间以及收敛性进行分析。因为实验结果具有随机性，本文在每个数据集上进行5次实验。对于模型的运行时间，选择GCFM、GEAM两个模型与AGCFN进行对比，其对比结果如表4所示。

如表4所示，在ACM数据集上，GCFM、GEAM与AGCFN模型5次的运行平均时间分别为64.76 s、123.94 s、58.59 s；在DBLP数据集上分别为193.28 s、265.01 s、190.09 s；在IMDB数据集上分别为103.57 s、189.11 s、112.47 s。可以看出，AGCFN的运行时间与GCFM运行时间相近，说明AGCFN在具有较高精度的情况下，没有付出过多的时间代价。而GEAM的运行时间较长是因为它的自关注与自适应融合机制需要进行大量计算。此外，可以看出，多层网络的网络层数与节点数量会影响模型的运行时间，这也从实验角度验证了本文的时间复杂度分析。

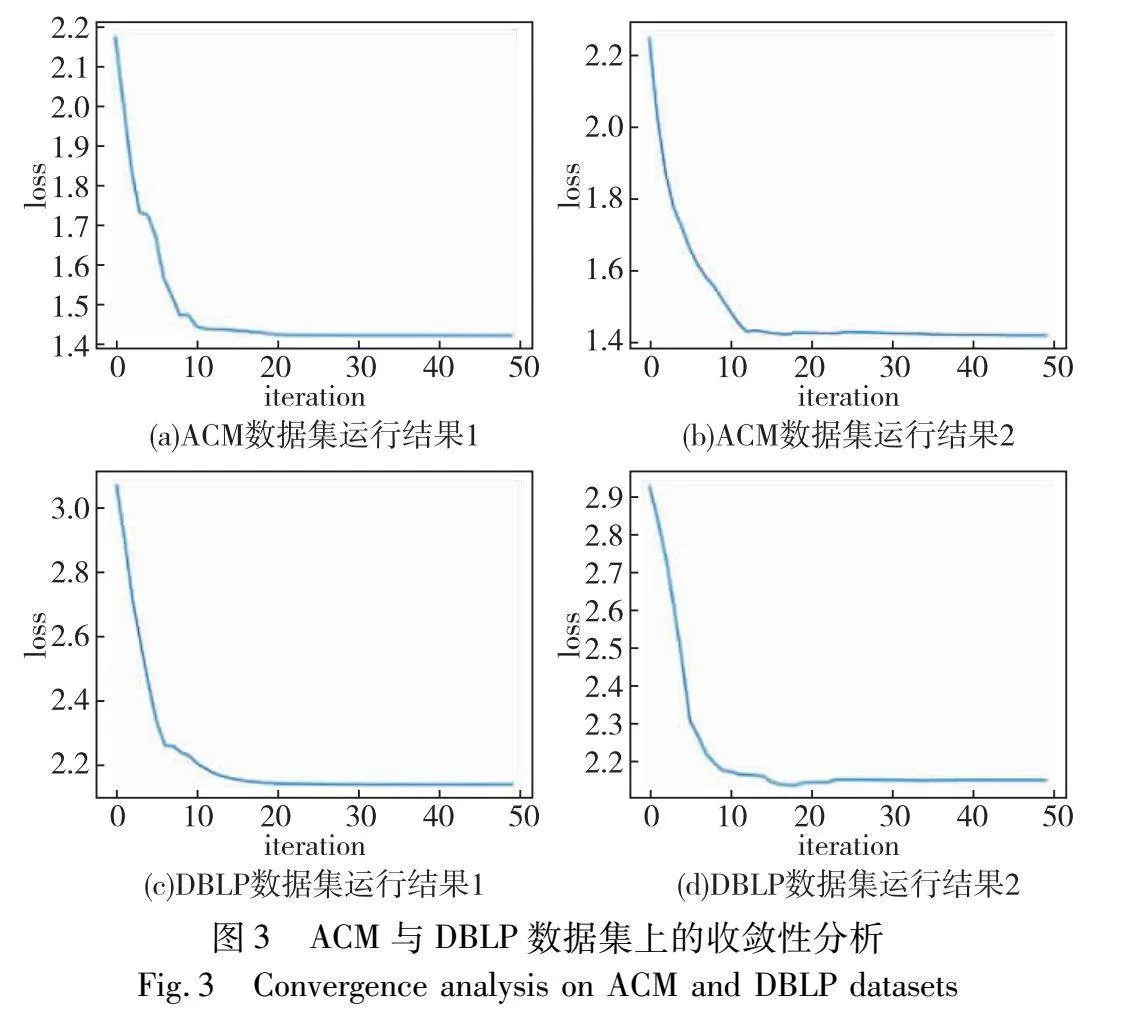
对于模型的收敛性，实验结果如图3所示，因为在实验中模型收敛性差距很小，并且在IMDB数据集上的表现情况与ACM和DBLP数据集上的表现情况相近，所以为了避免冗余，图3展示在ACM和DBLP数据集中进行两次实验的结果。

图3中，每个子图的横坐标代表迭代次数，本节将最大迭代次数设置为50。纵坐标代表损失值。其中图（a）和（b）为在ACM数据集上的实验结果图（c）和（d）表示在DBLP数据集上的实验结果。从图中可以看出，在两个数据集上，随着迭代次数的增加，损失函数逐渐减小并趋于稳定，虽然图（c）具有一定波动性，但是在迭代20轮以后也可以很快趋近于固定值。因此可以从实验角度得出，AGCFN模型是可以随着训练次数增加而快速收敛的。

3.7 超参数分析

为了探究超参数取值对模型的影响，本节设计了超参数实验。对于式（23）提到的两个用来度量KL散度损失和模块度最大化模块损失的超参数λ和η，对其敏感性进行分析。对于超参数λ，实验设计它的取值为λ={0.1，0.3，0.5，0.7，09，10}。对于超参数η，设计它的取值为η={001，003，005，007，0.09，0.10}。实验使用ACM数据集进行实验，实验结果如图4所示。

从图4中可以看出，AGCFN对自训练模块的KL损失的敏感度大于对模块度最大化模块的损失。但总的来说，AGCFN模型对超参数不敏感。实际中选择两个超参数λ和η的值分别为0.1和0.01。

4 实例分析

本章通过在ACM数据集上进行实例分析以展现AGCFN模型的有效性。具体而言，使用Gephi工具对AGCFN的社团检测结果进行直观展示，因为ACM数据集节点数量较多，为了更清晰地展现AGCFN的效果，从其三个社团分别随机选取若干节点进行可视化。随机抽取的节点编号分别为499，511，562，622，829，858，1023，1078，1143，1194，1382，1792，1803，1944，2230，2522，2540，2703，2754，2790，2897，2987，3014。为了直观地展示与分析，将其进行重新编号，形成0～22号节点。社团检测结果如图5所示，其中（a）为真实社团情况，（b）为AGCFN社团检测结果。依此验证AGCFN模型的有效性。

5 结束语

本文提出了一个新的社团检测模型AGCFN。通过构建自编码器模块、MGCAE模块、多层信息融合模块、模块度最大化模块和自监督模块，使得模型能够同时考虑多层网络节点内容信息和层间信息。自编码器模块与MGCAE模块配合进行每个网络层的两种信息提取；随后多层信息融合模块将其进行融合，得到每个节点的综合表示；自监督模块与模块度最大化模块用来进行损失度量，进而得到完整的损失函数，以完成模型的自训练与收敛。最后通过实验验证了AGCFN模型及所提各个模块的有效性。当前模型仅在中等规模数据集上进行了实验，然而现实中存在节点规模庞大的数据集，未来工作将进一步研究分析，使模型适用于大规模节点的网络。

参考文献：

［1］宗传玉， 李箬竹， 夏秀峰. 基于位置社交网络的用户社区和属性位置簇搜索 ［J］. 计算机应用研究， 2023， 40（9）： 2657-2662. （Zong Chuanyu， Li Ruozhu， Xia Xiufeng. User community and attribute location cluster search in location-based social networks ［J］. Application Research of Computers， 2023， 40（9）： 2657-2662.）

［2］Park C， Kim D， Han J，et al. Unsupervised attributed multiplex network embedding ［C］// Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA：AAAI Press，2020： 5371-5378.

［3］冯兴杰， 生晓宇. 基于图神经网络与深度学习的商品推荐算法 ［J］. 计算机应用研究， 2021， 38（12）： 3617-3622. （Feng Xingjie， Sheng Xiaoyu. Item recommendation algorithm based on GNN and deep learning ［J］. Application Research of Compu-ters， 2021， 38（12）： 3617-3622.）

［4］Zhou Xinchuan， Su Lingtao， Li Xiangju，et al. Community detection based on unsupervised attributed network embedding［J］. Expert Systems with Applications， 2023， 213： 118937.

［5］Berahmand K， Mohammadi M， Saberi-Movahed F，et al. Graph regularized nonnegative matrix factorization for community detection in attributed networks［J］. IEEE Trans on Network Science and Engineering， 2022， 10（1）： 372-385.

［6］Huang Xinyu， Chen Dongming， Ren Tao，et al. A survey of community detection methods in multilayer networks［J］. Data Mining and Knowledge Discovery， 2021， 35： 1-45.

［7］Boutemine O， Bouguessa M. Mining community structures in multidimensional networks［J］. ACM Trans on Knowledge Discovery from Data， 2017， 11（4）： 1-36.

［8］Gao Xubo， Zheng Qiusheng， Verri F A N，et al. Particle competition for multilayer network community detection ［C］// Proc of the 11th International Conference on Machine Learning and Computing. New York： ACM Press， 2019： 75-80.

［9］Cai Xiang， Wang Bang. A graph convolutional fusion model for community detection in multiplex networks［J］. Data Mining and Knowledge Discovery， 2023， 37（4）： 1518-1547.

［10］Wang Bang， Cai Xiang， Xu Minghua，et al. A graph-enhanced attention model for community detection in multiplex networks［J］. Expert Systems with Applications， 2023， 230： 120552.

［11］Li Chunying， Guo Xiaojiao， Lin Weijie，et al. Multiplex network community detection algorithm based on motif awareness［J］. Know-ledge-Based Systems， 2023， 260： 110136.

［12］Liu Xingyu， Cheng Junwei， Cheng Hao，et al. Self-supervised community detection in multiplex networks with graph convolutional autoencoder ［C］// Proc of the 26th International Conference on Computer Supported Cooperative Work in Design. Piscataway，NJ：IEEE Press， 2023： 1378-1383.

［13］Magnani M， Hanteer O， Interdonato R，et al. Community detection in multiplex networks［J］. ACM Computing Surveys， 2021， 54（3）： 1-35.

［14］Pramanik S， Tackx R， Navelkar A，et al. Discovering community structure in multilayer networks ［C］// Proc of IEEE International Conference on Data Science and Advanced Analytics. Piscataway，NJ：IEEE Press， 2017： 611-620.

［15］Shao Minglai， Lin Yujie， Peng Qiyao，et al. Learning graph deep autoencoder for anomaly detection in multi-attributed networks［J］. Knowledge-Based Systems， 2023， 260： 110084.

［16］Newman M E J. Fast algorithm for detecting community structure in networks［J］. Physical Review E， 2004， 69（6）： 066133.

［17］He Chaobo， Zheng Yulong， Cheng Junwei，et al. Semi-supervised overlapping community detection in attributed graph with graph convolutional autoencoder［J］. Information Sciences， 2022， 608： 1464-1479.

［18］Bo Deyu， Wang Xiao， Shi Chuan，et al. Structural deep clustering network ［C］// Proc of Web Conference. New York： ACM Press， 2020： 1400-1410.

［19］Fan Shaohua， Wang Xiao， Shi Chuan，et al. One2multi graph autoencoder for multi-view graph clustering ［C］// Proc of Web Conference. New York： ACM Press， 2020： 3070-3076.

［20］Liu Weiyi， Chen P Y， Yeung S，et al. Principled multilayer network embedding ［C］// Proc of IEEE International Conference on Data Mining Workshops. Piscataway，NJ：IEEE Press， 2017： 134-141.

［21］Nie Feiping， Li Jing， Li Xuelong. Self-weighted multiview clustering with multiple graphs［C］//Proc of IJCAI. San Francisco： Morgan Kaufmann Publishers， 2017： 2564-2570.