编码区块链中存储分配的分布式学习协议

摘 要：编码区块链利用纠错码技术，将区块分为多个编码片段并分布式存储于节点中。其主要目的在于减少参与者或节点的存储需求，实现高效的存储和容错能力。然而，节点随机存储任意数量的编码片段，导致编码片段分布不均匀，从而增加节点尝试解码区块时的通信成本以及关键节点的存储开销。为此，提出一种基于强化学习的分布式协议，用来合理分配节点存储的编码片段以降低存储开销和通信成本。具体而言，节点在解码任意区块时计算存储奖励，该奖励与编码片段的存储成本和节点尝试解码区块时产生的通信成本呈反比关系。学习收敛后与现有的集中式和分布式区块链编码存储方法进行了比较，研究结果表明，节点的奖励提高了7%，且节点的通信成本降低了55%。综上，基于强化学习的分布式协议为编码区块链存储和传输性能的提升提供了有效的解决方案。

关键词：编码；纠错码；分配；恢复；分布式

中图分类号：TP311.1 文献标志码：A 文章编号：1001-3695（2024）10-006-2918-08

doi：10.19734/j.issn.1001-3695.2023.12.0631

Distributed learning protocol for storage assignment in coded blockchain

Yang Changlin1， 2， Niu Xingyu1

（1.School of Computer Science， Zhongyuan University of Technology， Zhengzhou 451191， China; 2. School of Software Engineering， Sun YatSen University， Zhuhai Guangdong 519082， China）

Abstract：Coded blockchain leverages error correction codes to create multiple coded fragments that are then stored in a distributed manner by nodes. Its primary objective is to reduce the storage requirements of participants or nodes， achieving efficient storage and fault tolerance. However， nodes randomly store arbitrary coded fragments， which leads to high communication cost when a node attempts to decode a block. To this end， this paper proposed a novel reinforcement learning inspired distributed protocol to efficiently assign coded fragments to nodes. Specifically， nodes learn to store coded fragments based on a feedback signal that related to the storage cost of coded fragments and the communication cost incurred during block decoding attempts. After convergence， it compared the proposed protocol with existing centralized and distributed blockchain encoding storage methods. The results show that nodes have 7% higher reward， and critically， their communication cost is lower by 55%. In summary， the proposed reinforcement learning-based distributed protocol provides an effective solution for enhancing the storage and transmission performance of encoded blockchains.

Key words：coding; error correction codes; assignment; recovery; distributed

0 引言

区块链是一种无须任何中间方即可促进多方之间交易的技术。其关键特性包括分布式架构、安全性、不可窜改性和透明性，已在金融、医疗保健、物联网（IoT）和教育等不同领域得到了广泛应用［1］。然而，区块链存在存储可扩展性问题［2］，因为每个参与者都存储整个区块链的副本，该副本的数量级为千兆字节，并随时间不断增长。因此，区块链的运行依赖于拥有充足资源的节点，进而带来了安全问题。该安全问题涉及到资源丰富节点的垄断和操控，威胁了区块链的去中心化和抗攻击性能。

为了扩大区块链的规模，业界和学术界提出了许多存储方法，包括轻节点、分片、侧链和剪枝等［3］。然而，这些方法都有缺点。例如，轻节点和侧链都缺乏验证所有交易的能力，这意味着它们容易受到数据可用性攻击［4］。至于分片方法，其安全级别随着每个分片中恶意节点数量的增加而降低［5］。修剪会导致永久性数据丢失［3］。

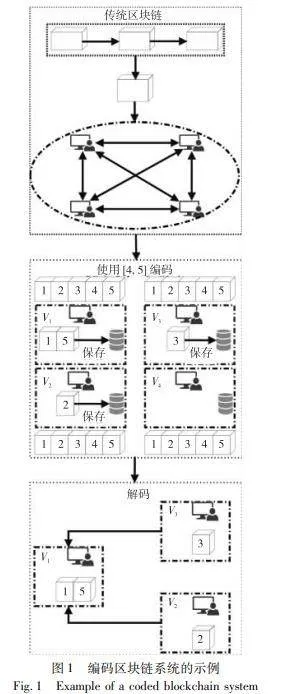
与上述方法不同，编码区块链利用纠删码技术来提高传统区块链的存储效率和容错能力［3］。如图1所示，每个节点独立地将区块编码成编码片段并根据存储分配策略存储。当一个节点（如节点v1）需要恢复一个区块时，它会从其他节点收集编码片段。此示例使用一个［4，5］编码，这意味着解码需要四个唯一的编码片段。在编码区块链系统中，一个区块被分为k个片段，然后使用Reed-Solomon码或喷泉码等纠错码进行编码，生成m（m≥k）个编码片段。编码区块链的另一个优点是它能够抵御节点故障［6］。

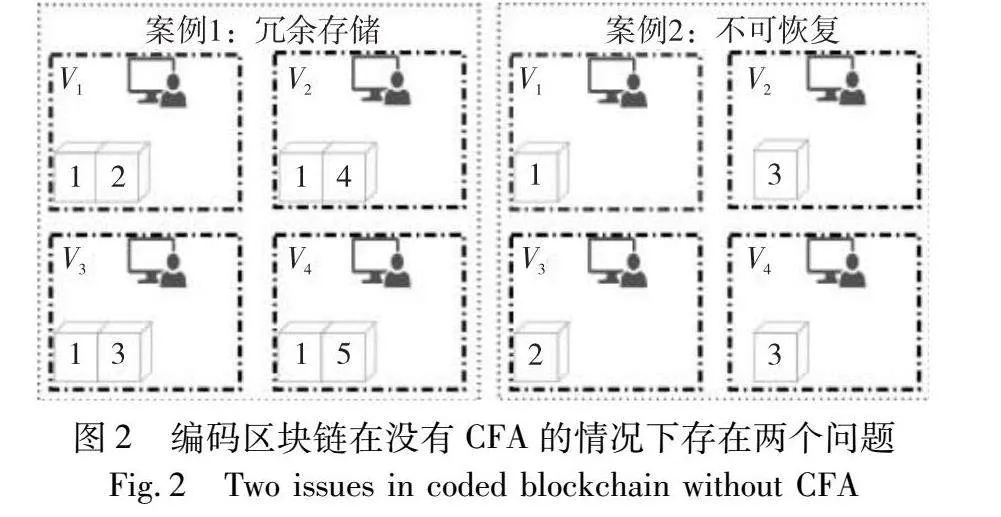
编码区块链面临的一个关键问题涉及到如何合理分配编码片段给节点，本文将其称为编码片段分配（CFA）问题。早期的编码区块链研究主要关注于区块编码策略，却忽视了CFA问题。换言之，它们的策略是在节点上随机存储任意数量的编码片段。这样的做法导致编码片段分布不均，从而增加了节点尝试解码区块时的通信成本，因为节点必须从远处的节点获取编码片段。图2展示了在没有考虑CFA的编码区块链中存在的另外两个问题。第一个问题是存储浪费，靠近的节点存储相同的编码片段，这不利于解码并增加了节点的存储负担，如案例1。第二个问题是无法保证区块的完全恢复，因为节点存储的编码片段数量不足以确保对区块的解码，如案例2。

现有的解决CFA问题的方法采用集中式或分布式分配方法。然而，这些方法有一个或多个缺点［3］。例如，中心化的分发方法与区块链系统的去中心化性质相矛盾［7］。另一方面，分布式分配方法未考虑参与者在重建区块时产生的通信成本［8］。此外，先前的分布式CFA解决方案并未对从对等节点检索的编码片段进行验证。

本文引入了一种分布式学习协议，用于将编码片段合理地分配给节点。该协议充分考虑了区块链系统的动态特性，其中节点独立进行存储、编码、解码区块以及加入/离开网络的操作。通过使用该协议，节点在解码区块时能够了解编码片段的分配情况，特别是在分配时考虑了解码成本以及来自其他节点发送的编码片段的完整性。节点维护其存储的编码片段的“状态”，并根据与存储成本、通信成本以及当前网络拓扑相关的“奖励”，采取“行动”来调整其编码片段集。

与现有的解决CFA问题的方法相比，基于强化学习的分布式协议能够更智能地解决CFA问题。这一协议允许每个节点根据其解码经验计算奖励，从而实现更合理的编码片段分配策略，并且根据网络状态变化实时调整存储的编码片段。同时，该协议无须节点间建立信任关系，每个节点都独立执行编码、解码和验证，并基于编码片段的可解码性定位诚实和恶意节点，因此，更适用于现有开放式的区块链系统。在仿真实验中，本文协议与文献［7］提出的CSA算法进行了比较，这是由于目前仅有文献［7］针对编码片段分配问题进行了讨论，并提出了可行方法。

综上，本文作出了以下贡献：

a）本文首次提出解决CFA问题的分布式学习协议，使每个节点能够学习如何合理地分配和重新分配编码片段。具体而言，节点可以根据其解码经验计算奖励，从而实现更智能的分配策略。此外，该协议适用于无信任的区块链系统。因为每个节点都独立执行编码、解码和验证，不依赖其他节点。

b）本文首次对所提出的学习协议进行研究，并与现有解决CFA问题的集中式和分布式启发式算法进行比较。结果表明，就总体奖励而言，所提出的协议比现有算法高出7%。此外，当网络拓扑发生变化并需要重新分配编码片段时，其重新分配编码片段所产生的通信成本比现有算法低55%。

1 相关工作

之前的工作已经设计了各种策略来编码区块链。例如，文献［9］采用纠删码来对区块文件进行编码分片存储，并随机分配给任意节点。Dai等人［10］采用网络编码，每个节点只存储一个编码片段。文献［11，12］中的工作结合拜占庭容错（BFT）共识算法和纠删码，每个节点存储一部分编码片段。文献［13］利用密钥共享、私钥加密和分布式存储来减少节点的存储需求。在文献［14］中，每个节点在{1，2，…，k}内随机生成一个数字d，节点从一组k个区块中随机选择d个区块，对这d个区块执行按位异或操作，生成所谓的液滴并进行存储。文献［15］介绍了一种新型区块链存储优化策略，利用纠删码技术对区块数据进行编码，并通过引入节点分组存储的方式，将编码后的区块数据以组为单位进行存储。这一策略旨在减少每个节点的存储负担，通过让每个组内的节点仅存储部分区块数据来实现存储空间的降低。然而，这些工作都没有明确说明如何在节点之间分配编码片段。这意味着节点会存储重复的片段，并且如果某些节点离开网络，会导致解码时编码片段数量不足，从而引发解码失败。

一些工作提出了集中式的分配策略，其中选举产生的节点或网络运营商决定每个节点的编码片段分配。例如，在文献［16］中，一组节点中的领导者负责对数据进行编码并将其分发给组内的节点。在文献［17］中，领导者（服务器）将一个区块编码成多个编码片段，并将其分发到客户端节点，其中每个客户端节点存储一个编码片段。Yang等人［7］将CFA问题制定为整数线性规划（ILP），他们还提出了一种由网络运营商负责运行的集中式启发算法，用来确定存储分配。Yu等人［17］在实用拜占庭容错（PBFT）系统中提出了一种编码区块链文件存储系统。在每个区块生成轮次中，矿工对挖掘的区块进行编码，并将编码片段分发到其他节点。Li等人［18］根据解码失败的整体概率确定每个节点存储的编码片段。

在分布式分配方法方面，每个节点根据自身对网络的观察来决定存储的编码片段，旨在减少存储并确保区块仍然可解码。Perard等人［19］引入了一种仅存储编码片段的编码节点，区块编码片段的数量随着区块的年龄增加而减少。Yang等人［7］概述了一种分布式协议，该协议在新节点加入或离开网络时调整节点的存储需求。如果节点无法使用附近邻居的编码片段解码区块，它会联系更远的节点以获取编码片段。文献［8］提出了一种分布式协商协议，节点使用该协议来交换编码片段，它减少了重复片段的数量，并确保节点存储足够数量的编码片段以解码区块。然而，该协议缺乏验证方案来检查编码片段的有效性。此外，文献［20］采用基于纠删码和拜占庭容错算法的编码方法，每个节点根据共识节点公钥列表分配存储编码区块，以降低区块链系统的存储冗余度，提高可扩展性。

目前的编码片段分配方法有几个缺陷。它们会不合理地将编码片段分配给节点，导致那些拥有更多片段的节点在解码过程中具有更高的通信成本。也可以说，它们必须在解码过程中提供更多编码片段。此外，编码片段会集中在某些节点上，因此当节点发生故障或离开网络时，存在数据丢失的风险。集中式的分发方法不适用，因为区块链系统需要分布式的解决方案。最后，分布式方法只考虑节点是否诚实，并不考虑区块恢复期间的通信成本。因此，本文提出了一种具有以下特点的分布式协议：

a）确保节点或参与者具有较小的存储和通信成本。

b）不需要领导节点。

c）从自身的解码过程中学习存储分配。

2 系统模型

本文旨在解决区块链系统中的存储可扩展性问题以及编码区块链中的编码片段分配（CFA）问题。在系统模型部分，本文详细阐述了节点如何对区块进行编码和解码，并引入了网络和节点模型。本文系统模型的设计目标是通过提出一种基于强化学习的分布式协议，使节点能够合理地调整编码片段的分配策略，从而降低存储和通信成本。

2.1 编码区块链模型

所有区块都采用相同的编码策略进行编码，该策略由以下三个基本功能组成。

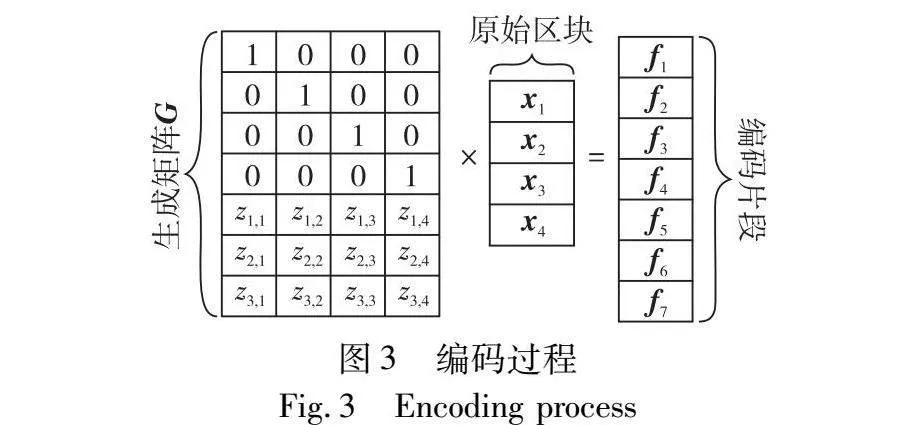
a）编码。每个节点将一个区块（如X）划分为k个片段，记为X={x1，x2，…，xk}。然后，它们使用Reed-Solomon纠错码对这k个片段进行编码。具体地，节点将所述编码的生成矩阵G与k个片段组成的列向量相乘，得到编码片段{f1，f2，…，fm}，每个编码片段的大小均为λ位。为了获得每个编码片段fj，j∈{1，2，…，m}，其计算表达式如下：

fj=x1×G［j，1］+x2×G［j，2］+…+xk×G［j，k］（1）

实际上，矩阵G可以是一个拥有m行和k列的范德蒙矩阵。它由两部分组成（图3）：一部分是一个k×k对角矩阵，另一部分是一个具有m－k行和k列的奇偶校验矩阵，其中奇偶校验矩阵的每个元素都是一个伪随机数，表示为{z1，1，z1，2，…，zm－k，k}。图3显示了一个编码过程的示例，其中m=7且k=4。

b）存储。编码片段由节点负责分发和存储。为了保存编码片段的记录，节点具有每个编码片段的索引，索引的集合表示为J={1，2，…，m}。

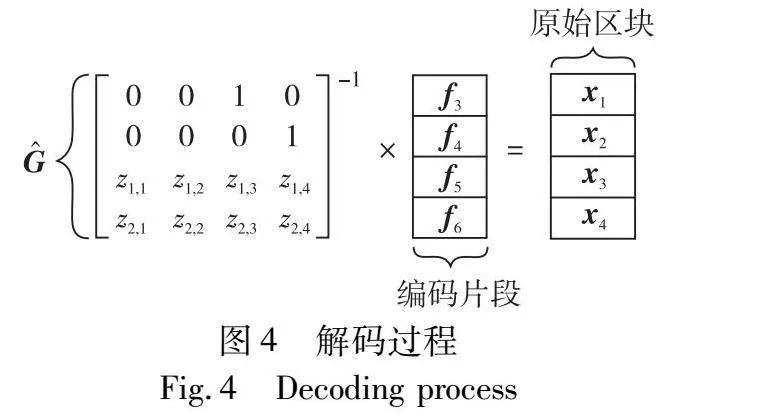
c）解码。为了解码一个区块，节点必须下载至少d个编码片段。一般来说，d≥k，并且d的具体取值取决于所采用纠错码的类型。在本文中，假设d=k，即采用最大距离可分离（MDS）代码。根据文献［21］，节点使用Merkle树来验证编码片段的完整性。验证通过后，节点通过从矩阵G中选择对应于k个编码片段的行来构造可逆矩阵G^。节点通过将G^的逆乘以由这k个编码片段组成的列向量，来恢复原始区块X。具体计算如下：

X=G^－1×［f1，f2，…，fm］（2）

图4显示了解码过程的示例，其中m=7且k=4。

2.2 网络模型

本文将编码区块链网络建模为一个具有n个节点的图（V，L），其中V是节点集，L为链接集。该网络应用［7］中的h跳定位特性表示其中每个节点需要从距离不超过h跳的节点获取足够数量的编码片段进行解码，并使用hv，u表示节点v和u之间的最小跳数。对于节点v，其h跳邻居为

Hh（v）={u：u∈V，hv，u≤h}（3）

在解码区块时，节点v将从h跳内的邻居节点获取编码片段，并使用B^（v）存储从这些邻居节点下载的编码片段的索引。此外，B（v）表示节点v存储的编码片段的集合。为了保证编码片段的及时响应，节点设有超时或最大等待时间，如果发生超时，节点将重新选择一个新的邻居节点来请求编码片段。

2.3 节点模型

每个节点维护自身的状态空间和动作空间，并接收奖励。假设节点在每个时刻t执行一个动作。

a）状态。令sv（t）为时刻t时节点v存储的编码片段数量，其中sv（t）=|B（v）|。节点v的状态空间Sv（t）包含sv（t）可以取值的所有数值。所有节点都设置其存储上限k，以确保它们不会存储不必要的编码片段，节点v∈V的状态空间Sv（t）为

Sv（t）={sv（t）|sv（t）∈{0，…，k}}（4）

b）动作。所有节点都独立地从相同的动作空间中采取行动。在每个时刻t，处于状态sv（t）的节点v根据Q（sv（t），av（t））的值来采取动作av（t），其中动作av（t）来自动作空间Av（t）。正式地，节点v的动作空间Av（t）为

Av（t）={av（t）|av（t）∈{－1，0，1}}（5）

其中每个动作av（t）都在集合{－1，0，1}中取一个值。如果节点v设置av（t）=1，则它在t时刻时从距离超过h跳的邻居节点处获得一个编码片段，该编码片段必须与其在B（v）中存储的编码片段不同。另一方面，如果av（t）=－1，则节点v从其存储中随机删除一个编码片段。最后，对于av（t）=0，节点v在时刻t时保持其编码片段不变。

c）奖励。奖励考虑了存储和通信成本。此外，为了权衡存储和通信成本，奖励引入权重参数ε∈（0，1］，其计算表达式如下：

Rv（t）=1λ×sv（t）+ε×D（v）（6）

其中：ε是平衡存储和通信成本影响的权重因子；λ表示编码片段的大小（以比特为单位）；D（v）表示节点v解码区块时的通信成本。

在此背景下，值得注意的是奖励并不取决于节点的“动作”，而是取决于其“状态”。换句话说，如果节点存储少量编码片段，并且产生较小的通信成本，例如当节点在解码期间尝试检索编码片段时，所有编码片段都可以从附近的节点获得，那么该节点具有较高的“状态奖励”。

3 可验证的低成本解码过程

在介绍协议细节之前，本文首先概述节点执行的解码过程，将文献［7， 21］中的解码过程进行结合。简而言之，文献［21］使用Merkle树来验证编码片段，相较于文献［19］的方法在计算成本上更低。另一方面，文献［7］从位于一跳或多跳之外的节点获取编码片段。

执行解码的节点（例如v）被称为请求者。它还记录通信成本D（v），用于计算第2章中的奖励。向节点v发送编码片段的其他节点被称为响应者。接下来，本文解释请求者和响应者。

a）请求者。算法1显示了请求者v的操作步骤。其输入是：（a） B（v）；（b） 其拥有的编码片段的索引集合，即B^（v），最初设置为B^（v）=B（v）；（c） 从其他节点检索的编码片段数量，即z=k－|B^（v）|；（d） 用于查找节点以获取编码片段的跳数，即，最初设置为=0。

在解码过程中，当节点v的编码片段不足时，即z>0，它将加1，旨在发现更多的邻居。它构造了一个集合U，其中包含距离它恰好跳的节点。节点v从U中随机选择一个节点u，并向其发送一个REQ_BLOCK消息，其中包括节点u的地址、B^（v）中的索引以及所需的编码片段的数量z。如果节点v在给定的超时时间内收到响应，它会提取编码片段fj及其相应的Merkle树路径pj，见算法1第10行。然后，节点v通过验证功能确保接收到的编码片段fj的完整性，这包括构建一棵Merkle树，将其叶子作为编码片段，并使用节点存储的Merkle树根来进行验证。

如果编码片段有效，则节点v将其添加到B^（v）中，将z的值减1，并将λ添加到通信成本中。请注意，如果响应节点的距离超过h跳，则节点v将独立存储该编码片段，即保持h跳定位特性，请参见算法1第15～17行。另一方面，如果编码片段无效或节点v尚未在超时时间内收到节点u的答复，则将u从U中删除，并向U中的另一个节点发送请求，直到U≠或z=0。

算法1 请求者

输入：B（v），z，B^（v），。

输出：D（v），B（v），B^（v）。

1 D（v）=0 // 解码区块时初始化节点v的通信成本

2 while z>0 do

3 =+1 // 增加跳数以发现更多邻居节点

4 U=H（v）－H－1（v） /* 构建包含距离节点v恰好跳的节点集合U */

5 while U= do

6 u=random.sample（U，1） /* 从集合U中随机选择一个节点u */

7 send（"REQ_BLOCK"，u，B^（v），z）

8 while not timeout do

9 if receive（"RPY_BLOCK"） then

10 ［fj，pj］=extract（"RPY_BLOCK"）

11 if verify（fj，pj） then

12 B^（v）=B^（v）∪{j} /*将接收到的编码片段索引添加到B^（v）中*/

13 D（v）=D（v）+λ // 更新通信成本

14  z=z－1

15 if >h then /*检查接收到的编码片段是否在h跳范围内*/

16 B（v）=B（v）∪{fj} /* 节点v存储编码片段fj以保持h跳定位 */

17 end

18 end

19 end

20 end

21 if z≤0 then

22 break

23 end

24 U=U－{u} // 从集合U中删除已处理的节点u

25 end

26 end

请求者算法（算法1）包含两个嵌套的while循环。在第一个while循环中，节点需要尝试构建集合U，其最坏情况下的时间复杂度是O（kn），其中k是每个节点最多存储的编码片段数量，n是节点的数量。在第二个while循环中，节点需要遍历集合U并执行相应的通信操作，其最坏情况下的复杂度是O（knlog n），其中log n是Merkle树的高度。算法1的时间复杂度为O（kn+knlog n），但由于通常关注增长最快的项，整体空间复杂度可以表示为O（knlog n）。对于空间复杂度，算法1主要占用空间的是节点维护的数据结构，包括B（v）、B^（v）和集合U。每个节点需要存储的编码片段数量最多为k，即|B（v）|≤k、|B^（v）|≤k。因此B（v）和B^（v）的空间复杂度都是O（k）。此外，在第一个while循环中，集合U涉及到存储所有节点的编号，因此集合U的空间复杂度是O（n）。综合考虑节点维护的数据结构和集合U，整体空间复杂度可以表示为O（n）。

b）响应者。响应者的伪代码如算法2所示。节点一旦收到REQ_BLOCK消息就成为响应者。收到此消息后，响应者节点（假设为u）提取索引集B^（v）和所需编码片段的数量z。它首先检查其存储的编码片段集合B（u）并构建一个互补集。如果z≤||，这意味着节点u存储的编码片段多于所需的编码片段数量。其次，它从中随机选择z个索引并重建集合^，请参见算法2第5行；否则，将^设置为整个互补集，请参见算法2第7行。接下来，对于每个编码片段fj（其中j∈^），节点u使用Merkle_tree_path函数来计算Merkle树路径pj。最后，它向节点v发送RPY_BLOCK消息，其中包含节点v的地址、编码片段fj以及对应的Merkle树路径pj。

算法2 响应者

输入：REQ_BLOCK，u，B^（v），z。

输出：RPY_BLOCK，v，fj，pj。

1 if receive（"REQ_BLOCK"） then

2 ［B^（v），z］=extract（"REQ_BLOCK"）

3 =B（u）－B^（v） // 计算互补集

4 if z≤|| then

5 ^=random.sample（，z） /* 从中随机选择z个索引来构建集合^ */

6 else

7 ^= /* 如果需要的编码片段数z超过可用编码片段数||，则使用整个互补集来构建集合^ */

8 end

9 for j∈^ do

10 pj=Merkle_tree_path（fj） /* 计算^中每个编码片段fj的Merkle树路径 */

11 send（"RPY_BLOCK"，v，fj，pj）

12 end

13 end

响应者算法（算法2）包括接收消息、提取消息信息、处理互补集和计算Merkle树路径等四个关键步骤。首先，接收和提取消息信息步骤的时间复杂度通常为常数时间，对整体复杂度的影响较小，因此被忽略。在处理互补集方面，响应者节点需要构建互补集和重建集合^，其中||≤k和|^|≤k，两个集合的时间复杂度都为O（k）。在计算Merkle树路径方面，对于每个在互补集中的编码片段，响应者节点需要计算Merkle树路径，其中每个编码片段计算的时间复杂度为O（log n）。因此，Merkle树路径计算的总时间复杂度为O（klog n）。对于空间复杂度，算法2主要占用空间的是节点维护的数据结构，包括B（u）、B^（v）、和^，其中|B（u）|≤k、|B^（v）|≤k、||≤k和|^|≤k。综上所述，算法2的总时间复杂度可以表示为O（klog n），而整体空间复杂度为O（k）。

在此背景下，值得注意的是响应者节点可以不回复请求消息。为此，编码区块链可以利用智能合约［22，23］以代币或硬币的形式激励响应者。另外，可以实施惩罚机制来驱逐自私节点，即诚实节点认为自私节点是恶意的并且不回复其请求。

4 CFA分布式学习协议

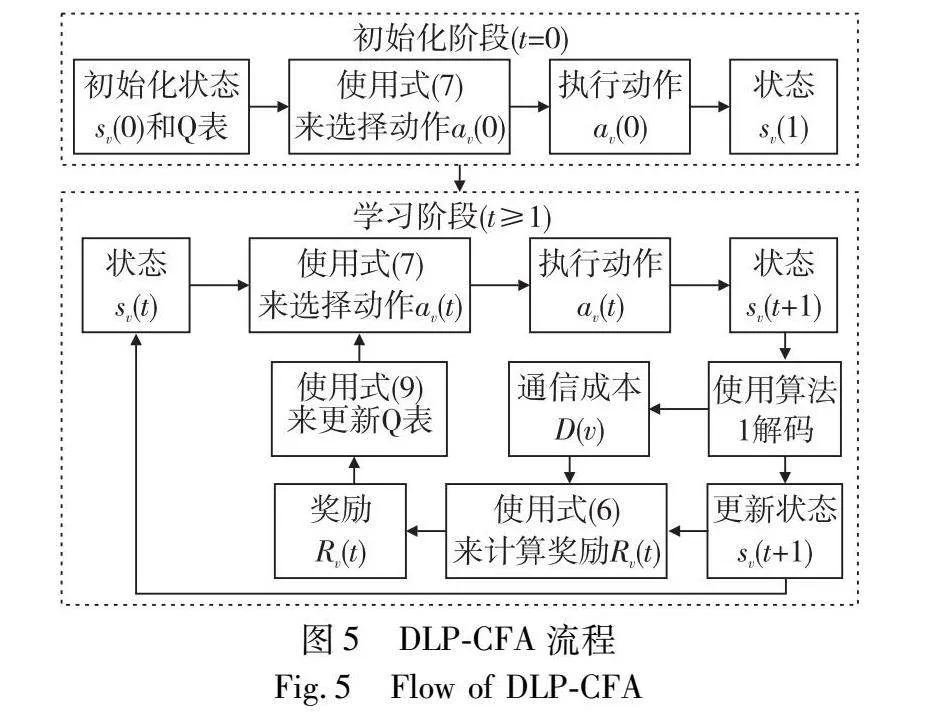
DLP-CFA可以分为初始化、学习两个主要阶段。DLP-CFA使节点能够学习和调整其存储的编码片段，如图5所示。本文采用状态-动作-奖励-状态-动作（SARSA）算法［24］中的Q表更新规则。

4.1 初始化阶段

节点的Q表跨越两个连续的时刻。因此，在第一个时刻，节点执行一个动作并且不更新其Q表。参考算法3，对于所有状态sv（t）∈Sv（t）和所有动作av（t）∈Av（t），节点v将其Q值初始化为零。它还通过从m个编码片段中随机选择k个编码片段，即其初始状态为sv（t）=k，来初始化编码片段集合B（v）。接下来，节点v使用玻尔兹曼策略［25］在初始状态sv（t）下选择一个初始动作av（t），其中选择动作av（t）的概率为

π（sv（t），av（t））=eφ（sv（t））Q（sv（t），av（t））∑b∈Av（t）eφ（sv（t））Q（sv（t），b）（7）

其中：

φ（sv（t））=ln c（sv（t））maxa，b∈Av（t）|Q（sv（t），b）－Q（sv（t），a）|（8）

这里，φ（sv（t））是时刻t时状态sv（t）的探索率；c（sv（t））表示节点v在时刻t之前经历状态sv（t）的次数。在开始学习时，玻尔兹曼策略会探索更多的状态，随后趋于收敛到具有较高Q值的状态，即更频繁地访问该状态。

最初，φ（sv（t））=0，节点v以相等的概率从Av（t）中选择一个动作。在此阶段，如果节点v恰好选择动作av（t）=1，则将其修改为av（t）=0，因为它不需要存储额外的编码片段。换句话说，在初始阶段，节点v只有在av（t）=－1时才执行该动作。最后，当av（t）=－1时，节点v随机删除其存储中的编码片段并进入学习阶段。

算法3 DLP-CFA初始化阶段

输入：h，m，k。

输出：sv（t），v，av（t），B（v），Q。

1 初始化Q（sv（t），av（t））=0，sv（t）∈Sv（t），av（t）∈Av（t）

2 B（v）=random.sample（{1，…，m}，k） /* 通过从m个编码片段中随机选择k个编码片段来初始化B（v） */

3 sv（t）=|B（v）| // 获取当前状态

4 使用式（7）来选择av（t）

5 if av（t）==1 then

6 av（t）=0

7 end

8 if av（t）==－1 then

9 B（v）=random.remove（B（v），1） /* 从B（v）中随机删除一个编码片段 */

10 end

算法3的时间复杂度主要涉及Q表和B（v）的初始化以及动作的执行。Q表初始化的时间复杂度为O（|Sv（t）|×|Av（t）|），其中|Sv（t）|=1和|Av（t）|=3。随机选择编码片段操作的时间复杂度为O（mk），而当动作av（t）=－1时执行动作的时间复杂度为O（m）。在最坏情况下，整体初始化阶段的时间复杂度可以表示为O（mk）。在空间复杂度方面，算法3的空间复杂度主要受节点的Q表和编码片段集合B（v）的影响。Q表的空间复杂度为O（|Sv（t）|×|Av（t）|），而编码片段集合B（v）的空间复杂度为O（|B（v）|），其中|B（v）|≤k。因此，整体空间复杂度为O（k）。

4.2 学习阶段

在学习阶段，每个时刻，节点会更新其存储的编码片段，即B（v），还更新其Q表。参考算法4，在将状态sv（t）初始化为当前存储的编码片段的数量|B（v）|之后，节点v使用玻尔兹曼策略选择一个动作。如果满足以下任一个条件：a） sv（t）=k且av（t）=1；b） sv（t）=0且av（t）=－1。节点将动作修改为零，即av（t）=0。这是因为在任何一种情况下，该节点都无法执行所需的操作。

如果选择的动作av（t）=1，则节点v需要获取一个编码片段来存储。具体来说，它需要获取一个编码片段进行存储，该编码片段在h跳内没有被任何节点存储，即Hh（v）中没有节点具有所请求的编码片段。为此，它以B（v）、z、B^（v）和作为输入运行算法1，其中B^（v）是通过上一个时刻的解码获得的，请参见算法4第15行。算法1从距离至少h+1跳的节点返回一个不在B^（v）中的编码片段。另一方面，如果av（t）=－1，则节点v只是删除一个其存储的编码片段。在此阶段，节点v的状态更改为sv（t+1），并更新|B（v）|。

在执行动作av（t）后，节点v解码一个区块。解码过程遵循第4章中的步骤，其中输入为z=k－|B（v）|、h=0和B^（v）=B（v）。解码后，节点v存储的编码片段数量会增加，这是因为节点v存储从距离超过h跳的节点检索到的编码片段。正如在4.2节中阐明的那样，节点v在执行一个动作和计算奖励时运行算法1。因此，节点的状态变化是由其“动作”和奖励计算引起的。

算法4 DLP-CFA学习阶段

输入：h，k，t，α，β，γ，σ，B（v），B^（v），Q。

输出：sv（t），av（t），B（v），Q，α。

1 sv（t）=|B（v）| // 获取当前状态

2 使用式（7）来选择av（t）

3 if （sv（t）==k and av（t）==1） or （sv（t）==0 and av（t）==－1）

4 av（t）==0 // 如果条件满足，则将动作av（t）修改为0

5 end

6 if av（t）==1 then

7 B（v）=Requester（B（v），1，B^（v），h） /* 如果条件满足，节点执行Requester函数获取一个编码片段 */

8 end

9 if av（t）==－1 then

10 B（v）=random.remove（B（v），1） /* 从B（v）中随机删除一个编码片段 */

11 end

12 z=k－|B（v）| // 计算解码所需编码片段个数z

13 =0

14 B^（v）=B（v）

15 D（v），B^（v），B（v）=Requester（B（v），z，B^（v），） /* 运行算法1获取编码片段并计算出节点v的通信开销 */

16 sv（t+1）=|B（v）| // 获取当前状态

17 计算奖励Rv（t）=1λ×sv（t+1）+ε×D（v）

18 使用式（9）来更新Q表

19 使用式（10）来计算αt－1

接下来，更新节点v的状态sv（t+1）。它使用式（6）计算奖励Rv（t），将sv（t）替换为sv（t+1）。最后，节点v将状态-动作对（sv（t－1），av（t－1））的Q值更新为

Q（sv（t－1），av（t－1））=Q（sv（t－1），av（t－1））+αt－1（Rv（t）+

γQ（sv（t+1），av（t+1））－Q（sv（t－1），av（t－1）））（9）

其中：γ是贴现率，而αt－1表示学习率。在每个时刻结束后，学习率都会降低，以确保收敛，具体如下［26］：

αt=α×βtσ（10）

其中：α是初始学习率；0<β<1是衰减率；σ是恒定步长。

算法4的时间复杂度主要受到动作执行和计算通信开销的影响。对于执行动作av（t）=1的情况，节点v执行Requester函数来获取一个编码片段。该函数的时间复杂度主要包括算法1的执行。由于只需要获取一个编码片段，该函数的时间复杂度为O（n+nlog n）。对于执行动作av（t）=－1的情况，节点执行删除操作的时间复杂度为O（k）。同时，计算通信开销的时间复杂度为O（kn+knlog n）。在最差情况下，总的时间复杂度可以表示为O（knlog n）。在空间复杂度方面，算法4主要占用空间的是节点维护的数据结构，包括B（v）、B^（v）和Q表，其中|B（v）|≤k、|B^（v）|≤k，而Q表的空间复杂度为O（|Sv（t）|×|Av（t）|）。因此，整体空间复杂度可以表示为O（k）。

5 仿真实验

本实验在一台搭载Intel Core i5-5287U处理器的笔记本电脑上进行，该处理器具有四个核心和八个线程，运行频率为29 GHz，内存为8 GB，硬盘容量为1 TB。本实验使用Python 3.9版本。网络拓扑是在一个面积为100 m2的区域内随机生成的，包含100个节点。如果两个节点的距离小于20 m，则它们是一跳邻居。本文将DLP-CFA中式（10）的学习率步长σ设置为50。假设所有区块的大小恒定为1 MB。本实验定义一个称为归一化奖励的度量，用R^（t）表示，它是所有节点的总体奖励。正式地，归一化奖励为

R^（t）=1n∑v∈VRv（t）（11）

该实验只考虑一个区块，因为所有块都使用相同的策略进行编码。该实验省略任何关于区块挖矿的讨论，有兴趣的读者可以参考文献［6］。仿真实验中，本文将DLP-CFA与现有的解决CFA问题的方法进行对比，即文献［7］中提出的集中式编码片段分配（CSA）算法和分布式动态调整（DA）算法。简而言之，在CSA算法中，一个中央控制器分配编码片段给所有节点，其目的是最大限度地降低总体存储和通信成本。使用DA算法，每个节点发现其h跳邻居处存储的编码片段，并动态调整其存储的编码片段。

5.1 k的影响

该实验首先研究DLP-CFA在不同k值下的收敛速度。该实验设置以下参数值：n=100、ε=0.9、h=2、m=200、α=0.1、γ=0.9和β=0.95。图6的结果表明，随着k的增加，DLP-CFA的收敛速度减少，并且归一化奖励收敛到比k较小时更高的值。这是因为较高的k值意味着较大的状态空间，从而减慢收敛速度。另一方面，归一化奖励随着k的增加而增加。因为编码片段的数量增加，每个编码片段的大小减小，从而降低节点存储相同编码片段集的概率。因此，DLP-CFA具有更高的归一化奖励或更高的收敛性和学习效率。本文注意到，当k=100时，DLP-CFA的归一化奖励在1 000个时间周期内收敛到0.010 7。在k=100时，与k的其他值相比，DLP-CFA收敛到更高的归一化奖励。

5.2 超参数α、β、γ、σ

为了研究上述超参数对DLP-CFA收敛性的影响，本文使用以下参数值：n=100、ε=0.9、h=2、m=200和k=100。

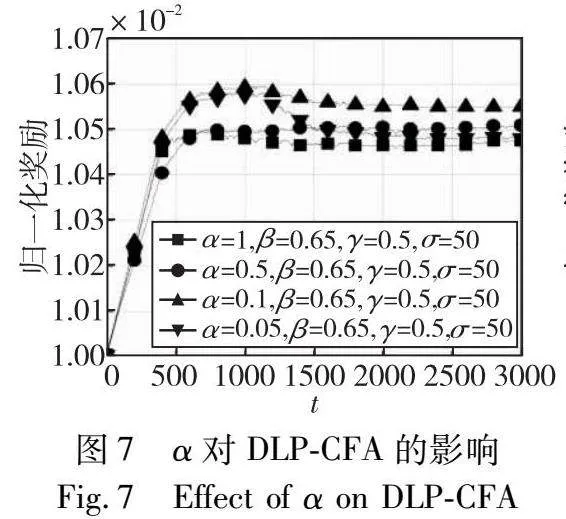
本实验首先考虑初始学习率α，将其设置为{1，0.5，0.1，0.05}中的一个值，其他三个参数固定为β=0.65、γ=0.6和σ=50。图7表明，当α减小时，DLP-CFA的收敛速度也增加。这是因为较小的α值意味着每个时期对Q的更新较小，这反过来又减慢了学习和收敛速度。结果表明，α=0.1导致DLP-CFA收敛到更高的归一化奖励。

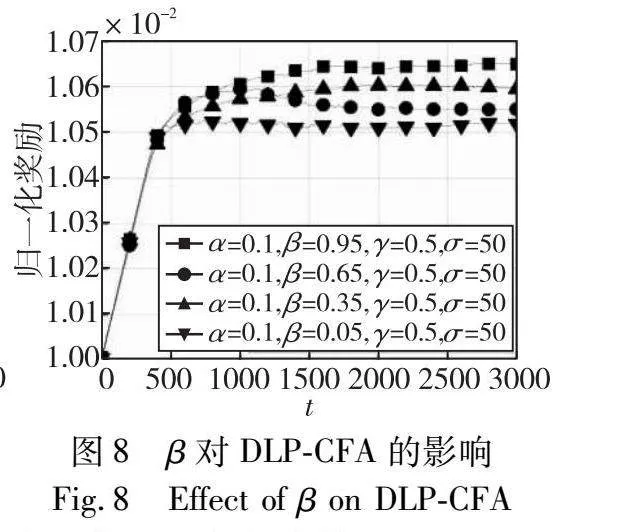
接下来，本实验研究衰减率β，其取值为{095，065，035，005}。本实验使用α=0.1，γ=0.6和σ=50。根据图8，随着β的增加，DLP-CFA的收敛速度降低。这是因为学习率α是衰减率β的函数，参见式（10）。因此，较大的β意味着较大的学习率，即学习率会随着时刻的增加而降低得更慢。结果表明，β=0.95使DLP-CFA能够收敛到更高的归一化奖励。

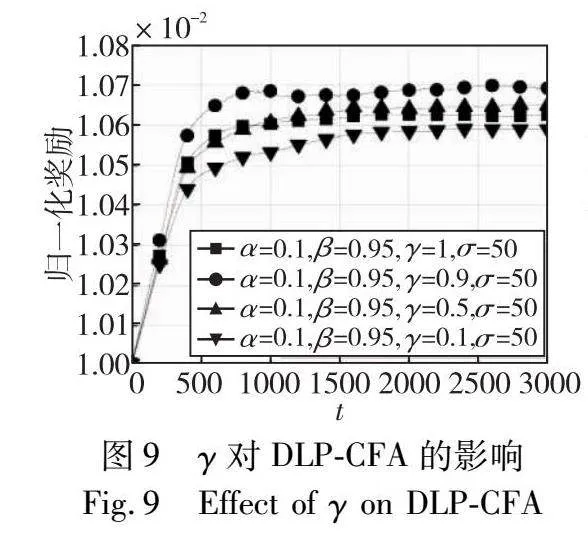
本实验现在研究范围内的贴现率γ。本实验设置α=0.1、β=0.95和σ=50。图9显示，具有较大折扣率的DLP-CFA需要更多的时间才能收敛。因为较小的γ表示更新在时刻t－1选择的状态-动作对的Q值，对于时刻t的Q值的影响较小，参见式（9）。此外，图9显示γ=0.9时具有最高的收敛归一化奖励。因为如果γ太小，DLP-CFA就会优先考虑即时奖励而不是长期收益。相反，如果γ太大，DLP-CFA会根据在时刻t下动作积极更新Q值。

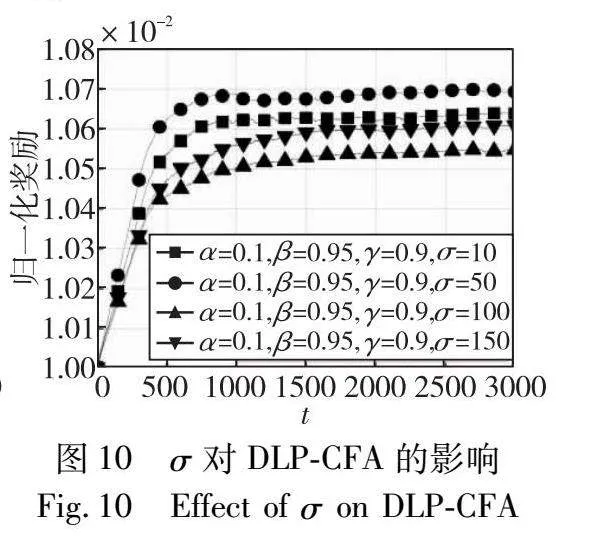
本实验还研究学习率步长σ，将其设置为集合{10，50，100，150}中的一个值，并设置α=0.1、β=0.95和γ=0.9。图10显示，DLP-CFA需要更多的时间周期才能以更大的步长收敛。原因与图8相同，因为α也是步长σ的函数。结果表明，σ=50时收敛到更高的归一化奖励。

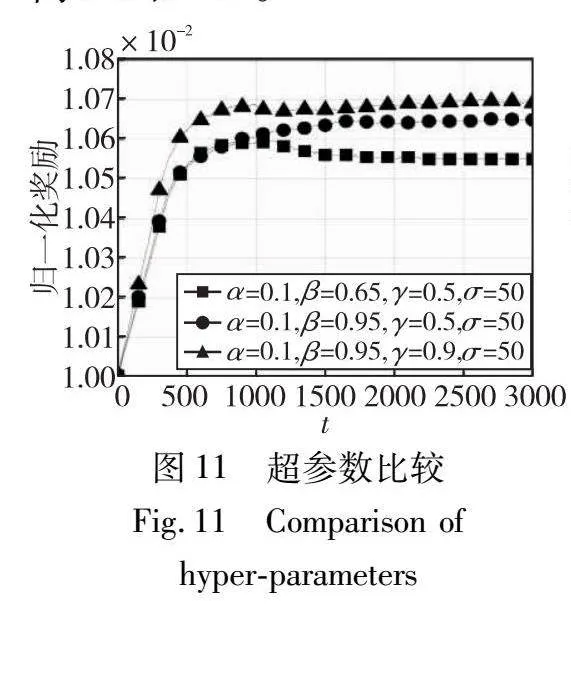
图11展示了上述结果中具有最大归一化奖励的参数，它表明α=0.1、β=0.95、σ=50和γ=0.9是很好的超参数选择。

5.3 与CSA和DA的比较

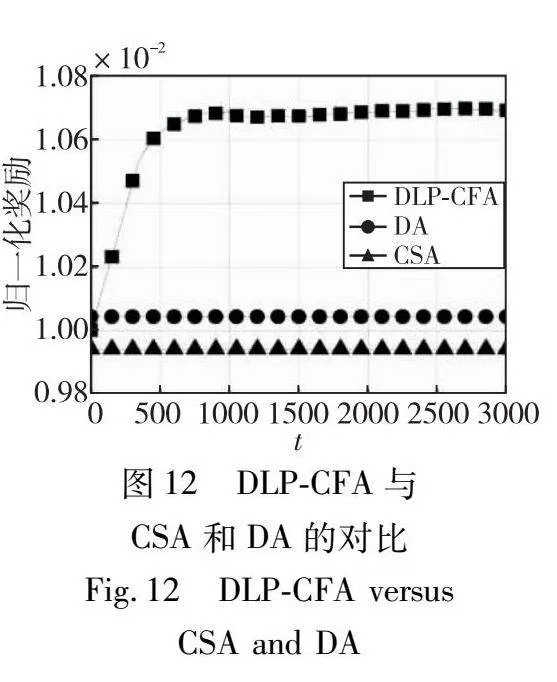
本实验研究了DLP-CFA的参数，并对其性能与CSA和DA进行了比较评估。本实验设置参数n=100、ε=0.9、h=2、k=100和m=200。DLP-CFA的超参数按照5.2节进行设置。从图12可以看出，DLP-CFA的归一化奖励分别比DA和CSA高6%和7%。

5.4 平均存储和通信成本

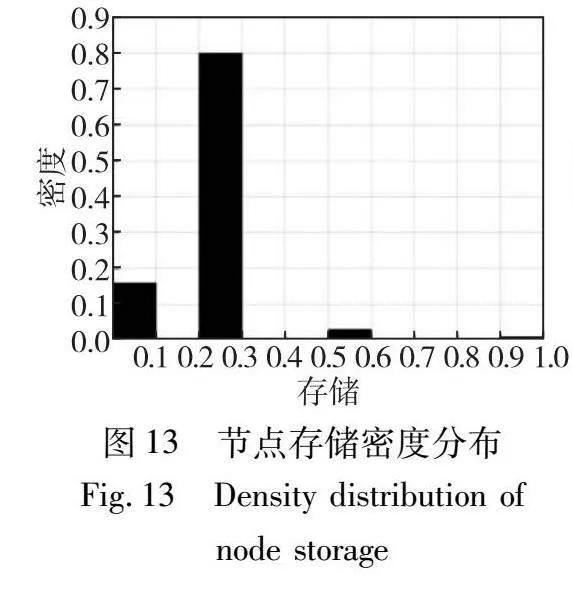
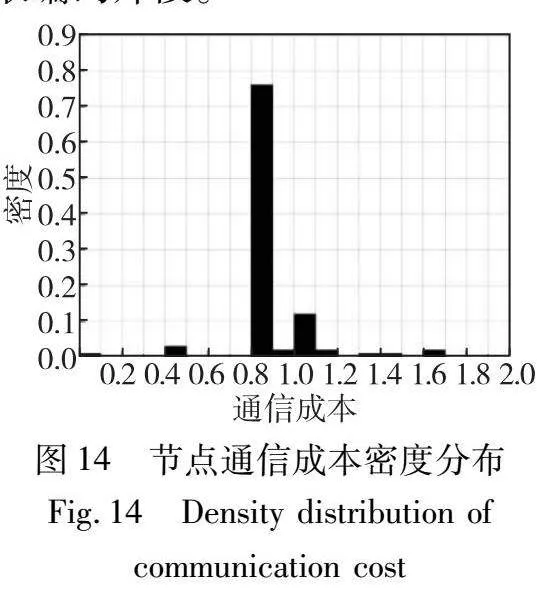
本实验现在研究使用DLP-CFA时的节点存储和通信成本，设置n=100、ε=0.9、h=2、k=100和m=200。图13显示，16％的节点存储少于10％的编码片段，即少于10个片段。另一方面，80%的节点存储10%～20%的编码片段，只有不到5%的节点存储超过50%的编码片段。从图14中可以看出，76%的节点从距离为一跳的节点获取编码片段。大约12%的节点从距离超过一跳的节点获取编码片段。

5.5 五个节点示例

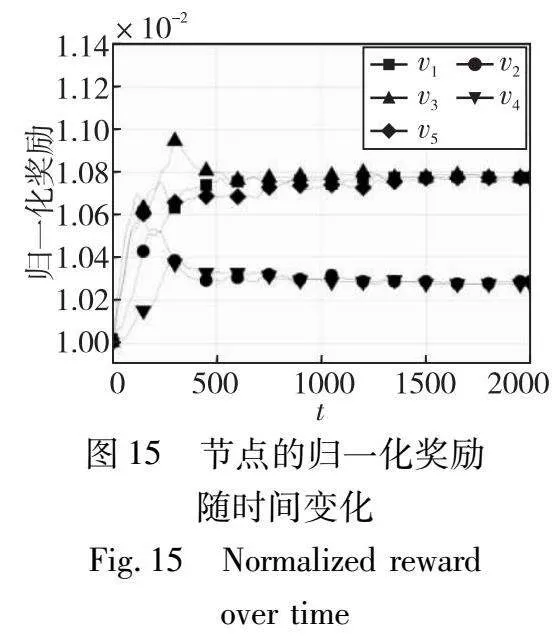
为了展示每个节点的实际存储演变，本实验研究了一个具有五个节点的示例网络。本实验展示了每个节点{v1，…，v5}在每个时期的归一化奖励、存储和通信成本。本实验设置ε=0.9、h=1、k=100和m=200。

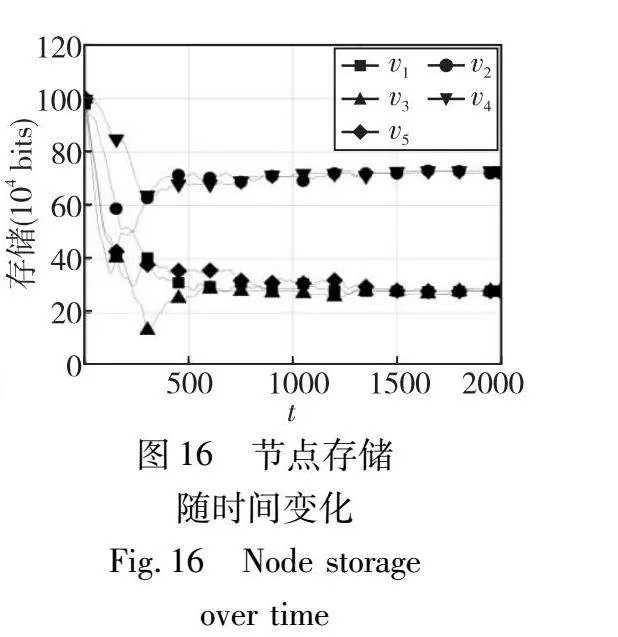
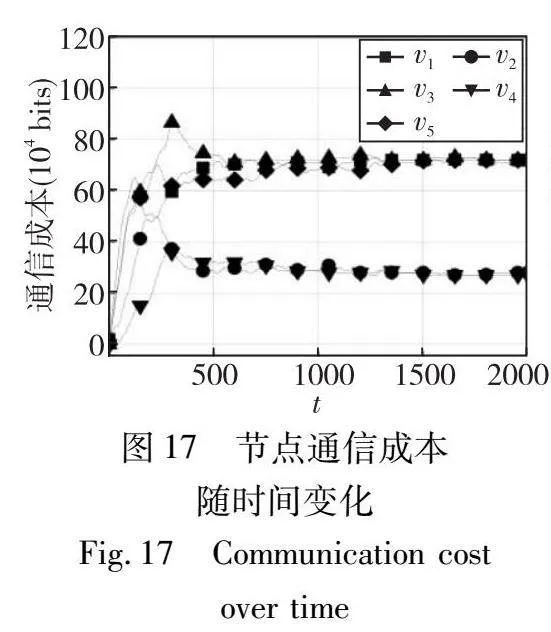
在图15～17中，本实验看到节点的存储量越高，通信成本就越低，反之亦然。如图16所示，节点存储水平在前300个时刻内迅速下降，这是因为最初所有节点都存储k个编码片段，这超出解码一个区块所需的编码片段的数量。在300～1 000个时间周期之间，节点v1、v3和v5的存储水平在收敛到最终值28之前波动，而节点v2和v4的存储水平在收敛到最终值71之前波动。

5.6 节点离开和加入

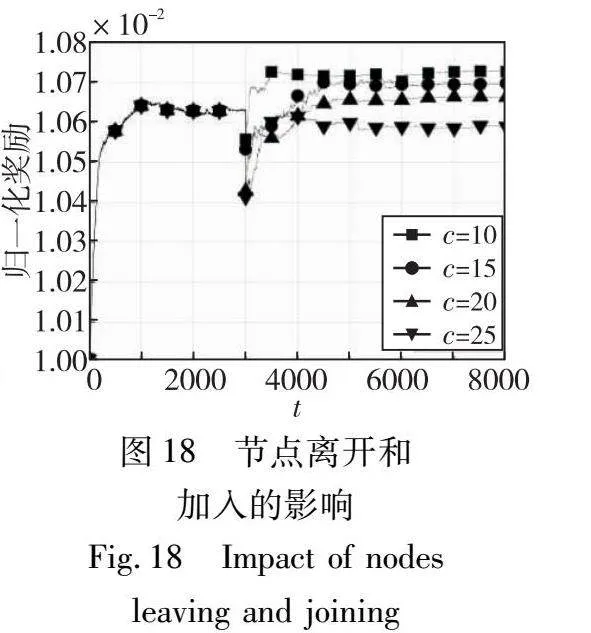
现在讨论一个动态场景，其中节点会随机离开并且新节点加入网络。本实验用c表示离开网络的节点数量和加入网络的新节点数。参数设置为n=100、ε=0.9、h=2、k=100、m=200和c={10，15，20，25}。在这个实验中，有c个随机节点在时刻t=3 000时离开网络，这标志着DLP-CFA达到稳定的编码片段分配状态。同时，c个新节点加入网络，但不存储任何编码片段，即需要从现有节点获取编码片段。

参考图18，随着更多的节点离开和加入，即较高的c值，DLP-CFA需要更多的时间才能收敛。这是因为更多的节点需要学习分配编码片段，并且节点之间存在更多的交互。此外，当c=10时，收敛后的归一化奖励增加，而当c=25时，收敛后的归一化奖励减少。这是因为当大量节点离开网络时，现有节点和新节点都需要存储新的编码片段以满足h跳定位属性。

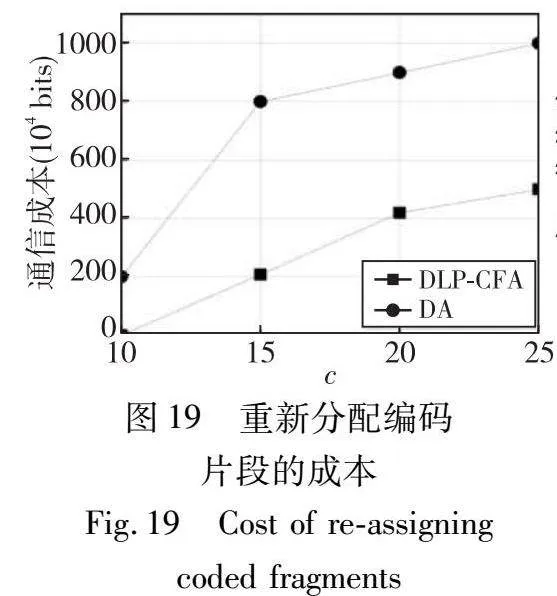
现在本实验研究在c个节点离开和加入网络后，导致编码片段重新分配的通信成本。图19显示DLP-CFA和DA的通信成本都随着c的增加而增加。这种增长可以归因于新节点数量的增加，这需要更多的编码片段重新分配给新加入的节点。此外，图19显示DLP-CFA的通信成本比DA低45%。

5.7 节点故障

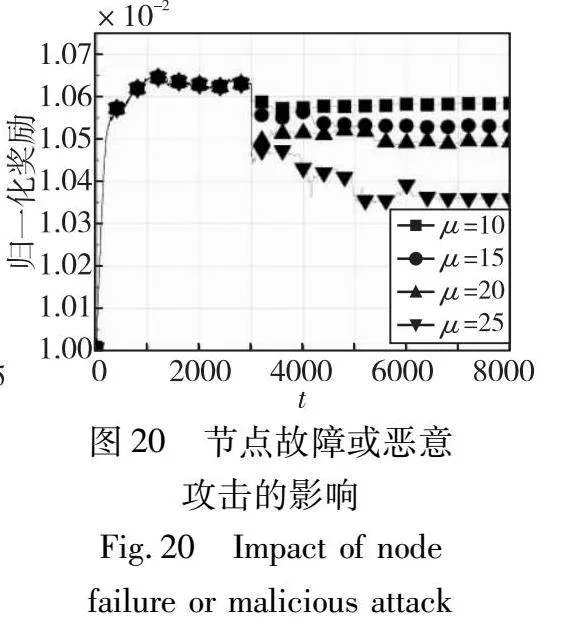
最后，本实验研究当μ个节点发生故障或受到攻击时的情况。在这种情况下，当一个节点发生故障或受到攻击时，可以通过其回复无效的编码片段来进行检测。实验中参数值设置为n=100、ε=0.9、h=2、k=100和m=200，μ从{10，15，20，25}中选择一个值。

从图20中可以看出，随着μ值增加，DLP-CFA收敛速度变慢，这是因为当具有所需编码片段的节点发生故障时，更多的编码片段变得不可使用。此外，归一化奖励随着μ值的增加而减少，这是因为大量节点故障意味着诚实节点需要存储更多的编码片段，以确保区块能够成功解码。然而，当有25个节点发生故障时，归一化奖励最多仅减少3%。

区块链编码存储方法已经在前期研究中［27］利用实际的比特币区块链数据进行了验证，其编码方法与本文方法相似，能够支撑本文方法在实际的区块链中应用的实用性，有效降低区块链节点存储开销。此外，本文方法在文献［27］的基础上进一步优化了节点存储编码数据的分配方法，降低传输成本并确保编码区块链的可解码性。

6 结束语

本文考虑了区块链系统中的分布式编码片段分配问题，为了解决此问题，提出了一种称为DLP-CFA的新颖协议，节点使用该协议以降低存储和通信成本的方式放置编码片段。所进行的模拟研究比较了现有的分布式和集中式算法。结果显示，DLP-CFA在总体奖励方面比这些算法高出7%。本文的研究还考虑节点离开/加入网络和节点故障的场景。结果表明，与之前的算法相比，DLP-CFA 降低了55%的通信成本。总体而言，本文提出的分布式学习协议在解决编码片段分配问题上取得了显著的进展。未来的研究将聚焦于区块链智能合约的数据编码存储问题，通过对智能合约进行编码，并考虑合约的调用频率，以进一步降低区块链存储成本和传输开销。

参考文献：

［1］Xie Junfeng， Yu F R， Huang Tao，et al. A survey on the scalability of blockchain systems ［J］. IEEE Network， 2019， 33（5）： 166-173.

［2］Si Honghao， Niu Baoning. Research on blockchain data availability and storage scalability ［J］. Future Internet， 2023， 15（6）： 212.

［3］Yang Changlin， Chin K W， Wang Jiguang，et al. Scaling blockchains with error correction codes： a survey on coded blockchains ［J］. ACM Computing Surveys， 2024，56（6）： 1-33.

［4］Yu Mingchao， Sahraei S， Li Songze，et al. Coded Merkle tree： solving data availability attacks in blockchains ［C］// Proc of International Conference on Financial Cryptography and Data Security. Cham： Springer， 2020： 114-134.

［5］Das S， Kolluri A， Saxena P，et al. On the security of blockchain consensus protocols ［C］// Proc of the 14th International Conference on Information Systems Security. Cham：Springer， 2018： 465-480.

［6］Wu Huihui， Ashikhmin A， Wang Xiaodong，et al. Distributed error correction coding scheme for low storage blockchain systems ［J］. IEEE Internet of Things Journal， 2020， 7（8）： 7054-7071.

［7］Yang Changlin， Wang Xiaodong， Ashikhmin A. Storage and communication tradeoff for wireless coded blockchains ［J］. IEEE Systems Journal， 2021， 16（2）： 2911-2922.

［8］Yang Changlin， Wang Xiaodong， Jiang Zigui，et al. On min-max sto-rage for resource—restricted clients in coded blockchain systems ［J］. IEEE Internet of Things Journal， 2023，10（20）： 17988-17999.

［9］赵国锋， 张明聪， 周继华， 等. 基于纠删码的区块链系统区块文件存储模型的研究与应用 ［J］. 信息网络安全， 2019 （2）： 28-35. （Zhao Guofeng， Zhang Mingcong， Zhou Jihua，et al. Research and application of block file storage model based on blockchain system of erasure code ［J］. Netinfo Security， 2019（2）： 28-35.）

［10］Dai Mingjun， Zhang Shengli， Wang Hui，et al. A low storage room requirement framework for distributed ledger in blockchain ［J］. IEEE Access， 2018， 6： 22970-22975.

［11］Qi Xiaodong， Zhang Zhao， Jin Cheqing，et al. BFT-Store： storage partition for permissioned blockchain via erasure coding ［C］// Proc of the 36th International Conference on Data Engineering. Pisca-taway， NJ： IEEE Press， 2020： 1926-1929.

［12］Qi Xiaodong， Zhang Zhao， Jin Cheqing，et al. A reliable storage partition for permissioned blockchain ［J］. IEEE Trans on Knowledge and Data Engineering， 2020， 33（1）： 14-27.

［13］Raman R K， Varshney L R. Coding for scalable blockchains via dynamic distributed storage ［J］. IEEE/ACM Trans on Networking， 2021， 29（6）： 2588-2601.

［14］Kadhe S， Chung J， Ramchandran K. SeF： a secure fountain architecture for slashing storage costs in blockchains ［EB/OL］. （2019-06-28） ［2023-12-16］. http：//arxiv.org/abs/1906.12140.

［15］张玉书， 何晓彤， 肖祥立， 等. 一种基于纠删码的区块链账本分组存储优化方法 ［J］. 计算机科学， 2023， 50（10）： 350-361. （Zhang Yushu， He Xiaotong， Xiao Xiangli，et al.

Grouping storage opimization method for blockchain ledger based on erasure code ［J］. Computer Science， 2023， 50（10）： 350-361.）

［16］Qu Bin， Wang L E， Liu Peng，et al. GCBlock： a grouping and co-ding based storage scheme for blockchain system ［J］. IEEE Access， 2020， 8： 48325-48336.

［17］Yu Ruize， Yang Changlin， Liu Ying. FSC： file storage in coded blockchain with C-PBFT consensus protocol ［C］// Proc of International Conference on Service Science. Piscataway， NJ： IEEE Press， 2022： 289-296.

［18］Li Chunlin， Zhang Jing， Yang Xianmin，et al. Lightweight blockchain consensus mechanism and storage optimization for resource-constrained IoT devices ［J］. Information Processing & Management， 2021， 58（4）： 102602.

［19］Perard D， Lacan J， Bachy Y，et al. Erasure code-based low storage blockchain node ［C］// Proc of IEEE International Conference on Internet of Things and IEEE Green Computing and Communications and IEEE Cyber， Physical and Social Computing and IEEE Smart Data. Piscataway， NJ： IEEE Press， 2018： 1622-1627.

［20］尹芙蓉， 朱承宇， 赵斌， 等. 基于CITA区块链的纠删码分片存储实现 ［J］. 华东师范大学学报： 自然科学版， 2021，2021（5）： 48-59. （Yin Furong， Zhu Chengyu， Zhao Bin，et al. Erasure code partition storage based on the CITA blockchain ［J］. Journal of East China Normal University： Natural Science， 2021，2021（5）： 48-59.）

［21］Miller A， Xia Yu， Croman K，et al. The honey badger of BFT protocols ［C］// Proc of the 26th ACM SIGSAC Conference on Computer and Communications Security. New York：ACM Press， 2016： 31-42.

［22］Zheng Zibin， Xie Shaoan， Dai Hongning，et al. An overview on smart contracts： challenges， advances and platforms ［J］. Future Generation Computer Systems， 2020， 105： 475-491.

［23］陈伟利， 郑子彬. 区块链数据分析： 现状、趋势与挑战 ［J］. 计算机研究与发展， 2018， 55（9）： 1853-1870. （Chen Weili， Zheng Zibin. Blockchain data analysis： a review of status， trends and challenges ［J］. Journal of Computer Research and Development， 2018， 55（9）： 1853-1870.）

［24］Wang Qiang， Zhan Zhongli. Reinforcement learning model， algorithms and its application ［C］// Proc of International Conference on Mechatronic Science， Electric Engineering and Computer. Pisca-taway， NJ： IEEE Press， 2011： 1143-1146.

［25］Singh S， Jaakkola T， Littman M L，et al. Convergence results for single-step on-policy reinforcement-learning algorithms ［J］. Machine Learning， 2000， 38： 287-308.

［26］She Daoming， Jia Minping. Wear indicator construction of rolling bearings based on multi-channel deep convolutional neural network with exponentially decaying learning rate ［J］. Measurement， 2019， 135： 368-375.

［27］Yang Changlin， Ashikhmin A， Wang Xiaodong，et al. Rateless coded blockchain for dynamic IoT networks ［EB/OL］. （2023-05-06）. https：//arxiv.org/abs/2305.03895.

［28］王锋， 张强， 刘扬， 等. 从扩展性角度看区块链 ［J］. 计算机应用研究， 2023， 40（10）： 2896-2907. （Wang Feng， Zhang Qiang， Liu Yang，et al. Research progress of blockchain from perspective of scalability ［J］. Application Research of Computers， 2023， 40（10）： 2896-2907.）

［29］胡宁玉， 郝耀军， 常建龙， 等. 基于变色龙hash的区块链可扩展存储方案 ［J］. 计算机应用研究， 2023， 40（12）： 3539-3544， 3550. （Hu Ningyu， Hao Yaojun， Chang Jianlong，et al. Scalable sto-rage scheme based on chameleon hash for blockchain ［J］. Application Research of Computers， 2023， 40（12）： 3539-3544， 3550.）