框架‑分布双段摇摆芯筒‑核心筒体系调谐减震机理及性能研究

摘要： 为了减小传统框架‑核心筒（FCT）结构体系筒体围合面积，进一步提高结构的经济性，提出框架‑分布芯筒‑核心筒（FDCT）高层结构体系；将分布芯筒与摇摆体系相结合形成框架‑分布摇摆芯筒‑核心筒（FDRCT）结构体系，旨在控制结构的变形模式。为了降低高阶振型对高层结构的不利影响，进一步提出具有调谐减震性能的框架‑分布双段摇摆芯筒‑核心筒（FDBRCT）结构体系。建立各结构的动力学模型和方程，并进行平稳随机振动分析，初步证明FDBRCT结构可以更为有效地降低结构的动力响应。对比FCT，FDCT，FDRCT以及FDBRCT结构的时程分析结果，FDCT结构由于刚度被削弱导致抗震能力下降，FDRCT改善了结构变形的不均匀程度，上部楼层加速度有所减小但顶层位移会增大。相较于FDRCT结构，FDBRCT结构的层间位移角最大值明显减小，变形更加均匀，适当降低了顶层位移响应以及内力需求，具备调谐能力的分布双段摇摆芯筒使FDBRCT结构在提高经济性的同时兼具更为优越的抗震、减震性能。

关键词： 框架‑核心筒结构； 分布摇摆芯筒； 分布双段摇摆芯筒； 高阶振型； 调谐减震

中图分类号： TU352.1；TU398+.2 文献标志码： A 文章编号： 1004-4523（2024）09-1593-13

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.016

1 概 述

框架‑核心筒（Frame‑Core Tube， FCT）结构体系是指由延性框架和核心筒组成的具有两道防线的双重抗侧力体系，结构示意图如图1（a）所示。由于具备抗震性能良好和功能灵活等优点，该体系已在超高层建筑中得到广泛应用。在该体系中，作为第一道防线的核心筒由于具备较大的抗侧刚度，承担了大部分水平作用力，而作为第二道防线的框架则主要承担竖向荷载，因此，整个结构的抗侧刚度主要是由核心筒提供的［1‑2］。

在FCT结构体系设计过程中，为了使结构具备足够的抗侧刚度和安全性，通常将核心筒的围合面积控制在比较保守的范围内。然而核心筒通常仅作为辅助设施空间，框架结构才是提供主要使用空间的部分，因此，FCT结构的经济性取决于核心筒围合面积占楼面面积的比例。为了提高结构的经济性，单纯地降低核心筒围合面积必然导致结构抗震性能下降。相关研究表明，在FCT结构体系中分散布置耗能连梁［3］、巨型支撑［4］和伸臂桁架［5］等构件，可以形成新的抗震防线并有效提高结构抗震、减震能力。根据目前高层筒体结构中的分散筒结构［6］以及多筒结构［7］的设计思路，同时结合附加分布式构件增加结构抗震防线的理念，可将传统FCT结构体系中核心筒的围合面积缩小，进而在核心筒周围选取合适的位置均匀并对称布置若干分布芯筒，形成框架‑分布芯筒‑核心筒（Frame‑Distributed Tube‑Core Tube， FDCT）高层结构体系，体系示意图如图1（b）所示。FDCT结构体系的筒体总围合面积小于传统的FCT结构体系，有效提高了结构的经济性以及布局灵活性。区别于传统的在结构中附加构件的理念，本文所提出的FDCT结构体系是在FCT结构体系基础之上进行了结构体系改进，其中的分布芯筒作为子结构形成了一道新的抗震防线，协调了传统FCT结构体系中核心筒与框架的抗震能力，避免了核心筒因刚度较大在地震作用下出现过早屈服破坏的问题。

由于筒体围合面积的降低造成了结构整体抗侧刚度偏小，地震作用下，FDCT结构体系的位移响应必然会增大，层间变形会更加不均匀，宜采取其他构造和措施进行性能提升。相关研究表明，弱化结构中刚度较大的构件基底约束，使其具备一定的摇摆能力，有助于结构层间位移角更加均匀，提高结构的抗震、减震能力。现有的实现摇摆体系的思路主要是将刚度较大的剪力墙［8］、内部填充墙［9］和桁架［10］等构件的基底约束进行释放，进而与框架结构相结合以达到控制结构变形的目的。基于摇摆体系的理念，考虑到FDCT结构体系中的分布芯筒也是刚度较大的构件，可将分布芯筒与摇摆体系相结合进而形成框架‑分布摇摆芯筒‑核心筒（Frame‑Distributed Rocking Tube‑Core Tube，FDRCT）高层结构体系，其结构体系示意图如图1（c）所示。地震作用下，FDRCT结构体系中的分布摇摆芯筒可以降低薄弱层的破坏，使结构变形更加均匀，控制结构的损伤模式，使结构具备更优异的减震能力。

由于高层结构体系的参与振型众多，其动力响应受高阶振型的影响较显著。在附加了摇摆体系的高层结构中，布置单段的摇摆构件对结构一阶振型的控制效果较为明显，但并没有消除高阶振型对动力响应的不良影响［11‑12］。相关研究表明：沿摇摆构件的高度方向有规律地额外布置若干铰接机制，在单段的摇摆构件基础之上形成双段或者多段的摇摆构件，以此来实现对结构高阶振型的控制，可进一步降低结构的动力响应。PANAGIOTOU等［13］提出了一种适用于钢筋混凝土高层墙体的双铰体系，以不同高度的FCT结构体系为数值分析模型，研究发现相较于单铰墙体，双铰墙体明显降低了结构在高阶模态影响下对弯矩和剪力的需求。WIEBE等［14‑15］对附加单段和双段摇摆钢框架的结构进行数值模拟分析并完成了8层缩尺结构振动台试验，对比分析了单段和双段摇摆钢框架对结构动力响应的控制效果。李国强等［16］分析了双段耗能摇摆结构体系的抗震机理，并对附加单段和双段耗能摇摆钢桁架的钢框架在地震下的动力响应进行对比分析。此外，根据双质量调谐阻尼器［17］以及悬吊双摆［18］的减震控制理论，可通过调节双段摇摆构件上摆和下摆所占的高度比例，改变相关质量和刚度灵活调控振动周期，实现对结构多阶振型的减震控制。BROUJERDIAN等［19］在具有自复位功能的单段可控摇摆墙的H，H和H（H为结构的高度）处额外附加了铰支座，并对附加不同双摆高度比例的双段摇摆墙‑框架结构进行了地震时程分析，结果表明，不同结构高度以及不同类型的地震动下，3种双段可控摇摆墙的减震效果各有不同，各种工况下的最优选择也不局限于其中一种类型。目前，在自由双段摇摆结构体系的研究方面，仅探究了将铰支座设置在H处的情况，且主要关注如何利用双段摇摆构件抑制结构高阶振型对动力响应的影响，缺乏关于调控上摆与下摆的高度比例的调谐优化研究。

随着摇摆结构高度的增加，受高阶模态的影响，地震作用下，需要增加摇摆构件的刚度和质量以满足结构的内力需求和牵引力需求，从而更好地控制结构的动力响应。对于本文中的FDRCT高层结构体系，一般会采取增大筒体墙的壁厚或者是提高筒体的围合面积占楼面面积比例的措施，但这必然会造成结构经济性下降。结合双段摇摆结构体系的设计理念，在FDRCT结构体系中的单段摇摆芯筒高度方向额外布置铰支座（以下简称为上部铰支座），使之改设为双段摇摆芯筒，形成框架‑分布双段摇摆芯筒‑核心筒（Frame‑Distributed Bi‑Rocking Tube‑Core Tube，FDBRCT）高层结构体系，旨在保证结构经济性的同时进一步降低结构的动力响应。FDBRCT结构体系示意图如图1（d）所示。

为了探究FDBRCT结构体系对高阶振型的控制效果以及通过自身调谐能力获得更为优越的抗震、减震性能，本文基于弹性地基梁的自由振动理论对上部铰支座的最佳位置进行了初步探索。根据FDCT结构、FDRCT结构和FDBRCT结构的简化动力学模型，基于平稳随机振动原理，分析了FDBRCT结构对动力响应的控制效果。在传统FCT结构基础上设计了FDCT结构、FDRCT结构和FDBRCT结构，并对四种结构进行了多遇地震和罕遇地震下的时程分析，进一步验证了FDBRCT结构的抗震、减震能力。

2 双段摇摆筒体调谐减震机理研究

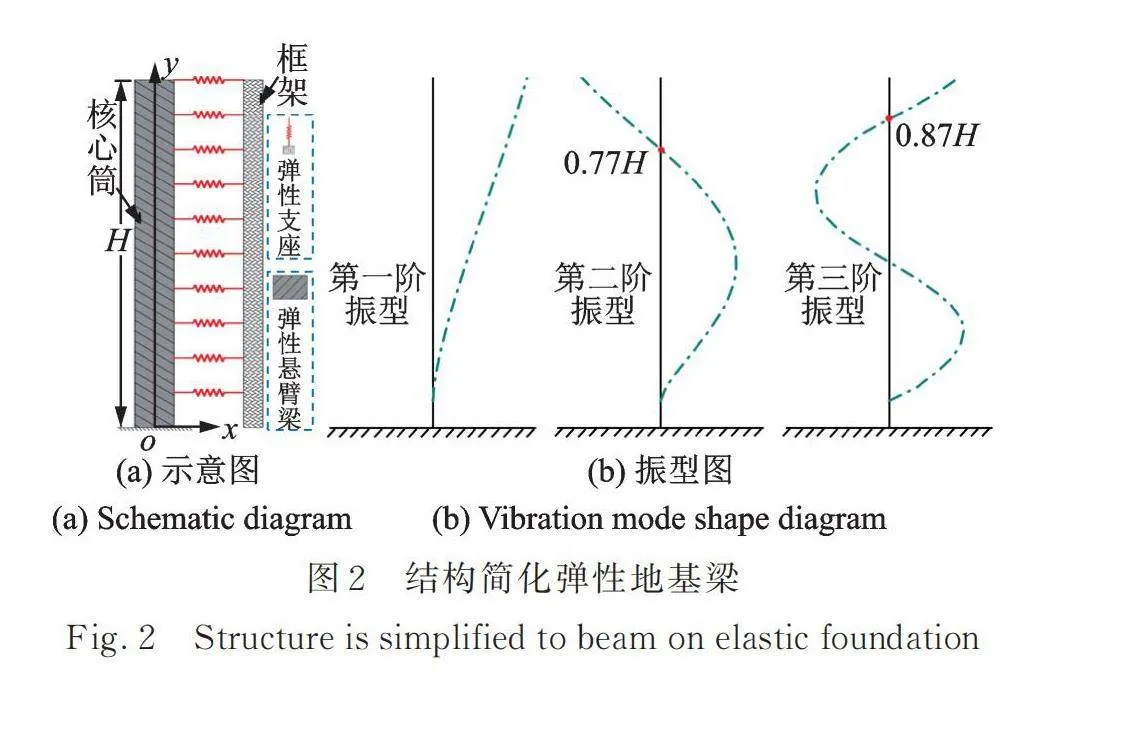
在FCT结构体系中，由于核心筒的刚度较大，结构的各阶振型由核心筒主导。双段摇摆体系的主要目的是通过降低结构动力响应受高阶振型的影响，达到抗震、减震的目的。本文基于自由振动理论求得FCT结构各阶振型函数，进而对FDBRCT结构中双段摇摆芯筒上部铰支座的最佳调谐位置进行探索。为了叙述方便，将上部铰支座以上的部分定义为上摆筒，其下部分为下摆筒。将FCT结构体系中的核心筒简化为悬臂梁，而与核心筒相连接的框架梁则可视为若干的弹性支座，整体结构可视为符合Winkler假定的弹性地基梁［20］，简化模型如图2（a）所示。根据弹性地基梁自由振动微分方程，可求解边界条件为一端固接一端自由的悬臂弹性地基梁的前三阶的振型函数，并获取相应的振型曲线，如图2（b）所示。

对于FDBRCT结构，其中的双段摇摆芯筒可视为在传统FCT结构体系中附加了一个等效双自由度体系，在振动过程中下摆筒与上摆筒之间将产生相互作用力，从而降低高阶振型的不利影响及整体动力响应。根据图2（b）中的振型曲线可知，第二阶振型曲线中正负方向的临界点位于0.77H附近，而结构振动的方向也可视为其自身振动时所受作用力的方向，据此可将上部铰支座设置在此临界点处以制约该振型对结构的影响。根据振型叠加法以及双段摇摆芯筒控制高阶振型的设计理念，虽然双段摇摆芯筒的设计理念主要是为了控制结构第二阶振型的影响，但是第三阶振型的作用也不能忽略，该振型的正负临界点位于0.87H附近。综上，可初步判定双段摇摆芯筒上部铰支座的最佳调谐位置处于0.77H～0.87H。经综合考虑，本文将上部铰支座设置在0.8H处的FDBRCT结构体系作为主要研究对象。

3 FDBRCT结构动力学分析模型

为了从动力学机理角度对FDCT结构、FDRCT结构和FDBRCT结构的抗震、减震性能进行初步探究和对比，分别建立三种结构的等效动力学模型。参考文献［19］对框架‑摇摆墙建立等效动力学模型，可将FDCT结构中的核心筒、框架和分布芯筒分别简化为单自由度体系，考虑等效刚度和阻尼后建立一个三自由度结构体系。将FDCT结构中的分布芯筒基底由固接改设为铰接，即可成为FDRCT结构。根据前文关于上部铰支座最优位置的设计思路，在FDRCT结构中分布摇摆芯筒的1.6h2（h2为分布摇摆芯筒的半高）处再附加铰接点，可形成具有附加分布双段摇摆芯筒的FDBRCT结构。三种体系的等效动力学模型如图3所示。

在FDCT结构动力学模型中，m0，k0和c0分别为核心筒的质量、刚度和阻尼系数；m1，k1和c1分别为框架的质量、刚度和阻尼系数；m2，k2和c2分别为分布芯筒的质量、刚度和阻尼系数；，和分别为核心筒的位移、速度和加速度；，和分别为框架的位移、速度和加速度；，和分别为分布芯筒的位移、速度和加速度；ag则为地面加速度。在FDRCT结构中，需要对分布摇摆芯筒关于摇摆的参数进行设定，而核心筒和框架的相关参数均与FDCT结构相同。如图3（b）所示，当分布摇摆芯筒受到外部激励其重心由o2摆动至z2过程中，x2为分布摇摆芯筒的相对位移；，和分别为分布摇摆芯筒的转角、角速度和角加速度。对FDBRCT模型，其分布双段摇摆芯筒中上摆筒和下摆筒的相关参数可根据单段的分布摇摆芯筒类推得到，如图3（c）所示，在单段分布摇摆芯筒相关参数基础之上，下角标为“2d”和“2u”分别表示下摆筒和上摆筒的参数。

根据图3（a）的动力学模型，建立FDCT结构的动力学方程如下：

（1）

（2）

（3）

由于FDCT结构的动力学方程与文献［15］所研究的双质量调谐阻尼器相同，在此不再详述。根据FDRCT结构动力学模型可知，分布摇摆芯筒在转动力矩、地震作用、重力和结构抗力综合作用下其质点由o2摆动至z2，由此可以建立FDRCT结构中框架和核心筒的动力学方程以及分布摇摆芯筒的力矩平衡方程式如下：

（4）

（5）

（6）

式中 I2为分布摇摆芯筒绕转动点的转动惯量，I2=（cos2α2+1/3）；R2为分布摇摆芯筒对角线长度的一半，=+；α2为分布摇摆芯筒对角线与高度方向的夹角，tanα2=b2/h2；b2为分布摇摆芯筒的半宽；g为重力加速度。

由图3（c）可知，附加双段摇摆体系的FDBRCT结构中上摆筒和下摆筒是并联关系，因此，在下摆筒的质点由o2d摆动至z2d和上摆筒的质点由o2u摆动至z2u的过程中，上摆筒和下摆筒之间将产生相互的作用力，参考FDRCT结构中单段分布摇摆芯筒的受力状态，可建立FDBRCT结构中关于框架和核心筒的动力学方程以及关于分布双段摇摆芯筒的力矩平衡方程式如下：

（7）

（8）

（9）

（10）

式中 I2d和I2u分别为下摆筒和上摆筒绕转动点的转动惯量。

在普通激励下，结构中摇摆构件的摆动角度一般不超过5°。因此，以分布双段摇摆芯筒的下摆筒为例，当转角θ2d<5°时，式（9）和（10）中的sinθ2d≈θ2d，cosθ2d≈1，且下摆筒在摆动过程中的相对位移x2d与质点o2d移动至z2d的水平位移分量相等，该值可表示为：

（11）

根据sinθ2d≈θ2d，并对上式进行求导可求得下摆筒的角加速度为。同理，上摆筒在摆动过程中的相对位移x2u与质点o2u移动至z2u的水平位移分量相等，而x2u实质上是下摆筒摇摆过程相对位移x2d与上摆筒自身摇摆过程产生的相对位移之和，因此，x2u可表示为：

（12）

由此，上摆筒的角加速度为。

4 结构平稳随机振动对比分析

为了探讨外部激励为地震作用时的结构力学性能，并考虑到地震动的强随机性及结构参数的影响，本文将FCT结构简化为两自由度线性模型、FDCT结构和FDRCT结构简化为三自由度线性模型、FDBRCT结构简化为四自由度线性模型。根据结构的动力学方程，以分布芯筒、分布摇摆芯筒和分布双段摇摆芯筒（下文总称为芯筒）的相关参数为变量，分别进行地震作用下的平稳随机振动分析，对比分析不同结构的减震效果。

对于多自由度线性结构，在平稳随机干扰Y（t）的作用下，结构的随机运动方程为：

（13）

式中 M，C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；，和分别表示结构的加速度、速度和位移响应过程；Y（t）为零均值的平稳随机过程；r为外部荷载的位置及幅值向量。

结构的质量矩阵和刚度矩阵可根据式（1）～（12）求得，由于FDBRCT结构受力特性最为复杂，限于篇幅，在此仅给出FDBRCT结构的质量矩阵和刚度矩阵，分别如下所示：

（14）

（15）

将结构的激励Y（t）转化为频域的函数，利用振型分解法将多自由度结构分解为多个单自由度结构，并计算其频响函数，进而求得结构平稳随机振动的位移响应自谱密度，对比结构在地震动下的位移动力响应。地震动加速度谱采用Clough‑Penzien谱，其功率谱密度函数为：

（16）

参考文献［22］，式中地基土卓越频率ωg取为13.96 rad/s，地基土阻尼比ζg取为0.8，第二个过滤层的卓越频率ωf取为2.09 rad/s，第二个过滤层的阻尼比取为0.8，谱强度因子S0取为0.021。

根据实际工程的设计经验，对进行平稳随机振动的结构线性模型各子结构的参数进行初始取值。在FCT结构中，核心筒质量取为5.8×106 kg，刚度为1.1×108 N/m，框架的质量为2×107 kg，刚度为4.7×107 N/m，FDCT结构、FDRCT结构和FDBRCT结构中的核心筒以及框架部分相关参数均与FCT结构相同。FDCT结构增设的分布芯筒初始质量设为2.3×107 kg，初始刚度设为8.9×107 N/m。分布芯筒基底约束释放形成分布摇摆芯筒后将导致筒体刚度下降，进而造成结构周期增大。可根据摇摆结构相关设计经验对FDRCT结构中分布摇摆芯筒参数进行设定，相较于分布芯筒，分布摇摆芯筒的周期增大20%～40%是较为适宜的，一般情况下可设定为30%。由结构的周期T、质量m和刚度k的关系式和可知，分布摇摆芯筒的刚度可设置为分布芯筒刚度的60%，而质量不变。而在FDBRCT结构中，首先在分布摇摆芯筒参数取值基础之上，根据下摆筒与上摆筒的高度比例4∶1，下摆筒的质量和刚度取为分布摇摆芯筒的80%，又由于上摆筒受双重摇摆机制控制，其刚度需要在比例取值基础上再进行40%折减，因此上摆筒的质量和刚度取为分布摇摆芯筒的20%和12%。

由于附加摇摆体系的结构动力学方程中需要确定摇摆构件的高度，参考文献［21］对摇摆刚体高度的计算方法，首先对FDRCT结构单段分布摇摆芯筒的高度进行计算。将没有附加分布摇摆芯筒的FCT结构的周期设为1.6 s，则其初始频率ωs=2π/1.6，引入频率参数p，p与ωs的关系取为ωs/p=10，因此，FDRCT结构模型中分布摇摆芯筒对角线的半长R2=3g/（4p2）=48.32 m，设tanα2=1/6，则分布摇摆芯筒的等效半高h2为47.67 m。根据分布摇摆芯筒的属性取值，可以得到FDBRCT结构理论模型中分布双段摇摆芯筒下摆筒和上摆筒的相关属性取值，其中h2d=47.67 m，h2u=9.53 m，R2d=38.95 m，R2u=12.41 m。结构的阻尼比为0.05，结构所在地区为8度区Ⅲ类场地，设计地震分组为一组。

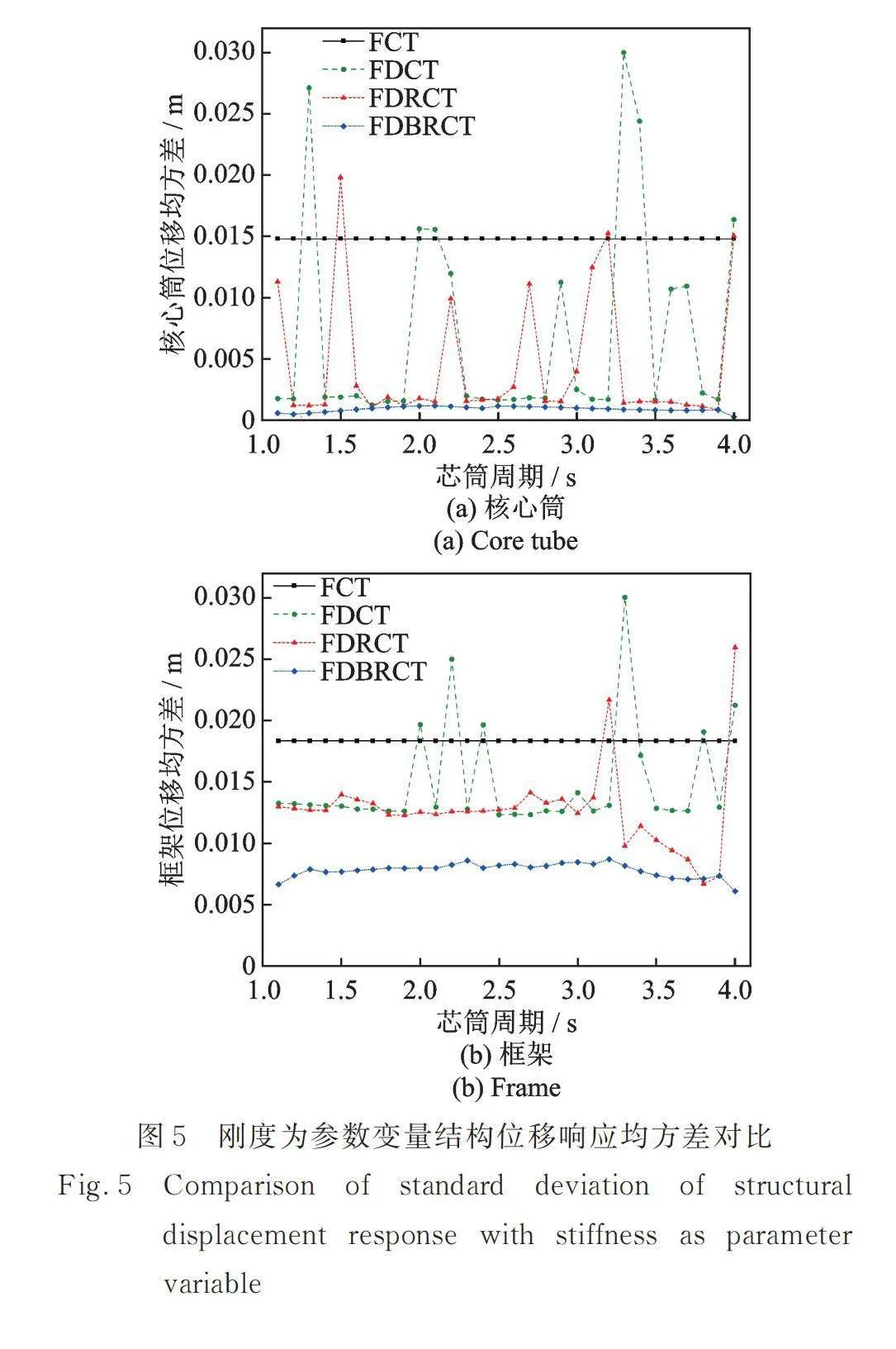
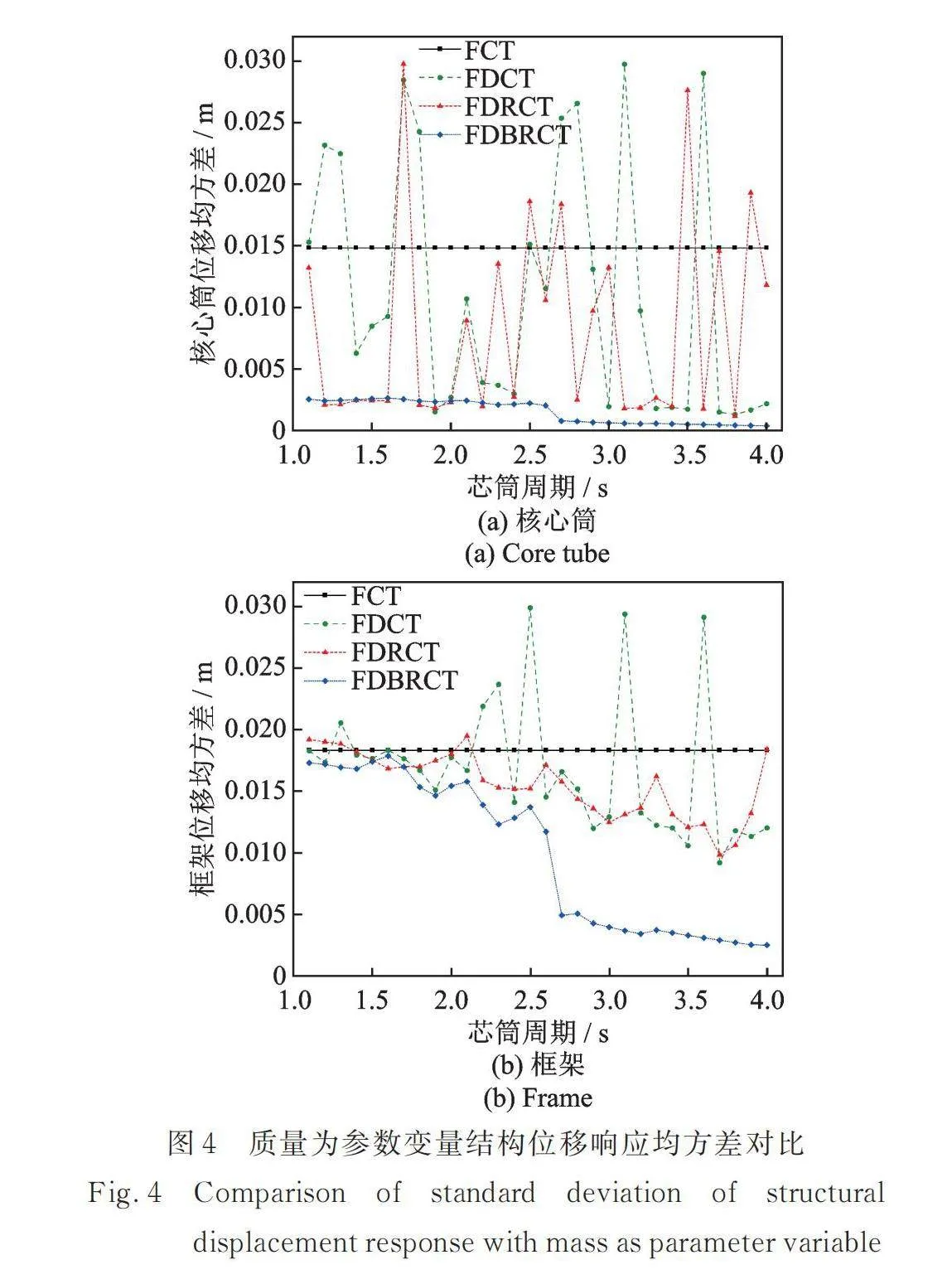
进行平稳随机振动分析时，首先根据工程设计经验，将结构中的芯筒的周期设定为以1.1～4 s，周期间隔取为0.1 s，共计30种工况，进而分别以分布（摇摆）芯筒以及下摆筒的初始刚度和初始质量为参照点，将其质量和刚度作为变量进行参数分析。根据不同结构的质量矩阵和刚度矩阵，参考图3中的结构动力学模型，求解结构中核心筒和框架的位移x0和x1的均方差，以此为对比依据分析结构在不同工况下的减震效果。图4和5分别为以芯筒的刚度和质量为变量得到的核心筒和框架的位移均方差对比图，其中FCT作为初始结构，其计算结果可以作为基准值，对FDCT结构、FDRCT结构和FDBRCT结构的结果进行对比。

从图4和5的结果可以看出：多数工况下FDCT结构和FDRCT结构的核心筒及框架位移响应均方差都要小于FCT结构，而FDRCT结构具备减震效果的工况多于FDCT结构，验证了分布芯筒与摇摆体系的结合可以使结构具备更优的减震性能。进一步观察FDBRCT结构的位移响应情况，可以发现绝大部分工况下其位移均方差都要小于FCT结构；且相较于FDRCT结构，FDBRCT结构的减震效果也更为优越和稳定。综上所述，在原结构中附加摇摆构件的FDRCT结构和FDBRCT结构展现出了显著且稳定的减震效果，而由于FDBRCT结构中分布双段摇摆芯筒所具备的调谐控制作用使结构的减震能力更为突出。

5 结构地震响应对比分析

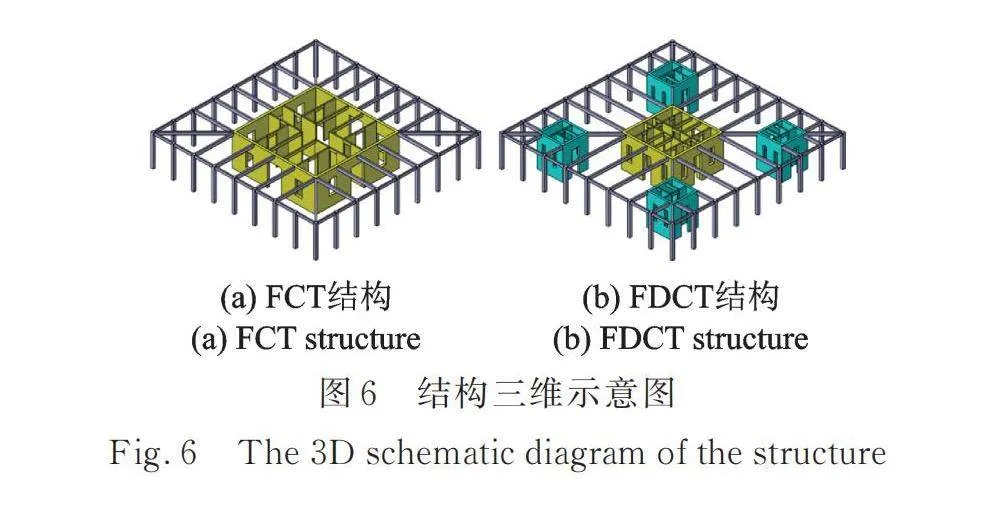
为进一步验证和研究FDBRCT结构的抗震、减震性能，将参考文献［23］设计的典型FCT结构作为原始模型，依据本文所提出的附加分布芯筒高层结构的设计理念，首先将FCT结构的核心筒围合面积进行适当缩小，并在结构中核心筒与框架角柱的连线位置中部均匀布置四个分布芯筒，进而形成FDCT结构，要求FDCT结构的筒体总围合面积要小于FCT结构，FCT结构与FDCT结构的结构示意图如图6所示。在FDCT结构中的分布芯筒基底布置铰接机制使之成为分布摇摆芯筒，即可成为FDRCT结构；在FDRCT结构基础之上依据前文所述的双段摇摆调谐减震理念在分布摇摆芯筒的0.8H处再布置第二个铰接机制形成FDBRCT结构。使用SAP2000有限元分析软件建立四种结构的模型，选取真实地震动时程并对结构的动力响应进行对比分析，探讨不同结构的抗震、减震性能。

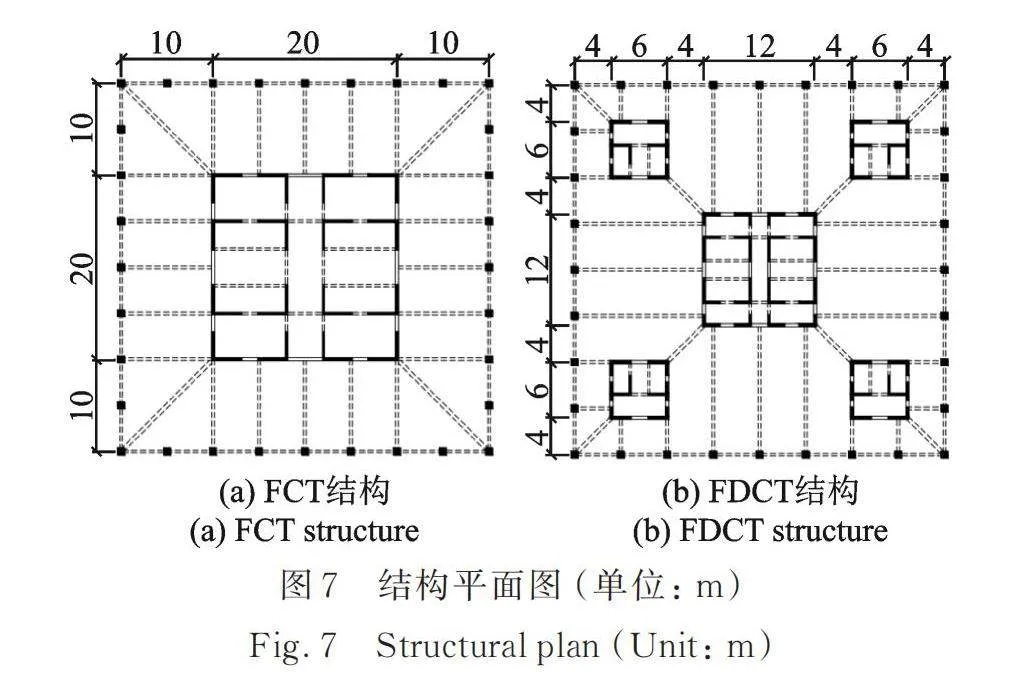
5.1 结构信息

FCT结构的总高为100 m，共25层，层高4 m，建筑总平面尺寸为40 m×40 m，其中核心筒的平面尺寸为20 m×20 m，筒体的围合面积占比为25%。而FDCT结构则是在FCT结构基础之上首先将核心筒的平面尺寸减小为12 m×12 m，增设的四个分布芯筒平面尺寸为6 m×6 m，此时筒体的总围合面积为18%。FCT结构的平面图如图7（a）所示，FDCT结构的平面图如图7（b）所示。FDRCT结构与FDBRCT结构仅是在FDCT结构的基础之上加入摇摆铰接机制，其他结构构件信息均相同。结构位于8度抗震设防区，场地类别为Ⅲ类，设计地震分组为第一组。

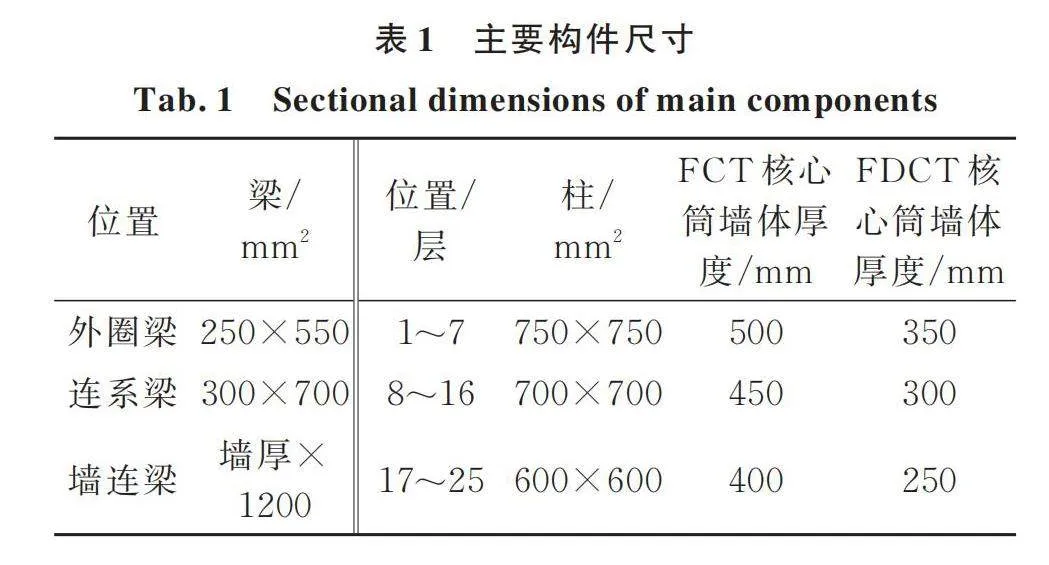
相对于FCT结构，虽然FDCT结构的筒体围合面积有所减小，但是筒体中墙体的数量即截面尺寸总和是有所增大的，基于本文提高框架‑核心筒结构经济性的思想，在FCT结构基础之上减小FDCT结构筒体外墙的壁厚，以实现控制结构建筑材料成本的目的，而其他结构构件的尺寸不变。FCT结构主要构件尺寸以及FDCT结构需要改变的构件尺寸如表1所示，其中分布芯筒墙体厚度与核心筒保持一致。根据表1的构件信息计算可知，相较于FCT结构，虽然FDCT结构的原材料用量依然会有所增加，但是FDCT结构的框架面积提高了7%，由此带来的建筑经济效益是明显的。综合比较，FDCT结构在经济性方面更有优势。结构的有限元模型中框架的梁柱均采用杆系单元，筒体中的墙体，弹性阶段采用壳UOcYy+hm6ENw2vgjyu/p8w==单元，而在弹塑性阶段则采用分层壳单元来模拟墙体的非线性行为。梁端和柱端在结构弹塑性阶段的变形采用塑性铰单元模拟；楼板采用壳单元进行建模。构件的纵筋型号均为HRB400，其屈服强度为413 MPa，极限强度为620 MPa。梁柱及筒体墙所使用混凝UOcYy+hm6ENw2vgjyu/p8w==土的抗压强度为60 MPa，板的则为35 MPa。

将FDCT结构中分布芯筒的基底约束释放并设置铰接节点即可成为FDRCT结构中的分布摇摆芯筒。而FDBRCT结构中除了在分布摇摆芯筒基底设置铰接点外，在该结构的80 m处即楼层的20层将芯筒墙体的底部分割并设置铰接点，即可成为具有调谐能力的分布双段摇摆芯筒，鉴于FDBRCT结构体系最为复杂，在此仅展示其有限元模型，如图8所示。而在实际工程当中，考虑到分布（双段）摇摆芯筒所具备的双向摇摆能力，参考文献［24］设计了芯筒中所需要的双向齿状铰支座，装置示意图如图9（a）所示，该铰支座可实现与墙体等宽，具备摇摆能力的同时也不影响筒体内部空间的使用。在摇摆结构中，通常与摇摆构件相连接的梁端部需要设置为铰接以保证转动能力，参考文献［25］设计了FDBRCT结构中与芯筒相连接框架梁的两端所需的铰接装置，装置示意图如图9（b）所示。

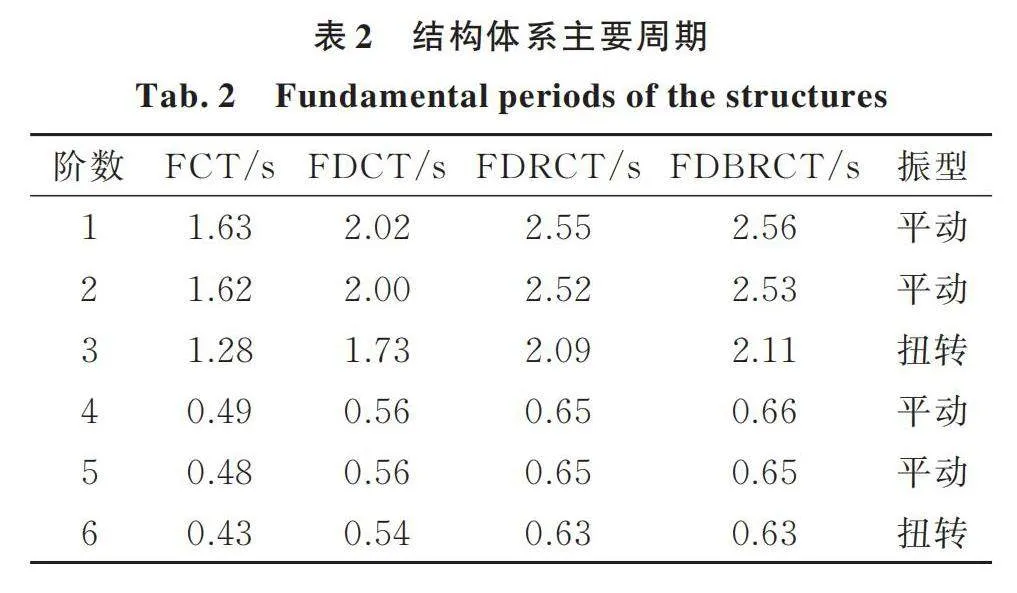
对FCT结构、FDCT结构、FDRCT结构和FDBRCT结构的有限元模型进行模态分析，各结构前六阶周期如表2所示。各个结构的振型相似，与FCT结构相比，本文提出的高层结构并没有改变原始结构的振动特性。FDCT结构相对于FCT结构周期增大的原因是筒体围合面积的减小，而由于摇摆体系的加入，FDRCT结构的周期将进一步减小。相对于FDRCT结构，FDBRCT结构的周期增幅不大，是由于具有调谐能力的分布双段摇摆芯筒中，上摆的高度比例偏小，因而对结构的刚度削弱程度较小。

5.2 分布双段摇摆芯筒调谐效果验证

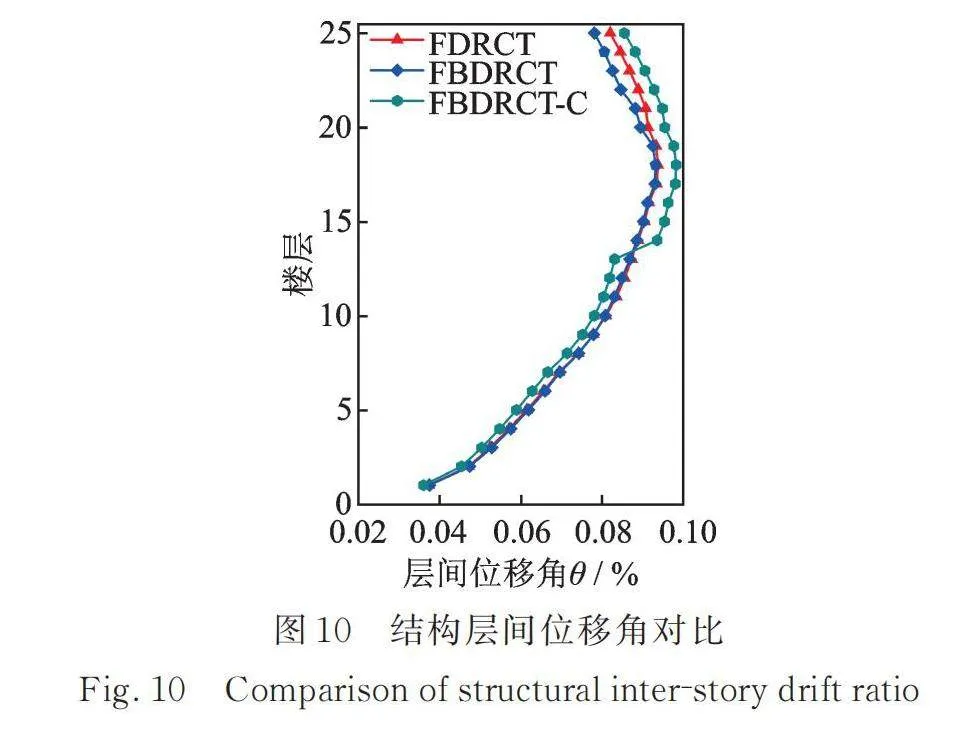
对于具有摇摆构件的高层结构体系，为了验证本文所提出的分布双段摇摆芯筒中，下摆筒与上摆筒的高度比例（下文简称为双摆芯筒比例）为8∶2相较于传统双段摇摆构件（比例为5∶5）具备更优的调谐作用，首先在FDBRCT结构有限元模型（双摆芯筒比例8∶2）基础之上，设计对比模型FDBRCT‑C结构，定义其分布双段摇摆芯筒中的上部铰支座设置在0.5H处（双摆芯筒比例5∶5）。以附加单段分布摇摆芯筒的FDRCT结构为参照模型，选取5组天然地震动，并对FDRCT结构、FDBRCT结构和FDBRCT‑C结构进行多遇地震下的动力时程分析，以结构层间位移角为判断依据对比FDBRCT结构和FDBRCT‑C结构相对于FDRCT结构的减震效果。

图10为附加不同比例双摆芯筒的结构在不同地震动下层间位移角均值对比图，可以看出，相较于附加分布摇摆芯筒的FDRCT结构，附加分布双段摇摆芯筒且比例为8∶2的FDBRCT结构中以上部铰支座为分界点，其层间位移角在上部铰支座之上的楼层减小，之下的楼层变化不大。原因在于输入的地震动为多遇地震，结构所受地震作用较小，此时的分布双段摇摆芯筒的摇摆功能只对结构起到了小幅度的控制作用，下摆筒所在位置的楼层基本与单段的分布摇摆芯筒作用相同，上摆筒由于双摇摆功能的影响对结构的上部楼层变形起到了一定的抑制作用。而对比双摆芯筒比例为5∶5的FDBRCT‑C结构，其层间位移角在上部铰支座之上的楼层层间位移角出现了明显的增大，在上部铰支座所处的楼层出现了明显的位移突变，不仅使结构的最大层间位移角有所增大而且结构变形的均匀程度下降也更为明显。综上所述，FDBRCT‑C结构对其变形模式产生了不利影响，而本文所提出的FDBRCT结构其附加的分布双段摇摆芯筒在多遇地震下对结构的控制作用略优于单段的分布摇摆芯筒，一定程度上验证了下摆筒与上摆筒的高度比例为8∶2使FDBRCT结构具备调谐减震的能力。

5.3 结构地震反应分析

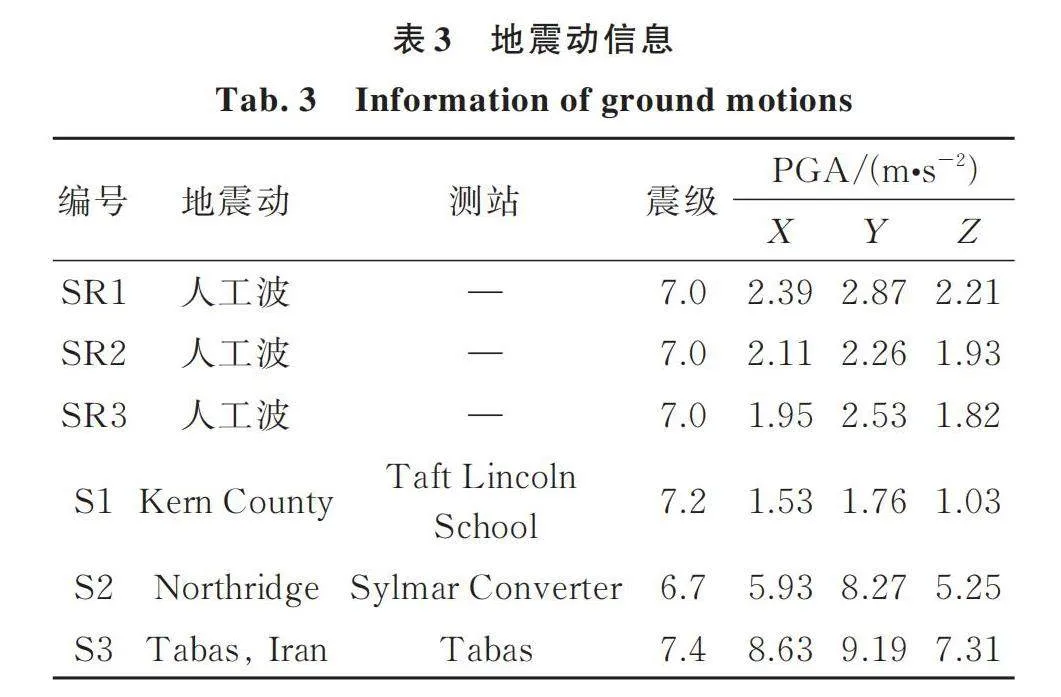
为了对比分析FCT结构、FDCT结构、FDRCT结构和FDBRCT结构在多遇地震及罕遇地震下的动力响应情况，并进一步探讨FDBRCT结构基于分布双段摇摆芯筒所实现的调谐减震的能力，本文选取3组人工地震动和3组天然地震动作为外部激励，地震动信息如表3所示。在进行地震动时程响应分析之前，首先将所有地震动统一按照加速度峰值为0.07g（多遇地震）和0.4g（罕遇地震）分别进行调幅，每组地震动的分量分别按照结构的X，Y和Z方向进行输入且加速度峰值按照0.85∶1∶0.65的比例进行再次调幅。

为了验证前文随机振动分析的基本结论，本文首先根据Clough‑Penzien功率谱和抗震设计反应谱生成了3组人工地震动，其频谱特征具有良好的统计意义。将相关地震动作为激励输入到有限元模型中进行弹性时程分析。结构顶层加速度响应的平均功率谱如图11所示。可以看出，相较于FCT结构，FDCT结构的功率谱峰值出现了增大，而FDRCT结构和FDBRCT结构则呈现不同程度的降低，二者均具备一定的减震能力，且具备调谐功能的FDBRCT结构的减震效果更优，该结论与前文平稳随机振动分析所得结论基本相符。

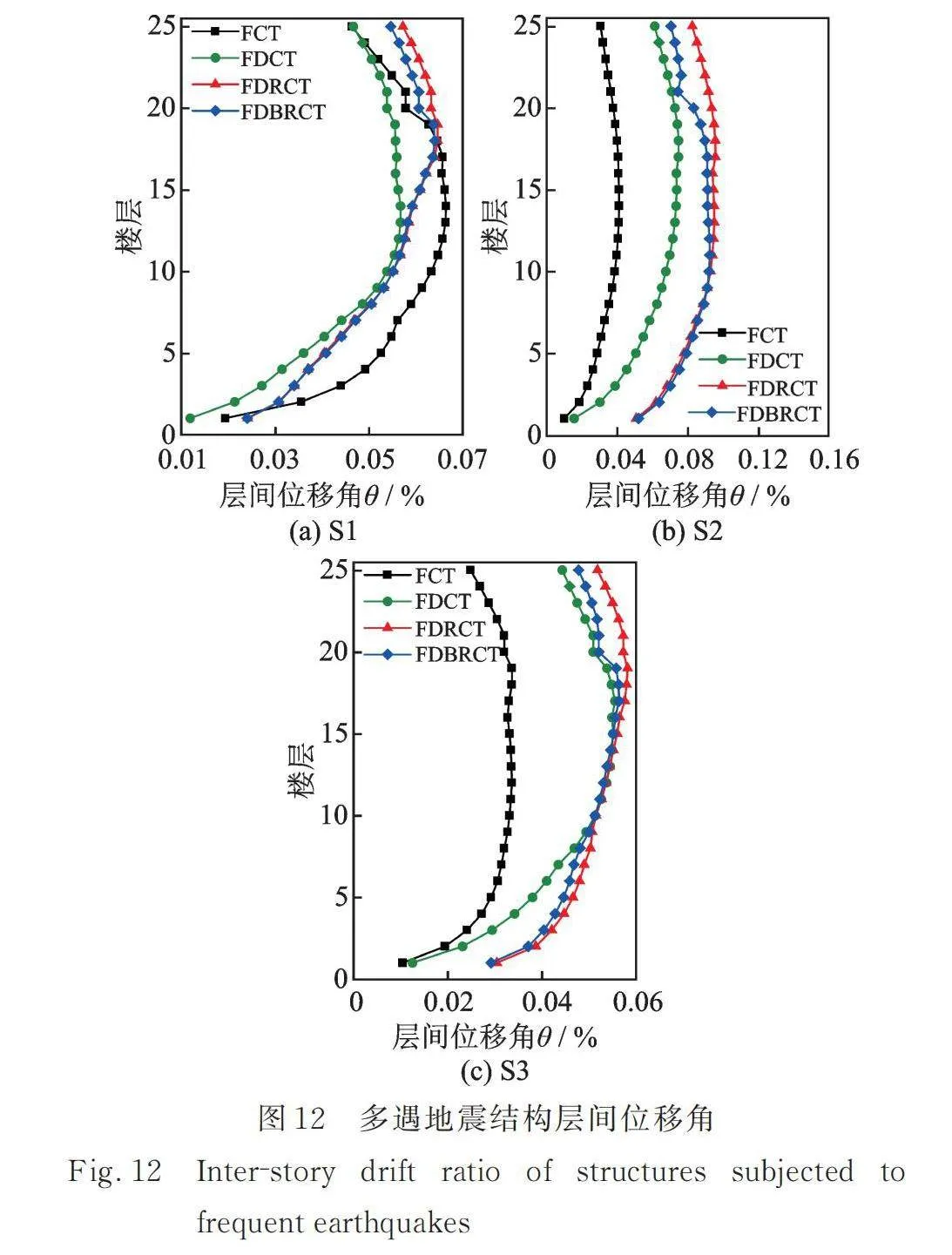
图12和13为不同结构在S1，S2和S3地震动的多遇地震以及罕遇地震下最大层间位移角对比图，四种结构层间位移角均未超过《建筑抗震设计规范》［26］所规定的框架‑核心筒结构在弹性状态下为1/800和塑性状态下为1/100的限值，说明四种结构的安全性均达到了设计要求。由于附加芯筒的高层结构体系其筒体的围合面积减少，结构整体的刚度有所下降，导致多数地震动下FDCT结构、FDRCT结构和FDBRCT结构的层间位移角均大于FCT结构。由于摇摆体系的加入，FDRCT结构的刚度进一步降低，因此层间位移角小于FDCT结构。但无论是在多遇地震还是在罕遇地震下，FDRCT结构的层间位移角都更为均匀，表明附加的分布摇摆芯筒有效地控制了结构的变形模式，减小了结构薄弱层破坏。多遇地震下，由于所受地震作用较小，结构的摇摆能力未能充分发挥，FDRCT结构层间位移角均匀性的提高程度要小于在罕遇地震下。

对比附加分布摇摆芯筒的FDRCT结构与附加分布双段摇摆芯筒的FDBRCT结构，同样是由于多遇地震下结构摇摆能力不足的原因，FDBRCT结构中仅有上部楼层的层间位移角有所减小，但是由于在多遇地震下结构依靠自身刚度足以抵抗地震破坏，所以FDBRCT结构中分布双段摇摆芯筒对结构减震能力提高幅度较小是可以接受的。而在罕遇地震下，相较于FDRCT结构，三条地震动下，FDBRCT结构最大层间位移角分别减小了12.1%，12.6%和10.3%，且在结构层间位移角较大的上部楼层整体都有所减小，显著提高了结构变形的均匀程度。通过对结构进行多遇地震与罕遇地震下的动力时程分析，更加全面地验证了FDBRCT结构中分布双段摇摆芯筒可以实现对结构的调谐减震作用，能够降低高阶振型对结构的不利影响。

采用层间位移集中系数（DCF）对结构各楼层层间变形的不均匀程度进行量化评价，DCF值越小表示结构楼层变形越均匀，相关表达式为：

（17）

式中 θi为第i层的层间位移角；zi为第i层的层高；H为结构总高度。多遇地震以及罕遇地震下，FCT结构、FDCT结构、FDRCT结构和FDBRCT结构的DCF值参见表4和5。

从表4和5可知，由于FDCT结构抗侧刚度较低，其DCF值要大于FCT结构。相较于FDCT结构，在多数地震动下加入摇摆机制的FDRCT结构DCF值明显减小。对比FDRCT结构和FDBRCT结构，多遇地震下FDBRCT结构的DCF值出现了小幅度增大，而在罕遇地震下由于摇摆功能得到更充分的发挥，FDBRCT结构的DCF值有所减小，结构变形更加均匀，证实了分布双段摇摆芯筒具有更为优良的减震效果。

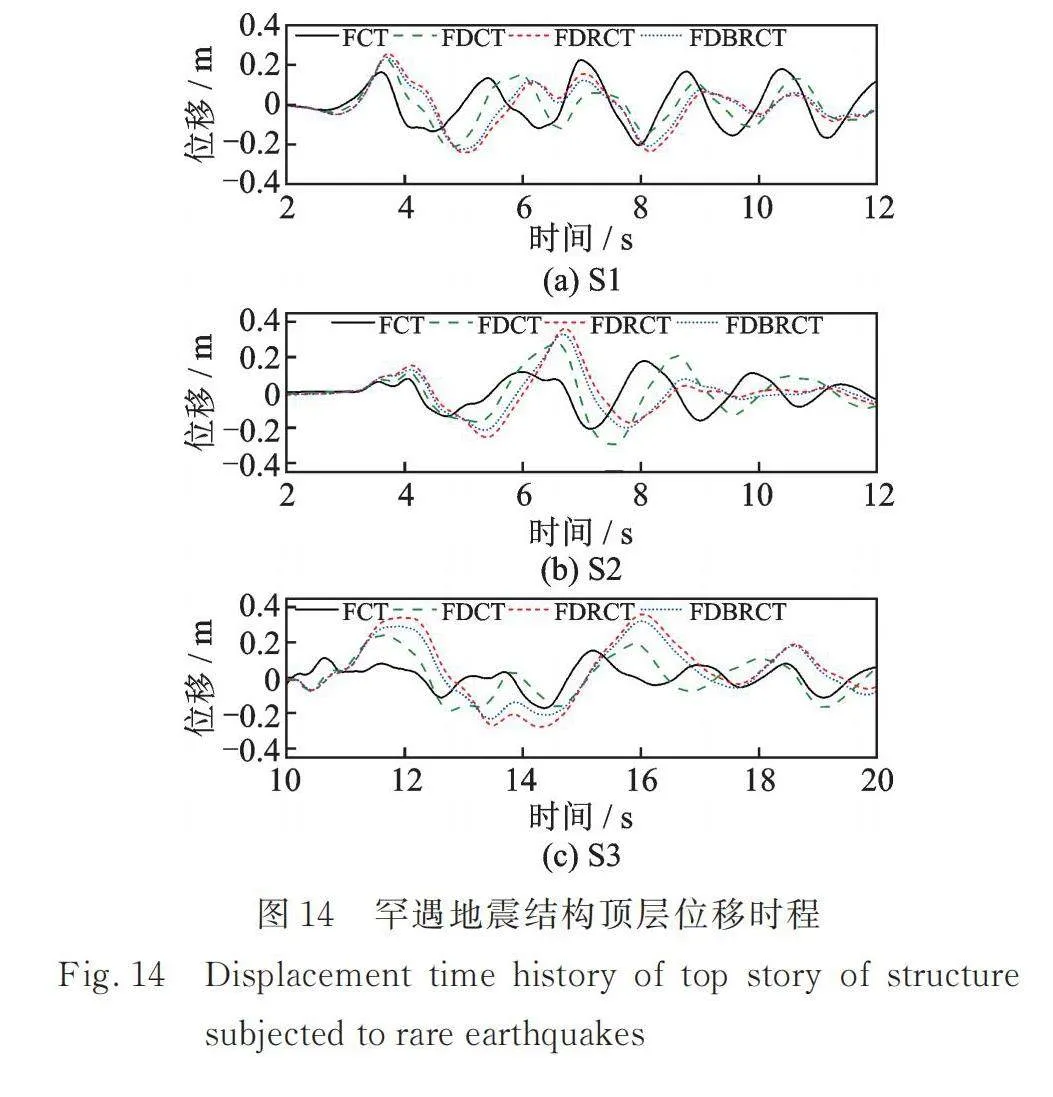
图14为四种结构在不同罕遇地震动时的顶层位移时程。通过对比可发现，由于结构刚度的下降，FDCT结构相对于FCT结构其顶层位移会整体增大，而附加摇摆体系后的FDRCT结构顶层位移会进一步增大，但是鉴于摇摆理念在于控制结构的变形模式使其更加均匀，顶层位移的适当增大是可以接受的。而当结构中附加分布双段摇摆结构之后，FDBRCT结构相较于FDRCT结构适当抑制了结构顶层位移响应，改善了单段摇摆构件使结构位移响应增大的不利影响。

结构在多遇地震下的加速度响应可以反映振时舒适度。由图15四种结构在不同地震动下层间加速度对比可知，相较于FCT结构，具有分布芯筒的FDCT结构的加速度响应出现一定程度的降低。而具有摇摆体系的FDRCT结构，加速度响应整体要小于FCT结构和FDCT结构，由于地震动的随机性，在S1和S3地震动下，FDRCT结构的各层加速度，尤其是在中上部楼层，减小幅度十分明显，由于结构较高楼层的加速度响应较为剧烈，因此FDRCT结构中分布摇摆芯筒能够有效提高结构振动舒适度。FDBRCT结构的各层加速度峰值与FDRCT结构基本一致，附加的分布双段摇摆芯筒相较于分布摇摆芯筒并不会对结构的加速度响应产生影响。

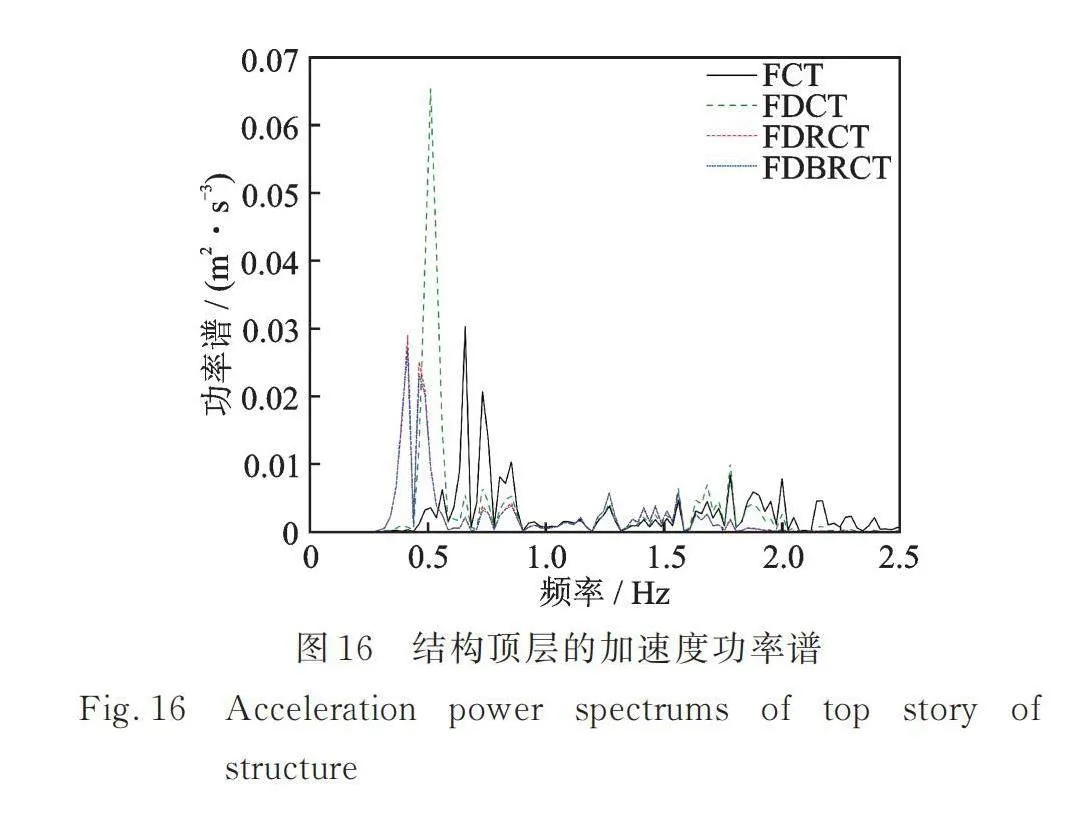
为了进一步验证FDBRCT结构相较于其他结构具备更优越的抗震、减震性能，选取S1地震波下的结构顶层响应结果并计算得到了四种结构的加速度功率谱，如图16所示。FDCT结构的功率谱曲线峰值和包络面积要大于FCT结构，而FDRCT结构和FDBRCT结构相对较小，从能量角度证明附加摇摆芯筒的结构具备更为优越的减震性能。相较于FDRCT结构，FDBRCT结构功率谱曲线峰值更小，充分说明附加分布双段摇摆芯筒可更为有效地提高结构的减震能力。

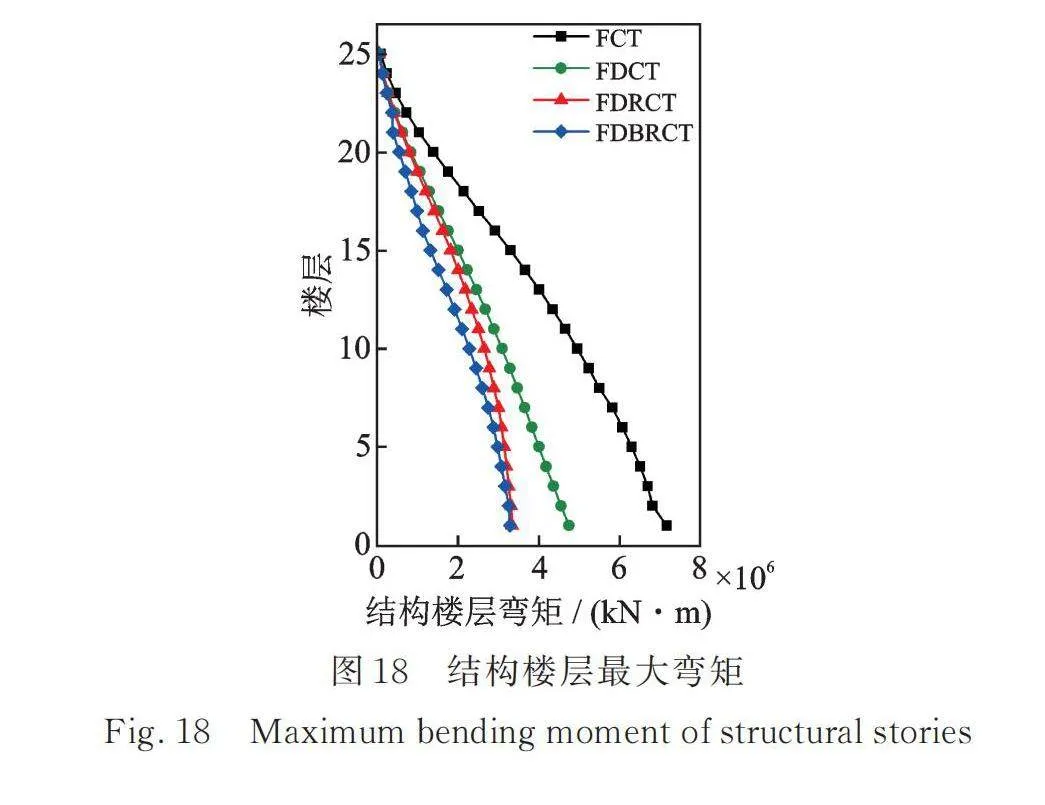
图17和18为S1地震波下不同结构的最大楼层剪力和弯矩对比图。可以看出，附加芯筒的高层结构可以有效地降低结构的内力，其中附加摇摆体系的结构降低幅度更大。相较于FDRCT结构，附加分布双段摇摆芯筒的FDBRCT结构降低了结构较低楼层的剪力，而中部楼层有所增加，由于结构较低楼层的剪力值较大，因此分布双段摇摆芯筒依然对控制结构剪力有良好的贡献。在控制楼层弯矩方面，FDBRCT结构的弯矩在整体上低于FDRCT结构，表明其降低了结构内力需求。鉴于高阶振型对高层结构的剪力和弯矩产生的不利影响更为显著，以上结果充分证明分布双段摇摆芯筒能够对结构高阶振型进行有效控制。

6 结 论

针对FCT结构筒体围合面积过大的不足，本文提出了附加分布芯筒的FDCT结构，摇摆体系与分布芯筒结合形成的FDRCT结构，旨在解决FDCT结构由于刚度下降造成的抗震性能不足等问题。为了降低高阶振型对结构的影响，根据弹性地基梁的振型曲线，同时基于调谐减震的理念，进一步提出附加下摆筒与上摆筒高度比例为8∶2的分布双段摇摆芯筒的FDBRCT结构。建立FDCT结构、FDRCT结构和FDBRCT结构的动力学模型和方程，分析结构在简谐激励以及地震动下的动力响应，基于有限元分析探讨FDBRCT结构调谐减震的性能。主要结论如下：

（1）根据FDCT结构、FDRCT结构和FDBRCT结构的动力学模型推导了结构的动力学方程，以芯筒的质量和刚度参数为变量对结构进行了简谐激励以及地震动下平稳随机振动分析，结果表明附加分布摇摆芯筒的FDRCT结构可以有效降低结构的动力响应，而附加分布双段摇摆芯筒的FDBRCT结构具备更为优越和稳定的减震效果。

（2）对比不同结构的有限元分析结果，附加分布芯筒的FDCT结构由于刚度的削弱造成了抗震能力的下降，因此相较于FCT结构其位移响应会有所增大。而附加分布摇摆芯筒的FDRCT结构可以使结构的层间位移角趋于均匀，减小结构薄弱层的破坏，加速度响应的降低提高了结构的舒适度，但是结构顶部位移有所增大。

（3）对比不同双摆芯筒比例的FDBRCT结构的有限元分析结果，验证了下摆筒与上摆筒高度比例为8∶2的分布双段摇摆芯筒具备更为优越的调谐减震效果。相较于FDRCT结构，多遇地震下FDBRCT结构减震作用不明显；罕遇地震下，由于摇摆作用的充分实现，FDBRCT结构的层间位移角最大值明显降低，且均匀程度进一步提高，更加有效地控制了结构的损伤模式。FDBRCT结构与FDRCT结构加速度响应基本相同，但可以降低结构顶部位移。FDBRCT结构有效降低了结构的内力需求。

（4）FDBRCT结构不但具备分布芯筒结构的经济性提升、布局更为灵活和多道抗震防线等优点，而且相较于单段的分布摇摆芯筒，具有调谐能力的分布双段摇摆芯筒抑制了高阶振型的影响且更为有效地提升了结构的抗震、减震性能。

参考文献：

［1］LIN T Y， STOTESBURY S D. Structural Concepts and Systems for Architects and Engineers［M］. New York： Van Nostrand Reinhold Publishing Company， 1988.

［2］包世华， 张铜生. 高层建筑结构设计和计算［M］. 北京： 清华大学出版社， 2013.

［3］ZHANG H， SU M Z， LIAN M， et al. Experimental and numerical study on the seismic behavior of high‑strength steel framed‑tube structures with end‑plate‑connected replaceable shear［J］. Engineering Structures， 2020， 223： 111172.

［4］LU X Z93YL/U53Mw5jJJbVpx4xBfoHVAx6isMSOtzEXfQ2wqU=， LU X， GUAN H， et al. Earthquake‑induced collapse simulation of a super‑tall mega‑braced frame‑core tube building［J］. Journal of Constructional Steel Research， 2013， 82： 59‑71.

［5］LU X Z， LIAO W J， CUI Y， et al. Development of a novel sacrificial‑energy dissipation outrigger system for tall buildings［J］. Earthquake Engineering and Structural Dynamics， 2019， 48（15）： 1661‑1677.

［6］王振宇， 刘晶波， 汪勇， 等. 超高层多筒巨型柱框架体系动力特性与地震反应研究［J］. 建筑结构学报， 2003， 24（1）： 54‑58.

WANG Zhenyu， LIU Jingbo， WANG Yong， et al. Study on dynamic properties and seismic responses of super high‑rise multitube‑megacolumn‑frame systems［J］. Journal of Building Structures， 2003， 24（1）： 54‑58.

［7］蒋济同， 王熙堃， 曹庆禺， 等. 高层混凝土建筑结构‑分散筒体体系初步研究［C］// 第七届全国现代结构工程学术研讨会论文集. 2007： 1746‑1749.

［8］尚庆学， 黄飒， 高生， 等. 装配式摇摆墙‑框架结构抗震性能试验研究［J］. 建筑结构学报， 2022， 43（8）： 12‑19.

SHANG Qingxue， HUANG Sa， GAO Sheng， et al. Experimental study on seismic performance of prefabricated rocking wall frame structure［J］. Journal of Building Structures， 2022， 43（8）： 12‑19.

［9］WU S J， PAN P， NIE X， et al. Experimental investigation on reparability of an infilled rocking wall frame structure［J］. Earthquake Engineering and Structural Dynamics， 2017， 46（15）： 2777‑2792.

［10］JIANG Q， WANG H Q， FENG Y L， et al. Experimental and numerical studies of a controlled rocking steel frame with buckling‑restrained columns［J］. Structures， 2020， 24： 690‑704.

［11］ERKMEN B. Effects of unbonded steel layout on seismic behavior of post‑tensioned precast concrete shear walls［J］. Bulletin of Earthquake Engineering， 2021， 19（1）： 179‑201.

［12］DEHCHESHMEH E M， BROUJERDIAN V. Determination of optimal behavior of self‑centering multiple-rocking walls subjected to far‑field and near‑field ground motions［J］. Journal of Building Engineering， 2021， 45： 103509.

［13］PANAGIOTOU M， RESTREPO， J I. Dual‑plastic hinge design concept for reducing higher‑mode effects on high‑rise cantilever wall buildings［J］. Earthquake Engineering and Structural Dynamics， 2009， 38（12）： 1359‑1380.

［14］WIEBE L， CHRISTOPOULOS C， TREMBLAY R， et al. Mechanisms to limit higher mode effects in a controlled rocking steel frame. 1： concept， modelling， and low‑amplitude shake table testing［J］. Earthquake Engineering and Structural Dynamics， 2013， 42（7）： 1053‑1068.

［15］WIEBE L， CHRISTOPOULOS C， TREMBLAY R， et al. Mechanisms to limit higher mode effects in a controlled rocking steel frame. 2： large‑amplitude shake table testing［J］. Earthquake Engineering and Structural Dynamics， 2013， 42（7）： 1069‑1086.

［16］李国强， 张文津， 王彦博， 等. 双段消能摇摆结构体系的地震反应特性研究［J］. 振动与冲击， 2021， 40（5）： 92‑101.

LI Guoqiang， ZHANG Wenjin， WANG Yanbo， et al. Seismic response characteristics of dual‑stage energy dissipation rocking structure system［J］. Journal of Vibration and Shock， 2021， 40（5）： 92‑101.

［17］LI C X， ZHU B L. Estimating double tuned mass dampers for structures under ground acceleration using a novel optimum criterion［J］. Journal of Sound and Vibration， 2006， 298（1‑2）： 280‑297.

［18］何浩祥， 许洪刚， 许维炳. 悬吊双摆动力特性分析及其在结构减振控制中的应用［J］. 振动工程学报， 2019， 32（2）： 305‑313.

HE Haoxiang， XU Honggang， XU Weibing. Dynamic characteristics of suspended double pendulum and its application in structural vibration control［J］. Journal of Vibration Engineering， 2019， 32（2）： 305‑313.

［19］BROUJERDIAN V， DEHCHESHMEH E M. Locating the rocking section in self‑centering bi‑rocking walls to achieve the best seismic performance［J］. Bulletin of Earthquake Engineering， 2022， 20（5）： 2441‑2468.

［20］王光远. 建筑结构的振动［M］. 北京： 科学出版社， 1978.

［21］MAKRIS N， AGHAGHOLIZADEH M. The dynamics of an elastic structure coupled with a rocking wall［J］. Earthquake Engineering and Structural Dynamics， 2017， 46（6）： 945‑962.

［22］薛素铎， 王雪生， 曹资. 基于新抗震规范的地震动随机模型参数研究［J］. 土木工程学报， 2003， 36（5）： 5‑10.

XUE Suduo， WANG Xuesheng， CAO Zi. Parameters study on seismic random model based on the new seismic code［J］. China Civil Engineering Journal， 2003， 36（5）： 5‑10.

［23］谢昭波， 解琳琳， 林元庆， 等. 典型框架‑核心筒单重与双重抗侧力体系的抗震性能与剪力分担研究［J］. 工程力学， 2019， 36（10）： 40‑49.

CHEA Cheav Por， XIE Linlin， LIN Yuanqing， et al. Study on seismic performance and collapse‑resistant capacity of typical frame‑core tube structures with single and dual lateral‑force resisting system［J］. Engineering Mechanics， 2019， 36（10）： 40‑49.

［24］QU Z， WADA A， MOTOYUI S， et al. Pin‑supported walls for enhancing the seismic performance of building structures［J］. Earthquake Engineering and Structural Dynamics， 2012， 41（14）： 2075‑2091.

［25］郑莲琼， 颜桂云， 魏常贵， 等. 钢质往复弯曲耗能铰滞回性能试验研究及理论分析［J］. 土木工程学报， 2020， 53（12）： 29‑43.

ZHENG Lianqiong， YAN Guiyun， WEI Changgui， et al. Experimental and numerical investigation of steel energy‑dissipating hinge under cyclic loading［J］. China Civil Engineering Journal， 2020， 53（12）： 29‑43.

［26］中华人民共和国住房和城乡建设部. 建筑抗震设计规范： GB 50011—2010［S］. 北京： 中国建筑工业出版社， 2010.

MOUHURD. Code for seismic design of buildings： GB 50011—2010［S］. Beijing： China Architecture and Building Press， 2010.

Study on tuned damping mechanism and performance of frame‑distributed bi‑rocking tubes‑core tube system

HE Hao‑xiang1， CHEN Yi‑fei1，2， CHENG Shi‑tao1， LAN Bing‑ji1

（1. Beijing Key Lab of Earthquake Engineering and Structural Retrofit，Beijing University of Technology， Beijing 100124， China；2. School of Civil Engineering， Luoyang Institute of Science and Technology， Luoyang 471023， China）

Abstract： In order to reduce the tube area proportion of the traditional frame‑core tube （FCT） structure system and improve the structural economy， a high‑rise structural system of the frame‑distributed tubes‑core tube （FDCT） is designed. The distributed tubes and rocking system are combined to form the frame‑distributed rocking tubes‑core tube （FDRCT） structural system， which can control the deformation mode of the structure. To reduce the adverse effects of higher modes on high‑rise structures， the frame‑distributed bi‑rocking tubes‑core tube （FDBRCT） structural system with tuned damping performance is further proposed. The dynamic models and equations of the structure are established， and the stationary random vibration analysis is carried out， which preliminarily proves that the FDBRCT structure can reduce the dynamic response of the structure more effectively. By comparing and analyzing the structural time‑history analysis results of the FCT， FDCT， FDRCT and FDBRCT， the seismic capacity of the FDCT structure decreases is due to the stiffness weakening. The FDRCT structure improves the uniform degree of structural deformation， and the upper floors acceleration decreases， but the roof displacement increases. Compared with the FDRCT structure， the maximum of inter‑story drift ratio of the FDBRCT structure increases significantly and the structural deformation is more uniform. Besides， the roof displacement response and internal force demand decrease appropriately. The distributed bi‑rocking tubes with tuned damping brings on better seismic capacity and damping performance of the FDBRCT structure， which can improve the economy at the same time.

Key words： frame‑core tube structure；distributed rocking tube；distributed bi‑rocking tube；higher order mode shape；tuned seismic mitigation

作者简介： 何浩祥（1978―）， 男， 博士， 教授， 博士生导师。E‑mail： hhx7856@163.com。