用于轮胎振动分析的壳模型优化研究

摘要： 虽然现有壳模型在0～500 Hz频带内精度高，适合用于轮胎结构振动分析，但由于模型中耦合了胎侧二维壳模型，导致胎冠振动模态难以分离，且模型自由度和所需输入参数增加。本文对该壳模型进行改进：在保持胎冠壳模型不变的基础上，应用轮胎环模型和板模型中对胎侧的近似方法，采用弹性基底代替胎侧二维壳模型，简化了原模型的边界条件并缩减了输入参数个数；针对改进后的壳模型建立了求解方法，实现了胎冠模态频率和振型的求解。并通过与实验数据的对比，验证了改进后的壳模型及其求解方法的正确性。

关键词： 轮胎振动； 壳模型； 边界条件； 模态频率； 模态振型

中图分类号： U461.1； U463.341 文献标志码： A 文章编号： 1004-4523（2024）09-1556-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.012

引 言

轮胎的振动特性和汽车的操纵特性与车内外噪声密切相关，因此轮胎结构振动性能是轮胎设计的关键。目前广泛采用的轮胎振动分析模型主要包括有限元模型和解析模型两类。其中，有限元模型的几何建模和模拟轮胎接地变形过程更加精确，但不适合用于分析轮胎结构振动机理，且计算效率较低；解析模型的几何建模过程需要进行许多简化，难以准确模拟接地变形过程，但可以体现轮胎中不同类型弹性波的传播和影响，且计算效率较高。

由于解析模型在分析轮胎振动机理及计算效率方面具有优势，因此一直是国内外科研机构的研究重点和热点。环（Ring）模型［1⁃7］、梁（Beam）模型［8⁃9］、壳（Shell）模型［10⁃18］和板（Plate）模型［19⁃20］等多种模型先后被建立。这些模型所适用的频率范围和应用场景不同。其中，环模型是二维模型，不包含沿轮胎横向传播的弹性波及对应模态，有效频率范围较窄（约到250 Hz）；梁模型和板模型忽略了轮胎曲率，因此无法用于滚动轮胎；板模型所能分析的频率最高，可达3000 Hz，但由于忽略了轮胎曲率，在100 Hz以下的频段内误差较大。

总结上述模型可知，从适用的频带范围及模型与实际轮胎的接近程度来看，壳模型是综合性能较好的轮胎振动解析模型。主要体现在：实际中轮胎结构噪声的主要关注频段是20～500 Hz，壳模型在该频段内具有较高精度；壳模型是三维模型，包含横向模态；壳模型可以模拟轮胎滚动。

关于壳模型的研究历史久远。Soedel［10］采用圆柱形薄壳近似轮胎，并从特征值和格林函数的角度研究了模型求解问题。Huang等［11］进一步研究了两端简支的旋转柱壳的动态响应求解问题，模型中考虑了由于内部气压和旋转离心力引起的周向预应力，也包含了应变的二阶非线性项，壳模型的边界（即胎冠两侧的边界）采用简支边界条件近似。Molisani等［12］研究了轮胎结构和声腔耦合模型，其中轮胎胎冠采用壳模型，胎侧假设为刚性，胎冠与胎侧相连处假设为简支边界条件。Kim等［13］进一步研究了旋转对壳模型振动响应的影响，分析了旋转带来的分岔现象。Bozdog等［14］采用曲面壳模拟轮胎外形，而并未采用常用的圆柱壳，曲面壳模型等效于同时对胎冠和胎侧进行建模，而边界条件只需在轮辋处给出。Lecomte等［15］提出了用于轮胎振动分析的壳模型，并深入研究了该模型的求解方法、模型参数获取方法以及与现有模型的差别。Alujevi等［16］深入研究了壳模型的模态频率和振型求解问题，该研究中模型采用的是自由边界条件。Yang等［17］研究了壳模型的模态频率求解问题，该论文的研究关注点与文献［16］类似，但相比文献［16］只考虑自由边界，该论文采用弹性基底（Elastic Foundation）作为边界条件，引入4个刚度变量，因此其边界条件更具一般性。黄海波等［18］建立了考虑横向弯曲振动的轮胎圆柱薄壳模型，采用径向、切向和侧向的线性等效弹簧代替胎侧和充气压力的弹性作用，并研究了固有频率的求解问题，模型中表示高阶振动时采用的横向傅里叶基函数是简支边界条件下的模态，因此该模型实际上隐含定义了胎冠边界条件为简支。

对比已建立的壳模型可知，文献［15］中建立的轮胎振动壳模型是建模过程简化较少且接近实际轮胎结构和工况的模型。该模型支持周向和横向的拉伸波和弯曲波，考虑了周向和横向的预应力及周向和横向的材料力学性能差异，且包含轮胎转速。特别的是，该模型未采用简支或自由等类型的理想边界模拟胎冠和胎侧连接处的边界条件，而是通过边界处的应力合力和形变位移连续，建立了胎冠⁃胎侧耦合系统。但是这种通过对胎侧建立壳模型形成耦合系统的方法，不但增加了系统的自由度，而且无法再直接分析胎冠的振动机理，阻碍了胎冠模态频率和振型的计算和分析；此外，对胎侧建模还会引入许多实际中难以获取的参数，如胎侧的拉伸刚度、半径、高度、线密度、损耗因子、预应力等，增加了该模型的实际应用难度。

实际上，已有的轮胎振动模型大都未对胎侧直接建模，而是采用弹性基底模拟胎侧作用（如前文所述的环模型和板模型），并取得了良好的效果。鉴于上述原因，本文对文献［15］中的壳模型进行改进，在保持胎冠壳模型不变的基础上，应用弹性基底代替胎侧壳模型，简化原模型的边界条件，缩减参数个数，并实现胎冠模态频率和振型的求解，推进该壳模型的实际工程应用。

1 胎冠壳模型

为明确相关参数的定义和相关变量的含义，简要介绍胎冠壳模型（见图1）［15］。如图1所示，笛卡尔坐标系是固定的惯性参考系，极坐标随胎冠旋转，分别指向径向、切向和横向。变形前壳上一点的位置向量为，其中，为圆柱半径，为胎冠横向的坐标。图1中，为胎冠宽度，为胎冠转速。壳上一点的变形表示为（u，v，w分别表示，，方向的变形分量）。则该模型的运动方程可通过哈密顿原理即如下变分方程推导得到：

（1）

式中 和表示变形的前、后时刻；表示壳变形和旋转过程的动能，可表示为：

（2）

式中 表示单位面积的胎冠质量；表示面积分；表示速度，表达式为：

。

式（1）中的表示变形应变能，表达式为：

（3）

式中 被积函数第一项中列向量中的元素为不同方向的线性应分变量，矩阵中的元素为拉伸刚度；被积函数第二项中列向量中的元素为不同方向的曲率，矩阵元素为弯曲刚度。

式（1）中的表示预应力引起的势能，表达式为：

（4）

式中 为单位周向距离上的横向预应力；为单位横向距离上的周向预应力；和分别表示横向和周向的二阶应变分量。

式（1）中的表示壳变形时内部压力所做的功，表达式为：

（5）

式中 为轮胎内部气压。

式（1）中的表示胎冠边界上应力所做的功，表达式为：

（6）

式中 ，和分别表示横向、切向和径向的应力合力；表示弯矩。这些边界应力合力的方向和符号约定如图2所示。另外需注意式（6）中的积分是在胎冠两侧边界上沿周向的一维积分，与式（3）～（5）在胎冠表面的面积分不同。

将式（2）～（6）代入式（1），通过变分运算可推导得到壳模型的运动方程为：

（7）

其中，变形和系数矩阵L的表达式分别如下：

其中：

此外，在变分过程中，还可推导得到周向预应力，边界应力合力表达式为：

（8）

（9）

（10）

（11）

2 胎冠壳模型边界条件改进

对于图1所示的胎冠壳模型，周向满足周期性边界条件，因此可用或作为傅里叶基函数展开，其中，为周向模态阶数；但是横向的傅里叶基函数是未知的，需由胎冠两侧的边界条件确定。如果采用简支等类型的理想边界条件，那么横向的傅里叶基函数存在解析表达式：或，其中，m为轴向模态阶数。但是这种理想边界条件不符合实际，没有考虑胎侧对胎冠的作用引起的横向模态变化。

解决上述问题有两种方案：一种是对胎侧进行建模，然后通过确保胎冠和胎侧连接处的应力合力连续和形变位移连续从而形成耦合系统；另外一种是采用弹性基底（即线性等效弹簧）代替胎侧作用。如引言中所述，第一种方案存在一些难点，实际应用性不足。因此，本文采用第二种方案与前文的胎冠壳模型进行结合，以解决上述难点，提升这一模型的实用性。

如图3所示，在所建立的壳模型的基础上，将胎侧作用等效为均布在胎冠壳模型两端的轴向、周向、径向和弯曲方向的线性弹簧，前三个方向与所建立的极坐标系方向对应，弯曲方向则与方向一致，它们对应的刚度分别为。由于伴随着壳模型的推导过程，同时得到了模型边界上的边界应力表达式（8）～（11），因此对于上述壳模型来说，采用这种等效方法非常适合，可以直接给出模型的边界条件如下：

在一侧：

（12）

在一侧：

（13）

3 改进后胎冠壳模型的求解方法

采用改进边界条件后，壳模型的求解实际上是联合求解式（7）给出的运动方程和式（12），（13）给出的边界条件。但是根据式（12）和（13）无法判断并给出横向的傅里叶基函数。为此，首先定义沿横向传播的弹性波为行波，横向波数为，然后通过边界条件确定真实的横向模态。因此，假设形变位移为：

（14）

式中 ，和分别为轴向、周向和径向形变位移幅值；为频率。

将式（14）代入运动方程（7）中，可得：

（15）

其中：

为使得式（15）有非零解，其左侧系数矩阵的行列式应为零，因此得到如下特征方程：

（16）

其中：

注意式（16）中包含横向波数和频率两个参数，也就是说该方程约束了和之间的关系，但是由于这两个参数相互关联，因此通过该方程无法求得壳模型的模态频率。模态频率的确定还需结合边界条件，即式（12）和（13）。具体方法如下。

首先给定一个频率，则通过式（16）可以求解出。由于式（16）是关于的8次特征方程，因此其有8个解。将给定的和其对应的8个解代入式（14）中的径向形变位移，可得：

（17）

其中：

（18）

式中 （=1，2，…，8）为对应每个解的复系数。

根据式（15），可以得到另两个方向形变位移幅值与径向形变位移幅值的关系如下：

（19）

其中：

因此，式（14）中的横向和切向形变位移可表示为：

（20）

其中：

（21）

将式（17）和（20）代入式（12）和（13），可以得到以（=1，2，…，8）为未知数的8阶线性方程组：

（22）

式中 为阶系数矩阵；为由（=1，2，…，8）组成的列向量。

如果矩阵行列式为0，也就是式（22）有非零解，那么此时所对应的频率即为壳模型的模态频率。计算时可以采用搜索的方法，对所关心频带内的每个频率重复上述过程，即可得到该频带内的模态频率，并可进一步得到该模态频率对应的振型。

但是这里需要注意一个难点：给定频率后，通过式（16）求解出的可能为复数根，也就是为复矩阵，因此通过搜索实频率，无法找到复矩阵的行列式等于0的位置，即无法确定模态频率。

解决上述难点的方法是对式（16）求解出的的根的形式进行讨论，并将每种的根的形式对应的形变位移转化为实系数表达式，进而代入边界条件确定模态频率。

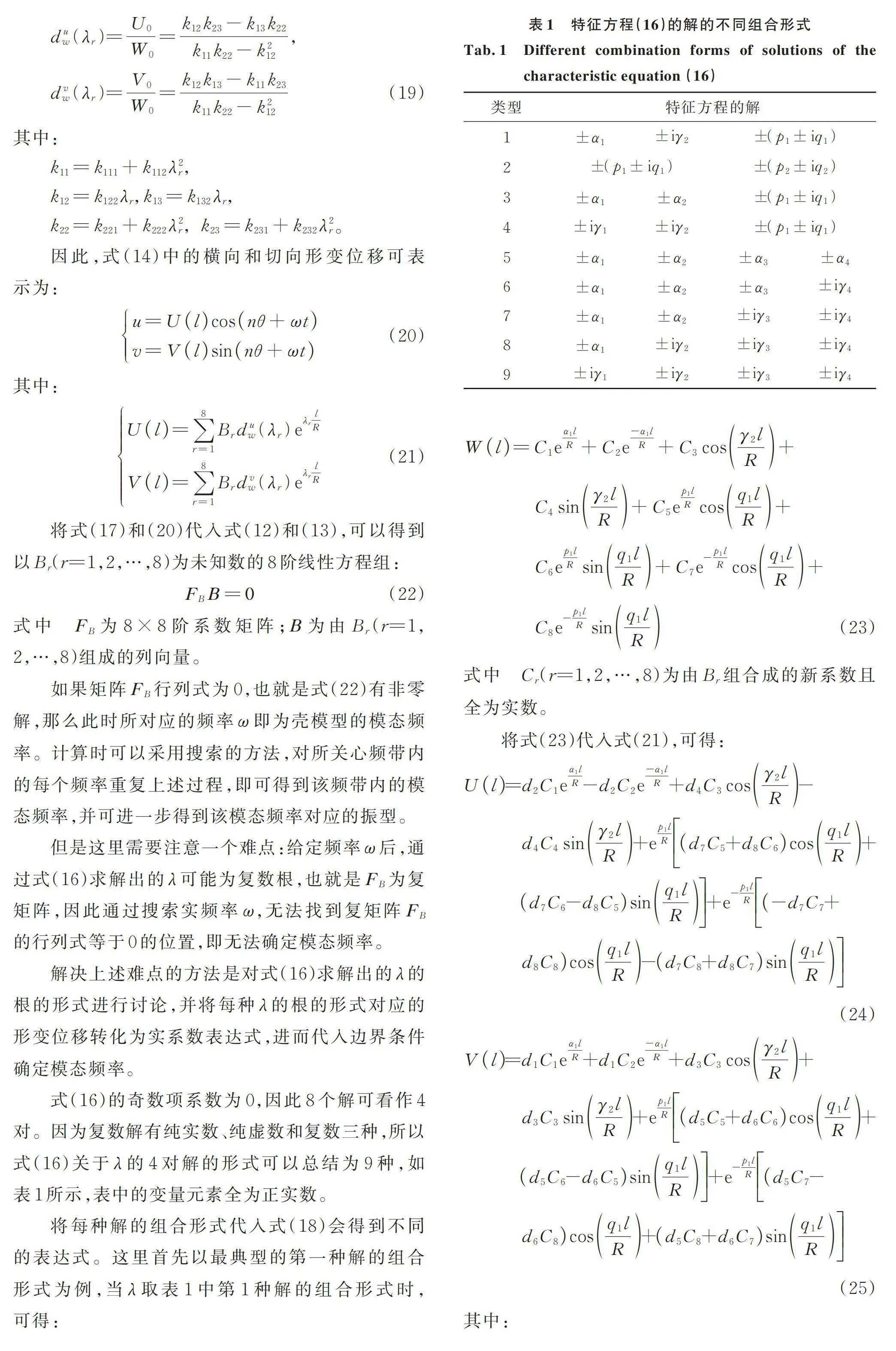
式（16）的奇数项系数为0，因此8个解可看作4对。因为复数解有纯实数、纯虚数和复数三种，所以式（16）关于的4对解的形式可以总结为9种，如表1所示，表中的变量元素全为正实数。

将每种解的组合形式代入式（18）会得到不同的表达式。这里首先以最典型的第一种解的组合形式为例，当取表1中第1种解的组合形式时，可得：

（23）

式中 （=1，2，…，8）为由组合成的新系数且全为实数。

将式（23）代入式（21），可得：

（24）

（25）

其中：

式中 real表示实部，img表示虚部。

将式（23）～（25）代入边界条件（12）和（13），可以得到以（=1，2，…，8）为未知数的8阶线性方程组：

（26）

式中 为由（=1，2，…，8）组成的列向量；为阶系数矩阵且其中元素全为实数。若方程（26）存在非零解，则行列式为零，此时所对应的频率即为壳模型的模态频率。

上述求解过程可总结如下：首先给定一个周向模态阶数和频率，求解式（16）得到（=1，2，…，8），针对每个根据公式（23）～（25）生成纯实数系数矩阵并计算的行列式；重复上述过程，计算频带内其他频率对应的的行列式；判别的行列式等于零时对应的频率，即为模态频率；计算模态频率下的非零系数，并代回公式（17）和（20），计算模态振型。

4 模型验证

为验证改进模型的准确性，以型号为205/55R16的轮胎为对象开展实验，该轮胎的相关参数如表2所示。实验测试了该轮胎的自由模态频率。实验时，在轮胎中间（即）圆周方向均匀布置了24个测点，并通过移动力锤的方式测试了每个测点处的力锤信号与固定粘贴的加速度传感器信号之间的频率响应函数（FRF），然后通过Test. Lab计算得到径向模态频率。

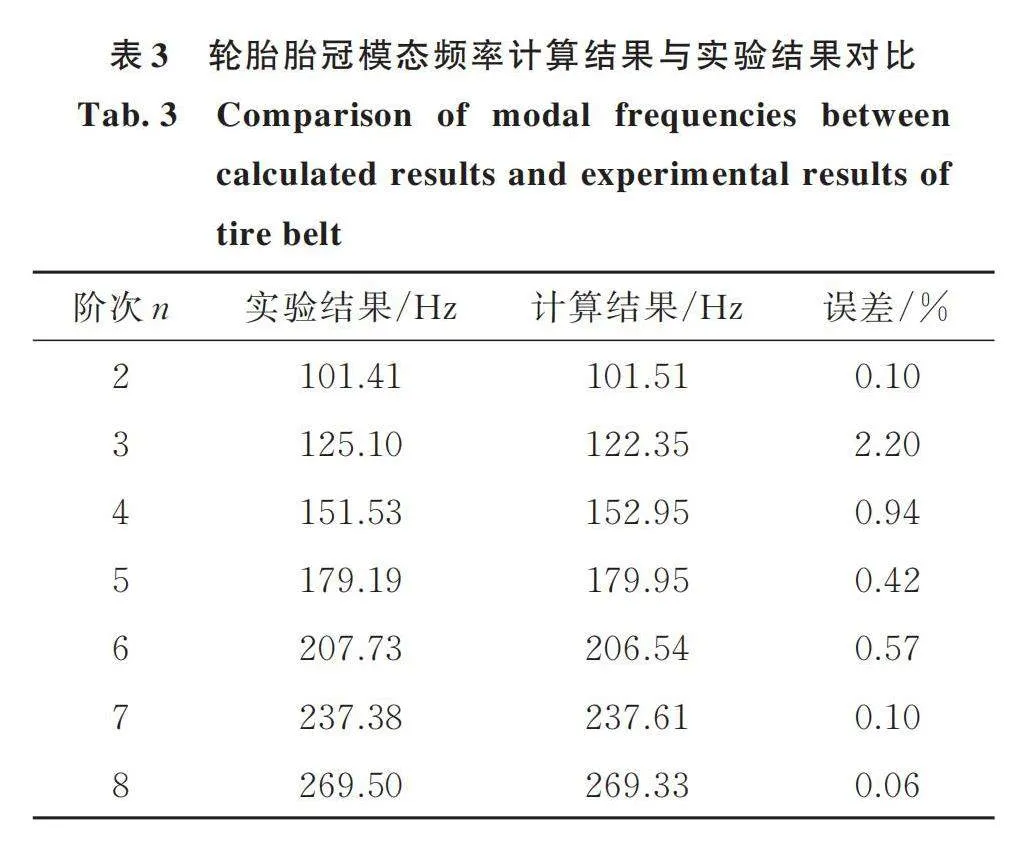
采用本文提出的改进壳模型计算得到的结果与实验结果的对比如表3所示，部分阶次的误差小于1%，部分阶次的误差接近2.5%。部分阶次误差稍大的原因在于：首先，模型采用了线性、各向同性等假设，如计算中假设了材料的轴向和横向特性相同，即且，但实际轮胎材料具有非线性且存在各向异性；其次，由于模态频率和轴向特征波数相互耦合，因此只能采用遍历搜索的方式，通过行列式数值的符号变化近似得到模态频率，因此计算过程存在误差；最后，部分输入参数是通过反演得到的，与实际参数之间存在误差。但是，总体上计算结果与实验结果吻合较好，从而证明了本文提出的改进壳模型的准确性。

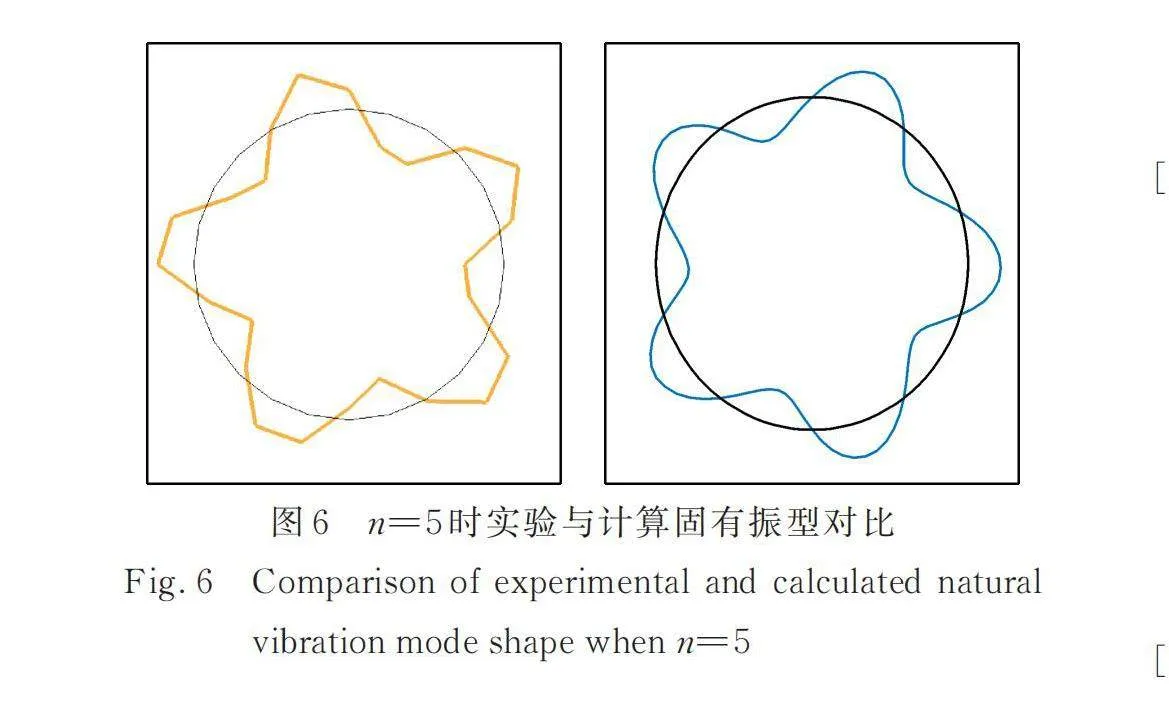
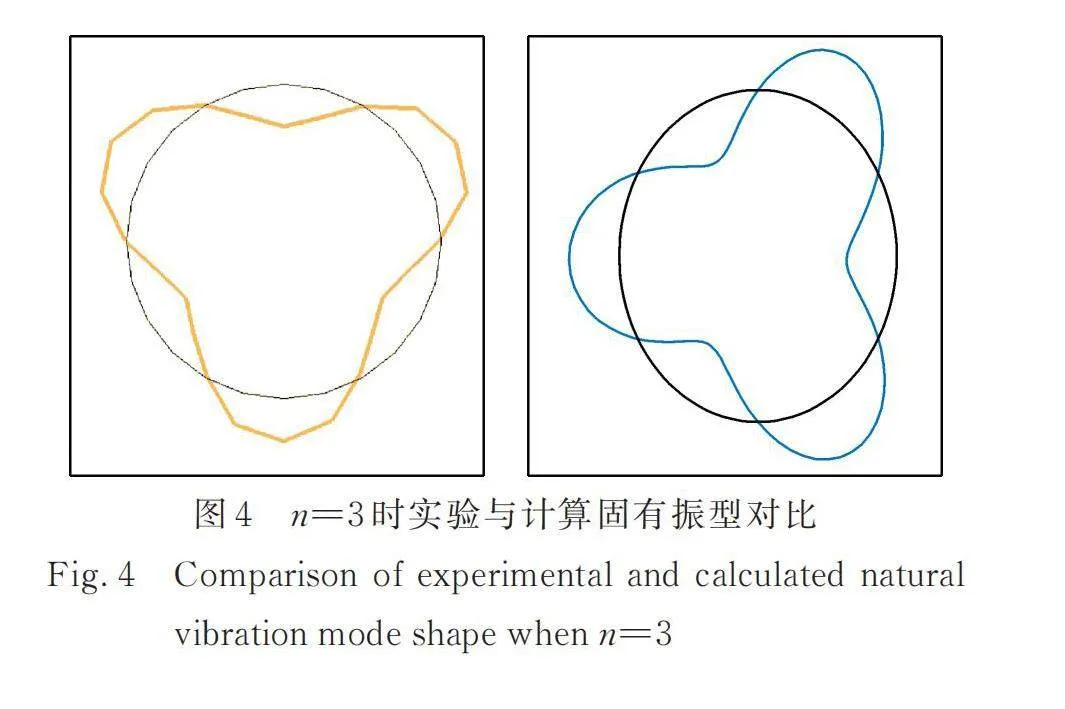
图4～6给出了实验获得的3～5阶模态振型，并与采用本文提出的改进壳模型计算得到的模态振型进行了对比。通过对比结果可以看出，计算结果与实验结果较为吻合，进一步说明了改进壳模型的准确性。

5 结 论

本文将轮胎环模型和板模型中近似胎侧的弹性基底方法用于改进壳模型中。与原模型相比，应用弹性基底后的模型去除了胎冠三维壳模型与胎侧二维壳模型的耦合，实现了实际中非常重要的胎冠振动模态的分离，减少了实际中难以获取的输入参数数目和模型求解的自由度。

针对改进的壳模型，本文详细讨论了模型求解过程中存在的难点，建立了胎冠模态频率和模态振型的求解方法，并通过实验验证了改进后的壳模型及其求解方法的正确性。

参考文献：

［1］Kung L E， Soedel W， Yang T Y. Free vibration of a pneumatic tire-wheel unit using a ring on an elastic foundation and a finite element model［J］. Journal of Sound and Vibration， 1986， 107（2）： 181-194.

［2］Huang S C， Soedel W. Effects of Coriolis acceleration on the free and forced in-plane vibrations of rotating rings on elastic foundation［J］. Journal of Sound and Vibration， 1987， 115（2）： 253-274.

［3］Kropp W. Structure-borne sound on a smooth tyre［J］. Applied Acoustics， 1989， 26（3）： 181-192.

［4］Gong S. A study of in-plane dynamics of tires［D］. Delft， Netherlands： Delft University of Technology， 1993.

［5］危银涛， 管迪华， 范成建. 关于轮胎的圈模型［J］. 汽车工程， 2001， 23（4）： 217-221.

Wei Yintao， Guan Dihua， Fan Chengjian. On the ring model of the tire［J］. Automotive Engineering， 2001， 23（4）： 217-221.

［6］Wei Y T， Nasdala L， Rothert H. Analysis of forced transient response for rotating tires using REF models［J］. Journal of Sound and Vibration， 2009， 320（1-2）： 145-162.

［7］郭孔辉， 邱恩超. 基于环模型的轮胎滚动接触有限元分析［J］. 吉林大学学报 （工学版）， 2011， 41（3）： 597-601.

Guo Konghui， Qiu Enchao. Finite element analysis of tire rolling contact based on ring supported on elastic foundation model［J］. Journal of Jilin University （Engineering and Technology Edition）， 2011， 41（3）： 597-601.

［8］Pinnington R J， Briscoe A R. A wave model for a pneumatic tyre belt［J］. Journal of Sound and Vibration， 2002， 253（5）： 941-959.

［9］Pinnington R J. A wave model of a circular tyre. Part 1： belt modelling［J］. Journal of Sound and Vibration， 2006， 290（1-2）： 101-132.

［10］Soedel W. On the dynamic response of rolling tires according to thin shell approximations［J］. Journal of Sound and Vibration， 1975， 41（2）： 233-246.

［11］Huang S C， Soedel W. On the forced vibration of simply supported rotating cylindrical shells［J］. The Journal of the Acoustical Society of America， 1988， 84（1）： 275-285.

［12］Molisani L R， Burdisso R A， Tsihlas D. A coupled tire structure/acoustic cavity model［J］. International Journal of Solids and Structures， 2003， 40（19）： 5125-5138.

［13］Kim Y J， Bolton J S. Effects of rotation on the dynamics of a circular cylindrical shell with application to tire vibration［J］. Journal of Sound and Vibration， 2004， 275（3-5）： 605-621.

［14］Bozdog D， Olson W W. An advanced shell thfupDDmA8mf3m8WMOo/efQ79L30g7cCOpvVTrsGd5p4s=eory based tire model［J］. Tire Science and Technology， 2005， 33（4）： 227-238.

［15］Lecomte C， Graham W R， Dale M. A shell model for tyre belt vibrations［J］. Journal of Sound and Vibration， 2010， 329（10）： 1717-1742.

［16］Alujevi N， Campillo-Davo N， Kindt P， et al. Analytical solution for free vibrations of rotating cylindrical shells having free boundary conditions［J］. Engineering Structures， 2017， 132：152-171.

［17］Yang Y B， Wei Y T. A unified approach for the vibration analysis of cylindrical shells with general boundary conditions［J］. Acta Mechanica， 2018， 229（9）： 3693-3713.

［18］黄海波， 余旭东， 叶方杰， 等. 考虑横向弯曲振动的轮胎圆柱薄壳模型［J］. 振动工程学报， 2020， 33（4）： 709-716.

Huang Haibo， Yu Xudong， Ye Fangjie， et al. A thin-walled cylindrical shell model for a tire considering transverse bending vibration［J］. Journal of Vibration Engineering， 2020， 33（4）： 709-716.

［19］Larsson K， Kropp W. A high-frequency three-dimensional tyre model based on two coupled elastic layers［J］. Journal of Sound and Vibration， 2002， 253（4）： 889-908.

［20］Andersson P， Larsson K. Validation of a high frequency three-dimensional tyre model［J］. Acta Acustica United with Acustica， 2005， 91（1）： 121-131.

Optimization of the shell model for tire vibration analysis

ZHANG Yong-bin， ZHANG Zhen-wei， ZHANG Xiao-zheng， BI Chuan-xing

（Institute of Sound and Vibration Research， Hefei University of Technology， Hefei 230009， China）

Abstract： The existing shell model is accurate in the frequency band of 0～500 Hz， making it highly suitable for tire vibration analysis. However， the modal properties of the tire belt cannot be obtained separately and the freedom as well as the number of parameters required by the model increases， because the shell model couples the tire belt and sidewall. Therefore， this shell model was improved in this paper. The shell model for simulating the tire belt remained unchanged， whereas， by using the method for approximating the sidewall used in the ring model and plate model of tire， the two-dimensional shell model for simulating the tire sidewall was replaced by an elastic foundation to simplify the boundary conditions of the tire belt and reduce the number of parameters related to the tire sidewall. The solving method for the improved shell model was developed to calculate the modal frequency and the modal shape of the tire belt. The validity of both the improved shell model and its solving method was demonstrated by an experiment.

Key words： tire vibration；shell model；boundary conditions；modal frequency；modal shape

作者简介： 张永斌（1982―），男，博士，教授，博士生导师。E-mail： ybzhang@hfut.edu.cn。