基于旋涡漂移假设的流线型闭口箱梁竖向涡振机理研究

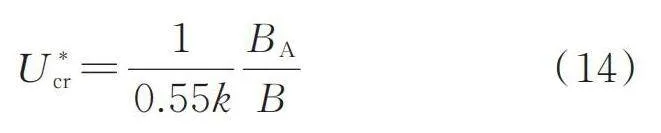
摘要： 旋涡脱落和漂移是桥梁涡振发生的关键流场特征，有必要从涡动力学的角度揭示涡振机理。以典型流线型闭口箱梁为例，从气动力做功能量角度，构建简化涡模型，并结合基于风洞试验的断面表面气动力时频特征和基于数值模拟方法的断面周围流场特性，揭示流线型闭口箱梁多阶涡振机理，验证上述模型。研究表明：分离涡斯托罗哈数表征旋涡气动力做功能量特征，其可表达为旋涡漂移速度与来流风速比值的正整数倍，即同一分离点可对应多个涡振锁定区。流线型箱梁断面存在3阶竖向涡振锁定区，其中，第2阶和第3阶涡振锁定区均由来流经过断面前缘附属设施时产生的大尺度旋涡，在分离点至断面尾缘之间发生周期性漂移诱导与维系。在第2和第3阶涡振锁定区内分离涡分别耗费约2个和1个振动周期完成从分离点至截面尾缘的漂移，即二者分别由该分离点诱发的2阶和1阶简化涡模式主导。该研究验证了简化涡方法推演桥梁断面周围旋涡演变特性的合理性。

关键词： 涡激振动； 旋涡漂移； 流线型箱梁； 简化涡模型

中图分类号： U441+.3 文献标志码： A 文章编号： 1004-4523（2024）09-1575-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.014

引 言

涡激振动是由气流绕经主梁表面时产生的规律性脱落旋涡引起的具有强迫和自激双重性质的自限幅风致振动现象。旋涡脱落、漂移及其非定常演化过程决定了断面表面气动力及其与结构运动之间的相位关系，实现风能向振动能量转化，进而导致结构涡振效应。涡振效应（振幅）又反过来决定旋涡脱落及漂移模式，如此循环往复。当气动力输能与结构阻尼比耗能达到能量平衡时，产生涡振极限环振动现象。在常遇风速范围内，大跨度桥梁存在发生多阶模态涡振风险［1‑2］。中国舟山西堠门大桥、武汉鹦鹉洲大桥和广东虎门大桥等均发生过高阶竖向涡振现象［3］。虽然涡激振动不会像颤振或驰振那样导致发散，但会影响行车安全，甚至诱发拉索参数共振等其他类型的气动不稳定问题［4］。

诸多学者从涡动力学角度分析了旋涡脱落、漂移与涡振现象之间的内在物理机制，并针对性提出相应抑振措施［5‑7］。PAÏDOUSSIS等［8］总结了不同断面涡振发生机制，指出类矩形断面或桥梁断面涡振主要与四种典型涡脱有关：前缘涡脱（LEVS）、后缘涡脱（TEVS）、交错边缘涡脱（AEVS）以及顶端撞击涡脱（ILEV）。SHIRAISHI等［9］进一步认为涡振驱动对应三类不同涡脱模式：第一类为断面运动导致前缘产生并在尾部交替脱落旋涡；第二类为断面运动导致前缘产生的分离涡和断面尾端产生的二次涡，即“双旋涡模式”［10］；第三类为断面尾部产生交替脱落旋涡 （如经典Karman涡）。上述涡脱模式中，第二和第三类被认为是桥梁断面最主要涡振驱动机制［11‑12］，分别可归类为单剪切层涡振驱动机制和双剪切层涡振驱动机制［13］。对于第二类涡脱模式驱动涡振机制（分离涡涡振），SHIRAISHI等［9］还基于流场特征，系统总结了旋涡沿断面漂移特征与涡振起振风速之间的关系。KUBO等［14］进一步研究发现，钝体断面的涡振形式（竖向和扭转）取决于旋涡在断面表面的空间分布模式。周志勇等［15］对近流线型箱梁断面周围流场研究发现，旋涡漂移对应升力漂移。周期性旋涡脱落与漂移过程对结构产生周期性的作用力，从而导致涡振发生。与一般桥梁断面相比，分离箱梁断面由于开槽的存在，抑制了分离涡在断面表面的横向漂移，但同时也引起了槽间涡漂移。LARSEN等［16］对分离双箱梁断面表面压力与流场特征研究发现，上游箱体尾部产生的分离涡沿槽间漂移及其对下游箱体前缘的撞击作用是涡振产生主要原因。此外，董佳慧等［17］、祝志文等［18］、马凯等［19］、李志国等［20］还采用数值模拟流场分析，从断面周围旋涡非定常演变的角度揭示了典型桥梁断面涡振机理和气动措施抑制机理。由上可知，旋涡脱落和漂移是桥梁断面涡振发生的共同流场特征，有必要提炼关键流场特征，从涡动力学的角度揭示涡振机理。

综上所述，国内外诸多学者基于桥梁断面周围绕流特征，从涡动力学角度定性分析了旋涡脱落和漂移与涡振发生之间的内在联系，归纳了一般桥梁断面或钝体断面（非开槽断面）分离涡涡振起振风速与旋涡漂移之间函数关系。然而，上述研究仍局限于对桥梁断面周围流场特征的简单归纳，难以体现涡激气动力时频空间特性及与之关联的“旋涡特征”，对桥梁断面多阶涡振产生机制尚不明晰。故有必要将涡振时断面气动力时空演变特征与流场特征物理性关联，由气动力时空分布特征推演关键流场特征——旋涡运动，将旋涡漂移、断面周期性运动与同步气动力三者紧密关联，构建简化涡模型，深入揭示桥梁断面涡振机理。

本文旨在简化涡振发生时断面‑流场之间复杂的流固耦合关系，构建基于旋涡气动力做功效应的简化涡模型。在此基础上，以典型流线型闭口箱梁为例，结合箱梁表面气动力时频特性与数值流场，验证上述简化涡模型，并揭示多阶竖向涡振机理。

1 简化涡模型

1.1 旋涡漂移假设

图1所示主梁断面，忽略来流在断面下表面的流动分离。假设气流绕经断面，在断面上表面分离点产生流动分离，生成分离涡，并沿来流方向漂移，即旋涡漂移。图1中，为上表面旋涡横向间距，为旋涡漂移距离，为旋涡漂移速度。

需要注意的是，图1中的旋涡是简化涡，是真实流场中分离涡的简化假设。在旋涡漂移过程中，分离涡对断面作用可采用集中力表达，即

（1）

式中 为空气密度；和分别为来流风速和断面宽度；为旋涡气动力系数。

假设旋涡沿断面上表面移动时保持不变，且旋涡漂移速度恒定，即忽略旋涡漂移过程中的非定常演变特性。分布气动力与涡激力相位差随坐标单调递增表征旋涡漂移［21］，旋涡漂移速度可由下式获得：

（2）

式中 和分别表示断面表面点和点处分布气动力与涡激力的相位差；和分别表示点K和点J距离前缘分离点的水平距离；为断面振动周期，，为断面竖向振动频率。

1.2 简化涡模式

旋涡横向间距与旋涡漂移速度的关系表示为：

（3）

竖向涡振的位移和速度可分别表示为：

（4a）

（4b）

式中 表示竖向涡振振幅；为断面振动与旋涡漂移起点之间相位差。当为零时，振动平衡位置对应旋涡漂移起点。

当断面表面相邻旋涡之间横向间距满足：

（5）

式中 取正整数，本文取1，2，3。单个振动周期内桥梁表面旋涡做功可表示为：

（6）

当断面表面相邻旋涡横向间距满足：

（7）

此时单个振动周期内桥梁表面旋涡做功可表示为：

（8）

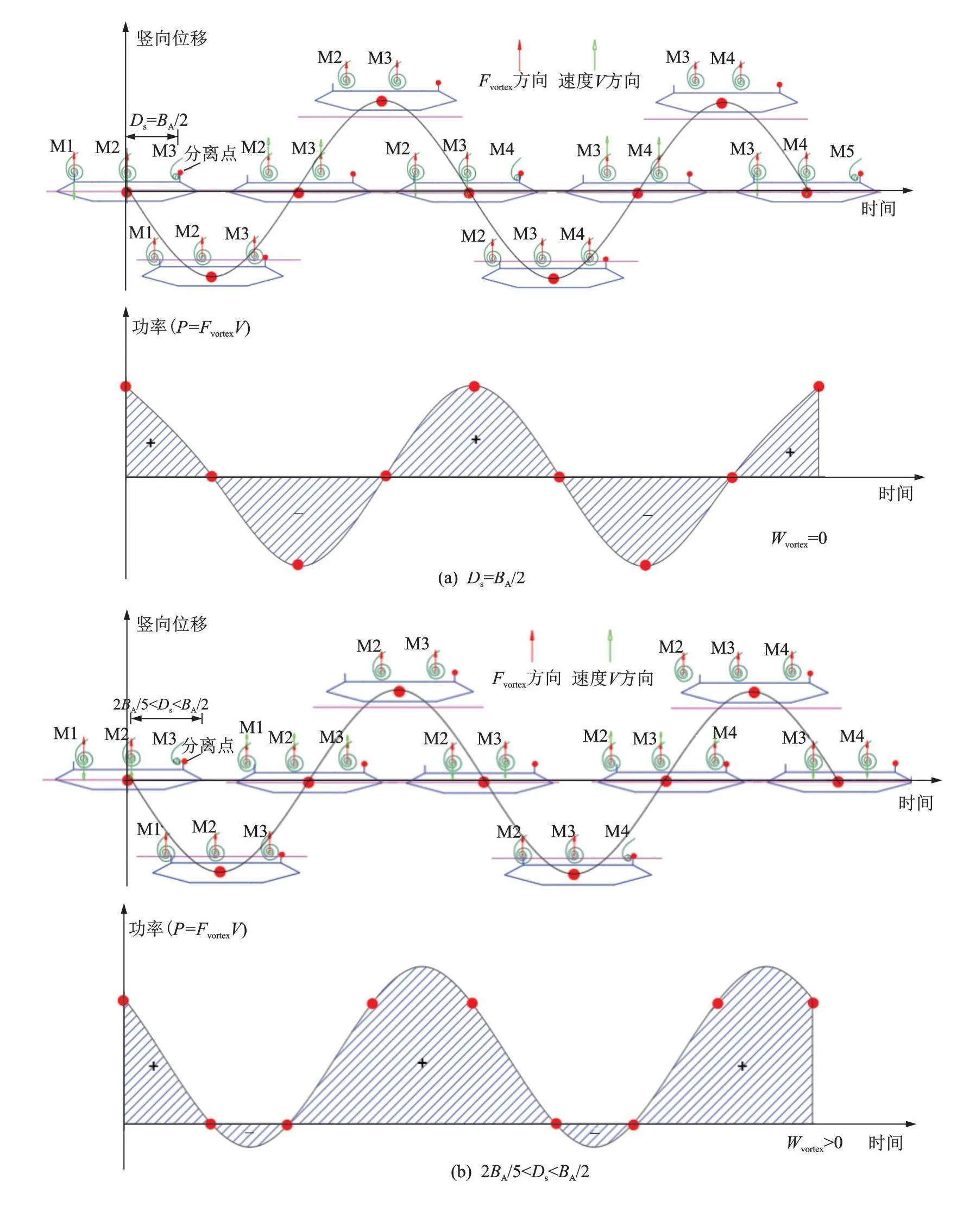
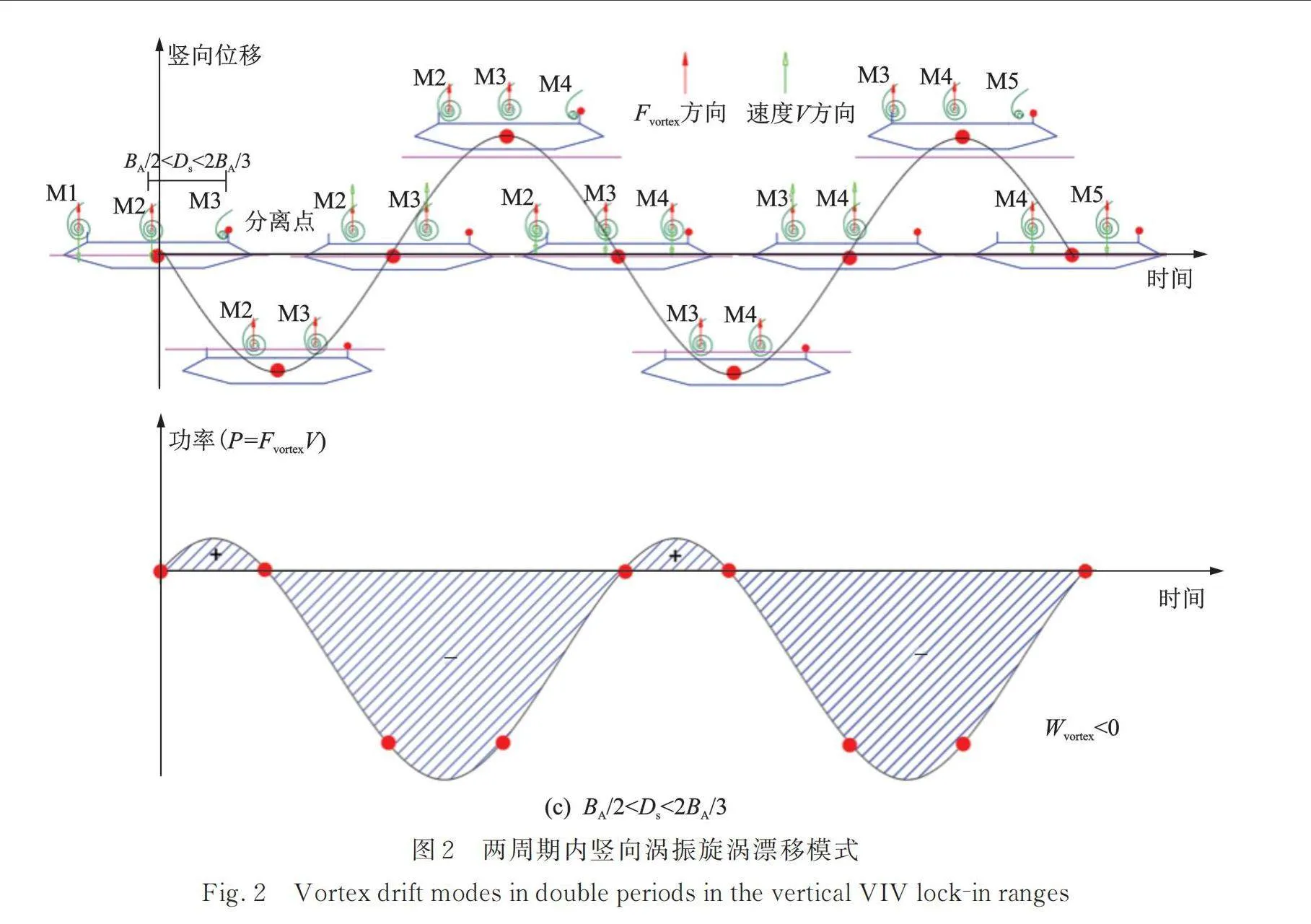
当旋涡气动力输入能量大于结构耗能时，即激发起振动，随着振动幅值增大，断面周围流场及旋涡气动力也随之变化，当旋涡气动力输入能量与结构耗散阻尼能量趋于平衡时，振动趋于稳定，即形成涡振极限环振动现象。忽略结构阻尼比效应，当时，旋涡气动力在单周期内做功为零，此时对应涡振状态。当，时，在，和三种情况下，断面振动两周期内竖向位移图及表面整体旋涡漂移模式和旋涡气动力做功如图2所示。上表面旋涡以命名，断面向上振动为正，向下振动为负。当时，表示漂移速度为的分离涡刚好经过2个竖向运动周期到达断面后缘，此时断面表面旋涡在单个周期内总体做功等于零，与文献［9］等流场观测相一致。需要注意的是，上述推导忽略后缘旋涡作用和结构阻尼比效应。

当忽略后缘旋涡的作用，旋涡漂移速度与断面振动周期之间关系可表示为：

（9）

涡振风速可表示为：

（10）

式中 为实际折减风速；为断面振动频率。则：

（11）

式中 为旋涡漂移速度与来流风速之比，即

（12）

则分离涡斯托罗哈数为：

（13）

由式（13）可知，分离涡斯托罗哈数可以表征旋涡气动力做功能量特征，与旋涡漂移距离、旋涡漂移速度及来流风速比值等相关。旋涡漂移速度与斯托罗哈数成正比，与周志勇等［15］流场观测相吻合。当取1时，对应分离涡1阶激励；当取值大于1时，对应分离涡阶激励，即斯托罗哈数为分离涡1阶激励时对应斯托罗哈数的倍。

1.3 多阶涡振

旋涡漂移速度与来流风速之比值可取值为0.50～0.60［9］。本文取值为0.55，结合式（13），则涡振风速可表示为：

（14）

对于存在个前缘分离点的单对称轴断面，存在个潜在涡振锁定区［22］。图3为上、下表面分别存在1个前缘分离点的单对称轴断面。图3中，为上表面旋涡漂移距离，为下表面旋涡漂移距离，此断面存在阶潜在涡振锁定区。在上述涡振锁定区内，当旋涡激励能量大于结构阻尼比耗能时，涡振发生［23］。需要注意的是，简化涡仅适用于涡振的稳定振幅状态。

以上从旋涡气动力做功角度，揭示了分离涡斯托罗哈数表征的多阶涡振能量特征。上述研究忽略旋涡非定常演化过程及结构阻尼比效应。

2 机理分析

2.1 试验概况

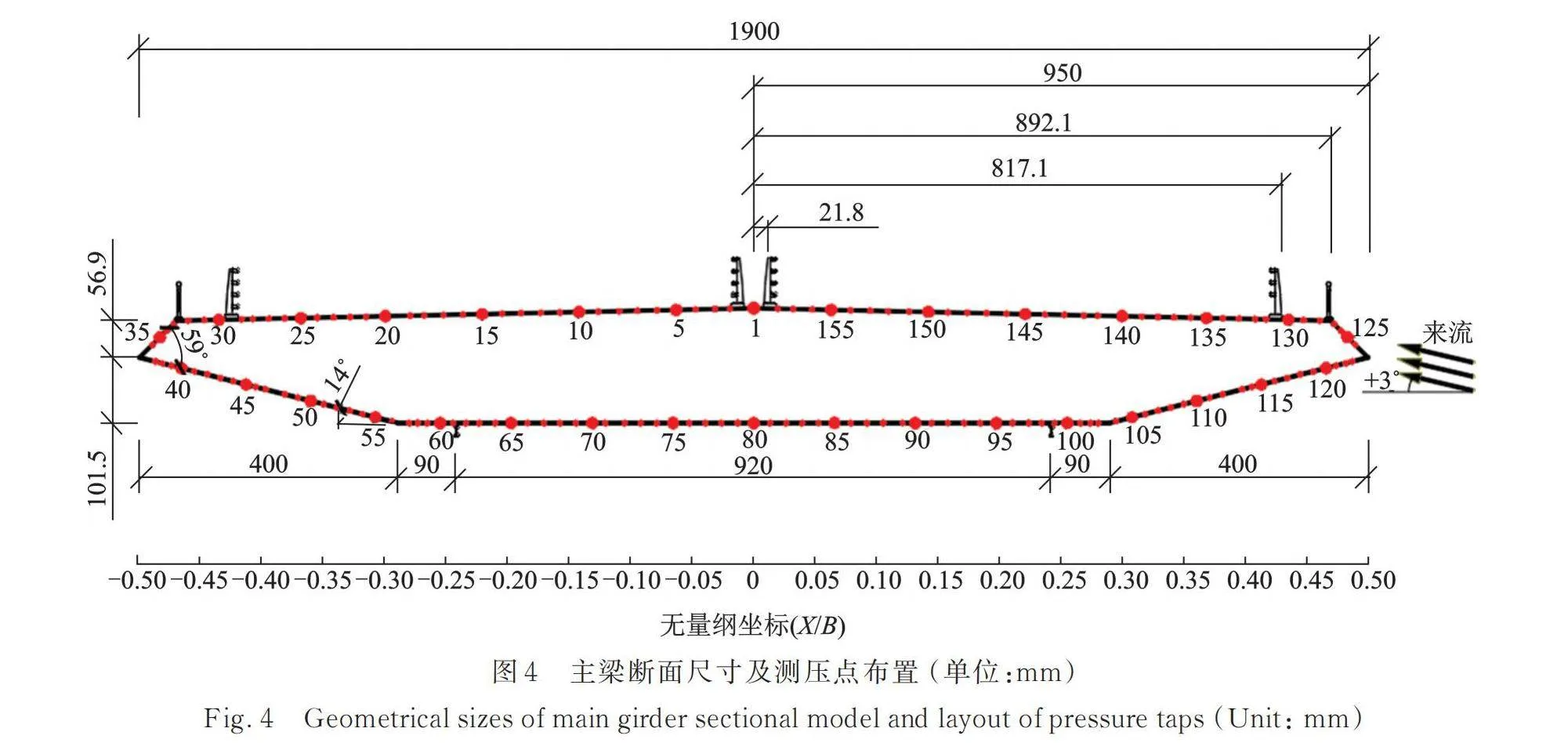
研究对象为+3°初始攻角下图4所示主梁断面，模型几何缩尺比为1∶20。模型中部断面布置测压孔，布置158个测点，主梁断面尺寸及测压点布置如图4所示。竖弯阻尼比为0.35%，竖向频率为3.32 Hz。总质量和总质量惯性矩分别为339.61 kg和168.12 kg·m2，试验详细介绍见文献［24］。主梁断面出现了明显的竖向涡振现象，涡振响应如图5所示。横坐标为折减风速，；纵坐标为归一化振幅，其中A为竖向涡振响应振幅，D为断面高度。折减风速小于2.07的风速范围内，存在3阶竖向涡振锁定区（以下统称为涡振锁定区）。其中，第2阶涡振锁定区起振风速为0.64，最大振幅对应折减风速为0.83。第3阶涡振锁定区起振风速为1.72，最大振幅对应折减风速为1.99。以下取折减风速0.83和1.99分别代表第2和第3阶涡振锁定区，进行气动力时频特性和数值流场分析。

2.2 旋涡漂移模式

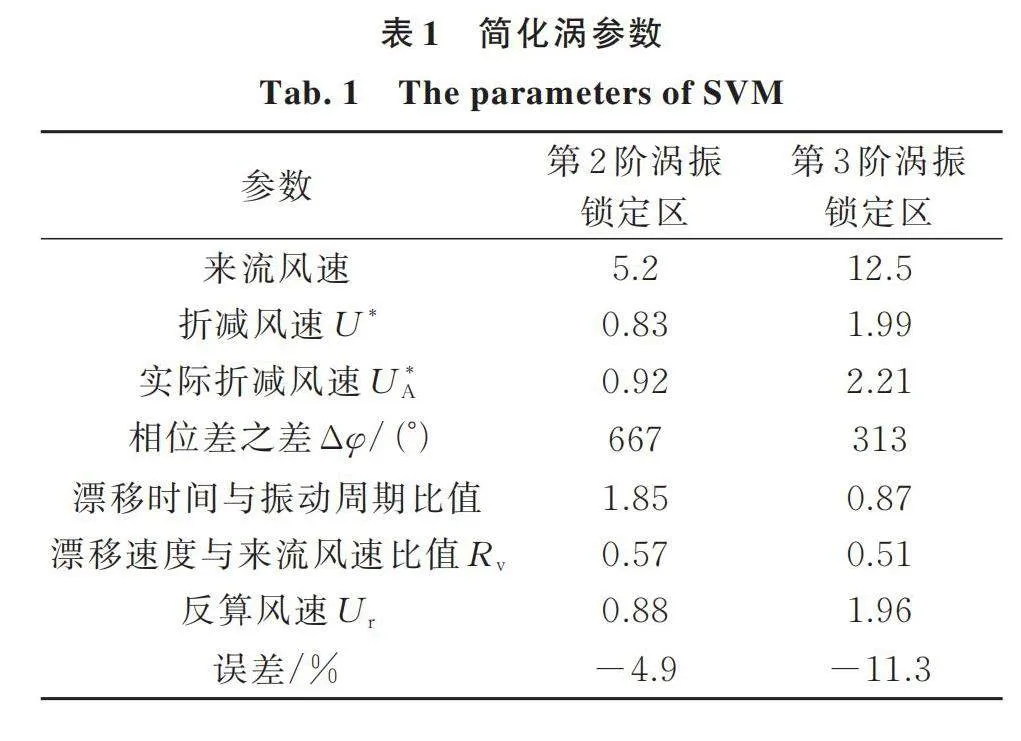
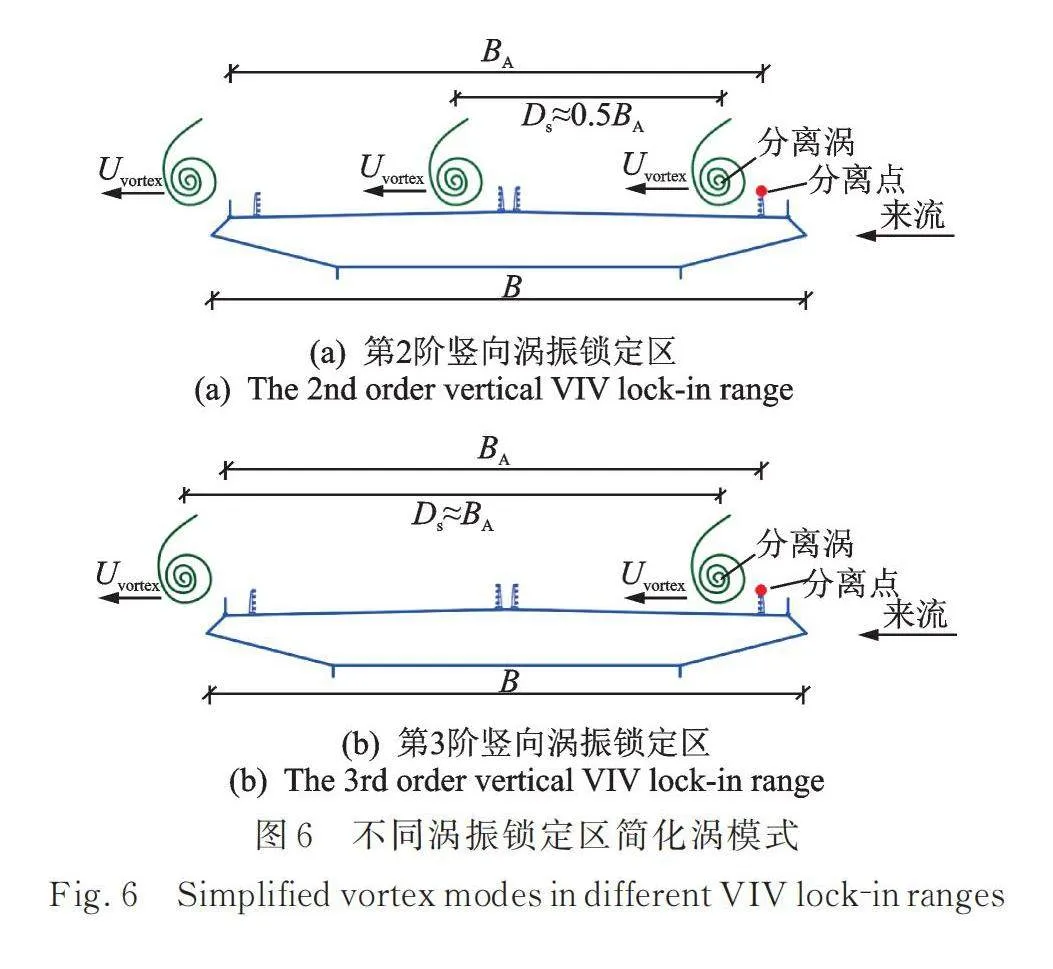
第2阶和第3阶竖向涡振锁定区旋涡漂移时间与振动周期比值分别接近于2和1，如表1所示。此外，下表面第2阶和第3阶竖向涡振锁定区相位差随坐标单调递减，且上游防撞栏杆与下游人行道栏杆处气动力与涡激力相位差之差远小于上表面，表明下表面没有明显的旋涡漂移［21］。表1列出了第2阶和第3阶竖向涡振简化涡参数。表1中，旋涡漂移速度由式（2）可得，旋涡漂移时间取为分离涡从上游防撞栏杆至下游人行道栏杆所用时间。实际折减风速由折减风速代入式（10）可得。反算风速由风速比值代入式（11）反算得到，第2阶和第3阶竖向涡振锁定区分别取为2和1。可知，各阶涡振反算风速与实际折减风速误差较小，表明上述涡振均由前缘分离涡诱导产生。第2阶和第3阶涡振锁定区分别由前缘附属设施诱发的2阶和1阶前缘分离涡主导，其简化涡模式如图6所示。

2.3 流场验证

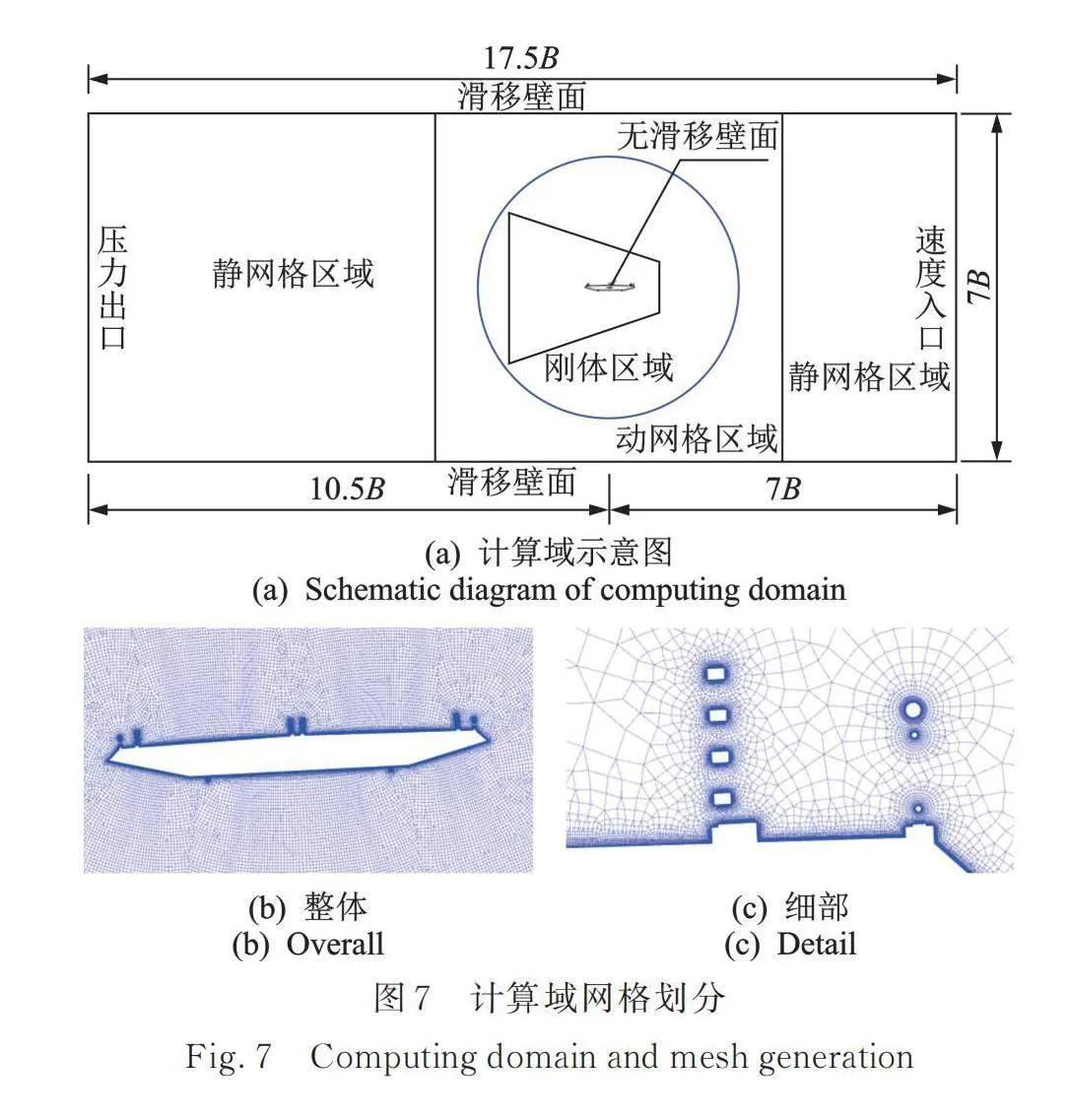
采用计算流体动力学软件Fluent进行数值模拟。计算域设置为长17.5B、宽7B的矩形区域，考虑到主梁断面在运动过程中所导致的网格变形等问题，采用分块的方式将网格分为静网格区域、动网格区域及刚体区域（圆形区域整体）。其中，静网格区域、动网格区域选用结构化网格，刚体区域选用非结构化网格+结构化网格，并对梯形区域进行局部加密。采用SIMPLE算法求解压力‑速度耦合方程，网格总数约为33万，时间步长设置为0.001 s，计算时长为60 s。绝大部分区域Y+值小于1，其中，附属设施如主梁上表面人行道栏杆、防撞栏杆及中央栏杆、下表面检修轨道附近Y+值范围为1～1.5。

计算域右侧边界设置为速度入口边界，左侧边界设置为压力出口边界。上、下边界采用滑移壁面，断面表面采用无滑移壁面边界条件，将主梁断面设置为Wall边界，湍流模型为SST k‑ω湍流模型，湍流强度取为0.5%，选择有限体积法求解控制方程。模型表面划分15层边界层，第一层厚度为0.02 mm，并以1.1的增长率向外扩散，计算域的设置和网格分区方式如图7所示。采用强迫振动方法对第2阶和第3阶竖向涡振锁定区典型风速（5.2 m/s和12.5 m/s）进行指定简谐运动，幅值取为图5试验测量值。

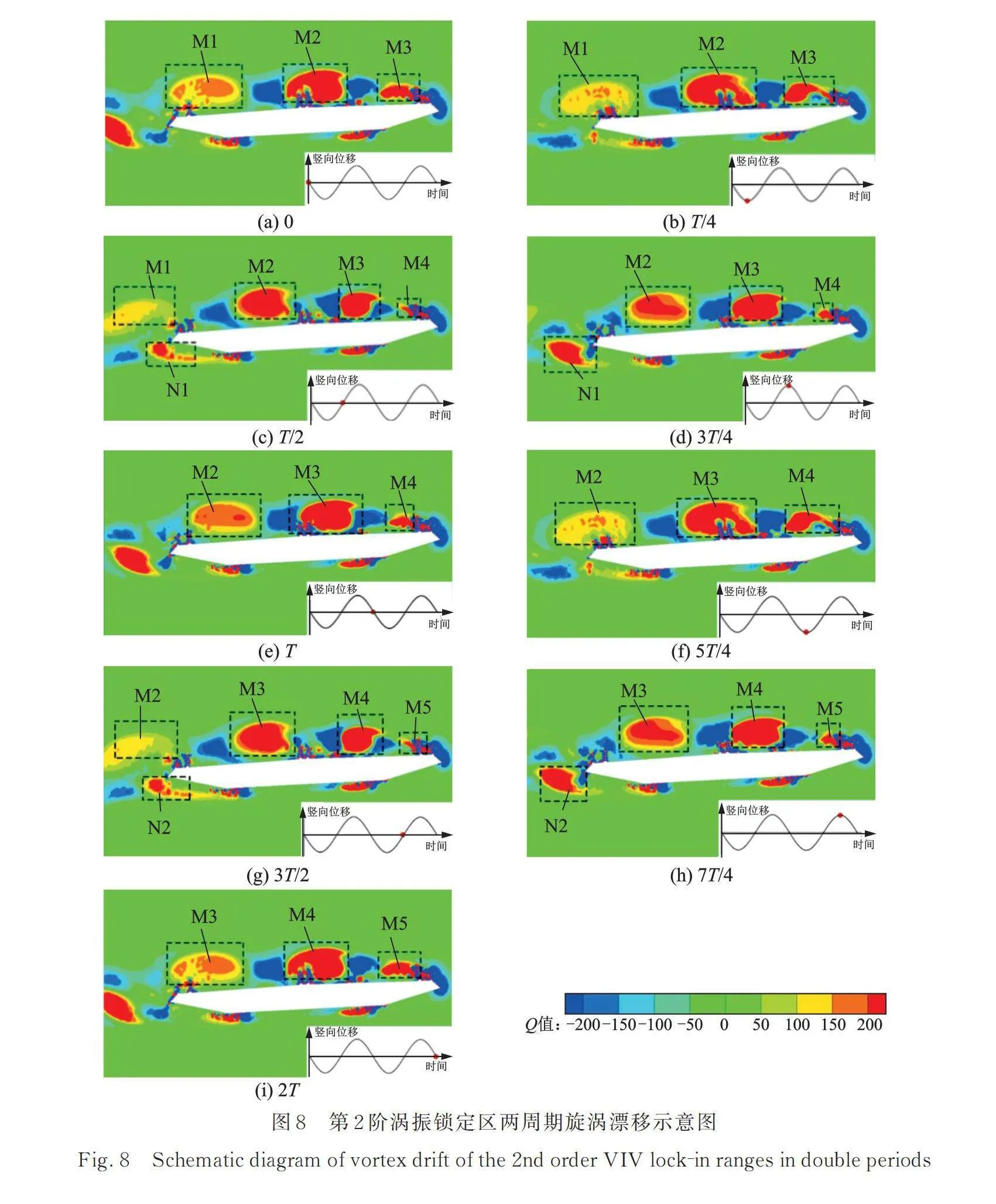
以第2阶涡振锁定区区断面上表面为例，两振动周期下的典型时刻旋涡漂移示意图如图8所示。本节利用Q准则［25］对断面附近旋涡进行了表征，其中准则定义流场中的速度梯度张量的第二矩阵不变量Q具有正值的区域为旋涡区域（图示红色区域）；当时，旋转速率小于应变速率，流体单元的运动是非旋转的（图示蓝色区域）。图8中，上、下表面旋涡分别以M，N命名。气流在断面上表面上游人行道栏杆处产生分离，在人行道栏杆与防撞栏之间形成分离泡，并在防撞栏处产生分离涡。时刻，断面上表面前缘存在一尺度较小的旋涡，断面中部（距断面前缘约）及后缘分别有大尺度旋涡和，其中旋涡即将脱落，旋涡在漂移过程中尺度逐渐增大；时刻，旋涡漂移至距断面前缘约处，旋涡从后缘脱落，此时前缘产生新的分离涡；时刻，旋涡漂移至断面中点处（距断面前缘约），旋涡即将脱落；时刻，旋涡漂移至距断面前缘约处时，旋涡脱落，前缘产生新的分离涡，此时表面旋涡分布与时刻一致；后续按此过程循环往复。故前缘分离产生旋涡从分离点漂移至断面尾缘需耗时约2个振动周期，与2.2节第2阶涡振锁定区简化涡模式相吻合。

对于第2阶涡振锁定区断面下表面，气流在上、下游检修轨道处流动分离，形成分离泡。并在下游检修轨道区域发展为较大尺度尾涡，上游检修轨道附近未发现较大尺度涡旋。其中尾涡与分别约于与时刻产生。即下表面尾涡相继产生旋涡漂移至同一位置其时间相隔。下表面与上表面旋涡从尾缘完全脱落时间约相差。对比上、下表面流场，可知上表面旋涡尺度远大于下表面旋涡，故前缘附属设施诱发的2阶前缘分离涡周期性漂移，即2阶简化涡模式，对第2阶涡振锁定区涡振起主导作用，与2.2节结论一致。

同理，对于第3阶涡振锁定区，断面时刻与时刻表面流场分布基本一致。上表面前缘分离产生旋涡从分离点漂移至断面尾缘需耗时约1个振动周期，旋涡漂移速度为第2阶涡振锁定区旋涡漂移速度的2倍，与2.2节第3阶涡振锁定区简化涡模式相吻合。下表面上游检修轨道附近无较大尺度涡旋，下游斜腹板存在较大尺度尾涡，如图9所示。上表面旋涡尺度远大于下表面旋涡，前缘附属设施诱发的1阶前缘分离涡周期性漂移，即1阶简化涡模式，对第3阶涡振锁定区涡振起主导作用。

3 结 论

基于简化涡模型，从能量视角建立旋涡漂移、断面周期性运动与同步气动力之间关系，以典型流线型闭口箱梁为研究对象，通过其发生涡振时气动力时频演变特性与流场特征，验证简化涡模型，揭示典型流线型箱梁多阶涡振机理。主要研究结论如下：

（1） 分离涡斯托罗哈数表征旋涡气动力做功能量特征，其可表达为旋涡漂移速度与来流风速比值的正整数倍，即同一前缘分离点对应个涡振锁定区。对于存在个前缘分离点的单对称轴断面，存在个潜在涡振锁定区。

（2） 前缘分离涡主导涡振可由分离涡斯托罗哈数表征，第2阶和第3阶竖向涡振锁定区分别由2阶和1阶简化涡模式下的前缘分离涡在断面进行漂移所诱发与维系。

（3） 简化涡模式和流场验证多阶涡振情况基本吻合，验证了用简化涡揭示多阶涡振机理的可行性。

研究构建的针对涡振的简化涡分析方法，在忽略结构阻尼比效应及绕流流场非定常演变效应的前提下，对涡振机理分析有较好效果。未来将进一步推广至扭转涡振、竖向与扭转涡振耦合以及开槽断面涡振机理分析。

参考文献：

［1］华旭刚， 黄智文， 陈政清. 大跨度悬索桥的多阶模态竖向涡振与控制［J］. 中国公路学报， 2019， 32（10）： 115-124.

HUA Xugang， HUANG Zhiwen， CHEN Zhengqing. Multi-mode vertical vortex-induced vibration of suspension bridges and control strategy［J］. China Journal of Highway and Transport， 2019， 32（10）： 115-124.

［2］许福友， 林志兴， 李永宁， 等. 气动措施抑制桥梁涡振机理研究［J］. 振动与冲击， 2010， 29（1）： 73-76.

XU Fuyou， LIN Zhixing， LI Yongning， et al. Vortex resonance depression mechanism of a bridge deck with aerodynamic measures［J］. Journal of Vibration and Shock， 2010， 29（1）： 73-76.

［3］GE Y J， ZHAO L， CAO J X. Case study of vortex-induced vibration and mitigation mechanism for long-span suspension bridge［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2022， 220： 104866.

［4］LI H， LAIMA S J， ZHANG Q Q， et al. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2014， 124： 54-67.

［5］高东来， 陈文礼， 杨文瀚， 等. 基于涡动力学的大跨度桥梁风效应流动控制［J］. 中国科学： 技术科学， 2021，51（5）： 517-529.

GAO Donglai， CHEN Wenli， YANG Wenhan， et al. Vortex dynamics-based flow control of wind effects on long-span bridges［J］. Scientia Sinica （Technologica）， 2021， 51（5）： 517-529.

［6］辛大波， 欧进萍. 定常吸气改善桥梁断面风致静力特性的数值［J］. 沈阳建筑大学学报（自然科学版）， 2008， 24（1）： 1-5.

XIN Dabo， OU Jinping. Numerical investigation in improving aerodynamic performances of drag force of cross section for bridge box girders by steady air-suction［J］. Journal of Shenyang Jianzhu University （Natural Science）， 2008， 24（1）： 1-5.

［7］李春光， 毛禹， 颜虎斌， 等. 基于吸气的流线型箱梁涡振主动流动控制试验研究［J］. 桥梁建设， 2022， 52（4）： 95-102.

LI Chunguang， MAO Yu， YAN Hubin， et al. Experimental study on active flow control of vortex-induced vibration of streamlined box girder based on suction［J］. Bridge Construction， 2022， 52（4）： 95-102.

［8］PAÏDOUSSIS M P， PRICE S J， LANGRE E D. Fluid-Structure Interactions： Cross-Flow-Induced Instabilities［M］. New York： Cambridge University Press， 2011.

［9］SHIRAISHI N， MATSUMOTO M. On classification of vortex-induced oscillation and its application for bridge structures［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1983， 14（1-3）： 419-430.

［10］胡传新， 赵林， 周志勇， 等. 流线型闭口箱梁抑流板抑制涡振机理研究［J］. 振动工程学报， 2020， 33（1）： 1-11.

HU Chuanxin， ZHAO Lin， ZHOU Zhiyong， et al. Suppressing mechanism of spoilers on vortex-induced vibrations around a streamlined closed-box girder based on characteristics of aerodynamic forces and flow field［J］. Journal of Vibration Engineering， 2020， 33（1）： 1-11.

［11］KOMATSU S， KOBAYASHI H. Vortex-induced oscillation of bluff cylinders［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1980， 6（3-4）： 335-362.

［12］MATSUMOTO M， SHIRAISHI N， SHIRATO H， et al. Mechanism of， and turbulence effect on vortex-induced oscillations for bridge box girders［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1993， 49（1-3）： 467-476.

［13］葛耀君， 赵林， 许坤. 大跨桥梁主梁涡激振动研究进展与思考［J］. 中国公路学报， 2019， 32（10）： 1-18.

GE Yaojun， ZHAO Lin， XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges［J］. China Journal of Highway and Transport， 2019，32（10）： 1-18.

［14］KUBO Y， HIRATA K， MIKAWA K. Mechanism of aerodynamic vibrations of shallow bridge girder sections［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1992， 42（1-3）： 1297-1308.

［15］周志勇， 毛文浩. 地面效应对近流线型断面涡激共振性能的影响［J］. 振动与冲击， 2017， 36（6）： 168-174.

ZHOU Zhiyong， MAO Wenhao. Ground effects on vortex-induced vibrations of a closed box girder［J］. Journal of Vibration and Shock， 2017， 36（6）： 168-174.

［16］LARSEN A， SAVAGE M， LAFRENIÈRE A， et al. Investigation of vortex response of a twin box bridge section at high and low Reynolds numbers［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2008， 96（6-7）： 934-944.

［17］董佳慧， 黄林， 王骑， 等. Π型钢-混叠合梁斜拉桥涡振性能及整流罩制振措施研究［J］. 振动与冲击， 2022， 41（16）： 50-57.

DONG Jiahui， HUANG Lin， WANG Qi， et al. Vortex-induced vibration performance of a cable-stayed bridge with a Π-shaped steel-concrete composite girder and aerodynamic countermeasure research［J］. Journal of Vibration and Shock， 2022， 41（16）： 50-57.

［18］祝志文， 石亚光， 颜爽. 带防撞栏杆扁平箱梁高阶模态涡激振动的CFD研究［J］. 振动与冲击， 2021， 40（10）： 228-234.

ZHU Zhiwen， SHI Yaguang， YAN Shuang. Investigation on vortex-induced high-mode vibrations of flat box girders with crash barriers based on CFD［J］. Journal of Vibration and Shock， 2021， 40（10）： 228-234.

［19］马凯， 胡传新， 袁万城， 等. 基于风洞试验和数值模拟的双矩形断面涡振气动干扰研究［J］. 振动与冲击， 2020， 39（1）： 157-168.

MA Kai， HU Chuanxin， YUAN Wancheng， et al. Aerodynamic interferences in vortex-induced vibration of dual-rectangular sections based on wind tunnel tests and numerical simulation［J］. Journal of Vibration and Shock， 2020， 39（1）： 157-168.

［20］李志国， 周强， 马存明， 等. 中央格栅抑制分离式双箱梁涡振的机理研究［J］. 桥梁建设， 2018， 48（1）： 19-24.

LI Zhiguo， ZHOU Qiang， MA Cunming， et al. Mechanism of suppressing vortex-induced vibration of twin-box girder using central grids［J］. Bridge Construction， 2018， 48（1）： 19-24.

［21］HU C X， ZHAO L， GE Y J. A simplified vortex model for the mechanism of vortex-induced vibrations in a streamlined closed-box girder［J］. Wind and Structures， 2021， 32（4）： 309-319.

［22］ZIADA S， ROCKWELL D. Oscillations of an unstable mixing layer impinging upon an edge［J］. Journal of Fluid Mechanics， 1982， 124： 307-334.

［23］NAKAMURA Y， NAKASHIMA M. Vortex excitation of prisms with elongated rectangular， H and perpendicular-to cross-sections［J］. Journal of Fluid Mechanics， 1986， 163： 149-169.

［24］YUAN W Y， LAIMA S J， CHEN W L， et al. Investigation on the vortex-and-wake-induced vibration of a separated-box bridge girder［J］. Journal of Fluids and Structures， 2017， 70： 145-161.

［25］NAKAMURA Y， OHYA Y， TSURUTA H. Experiments on vortex shedding from flat plates with square leading and trailing edges［J］. Journal of Fluid Mechanics， 1991， 222： 437-447.

Vertical vortex‑induced vibration mechanism of streamlined closed-box girder based on vortex drift hypothesis

HU Chuan-xin1， ZHAO Lin2， GONG Ling-long1， GE Yao-jun2

（1.School of Urban Construction， Wuhan University of Science and Technology， Wuhan 430065， China； 2.State Key Labortory of Disaster Reduction in Civil Engineering， Tongji University， Shanghai 200092， China）

Abstract： Vortex shedding and drift are key characteristics around the bridge girders during VIVs， and therefore it is necessary to reveal VIVs mechanisms of bridge girders from the perspective of vortex dynamics. A simplified vortex model was constructed from the perspective of aerodynamic work. Taking a typical streamlined-closed box girder as an example， a simplified wortex model was constructed from the perspective of aerodynamic work. Combined with the aerodynamic time-frequency characteristics of the bridge girder from wind tunnel experiments and the flow field characteristics around the girder based on numerical simulation method， the above model was verified and then the multi-order VIVs lock-in range mechanisms of the girder were revealed. The results indicate that the Strouhal number of the separation vortex characterizes energy effects of the vortex aerodynamics， which can be expressed as a positive integer multiple of the ratio of vortex-drift velocity to oncoming flow velocity， implying that a separation point can excite multiple VIVs lock-in ranges. There were 3 order lock-in ranges of vertical VIVs for the girder. Both the 2nd and 3rd lock-in ranges are excited and sustained by the large-scale separated vortexes separating at the leading edge and periodic drift in the drift distance between the separation point and the trailing edge. Especially， it takes about 2 and 1 vibration cycle for the separation vortexes to traverse the drift distance in the 2nd and 3rd order VIVs lock-in ranges， respectively. Therefore， they are dominated by the 2nd and 1st order simplified-vortex modes originating from the leading edge， respectively. This study verifies the rationality of the simplified-vortex model to deduce the vortices evolutionary characteristics around the bridge girder and provides a new methodology for VIVs mechanism of the bridge girders.

Key words： vortex-induced vibration（VIV）；vortex drift；streamlined box girder；simplified vortex model（SVM）

作者简介： 胡传新（1987―），男，博士。E-mail：chuanxin86@126.com。

通讯作者： 赵 林（1974―），男，博士，教授。E-mail：zhaolin@tongji.edu.cn。