高阻尼厚层橡胶支座力学性能试验研究

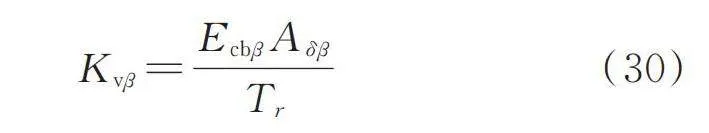
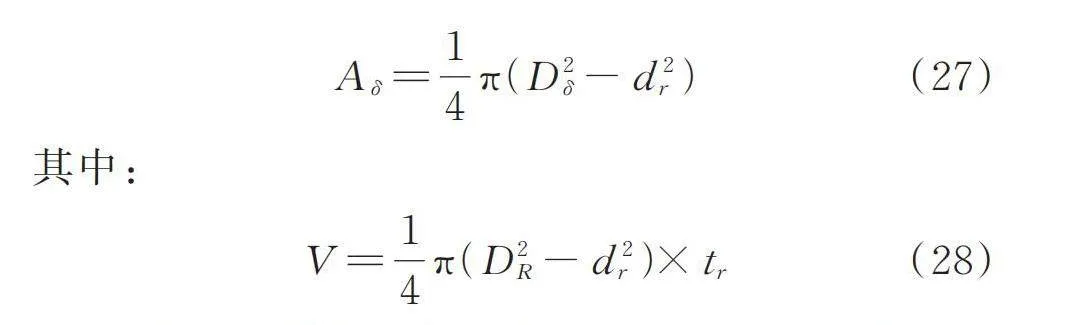
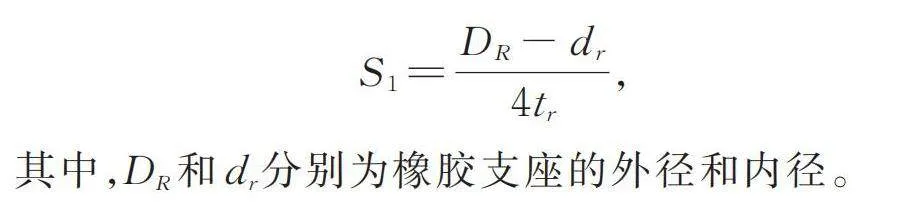
摘要： 为探究高阻尼厚层橡胶支座的力学性能，本文通过研究高阻尼厚层橡胶支座在竖向压应力作用下的水平剪切及竖向压缩的受力特征，建立了考虑水平剪切变形的力学模型，并提出了基于压应力变化的竖向刚度修正理论。为验证理论模型的准确性，分别设计了3种不同第一形状系数的高阻尼厚层橡胶支座来进行水平拟静力剪切和竖向压缩试验。结果表明：高阻尼厚层橡胶支座的等效水平刚度、等效阻尼比随内部钢板对橡胶的约束作用的变化而变化，在水平拟静力试验下，随支座水平剪切变形的增加呈现出先减小后增大的变化趋势，且随着竖向压应力的增大，水平等效刚度逐渐减小；在竖向压缩试验中，随着竖向压力的增大，竖向压缩刚度呈现非线性强化特征。通过理论与试验结果的对比分析可知：本文构建的水平剪切变形的力学模型可较好地描述高阻尼厚层橡胶支座水平剪切的力学性能，竖向刚度修正理论可以准确计算其竖向刚度，不同工况下与试验结果的偏差均在5%以内。

关键词： 高阻尼厚层橡胶支座； 压应力相关性； 剪应变相关性； 试验研究； 力学性能

中图分类号： TU352.12 文献标志码： A 文章编号： 1004-4523（2024）09-1584-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.015

引 言

近年来，隔震技术的发展已经逐渐成熟。传统的叠层橡胶支座和铅芯橡胶支座已经被广泛应用于隔震工程［1］。但是通过对铅芯橡胶支座的试验研究发现：传统铅芯橡胶支座在大位移变形时往往会因为铅芯挤压变形而不易复位，并且铅芯的大量应用不利于环境保护［2］。基于此，国内外学者对高阻尼橡胶支座进行了大量的研究［3］。

高阻尼橡胶隔震支座由于在其橡胶材料中添加炭黑、增塑剂等材料，并且由加劲钢板为其提供约束，使其具有较好的耗能性能和稳定的恢复力［4］。陈彦江等［5］研究了竖向压应力、水平剪切应变、加载频率等对高阻尼橡胶支座滞回性能的影响，结果表明：高阻尼橡胶隔震支座滞回曲线饱满，耗能能力稳定，不同的加载频率对其等效刚度和阻尼均有影响。魏威等［6］提出了一种高阻尼橡胶隔震支座考虑竖向压应力的速度相关性本构模型，且对隔震建筑在近断层地震作用下的响应进行了分析研究。雷拓等［7］研究了不同橡胶添加材料对高阻尼橡胶隔震支座的综合力学性能的影响。沈朝勇等［8］通过反复加载试验对高阻尼橡胶隔震支座剪应变相关性，压应力相关性，加载频率、温度相关性，老化性能等进行了研究，并提出了相关参数随剪应变变化的经验公式。

随着隔震技术的发展，竖向隔震尤其是三维隔震引起国内外学者的广泛关注［9］。李吉超等［10］对厚层橡胶支座进行了系统的试验研究，结果表明：厚层橡胶支座较传统橡胶支座竖向刚度更小，可以用于建筑、桥梁等结构的三维隔震。何文福等［11］对厚层橡胶支座的基本力学性能进行了研究，发现厚层橡胶支座在水平方向具有良好的力学性能，竖向具有较好的大变形能力，可以作为机械设备、精密仪器等的三维隔震装置。王涛等［12‑13］开发了一种三维隔震支座，由厚层橡胶支座和油阻尼器组成，用于核电厂三维隔震，通过对厚层橡胶支座的试验研究发现：厚层橡胶支座水平方向的剪切性能与普通橡胶支座差别不大，但是其竖向具有较大的变形能力，竖向刚度约为普通橡胶支座的1/8左右。何文福等［14］提出了一种建筑三维隔震/振支座，其由铅芯橡胶支座作为水平隔震元件，厚层橡胶支座作为竖向隔震元件，通过理论分析及实际项目应用分析发现：该建筑三维隔震/振支座可以用于轨交建筑的三维隔震/振。周颖等［15］将厚层橡胶支座用于上海莘庄地铁上盖结构并进行设计分析，结果表明：厚层橡胶支座不但可以实现隔震效果，同时结构的倾覆摇摆问题也没有出现。文献［16‑17］提出了一种新的高性能混合无源基底隔离系统，将基底隔离系统（BIS）与调谐串联质量阻尼器惯性器（TTMDI）集成在一起，称为BIS+TTMDI，其具有高控制效率、高鲁棒性、非常小的冲程和大幅降低的阻尼需求。

本文针对高阻尼厚层橡胶支座，建立了考虑水平剪切变形的力学模型，提出了水平方向刚度计算的解析理论公式和基于压应力变化的竖向刚度修正理论经验公式。此外，本文设计了3种不同第一形状系数的高阻尼厚层橡胶支座，并进行了水平拟静力剪切和竖向压缩试验。通过试验研究，分析了高阻尼厚层橡胶支座在竖向压应力作用下的水平剪切、竖向压缩及竖向破坏性能，并与理论计算结果进行对比分析。

1 高阻尼厚层橡胶支座力学性能

分析高阻尼厚层橡胶支座在准静态加载条件下产生的变形及受力特征，并做以下假定：（1）高阻尼厚层橡胶本体在加载过程中的任意时刻处于平衡状态；（2）高阻尼厚层橡胶某一点在任意时刻的内能密度完全由该时刻点的应变状态确定，即存在一个应变张量的标量弹性势能函数，对应变分量的导数是对应的应力分量。

根据第二类Piola‑Kirchhoff应力分析得到下式：

（1）

式中 C表示Cauchy‑Green变形张量；，分别表示橡胶材料在大、小变形下的应力状态；N表示组合成橡胶的非线性弹塑性弹簧个数；表示弹簧序号；gn表示各个弹簧之间的应力分摊比例，其中所有gn的总和为1；ln为各弹簧的应变速率；L为累计时间内的变形应变。

对于高阻尼厚层叠层橡胶，应变能函数W为：

（2）

式中 I1，I2，I3分别为Cauchy‑Green变形张量C的第一、第二、第三基本不变量，表达式为：

（3）

通过微元体分析变形可知，橡胶单元的组合变形为：

（4）

式中 ，和为单元节点变形前坐标；和为单元剪切变形量。

由式（1）～（4）可以得到变形体的变形梯度为：

（5）

橡胶单元的变形前后体积比为：

（6）

式（1）中的Cauchy‑Green变形张量为：

（7）

速度梯度张量和变形速度张量分别为：

（8）

（9）

式中 为速度场梯度的速度梯度张量。

通过得到的变形速度张量D，对D在0～t的累计时间内进行积分，得到橡胶单元的变形应变为：

（10）

式中 表示从变形开始时刻到当前时刻的变形路径；表示单位变形路径。

假设橡胶单元为不可压缩的，则第一不变量和第三不变量分别为：

（11）

（12）

式中 和分别表示1，2方向的应变量。

通过式（1）和（3）可得到应力为：

（13）

因此，橡胶单元的双向剪应变和剪应力的关系为：

（14）

（15）

根据Neo‑Hookean模型引入橡胶小变形下的应变能函数，为了考虑橡胶大变形下的性能状态，通过Yeoh模型构建橡胶应变能函数，如下式所示：

（16）

（17）

式中 ，和分别表示橡胶第一、第二和第三超弹性系数；表示在Neo‑Hookean模型下的第一不变量。通过这两个应变能函数所构建的两对应力‑应变关系曲线，并且并联一个弹性单元，共同组成高阻尼厚层橡胶支座滞回模型，如图1所示。

将式（16），（17）代入式（1），（14），（15）中，可以得到双向的剪应变和剪应力的关系为：

（18）

（19）

令，对式（18），（19）进行三向线积分得：

（20）

（21）

（22）

式中 表示单位应变速率。

对式（20），（21），（22）进行下一时刻的迭代可得：

其中，剪应变和剪应力对整体截面积分，可得到高阻尼厚层橡胶支座水平剪切滞回模型中非线性部分的位移变形和剪切恢复力。

2 压剪及竖向力学模型

厚层橡胶支座不同于叠层橡胶支座，利用现有竖向刚度计算方法得出结果与试验结果偏差较大［11］。主要原因是厚层橡胶支座的橡胶层较厚，橡胶层的竖向压缩变形较大，且内部钢板对橡胶层的约束作用较小。王涛等［13］通过修正单层橡胶的变形，利用积分修正的方式计算竖向刚度。何文福等［14］提出了考虑压应力变化的竖向刚度积分修正方法，通过对压缩模量、竖向变形等参数的修正，计算厚层橡胶支座竖向刚度。

厚层橡胶支座在竖向压应力作用下初始变形较大，其橡胶层直径、面积均会发生变化。而现有的竖向刚度计算理论没有考虑不同压应力作用下的刚度变化情况，因此本文在现有竖向刚度计算理论的基础上，提出了考虑压应力变化的竖向刚度修正计算理论。

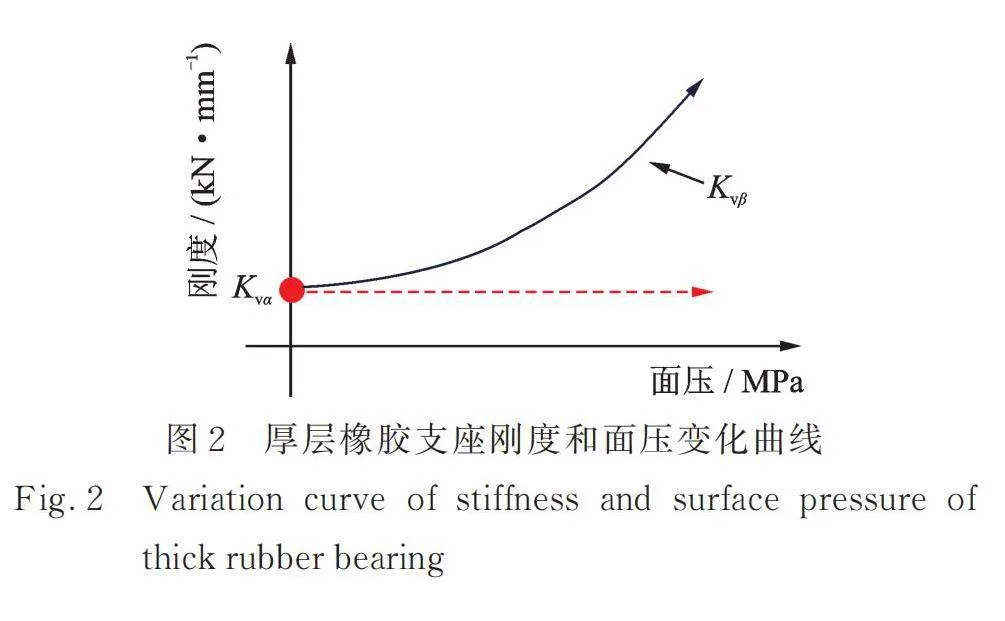
厚层橡胶支座的竖向刚度由初始面压作用下的瞬时刚度和工作面压作用下的强化修正刚度组成，即

（23）

如图2所示，为单层橡胶在压应力作用下对竖向变形的约束作用，其值随压应力的增大而逐渐增大。

在基于压应力变化的竖向刚度修正理论中，，的计算方法如下，其中α，β为指数修正系数，α，β的取值可通过对橡胶支座受压变形过程的试验进行标定得到。因此根据常规的橡胶支座竖向压缩刚度计算公式［17］，并对其采用α指数修正可得：

（24）

式中

A为铅芯橡胶支座截面面积；Tr为橡胶层总厚度；Eb为橡胶体积弹性模量；G为橡胶剪切模量；k为与硬度有关的弹性模量修正系数；S1为第一形状系数，表达式为：

，

其中，DR和dr分别为橡胶支座的外径和内径。

由于钢板对单层橡胶的约束面积不变，所以第一形状系数保持不变，弹性模量的修正计算方法如下：

（25）

考虑橡胶支座泊松比，即橡胶体积不可压缩，在受压状态下，其体积不变，如图3所示。

当竖向变形为时，单层橡胶在受压状态下的支座等效直径和等效面积的修正公式分别如下：

（26）

（27）

其中：

（28）

因此，厚层橡胶支座的竖向压应力由初始面压逐渐增加至工作面压时，其受约束作用下的等效面积的计算公式如下：

（29）

综上，工作面压作用下强化修正刚度的计算公式如下：

（30）

通过式（23）～（30）对厚层橡胶支座的竖向刚度进行修正，可得基于压应力变化的竖向刚度修正计算理论Kv，如下式所示：

（31）

3 试验研究及分析

3.1 试验简介

本次试验采用加载设备为15000 kN的动态压剪试验机，如图4所示，其竖向荷载为15000 kN，水平剪力为2000 kN，水平位移为1000 mm。试验过程中，竖向加载采用荷载控制，水平方向加载采用位移控制。

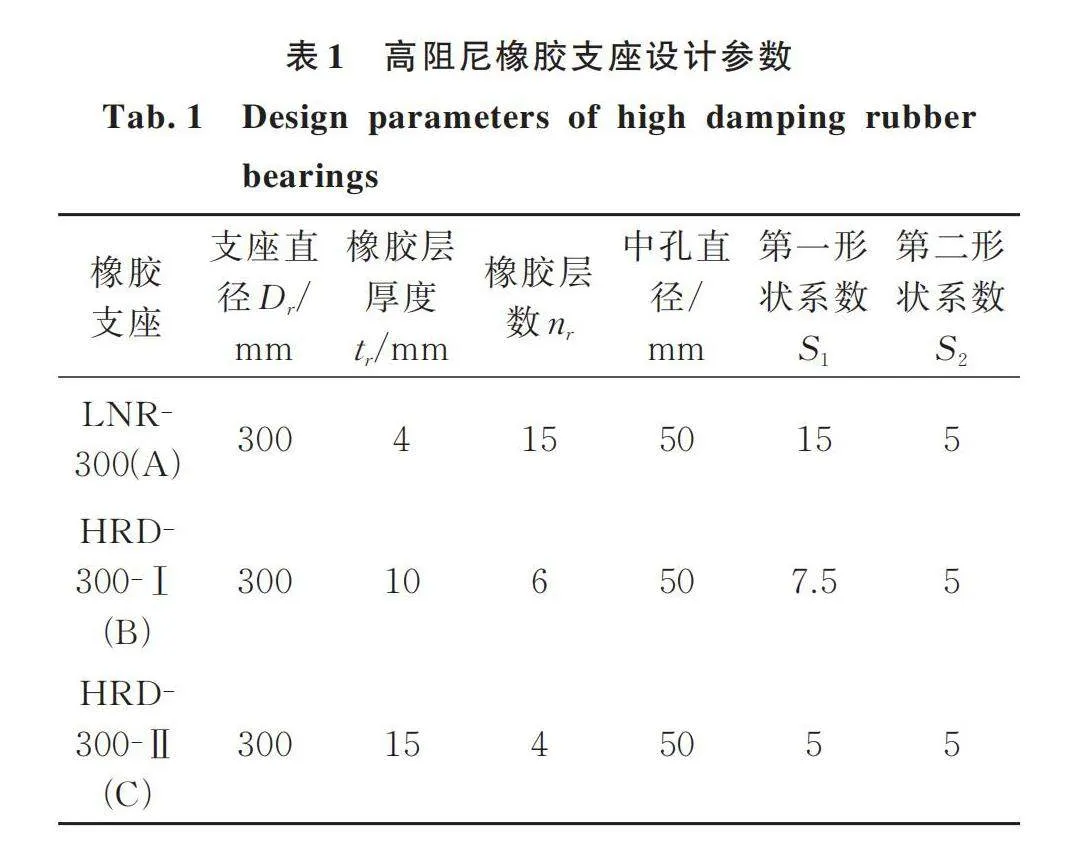
本次试验依据第二形状系数不变（S2=5）的原则，为了比较厚层支座和常规橡胶支座的力学性能差异，分别设计了3种不同第一形状系数的橡胶支座。其中，支座A的第一形状系数S1为15，为普通叠层橡胶支座；支座B和C的第一形状系数S1分别为7.5和5，为厚层橡胶支座。如表1所示，分别给出了3种不同橡胶支座的设计参数。

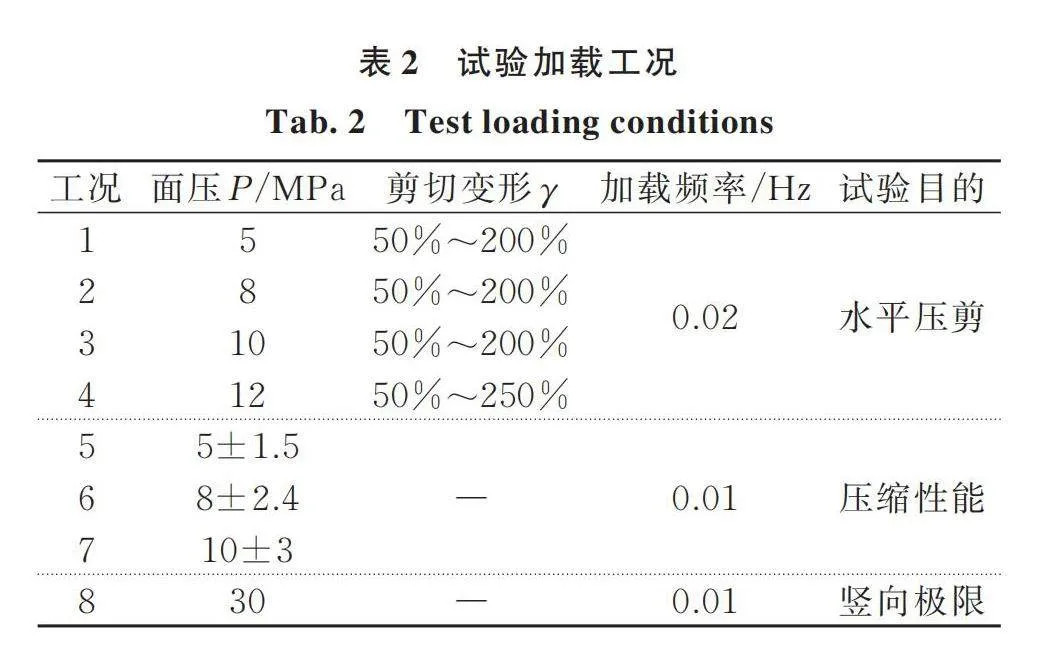
为了研究高阻尼厚层橡胶支座和叠层橡胶支座的水平剪切、竖向压缩及竖向极限性能，分别对不同形状系数的支座进行水平剪切及竖向压缩试验，试验加载工况如表2所示。

3.2 水平剪切试验

对高阻尼叠层橡胶支座和厚层橡胶支座进行水平剪切试验，其竖向压应力分别为5和10 MPa。图5分别给出了不同形状系数的高阻尼橡胶支座在相同压应力作用下的水平剪切滞回曲线。试验结果表明：

（1）在不同压应力作用下，高阻尼叠层橡胶支座和厚层橡胶支座的滞回曲线平滑且饱满，表现出稳定的力学性能。

（2）在5 MPa压应力作用下，高阻尼叠层橡胶支座的加载刚度和卸载刚度平行，其滞回曲线呈现出明显的梭形。在10 MPa压应力作用下，高阻尼厚层橡胶支座的加载刚度远小于卸载刚度，其滞回曲线由梭形变为S形，耗能能力显著增加。

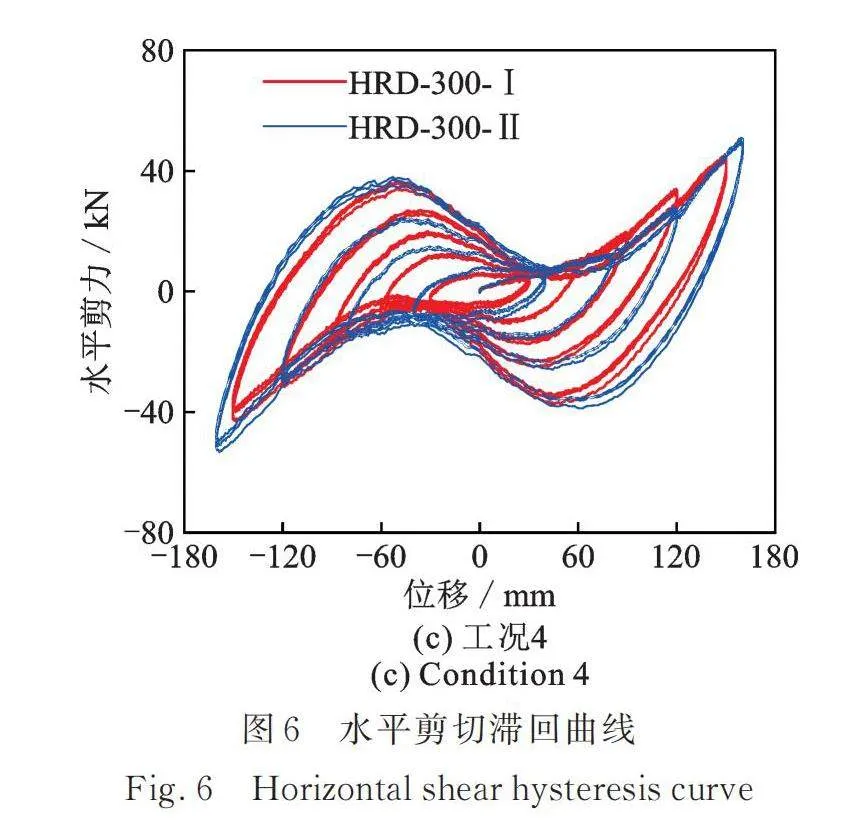
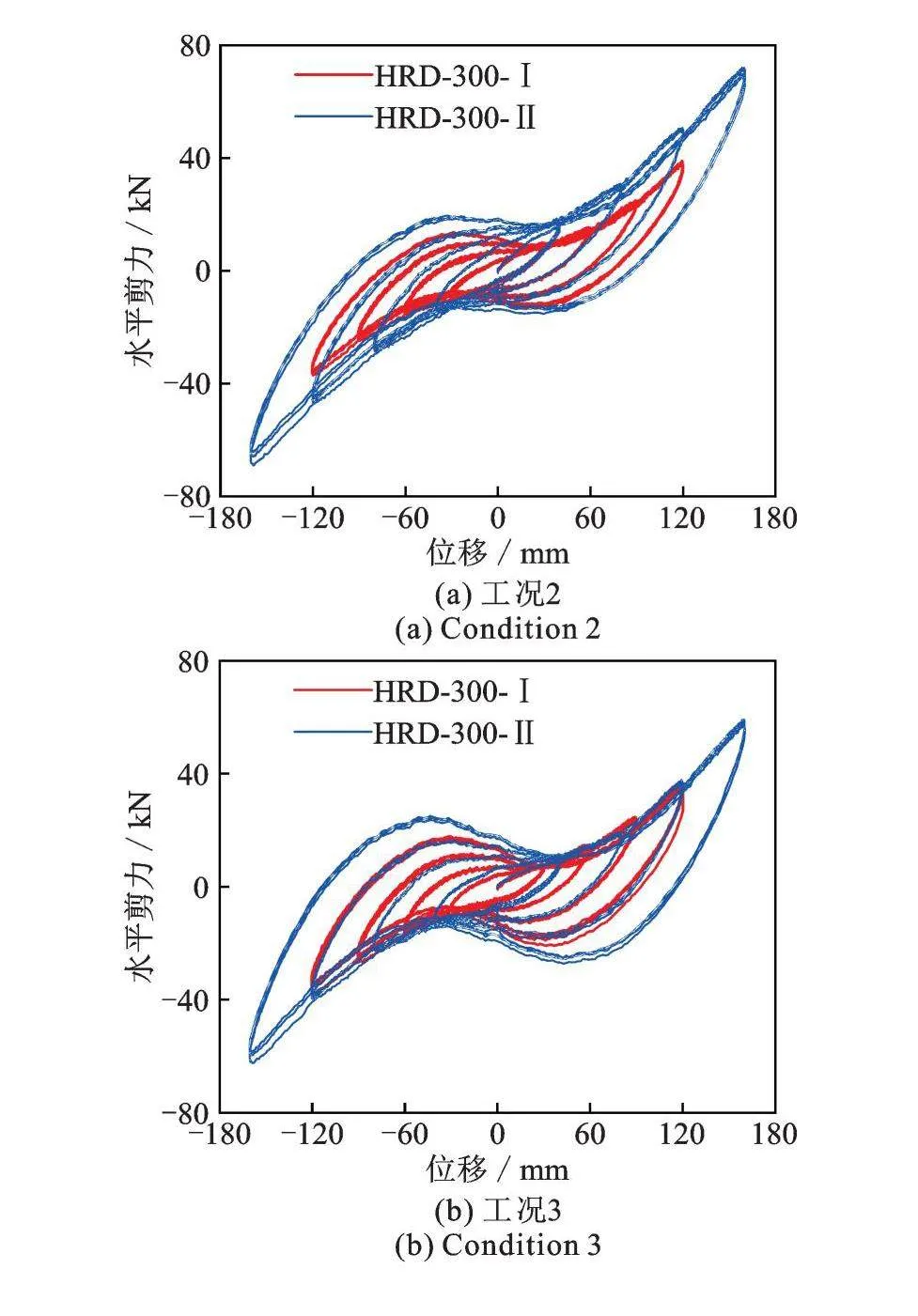
基于上述分析结果，为了分析高阻尼厚层橡胶支座在不同压应力作用下的水平剪切性能，对支座B和C在不同竖向压应力（8，10，12 MPa）作用下进行压剪试验，结果如图6所示。

由试验结果可知：在上述竖向压应力作用下，不同形状系数的高阻尼厚层橡胶支座除了呈现出相同的变化规律之外，其水平滞回曲线平滑且饱满，且随着竖向压应力的增大，滞回曲线由典型的梭形逐渐变为S形，耗能能力显著增加。

3.3 竖向压缩及极限性能试验

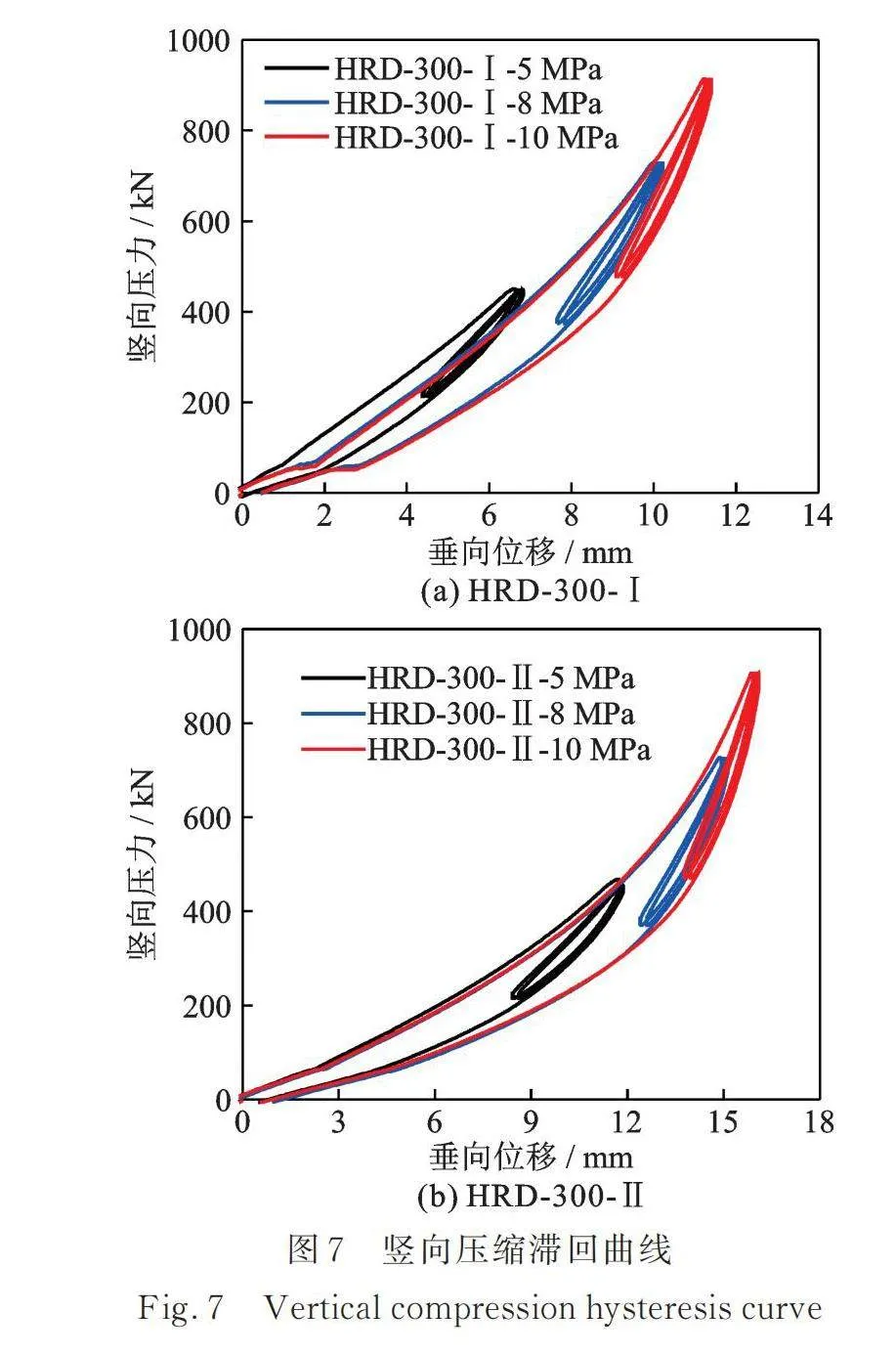
对高阻尼厚层橡胶支座进行竖向压缩试验，如工况5～7所示。图7给出了高阻尼厚层橡胶支座的竖向压缩滞回曲线。试验结果表明：（1）与普通叠层橡胶支座一样，高阻尼厚层橡胶支座的竖向刚度随压应力的增大而增大。（2）高阻尼厚层橡胶支座的竖向变形能力远大于普通叠层橡胶支座，在10 MPa竖向压应力作用下，支座的最大竖向变形约为16 mm。

如工况8所示，对高阻尼厚层橡胶支座进行竖向极限压缩试验，最大竖向压应力为30 MPa。如图8所示，在试验过程中，竖向压应力逐渐增大至30 MPa，支座没有出现明显破坏，可见支座的极限压应力大于30 MPa。图9给出了工况8作用下的竖向压缩曲线。由试验结果可知：高阻尼厚层橡胶支座在30 MPa的竖向压应力作用下，其加载曲线及卸载曲线平滑，最大竖向位移约为20 mm。

4 试验与理论对比分析

为了验证本文所提出的水平剪切变形和竖向刚度的计算理论，针对上述工况进行试验研究。限于篇幅，图10仅给出HDR‑300‑Ⅱ的试验与理论水平剪切滞回曲线的对比结果。通过对比分析可知：（1）高阻尼橡胶支座在同一竖向压应力作用下，随支座水平剪切变形的增加，由于支座内部钢板的转动，滞回曲线的形状逐渐由梭形转变为S形。（2）通过理论计算得到支座的剪切变形和恢复力与试验结果基本相同，其滞回曲线表现出了较好的耗能能力。

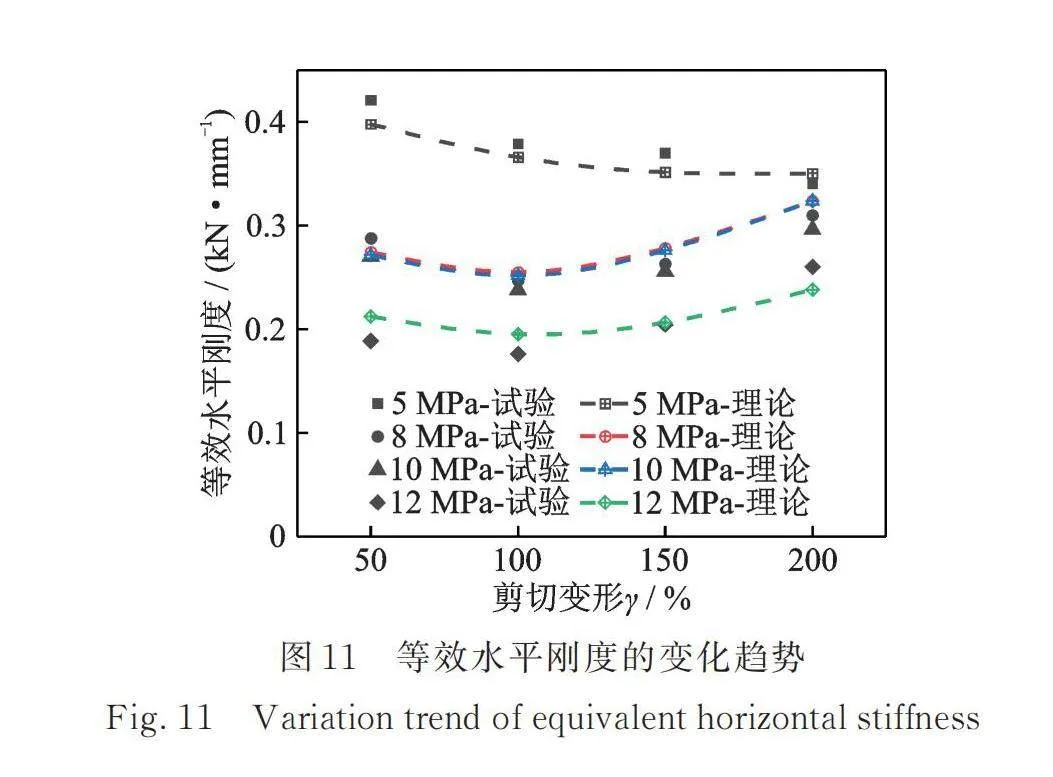
图11给出了等效水平刚度随不同剪切变形的变化趋势。当竖向压应力为5 MPa时，高阻尼厚层橡胶支座的加载刚度和卸载刚度平行，等效水平刚度随剪切变形的增加而减小，支座内部的钢板没有发生转动。

当竖向压应力分别为8，10，12 MPa时，厚层橡胶支座内部钢板随剪切变形的增加而逐渐发生转动，对单层橡胶的约束作用增强。等效水平刚度在内部钢板未发生转动时，随剪切变形的增加而减小；在内部钢板发生转动时，由于对单层橡胶的约束作用增强，等效水平刚度逐渐增大。

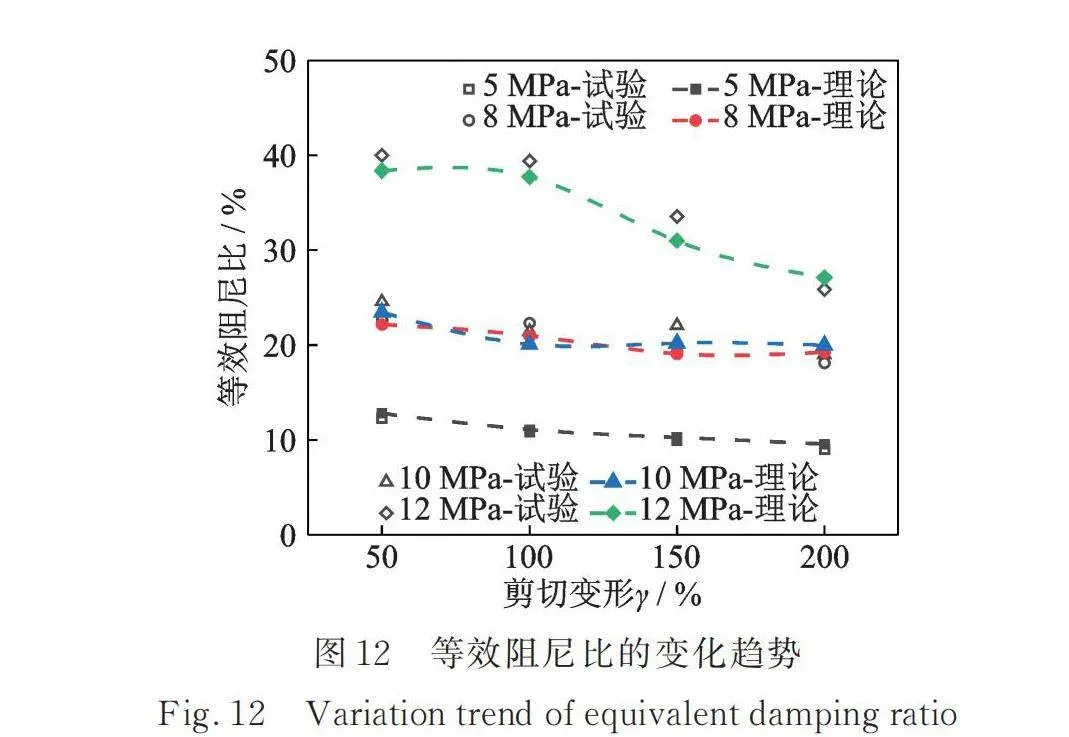
图12给出了不同压应力作用下等效阻尼比的变化趋势。在5 MPa竖向压应力作用下，其等效阻尼比随剪切变形的增加而减小；在8，10，12 MPa竖向压应力作用下，由于内部钢板转动约束作用，其等效阻尼比在不同剪切变形作用下基本保持稳定。

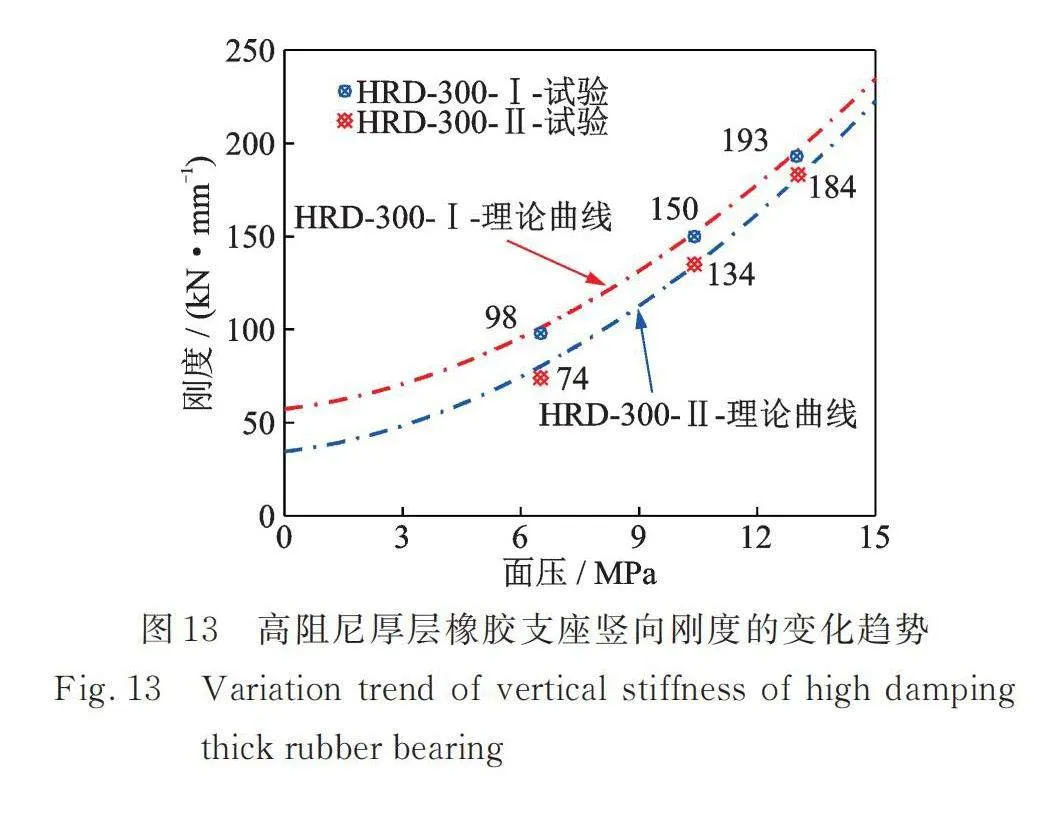
高阻尼厚层橡胶支座的竖向刚度计算理论在传统叠层橡胶支座修正的基础上得到，如式（24），（25）所示，其中修正系数α=0.9，β=0.1。

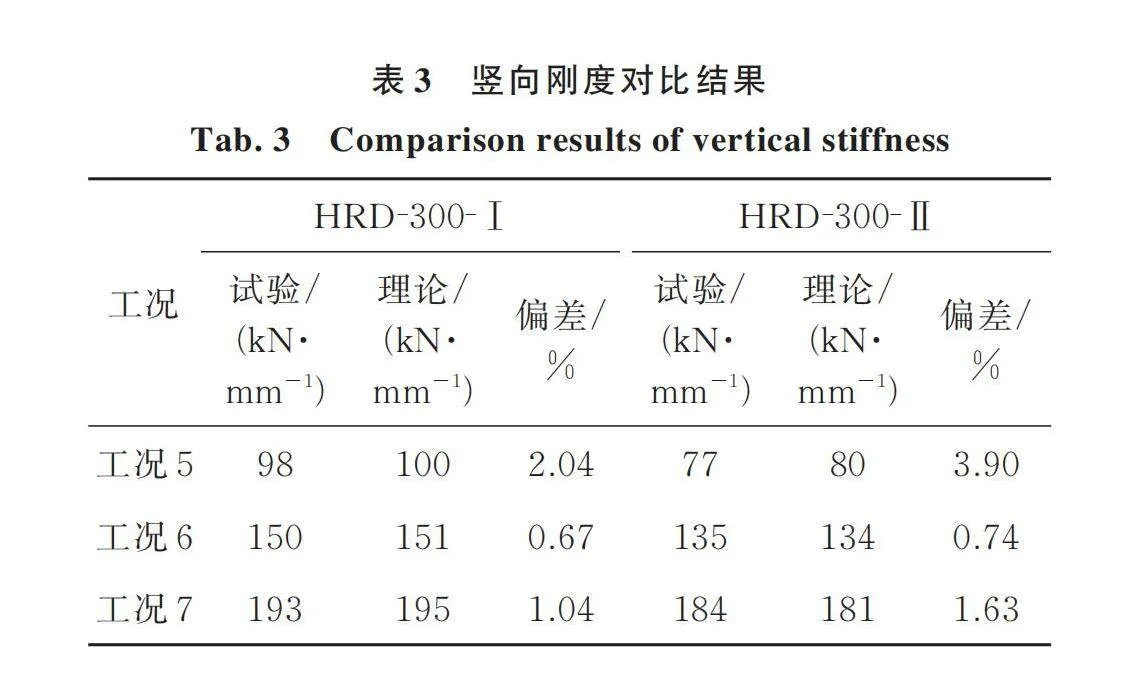
表3给出了高阻尼厚层橡胶支座竖向刚度理论和试验的对比结果。不同于叠层橡胶支座，厚层橡胶支座由于其具有较大的竖向变形能力，且竖向变形速率逐渐减小，通过修正公式计算的理论结果与试验结果的误差均在5%以内。

如图13所示，高阻尼厚层橡胶支座竖向刚度随着竖向压力的增大，呈现出非线性强化特征。

5 结 论

本文建立了高阻尼厚层橡胶支座水平剪切变形、恢复力的计算理论，且通过考虑厚层橡胶支座竖向变形的非线性特征，采用指数修正方法得到了基于面压的竖向刚度计算公式。通过试验结果与理论结果的对比分析，可得到主要结论如下：

（1）本文提出了考虑橡胶大变形的水平剪切变形、恢复力的计算方法，并推导出了厚层橡胶支座考虑竖向非线性变形的竖向刚度的指数修正公式。

（2）在竖向压应力作用下，不同形状系数的高阻尼厚层橡胶支座呈现出相同的变化规律，其水平滞回曲线平滑且饱满，随着竖向压应力的增大，滞回曲线由典型的梭形逐渐变为S形，耗能能力显著增加。

（3）高阻尼厚层橡胶支座的等效水平刚度、等效阻尼比在8，10，12 MPa竖向压应力作用下，由于内部钢板转动，对橡胶层的约束作用增强，呈现出先减小后增大的变化趋势。

（4）高阻尼厚层橡胶支座的竖向刚度通过建立的竖向刚度计算理论得到的结果与试验结果吻合，误差均在5%以内。

参考文献：

［1］Kelly J M. Earthquake-Resistant Design with Rubber［M］. Berlin， Germany： Springer-Verlag， 1993.

［2］薛彦涛. 建筑结构隔震技术现状与应用［J］. 建筑结构， 2011， 41（11）： 82-87.

Xue Yantao. Status and application of base-isolation technique of buildings［J］. Building Structure， 2011， 41（11）： 82-87.

［3］葛庆子， 杨毅坚， 戴靠山， 等. 高阻尼橡胶支座力学性能研究综述［J］. 建筑结构， 2022， 52（12）： 70-79.

Ge Qingzi， Yang Yijian， Dai Kaoshan， et al. Review of mechanical properties of high damping rubber bearing［J］. Building Structure， 2022， 52（12）： 70-79.

［4］郑杰， 顾冉星， 贾俊峰， 等. 高阻尼橡胶隔震支座力学性能研究及其桥梁工程应用进展［J］. 防灾科技学院学报， 2022， 24（2）： 1-15.

Zheng Jie， Gu Ranxing， Jia Junfeng， et al. Mechanical properties of high damping rubber isolation bearings and its application in bridge engineering［J］. Journal of Institute of Disaster Prevention， 2022， 24（2）： 1-15.

［5］陈彦江， 郭凯敏， 李勇， 等. 桥梁高阻尼隔震橡胶支座性能试验研究［J］. 振动与冲击， 2015， 34（9）： 136-140.

Chen Yanjiang， Guo Kaimin， Li Yong， et al. Behavior of high damping seismic isolation rubber bearings for bridges［J］. Journal of Vibration and Shock， 2015， 34（9）： 136-140.

［6］魏威， 袁涌， 谭平， 等. 考虑压力影响的高阻尼橡胶隔震支座速度相关性本构模型及其地震响应研究［J］. 土木工程学报， 2020， 53（2）： 23-32.

Wei Wei， Yuan Yong， Tan Ping， et al. A rate-dependent constitutive model of high damping rubber bearings considering the influence of compressive load and its effect on the seismic response［J］. Chinese Civil Engineering Journal， 2020， 53（2）： 23-32.

［7］雷拓， 张永旺， 杨永睿， 等. 高阻尼隔震支座复合橡胶材料制备及性能研究［J］. 土木工程学报， 2018， 51（增刊1）： 1-7.

Lei Tuo， Zhang Yongwang， Yang Yongrui， et al. Composite material preparation and properties research of high damping isolation bearing［J］. Chinese Civil Engineering Journal， 2018， 51（Sup1）： 1-7.

［8］沈朝勇， 周福霖， 崔杰， 等. 高阻尼隔震橡胶支座的相关性试验研究及其参数取值分析［J］. 地震工程与工程振动， 2012， 32（6）： 95-103.

Shen Chaoyong， Zhou Fulin， Cui Jie， et al. Dependency test research of mechanical performance of HDR and its parameter value analysis［J］. Earthquake Engineering and Engineering Dynamics， 2012， 32（6）： 95-103.

［9］Newland D E， Hunt H E M. Isolation of buildings from ground vibration： a review of recent progress［J］. Proceedings of the Institution of Mechanical Engineers. Part C： Journal of Mechanical Engineering Science， 1991， 205（1）： 39-52.

［10］李吉超， 尚庆学， 罗清宇， 等. 厚层橡胶支座的力学性能试验研究［J］. 振动与冲击， 2019， 38（9）： 157-165.

Li Jichao， Shang Qingxue， Luo Qingyu， et al. Tests for mechanical performance of thick rubber bearings［J］. Journal of Vibration and Shock， 2019， 38（9）： 157-165.

［11］何文福， 刘文光， 杨彦飞， 等. 厚层橡胶隔震支座基本力学性能试验［J］. 解放军理工大学学报 （自然科学版）， 2011， 12（3）： 258-263.

He Wenfu， Liu Wenguang， Yang Yanfei， et al. Basic mechanical properties of thick rubber isolators［J］. Journal of PLA University of Science and Technology （Natural Science Edition）， 2011，12（3）： 258-263.

［12］王涛， 王飞， 丁路通. 核电厂三维隔震技术的理论和试验研究［J］. 土木工程学报， 2012， 45（增刊1）： 238-242.

Wang Tao， Wang Fei， Ding Lutong. Theoretical and experimental study on three-dimensional base-isolated nuclear power plant［J］. Chinese Civil Engineering Journal， 2012， 45（Sup1）： 238-242.

［13］王涛， 李吉超， 王飞. 针对核电厂三维隔震的厚层橡胶支座力学性能研究［J］. 核动力工程， 2015， 36（5）： 37-40.

Wang Tao， Li Jichao， Wang Fei. Experimental study on thick rubber bearings of three-dimensional isolation of nuclear power plants［J］. Nuclear Power Engineering， 2015， 36（5）： 37-40.

［14］何文福， 罗昊杰， 许浩， 等. 轨交沿线建筑三维隔震/振支座力学性能试验研究及应用分析［J］. 振动工程学报， 2020， 33（6）： 1112-1121.

He Wenfu， Luo Haojie， Xu Hao， et al. Experimental study and application analysis of mechanical performance of 3D isolation/vibration bearings along railway lines［J］. Journal of Vibration Engineering， 2020， 33（6）： 1112-1121.

［15］周颖， 陈鹏， 陆道渊， 等. 地铁上盖多塔楼隔震与减振设计研究［J］. 土木工程学报， 2016， 49（增刊1）： 84-89.

Zhou Ying， Chen Peng， Lu Daoyuan， et al. Design and seismic response analysis for multiple buildings with large podium using inter-story isolation technology［J］. Chinese Civil Engineering Journal， 2016， 49（Sup1）： 84-89.

［16］Li C X， Chang K， Cao L Y， et al. Performance of a nonlinear hybrid base isolation system under the ground motions［J］. Soil Dynamics and Earthquake Engineering， 2021， 143： 106589.

［17］Cao L Y， Li C X. A high performance hybrid passive base-isolated system［J］. Structural Control and Health Monitoring， 2022， 29（3）： e2887.

Experimental research on mechanical properties of high damping thick rubber bearings

KUANG Cheng-gang1， TAN Ping1， CHEN Mu-feng2， LI Zhi-xiang3， LUO Hao-jie4

（1.School of Civil Engineering， Guangzhou University， Guangzhou 510006， China； 2.School of Civil Engineering， Guangzhou Institude of Science and Technology， Guangzhou 510540， China；3.Zhen’an Technology Co.， Ltd.， Kunming 650217， China；4.Shanghai Xinlan Real Estate Development Co.， Ltd.， Shanghai 200071， China）

Abstract： In order to explore the mechanical properties of high-damping thick-layer rubber bearings， this paper studies the force characteristics of horizontal shear and vertical compression of high-damping thick-layer rubber bearings under vertical compressive stress. A model considering horizontal shear deformation is established， and a vertical stiffness correction theory is proposed based on compressive stress changes. To verify the accuracy of the theoretical model， three types of high-damping thick-layer rubber bearings with different first shape coefficients were designed for horizontal quasi-static shear and vertical compression tests. The results show that the equivalent horizontal stiffness and equivalent damping ratio of the high-damping thick-layer rubber bearing are changed by the restraint effect of the internal steel plate. As the vertical compressive stress increases， the horizontal equivalent stiffness gradually decreases. In the vertical compression test， as the vertical pressure increases， the vertical compressive stiffness presents nonlinear strengthening characteristics. Through the comparative analysis of theoretical and experimental results， it can be seen that the mechanical model of horizontal shear deformation constructed in this paper can better describe the mechanical properties of high-damping thick-layer rubber bearing in horizontal shear， and the vertical stiffness correction theory can accurately calculate its vertical stiffness. The deviations from the test results under different working conditions are all within 5%.

Key words： high damping thick rubber bearing；compressive stress correlation；shear strain correlation；experimental research；mechanical properties

作者简介： 匡成钢（1987—），男，博士研究生。E-mail： 349877696@qq.com。

通讯作者： 谭 平（1973—），男，博士，教授。E-mail： tanping2000@hotmail.com。