含中介轴承波纹度的双转子系统振动特性分析

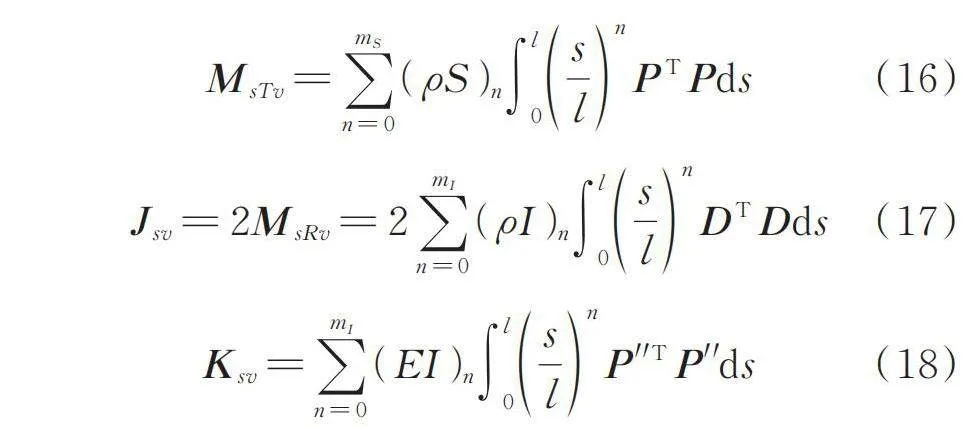
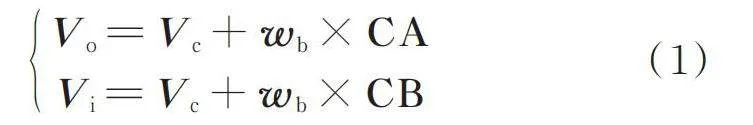
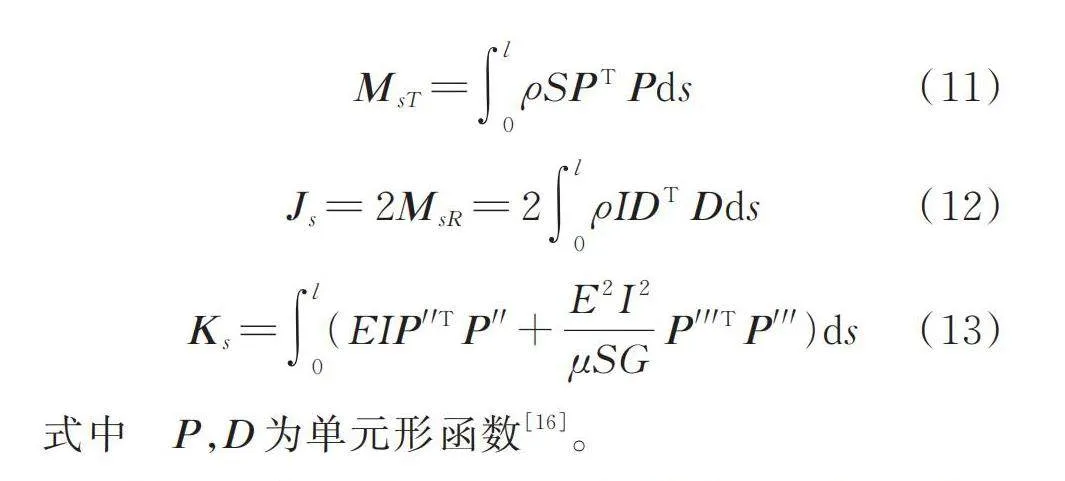
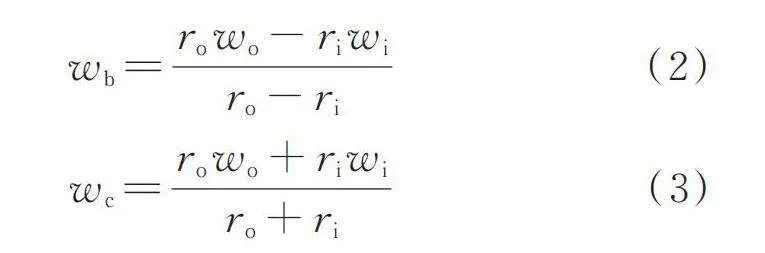
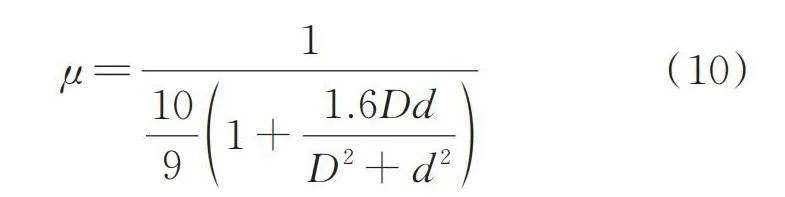
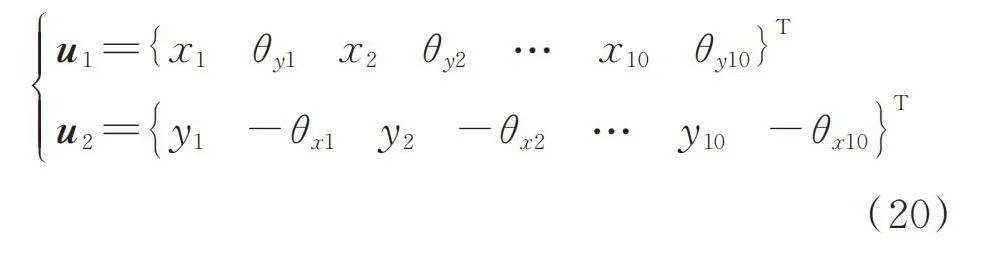
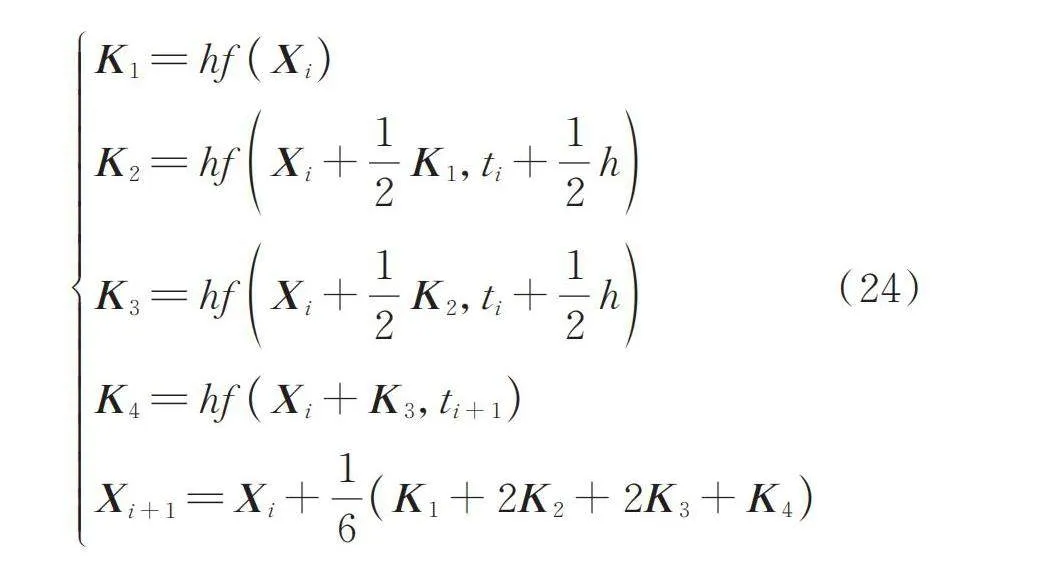
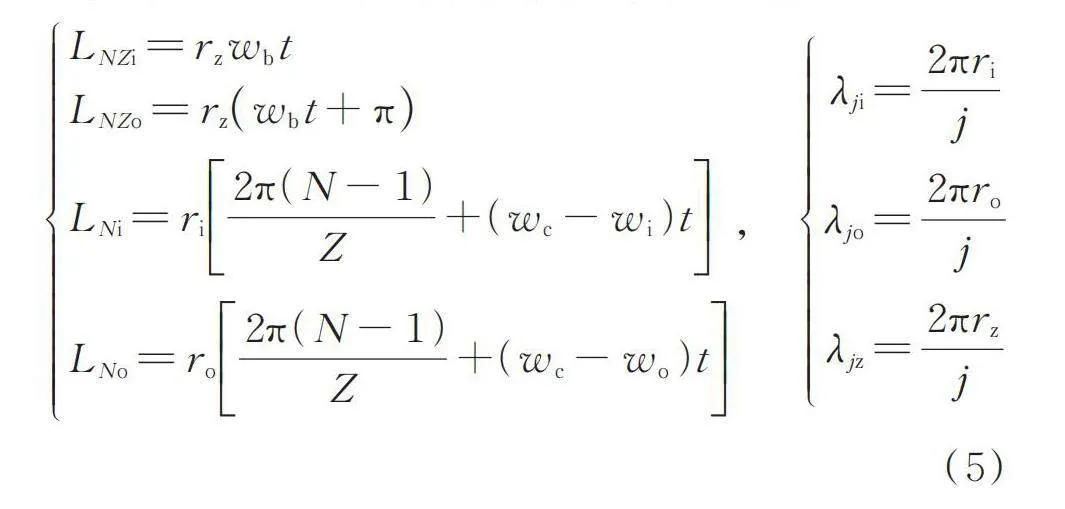
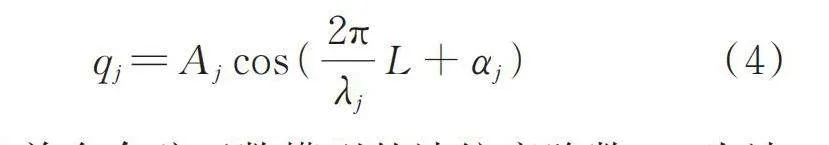
摘要： 针对双转子系统中存在中介轴承波纹度的问题，以含变截面外转子的双转子⁃轴承系统为研究对象，考虑中介轴承滚动体和内、外圈滚道波纹度，基于有限元法建立了双转子⁃轴承系统的动力学模型，采用四阶Runge⁃Kutta数值解法求解方程，分析了波纹度激励对系统频谱特征和幅频响应曲线的影响。结果表明：内、外圈滚道存在波纹度时系统会出现内、外转子转频和保持架转频的组合频率，滚动体存在波纹度时系统会出现偶数倍的滚动体自转频率；考虑转子不平衡激励，外圈滚道波纹度会增大外转子主激励的共振区域的振动，且随着波纹度幅值的增加，系统的振动会在整个转速范围内增大，而内圈滚道波纹度与不平衡激励两者的振动响应会在内转子主激励的第二次共振区域出现近似同频反相的现象，系统的振动会随着波纹度幅值的增加而降低，在其他区域的振动会增大，相对于高转速区域，滚动体波纹度对低转速区域的振动特性会有较大影响。

关键词： 转子动力学； 双转子系统； 中介轴承； 波纹度； 幅频响应

中图分类号： O347.6； TH113； TH133 文献标志码： A 文章编号： 1004-4523（2024）09-1523-12

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.009

引 言

现代燃气轮机和航空发动机一般采用有中介轴承支承的双转子结构形式，中介轴承（一般为圆柱滚子轴承或深沟球轴承）［1］的存在增大了高、低压转子的动力学耦合效应。由于机械加工误差不可避免，中介轴承内圈、外圈滚道和滚动体表面会产生波纹度，而波纹度又是转子⁃轴承系统振动的重要激励源之一，会使双转子⁃轴承系统表现出更为复杂的动力学特性。因此，有必要对含中介轴承波纹度的双转子系统振动特性展开研究。

对于单转子⁃轴承系统，顾晓辉等［2］考虑了球轴承内、外圈滚道波纹度、径向游隙和非线性赫兹力，研究了波纹度最大幅值和转速对单转子⁃轴承系统非线性振动的影响，并用关联维数判别了系统波纹度故障的程度。Wang等［3］考虑了滚子轴承的波纹度和径向游隙，建立了转子⁃滚动轴承的四自由度动力学方程，通过分岔图、庞加莱截面图和频谱图等分析了系统响应的稳定性。Zhang等［4］考虑了球轴承波纹度、不平衡力和滚动体的变柔度振动，提出了一个全面的转子⁃轴承系统动力学模型，深入讨论了轴承波纹度的幅值和初相角、转子偏心、轴承预紧力和旋转系统阻尼对系统失稳区域的影响。康锋等［5］考虑了薄壁滚动轴承内、外圈滚道波纹度、径向间隙等非线性因素，建立了薄壁轴承⁃转子系统非线性动力学模型，分析了系统的强迫振动特性。刘永葆等［6］以某船用燃气轮机低压转子系统为研究对象，建立了轴承波纹度故障下的双跨三支承滚动轴承转子系统的动力学模型，研究了波纹度最大幅值和波纹度个数对系统的非线性动力学特性影响规律。余登亮等［7］建立了球轴承内、外圈表面的波纹度模型，研究了含波纹度滚动轴承支撑下裂纹转子系统发生碰摩故障时的动力学特性。Nan等［8］考虑轴承波纹度故障、不平衡激励、非线性Hertz接触力、变柔度振动以及轴材料的物理非线性刚度等，建立了一种新的滚动轴承支承的非线性转子模型，研究了波纹度、间隙和质量偏心对动力学行为的影响。Harsha等［9］考虑了球轴承内、外圈滚道波纹度和滚珠与滚道之间的非线性接触力，对球轴承支承的刚性转子的稳定性进行了研究。

在双转子⁃轴承系统方面，考虑轴承波纹度的双转子系统动力学特性的研究较少，Lu等［10］、Ma等［11］基于有限元法建立了双转子系统的动力学方程，考虑中介轴承的径向游隙等非线性因素，分析了径向游隙对系统非线性振动的影响，没有考虑中介轴承波纹度的影响。侯磊等［12］考虑了中介轴承内、外圈滚道波纹度，用单个正弦函数表达波纹度波形，应用拉格朗日方程建立了双转子⁃轴承系统的动力学模型，主要从分岔图和庞加莱截面图角度分析了转速、波纹度幅值等参数对系统的非线性动力学行为。李静等［13］建立了考虑中介轴承内圈滚道波纹度的双转子系统模型，将波纹度模型简化为单个正弦函数形式，从时变刚度曲线、幅频响应曲线、分岔图以及庞加莱截面图方面，对比分析了理想中介轴承和考虑内圈滚道波纹度时双转子⁃轴承系统的动力学特性，发现波纹度使双转子系统运动更加复杂。

上述研究工作主要分析了单转子⁃轴承系统存在波纹度时的振动特性，少量工作针对双转子⁃轴承系统探索了内、外圈滚道波纹度对系统分岔和混沌特性的影响规律，对双转子系统振动特性的研究都鲜有考虑到滚动体波纹度的影响。本文将以双转子⁃轴承系统为研究对象，考虑中介轴承滚动体和内、外圈滚道的波纹度，将波纹度模型简化为多个周期性的余弦函数的叠加，利用有限元法建立了含变截面外转子的双转子⁃轴承系统的动力学模型，对波纹度激励下双转子⁃轴承系统的振动频谱特征和幅频响应特性开展研究。

1 双转子⁃轴承系统的动力学建模

1.1 中介轴承波纹度模型的建立

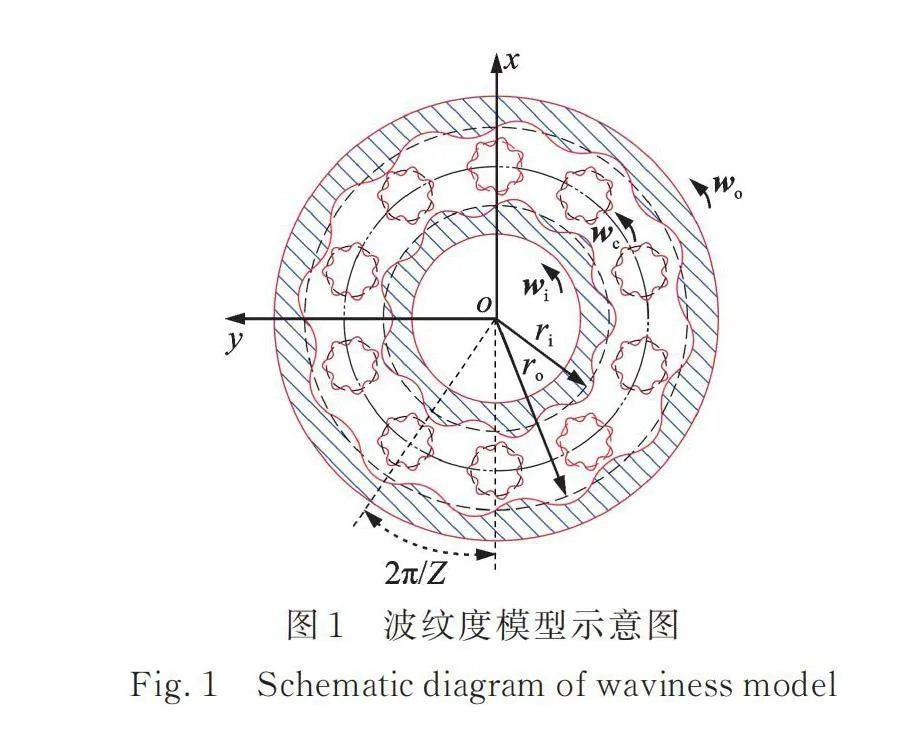
理想滚动轴承的内、外圈滚道和滚动体表面为光滑曲面，但由于机械加工误差，实际会产生带波纹度的轴承表面。此时滚动体与内、外圈滚道接触面的曲率半径是时变的，导致接触力也是时变的。本文研究的中介轴承为滚珠轴承，轴承外圈滚道刚性固定在外转子上，随外转子同速转动，内圈滚道刚性固定在内转子上，随内转子同速转动。如图1所示为轴承内圈、外圈滚道和滚动体波纹度模型的示意图。将轴承波纹度简化为多个余弦函数的叠加［3］，叠加的数目和波纹度的阶数有关。

建立波纹度模型之前，首先通过理论力学推导滚动体的自转速度，假设滚动体与滚道之间为纯滚动，无滑动，在接触点上两表面的线速度相等，接触角为0°。如图2所示为滚动体和内、外圈滚道之间的运动关系图。

设轴承内、外圈滚道同向旋转，外圈滚道转速大于内圈滚道转速；，两点分别为滚动体与外圈滚道和内圈滚道的接触点，为滚动体中心；，，分别为，，三点的线速度；，，分别为内圈、外圈滚道和保持架转速，，，分别表示它们的大小；为滚动体自转速度；CA代表由C点指向A点的矢量；CB代表由C点指向B点的矢量；，，分别为内圈、外圈滚道半径和滚动体半径，则由刚体平面运动可得：

（1）

则内、外圈滚道同向旋转时滚动体自转速度大小和保持架的旋转速度大小分别为：

（2）

（3）

对于波纹度模型，设单个余弦函数的表达式为：

（4）

式中 j为单个余弦函数模型的波纹度阶数；为波纹度的幅值；为波纹度波纹的波长；为某时刻距离参考点的弧长；为波纹度的初始接触角；内圈、外圈滚道和滚动体的波纹度参数表达式如下：

（5）

式中 为滚动体编号；为滚动体个数；，分别为某时刻第个滚动体和内圈、外圈滚道接触点相对滚动体参考点运动的距离；，分别为某时刻第个滚动体和内圈、外圈滚道接触点相对内圈、外圈滚道参考点运动的距离；，，分别为内圈、外圈滚道和滚动体波纹度波纹的波长。

滚动轴承工作时，由于滚动体的旋转路径不可预测，假设滚动体表面波纹度仅具有平面运动，和分别为第个滚动体与内圈、外圈滚道接触时的滚动体波纹度，和分别为第个滚动体与内圈、外圈滚道接触时内圈和外圈滚道的波纹度，则将式（5）代入式（4），并叠加多个余弦函数可得内圈、外圈滚道以及滚动体的波纹度表达式为［3］：

（6）

式中 为多个余弦函数叠加模型的波纹度阶数，在后文中简称为波纹度阶数；，，分别为内圈、外圈滚道和滚动体的波纹度幅值；，，分别为内圈、外圈滚道和滚动体波纹度的初始接触角度。

1.2 考虑波纹度的中介轴承弹性恢复力建模

考虑中介轴承为深沟球轴承，根据滚动轴承Hertz接触理论，第个球与内、外圈滚道接触时的接触力为［14］：

（7）

式中 为第个滚动体与滚道之间的弹性变形；为滚动体与内、外圈滚道之间的等效Hertz接触刚度；为Heaviside阶跃函数。

设轴承径向游隙为，内圈滚道在方向和方向移动了距离和，外圈滚道在方向和方向移动了距离和，则考虑轴承波纹度的弹性变形为：

（8）

式中 为中介轴承第个滚动体的位置角，即，则可得轴承的总弹性恢复力在方向和方向的分力为：

（9）

1.3 双转子⁃轴承系统动力学建模

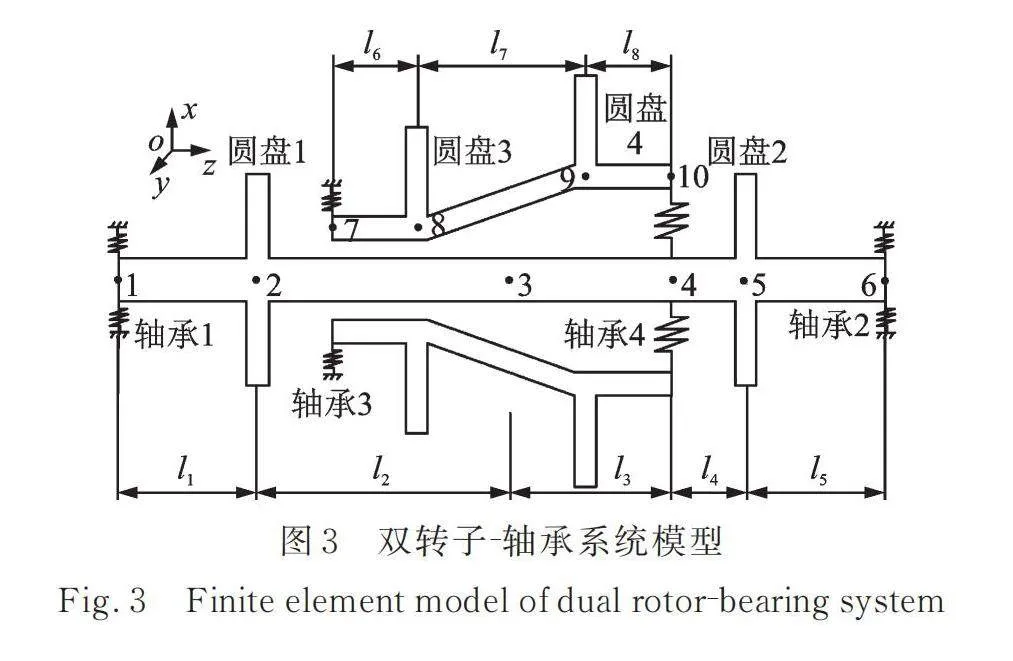
参考文献［15］，建立了本文的双转子⁃轴承系统模型，如图3所示。轴承1和2为内转子的支承轴承，轴承3为外转子的支承轴承，轴承4为中介轴承。根据圆盘和轴承的位置，将内转子划分为6个节点，外转子划分为4个节点，其中8，9节点之间的轴段单元为变截面形式。

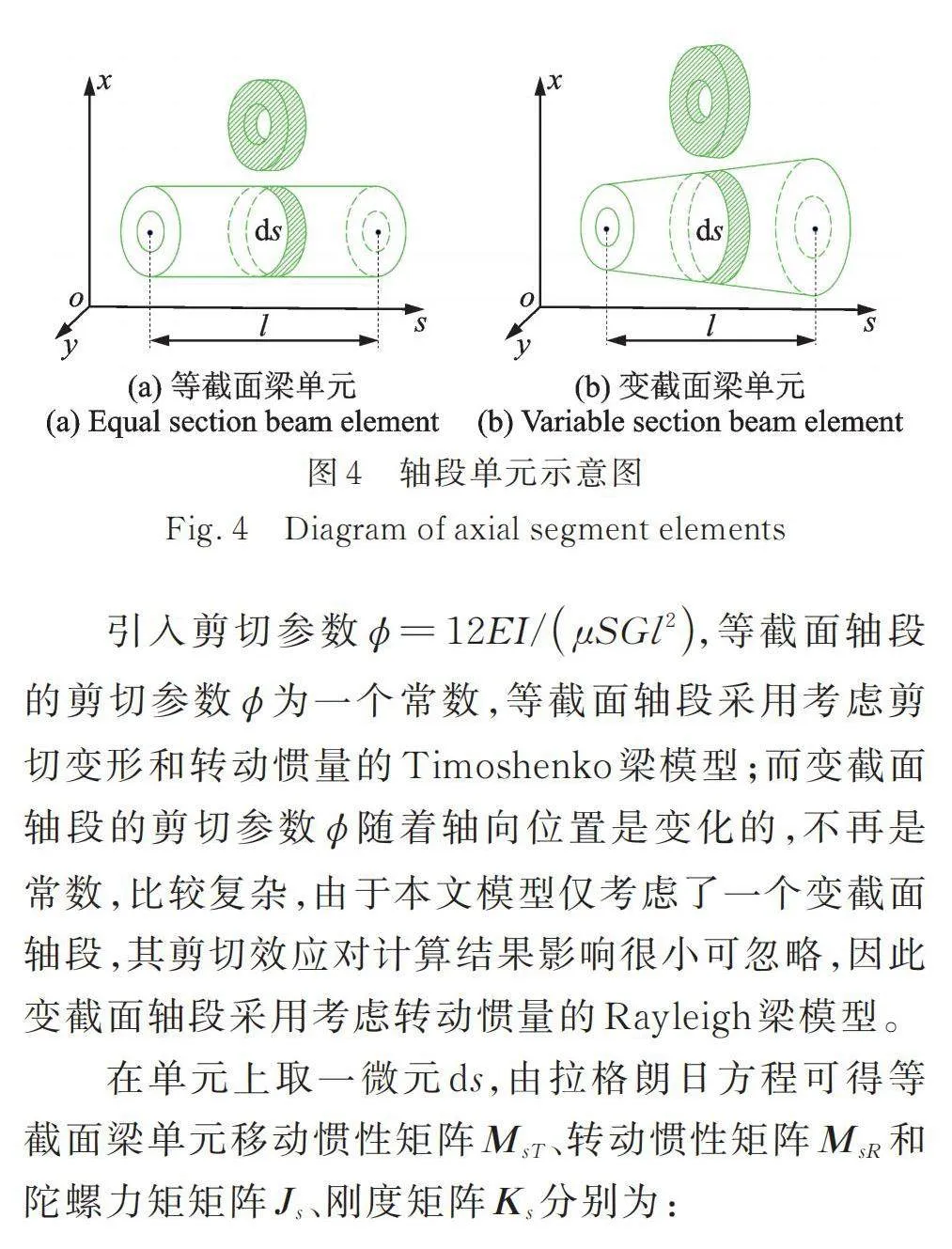
等截面和变截面轴段单元示意图如图4所示，变截面轴段采用锥形梁单元。设轴段单元的长度为，密度为，拉压弹性模量为，泊松比为，剪切弹性模量为，横截面面积为，截面对中性轴的惯性矩为，为截面剪切系数，即：

（10）

式中 ，分别为圆截面的内径和外径。

引入剪切参数，等截面轴段的剪切参数为一个常数，等截面轴段采用考虑剪切变形和转动惯量的Timoshenko梁模型；而变截面轴段的剪切参数随着轴向位置是变化的，不再是常数，比较复杂，由于本文模型仅考虑了一个变截面轴段，其剪切效应对计算结果影响很小可忽略，因此变截面轴段采用考虑转动惯量的Rayleigh梁模型。

在单元上取一微元，由拉格朗日方程可得等截面梁单元移动惯性矩阵、转动惯性矩阵和陀螺力矩矩阵、刚度矩阵分别为：

（11）

（12）

（13）

式中 ，为单元形函数［16］。

推导变截面梁单元矩阵时，横截面面积、截面对中性轴的惯性矩不再是一个常数，而是根据截面形状随着轴向位置变化的。可将单元内参数随着轴向距离的变化关系式展开为多项式的形式，再进行积分累加可得到变截面梁单元矩阵［17］。建立变截面梁问题的关键在于将轴段截面的变化参数展开为多项式的形式，和根据截面变化形状可直接展开为多项式或者通过泰勒展开得到其多项式如下：

（14）

（15）

式中 和分别表示S和I展开多项式的最高次数；n表示多项式连加求和中的一个过程变量。考虑变截面梁为线性变化，由拉格朗日方程可得线性锥形梁单元移动惯性矩阵、转动惯性矩阵、陀螺力矩矩阵、刚度矩阵分别为：

（16）

（17）

（18）

利用有限元法单元组合规则，可得双转子⁃轴承系统的运动微分方程为：

（19）

式中 ，，分别为内、外转子的总质量矩阵、总回转矩阵和总刚度矩阵；为瑞利阻尼矩阵；，为转子的不平衡力；为圆盘的重力；，为轴承非线性弹性恢复力；，为内、外转子的广义位移向量，即：

（20）

2 有限元模型验证及求解方法

2.1 有限元模型验证

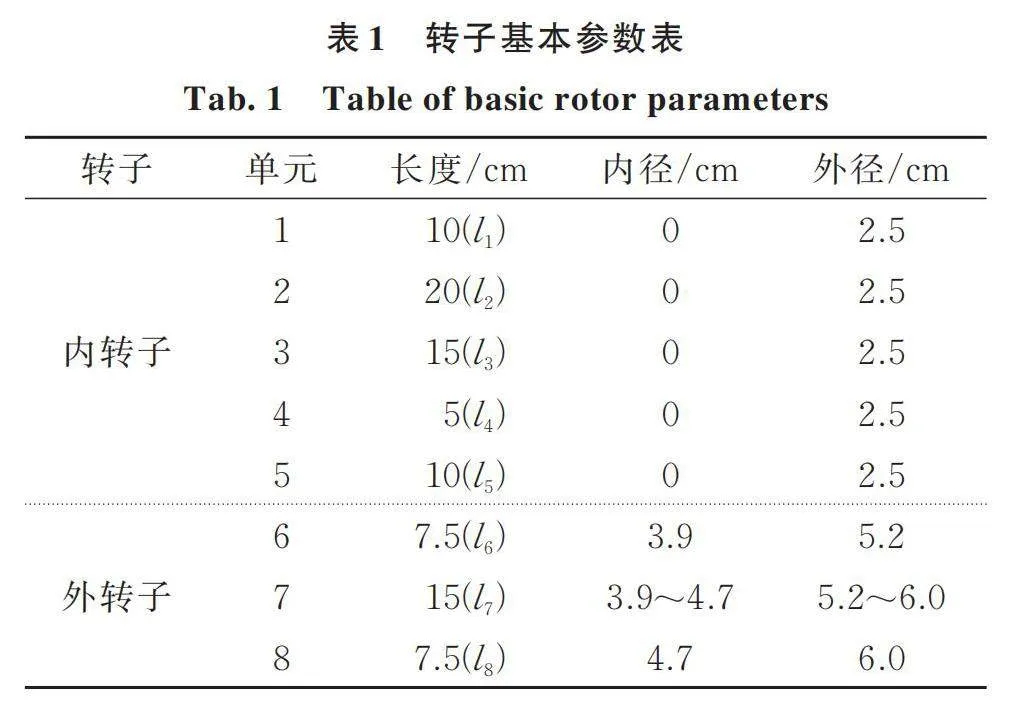
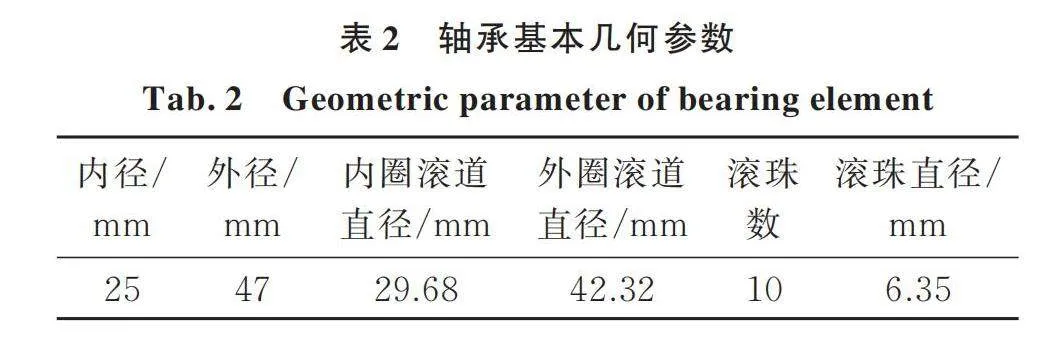
内、外转子参数如表1所示。圆盘1和2的参数相同，质量、极转动惯量和直径转动惯量分别为9.683 kg，0.049 kg·m²，0.0245 kg·m²；圆盘3和4的参数相同，质量、极转动惯量和直径转动惯量分别为9.139 kg，0.04878 kg·m²，0.02439 kg·m²；内、外转子材料密度为7800 kg/m3；泊松比为0.3；拉压弹性模量为2.11011 Pa。将支承轴承线性化处理，x和y方向的刚度相同，支承轴承1，2，3的刚度分别为，， N/m。中介轴承为深沟球轴承6005，基本几何参数如表2所示，其等效接触刚度kb由文献［1］中的方法计算为8.4922×109 N/m1.5。

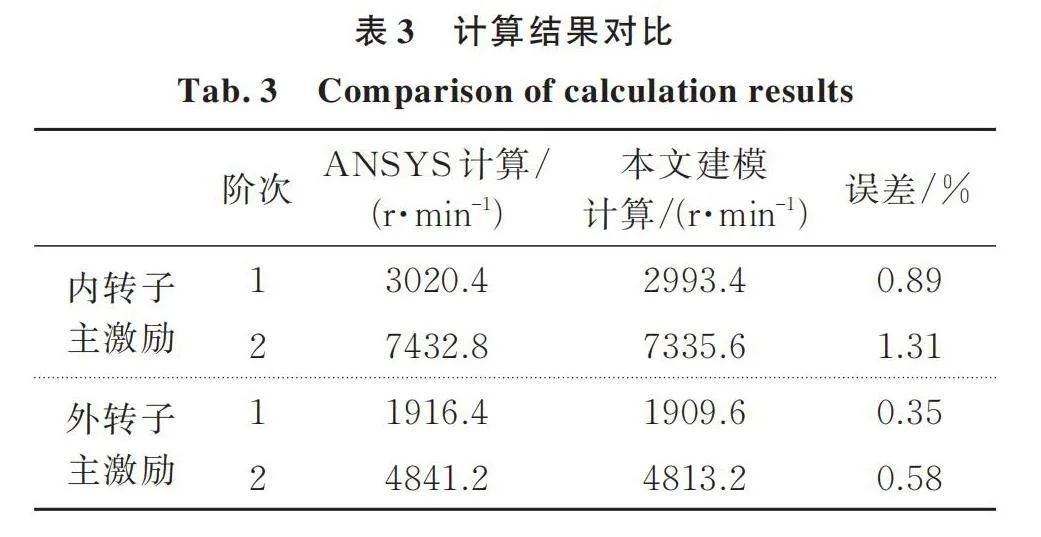
为验证本文所编写的双转子⁃轴承系统有限元计算程序是有效可行的，将使用ANSYS软件计算双转子⁃轴承系统的临界转速和本文编写有限元程序计算的结果进行对比，先假设中介轴承两个方向的刚度均为8.75106 N/m［15］，内、外转子转速比为1.5。如图5所示为ANSYS建立的双转子⁃轴承系统有限元模型，转子采用BEAM188单元模拟，轴承采用COMBI214单元模拟，圆盘采用MASS21单元模拟。如图6所示为以内转子转速为横轴的Campbell图，图中斜率为ki和ko的直线分别代表内、外专子的同步激励线，A点和B点分别为内转子主激励的前两阶临界转速，C点和D点分别为外转子主激励的前两阶临界转速，临界转速计算结果如表3所示。可知本文求解的临界转速和ANSYS求解的结果最大误差为1.31%，证明了本文所编写的有限元计算程序的正确性。

2.2 系统动力学响应求解方法

由于系统方程中含中介轴承非线性恢复力，四阶Runge⁃Kutta数值积分法可以直接应用于非线性系统，本文采用四阶Runge⁃Kutta法求解方程，设系统振动微分方程为：

（21）

式中 分别为系统质量矩阵、阻尼矩阵、刚度矩阵、外力向量和所求位移向量。

首先需要将方程降阶，即定义一个新的向量，并对求导，即：

（22）

（23）

设步长为，在时刻处计算的递推公式为：

（24）

3 波纹度对系统响应频谱特征分析

为研究波纹度激励对双转子⁃轴承系统响应频谱特征的影响，以内圈滚道波纹度、外圈滚道波纹度和滚动体波纹度为控制变量分别分析，设内圈、外圈滚道波纹度幅值均为5 μm，滚动体波纹度幅值为2 μm，内圈、外圈滚道和滚动体波纹度初始接触角度分别为，和，轴承径向游隙为4 μm，内、外转子转速比为1.5，取图3中内转子节点2处的垂直方向振动响应为研究对象。

3.1 外圈滚道波纹度的影响

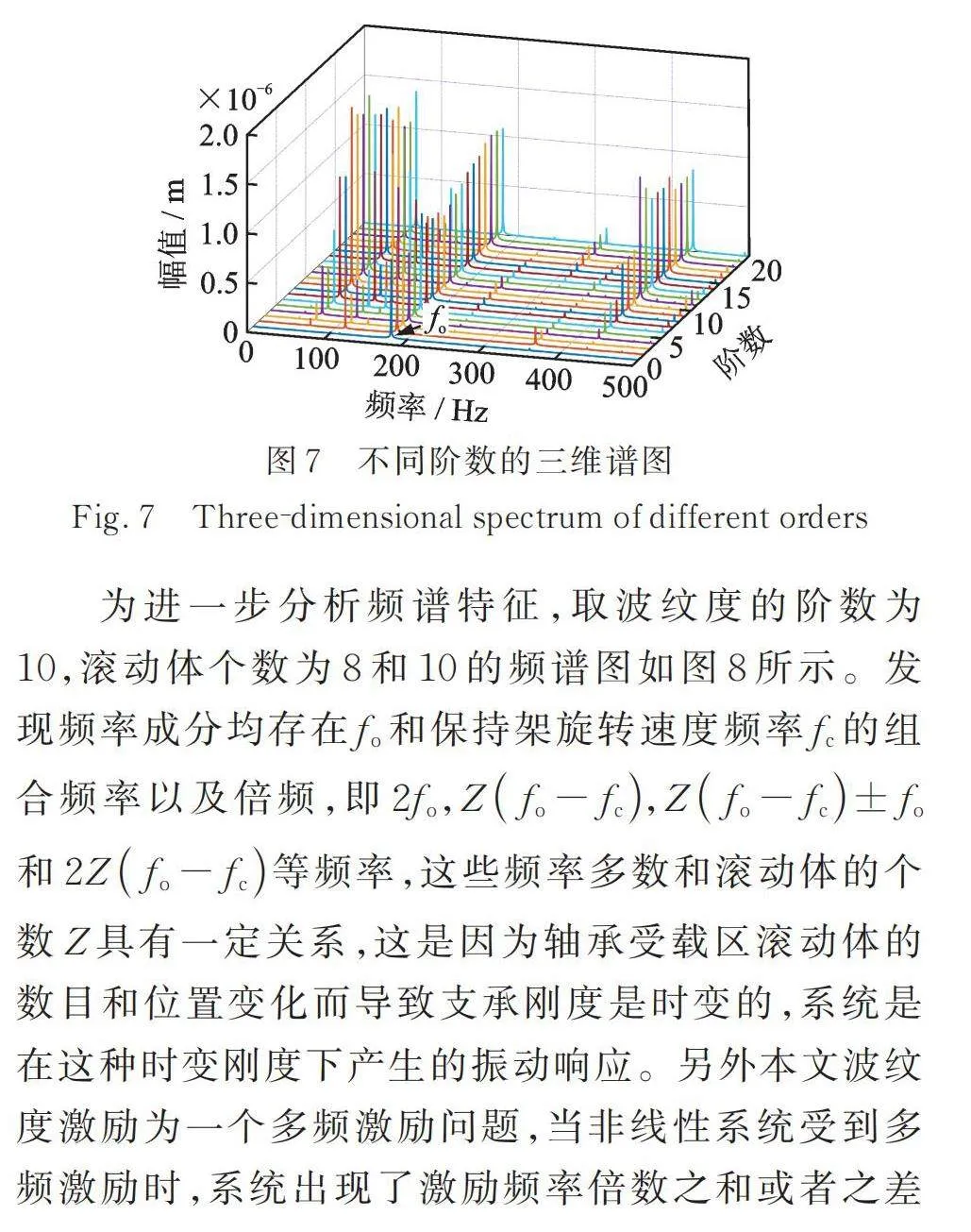
仅考虑外圈滚道波纹度时，取内转子转速为7200 r/min，波纹度阶数为1～20阶的三维谱图如图7所示。外圈滚道波纹度阶数为1时，频谱图中会出现外圈旋转频率，其他频率成分不明显。在计算的不同阶数下，随着阶数的增加，频谱图中均出现了相同的外圈滚道波纹度引起的特征频率。

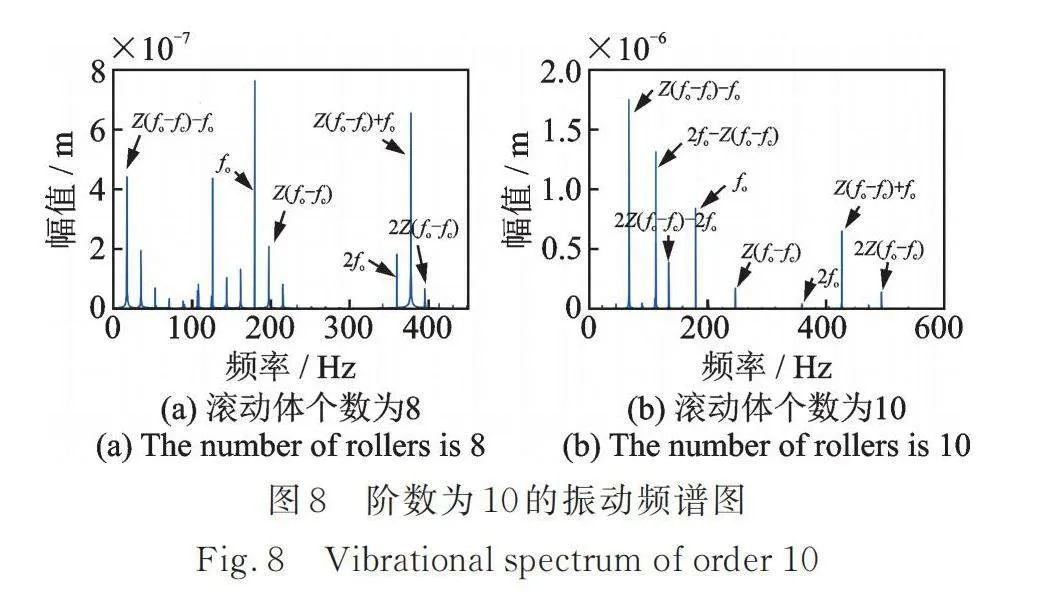
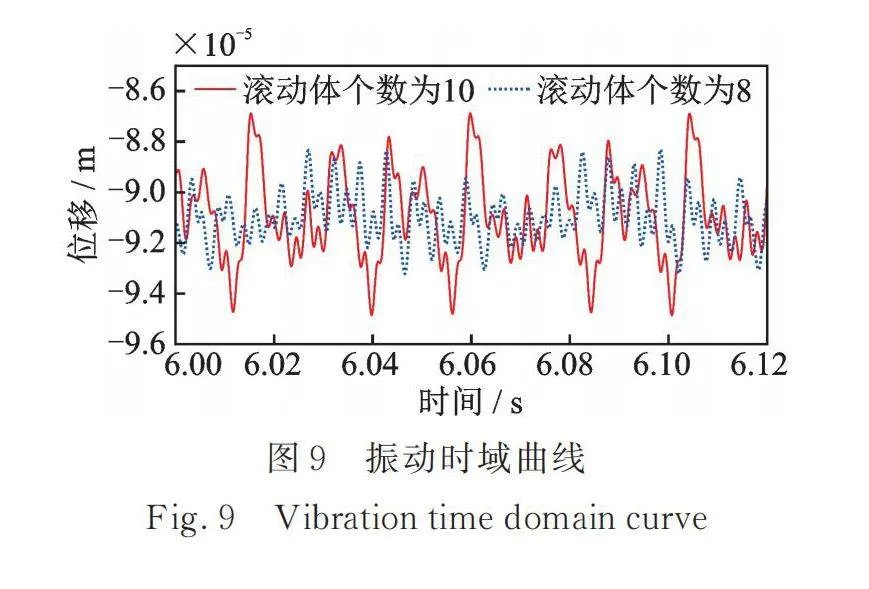
为进一步分析频谱特征，取波纹度的阶数为10，滚动体个数为8和10的频谱图如图8所示。发现频率成分均存在和保持架旋转速度频率的组合频率以及倍频，即，，和等频率，这些频率多数和滚动体的个数Z具有一定关系，这是因为轴承受载区滚动体的数目和位置变化而导致支承刚度是时变的，系统是在这种时变刚度下产生的振动响应。另外本文波纹度激励为一个多频激励问题，当非线性系统受到多频激励时，系统出现了激励频率倍数之和或者之差的组合振动现象。绘制两种工况下的时域曲线如图9所示。对比频谱和时域曲线可知滚动体个数为10时的振动响应相对滚动体个数为8时更剧烈，这是因为此时波纹度阶数为10，与滚动体个数相等，这和文献［18］单转子⁃轴承系统得出的结论相同，即波纹度阶数与滚动体个数相等时，系统会出现较大振动。

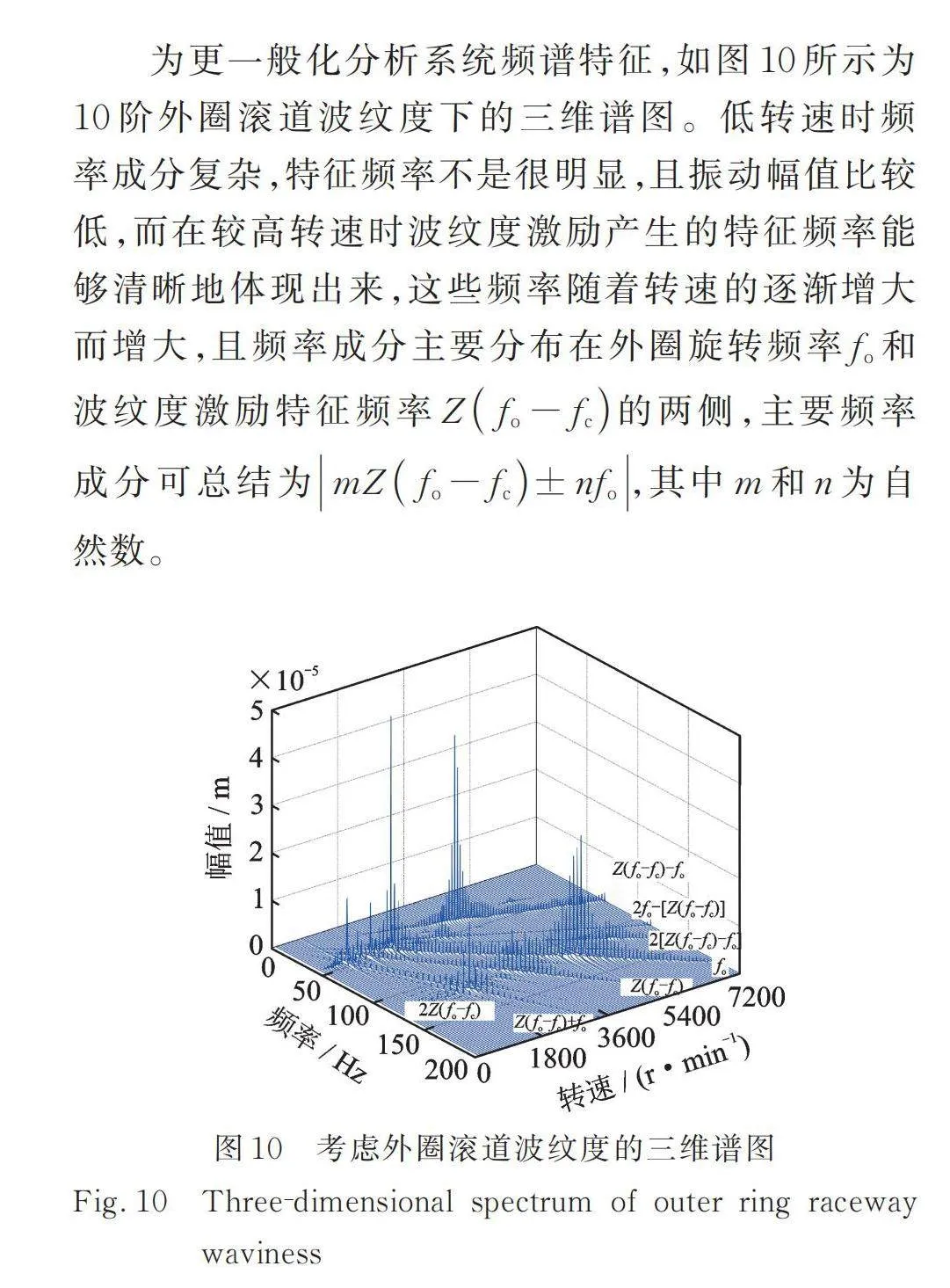
为更一般化分析系统频谱特征，如图10所示为10阶外圈滚道波纹度下的三维谱图。低转速时频率成分复杂，特征频率不是很明显，且振动幅值比较低，而在较高转速时波纹度激励产生的特征频率能够清晰地体现出来，这些频率随着转速的逐渐增大而增大，且频率成分主要分布在外圈旋转频率和波纹度激励特征频率的两侧，主要频率成分可总结为，其中和为自然数。

3.2 内圈滚道波纹度的影响

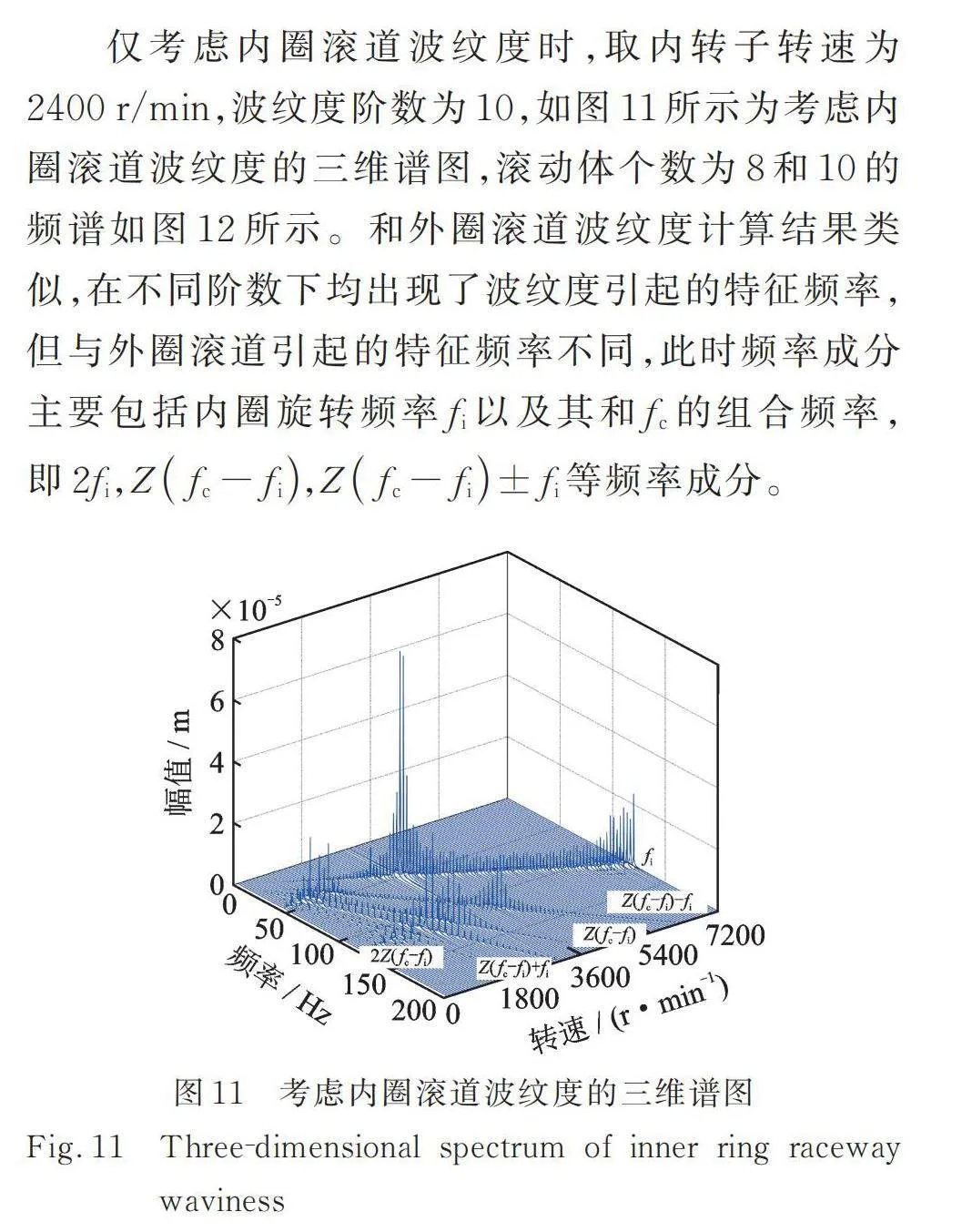
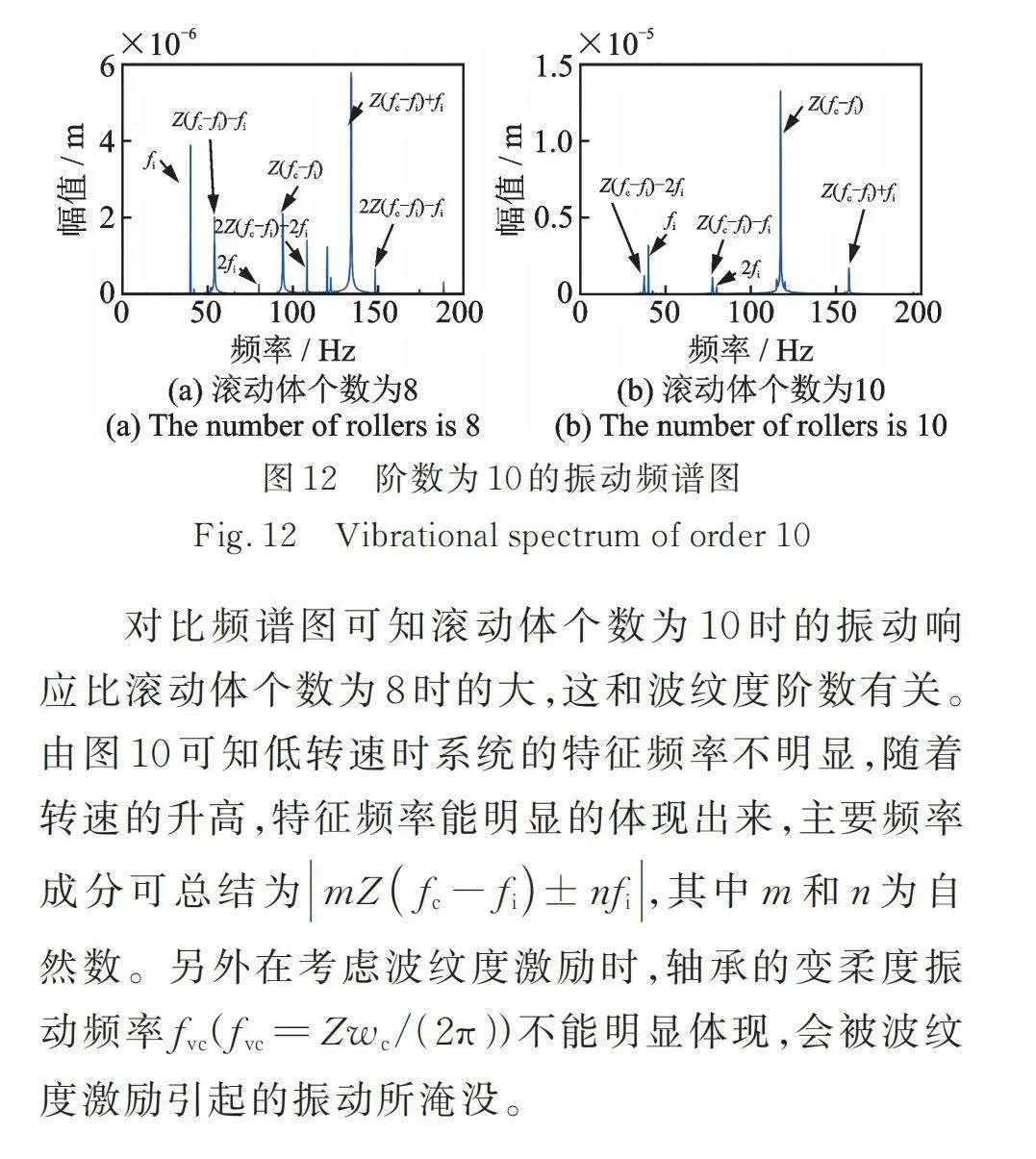
仅考虑内圈滚道波纹度时，取内转子转速为2400 r/min，波纹度阶数为10，如图11所示为考虑内圈滚道波纹度的三维谱图，滚动体个数为8和10的频谱如图12所示。和外圈滚道波纹度计算结果类似，在不同阶数下均出现了波纹度引起的特征频率，但与外圈滚道引起的特征频率不同，此时频率成分主要包括内圈旋转频率以及其和的组合频率，即，，等频率成分。

对比频谱图可知滚动体个数为10时的振动响应比滚动体个数为8时的大，这和波纹度阶数有关。由图10可知低转速时系统的特征频率不明显，随着转速的升高，特征频率能明显的体现出来，主要频率成分可总结为，其中和为自然数。另外在考虑波纹度激励时，轴承的变柔度振动频率（）不能明显体现，会被波纹度激励引起的振动所淹没。

3.3 滚动体波纹度的影响

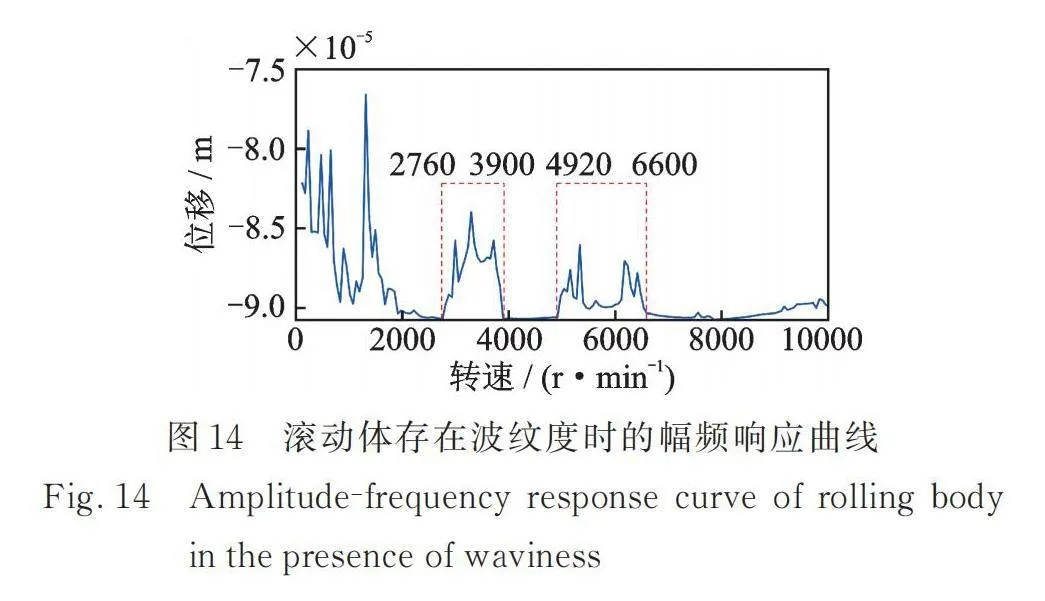
仅考虑滚动体波纹度时，取波纹度阶数为10，认为所有滚动体具有相同的波纹度，如图13所示为考虑滚动体波纹度的三维谱图。系统在整个转速范围内存在偶数倍的球自转频率和一些100 Hz以内的其他低频频率，这些低频频率是系统考虑波纹度而产生的系统共振频率，和此时刻系统的固有特性有关。绘制系统的幅频响应曲线如图14所示。发现系统在0～2000 r/min转速范围内振动比较复杂，且振动相对高转速时较大，从瀑布图中看出振动频率成分主要为偶数倍的球自转频率，系统共振频率的幅值较小；而在2760～3900 r/min和4920～6600 r/min区域内的振动频率主要为系统的共振频率，偶数倍球自转频率的振动幅值较小。

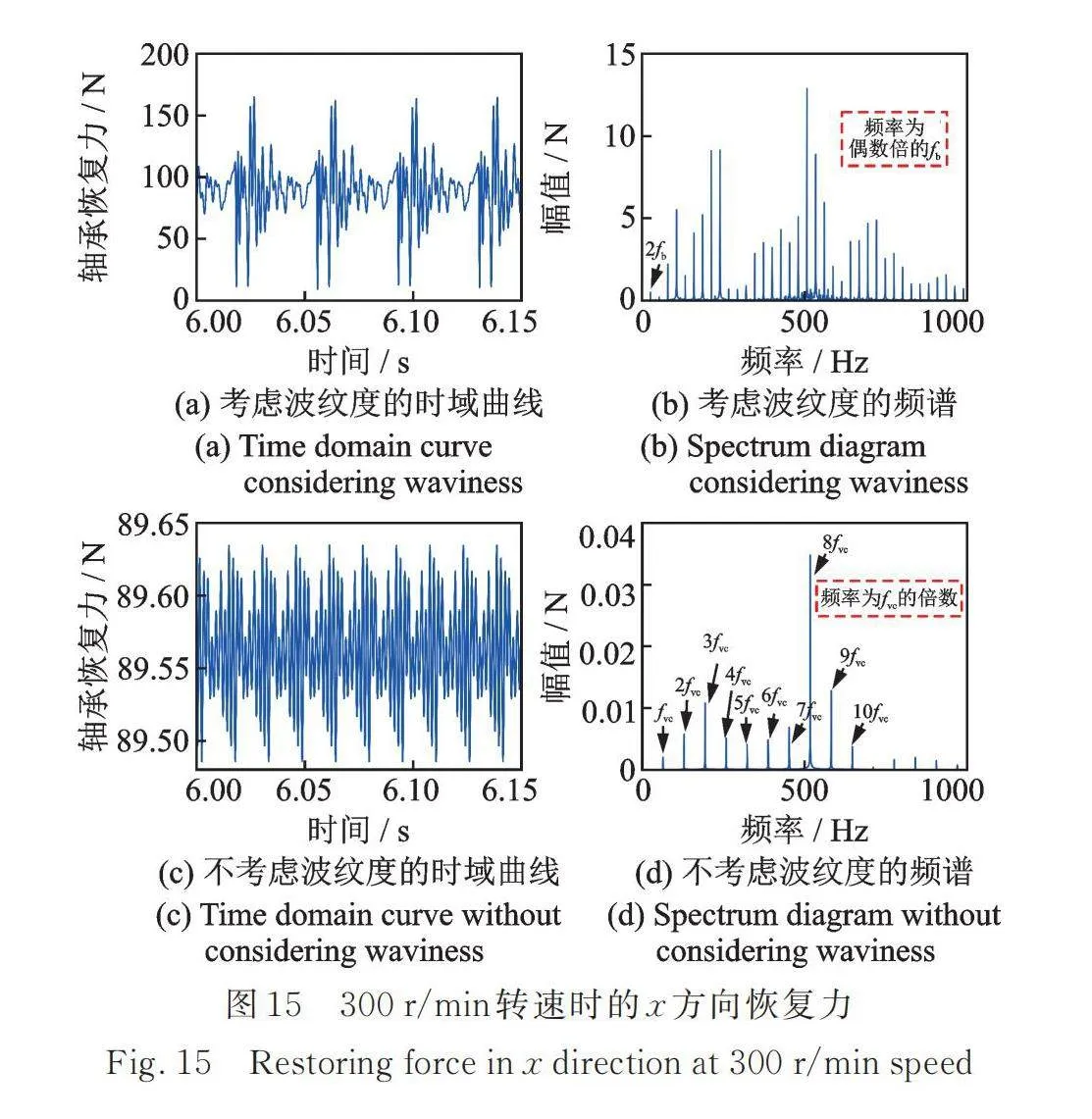
本文从轴承恢复力的角度分析系统在0～2000 r/min低转速范围内比高转速时振动相对较大的原因，内转子转速分别为300 r/min和4800 r/min时考虑波纹度与不考虑波纹度的轴承恢复力时域和频域图如图15，16所示。由于波纹度的存在，内转子转速为300 r/min时的轴承弹性恢复力会在一段时间内较平缓，然后会突然变化剧烈，类似冲击一样的变化趋势，导致低转速下系统振动过大；而在较高转速如内转子转速为4800 r/min时，轴承的弹性恢复力是相对比较连续的，没有明显冲击特征。另外球的自转频率是随着转速的增大而增大的，低转速时球波纹度波峰和内、外圈滚道接触时间间隔相对高转速时较长，导致在相同时间段高转速和低转速时的轴承恢复力时域曲线特征有差别，从而影响系统的振动响应。

对轴承弹性恢复力进行傅里叶变换，不考虑轴承波纹度时的轴承恢复力频率主要为轴承变柔度振动频率及其倍频，而考虑轴承波纹度比不考虑波纹度时的频谱成分丰富且复杂，主要有系统的共振频率，还有，，等偶数倍的球自转频率，出现偶数倍是因为滚动体不仅和内圈接触，还和外圈接触，波纹度激励由两部分激励共同组成。

通过上述分析，滚动体存在波纹度时，系统响应会出现偶数倍的球自转频率，低转速时频率成分幅值较大，高转速时频率成分幅值较小，且会存在和系统共振的频率成分。

4 波纹度对系统幅频响应的影响

本节考虑内、外转子的不平衡力，设内转子2节点有9.68310-5的不平衡量，外转子8节点上有9.13910-5的不平衡量，初相位均为0，波纹度模型参数同前文所述，分别对仅考虑波纹度、仅考虑不平衡力以及同时考虑两者的幅频响应进行计算，探究考虑波纹度激励下系统的振动响应。

4.1 考虑外圈滚道波纹度对系统响应的影响

如图17所示为考虑外圈滚道波纹度和转子不平衡激励时的幅频曲线对比图。高转速时主要是由转子不平衡引起的振动，轴承的波纹度对振动响应特性影响较小；而在低转速时波纹度激励会在一些转速下引起共振，不能忽略其对系统的影响。

仅考虑转子不平衡力时，在一定转速范围内，幅频响应曲线中会出现四个共振峰，是由内、外转子不平衡引起的共振，在线性领域内可解释为由内转子和外转子主激励的前两阶临界转速引起的共振，即共振峰对应的转速可称为临界转速。

仅考虑轴承外圈滚道波纹度时，低转速下会出现几个振动较大的区域，这是由波纹度激励引起的，振动频率成分主要为外圈滚道波纹度故障对应的特征频率。但随着转速的升高，转子不平衡力逐渐增大，对系统的振动响应起主导作用，而波纹度激励引起的振动会趋于平缓，对系统振动响应影响较小。高转速下波纹度激励引起的振动响应中存在很多高频成分，且可认为滚动体滚过波纹度波峰或波谷的时间较短，轴承恢复力较为连续，波纹度对系统振动影响较小。

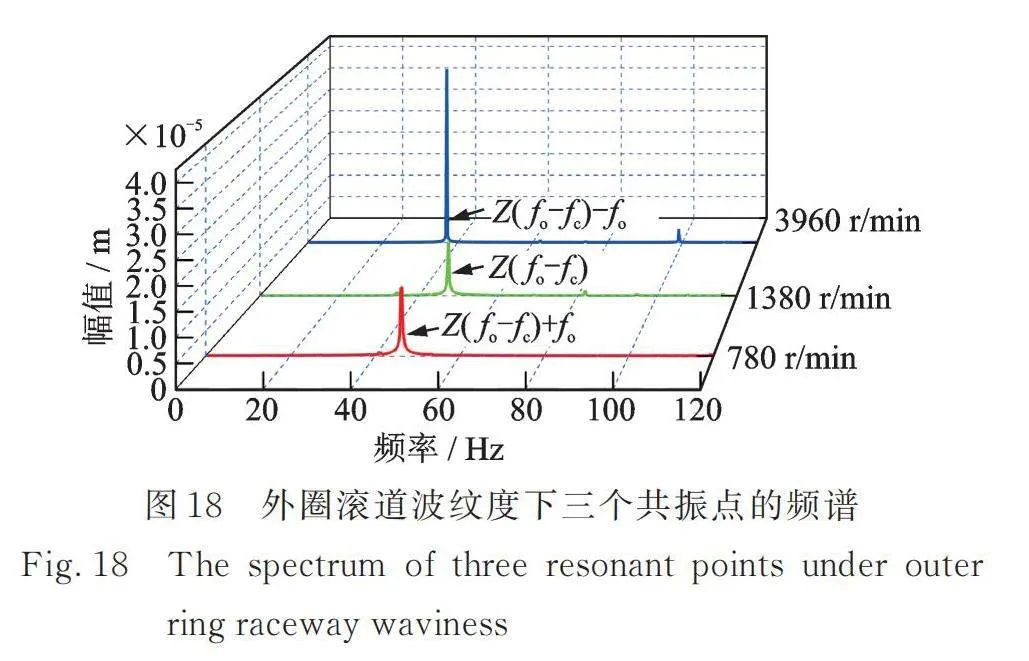
同时考虑转子不平衡力和外圈滚道波纹度时，图17中出现了7个共振峰，对应转速分别为：780，1380，1920，3000，3960，4920，7500 r/min。其中780，1380和3960 r/min时的振动主要是由保持架转频和外转子转频的组合频率引起的系统共振。如图18所示为这三个共振点的频谱分析，其主导的频率分别为，以及。

而1920 r/min和4920 r/min时的振动是外转子不平衡和外圈滚道波纹度激励共同引起的，主要频率成分为，这两个转速附近分别可称为外转子主激励的第一次和第二次共振区域；3000 r/min和7500 r/min时主要是由内转子不平衡引起的振动，主要频率成分为，这两个转速附近分别可称为内转子主激励的第一次和第二次共振区域，此时外圈滚道波纹度激励对这两个区域的振动几乎没有影响。通过上述分析，在考虑外圈滚道波纹度时，系统振动特性变得更复杂，波纹度激励不仅会增大低转速区域的振动，还会对外转子主激励的共振区域振动产生影响。

4.2 考虑内圈滚道波纹度对系统响应的影响

如图19所示为考虑内圈滚道波纹度和转子不平衡激励时的幅频曲线对比图。和考虑外圈滚道波纹度结果类似，系统的幅频响应曲线中也出现了多个共振峰，共振峰的出现主要由转子的不平衡力和内圈滚道波纹度激励引起。出现的共振峰对应的转速分别为720，960，1320，1920，3000，4920，7500 r/min。其中720，960以及1320 r/min时的振动主要是由保持架转频和内转子转频的组合频率引起的系统共振，如图20所示为这三个共振点的频谱分析，其主导的频率分别为，以及。

外转子主激励的第一次共振区域（1920 r/min附近）和第二次共振区域（4920 r/min附近）的振动主要是由外转子不平衡引起的，内圈滚道波纹度的影响较小。而在内转子主激励的第一次共振区域（3000 r/min附近）和第二次共振区域（7500 r/min附近）的振动主要是由内转子不平衡和内圈滚道波纹度引起的，但是发现在第二次共振区域内圈滚道波纹度激励降低了转子不平衡引起的振动，为分析这个现象，如图21所示为7500 r/min时三种工况的时域曲线。由图21可知仅考虑内圈滚道波纹度和仅考虑转子不平衡力时的振动响应可近似认为同频反相，因此两种激励共同作用时系统振动会降低。

通过上述分析，可知考虑内圈滚道波纹度时，共振峰同样会在低转速区域增多，而且内圈滚道波纹度激励会对内转子主激励的共振区域振动产生较大影响，而对外转子主激励的共振区域影响较小。

4.3 考虑滚动体波纹度对系统响应的影响

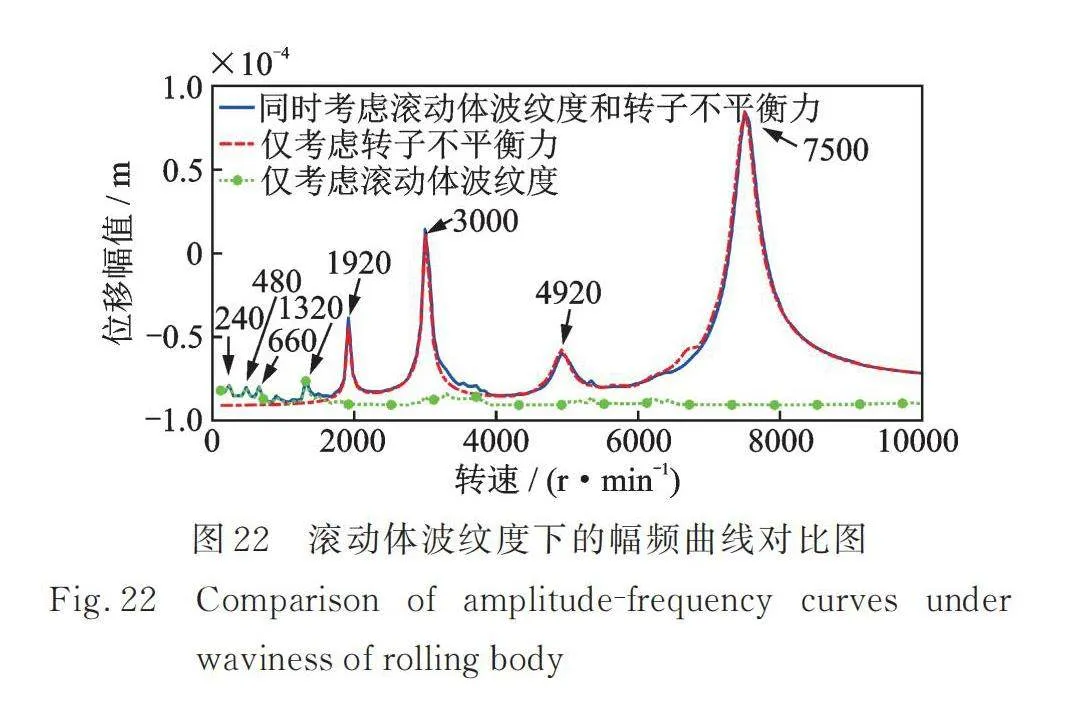
如图22所示为考虑滚动体波纹度影响的三种工况的幅频响应对比图。对比发现低转速时系统振动响应主要是由滚动体波纹度激励引起的，会引起系统产生几个振动较大区域，此时转子的不平衡力对系统响应影响较小。而高转速情况下则相反，系统的响应主要是由转子不平衡引起的，滚动体波纹度激励引起的振动响应几乎可以忽略。这是因为转子的不平衡力是随着转速的升高而增大的，低转速时转子的不平衡力相对滚动体波纹度激励较弱。

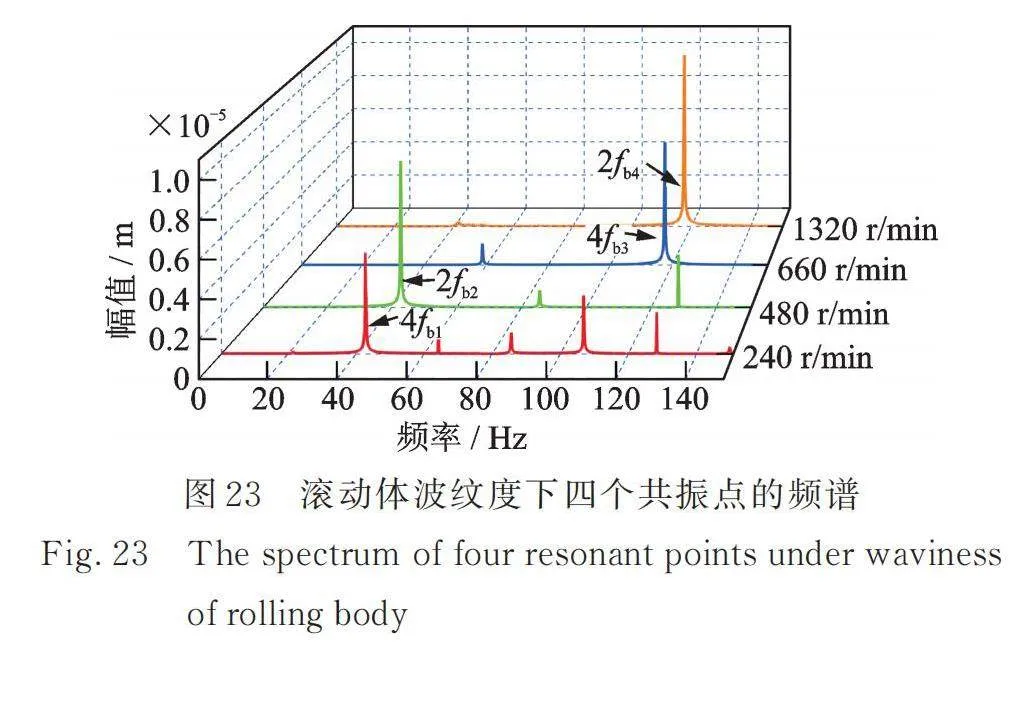
另外图中共振峰对应的转速分别为240，480，660，1320，1920，3000，4920，7500 r/min。其中前四个转速振动过大主要是由波纹度激励频率与此时系统的固有频率相近引起的系统的共振，如图23所示为这四个共振点的频谱分析，其主导的频率主要为偶数倍的滚动体自转频率。其他四个共振峰是由转子不平衡引起的。结合图13三维谱图可知，虽然滚动体波纹度激励会引起高转速下的一些区域产生系统共振，但是在考虑转子不平衡力时，波纹度对高转速区域振动的影响较小，而对低转速区域的振动则有一定程度的影响。

5 波纹度幅值对振动响应的影响

转子⁃轴承系统在正常运转过程中，由于轴承摩擦、润滑以及疲劳等原因，轴承波纹度的幅值可能会发生变化，因此研究波纹度幅值变化对系统振动响应的影响很有必要。

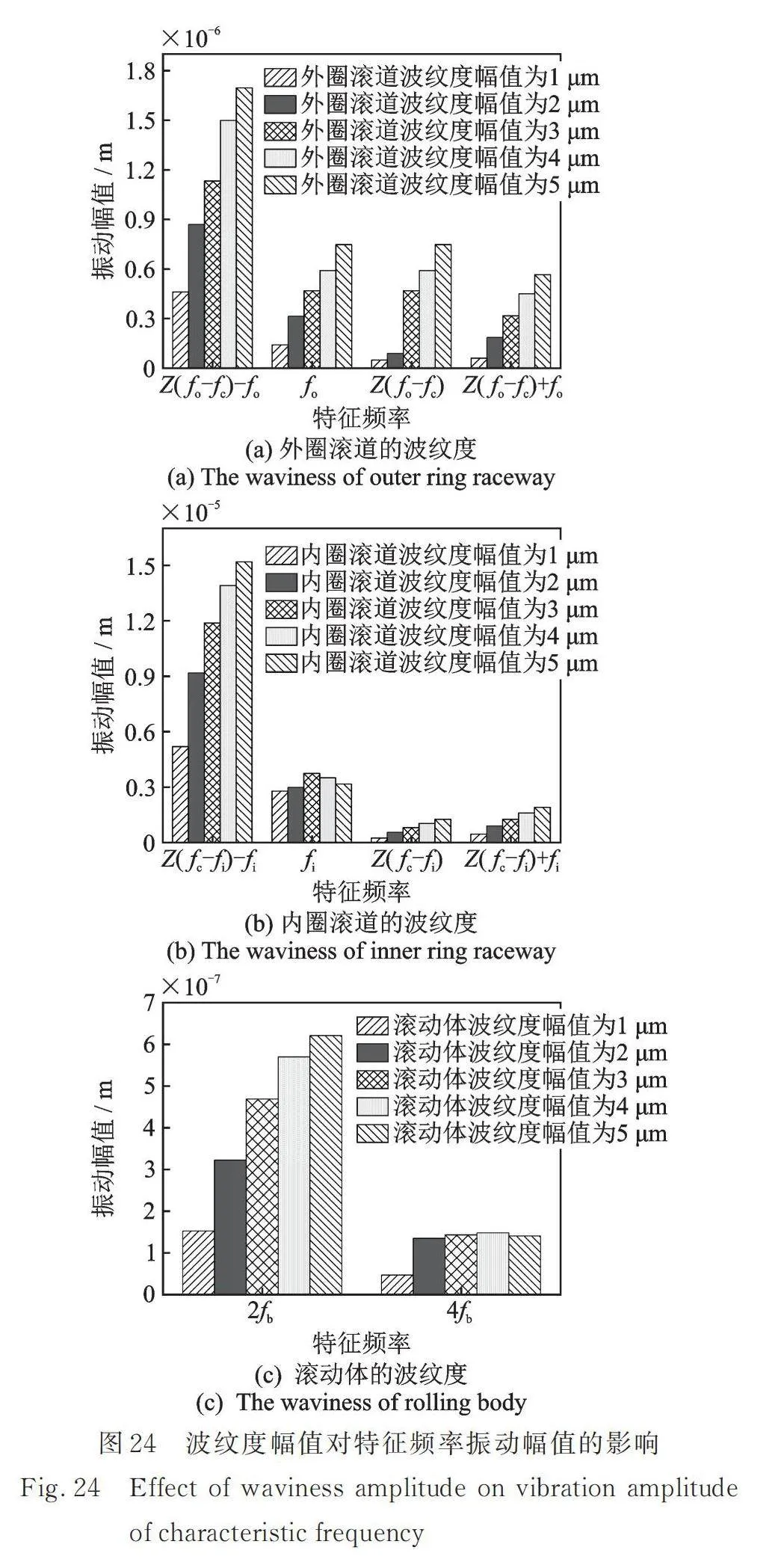
5.1 波纹度幅值对特征频率响应的影响

为研究波纹度幅值对波纹度激励下的响应特征频率幅值的影响，设内圈滚道、外圈滚道和滚动体波纹度幅值分别为5，4，3，2和1 µm，考虑内、外圈滚道波纹度时的转速与上文相同，考虑滚动体波纹度时取非共振区域内转子转速为2400 r/min。计算得到相应特征频率的振动幅值随波纹度幅值的变化规律如图24所示。

5.2 波纹度幅值对振动幅频响应的影响

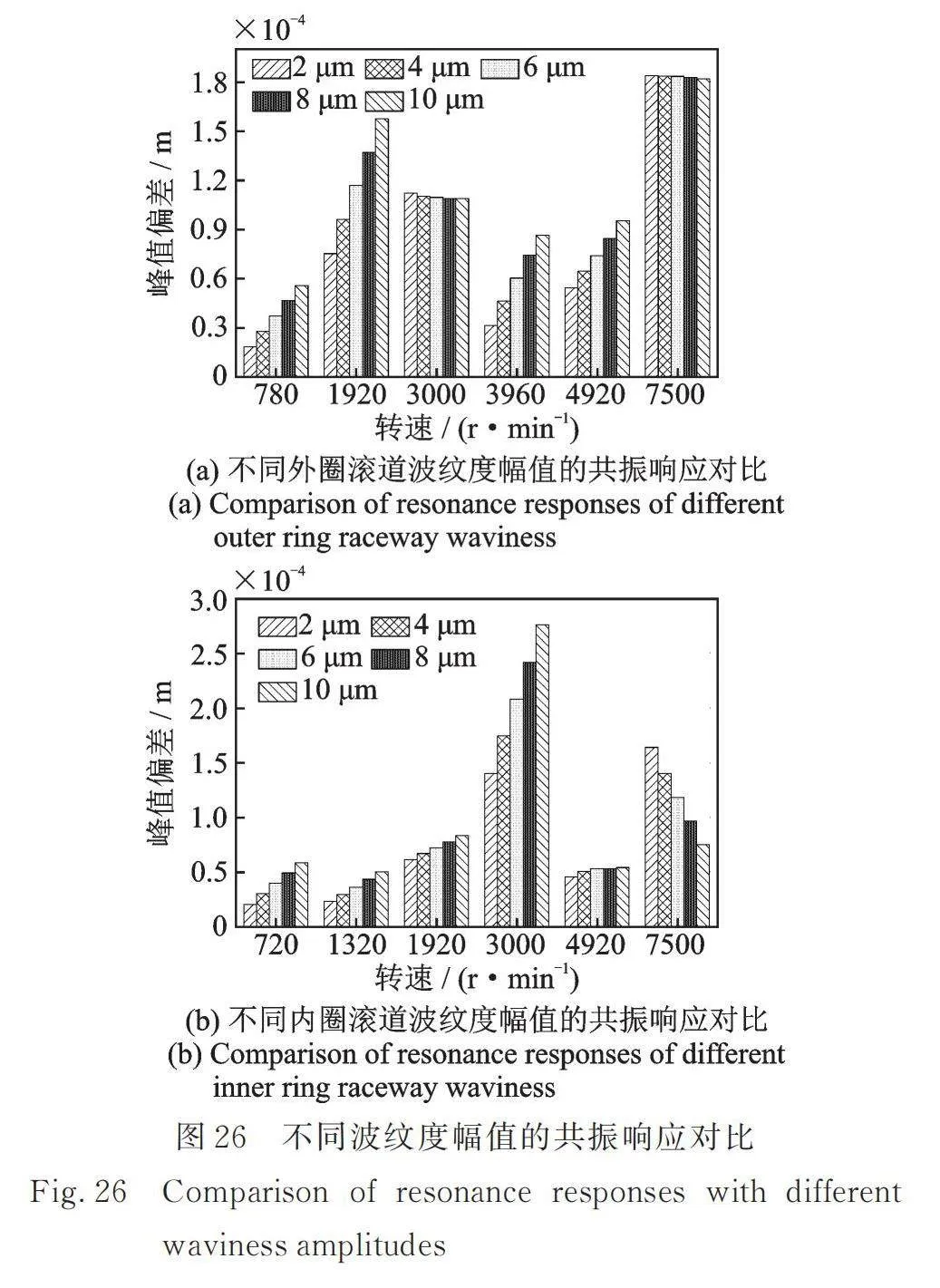
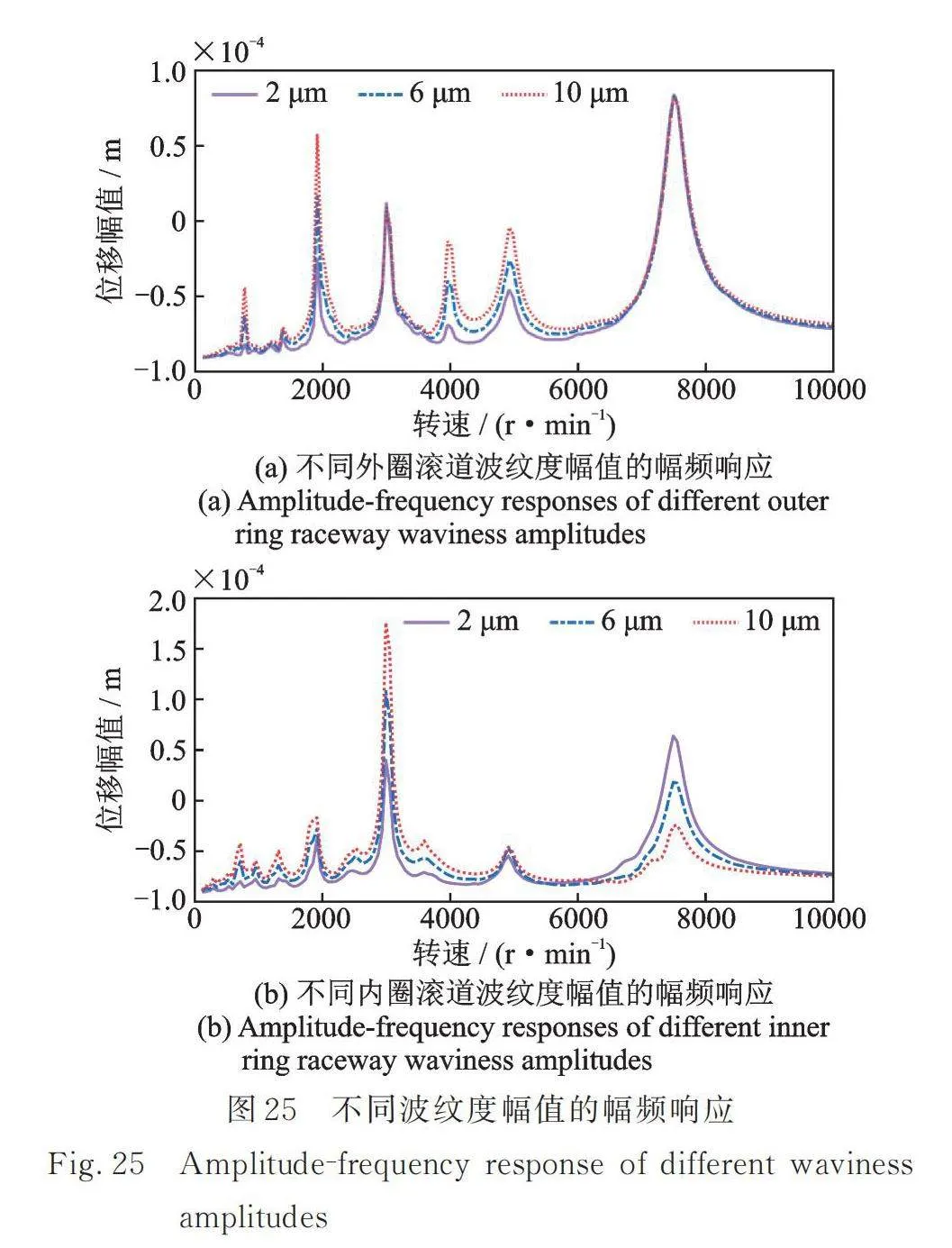
由于滚动体波纹度对高转速区域幅频响应影响较小，本小节主要研究内、外圈滚道波纹度幅值对在波纹度激励下系统振动幅频响应的影响，设内、外圈滚道波纹度幅值分别为2，4，6，8和10 µm，如图25所示为不同波纹度幅值下的系统幅频响应图，为方便比较，图中仅绘制了三个波纹度幅值下的幅频响应曲线。

不同波纹度幅值下幅频响应曲线的共振响应对比如图26所示，其中峰值偏差为位移最大值与平均值的差。发现随着外圈滚道波纹度幅值的增加，转速为780，1920，3960以及4920 r/min对应的振动峰值偏差会有明显的增加，这是因为波纹度激励对这些共振峰的形成具有较大贡献，然而对于转速3000 r/min和7500 r/min时的共振峰影响较小，因为产生此共振峰的原因主要是内转子的不平衡力，外圈滚道波纹度的影响较小。随着内圈滚道波纹度幅值的增加，低转速区域的振动和内转子主激励的第一次共振区域振动会明显增大，然而在内转子主激励的第二次共振区域则相反，波纹度幅值越大，响应越小。结合前文分析，这是因为在此共振区域内波纹度激励和转子不平衡引起的振动响应可近似认为同频反相，波纹度激励引起的振动响应增大，转子不平衡振动响应不变，这将会导致系统振动降低。

总体来看，轴承波纹度幅值对系统振动会有一定的影响，可能会出现系统振动过大的现象，在一些区域也有可能会降低系统振动，因此在实际工作情况下，为减小转子⁃轴承系统的振动和噪声，控制波纹度幅值具有一定的必要性。

6 结 论

本文考虑中介轴承内圈、外圈滚道和滚动体波纹度，基于有限元法建立了含变截面外转子的双转子⁃轴承系统，分别研究了内圈、外圈滚道和滚动体波纹度激励下的频谱特征，分析了波纹度激励对系统振动特性的影响，得出如下结论：

（1）考虑内、外圈滚道波纹度时，低转速时特征频率成分不太明显，而较高转速时频率成分会明显体现出来，为内、外转子转频和保持架转频的组合频率。

（2）外圈滚道存在波纹度时，其故障特征频率可总结为；内圈滚道存在波纹度时，其故障特征频率可总结为；滚动体存在波纹度时，系统响应会出现偶数倍的球自转频率，低转速时频率幅值较大，高转速时频率成分幅值较小且会存在和系统共振的频率成分。和为自然数，当和取较小值时，频率成分较明显；当和取较大值时，频率成分存在，但不明显。

（3）考虑转子不平衡和轴承波纹度两种激励时，较低转速时内、外圈滚道和滚动体波纹度均会对系统的振动有较大影响，会增大系统的振动。而在较高转速时，滚动体波纹度对系统响应的影响可以忽略，外圈滚道波纹度会增大外转子主激励的共振区域的振动，内圈滚道波纹度会增大内转子主激励的第一次共振区域的振动，而在内转子主激励的第二次共振区域两种激励引起的振动响应近似同频反相，会降低系统的振动。

（4）随着外圈滚道波纹度幅值的增加，系统在整个转速范围内的振动会增大，随着内圈滚道波纹度幅值的增加，在内转子主激励的第二次共振区域的振动会降低，其他转速区域内的振动会增大。

本文以双转子⁃轴承系统为研究对象，分析了中介轴承滚动体和内、外圈滚道波纹度下系统的振动特性，并对比分析了滚动体波纹度故障与内、外圈滚道波纹度故障的特征差异，可为双转子⁃轴承系统的故障诊断、振动控制以及结构设计提供参考意见。

参考文献：

［1］崔江. 双转子-滚动轴承系统的动力学特性研究［D］. 哈尔滨：哈尔滨工业大学， 2017.

Cui Jiang. Dynamic characteristic research of dual rotor-rolling bearing systems［D］. Harbin：Harbin Institute of Technology， 2017.

［2］顾晓辉，杨绍普，刘永强，等.表面波纹度对滚动轴承-转子系统非线性振动的影响［J］.振动与冲击， 2014，33（8）：109-114.

Gu Xiaohui， Yang Shaopu， Liu Yongqiang， et al. Effect of surface waviness on nonlinear vibration of a rotor with ball bearings［J］. Journal of Vibration and Shock， 2014， 33（8）： 109-114.

［3］Wang L， Cui L， Zheng D ， et al. Nonlinear dynamics behaviors of a rotor roller bearing system with radial clearances and waviness considered［J］. Chinese Journal of Aeronautics， 2008， 21（1）：86-96.

［4］Zhang X， Han Q， Peng Z， et al. A comprehensive dynamic model to investigate the stability problems of the rotor⁃bearing system due to multiple excitations［J］. Mechanical Systems & Signal Processing， 2016， 70-71：1171-1192.

［5］康锋，张耀强，杨茹萍，等.考虑波纹度的薄壁轴承-转子系统非线性强迫振动分析［J］.振动与冲击，2017，36（1）：96-101.

Kang Feng， Zhang Yaoqiang， Yang Ruping， et al. Forced vibration of a thin walled bearing-rotor system considering waviness［J］. Journal of Vibration and Shock， 2017，36（1）：96-101.

［6］刘永葆，李默，黄海涛，等.波纹度故障下低压转子系统的非线性动力学研究［J］.海军工程大学学报，2020，32（1）：50-56.

Liu Yongbao， Li Mo， Huang Haitao， et al. Research on nonlinear dynamics of low-pressure rotor system with waviness fault［J］. Journal of Naval University of Engineering， 2020，32（1）：50-56.

［7］余登亮，南国防，姜珊，等.滚动轴承支承下转子系统耦合故障动力学研究［J］. 计算物理， 2022，39（6）：733-743.

Yu Dengliang， Nan Guofang， Jiang Shan， et al. Research on coupling fault dynamics of rotor system supported by rolling bearing［J］. Chinese Journal of Computational Physics， 2022，39（6）：733-743.

［8］Nan G F， Zhang Y， Zhu Y J， et al. Nonlinear dynamics of rotor system supported by bearing with waviness［J］. Science Progress， 2020， 103（3）：1-29.

［9］Harsha S P， Kankar P K. Stability analysis of a rotor bearing system due to surface waviness and number of balls［J］. International Journal of Mechanical Sciences， 2004， 46（7）： 1057-1081.

［10］Lu Z Y， Wang X D， Hou L， et al. Nonlinear response analysis for an aero engine dual-rotor system coupled by the inter-shaft bearing［J］. Archive of Applied Mechanics， 2019， 89（7）： 1275-1288.

［11］Ma X X， Ma H， Qin H Q， et al. Nonlinear vibration response characteristics of a dual-rotor-bearing system with squeeze film damper［J］. Chinese Journal of Aeronautics， 2021， 34（10）： 128-147.

［12］侯磊，符毅强，陈予恕.考虑中介轴承波纹度的双转子系统的非线性振动［J］.航空动力学报，2017，32（3）：714-722.

Hou Lei， Fu Yiqiang， Chen Yushu. Nonliner vibration of dual-rotor system with surface waviness in inter-shaft bearing［J］. Journal of Aerospace Power， 2017，32（3）：714-722.

［13］李静，曹树谦，郭虎伦.中介轴承波纹度对双转子系统动力学特性的影响［J］.机械科学与技术，2020，39（11）：1794-1804.

Li Jing， Cao Shuqian， Guo Hulun. Effects of surface waviness of intershaft bearing on dynamic characteristics of dual rotor system［J］. Mechanical Science and Technology for Aerospace Engineering， 2020，39（11）：1794-1804.

［14］Jin Y， Lu K， Huang C， et al. Nonlinear dynamic analysis of a complex dual rotor-bearing system based on a novel model reduction method［J］. Applied Mathematical Modelling， 2019， 75： 553-571.

［15］Fei Z X， Tong S G， Wei C. Investigation of the dynamic characteristics of a dual rotor system and its start-up simulation based on finite element method［J］. Journal of Zhejiang University-SCIENCE A （Applied Physics & Engineering）， 2013， 14（4）： 268-280.

［16］张文.转子动力学理论基础［M］.北京：科学出版社，1990.

［17］He P， Liu Z S， Li C. An improved beam element for beams with variable axial parameters［J］. Shock and Vibration， 2013， 20（4）： 601-617.

［18］张耀强， 陈建军， 邓四二，等.考虑表面波纹度的滚动轴承-转子系统非线性动力特性［J］.航空动力学报，2008，23（9）：1731-1736.

Zhang Yaoqiang， Chen Jianjun， Deng Sier， et al. Nonlinear dynamic characteristics of a rolling bearing-rotor system with surface waviness［J］.Journal of Aerospace Power， 2008， 23（9）：1731-1736.

Analysis of vibration characteristics of a dual rotor system with inter-shaft bearing waviness

LIU Kun-peng1， LIU Hong-da2， SHI Xiu-jiang1， WANG Dong-hua1， LI Wan-you1

（1.College of Power and Energy Engineering， Harbin Engineering University， Harbin 150001， China； 2.No.703 Research Institute of CSSC， Harbin 150078， China）

Abstract： Aiming at the issue of inter-shaft bearing waviness in a dual rotor system， the dual rotor-bearing system of external rotor with variable cross section was taken as the research case. The dynamic model of the dual rotor-bearing system was established based on the Finite Element Modeling （FEM）. The waviness of the inner and outer ring raceways and the rolling body of the inter-shaft bearing were considered in the model. The fourth order Runge-Kutta numerical method was used to solve the equations， and the influence of waviness excitation on the amplitude-frequency response curve and spectral characteristics of the system was analyzed. The results show that when there is waviness in the inner and outer ring raceways， the system exhibits a combination frequency of the inner and outer rotor rotation speed frequency as well as cage rotation speed frequency. And when there is waviness in the rolling body， the system has an even times of the rolling body self-rotation speed frequency. When the rotor is unbalanced， the outer ring raceway waviness will amplify vibrations in the resonance region of the outer rotor main excitation. The vibration of the system will increase in the whole speed range with the increase of the waviness amplitude， while the vibration responses of the inner ring raceway waviness and the unbalanced excitation will appear similar to the same frequency and reverse phase phenomenon in the second resonance region of the inner rotor main excitation. The vibration of the system will decrease with the increase of waviness amplitude， while the vibration in other regions will increase. Compared with the high rotating speed region， the waviness of the rolling body significantly impacts on the vibration characteristics in the low rotating speed region.

Key words： dynamics of rotor；dual rotor system；inter-shaft bearing；waviness；amplitude-frequency response

作者简介： 刘坤鹏（2000―），男，博士研究生。电话：（0451）82588833；E-mail：liukunpeng@hrbeu.edu.cn。

通讯作者： 王东华（1981―），男，博士，副教授。电话：（0451）82589199；E-mail：wangdonghua@hrbeu.edu.cn。