基础冲击作用下弹性支撑的电磁轴承‑柔性转子系统振动特性及瞬态振动主动抑制策略

摘要： 本文将电磁轴承‑柔性转子系统安装在弹性支撑的基础上，研究了双半正弦波、半正弦波、正弦波、三角波和双三角波5种冲击激励下弹性支撑基础的振动特性，得到了不同冲击激励参数对弹性支撑基础的加速度的影响规律。为了抑制基础冲击激励条件下弹性支撑的电磁轴承‑柔性转子系统的振动，提出了一种基于基础加速度的转子系统瞬态振动补偿控制策略。在设计的电磁轴承‑柔性转子系统试验平台上，进行了多种冲击激励条件下弹性支撑基础的振动特性试验，以及安装在弹性支撑基础上的电磁轴承‑柔性转子系统的瞬态振动抑制试验。结果表明：冲击激励下，弹性支撑基础的加速度和电磁轴承‑柔性转子振动均表现出明显的冲击特征，振动的特性随着冲击激励形式的不同而变化。基于基础加速度的转子系统瞬态振动补偿控制策略能够有效地抑制基础冲击激励对转子振动的影响。

关键词： 转子动力学； 电磁轴承； 振动抑制； 基础冲击； 前馈补偿

中图分类号： O347.6； TH133.3 文献标志码： A 文章编号： 1004-4523（2024）09-1513-10

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.008

引 言

电磁轴承（Active Magnetic Bearings， AMBs）是一种新型的转子支承，除了支撑转子外，作为一种特性可控的执行器，还能够对转子在不同激励条件下的振动进行有效的控制。

目前对AMBs‑转子系统振动主动控制的研究主要是针对稳定的激励状态，如同步不平衡激励、多频激励等。但随着AMBs的普及性应用，支撑在AMBs上的一些旋转机械在工作过程中可能会受到周围环境的影响，如冲击、地震等，从而影响到系统的可靠性。冲击是一种剧烈变化的瞬态激励，使转子系统的振动瞬间增大［1‑2］。由于AMBs能够给转子提供的刚度较小，因此受到冲击后，转子的瞬态振动可能会导致转子与备用轴承之间发生碰撞，危害转子系统的安全。为了保证AMBs‑转子系统在冲击环境下仍然具有良好的特性，有必要对冲击激励作用下AMBs‑转子系统的振动特性开展研究，以便事先采取必要的措施。

转子受到的基础冲击激励可分为两类，一类是基础与转子系统整体做冲击运动，从而使转子承受惯性冲击激励，如地震造成的冲击或在振动台上进行的基础冲击试验［3］。这类基础冲击通常无法精确获得冲击激励力，也无法获得基础的力学模型，所以只能将转子系统承受的冲击激励用基础的运动参数来描述。另一类是基础受到冲击作用后产生冲击响应，基础的冲击响应使转子系统承受额外的载荷，如爆炸对舰船的冲击。第一类基础冲击是基于基础响应已知的情况，第二类基础冲击是基于基础所受载荷已知而响应未知的情况，因此，第一类基础冲击可以看作是第二类基础冲击的简化。

实际工程中的冲击激励是十分复杂的，为了进行理论分析，通常都会对其进行简化。如海军设备抗冲击标准［4］主要将冲击激励简化为双半正弦波、半正弦波、正弦波、三角波和双三角波等。其中，半正弦波和双三角波最常用。LEE等［5］将滚动轴承支承的转子系统固定在振动台上，研究了半正弦冲击激励下转子系统的响应。之后，LEE等［6］又建立了基础‑轴承‑转子系统的动力学模型，研究了基础半正弦冲击下转子相对于基础的瞬态振动。WANG等［7］和贺少华等［8］将爆炸对舰船的冲击激励简化为双三角波，分别研究了舰船抗冲击性能的优化以及冲击激励下舰船的响应。

针对基础冲击激励条件下转子系统动力学的研究，目前大多集中于基础冲击激励对转子响应的影响，研究对象主要为机械轴承支承的转子系统［9‑11］。对于基础冲击激励条件下AMBs‑转子系统的研究还相对较少。ZHU［12］对AMBs‑刚性转子系统在基础锤击激励下的性能进行了测试，发现一般控制器的抗冲击能力非常有限，大的基础冲击会导致转子与定子之间发生碰摩。SU等［13］建立了AMBs‑保护轴承‑转子系统模型，研究了梯形波、三角波等冲击激励作用下转子系统与保护轴承间的非线性行为。鲜有关于基础冲击激励如何影响弹性支撑的AMBs‑转子系统的振动特性以及如何有效抑制基础冲击激励的影响的报道。

本文将AMBs‑转子系统安装在弹性支撑的基础上，首先建立了冲击激励条件下弹性支撑的AMBs‑柔性转子系统动力学方程。然后，对比分析了双半正弦波、半正弦波、正弦波、三角波和双三角波冲击激励下弹性支撑基础的加速度响应，研究了冲击幅值和持续时间等参数对基础加速度响应的影响。针对基础冲击激励条件下传统PID控制对AMBs‑转子系统振动抑制能力有限的问题，设计了一种基于基础加速度的瞬态振动补偿控制策略。最后，在搭建的弹性支撑的AMBs‑柔性转子系统试验平台上，进行了多种冲击激励条件下弹性支撑基础的振动特性试验，以及AMBs‑柔性转子系统的瞬态振动抑制试验，对理论分析的正确性以及所提控制策略的有效性进行了验证。

1 基础冲击激励条件下弹性支撑的AMBs‑柔性转子系统的动力学模型

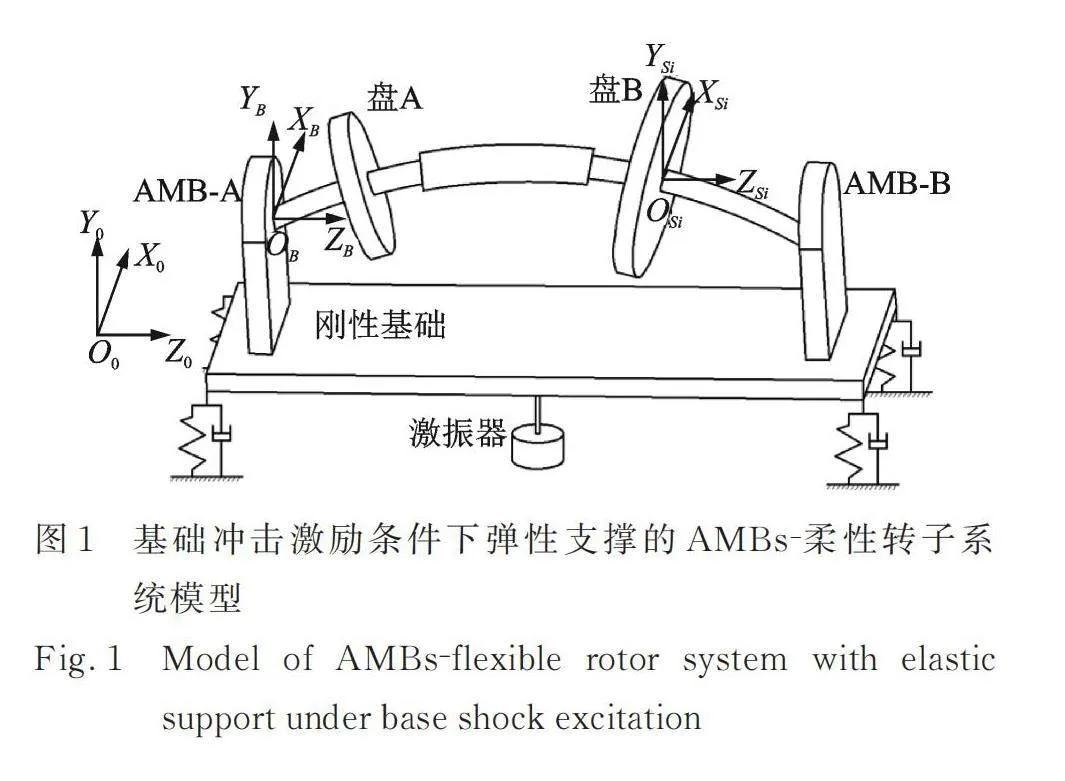
图1为基础冲击激励条件下弹性支撑的AMBs‑柔性转子系统模型。多盘柔性转子由两端的电磁轴承AMB‑A和AMB‑B支承在基础上，基础由4个弹簧‑阻尼支点支承在地面上，基础下方与激振器传力杆固连，以对基础施加冲击激励。

假设基础为刚体，为了便于描述转子的运动，使用了3套坐标系。其中：

（1）坐标系为相对于地面静止的空间参考坐标系，简称空间参照系，空间参照系是一个广义的参照系，原点可位于空间的任意一点。

（2）坐标系为固连于运动基础的坐标系，随着基础一同运动，简称基础坐标系。坐标系原点位置与转子静态悬浮时，AMB‑A端的转子截面轴心重合。纵轴沿转子轴线方向由AMB‑A指向AMB‑B，立轴垂直基础底面向上，横轴方向符合右手定则。

（3）坐标系为沿转子轴线任意截面的局部固定坐标系，坐标系原点为所在截面轴心，各坐标轴与坐标系对应坐标轴平行。转子运转过程中，坐标系随所在转子截面轴心平动，但不随转子所在截面转动。在用有限元对转子进行离散化建模时，每个单元节点所在截面都有一个局部固定坐标系，因此坐标系代表了一组坐标系。

在空间参照系中，基础在激振器产生的冲击激励作用下带动转子进行运动，使转子系统承受额外的载荷，从而对转子的振动产生影响。基础在各个时刻的姿态、空间位置以及位移，在空间参照系中描述；使用原点位置的速度和加速度代表各个时刻基础的运动信息，运动信息在基础坐标系中描述，转子基础沿，及的平动速度为，和，转动速度为，和。忽略转子各个位置相对于基础的轴向运动，转子各截面轴心相对于基础的径向平动位移和速度在基础坐标系中描述；转子各截面轴心相对于基础的径向转动位移和速度在局部坐标系中描述。

本文将基础冲击激励条件下弹性支撑的AMBs‑柔性转子系统的建模分为两部分，一部分是基础激励条件下AMBs‑柔性转子系统的动力学建模，另一部分是冲击激励作用下弹性支撑基础的动力学建模。

1.1 基础激励条件下AMBs‑柔性转子系统的动力学建模

采用有限元法将转子离散为N个节点，每个节点包含4个自由度。转子轴段采用考虑截面惯性及剪切效应的Timoshenko梁单元进行建模，圆盘采用具有等效质量和等效转动惯量的刚性圆盘单元建模，在AMBs位置节点处用对应的广义力来等效AMBs对转子的作用。

利用Lagrange方程建立基础激励条件下AMBs‑柔性转子系统的动力学方程为［14］：

（1）

式中 ，，分别为4N×4N维质量矩阵、陀螺矩阵和刚度矩阵；为转子转速；和分别为基础转动激励引起的4N×4N维附加阻尼矩阵和附加刚度矩阵；为4N×1维电磁力向量；为4N×1维不平衡力向量；为4N×1维基础激励载荷向量；为4N×1维重力载荷向量；为柔性转子4N×1维广义位移向量。

AMBs采用差动模式，线性化后AMBs的电磁力向量为：

（2）

式中 及分别为AMBs的电流‑刚度及位移‑刚度系数矩阵；为AMBs的控制电流向量；为克服转子重力影响的电流；转子在重力和的作用下保持静态悬浮，因此在转子动力学研究中通常不考虑重力及电磁力分量的影响，此时式（1）变为：

（3）

对于图1所示的AMBs‑柔性转子系统，假设AMBs分别在第a个节点和第b个节点处，设和分别为AMB‑A和AMB‑B的位移‑刚度系数，则矩阵为：

（4a）

式中 位置在矩阵的第4a-3行、第4a-2行，位置在第4b-3行、第4b-2行对角线处，其余元素均为0。

同理，令和分别为AMB‑A和AMB‑B的电流‑刚度系数，则矩阵为：

（4b）

其中，省略号处元素均为0。

对应的控制电流向量为：

（4c）

式中 表示AMB‑n轴承的m自由度对应的控制电流。

式（3）中基础转动激励引起的转子附加矩阵以及激励载荷向量可表示为［14］：

（5a）

（5b）

（5c）

式中 及（）为与转子结构相关的4N×4N维矩阵； （）为与转子结构相关的4N×1维向量，具体形式可见参考文献［9，14］。

1.2 冲击激励作用下弹性支撑基础的动力学模型

假设基础的冲击是在基础沿轴线的平动自由度方向，则根据图1，基础的运动微分方程可表示为：

（6）

式中 为基础的总质量；（）和（）为基础左端（右端）弹性支撑的刚度和阻尼系数；/为转子在AMB‑A/‑B位置沿方向相对于基础的位移，为式（3）中向量的对应AMBs自由度的元素；为基础受到的冲击激励力。

如果基础只有沿轴线的平动自由度方向的运动，则基础运动的加速度为，即有，沿的冲击载荷作用下，式（5）可简化为：

（7）

联立式（3）～（6），即为弹性支撑的AMBs‑柔性转子系统的动力学方程。

式（3）和（6）中均含有AMBs的控制力项，表明了转子与基础之间通过AMBs相互影响。

2 冲击激励条件下弹性支撑基础的瞬态振动加速度特性

冲击激励作用于图1所示系统时，弹性支撑基础会产生振动加速度。假设AMBs‑柔性转子系统处于稳定悬浮状态，AMBs采用PID控制，转子结构参数见文献［15］，其中转子质量为17 kg，基础及控制参数如表1所示。

2.1 冲击激励类型对弹性支撑基础瞬态加速度的影响

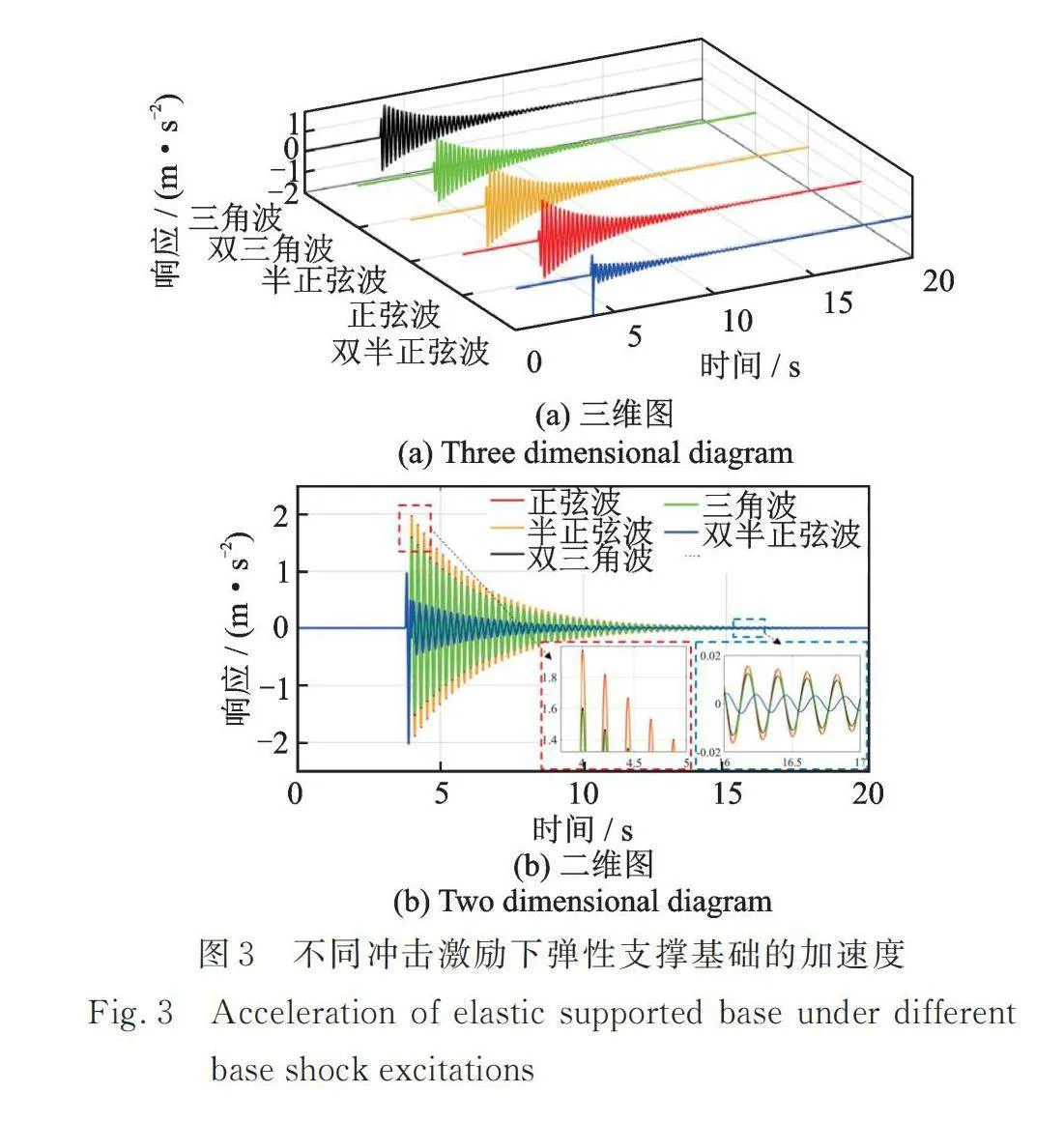
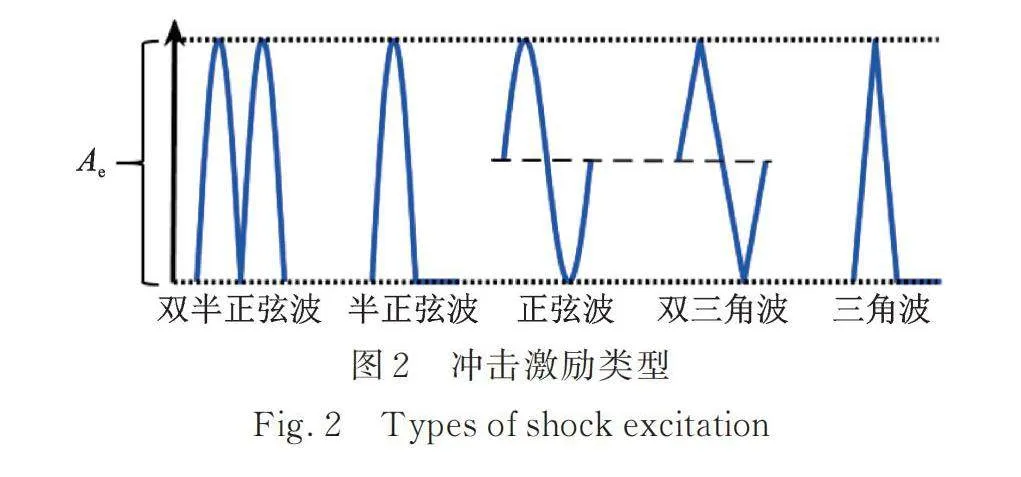
图2为常见的基础冲击激励的类型，包括半正弦波、三角波、双半正弦波、正弦波以及双三角波。为了保证激励的幅值相同，令半正弦波、双半正弦波和三角波的峰值与正弦波、双三角波的峰峰值相等，均为Ae；为了保证激励的周期相同，令各个波的持续时间相同。

图3为转子静态稳定悬浮时，不同形式冲击激励作用下弹性支撑基础的瞬态加速度时间历程。

由图3可见，半正弦波、正弦波、三角波和双三角波冲击激励作用下，基础的加速度响应突然增大，然后振荡衰减，呈现明显的冲击特征。其中，半正弦波和正弦波引起的冲击响应大于三角波和双三角波激励下的响应，表明同等幅值和持续时间的半正弦波/正弦波对基础的影响更大。正弦波（双三角波）比半正弦波（三角波）多了一个反向加载的过程，但弹性支撑基础的加速度响应并无显著差别，正弦波（双三角波）冲击下的基础加速度响应仅仅略大于半正弦波（三角波）激励下的基础加速度响应。根据图3（b），随着时间的推移，半正弦波、正弦波、三角波和双三角波冲击激励作用下弹性支撑基础的加速度幅值基本一致，表明系统的镇定时间基本相同。

双半正弦波冲击激励下，弹性支撑基础瞬间响应一个正向脉冲加速度和一个反向脉冲加速度，之后响应瞬间减小，接着缓慢振荡衰减。与同等幅值和持续时间的其他冲击载荷相比，双半正弦波冲击激励使弹性支撑基础的加速度幅值整体更小，但变化更剧烈。

2.2 冲击激励持续时间对弹性支撑基础瞬态加速度的影响

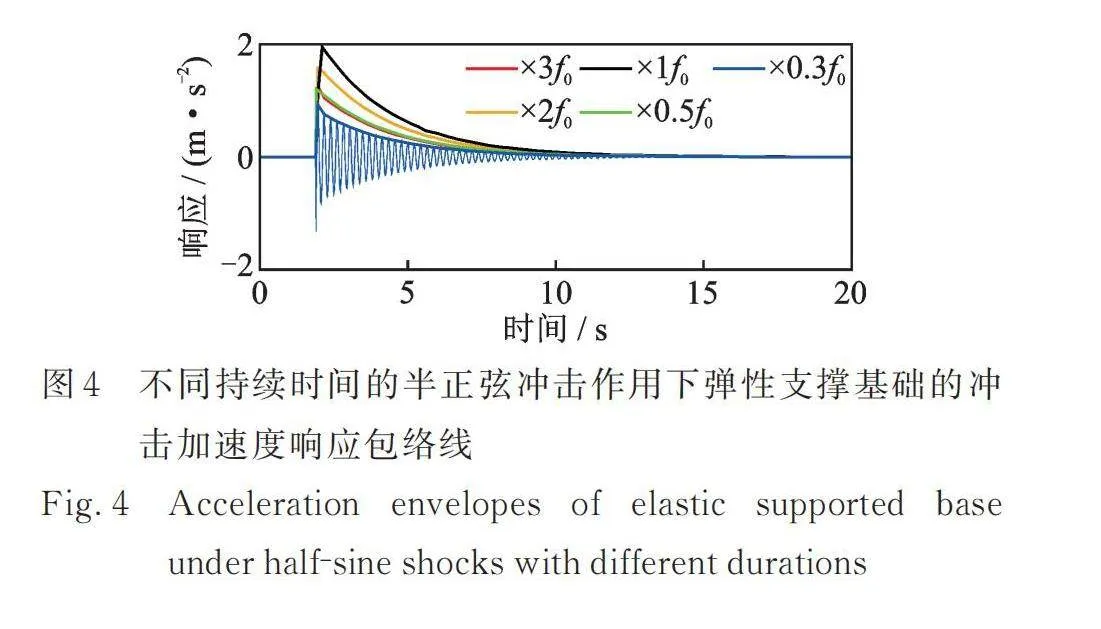
冲击激励的持续时间是一个重要的参数，决定了各个响应波形的周期以及激励对弹性支撑基础的作用时间。由2.1节可知半正弦波和正弦波冲击对弹性支撑基础的影响最大，而半正弦波是最常见的冲击载荷类型，因此本节利用半正弦波冲击激励分析冲击持续时间对弹性支撑基础加速度的影响。

由表1的数据可以确定出弹性支撑集成的平动固有频率为f0=4.7 Hz，分别令半正弦波的持续时间换算为×0.3f0，×0.5f0，×1f0，×2f0，×3f0，得到弹性支撑基础的冲击加速度包络线如图4所示。可见，当冲击载荷持续时间（频率）越接近系统的固有频率时，弹性支撑基础的冲击加速度幅值越大。随着时间的推移，各工况下弹性支撑基础的冲击加速度几乎同时衰减到0。

2.3 冲击激励幅值对弹性支撑基础瞬态加速度的影响

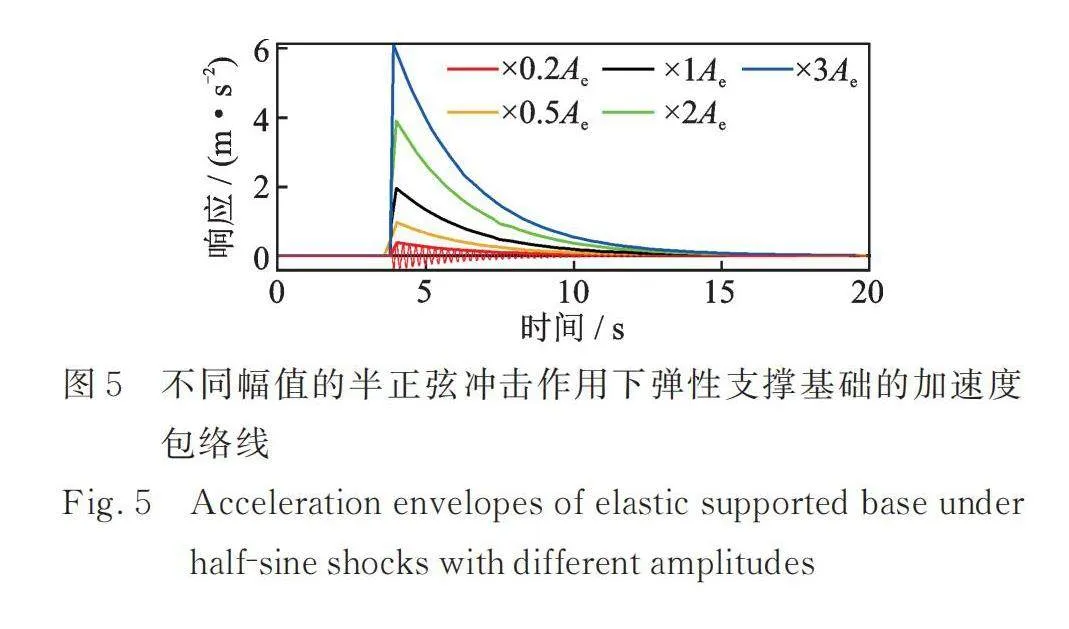
为了研究冲击激励幅值对弹性支撑基础振动的影响，针对半正弦冲击载荷，得到不同冲击载荷幅值条件下弹性支撑基础的冲击加速度包络线如图5所示。可见，基础冲击加速度的峰值随冲击激励幅值的增加呈线性增加，且各激励幅值下加速度的包络线形状相近。

2.4 转子不平衡激励对弹性支撑基础瞬态加速度的影响

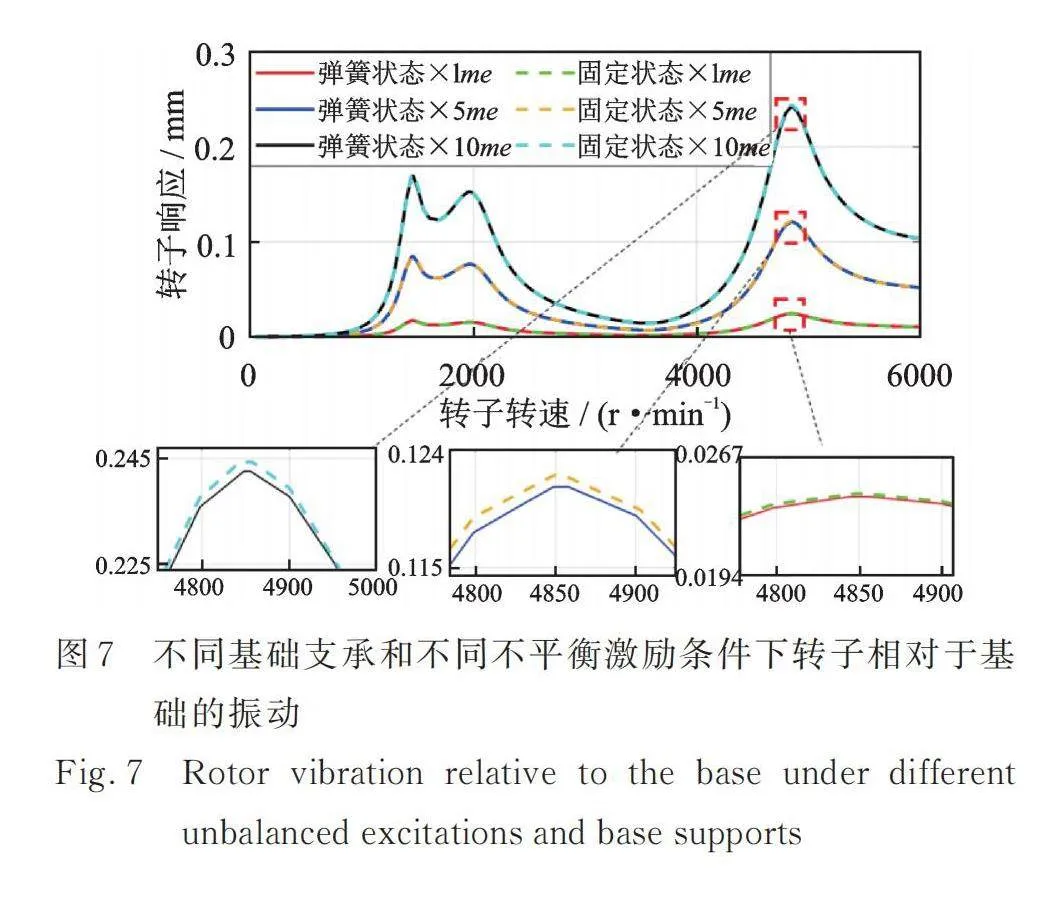
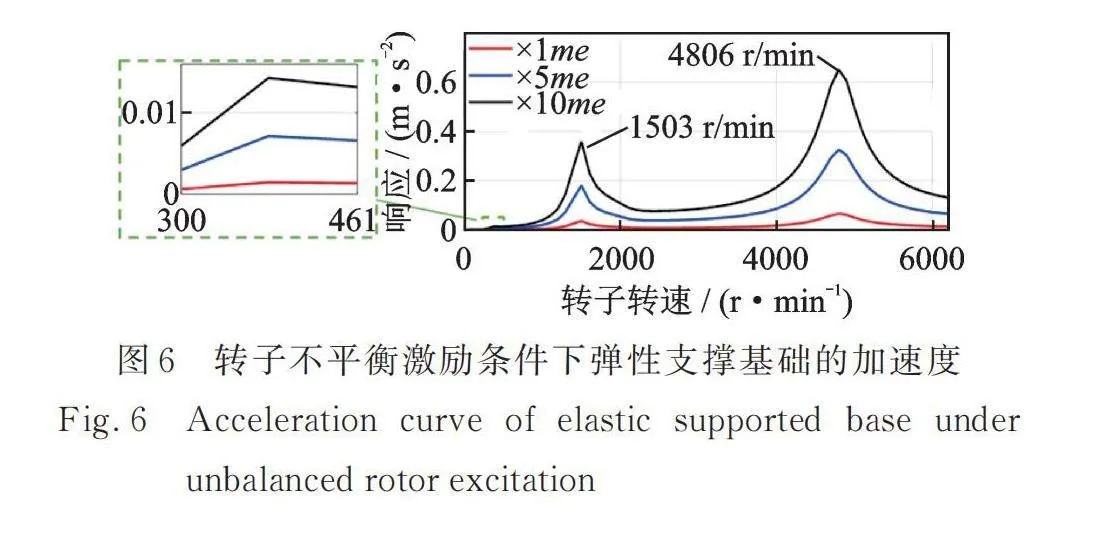
为了分析转子不平衡激励对弹性支撑系统的影响，图6给出了0～6000 r/min转速范围内弹性支撑基础的加速度变化。其中盘A/盘B的基准不平衡量为同相1 g·cm/5 g·cm，计算中的不平衡量分别为基准不平衡量（me）的1，5和10倍。图7为不同基础支承和不同不平衡量条件下，转子相对于基础的振动响应曲线。

由图6和7可得，转子不平衡对弹性支撑系统振动的影响随着不平衡量的增大而线性增大，且在转子平动临界转速和一阶弯曲临界转速位置影响显著。当不平衡量为5倍基准不平衡量时，弹性支撑基础的加速度最大仅为0.3 m/s2，因此当转子平衡精度较高时，可以忽略转子不平衡对弹性支撑基础的影响。

转子相对于基础的振动幅值随不平衡量的增大而线性增大。与基础固定状态相比，基础弹簧支承状态下转子相对于基础的振动在临界转速附近，尤其是一阶弯曲临界转速附近略有下降，但振动幅值在整体上仍然和基础固定状态下相当，说明基础的支承状态对转子系统的不平衡响应影响较小。

3 基于基础加速度的转子系统瞬态振动补偿控制

冲击激励作用下，基础带动AMBs‑柔性转子系统产生瞬时的加速度，使AMBs‑柔性转子系统相对于基础的振动瞬间增大［1］，可能导致转子与备用轴承之间出现碰撞，不利于转子的安全运行。为了减小冲击激励对AMBs‑柔性转子系统瞬态振动的影响，控制器必须对这种瞬态振动有足够快的反应和有效的控制。基于此，本节设计了一种基于基础加速度的转子系统瞬态振动前馈补偿控制器。

3.1 基于基础加速度的瞬态振动前馈补偿控制算法

控制器，如最常见的PID控制器，通常是基于反馈原理来对AMBs‑柔性转子系统的特性进行调节，即扰动对被控对象已经造成了影响，控制器基于这些影响进行调节。反馈控制器从原理上决定了扰动必须对被控对象产生一定的影响，因此，对于这种突变扰动的抑制能力有限。如若能在线获知扰动的信息，在扰动作用于转子的同时，对转子施加一个AMBs控制力，则能够大大降低扰动对转子的影响。

基于上述原理，提出如图8所示的基于基础加速度前馈补偿的AMBs‑柔性转子系统瞬态振动控制策略。主要由两部分组成：一部分是基于转子位移的主控制器反馈回路，主要用于保持转子系统稳定，并对扰动的影响具有一定的反馈调节作用；另一部分是前馈通路，主要用于提前获知基础的冲击扰动，并产生补偿电流对其进行补偿。

利用加速度传感器可获得基础沿方向的加速度。将基础加速度和结构参数代入式（7），即可得到冲击载荷下转子受到的附加载荷向量。

由式（3）可得，s时刻由基础激励载荷引起的转子响应为：

（8）

式中 为虚数单位；；为振动角频率。

假设s时刻，前馈补偿算法得到的4×1维电流向量为，则前馈补偿电磁力为：

（9）

相应的前馈补偿电磁力造成的转子响应为：

（10）

定义：

（11）

实际工程中，转子承受的基础运动激励载荷通常为低频载荷［16］。进而，式（11）可简化为：

（12）

经前馈补偿，基础激励载荷造成的转子残余响应为：

（13）

如果关注的响应并不是整个转子，而是转子上容易发生碰磨的位置，如圆盘、AMBs位置等，则：

（14）

式中 为所关注响应位置的自由度（以下称目标节点自由度）的选择矩阵。

为表征前馈补偿控制对基础激励条件下目标节点自由度响应的补偿程度，选择目标函数为：

（15）

式中 “*”表示矩阵或向量的共轭转置。

令目标函数J对前馈补偿电流的导数为0，得到极值条件为：

（16）

求解得：

（17）

其中，，由于矩阵不一定可逆，此处用伪逆来近似求解。式（17）即为基于基础加速度的前馈补偿电流的数学模型。

又由于：

（18）

因此式（17）是取得极小值的解。

3.2 补偿电流误差的修正

由式（17）可知，前馈补偿电流的求解不仅与基础运动参数相关，还与转子系统的动力学模型有关。实际的转子系统，由于加工、装配及测试误差等原因，可能与理论模型之间存在误差，这就导致理论模型求解的前馈补偿电流与实际的最佳补偿电流之间存在误差，进而影响补偿效果。为了解决该问题，引入修正系数矩阵，令：

（19）

式中 ，为AMBs的数目。对于第个AMB，和分别对应和方向的补偿电流修正系数。

试验中调节修正系数矩阵的步骤为：

（a）在转子悬浮或低转速条件下，针对各个电流通道，给定修正系数初值为1。给基础施加恒定的正弦激励，获得正弦激励下的转子响应。

（b）试探性改变修正系数，得到此时正弦激励下转子的响应，并与前一修正系数下的结果对比。若响应幅值减小则继续沿该方向调节修正系数，否则反向调节。重复该步骤直至基础冲击激励下转子响应达到最小。

4 试验结果与分析

为了验证冲击激励下弹性支撑基础的加速度特性，以及基于基础加速度的瞬态振动前馈补偿算法的有效性，在图9所示的试验平台上，进行了冲击激励条件下弹性支撑基础的振动特性试验及转子瞬态振动控制试验。

刚性基础平板由4个弹簧悬挂在铝合金框架上，使整个转子系统试验平台实现弹性支撑状态。AMBs及驱动电机等都固定在刚性基础平板上。弹性支撑的基础平板和AMBs转子系统共同组成弹性支撑系统。试验平台的基础参数如表1所示，转子参数见文献［15］。转子由电机拖动，电机与转子之间用柔性连轴器连接，电机的转速通过变频器进行控制。刚性基础平板下方固定有激振器，通过传力杆与基础平板固连，以实现对基础的激振。激振器的驱动电流由独立的功率放大器提供，通过调节激振器功放的增益，来改变激振器的输出幅值，驱动信号由信号发生器输入到功率放大器。

在2个轴承座位置的基础平板上，分别安装了两个ICP型加速度传感器来采集基础的加速度。在轴承座侧面端盖上安装有电涡流传感器，用来测量AMBs处转子的位移。由于电涡流传感器非常靠近AMBs，可近似等效为同位系统。试验中采用dSPACE （DS1103）作为控制器，采集的基础加速度和转子位移实时地传输到dSPACE，以实现对转子系统振动的主动控制。

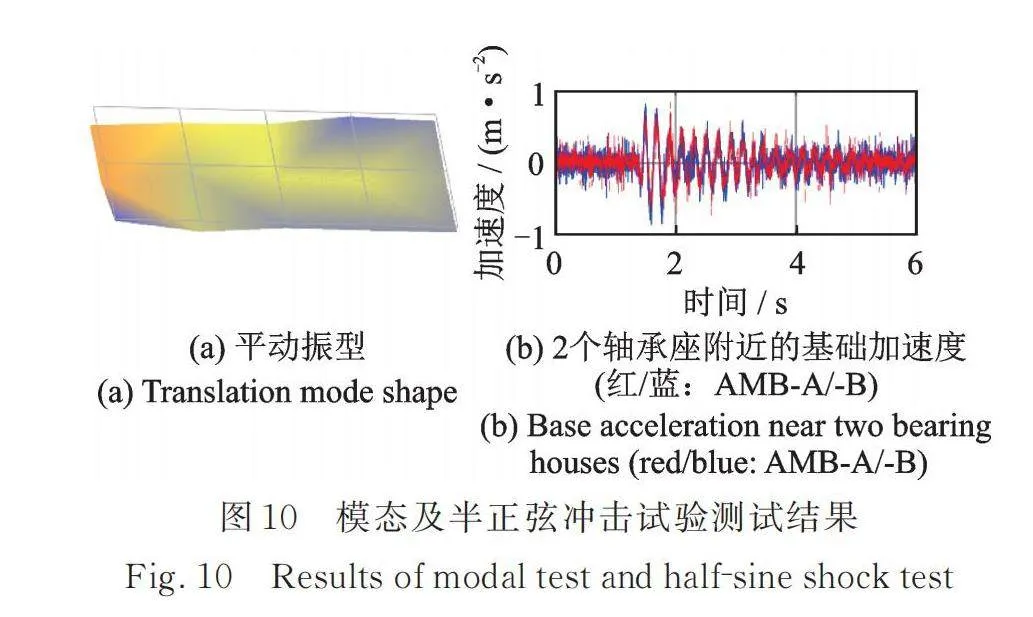
将弹性支撑的基础以及基础上的转子系统合称为弹性支撑系统，对整个弹性支撑系统进行模态测试，图10（a）为得到的基础沿竖直方向的刚体平动振型，对应的频率为5 Hz。由于激振器输出功率有限，根据2.2节的分析结果可知，只需要令图2中各脉冲的持续时间均为0.2 s，就能够激发弹性支撑基础纯刚体平动模态的振动。图10（b）为半正弦冲击下，底板2个轴承座附近的基础加速度的时间历程，可见2个轴承座附近的基础加速度几乎一样，此时基础呈现出显著的平动冲击特征。

4.1 冲击激励下基础的瞬态加速度特性

调节激振器的功放增益至×1，×1.5，×2三挡，分别对应激振器的不同输出，得到图2中各冲击载荷下基础的加速度响应时间历程如图11所示，其峰值用对应的虚线来表示。

结果表明，冲击激励条件下基础的加速度响应与图3类似，即：双半正弦冲击下基础产生一个明显的正向脉冲和反向脉冲后，逐渐振荡衰减至0；半正弦、正弦、三角以及双三角冲击下，基础的加速度突然增大然后振荡衰减。在相同的激励幅值和持续时间下，（半）正弦波激起的基础加速度峰值比双三角波激起的更大。

冲击激励的幅值越大，基础瞬态加速度的峰值越大，但不同幅值的冲击激励下，基础瞬态加速度响应的衰减时间基本相同。

4.2 冲击激励下AMBs‑柔性转子系统在静态悬浮时的瞬态振动特性

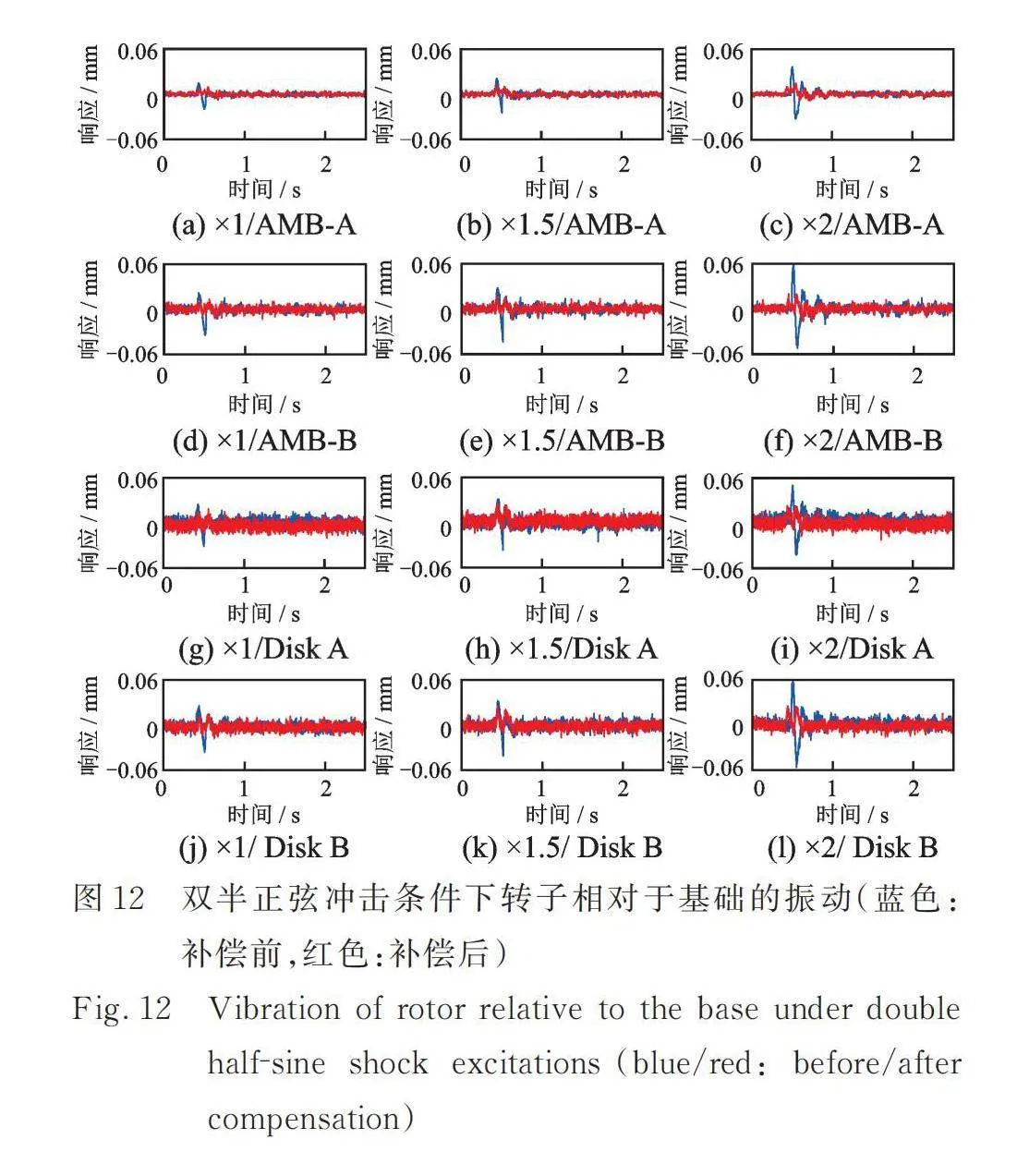
图12给出了AMBs‑柔性转子系统处于静态悬浮状态时，在图11（a）的双半正弦基础冲击激励下，前馈补偿前后转子相对于基础的瞬态振动响应时间历程。图12中标题×L/P表示功放增益为×L挡时转子上P位置的响应。

前馈补偿前，基础冲击激励下转子的瞬态响应有一个明显正向脉冲和反向脉冲，与基础的加速度冲击响应一致。整个转子相对于基础的瞬态振动随着冲击激励幅值的增大而增大，且基本呈线性变化。转子AMB‑A端由于联轴器与电机相连，在联轴器的约束下该端的振动较AMB‑B端的振动小。前馈补偿后，基础冲击激励下转子的瞬态响应被大幅抑制，且AMBs位置的抑制效果要优于盘位置。

图13为在图11中半正弦、正弦、三角、双三角冲击激励的作用下，AMBs‑柔性转子系统相对于基础的瞬态振动时间历程。为了节约篇幅，图中仅给出基础受到2倍幅值冲击激励条件下，AMB‑B位置处转子瞬态振动时间历程，其余位置的结果与之类似。

结果表明，在半正弦、正弦、三角、双三角冲击激励条件下，转子相对于基础的瞬态振动均呈现突然增大，然后振荡衰减的特征，且与基础的加速度冲击响应具有一致性。同等幅值的冲击载荷下，（半）正弦冲击对转子振动的影响较（双）三角冲击更加明显。前馈补偿后，冲击激励对AMBs‑柔性转子系统瞬态振动的影响被大幅抑制，转子的瞬态振动时间历程不再有明显的冲击特征。

4.3 冲击激励下AMBs‑柔性转子系统在恒速运行时的瞬态振动特性

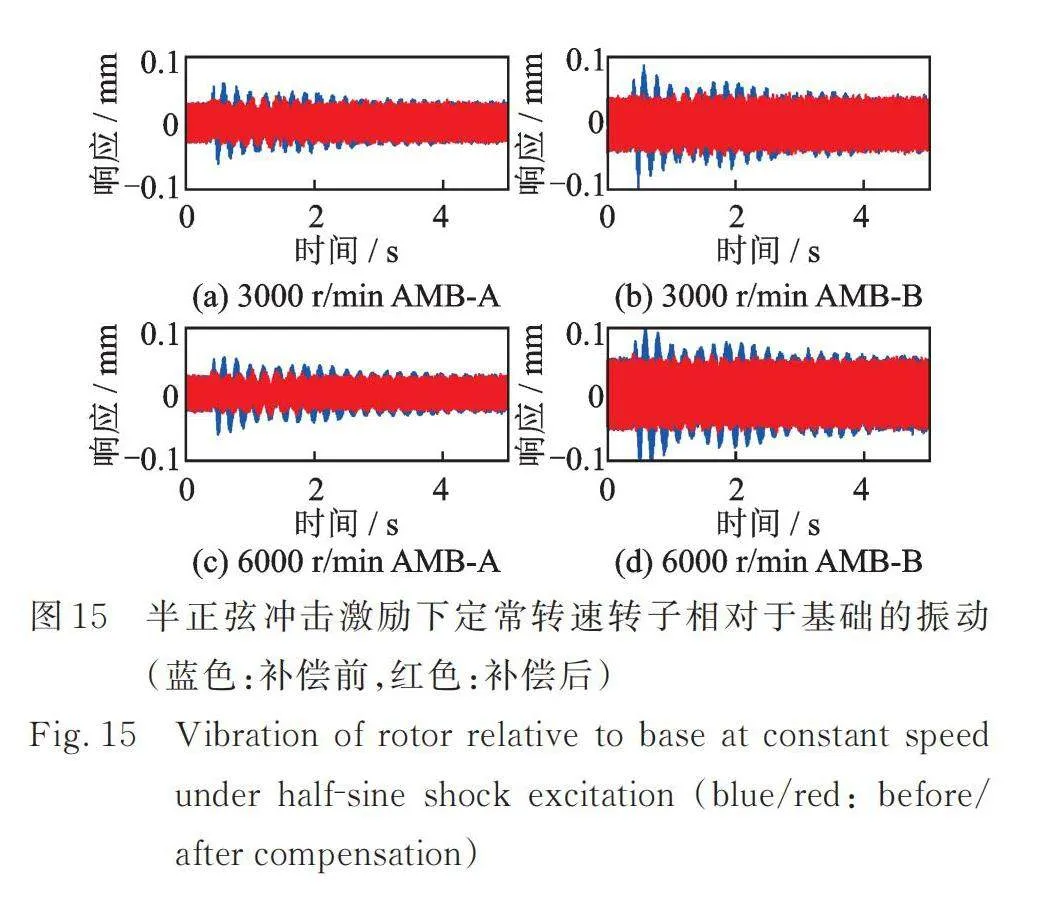
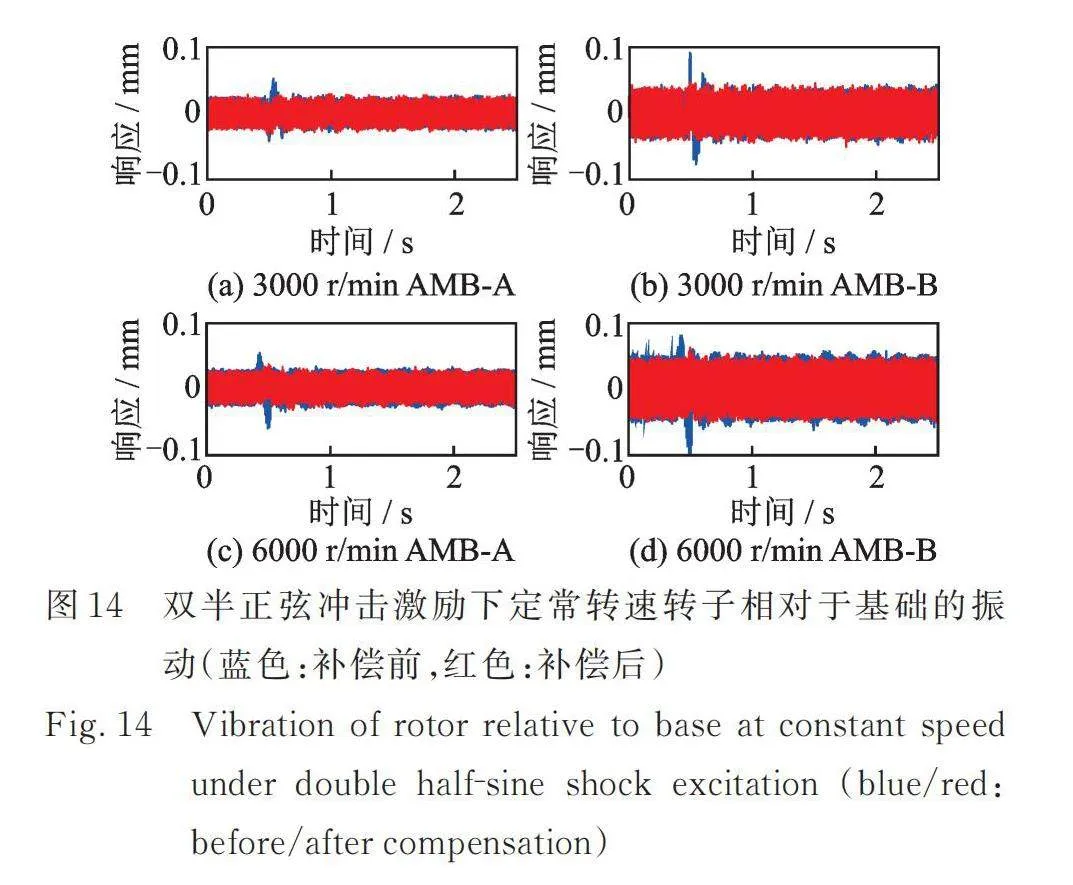
试验转子的一阶弯曲临界转速为4850 r/min左右，为了分析冲击激励对刚性转速区及柔性转速区转子瞬态振动的影响，分别在转子处于3000 r/min和6000 r/min时，进行了基础冲击激励试验，冲击激励如图11所示，得到的试验结果如图14和15所示。根据图13，半正弦、正弦、三角、双三角冲击激励作用下，AMBs‑柔性转子系统的瞬态振动相似，为节约篇幅，图14和15仅给出2倍幅值的双半正弦和半正弦冲击激励条件下转子AMBs位置的响应。

基础冲击激励条件下，恒速运行时转子相对于基础的振动是不平衡振动和冲击振动的叠加。在刚性转速区和柔性转速区，基础冲击激励对转子瞬态振动的影响规律相同，且与图11中的基础加速度响应具有一致性。前馈补偿前，双半正弦冲击使转子系统的瞬态响应产生一个正向和反向脉冲，然后迅速衰减至与不平衡响应相当的幅值。与静态悬浮状态相比，转子瞬态振动衰减的过程相对不明显。半正弦冲击使转子响应瞬间增大，然后振荡衰减。前馈补偿后，基础冲击激励下的转子响应几乎没有明显变化，说明了所设计的前馈补偿算法能够对恒定转速工况下转子的瞬态振动进行有效的抑制。

5 结 论

本文分析了半正弦波、三角波、双半正弦波、正弦波以及双三角波冲击激励条件下，弹性支撑基础以及弹性支撑的AMBs‑柔性转子系统的振动特性。为了抑制基础冲击激励对AMBs‑柔性转子系统瞬态振动的影响，设计了一种基于基础加速度的瞬态振动前馈补策略法。通过仿真和试验，得到了如下结论：

（1）冲击激励下，弹性支撑基础的加速度瞬间增大，表现出显著的冲击特征。双半正弦波使弹性支撑基础的加速度瞬间产生一个正向和反向脉冲，然后振荡衰减；（半）正弦和（双）三角冲击使弹性支撑基础的加速度瞬间增大，然后振荡衰减，且同等冲击幅值的情况下，（半）正弦冲击对基础瞬态加速度的影响较（双）三角冲击更大。

（2）将弹性支撑基础和固定在基础上的AMBs‑柔性转子系统看作弹性支撑系统，基础冲击激励的持续时间越接近弹性支撑系统的固有周期，则冲击激励对系统瞬态振动的影响越大。

（3）冲击激励条件下，AMBs‑柔性转子系统的瞬态振动与基础的瞬态加速度具有一致性，呈现出明显的冲击特征，且瞬态振动的幅值随冲击激励幅值的增大而增大。

（4）无论在转子静态悬浮状态还是恒速运转状态，应用基于基础加速度的转子系统瞬态振动前馈补偿策略后，转子相对于基础的瞬态振动几乎不再受基础冲击激励的影响，转子响应的冲击特征得到了有效的抑制，验证了本文所提算法的有效性。

参考文献：

［1］陈伟， 吴泽宇， 韩佳奇， 等. 突加基础冲击激励下转子系统振动特性试验［J］. 航空动力学报，2023， 38（4）： 878‑888.

CHEN Wei， WU Zeyu， HAN Jiaqi， et al. Test on vibration characteristics of rotor system under sudden base shock excitation［J］. Journal of Aerospace Power，2023， 38（4）： 878‑888.

［2］杨泽东. 突加高能基础激励载荷作用下转子系统响应特性及稳定性研究［D］. 南京：南京航空航天大学，2020.

YANG Zedong. Study on response characteristics and stability of rotor system under sudden high energy excitation load［D］. Nanjing： Nanjing University of Aeronautics and Astronautics， 2020.

［3］GAGANIS B J， ZISIMOPOULOS A K， NIKOLAKOPOULOS P G， et al. Modal analysis of rotor on piecewise linear journal bearings under seismic excitation［J］. Journal of Vibration and Acoustics， 1999， 121： 190‑196.

［4］张晓阳， 刘建湖， 潘建强， 等. 各主要海军国家设备抗冲击标准之评述［J］. 船舶力学， 2011， 15（11）：1322‑1334.

ZHANG Xiaoyang， LIU Jianhu， PAN Jianqiang， et al. Review on anti‑shock criteria for equipments in some primary navy countries［J］. Journal of Ship Mechanics， 2011， 15（11）： 1322‑1334.

［5］LEE A S， KIM B O，KIM Y C. A finite element transient response analysis method of a rotor‑bearing system to base shock excitations using the state‑space Newmark scheme and comparisons with experiments［J］. Journal of Sound & Vibration， 2006， 297： 595‑615.

［6］LEE A S， KIM B O. Construction of shock response map for a flexible rotor‑bearing system with mount system to base excitations using the FE transient analysis method［C］∥Proceedings of ASME Turbo Expo. Vancouver，Canada， 2011： 291‑298.

［7］WANG Yu， CHEN Xinglin， LI Guangmin. The optimum design of ship turbo generator reducer based on shock characteristics［J］. Applied Mechanics and Materials， 2010， 39： 157‑162.

［8］贺少华， 吴新跃. 舰载旋转机械基础冲击响应建模和数值计算［J］. 爆炸与冲击， 2011， 31（6）： 561‑566.

HE Shaohua， WU Xinyue. Shock response modeling and computation of shipboard rotating machinery subjected to base‑transferred shock force［J］. Explosion and Shock Waves， 2011， 31（6）： 561‑566.

［9］陈曦. 基础运动激励条件下转子系统动力学特性研究［D］. 西安： 西北工业大学，2019.

CHEN Xi. Dynamic characteristics of rotor‑bearing system subjected to base motions［D］. Xi’an： Northwestern Polytechnical University， 2019

［10］赵元松， 贺少华， 吴新跃. 舰船旋转机械基础冲击动力学理论与实验研究［J］. 船舶力学， 2014， 18（8）： 1005‑1012.

ZHAO Yuansong， HE Shaohua， WU Xinyue. Experimental verification for modeling of rotating machinery under base‑transferred shock excitations［J］. Journal of Ship Mechanics， 2014， 18（8）： 1005‑1012.

［11］彭刚， 李超， 曹冲， 等. 冲击激励转子系统动力学响应及安全性设计［J］. 推进技术， 2018， 39（5）： 1111‑1121.

PENG Gang， LI Chao， CAO Chong， et al. Dynamic response and safety design of rotor system with impact excitation［J］. Journal of Propulsion Technology， 2018， 39（5）： 1111‑1121.

［12］ZHU Changsheng. Effect of impact on the dynamics of a rotor supported on active magnetic bearings［C］∥Proceedings of IMAC‑21 Conference & Exposition on Structure Dynamics. Florida， USA， 2003.

［13］SU Y， GU Y P， KEOGH P S， et al. Nonlinear dynamic simulation and parametric analysis of a rotor-AMB‑TDB system experiencing strong base shock excitations［J］. Mechanism and Machine Theory， 2021， 155： 104071.

［14］祝长生，陈拥军．机动飞行时发动机转子系统动力学统一模型［J］．航空动力学报，2009，24（2）：371‑377．

ZHU Changsheng， CHEN Yongjun. General dynamic model of aeroengine’s rotor system during maneuvering flight［J］.Journal of Aerospace Power，2009，24（2）：371‑377．

［15］李翁衡，祝长生. 基于刚性转子模型辅助线性自抗扰的电磁轴承‑柔性转子系统过二阶弯曲临界转速振动控制［J］. 中国电机工程学报，2023， 43（6）： 2413‑2425.

LI Wengheng，ZHU Changsheng. Vibration control of an active magnetic bearing‑flexible rotor system passing the second bending critical speed based on linear active disturbance control assisted by rigid rotor model［J］. Proceedings of the CSEE，2023， 43（6）： 2413‑2425.

［16］SUZUKI Y. Acceleration feedforward control for active magnetic bearing systems excited by ground motion［J］. IEE Proceedings-Control Theory and Applications， 1998， 145（2）：113‑118.

Vibration characteristics and active control strategy of an active magnetic bearing‑flexible rotor system with elastic support under impact load

ZHANG Peng， ZHU Chang‑sheng， LI Weng‑heng

（College of Electrical Engineering， Zhejiang University， Hangzhou 310027，China）

Abstract： Impact load is a common load， but it is also very special. Compared with other persistent loads， impact load has the characteristics of short duration and large output energy， leading to the transient vibration which may affect the system’s operation safety. In this paper， the active magnetic bearing （AMB）‑flexible rotor was installed on an elastically supported base. The vibration characteristics of the elastic supported base under five types of impact loads， including double half‑sine wave， half‑sine wave， sine wave， triangle wave， and double triangle wave， were investigated. The influence of different impact load parameters on the acceleration of the base was obtained. In order to suppress the rotor vibrations， relative to the base induced by impact loads， a transient vibration compensation control strategy based on the base acceleration was derived. The theoretical and experimental results indicate that the elastic supported base and the AMBs‑flexible rotor system installed on it both exhibit obvious impact characteristics under impact loads. These impact characteristics vary with different types of impact loads. The effect of base shock excitations on the rotor vibration can be effectively suppressed by the proposed algorithm.

Key words： dynamics of rotor； active magnetic bearing；vibration suppression； base shock；feed‑forward compensation

作者简介： 张 鹏（1992―），男，博士研究生。 E‑mail： zhang_peng@zju.edu.cn。

通讯作者： 祝长生（1963―），男，博士，教授。 E‑mail： zhu_zhang@zju.edu.cn。