采用过滤白噪声模型的地震动时域降维表达

摘要： 随机地震动模拟一般有频域和时域两大类方法。本文基于单重过滤白噪声时域模型，建议了平稳地震动过程和全非平稳地震动过程模拟的时域表达。本质上，时域表达可视为一系列标准正交随机变量所调制的确定性函数的线性叠加，而正交随机变量集则可定义为随机正交函数形式来实现高效降维。为此，通过引入三类随机正交函数，即非高斯型的Legendre正交多项式、Hartley正交基和高斯型的Hartley正交基，均可实现仅用一个基本随机变量在时域模型上精细表达地震动加速度过程。平稳地震动过程的数值算例表明了本文方法的有效性，且优于Monte Carlo方法；全非平稳地震动的算例分析则表明了本文方法的工程适用性。

关键词： 地震动过程； 时域表达； 过滤白噪声； 降维模拟

中图分类号： P315.9； TU311.3 文献标志码： A 文章编号： 1004-4523（2024）09-1493-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.006

引 言

中国位于环太平洋地震带与欧亚地震带之间，是一个地震频发的国家。强烈地震会造成工程结构的破坏，危害人类生命安全，造成重大经济损失，因此，对工程结构进行合理的抗震分析具有重要意义［1］。目前，工程中常挑选若干实测强震记录对结构进行抗震分析，这虽然便于工程应用，但由于实测记录数量有限以及具体场地条件的限制，无法满足工程抗震精细化分析的需求。因此，地震动过程的人工合成方法逐渐受到工程界和学术界的广泛关注。一般而言，随机地震动的模拟方法可分为时域方法和频域方法两大类。频域方法主要适用于平稳过程的模拟，对于全非平稳地震动过程，往往需要引入时频调制函数，由于时频调制函数和平稳功率谱一般为慢变函数，因而难以很好地刻画地震动局部的时频全非平稳性，而且模拟时需要进行时频域转换，不可避免地引入误差［2］。时域方法的模拟直接在时域上进行，且通过强度调制函数和时变滤波器，可实现时频全非平稳，无需进行时频域的转换。为此，本文主要研究地震动模拟的时域方法。

地震动模拟的时域方法大致可分为调幅过滤白噪声模型，时变ARMA模型等。时变ARMA模型本质上是一类机器学习模型，李英民等［3］对这类模型进行了较为系统的研究。由于时变ARMA模型的参数较多，且模型需要进行判阶，因此本文仅研究调幅过滤白噪声模型，该模型的发展有着悠久的历史。Housner［4］率先提出采用随机过程理论来模拟地震动加速度过程的思想。Bycroft［5］正式提出了平稳白噪声地震动模型。然而，平稳白噪声模型无法体现真实地震动的非平稳性，因此Shinozuka等［6］、Amin等［7］、Iyengar等［8］分别建议了强度调制函数来构造非平稳地震动模型。Yeh等［9］基于平稳滤波器构造高斯过滤白噪声的地震动模型，并通过识别目标地震动的累积能量和向上穿零次数来确定其模型参数。随后，Beck等［10］、Rezaeian等［11］、Vetter等［12］提出和发展了基于调幅过滤白噪声的时域模型。该模型是一种半物理、半数据驱动模型，它以白噪声过程作为原始随机信号，经时变的滤波器过滤，最后通过调制函数来获得全非平稳地震动。基于调幅过滤白噪声的时域模型标志着地震动模拟的时域方法已趋于成熟，具有广泛的应用前景。

在随机地震动模拟的频域方法中，无论是地震动过程的源谱表达［13］，还是地震动随机场的离散表达［14‑15］（谱表示与POD）以及连续表达［16］（波数谱），均可看作是一系列正交随机变量与确定性函数之积的线性组合形式，这为引入随机正交函数的约束来实现正交随机变量集的高效降维提供了便利［17］。在本质上，随机地震动模拟的时域方法也可看作类似形式，即一系列标准正交随机变量所调制的确定性函数的线性叠加。因此，时域方法同样也可以引入随机正交函数来实现高效降维。而且，由于降维方法所生成的代表性样本具有赋得概率，且构成一个完备的概率集，可与第三代结构设计理论相结合［18‑20］，实现复杂工程结构的精细化动力响应分析与整体可靠度计算。

1 平稳地震动过程的单重过滤白噪声模型

在地震工程中，平稳单重过滤白噪声模型是指将地表土层视为单自由度的线性滤波器，而地震引起基岩运动的加速度过程假定为一个零均值的白噪声过程，其双边功率谱密度为。于是，地表土层的运动方程［21］为：

（1）

式中 分别为地震地面相对于基岩的加速度、速度和位移响应；分别为地表土层的卓越圆频率和阻尼比。

考虑到初始条件为零，根据Duhamel积分［21］，地震地面的相对位移响应为：

（2）

式中 “*”表示卷积符号；为相对位移的单位脉冲响应函数，即：

（3）

式中 。

根据卷积运算的微分性质，地震地面的相对速度响应为：

（4）

式中 为相对速度的脉冲响应函数，其表达式为：

（5）

于是，地震地面的绝对加速度可以表示为：

（6）

最后，将式（2）及式（4）代入到式（6）中，并利用式（3）和式（5），即可得到地震地面绝对加速度的单重过滤白噪声表达式：

（7）

式中 表示绝对加速度的脉冲响应函数，即：

（8）

在式（2），（4）及式（7）中，平稳白噪声过程应当满足如下条件：

（9）

式中 E［］表示数学期望；为Dirac函数。

式（7）即为单重过滤白噪声的时域模型，而对应的频域模型就是地震工程中著名的Kanai‑Tajimi谱［22］：

（10）

2 基于时域模型的平稳地震动过程模拟

为了便于模拟，对于平稳地震动加速度过程，需要将式（7）写成分段积分的形式：

（11）

式中 经过k个时间步长后的时刻，为时间离散步长；表示地震动模拟持时T的时间离散项数；表示模拟时间t的时间离散项数。

在微小时间段内，假定为一常数，且略去式（11）中的最后一项。于是，式（11）可以近似写成：

（12）

若令：

（13）

可以证明，（）是一组零均值的正交随机变量。事实上有：

（14）

（15）

式中 为Kronecker符号。

进一步，将随机变量进行标准化处理，即。于是，式（12）还可以简写成：

（16）

式中 为一组标准正交随机变量集，即满足如下的基本条件：

， （17）

3 基于时域模型的全非平稳地震动过程模拟

对于全非平稳地震动加速度过程，本文采用强度调制函数和时变的场地参数来描述时‑频全非平稳性。为此，根据式（7），全非平稳地震动加速度过程的时域模型为：

（18）

其中

（19）

在式（18）中，由于大括号内的部分是一个具有时变频率成分的标准化过程（单位方差过程）。因此，强度调制函数就完全控制了过程的时间非平稳性，而脉冲响应函数（滤波器）及其时变参数则控制了过程的频谱非平稳性。

一般地，强度调制函数可选用三段式模型［7］：

（20）

式中 参数，为地震动过程的标准差函数的最大值，变量c控制强度调制函数下降段的衰减速度。

对于脉冲响应函数的表达式（8），其参数采用如下的线性时变形式［23］：

（21）

式中 与分别为场地土卓越圆频率和阻尼比的均值；a，b为场地土参数随时间变化的速率。

同样地，为了便于模拟，首先将式（18）中大括号内的部分写成如式（11）所示的分段积分形式；然后，在微小时间段内，假定为一常数，且略去大括号内的最后一项，得到：

（22）

PIEMfolXGCQsqZhPkk5pd07v6ct3Zrn64KEN1kjh6bM=其中

（23）

最后，定义随机变量，并进行标准化处理，即可得到式（22）的简写形式：

（24）

其中

（25）

值得指出的是，几乎在以往所有的文献里，都直接将随机变量集当作是一组相互独立的标准高斯随机变量。这从Monte Carlo模拟的角度是十分方便的。但是，在本质上，随机变量集应当是一组标准正交随机变量，而且它们的概率分布也没有给定，这恰为正交随机变量集的降维提供了必要条件。此外，从式（16）及式（24）还可知，随机过程的时域表达与Karhunen‑Loève分解具有相同形式，他们都是将随机过程表达为一系列确定性函数与正交随机变量之积的线性组合形式。从这一意义来看，Karhunen‑Loève分解可以视为是随机过程时域表达的一种形式。

4 正交随机变量集的降维表达

为了实现地震动过程时域表达的降维模拟，根据随机正交函数的降维思想［13‑17］，可以方便地构造以下三类正交随机变量集的随机正交函数形式［17］。

对于Legendre正交多项式，构造标准正交随机变量集的随机正交函数表达式为：

（26）

式中 基本随机变量服从区间上的均匀分布；为Legendre正交多项式函数，其递推公式为：

（27）

对于三角函数形式（Hartley正交基），可构造标准正交随机变量集的随机正交函数为：

（28）

式中 基本随机变量服从区间上的均匀分布；常数通常取为。

上述两类随机正交函数形式所构造的（）一般都是非高斯型的标准正交随机变量。为了构造高斯型的标准正交随机变量集，根据式（28），并利用反变换法［17］，可得：

（29）

式中 为标准高斯分布函数的反函数；基本随机变量服从区间上的均匀分布；常数通常取为。式（29）是基于Hartley正交基的高斯标准正交随机变量集，简称为高斯型的Hartley正交基。

在式（26），（28）及式（29）中，i是j （）的重新排序，即i与存在着某种确定性的一一映射关系。这种一一映射关系通常可采用MATLAB工具箱中的rand（‘state’，0）和temp=randperm（N）函数来实现，即它们之间的一一映射关系为。这一映射关系恰为降维模拟方法的一个充分条件。

5 数值算例

5.1 平稳地震动过程的降维模拟分析

在应用式（16）和式（26），（28），（29）来模拟平稳地震动加速度过程时，需要首先确定时域模型的参数取值和基本随机变量的代表性点集。

对于地震动单重过滤白噪声模型，谱强度可按如下的公式计算［13，24］：

（30）

式中 为谱强度因子为1时的功率谱面积；为地震动峰值加速度的均值；为峰值因子。

在本算例中，以场地类别Ⅱ为例，地震动峰值加速度均值，峰值因子，场地土参数，；地震动模拟持时，时间步长。基本随机变量的离散代表点公式如表1所示，其中代表点的数量，422，626三种情况。

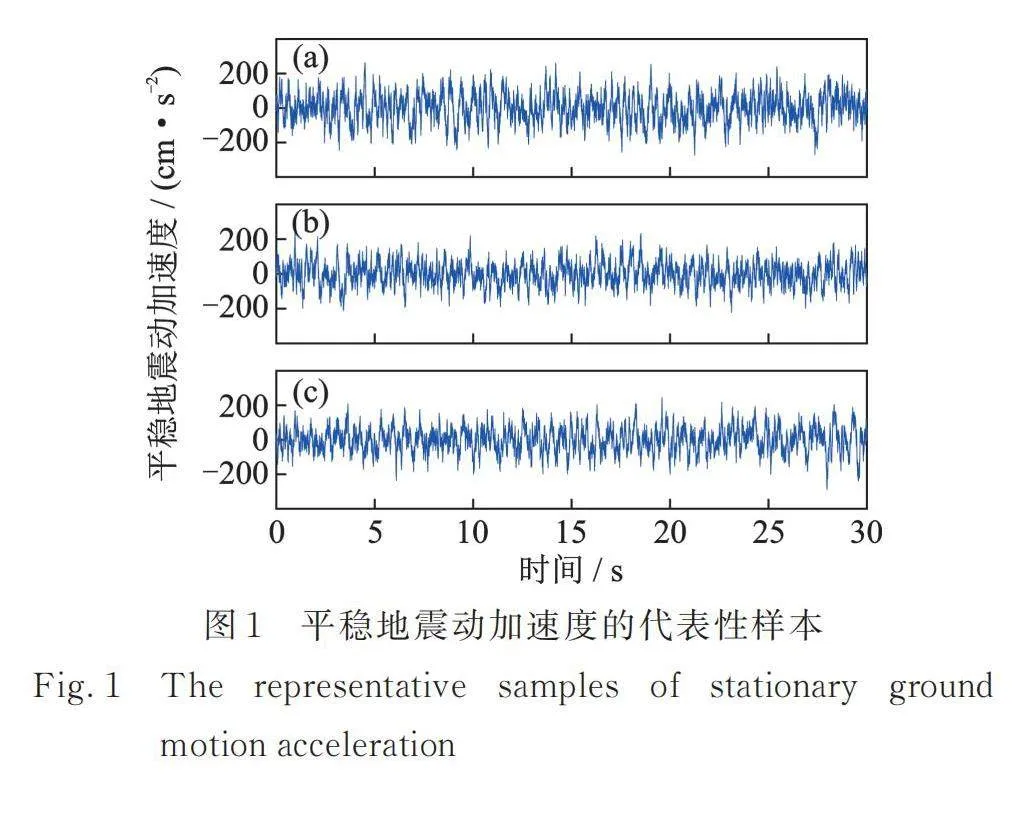
图1为三类随机正交函数降维方法生成的平稳地震动加速度代表性样本，图1中（a），（b），（c）分别采用了Legendre正交多项式、Hartley正交基以及高斯型的Hartley正交基。可见，代表性样本均具有良好的平稳特性。

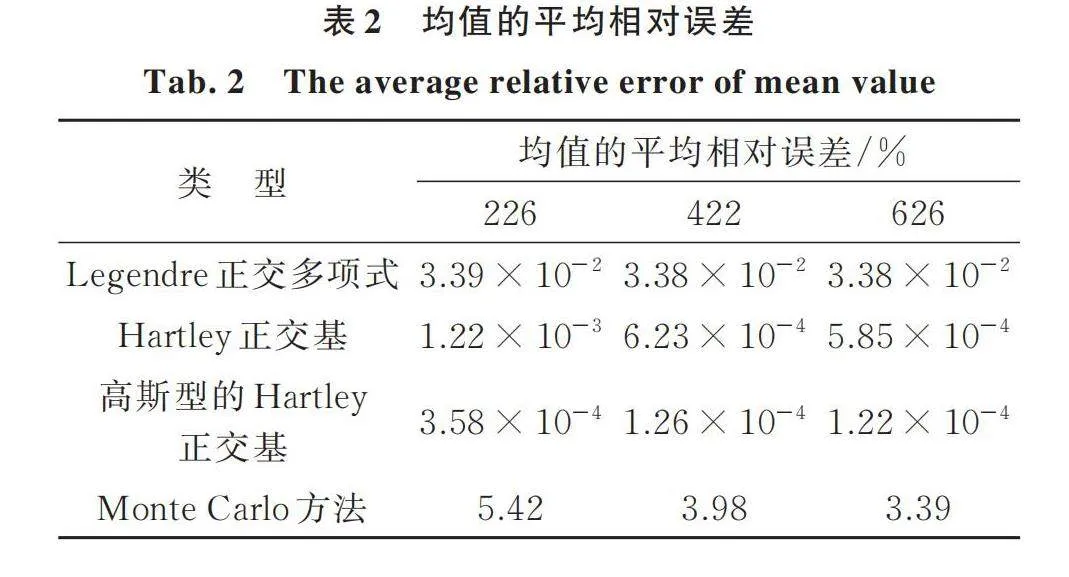
为了进一步说明降维方法的有效性，现将本文方法与Monte Carlo方法进行对比分析。图2为平稳地震动加速度过程的均值和标准差的模拟值与目标值比较，其中图2（a）采用了Hartley正交基（非高斯型）的降维方法，图2（b）采用了相互独立的标准高斯随机变量的Monte Carlo方法。直观地看，本文降维方法模拟平稳地震动加速度过程的均值明显优于Monte Carlo方法；对标准差而言，两种方法的差异性不大。表2和表3分别给出了均值和标准差的平均相对误差，由表可见，对于三类随机正交函数的降维方法，所生成平稳地震动加速度过程的代表性样本集合的误差均比较接近，说明降维方法具有普适性。同时，高斯型的Hartley正交基模拟精度最高，Hartley正交基次之，Legendre正交多项式相对较差。因此，若对模拟精度要求较高时，可选用高斯型的Hartley正交基。此外，对于每一类随机正交函数，随着代表性样本数量的增加，均值和标准差的平均相对误差都是逐渐减小的，这表明降维方法具有良好的鲁棒性。

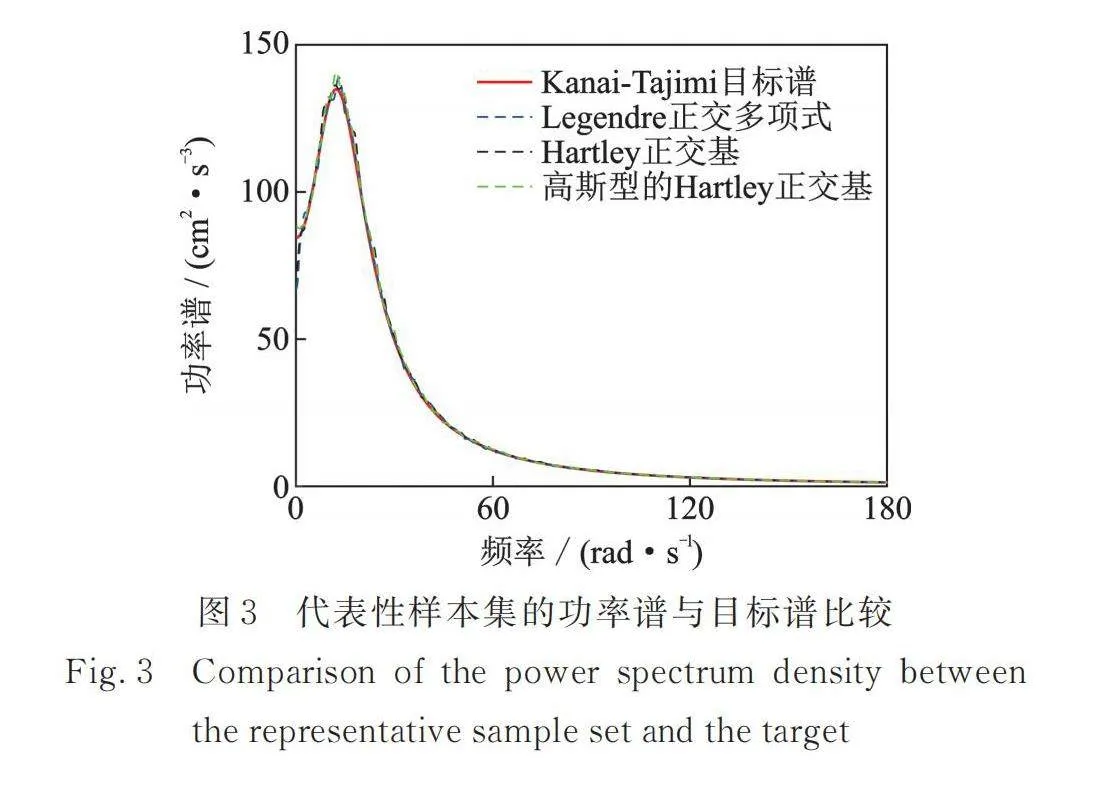
利用三类随机正交函数的降维方法，生成平稳地震动加速度过程的代表性样本集，图3为422条代表性样本集的单边功率谱与单边目标谱的比较。可见，代表性样本集的功率谱与目标谱拟合良好。

表4给出了代表性样本集的功率谱平均相对误差。在总体上，三类随机正交函数的降维方法要比Monte Carlo方法的平均相对误差略小。而且随着代表性样本数量的增加，功率谱平均相对误差逐渐减小。这进一步说明了随机正交函数降维方法的有效性和优越性。

5.2 全非平稳地震动过程的降维模拟分析

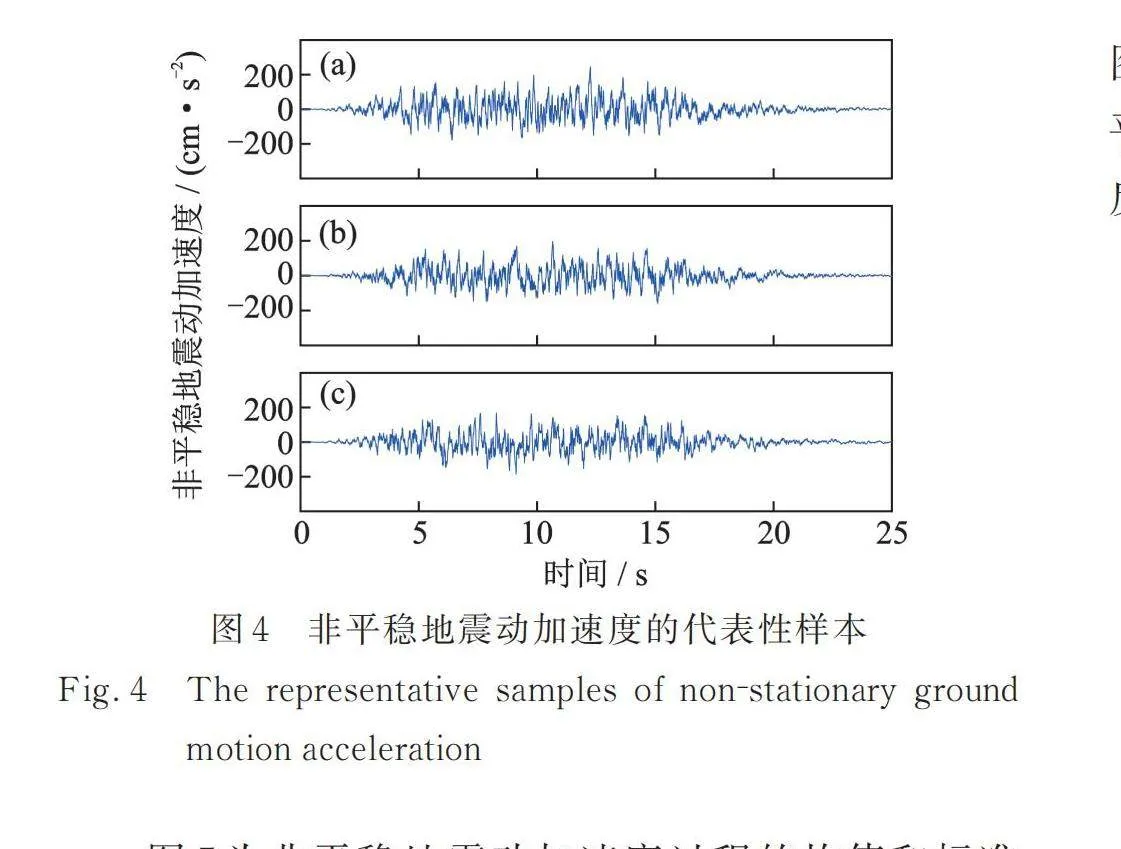
在全非平稳地震动过程的降维模拟中，以场地类别Ⅱ和设计地震分组第二组为例。其中，地震动峰值加速度均值，峰值因子；场地土参数，，，；地震动模拟持时，时间步长；强度调制函数参数，，，。基本随机变量的离散代表点公式如表1所示，其中代表点的数量。图4为三类随机正交函数降维方法所生成的全非平稳地震动加速度代表性样本，图4中（a），（b），（c）分别采用了Legendre正交多项式、Hartley正交基以及高斯型的Hartley正交基。显然，代表性样本均具有良好的强度和频率非平稳特性。

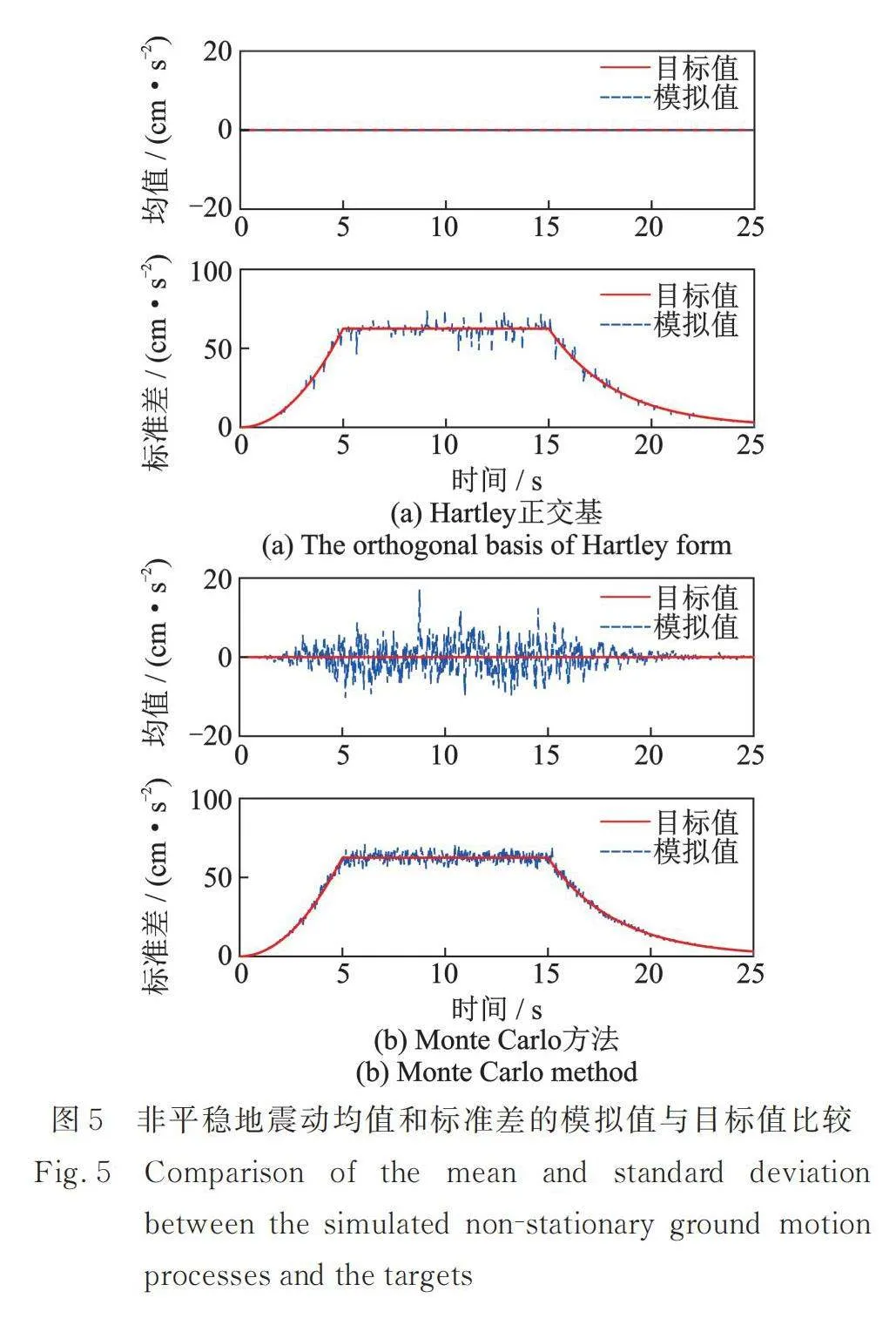
图5为非平稳地震动加速度过程的均值和标准差的模拟值与目标值比较，其中图5（a）采用了Hartley正交基（非高斯型）的降维方法，图5（b）采用了相互独立的标准高斯随机变量的Monte Carlo方法。可见，本文建议的降维方法模拟非平稳地震动加速度过程的均值和标准差都优于Monte Carlo方法。

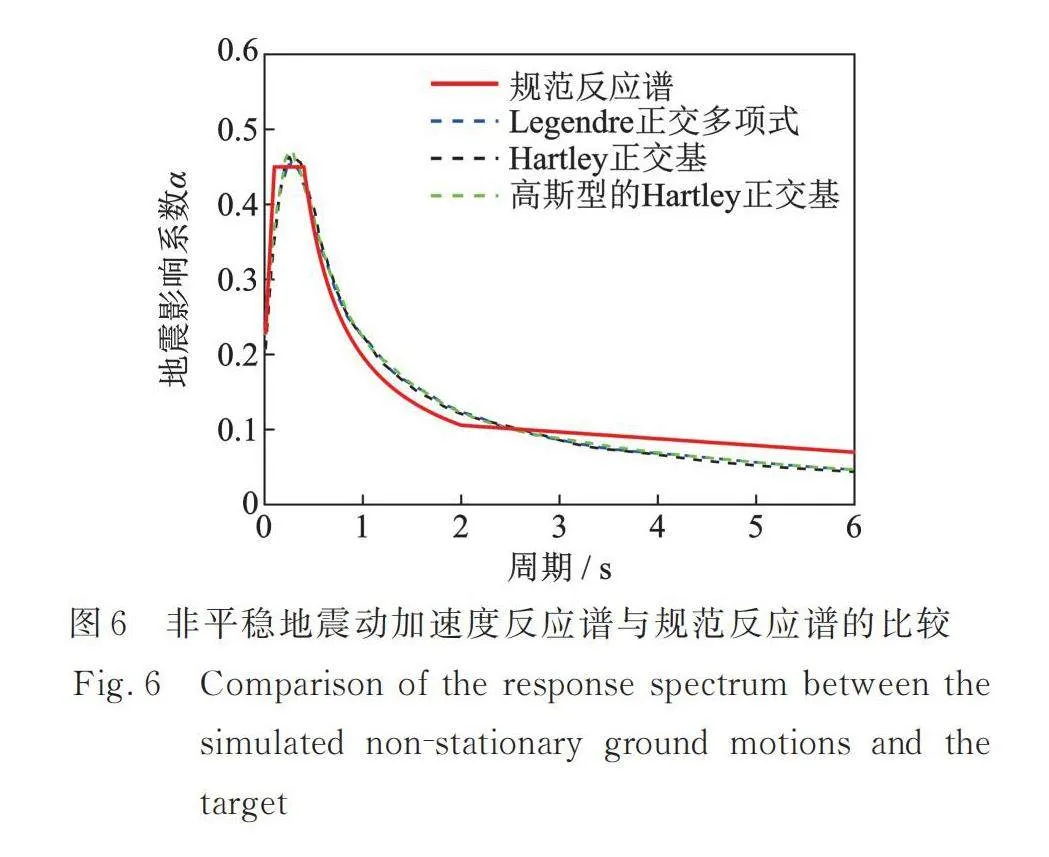
为进一步从地震反应谱来阐明本文降维方法的工程适用性，图6给出了三类随机正交函数降维方法所生成的非平稳地震动加速度反应谱与规范反应谱的比较，其中规范反应谱对应于《建筑抗震设计规范》［25］中场地类别Ⅱ和设计地震分组第二组。从图6可知，三类随机正交函数降维方法所生成的非平稳地震动加速度反应谱几乎重合，且它们与规范反应谱拟合良好。

6 结论与展望

基于时域的单重过滤白噪声模型，给出了平稳地震动加速度过程模拟的时域表达，进一步通过引入强度调制函数以及场地土的时变参数模型，建立了全非平稳地震动加速度过程模拟的时域表达。在此基础上，通过引入标准正交随机变量集的三类随机正交函数形式，实现了地震动加速度过程的降维模拟。其结论与展望如下：

（1） 在平稳地震动过程和非平稳地震动过程模拟的时域表达中，都是通过一系列标准正交随机变量来实现的。而传统的Monte Carlo方法则是利用一系列相互独立的标准高斯随机变量。然而，标准正交随机变量集可以通过基本随机变量的正交函数（即随机正交函数）来实现降维。事实上，随机过程模拟的时域表达与频域表达均可通过随机正交函数来实现其降维模拟。

（2） 对于平稳地震动加速度过程，其时域表达中包含了时间步长，因此需要足够小的时间步长才能获得理想的模拟效果。为此，可以像全非平稳地震动加速度过程模拟的时域表达，采用标准化过程来消除时间步长的影响，从而提高模拟效率。

（3） 随机正交函数降维方法的最大优点在于实现了仅用一个基本随机变量即可精细地表达地震动加速度过程，从而仅需数百条代表性样本就能在全概率上反映地震动过程的概率信息。这为结合概率密度演化理论进行复杂工程结构的精细化抗震分析提供了重要基础。

（4） 本文仅给出了单重过滤白噪声模型，事实上，还可以推导出二重过滤白噪声等模型。而且，对于非平稳地震动加速度过程的时域表达，也可以给出不同的强度调制函数和场地土的时变参数模型。这将在后续研究中进一步完善。

参考文献：

［1］杨庆山， 田玉基. 地震地面运动及其人工合成［M］. 北京： 科学出版社， 2014.

Yang Qingshan， Tian Yuji. Earthquake Ground Motions & Artificial Generation［M］. Beijing： Science Press， 2014.

［2］欧进萍， 王光远. 结构随机振动［M］. 北京： 高等教育出版社， 1998.

Ou Jinping， Wang Guangyuan. Random Vibration of Structure［M］. Beijing： Higher Education Press， 1998.

［3］李英民， 刘立平. 工程结构的设计地震动［M］. 北京： 科学出版社， 2011.

［4］Housner G W. Characteristics of strong-motion of earthquakes［J］. Bulletin of the Seismological Society of America， 1947， 37（1）： 19-31.

［5］Bycroft G N. White noise representation of earthquakes ［J］. Journal of the Engineering Mechanics Division， 1960， 86（2）： 1-16.

［6］Shinozuka M， Deodatis G. Stochastic process models for earthquake ground motion［J］. Probabilistic Engineering Mechanics， 1988， 3（3）： 114-123.

［7］Amin M， Ang A. Non-stationary stochastic model of earthquake motion［J］. Journal of the Engineering Mechanics Division， 1968， 94（2）： 559-584.

［8］Iyengar R N， Iyengar K T S R. A nonstationary random process model for earthquake accelerograms［J］. Bulletin of the Seismological Society of America， 1969， 59（3）： 1163-1188.

［9］Yeh C H， Wen Y K. Modeling of nonstationary ground motion and analysis of inelastic structural response［J］. Structural Safety， 1990， 8（1-4）： 281-298.

［10］Beck J L， Papadimitriou C. Moving resonance in nonlinear response to fully nonstationary stochastic ground motion［J］. Probabilistic Engineering Mechanics， 1993， 8（3-4）： 157-167.

［11］Rezaeian S， Der Kiureghian A. A stochastic ground motion model with separable temporal and spectral nonstationarities［J］. Earthquake Engineering and Structural Dynamics， 2008， 37（13）： 1565-1584.

［12］Vetter C R， Taflanidis A A， Mavroeidis G P. Tuning of stochastic ground motion models for compatibility with ground motion prediction equations［J］. Earthquake Engineering and Structural Dynamics， 2016， 45（6）： 893-912.

［13］Liu Z J， Liu W， Peng Y B. Random function based spectral representation of stationary and non-stationary stochastic processes［J］. Probabilistic Engineering Mechanics， 2016， 45： 115-126.

［14］Liu Z X， Liu Z J， Ruan X X， et al. Spectral representation-based dimension reduction for simulating multivariate non-stationary ground motions［J］. Soil Dynamics and Earthquake Engineering， 2018， 114： 313-325.

［15］刘章军， 刘子心， 阮鑫鑫， 等. 地震动随机场的POD降维表达［J］. 中国科学： 技术科学， 2019， 49（5）： 589-601.

Liu Zhangjun， Liu Zixin， Ruan Xinxin， et al. POD-based dimension reduction representation of stochastic ground motion fields［J］. Scientia Sinica （Technologica）， 2019， 49（5）： 589-601.

［16］Ruan X X， Liu Z J， Liu Z X， et al. Dimension-reduction representation of stochastic ground motion fields based on wavenumber-frequency spectrum for engineering purposes［J］. Soil Dynamics and Earthquake Engineering， 2021， 143： 106604.

［17］Liu Z J， Liu Z X， Peng Y B. Dimension reduction of Karhunen-Loeve expansion for simulation of stochastic processes［J］. Journal of Sound and Vibration， 2017， 408： 168-189.

［18］Li J， Chen J B. Stochastic Dynamics of Structures ［M］. Singapore： John Wiley & Sons， 2009.

［19］Li J， Chen J B. The principle of preservation of probability and the generalized density evolution equation［J］. Structural Safety， 2008， 30（1）： 65-77.

［20］李杰. 工程结构可靠性分析原理［M］. 北京： 科学出版社， 2021.

Li Jie. Fundamental of Structural Reliability Analysis ［M］. Beijing： Science Press， 2021.

［21］刘章军，陈建兵，彭勇波. 结构动力学［M］. 北京：中国建筑工业出版社， 2022.

［22］Kanai K. An empirical formula for the spectrum of strong earthquake motions［J］. Bulletin of Earthquake Research Institute， 1961， 39（1）： 85-95.

［23］刘章军， 刘子心. 基于规范反应谱的全非平稳地震动过程模拟［J］. 振动工程学报， 2017， 30（3）： 457-465.

Liu Zhangjun， Liu Zixin. Simulation of fully non-stationary ground motion based on seismic design response spectrum［J］. Journal of Vibration Engineering， 2017， 30（3）： 457-465.

［24］Seya H， Talbott M E， Hwang H H M. Probabilistic seismic analysis of a steel frame structure［J］. Probabilistic Engineering Mechanics， 1993， 8（2）： 127-136.

［25］中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局. 建筑抗震设计规范：GB 50011—2010 ［S］. 北京： 中国建筑工业出版社， 2010.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China， General Administration of Quality Supervision， Inspection and Quarantine of the People’s Republic of China. Code for seismic design of buildings： GB 50011—2010［S］. Beijing： China Architecture & Building Press， 2010.

Dimension-reduction representation of seismic ground motion using filtered white noise model in time domain

LIU Zhang-jun1， FAN Ying-fei1， Jiang Yun-mu1， Ruan Xin-xin1， Liu Zi-xin2

（1.School of Civil Engineering and Architecture， Wuhan Institute of Technology， Wuhan 430074， China；2.Key Laboratory of Building Collapse Mechanism and Disaster Prevention，Institute of Disaster Prevention，China Earthquake Administration， Sanhe 065201， China）

Abstract： There are two kinds of stochastic seismic ground motion simulation methods： frequency-domain methods and time-domain methods. Based on the time-domain model of single filtered white noise， this paper proposes the time-domain representation for simulating stationary and non-stationary seismic ground motion processes. In essence， the time-domain representation can be regarded as linear superposition of deterministic functions modulated by a series of standard orthogonal random variables， and the set of orthogonal random variables is defined as the form of random orthogonal functions to achieve efficient dimension-reduction. Therefore， by introducing three kinds of random orthogonal functions， i.e.， Legendre orthogonal polynomial of non-Gaussian type， Hartley orthogonal basis and Hartley orthogonal elementary of Gaussian type， the acceleration process of seismic ground motion can be accurately represented in the time-domain model with only one elementary random variable. Numerical examples of seismic stationary ground motion process show the effectiveness of the proposed method， which is superior to the Monte Carlo method. The analysis of fully nonstationary seismic ground motion shows the engineering applicability of the proposed method.

Key words： ground motion process；time domain representation；filtered white noise model；dimension-reduction simulation

作者简介： 刘章军（1973―），男，博士，教授，博士生导师。E-mail： liuzhangjun73@aliyun.com。

通讯作者： 刘子心（1988—），女，博士，副教授，硕士生导师。E-mail： liuzixin@cidp.edu.cn。