非线性随机响应单侧尾部分布的代理模型算法

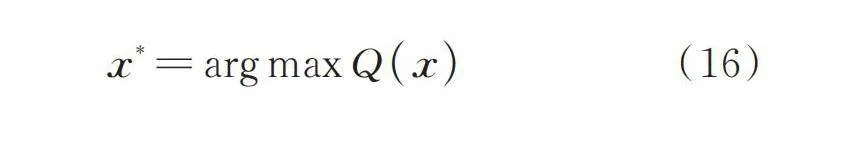
摘要： 对于大型复杂结构的非线性随机响应，随机模拟法是较为实用的工程分析方法。然而对于需要大量样本的尾部概率估计，高昂的计算成本限制了该类方法的应用。为了降低计算成本，开发了基于主动学习的高斯过程代理模型算法，但其主动学习优化策略仍需进一步完善，以满足工程中对单侧尾部概率分布估计精度的需求。为此提出了一种具有智能关注功能的搜索函数，构建了针对工程中事故风险极高的单侧尾部的算法。以地铁隧道环梁和衬砌间复杂粘结滑移行为为例，验证了该算法的有效性。相比原有算法，本文算法对单侧尾部概率的估计误差降低了30%。本文算法能更精确地估计复杂结构随机响应分布的单侧尾部概率，进而估计极端事故的发生概率，为风险测度和防灾管理决策提供量化分析依据。

关键词： 随机振动； 非线性响应； 高斯过程代理模型； 主动学习； 尾部概率

中图分类号： O324； O322 文献标志码： A 文章编号： 1004-4523（2024）09-1485-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.005

引 言

过去数十年里，为适应复杂结构的工程可靠性设计，结构随机响应［1‑2］研究得到了长足发展，产生了随机有限元［3］、随机摄动［4］、概率密度演化［5］和随机模拟［6］等分析方法。但大部分方法在实际应用中仍面临两个挑战，一是很难深度嵌入商业用软件，二是对极小概率事件估计的计算成本过高。

为了解决第一个问题，基于代理模型的随机模拟法被提出来［7］。代理模型是对原始复杂模型的近似，它能够在保持合理精度的同时，大幅降低计算成本，更加便捷地实现直接随机模拟分析，从而为工程不确定性量化估计提供更具效率的解决方案。

高斯过程模型［8］是目前常用的代理模型，作为一种非参数模型，可以灵活拟合复杂的非线性关系，更重要的是，它能够量化估计响应预测的不确定性，并得到预测结果的置信区间，这对于提升评估预测结果的有效性具有显著作用。另外，近些年快速发展的神经网络模型也成为代理模型的有效备选方案［9］。结合高斯过程的不确定性量化特性和深度学习的高表达性的深度高斯过程［10］是目前最前沿的方向之一。

KAYMAZ［11］首次将高斯过程模型作为代理模型引入结构随机响应分析领域，但需要通过进一步的自适应实验设计策略对该模型进行优化。BICHON等［12］和SCHÖBI等［13］提出主动学习策略，通过专门设计新增实验样本以优化模型。ECHARD等［14］通过几个算例验证了该主动学习策略对处理高非线性、不可微、非凸等问题的有效性。但文献［14］采用的算法的优化目标仅限于估计指定阈值的失效概率，而工程中往往更关注高风险区间的分布函数，因此该方法只能逐一迭代地更改阈值，利用离散的计算结果来表征随机响应，分析效率尚不能满足实际工程分析需求。

基于主动学习的高斯过程算法（Active Learning‑Based Gaussian Process， AL‑GP）能同时估计累积和互补累积分布函数［15］。相较于传统的针对特定阈值的方法，该算法采用以某个区间为优化目标的策略，能够更清楚地描述概率分布。

一些罕见但危害重大的事故通常呈现为小概率的分布函数的“尾部”事件［16］，现有的AL‑GP方法提供了估计尾部概率的解决方案，但在实际工程应用中，对尾部概率估计的精度仍然不足，尤其是在计算复杂非线性结构响应的尾部概率时，其计算效率需要进一步提高。

为了使AL‑GP更精确、高效地估计尾部小概率，本文提出一个对尾部区间更具智能关注能力的搜索函数，并建立相应算法，显著降低非线性结构响应的单侧尾部估计误差。另外，为了验证本算法在实际工程结构上的计算效率，实现算法程序与商业有限元软件的交互结合，开发出一个随机响应分析平台，以便快速求解结构响应的单侧尾部概率。本文以来自实际工程的案例——地铁隧道环梁和衬砌间的粘结滑移行为分析，验证了算法的有效性。

1 针对单侧尾部的AL‑GP算法

结构随机响应分析中，给定输入的联合随机参数x，需要关注输出的结构响应Y的随机性。从x到Y的确定性映射关系G（·）为：

（1）

虽然式（1）形式简洁，但G（·）在复杂结构中代表着一个计算成本极高的数值模型。这使得基于式（1），难以通过直接随机模拟法估计Y的随机性。直接随机模拟法，即蒙特卡罗模拟法（Monte Carlo Simulation， MCS）适用性极强，可以应用于非侵入式有限元计算，但由于它需要对每个随机参数样本执行一次完整的数值模拟计算，因此应用在规模庞大的复杂结构中会非常耗时。故本文提出了尾部敏感的学习算法，不仅拟合出了替代G（·）的快速代理模型M（·），还对单侧尾部的计算实现了优化。

（2）

式中 F（·）为分布函数；y为结构响应Y的变量形式；n为随机参数样本总量；为指示函数，其中时=1，否则= 0。

1.1 针对单侧尾部的AL‑GP算法的流程

如图1所示，本节介绍的算法是对AL‑GP算法的针对性改进，使其更适用于具有单侧尾部风险的分布。为了满足关注单侧尾部的要求，开发了一个搜索函数，分析步骤如下：

（1）使用拉丁超立方抽样法，针对变量——混凝土强度、钢材（螺栓）屈服强度、极限强度、弹性模量生成初始训练集Xs，再用G（·）计算出对应的精确输出变量Y，本文中为螺栓滑移量。

（2）使用训练集｛Xs ， Y｝训练高斯过程代理模型，核函数选用高斯核函数。

（3）生成一个大样本量的备选集Xc，计算对应的三重估计。

（4）计算损失函数，如果停止准则被满足，则结束算法，否则进入步骤（5）。

（5）利用本文提出的搜索函数，找到误差最大的。

（6）在Xc中搜索，找到使学习函数最大的样本x*，并计算出其对应的真实值y*。

（7）将｛x*，y*｝增加进｛Xs ， Y｝。

（8）返回到步骤（2）。

1.2 样本初始化

初始训练集Xs可由分层抽样法得到，如拉丁超立方［17］抽样法。本文的初始训练集样本个数设置为20个。虽然这个数量可以是任意值，但考虑到唯一确定包含n个变量的二次多项式需要至少［（n+1）⋅（n+2）/2］个样本（样本数量需要大于系数数量，变量n的二次多项式具有［（n+1）（n+2）/2］个系数），本算例中变量个数为4，那么样本个数最好大于16。保守起见，初始训练集样本个数取为20。

备选集Xc可根据变量的概率密度函数用直接抽样法得到， 样本规模为106。此样本规模确保了当尾部概率大于10-3时，变异系数始终小于5%。

1.3 的三重估计

在利用训练集Xs完成高斯过程代理模型的超参数取值后，下一步要预测备选集Xc的响应量。高斯过程预测的具体原理［18］不在此赘述，主要介绍如何对初步训练后的高斯过程模型进一步优化。最终不仅要得到确定性的预测值，还需要得到预测结果的置信区间，以便衡量代理模型的不确定性，为后期优化提供依据。基于高斯过程中对所有输出变量具有多元联合高斯分布的假定，任意一个输出值都符合高斯分布。故只需要在中心预测的基础上加减一定的标准差得到上、下限值，被称为三重预测：

（3）

式中 ；为新增训练样本的预测均值；为新增训练样本的预测标准差；k值代表置信水平。对，的三重预测模型分别为，，。比如，意味着用 作为备选集Xc对应的Y。

综上，根据式（2）和（3）， 结构响应Y的累积分布函数（Cumulative Distribution Function， CDF）同样具有三重预测：

（4）

式中 。备选集Xc 需要保持一致以确保。

1.4 误差函数

虽然三重预测提供了置信范围，但还需要一个综合指标（即误差函数）评估模型的不确定性。当置信范围较小时，预测的确定性程度较高；而当置信范围较大时，预测的不确定性较高，可能无法满足工程分析需求，就需要修改代理模型。为了衡量模型的不确定性以便做出是否修改模型的决策，需要将这个置信范围积分，具体表示为：

（5）

式中

（6）

为了避免式（6）中的分母为0，将积分范围由原始范围变换为（）。这个新的积分范围就是工程分析需要关注的概率分布区间。式（6）的分母形式有助于关注双侧尾部。

阈值ε可设置为：

（7）

式中 为一个特定值，表示式（6）应该平均地小于，一般设为0.1。

1.5 学习函数

在完成上述定量评估后，如果误差没能低于阈值，就需要优化代理模型。对高斯过程模型来说，增加训练样本数量是最直接的优化方式，然而，如何增加训练样本决定了优化的效率，定义学习函数为：

（8）

式中 为误分类概率；Φ［·］为标准高斯分布的CDF；y'为结构响应Y的关键值；为新增训练样本的中心预测值。式（8）意味着新增的样本既要接近y'，又要预测标准差高，才能使误分类概率最高。通常情况下，使误分类概率最高的样本是最值得学习的样本。因此，如何发现最优的y' 就成为一个关键问题，为此本文提出了一个新颖的搜索函数来寻找y'。

2 带激活函数的搜索函数

提出一个带激活函数的搜索函数是本文对原有AL‑GP方法最主要的改进。在原始的AL‑GP算法中，有一个关注单侧尾部的方案，即将式（6）分母改为或。可以观察到这个关注单侧尾部的方案并不是原方法精心设计的，因为原方法的本意是对偶地关注双侧尾部。受到函数形式的限制，它对单侧尾部的重视能力是有限的，这可能导致它无法满足实际工程对单侧尾部估计精度的要求。在实际工程中，极端灾难事件往往只发生在结构响应量分布的单侧尾部，但造成的损失又是巨大的，其风险不可忽略，需要更精准的估计。

因此，有必要通过改进，赋予搜索函数一种智能的关注功能，加大对极端事件的关注程度，以提高对风险极大的单侧尾部的估计精度。在式（5）中对误差函数定义的基础上，常规做法是定义搜索函数为找到使误差函数W*（·）最大的y'。但如上所述，还要考虑极端事件的风险，故不妨从风险视角出发，对误差函数加权，形成新的搜索函数，具体表示为：

（9）

式中 表示一个以 y' 为中心，且参数为ω的高斯核函数，用于实现误差的局部化而不仅仅只考虑点误差；α（y'） 表示激活函数；的形式见式（6）。

由于风险函数往往是单调非线性的，神经网络中的激活函数正好具有这种性质，因此选取了三种激活函数作为可能的选项，分别是Sigmoid，tanh和ReLU。本文提供的函数形式是递增的，意味着关注程度随响应量值的增加而增加，即搜索函数更关注分布的右尾。另外，简单地用代替即可实现关注对象的对称翻转，以便关注分布的左尾。下面介绍最终的搜索函数。

激活函数，式（9）展开为：

（10）

式中 ；的定义域为［-3， 3］。

激活函数，式（9）展开为：

（11）

式中 ；的定义域为［0， 1.85］。

激活函数，式（9）展开为：

（12）

式中 ；的定义域为［0，0.95］。

三种函数的值域上限都约为0.95，以方便等效对比。

该搜索函数将模型不确定性和风险相结合，定义了一个评价结构响应Y关键程度的指标。使这个指标最大的就是式（8）的学习函数定义中的关键值：

（13）

其中高斯核区域被［ylower， yupper］截断，归一化常数Z设置为：

（14）

σ（y'）在下式中求解，这是AL‑GP的简化方法。基本原理是在Xc中找到y'的最近点，用最近点的σ值代替σ的精确值。

（15）

通过搜索函数，找到了结构响应Y的关键值，为随后学习函数的使用扫清了障碍。有了，问题重新回到最初，即寻找使学习函数最大的新增训练样本：

（16）

3 算例分析

盾构隧道是城市地铁首选的施工方法，具有许多优点。然而，在软土地区，地铁运营过程中可能会出现不均匀沉降，这会影响盾构隧道的长期性能。考虑到中国有些大型城市位于软土地区［19］，不均匀沉降的潜在风险值得关注。

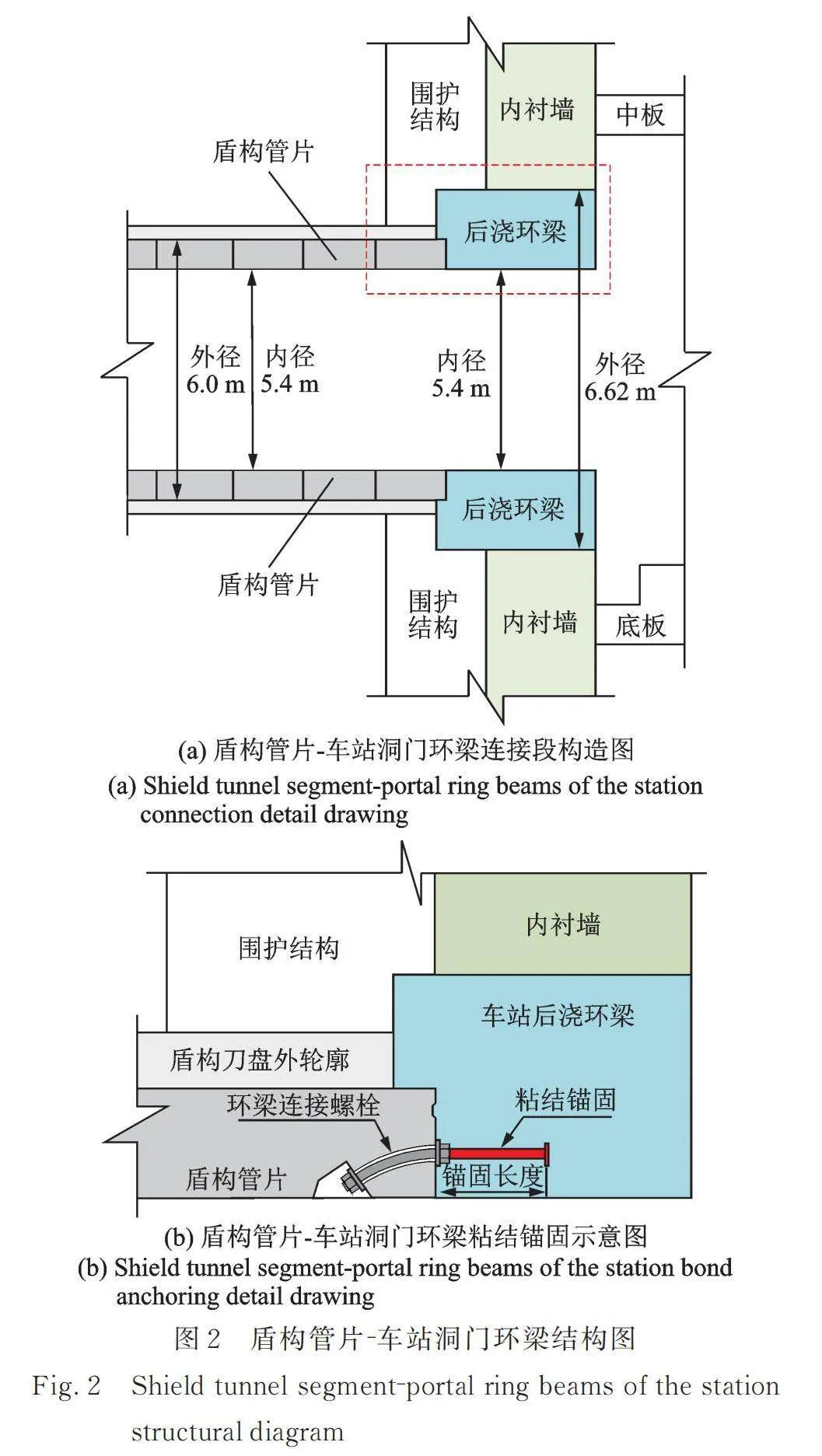
如图2所示，在盾构管片和车站后浇环梁的连接段，由于两者在结构形式和荷载方面存在显著差异，纵向不均匀沉降更容易发生。在这种情况下，如果埋入环梁的螺栓锚固长度不足，可能导致螺栓与混凝土发生较大的相对滑移，进而导致纵向环缝张开［20］，引发渗漏问题，甚至可能导致盾构管片与车站后浇环梁受拉破坏。这不仅会影响地下结构的防水性和耐久性，还有可能威胁整个地下空间的安全。

如果按照可靠性规范严格设计，这种事故发生的概率很小，但一旦发生，可能造成巨大损失。因此，这属于典型的小概率大损失事件。可使用本文提及的方法量化估计这种灾害风险。

以某地铁车站为例，盾构管片与车站后浇环梁连接段构造如图2所示，后浇环梁采用C35混凝土；盾构管片采用C50混凝土。管片与后浇环梁纵向通过10根M27螺栓连接，螺栓机械强度为8.8级，长0.5 m，细部构造如图2所示。连接段螺栓左端通过手孔与管片连接，与混凝土没有接触；右端预埋入后浇环梁，埋入长度为0.25 m。

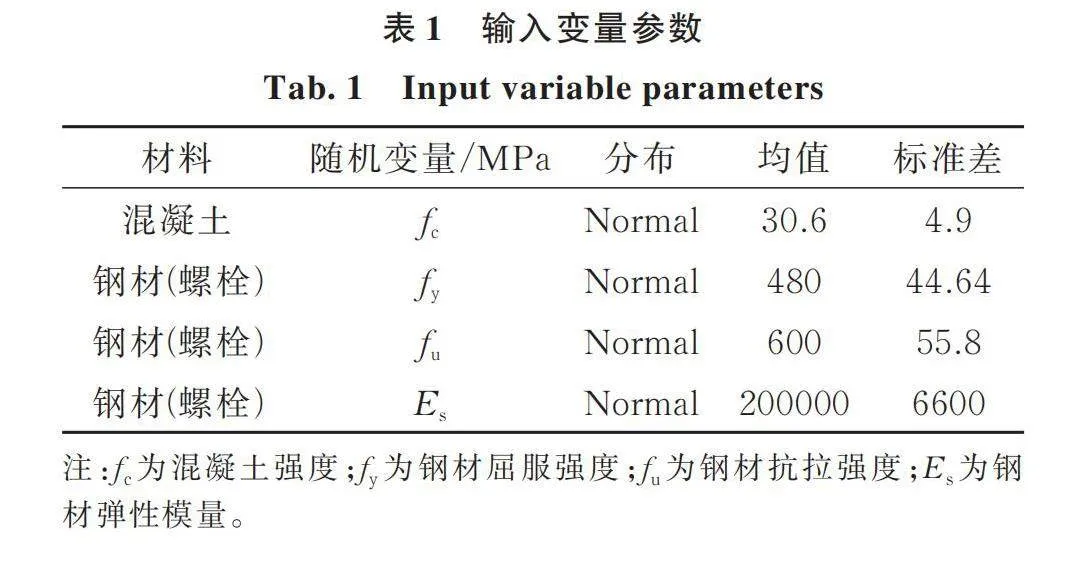
3.1 结构参数随机性

结构随机源及其分布统计量［21‑22］如表1所示：

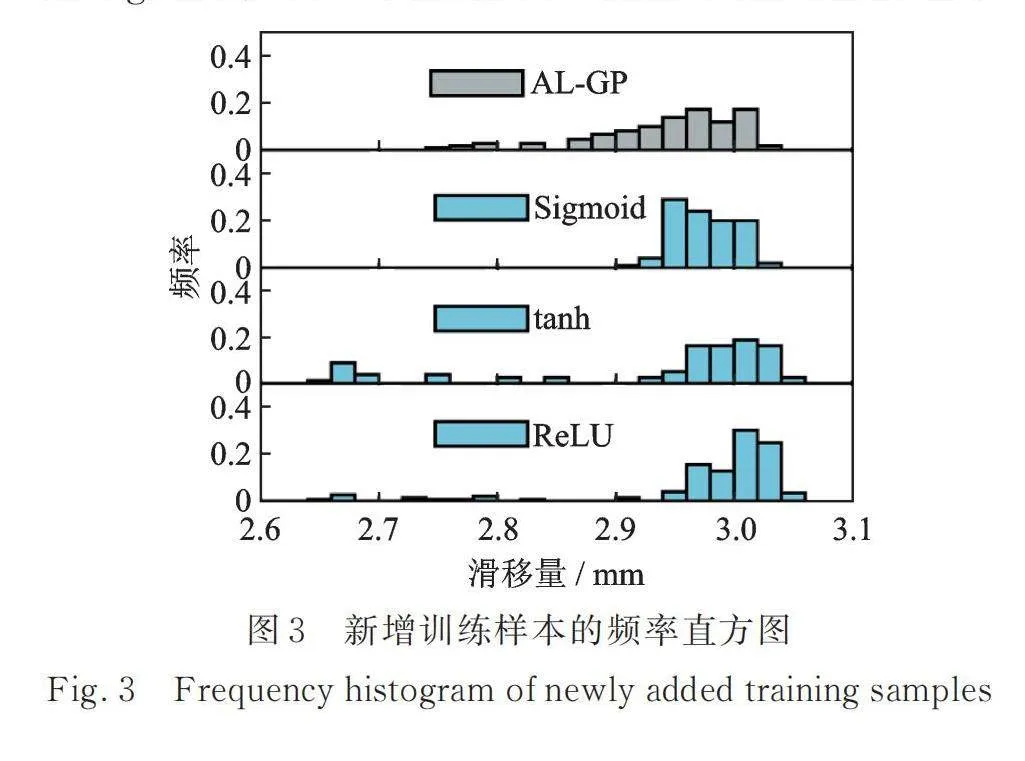
3.2 新增训练样本的分布

过大的滑移量是钢筋混凝土结构粘结锚固破坏的重要表征。因此需要重点关注滑移量分布函数的右尾。为了对比AL‑GP和本文算法，之后讨论的AL‑GP算法是式（6）分母改为的关注单侧右尾的形式。从图3反映的计算结果可以看到，与既有的AL‑GP算法相比，本文提出的针对单侧尾部的算法能够更有效地将新增训练样本集中在单侧尾部区域。这为代理模型在结构响应的尾部具备更出色的预测能力打下基础。另外，显然不同的激活函数导致不同的样本点分布，这与激活函数的形式有关。在高斯过程预测中，预测值是训练样本输出值的线性组合，特定概率区间内投入的训练样本越多，预测不确定性就会越低。而由图3可以看出，相比Sigmoid，ReLU函数将更多的样本投入在极端小分位点区域，因此ReLU函数更适合事故分位点极端小的结构响应，而Sigmoid函数则适合分位点较大的结构响应。

3.3 单次算法运行中的误差迭代

误差是评价模型不确定性的指标，在向右尾新增更多训练样本后，误差的迭代变化反映了模型精度的变化。由于只关注右尾的模型精度，因此将误差积分范围［ylower，yupper］设为。由于没有对误差积分范围细化，三种激活函数的表现近似，这里仅对比AL‑GP 和采用Sigmoid激活函数的本文算法的表现，结果如图4所示。尽管高斯过程模型由于超参数选取导致其具有固有的随机性，误差下降并非完全连续，但仍能观察到误差下降呈现先急后缓，逐渐收敛的趋势。而值得注意的是，本文算法随着迭代次数的增加，误差下降速度更快，并且收敛到一个更低的水平。该结果源于高斯过程预测可以看作线性平滑器［18］，预测值是训练样本输出值的线性组合。由图3可以看出，在相同迭代次数下，采用本文算法投入的训练样本，输出值更多地分布在单侧尾部，因此该区域的预测误差会更快下降。而由于高斯过程是一种概率模型，它对于任意给定的输入，会输出一个概率分布而不是一个确定的数值。随着样本数量的增加，模型的不确定性可能会减小，但不会完全消失。因此本文算法只能有限度地提高精度。

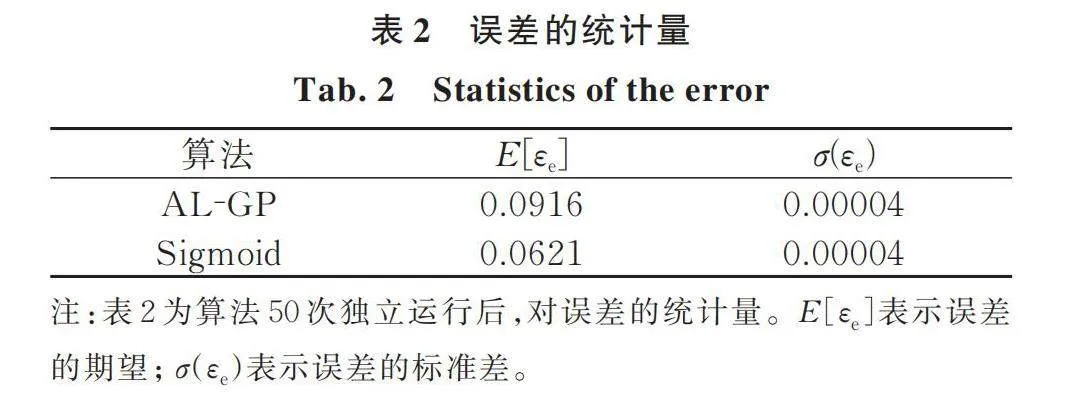
3.4 算法大量运行后误差的统计量

为了避免计算仅仅运行一次可能存在的偶然性，本节需要观察多次运行后计算误差的统计量，结果如表2所示。本文算法在误差期望上相较于既有算法降低了30%，这意味着代理模型在右尾上能达到更高的收敛精度。而且，极低的标准差意味着结果的稳定性好。总体来看，相较于既有算法，采用Sigmoid激活函数的本文算法在滑移量的右尾部分能够实现更为精确的预测，并且结果表现稳定。

3.5 互补累积分布函数的迭代

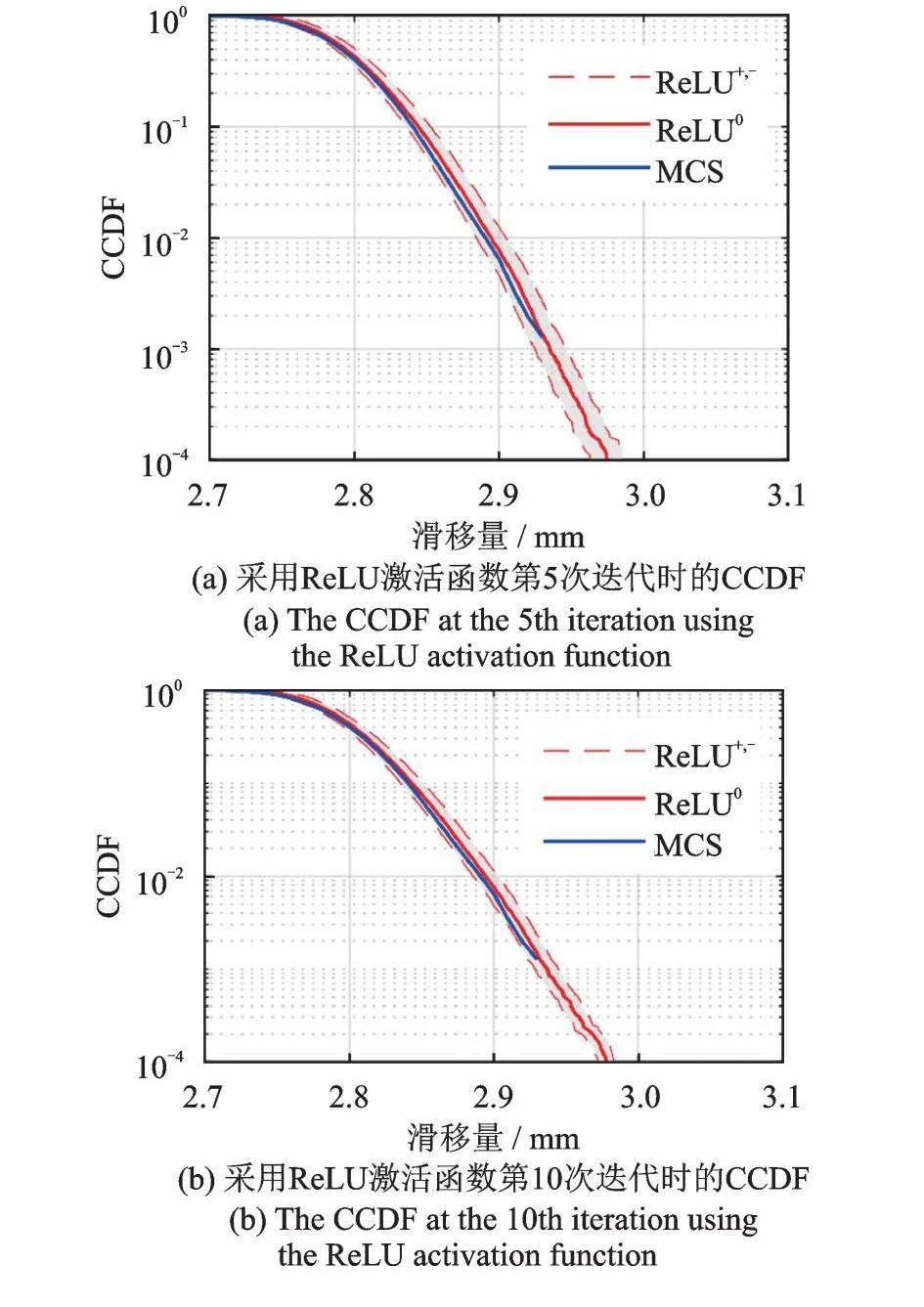
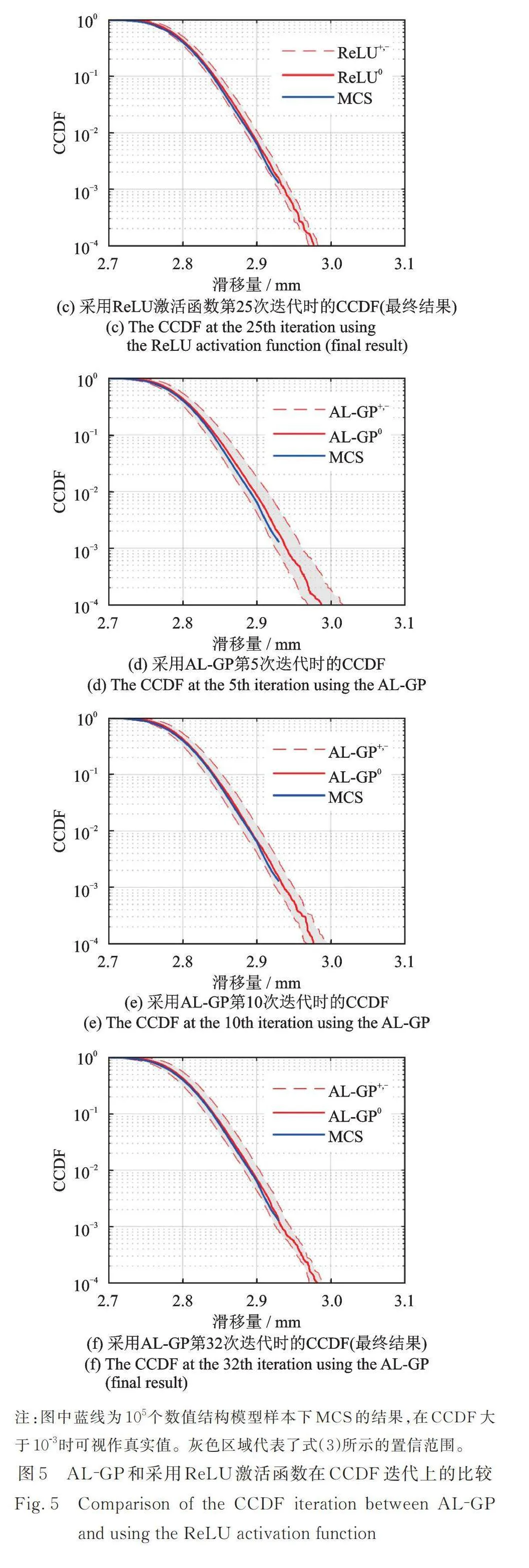
虽然上述结果表明代理模型的误差足够小，但仍然存在一个疑问，即代理模型是否足够接近于复杂结构数值模型。因此需要验证基于代理模型预测的结构响应量的分布函数是否与复杂数值模型一致。相较于概率密度函数，本文选择了互补累积分布函数［23］（Complementary Cumulative Distribution Function，CCDF），因为它更能反映结构响应量的右尾部分。将AL‑GP算法和本文算法中CCDF函数的迭代情况进行了比较，结果如图5所示。

正如3.3和3.4节所述，相较于AL‑GP算法，本文提出的算法训练的代理模型具有更低的不确定性，这在CCDF图中表现为灰色区域更为紧凑。同时，红色实线与蓝线高度重合，说明代理模型与真实复杂结构模型得到的随机响应极为接近，充分验证了代理模型的正确性。这进一步证明了本算法在处理复杂非线性结构模型时的有效性。

4 结 论

本研究旨在改善结构随机响应分析的预测精度和计算效率，提高对结构响应单侧尾部的关注。提出了一种基于主动学习的高斯过程算法。设计了针对单侧尾部的AL‑GP算法的流程，包括学习函数和搜索函数，以便更有效地寻找新增训练样本，实现主动学习的模型优化。得到的主要结论如下：

（1）由于导入本文提出的搜索函数，本文算法在新增训练样本的选择和分布上能够更好地关注单侧尾部，更好地拟合复杂结构模型的尾部概率分布。误差迭代结果显示本文算法在误差下降速度和最终收敛水平上表现得更加出色，误差降低了30%。多次运行的误差统计量分析也验证了本文算法的优势。

（2）在验证代理模型的准确性方面，比较了本文算法与复杂结构数值模型的CCDF函数，结果表明本文提出的代理模型预测的结构响应量的分布函数与真实模型非常接近。

本文提出的算法能够更有效地拟合结构非线性随机响应的尾部概率分布，有利于更准确地评估结构响应的风险。

参考文献：

［1］李英民，杨成，赖明.结构非线性地震反应分析的改进能力‑需求曲线方法［J］.世界地震工程，2003，19（4）：28‑33.

LI Yingmin， YANG Cheng， LAI Ming. Improved capacity‑demand‑diagram methods for analysis of structural nonlinear seismic responses［J］. World Earthquake Engineering，2003，19（4）：28‑33.

［2］杨成，陈云羿，廖伟龙，等.基于弹塑性限位装置的基础隔震建筑地震碰撞行为［J］.建筑结构学，2021，42（10）：67‑75.

YANG Cheng， CHEN Yunyi， LIAO Weilong， et al. Collision behaviors of base‑isolation structures with elastoplastic horizontal displacement stopper［J］. Journal of Building Structures， 2021，42（10）：67‑75.

［3］陈喆，何欢，陈国平，等.考虑不确定性因素的有限元模型修正方法研究［J］.振动工程学报，2017，30（6）：921‑928.

CHEN Zhe， HE Huan， CHEN Guoping， et al. The research of finite element model updating method considering the uncertainty［J］. Journal of Vibration Engineering， 2017，30（6）：921‑928.

［4］任勇生，张玉环，时玉艳.考虑不可伸长和材料内阻的旋转复合材料轴的非线性自由振动分析［J］.振动工程学报，2018，31（3）：468‑482.

REN Yongsheng， ZHANG Yuhuan， SHI Yuyan. Nonlinear free vibration analysis of an in‑extensional rotating composite shaft with material internal damping［J］. Journal of Vibration Engineering， 2018， 31（3）： 468‑482.

［5］李杰，陈建兵. 随机结构动力可靠度分析的概率密度演化方法［J］. 振动工程学报，2004，17（2）：121‑125.

LI Jie， CHEN Jianbing. Probability density evolution method for reliability analysis of stochastic structural［J］. Journal of Vibration Engineering， 2004， 17（2）： 121‑125.

［6］苏成，黄欢，徐瑞，等.大规模非线性系统随机振动显式迭代Monte Carlo模拟法［J］.振动工程学报，2014，27（2）：159‑165.

SU Cheng， HUANG Huan， XU Rui， et al. Random vibration analysis of large‑scale nonlinear systems by explicit iteration Monte Carlo simulation method［J］. Journal of Vibration Engineering， 2014， 27（2）： 159‑165.

［7］张军红，韩景龙.含区间不确定性参数的机翼气动弹性优化［J］.振动工程学报，2011，24（5）：461‑467.

ZHANG Junhong， HAN Jinglong. Aeroelasticity optimization of wing including interval uncertainty parameters［J］. Journal of Vibration Engineering， 2011， 24（5）： 461‑467.

［8］高海洋，郭杏林，韩放，等.连续体结构裂纹识别的Kriging代理模型求解策略［J］.振动工程学报，2013，26（6）：879‑885.

GAO Haiyang， GUO Xinglin， HAN Fang， et al. Strategy of crack identification for continuum structure based on Kriging surrogate model［J］. Journal of Vibration Engineering， 2013， 26（6）： 879‑885.

［9］EASON J， CREMASCHI S. Adaptive sequential sampling for surrogate model generation with artificial neural networks［J］. Computers & Chemical Engineering， 2014， 68： 220‑232.

［10］PANG G F， YANG L， KARNIADAKIS G E. Neural-net‑induced Gaussian process regression for function approximation and PDE solution［J］. Journal of Computational Physics， 2019， 384： 270‑288.

［11］KAYMAZ I. Application of kriging method to structural reliability problems［J］. Structural Safety， 2005， 27（2）： 133‑151.

［12］BICHON B J， ELDRED M S， SWILER L P， et al. Efficient global reliability analysis for nonlinear implicit performance functions［J］. AIAA Journal， 2008， 46（10）： 2459‑2468.

［13］SCHÖBI R， SUDRET B， MARELLI S. Rare event estimation using polynomial‑chaos kriging［J］. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems， Part A： Civil Engineering， 2017， 3（2）：D4016002.

［14］ECHARD B， GAYTON N， LEMAIRE M. AK-MCS： an active learning reliability method combining Kriging and Monte Carlo Simulation［J］. Structural Safety， 2011， 33（2）：145‑154.

［15］WANG Z Q， BROCCARDO M. A novel active learning-based Gaussian process metamodelling strategy for estimating the full probability distribution in forward UQ analysis［J］. Structural Safety， 2020， 84： 101937.

［16］BRAZAUSKAS V， KLEEFELD A. Modeling severity and measuring tail risk of norwegian fire claims［J］. North American Actuarial Journal，2016， 20（1）：1‑16.

［17］孙国华，顾强，方有珍，等.半刚接钢框架内填暗竖缝RC墙结构基于性态的地震易损性分析［J］.振动工程学报，2016，29（3）：410‑419.

SUN Guohua， GU Qiang， FANG Youzhen， et al. Performance‑based seismic fragility analysis of partially-restrained steel frame with concealed vertical slit RC infill walls［J］. Journal of Vibration Engineering， 2016， 29（3）： 410‑419.

［18］RASMUSSEN C E， WILLIAMS C K I. Gaussian Processes for Machine Learning［M］. Cambridge： The MIT Press， 2005.

［19］汪小兵，王如路，刘建航.上海软土地层中运营地铁隧道不均匀沉降的治理方法［J］.上海交通大学学报，2012，46（1）：26‑31.

WANG Xiaobing， WANG Rulu， LIU Jianhang. Disposal method of unequal settlement of metro tunnel in operation in Shanghai soft ground［J］. Journal of Shanghai Jiao Tong University， 2012， 46（1）： 26‑31.

［20］郑永来，韩文星，童琪华，等.软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究［J］.岩石力学与工程学报，2005，24（24）：4552‑4558.

ZHENG Yonglai， HAN Wenxing， TONG Qihua， et al. Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil［J］. Chinese Journal of Rock Mechanics and Engineering， 2005， 24（24）： 4552‑4558.

［21］NOWAK A S， RAKOCZY A M， SZELIGA E K. Revised statistical resistance models for R/C structural components［C］∥Andy Scanlon Symposium on Serviceability and Safety of Concrete Structures： from Research to Practice. American Concrete Institute， 2011.

［22］MIRZA S A， SKRABEK B W. Reliability of short composite beam‐column strength interaction［J］. Journal of Structural Engineering， 1991， 117（8）： 2320‑2339.

［23］SÂRBU A， BECHET A， BĂLAN T， et al. Using CCDF statistics for characterizing the radiated power dynamics in the near field of a mobile phone operating in 3G+ and 4G+communication standards［J］. Measurement， 2019， 134： 874‑887.

A surrogate algorithm for the one‑sided tail of structural random nonlinear response

YIN Wei‑hao1， YANG Hai‑ting1， HUANG Yan‑wen1， YANG Cheng2， LÜ Da‑gang3

（1.School of Civil Engineering， Southwest Jiaotong University， Chengdu 610031， China； 2.National Engineering Research Center of Geological Disaster Prevention Technology in Land Transportation， Southwest Jiaotong University， Chengdu 610031， China； 3.School of Civil Engineering，Harbin Institute of Technology，Harbin 150001，China）

Abstract： In the realm of stochastic nonlinear response analysis for large and intricate structures， the Monte Carlo simulation method stands out as a pivotal approach. However， its widespread practicality is hampered by its exorbitant computational cosJHR0wxztfnXsLPNmehNr4A==ts. To surmount this challenge， researchers have endeavored to develop the active learning‑based Gaussian process surrogate model algorithm. Despite its promise in reducing computational expenses， the optimization strategy associated with active learning necessitates further refinement to meet the exacting demands of engineering applications. For this purpose， we introduce a search function endowed with ‘intelligent’ attention capabilities. This function is meticulously crafted to concentrate on exceedingly high‑risk one‑sided tail events in engineering scenarios. By incorporating this search function， we have engineered an algorithm that surpasses existing methodologies. Our algorithm finds successful application in the analysis of complex adhesive anchoring structures within subway tunnel rings and linings. Compared to conventional methodologies， our algorithm exhibits a remarkable 30% reduction in the estimation error of single‑tailed probabilities. This advancement facilitates a more precise estimation of the one‑tailed probability distribution governing the stochastic response of complex structures. Consequently， it enhances the precision of assessing the occurrence probability of extreme events. These findings yield invaluable insights for decision‑making processes in pertinent engineering domains and insurance sectors.

Key words： random vibration； nonlinear response；Gaussian process surrogate model；active learning；tail probability

作者简介： 尹炜浩（1999―），男，硕士研究生。E‑mail： 1134343712@qq.com。

通讯作者： 杨 成（1977―），男，博士，副教授。E‑mail： yangcheng@swjtu.edu.cn。