人体分布式动力学模型及其参数识别

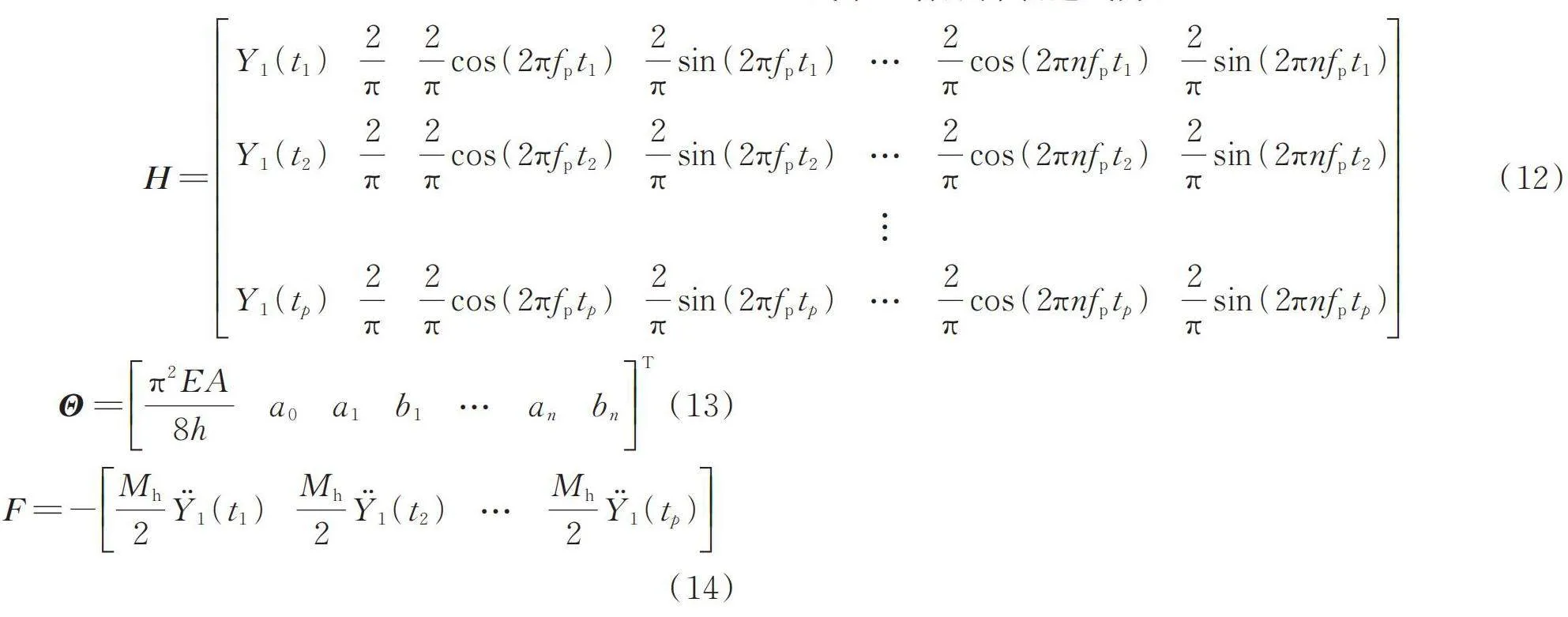
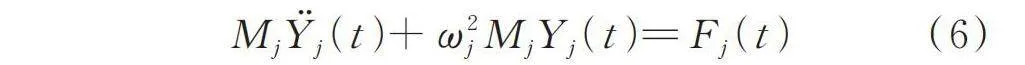
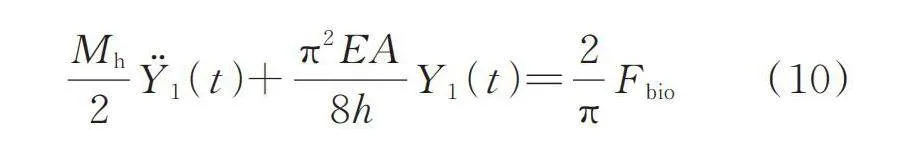
摘要： 建立人体动力学模型获取人体自振频率是土木工程、机械工程、交通工程、航空航天、康复医学等许多领域的共性科学问题，以往研究最常采用的弹簧⁃质量块⁃阻尼器集中质量模型，与实际人体质量、刚度沿身高的分布式特性并不相符。本研究提出含有生物自驱力的人体分布参数动力模型，理论上推导了自振频率的表达式，并据此提出了基于步态测试技术的频率识别算法。组织了247名测试者进行步态试验，识别了每位测试者的人体刚度和自振频率，进一步研究了识别参数的概率分布特征，并通过与以往研究结果对比、不同年龄段统计分析等，多角度验证了所提模型的合理性和适用性。

关键词： 人体动力学模型； 参数识别； 分布参数模型； 弹簧⁃质量块⁃阻尼器模型

中图分类号： R318.01； TB18 文献标志码： A 文章编号： 1004-4523（2024）09-1468-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.003

引 言

建立人体动力学模型并研究人体刚度、自振频率等特性是生物力学［1］、车辆工程［2］、航空航天［3］以及土木工程［4］等领域的共性科学问题，用于研究车辆、飞行器对乘客的影响、人体运动（如步行、跳跃、跑步等）对结构物的影响以及评价人体自身健康状态等。

目前各领域中最常见的是集中参数模型，即“弹簧⁃质量块⁃阻尼器”（Spring Mass Damper， SMD）人体动力学模型，根据质量块数量再分为单自由度和多自由度模型。

在人致结构振动研究领域，早期研究者基于人体拥有质量、耗能特性和弹性特质的现实，将人体模拟成SMD系统，相关研究呈现出先“静”（静止的人）后“动”（运动的人）、先“单”（单自由度）后“多”（多自由度）的趋势。Foschi等［5］最早使用单自由度SMD模型对静止人体进行建模，成功解释了人对结构动力特性改变的原因。Folz等［6］延续前者的研究内容，将SMD模型扩展为2自由度和11自由度系统，研究不同人体模型对耦合作用的影响。文献［7⁃8］尝试使用SMD模型来模拟运动的人，以研究不同运动姿势下人体与结构的耦合作用。

集中质量模型的分析和计算相对便捷，但其分析精度受质量数（自由度数目）的影响，数目越多，精度也就越高。然而，对人体这样具有分布性质的体系而言，原则上要取无限多个自由度数目才能收敛于精确解。此外，采用集中质量模型，需要人为假定集中质量点的数量、位置以及各质点质量的分配比例，集中质量的物理意义也较不明确，因此实际应用中大多采用最简单的单质点模型。与一般动力学系统建模类似，除去集中质量模型还可以建立动力系统的分布参数动力学模型，可更合理地反映人体的物理特性。Kitazaki等［9］将人体脊柱作为刚性元件的层状结构，把椎间盘作为可变形元件，采用有限元法进行分析，这一方法虽有别于传统的集中质量模型，且具备一定程度的分布参数方法的思想，但仍不是真正意义上的分布参数模型。据作者目前所知，尚未有关于人体分布参数动力系统建模的公开研究。

为此，本文提出人体分布参数动力模型，基于理论解建立模型参数的识别算法，结合人体步态试验的时程结果识别获取不同测试者的人体刚度和自振频率，并针对两者的概率分布进行拟合和分析。此外，横向对比了本研究结果与以往研究结果，纵向对比了不同年龄段的人体参数，论证了所提模型的合理性和适用性。

1 人体动力学模型

1.1 集中质量模型

与静止人体模型不同，运动人体的动力学模型应同时考虑人的生物特性和主动作用。Zhang等［10］提出了含有生物自驱力的SMD模型并用该模型模拟行人的机械性能，如图1所示。该模型采用成对的生物自驱力模拟行走过程中人体肌肉的主动作用，考虑生物能的供给，作为行人竖向振动的激励，以此建立行人与结构耦合振动的系统。该研究通过设计人行桥的人致振动试验，识别了行人SMD的模型参数，以验证SMD模型模拟行人的适用性。该SMD模型的运动方程为：

（1）

式中 Mh，Ch和Kh分别表示行人的质量、阻尼和刚度；u为行人质心在生物自驱力下的位移响应；Fbio为生物自驱力。一般情况下，行人正常行走是一个周期/近周期运动，假定行人按照固定步频行走，此时可使用傅里叶级数来表示生物自驱力，如下所示：

（2）

式中 a0，ai和bi为傅里叶级数系数，也是各阶生物力系数；n为傅里叶级数模型的阶数；fp为行人行走的步频。

上述含有内部成对生物自驱力的人体SMD模型有着较高的实用性和便捷性，为其他学者所使用。Wang等［11⁃12］基于该模型，采用粒子滤波分步系统识别方法，识别了人体行走、屈伸律动（bounce）运动状态下的机械性能参数。

1.2 分布质量模型

集中质量模型因简单、实用，成为研究人体动力学时最常使用的模型，但其分析精度受所采用的质点数的影响，需要增加质点数以提升精度。对于人体这样具有典型分布性质的体系而言，需要取较多自由度数目才能得到满意的精度。然而，集中质量模型需要人为假定集中质点的数量、位置和质量分配比例，模型的物理意义也不明确。在不同学科领域中，集中质量的取值根据研究目的和应用的不同也有所不同，缺乏合理的选取原则。

考虑到分布参数动力学模型可更合理地反映人体的物理特性，本研究延续含生物自驱力SMD模型的思路，提出含生物自驱力的分布质量人体模型，如图2所示。

仅考虑轴向振动，可忽略阻尼对轴向行为的影响［13］，则轴向运动偏微分方程为：

（3）

式中 为人体分布质量，定义为人体质量Mh与身高h之比，即；EA为人体分布等效轴向刚度；为轴向生物分布力，定义为生物自驱力Fbio与人体身高h之比，即；x和t为位置和时间参数。

利用经典动力学理论的振型叠加法，人体轴向位移响应可表示为：

（4）

式中 us为人体轴向位移响应；j表示振型阶数；Yj（t）为第j阶振型的正则坐标；ϕj（x）表示第j阶轴向振动振型：

（5）

从而可得式（3）所对应的正则坐标运动方程：

（6）

式中 Mj为广义质量；ωj为第j阶轴向振动圆频率；Fj为广义荷载，表达式分别为：

（7）

（8）

（9）

考虑到步行荷载的窄带特征、人体步行时趋向省力舒适（低频）的自适应性，以及本研究只关注人体基频，为了提高识别算法的效率，本模型仅考虑对运动响应贡献最大的第一阶振型，即j=1，代入式（7）～（9），进一步再代入式（6），得到该模型的运动方程为：

（10）

基于此，人体在每个步行时刻ti（i=1，2，…，p）的运动方程可用矩阵形式表示：

（11）

式中 各矩阵表达式为：

（12）

（13）

（14）

一阶正则坐标Y1可由试验所测的人体轴向位移响应us计算得到，具体计算公式为：

（15）

Θ中的元素是待识别的人体机械性能参数，H和F中的参数均可由步态试验测量得到，其中假定人体刚度参数EA在行走过程中是时不变的，采用最小二乘法，可得到人体刚度和各阶生物力系数。具体计算公式为：

（16）

2 步态试验

为了验证上述分布参数模型的合理性和适用性，本研究设计了步态试验，利用三维光学运动捕捉技术（3D Motion Capture）获取行人正常行走时的位移响应，进而根据以上推导的算法，识别获得人体机械性能参数。

2.1 试验方案

试验在上海市某医院生物力学实验室开展，实验室内设有一工作区域，四面设有16台Vicon T40s红外线高速摄像机，中部地面内嵌4块AMTI OR6⁃7三维测力台及一块FOOTSCAN三维足底压力板，实验室环境如图3所示，图中铺设地毯的区域为测试者的主要试验活动范围。

试验采用Vicon三维光学捕捉运动系统，其基本原理是利用高速红外摄像头（采样频率为100 Hz）和固定在人体关键点上的反光标记物（称为“Marker”，空间定位精度为0.1 mm）来捕捉步行过程中人体关节及关键部位的三维运动轨迹。图4展示了本研究中某一位测试者的某次步行试验，采用了39 Marker点布置方式，具体布置详见文献［14］。

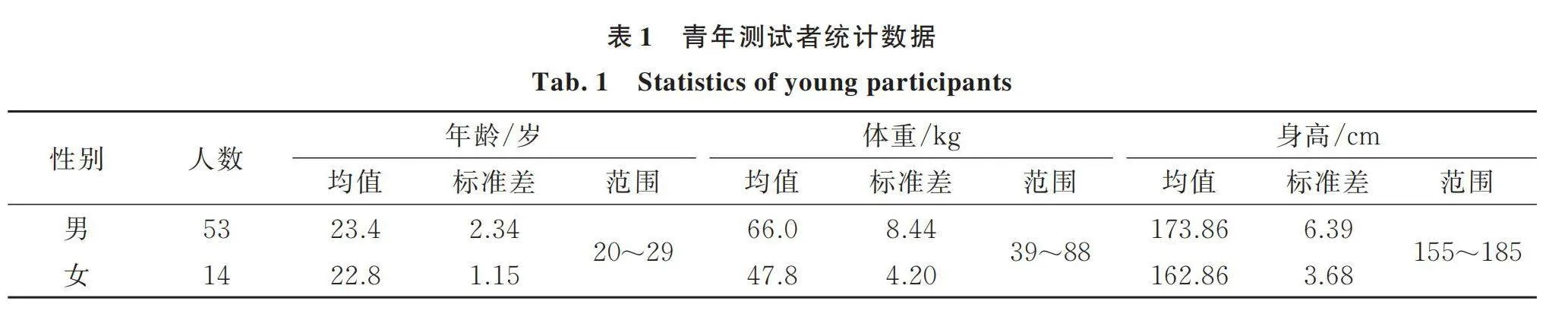
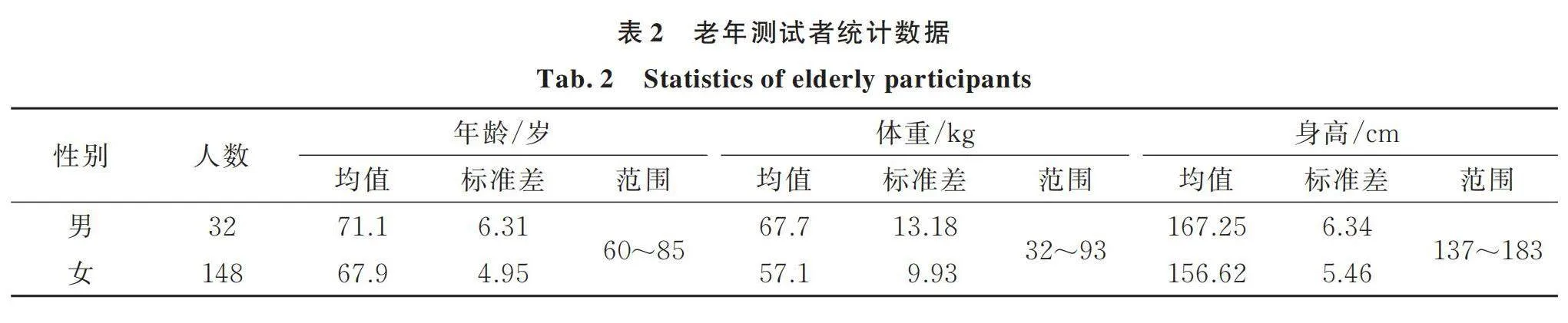
本次试验共募得247位测试者，包括85名男性及162名女性，年龄段覆盖20～29岁（青年）和60～85岁（老年），其统计特征如表1和2所示。试验获得了该医院伦理委员会的批准。

此外，在Scientific Data上收集了50名外国人的步态试验公开数据（详情：25名男性与25名女性，年龄范围：6～72岁，体重范围：18.2～110 kg，身高范围：116.6～187.5 cm）［15］。

本研究中每位测试者步态试验的基本步骤为：

（1） 熟悉并确认试验须知、要求和潜在风险；

（2）登记姓名、性别和年龄等基本信息，并测量其身高和体重；

（3）穿上指定服装，由实验室人员在测试者身上的关键点贴上Marker；

（4）熟悉实验室环境及实验要求，预演步行直至步态自然舒适并符合要求；

（5）记录其站立静态时各Marker的三维位置；

（6）选择其认为最舒适自然的步频和步速行走，完成10次正式步行试验。

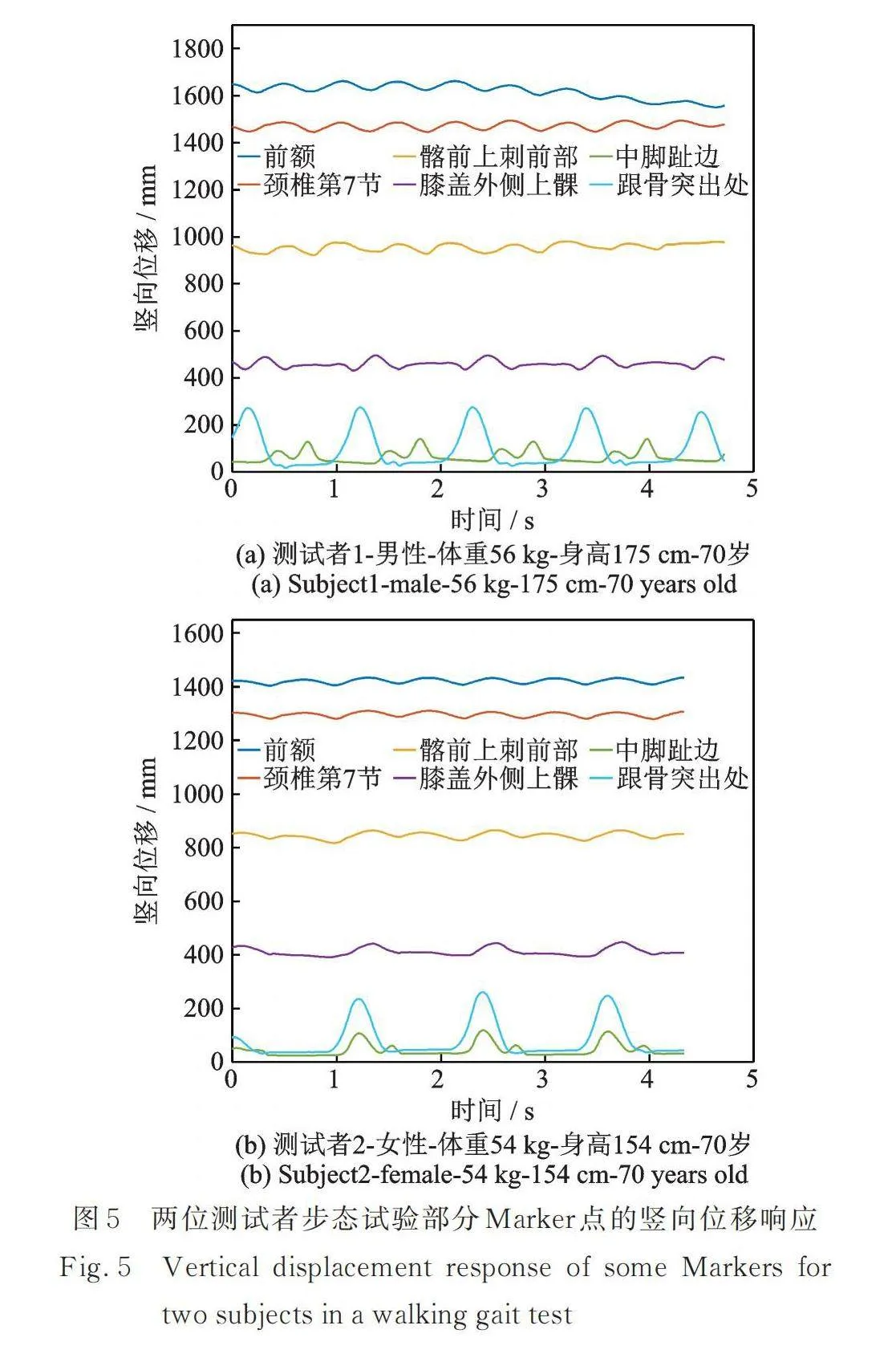
2.2 典型试验结果

图5展示了两位同龄测试者：（a）测试者1⁃男性⁃体重56 kg⁃身高175 cm⁃70岁；（b）测试者2⁃女性⁃体重54 kg⁃身高154 cm⁃70岁，完成一次行走时部分Marker点的竖向空间轨迹。其中，已有研究［16］表明C7点（颈椎第7节突出部位）位于人体中轴线上，脂肪覆盖少，测量结果清晰稳定，并且因其棘突明显，易于定位，能较好地减小Marker粘贴位置的偏差，推荐C7点作为特征点代表人体重心运动，因此该点轨迹将用于后续人体动力参数的识别。

3 参数识别

3.1 参数识别步骤

利用本文1.2节所阐述的分布参数模型的理论推导和识别算法，对于测试者的每一次行走，按如下步骤识别行人的刚度和自振频率：

（1）导入测试者质量Mh和身高h，记录其站立静止时C7点的竖向位置信息，记为hC7；

（2）提取行走过程中C7点的竖向响应u0（t），并进行去趋势项处理，处理后的时程记为u（t）；

（3）对u（t）进行谱分析获得测试者在该次行走中的步频，记为fp；

（4）根据式（15）计算一阶正则坐标Y1（t），并通过微分运算得到；

（5）根据式（12）～（14）建立分布式模型的运动识别矩阵，其中生物自驱力取前3阶；

（6）根据式（16）解出最小二乘意义下的人体动力参数矩阵Θ，得到该测试者的刚度、各阶生物自驱力系数，人体自振频率的计算公式为：

（17）

3.2 识别实例

根据以上识别步骤，以2.2节展示的男性测试者（体重56 kg⁃身高175 cm⁃70岁）的一次行走数据为例，展示其动力参数识别的过程和结果。

该测试者的体重Mh为56 kg，身高h为175 cm，其站立静止时C7⁃Marker点的竖向位置hC7为149.91 cm。提取出行走时C7点的竖向振动信息u0（t），并对其做去趋势项处理得到u（t），再利用式（15）计算得Y1（t），三者时程图如图6所示，计算得到的时程如图7所示。对u（t）进行频域分析，获得该测试者在该次行走中的步频fp为1.822 Hz。

将以上结果代入式（12）～（14）中建立对应的运动矩阵，由式（16）解得本例中人体等效轴向刚度EA/h为2570.4 N/m，进一步根据式（17）计算得到对应的人体自振频率为1.689 Hz。

4 识别结果讨论

本节通过多角度参数对比和分析，讨论分布参数人体模型的合理性和适用性。

4.1 整体结果分析

为方便比较，将每位测试者10次步行试验识别结果的均值作为其代表参数。图8展示了247名中国测试者与50名外国测试者的人体动力参数识别结果，经过单因素方差分析，在显著性水平α=0.01的情况下，两者间没有显著的分布差异，因此后续将合并分析。结果显示，人体自振频率和人体刚度随步频的分布较为离散，反映出很强的个体差异性。Pearson相关分析显示，频率呈现随步频弱增加的趋势（r=0.30，P<0.01），刚度变化则无明显的趋势（r=0.19，P<0.01），以上相关性分析中r表示相关系数，P值表征统计显著性。

所有测试者的人体动力参数的统计特征如表3所示，频率的变化范围为1.00～3.88 Hz，均值为1.70 Hz，标准差为0.36 Hz；刚度变化范围为820.1～15584.2 N/m，均值为2865.2 N/m，标准差为1765.4 N/m。

4.2 参数概率分布

4762893ddf186736cd2c8d08b356a805以往的研究中，Nimmen等［8］因样本量较少，故而假定人体参数均服从高斯正态分布，本研究针对“行走”这一运动形式所识别的人体自振频率和刚度参数进行了概率分布的拟合（如图9所示），经K⁃S检验，发现两者并不服从正态分布。图9数据分布具有显著的厚尾特性，因而更适合采用t⁃Location⁃Scale（t位置尺度）分布，该分布的概率密度函数为：

（18）

式中 Γ（·）为伽马函数；μ为位置参数；σ为尺度参数；ν为形状参数。该分布的统计指标均值和方差的表达式分别为：

（19）

（20）

t分布相关的位置参数、尺度参数和形状参数也显示于图9中。

4.3 与已有研究结果对比

Nimmen等［8］发现人体的机械性能参数主要取决于身体的姿势，且运动中的人体参数与静止的人体参数差别很大［17］。因此，将本文识别结果与已有模拟行走运动形式的研究结果进行了对比，如表4所示。

由于本研究的测试样本数量高出现有研究1～2个量级，且样本包含国内和国外的青年人与老年人，因此参数变化区间更宽是合理的，但本文结果与已有研究结果大致处于同一量级内。所提模型的合理性可进一步通过具体对比体现，例如Nimmen等［8］采用“跨步”的静止姿态来模拟步行动作并识别人体参数，由于此时测试者身体肌肉处在紧绷状态，所识别的参数并非真正运动中行人的参数，因此所得频率上下限均高于本文结果。张梦诗等［17］测试的样本偏少，且均为身体健康、年龄相仿的学生群体，其频率值和刚度变化较小。

4.4 不同年龄段对比

联合国世界卫生组织对年龄的划分标准规定：44岁以下为青年，45岁以上为中老年。本文将测试者按照以上标准划分成青年组和中老年组，分别有109名和188名，两组测试者的人体自振频率和人体刚度的概率分布直方图如图10所示。

由图10可知，中老年虽然样本数量多，但人体自振频率和刚度分布较集中，且总体上数值偏低，表明其人体刚度较小，符合中老年人骨骼和肌肉质量下降的特征。与之对比，青年人的频率和刚度分布较宽泛，且整体数值高于中老年人，一方面反映出青年人群体的骨骼、肌肉质量整体较高（因而刚度大、频率高）；另一方面也反映出青年人群体具有更显著的个体差异性。两组人群的参数统计特征如表5所示，青年人的均值和标准差都显著高于中老年人。

以上结果均表明分布式参数模型符合人体生理特点，能更准确地反映理论模型中人体机械性能的物理基础，即骨骼、肌肉质量以及密实程度。

5 结 论

针对现有人体集中质量力学模型物理意义不明确的问题，本研究提出了人体分布式参数动力模型，给出了模型的参数识别算法，应用于247名测试者的三维步态试验数据，成功识别得到每位的人体刚度和自振频率，参数的分布范围与已有研究的整体范围相近。

对识别参数的统计分析发现：人体自振频率和刚度服从t⁃Location⁃Scale分布；中老年人的自振频率和刚度分布较集中，总体数值偏低，而青年人的自振频率和刚度分布较宽泛，总体数值较高，符合青年人骨骼肌肉质量优于中老年人的特征。

理论分析以及试验结果的多角度对比分析，验证了人体分布式动力模型的合理性和适用性。本文提出的分布式人体模型可用于人体立姿轴向振动的研究，国内许多大城市公共交通（公交车、地铁）上的乘客大多数是立姿，且公共交通的振动对人体长期的影响不可忽视，此外许多行业的工人需要立姿作业，日常暴露于振动中，而国内对于人体立姿振动的研究较少［18］，本文所提模型可用于确定人体立姿轴向振动的参数，为国际标准ISO 5982：2019和国内标准GB/T 16440—1996补充材料。所提模型也具有显著的多学科应用前景，例如土木工程中人⁃结构相互作用分析、机械和交通领域中动力装置对人体的影响以及医学领域中人体健康监测研究等。

参考文献：

［1］Edwards M H， Gregson C L， Patel H P， et al. Muscle size， strength， and physical performance and their associations with bone structure in the Hertfordshire Cohort Study［J］. Journal of Bone and Mineral Research， 2013， 28（11）： 2295-2304.

［2］张鄂， 刘明利， 邵晓春， 等. 动态环境人-车系统的人体振动特性研究与仿真［J］. 工程设计学报， 2009， 16（3）： 166-171.

Zhang E， Liu Mingli， Shao Xiaochun， et al. Study and simulation on human body vibration characteristics of human-vehicle system in dynamic environment［J］. Chinese Journal of Engineering Design， 2009， 16（3）： 166-171.

［3］杨智春， 颜璘娟. 飞机应急着陆时的人体冲击响应研究［J］. 振动与冲击， 2009， 28（5）： 10-12.

Yang Zhichun， Yan Linjuan. Effects of passenger seat stiffness on the impact responses of human body during aircraft force-landing［J］. Journal of Vibration and Shock， 2009， 28（5）： 10-12.

［4］张梦诗， 陈隽， 徐若天. 竖向行人-结构相互作用中的行人MD及SMD模型参数识别［J］. 振动工程学报， 2016， 29（5）： 814-821.

Zhang Mengshi， Chen Jun， Xu Ruotian. MD and SMD model parameters of pedestrians for vertical human-structure interaction［J］. Journal of Vibration Engineering， 2016， 29（5）： 814-821.

［5］Foschi R O， Gupta A. Reliability of floors under impact vibration［J］. Canadian Journal of Civil Engineering， 1987， 14（5）： 683-689.

［6］Folz B， Foschi R O. Coupled vibrational response of floor systems with occupants［J］. Journal of Engineering Mechanics， 1991， 117（4）： 872-892.

［7］Shahabpoor E. Dynamic interaction of walking humans with pedestrian structures in vertical direction experimentally based probabilistic modelling［D］. Sheffield： University of Sheffield， 2014.

［8］Nimmen K V， Maes K， Živanović S， et al. Identification and modelling of vertical human-structure interaction［C］//Proceedings of the 33rd IMAC， Springer International Publishing， 2015： 319-330.

［9］Kitazaki S， Griffin M J. A modal analysis of whole-body vertical vibration using a finite element model of the human body［J］. Journal of Sound and Vibration， 1997， 200（1）：83-103.

［10］Zhang M S， Georgakis C T， Chen J. Biomechanically excited SMD model of a walking pedestrian［J］. Journal of Bridge Engineering， 2016， 21（8）： C4016003.

［11］Wang H Q， Chen J， Brownjohn J M W. Parameter identification of pedestrian’s spring-mass-damper model by ground reaction force records through a particle filter approach［J］. Journal of Sound and Vibration， 2017， 411： 409-421.

［12］Wang H Q， Chen J， Nagayama T. Parameter identification of spring-mass-damper model for bouncing people［J］. Journal of Sound and Vibration， 2019， 456： 13-29.

［13］Clough R W， Penzien J. Dynamics of Structures［M］. Third Edition. Berkeley： Computers & Structures Inc.， 2003.

［14］陈隽， 王玲， 陈博， 等. 跳跃荷载动力特性与荷载模型实验研究［J］. 振动工程学报， 2014， 27（1）： 16-24.

Chen Jun， Wang Ling， Chen Bo， et al. Dynamic properties of human jumping load and its modeling： experimental study［J］. Journal of Vibration Engineering， 2014， 27（1）： 16-24.

［15］Lencioni T， Carpinella I， Rabuffetti M， et al. Human kinematic， kinetic and EMG data during different walking and stair ascending and descending tasks［J］. Scientific Data， 2019， 6（1）： 309.

［16］Han Z P， Brownjohn J M W， Chen J. Structural modal testing using a human actuator［J］. Engineering Structures， 2020， 221：111113.

［17］张梦诗. 行人与结构耦合振动分析理论与实验研究［D］. 上海： 同济大学， 2016.

Zhang Mengshi. Analytical theory and experimental study on coupled vibrations of pedestrians and structures［D］. Shanghai： Tongji University， 2016．

［18］董大仟， 何青， 杨昆. 人体振动的研究进展概述［C］//第八届全国振动理论及应用学术会议论文集摘要. 上海， 2003： 226-227.

Dong Daqian， He Qing， Yang Kun. Review the research of human body to vibration［C］//Proceedings of the 8th National Conference on Vibration Theory and Application. Shanghai， 2003： 226-227.

Modeling and parameter identification of distributed parameter dynamics model for a human body

CHEN Zhe-yao1， WANG Hao-qi1， CHEN Jun1， ZHAO Yong-fang2， GUO Hai-ling2

（1.College of Civil Engineering，Tongji University，Shanghai 200092，China； 2.Shuguang Hospital Affiliated to Shanghai University of Traditional Chinese Medicine，Shanghai 201203，China）

Abstract： Establishing human body dynamics model to obtain human natural vibration frequency is a common scientific challenge in various fields such as civil engineering， traffic engineering， aerospace， rehabilitation medicine and so on. The spring-mass-damper （SMD） model is most commonly used in previous studies， which actually is not consistent with the distribution characteristics of human mass and stiffness along the height. In this study， a distributed parameter dynamics model of the human body with a pair of biomechanical forces is proposed， and the analytical solution of human natural frequency is theoretically derived. Therefore， a frequency recognition method based on gait tests is proposed. 247 subjects are organized to conduct gait tests， and their stiffness and natural frequency are identified. The rationality and applicability of the proposed model are verified from multiple perspectives： by fitting the probability distribution of results， comparing the results with other researches， and analyzing the results across different age groups.

Key words： human body dynamics model；parameter identification；distributed parameter model；spring-mass-damper model

作者简介： 陈哲瑶（1998―），女，硕士研究生。电话：（021）65985270；E-mail：chzhyao@tongji.edu.cn。

通讯作者： 陈 隽（1972―），男，博士，教授。电话：（021）65985270；E-mail：cejchen@tongji.edu.cn。