结合传递比与栈式自编码器的结构损伤识别

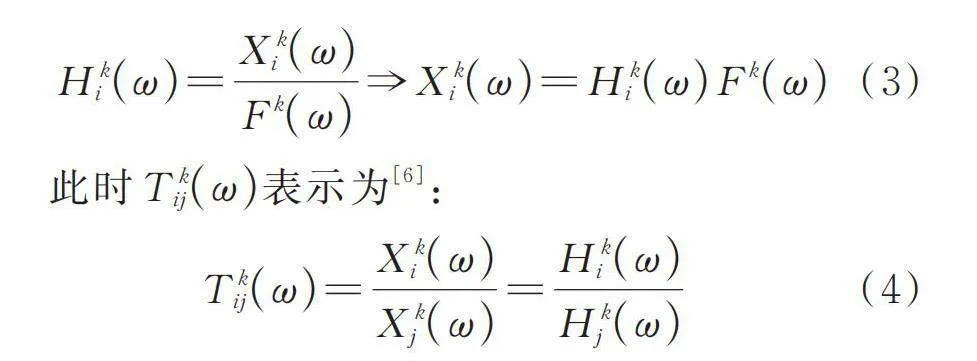
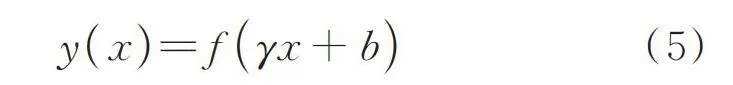
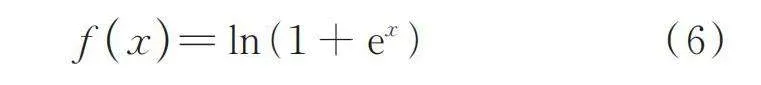
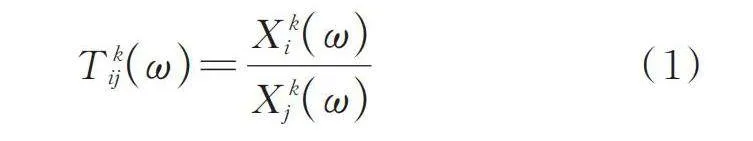
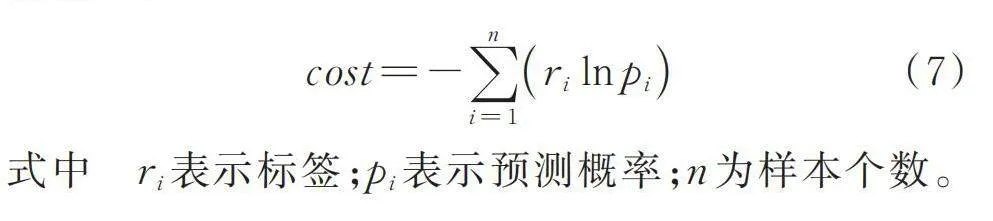
摘要： 如何从土木结构响应数据中挖掘损伤特征并有效分类，是实现损伤模式识别的关键。为此，以框架结构为分析对象，搭建设有自编码器隐藏层和Softmax分类层的栈式自编码器网络，采用无监督联合有监督的混合学习机制；基于有限元分析获取框架不同工况下的传递比函数值，构建训练集、验证集和测试集样本；通过预训练确定自编码器隐藏层的参数值如权重和偏置值，避免网络出现过拟合；采用微调方式进一步调整预训练后的网络参数值，再结合验证集实现对网络超参数的调整；将实测传递比数据输入网络，实现对框架节点损伤的评估。结果表明：所提方法能有效进行损伤特征的提取和分类，准确识别框架节点的单、双损伤工况，相较于传统浅层神经网络具有更高的识别准确度和更好的抗噪性。

关键词： 损伤识别； 栈式自编码器； 混合学习机制； 传递比函数； 框架结构

中图分类号： TU312+.3； TU391 文献标志码： A 文章编号： 1004-4523（2024）09-1460-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.002

引 言

土木结构可以通过系统参数的变化估计或损伤模式的归类来判断结构是否发生损伤，属于反问题求解［1］或模式识别过程［2］，常采用频域响应如模态频率、振型和频响函数等构建目标函数［3］。但模态参数包含的结构信息有限，实践应用存在较大局限性：比如结构频率对局部损伤引起的变化不敏感，且容易被环境因素（温度）导致的频率变化所掩盖［1］；构造光滑的模态振型需要足够的传感器数量，分析振型数量远小于结构的自由度数目，同时振型易受环境噪声的影响［4］。表示结构输入⁃输出关系的频响函数虽然包含了更多结构信息，但在实际测试中难以获取频响函数逆矩阵，反问题求解过程容易产生病态矩阵问题，且对土木结构而言，在环境激励下无法获取频响函数［5］。

和频响函数不同，传递比函数反映的是系统输出⁃输出之间的关系［6］，更适合于仅知道响应的服役状态下的土木结构动力分析，包含更多的结构信息，同时无需进行模态参数识别，更有利于损伤识别问题的求解［7⁃10］。Cheng等［9］研究了传递比函数构造的损伤指标与结构损伤间的关系，发现信号输入位置与识别损伤区域相关。Schallhorn等［10］结合传递比函数、相干函数构建了一种概率损伤指标，在识别桥梁构件裂缝的同时评估桥梁的健康状况。但现有研究大多通过中间参数寻找传递比函数与结构损伤间的关系，实际计算过程往往较为繁琐，不利于处理大量响应数据和提高损伤评估的实时性。此外，现有损伤指标一般只包含传递比函数的幅值、峰值或反共振频率等部分信息，未对传递比函数中的其他结构信息进行充分挖掘，因此面临着函数曲线的高维数据分析、压缩和特征提取问题。

人工神经网络在结构损伤识别上已有较长时间的应用，包括早期的传统浅层神经网络和近年来兴起的深度神经网络［11］。浅层神经网络的拓扑相对简单，通常只有一、两个隐藏层，损伤识别应用时输入层的神经元个数也不多，输入的往往是模态频率、振型和曲率［12］等低维数据，在特征提取和模式分类上的效果一般。而拓扑更复杂、学习能力更强的深度神经网络能够处理模式复杂、数量庞大的高维度数据，对分类问题也有较好的泛化能力［13］，已经在图像识别、语音转换等领域获得了应用［14］，在结构健康监测领域的异常数据检测［15］、数据压缩与重构［16］、数据恢复［17］等方面也取得了一定进展，展现了从高维度数字信号中提取特征的能力。Bao等［15］通过计算机视觉将大跨度斜拉桥的加速度响应数据转换为图矢量，再利用深度神经网络获取数据的异常分布情况及传感器的异常计数结果。为更好地对监测数据进行压缩与重构，Ni等［16］提出了一种自编码结构的卷积神经网络，编码部分采用一维卷积神经网络对加速度时程数据进行压缩和特征提取，解码部分的卷积神经网络则对压缩数据进行恢复，实现加速度数据的高精度重构。Jiang等［17］提出一种新的数据驱动神经语义恢复框架，利用卷积神经网络和编码器架构捕获加速度响应数据的整体语义特征，在数据高度缺失的情况下仍能保障良好的恢复精度和鲁棒性。为此，可尝试将深度神经网络进一步应用于结构损伤识别问题的求解上。

本文提出了一种结合传递比函数和栈式自编码器（Stacked Auto⁃Encoder， SAE）的损伤识别方法，利用栈式自编码器特征提取层进行传递比数据压缩和损伤特征提取，再结合Softmax多模式分类器进行特征分类，实现无监督和有监督学习的有机结合，既能够解决采用传统模态参数时损伤识别准确度不高的问题，又能够突破传统浅层神经网络在数据压缩、特征提取和多模式分类上的局限性，便于工程实际应用。

1 结构传递比函数

传递比函数包含被测结构完整的模态信息，对局部损伤很敏感，损伤会引起传递比函数幅值及对应频率的变化，变化量随着损伤程度增大而增大。此外，工程结构损伤识别往往依赖于激励⁃响应信号分析所获取的动力特征，但对实际土木工程结构而言，环境激励下的激励力未知，只能采集响应数据，无法获取频响函数，而传递比函数不涉及激励的测量，可采用响应谱计算，且对加速度、速度和位移响应都适用，应用上更方便［6］：

（1）

为提高传递比函数的信噪比，动力测试中传递比函数可定义为［18］：

（2）

式中 表示在点激励系统时响应点i和j之间的传递比函数；表示i点的响应谱，表示j点的响应谱；为的共轭复数。

当采用神经网络进行分析时，往往需要大量的样本，此时可通过有限元模拟获取。因为存在激励力测量问题，可通过结构的频响函数计算，其为系统响应X与激励F的比值［19］：

（3）

此时表示为［6］：

（4）

可见，式（2）和（4）分别适用于激励力无法测量和可以获取的情况。

2 损伤识别用栈式自编码器

2.1 栈式自编码器

常规SAE是由多个自编码器（Auto‑Encoder， AE）结合逐层贪婪学习策略得到的一种深度神经网络［20］，每个AE本质上也是一个包含输入层、隐藏层（称为AE隐藏层）和输出层的无监督学习网络，使得SAE拥有自动对输入数据进行压缩和特征提取的能力。SAE的隐藏层也称为特征提取层，体现为AE隐藏层的堆叠，1个AE训练1个隐藏层，前1个AE隐藏层提取的特征信息作为后1个AE的输入和输出，以进一步提取原始输入数据的高阶抽象特征，从而完成对原始输入数据的逐步压缩和特征提取。

本文采用的SAE网络由输入层、特征提取层、分类层和输出层4部分组成，拓扑如图1所示［20］。输入层是SAE的入口，传递比函数值作为该层神经元的输入；特征提取层即为堆栈的AE隐藏层，实现对输入的高维传递比的压缩和特征提取；分类层可视为一个全连接神经网络的隐藏层，可采用Softmax函数作为激活函数，输入为最后一个隐藏层的输出，输出为整个SAE网络的输出，最终实现对特征的有效分类。由于AE采用无监督学习方式，而Softmax分类器属于有监督学习，因此整个SAE网络结合了无监督和有监督学习的优点，实现混合学习机制，以达到高效数据压缩和分类的目的。要说明的是，分类层采用的Softmax函数也可用其他函数（比如Sigmoid函数）进行替换，但Softmax函数更适合于互斥多类别分类问题，能够直接输出样本数据属于各类别的概率，提高分类效率，便于复杂损伤特征下的分类。

SAE网络通过TensorFlow平台构建［21］，每个神经元的计算式为［22］：

（5）

式中 x和y分别表示神经元的输入和输出；为权重；为偏置；表示激活函数，常见的激活函数有，，函数等，其中函数能够有效防止某些神经元死亡和输出偏差移动的问题，是一种更加近似生物神经的激活函数［23］，可用于AE隐藏层。函数定义为：

（6）

最后，损失函数cost可以评估网络预测值和真实值间的误差，准确率是所有预测结果中正确预测的样本占比，本文微调训练时采用交叉熵作为损失函数［22］：

（7）

式中 表示标签；表示预测概率；n为样本个数。

2.2 样本集生成

如第1节所述，本文通过有限元分析获取结构传递比值，作为SAE网络的数值样本。样本集包含三种［22］：训练网络参数的训练集，训练超参数和检验模型性能的验证集，检验最终模型泛化能力的测试集，常用的占比为3∶1∶1［24］。这里“网络参数”指SAE网络中的权重和偏置，“超参数”指网络的学习率、训练次数、训练批次、隐藏层数及相应的神经元数等。

为尽可能涵盖结构可能损伤情况，神经网络样本集需要考虑很多种损伤模式和损伤程度，使得样本量十分庞大，增加了网络的训练时间和计算成本。为此，本文将框架损伤位置作为试验因素，损伤程度作为试验水平，利用实验设计方法来减少样本量。单（框架节点）损伤工况采用单因素、多水平设计，多损伤工况采用多因素、多水平的均匀设计［25］。此外，实测结构响应往往包含大量的环境噪声，为提高SAE网络对环境噪声的鲁棒性，可在数值样本生成过程中加入高斯白噪声，使得传递比函数值为带噪声值。

3 基于SAE的损伤识别流程

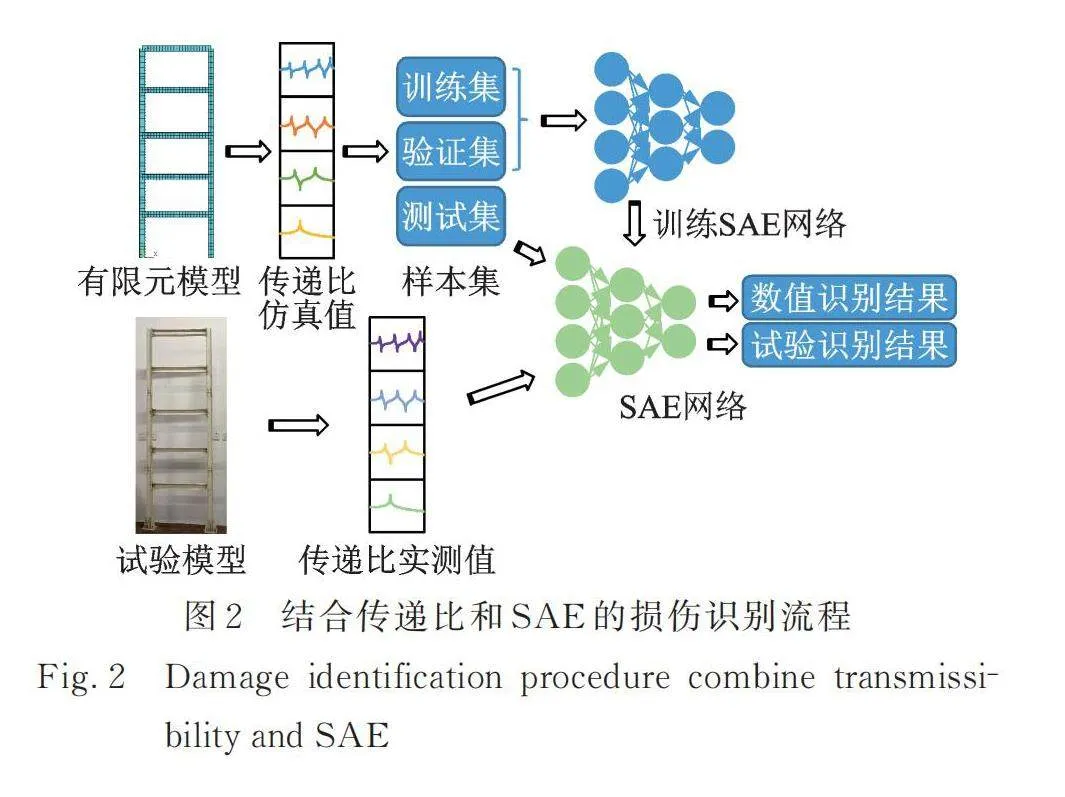
以框架结构为例，结合传递比和SAE的损伤识别流程如图2所示。首先，搭建SAE网络拓扑，设置输入层、输出层神经元个数，初设AE层层数和神经元个数、分类层的神经元个数（在训练和验证过程中调整），同时设置学习率和训练批次数目等；其次，建立试验框架的有限元模型，通过有限元分析获取训练集、验证集和测试集样本，均包含不同工况下的传递比数值；接着，采用混合学习机制，通过预训练和验证过程确定SAE网络拓扑和权重等参数，其中训练集用于确定网络权重、偏置等参数，验证集用于确定网络超参数如隐藏层及其神经元的数目；随后，利用测试集评价SAE网络对未知样本的预测准确度；最后，将试验框架实测的传递比值代入SAE网络，实现对框架节点的损伤识别。

更具体地，网络训练过程包括AE隐藏层预训练和网络微调两个步骤。预训练是对AE隐藏层逐层训练，属于无监督学习过程，起到数据压缩和特征提取作用，能够得到与训练集相关的AE隐藏层权重w和偏置b，避免SAE网络出现过拟合问题［26］；微调则是将所有的AE层和分类层同时训练，进一步调整预训练后的网络参数值，使整个SAE网络对已有样本有更好的拟合，对未知样本有着更好的预测效果。

网络验证过程则是将验证集代入前述训练后的SAE网络，通过损失函数值和样本验证准确率来判断网络是否符合要求。若损失和准确率满足要求，则保存当前网络的各参数（权重、偏置和超参数）；反之，则对网络超参数（隐藏层个数、神经元个数、学习率和训练批次数目）进行调整，然后重新预训练和微调，直到代入验证集后的SAE网络能够输出符合要求的结果，此时网络训练完成。

4 试验钢框架算例

采用一榀5层试验钢框架验证所提方法的可行性，如图3所示。框架全高1835 mm，宽600 mm；梁截面尺寸，柱截面尺寸，梁和柱通过螺栓实现刚性连接，框架底部通过螺栓固接在工字钢基座上。钢材的实测弹性模量为212 GPa，密度为。为获取框架节点加速度响应，采用锤击法激励框架，激励点位于J6（图3），加速度传感器布设于J1～J5上，通过动态测试系统采集各测点的加速度时程数据，采样频率为2 kHz。

4.1 SAE网络初设置和有限元建模

框架损伤识别所用的SAE网络包含输入层、特征提取层、分类层和输出层。输入层有648个神经元，与传递比数据量相同（4个传递比函数，每个函数有162个数值，故相应地有4×162=648个神经元）；输出层有19个神经元，与损伤模拟工况数目相同。构建的SAE网络拟实现对0～157 Hz频段内的传递比数据压缩提取特征，该频段包含了框架第1，2阶频率。

为生成SAE网络所需的训练样本，建立了钢框架的有限元模型设定，几何尺寸与试验模型相同，材料特性由实测得到，梁柱采用梁单元模拟，节点处采用弹簧单元连接，所建立的模型为图2中的框架有限元模型，网格划分后共包含268个梁单元和30个弹簧单元。

4.2 生成样本集

如前所述，输入SAE网络的样本包括训练集、验证集和测试集，其中训练集需要包含各种节点损伤位置和程度组成的不同工况，传递比样本均由有限元模型计算得到。

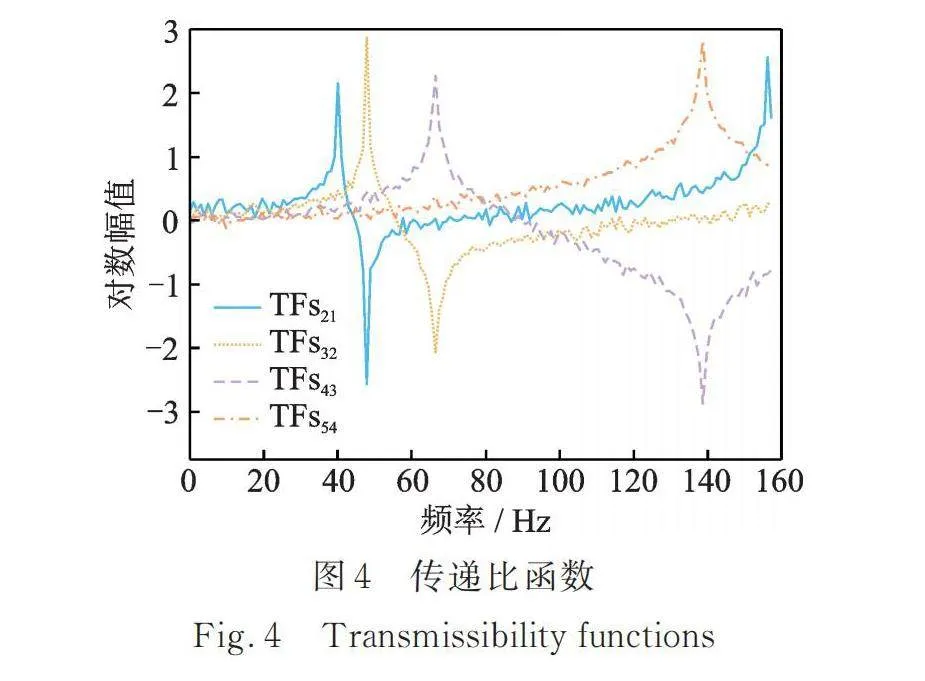
损伤以梁柱节点刚度损失进行模拟，单节点损伤J1～J10共10个工况，样本损伤程度由3%～30%均匀分布，步长为3%；双节点损伤以相邻节点为主，比如J1+J2，J2+J3，…，J9+J10共8种不同的工况（不包含J5+J6），损伤程度根据均匀设计表格进行取值，损伤程度也为3%～30%。此外，未损伤框架也作为独立工况加入样本集，因此一共19个工况（对应输出层19个神经元）。为模拟实际情况，各工况传递比函数值添加了1%～10%高斯白噪声，如图4所示。

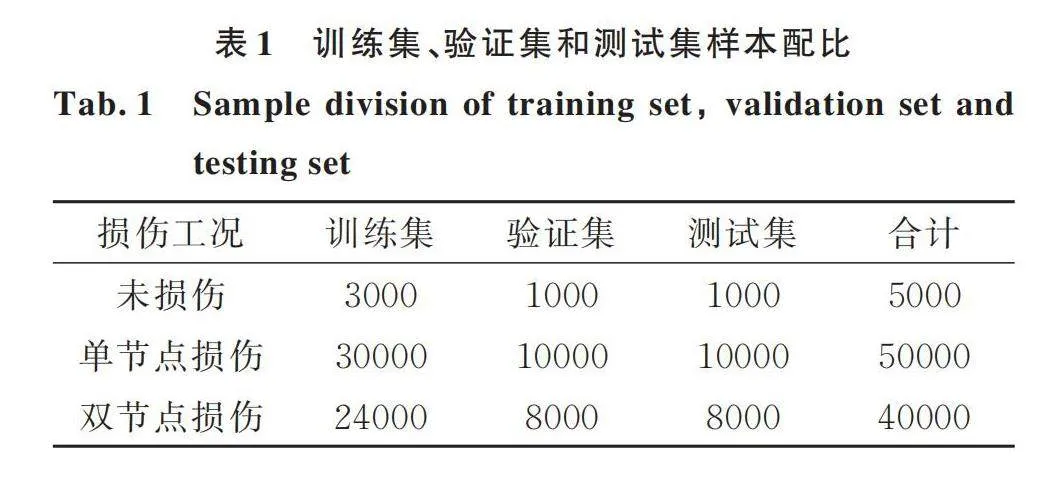
如2.2节所述，训练集、验证集、测试集的样本数比例为3∶1∶1。对于未损伤工况，均匀抽取40%样本，验证集和测试集各半，剩余的60%样本作为训练集；对于单节点损伤工况，选取损伤程度9%和21%的样本作为测试集，15%和27%的样本作为验证集，剩余的样本组成训练集；对于双节点损伤工况，取均匀设计表格中水平3和7作为测试集，水平5和9作为验证集，其他的样本作为训练集。样本总数为95000个，各样本集分配如表1所示，1个样本包含由5个响应测试点计算的4个传递比函数。

4.3 SAE网络训练、验证和测试

基于TensorFlow平台搭建SAE网络，采用Adam优化算法，初设训练批次数目为100、学习率为0.00005，每个AE隐藏层的预训练次数为20，微调的训练次数为500。经过预训练、微调和验证，确定隐藏层个数为4，各层神经元个数分别为500，350，200，3；分类层神经元个数为19。

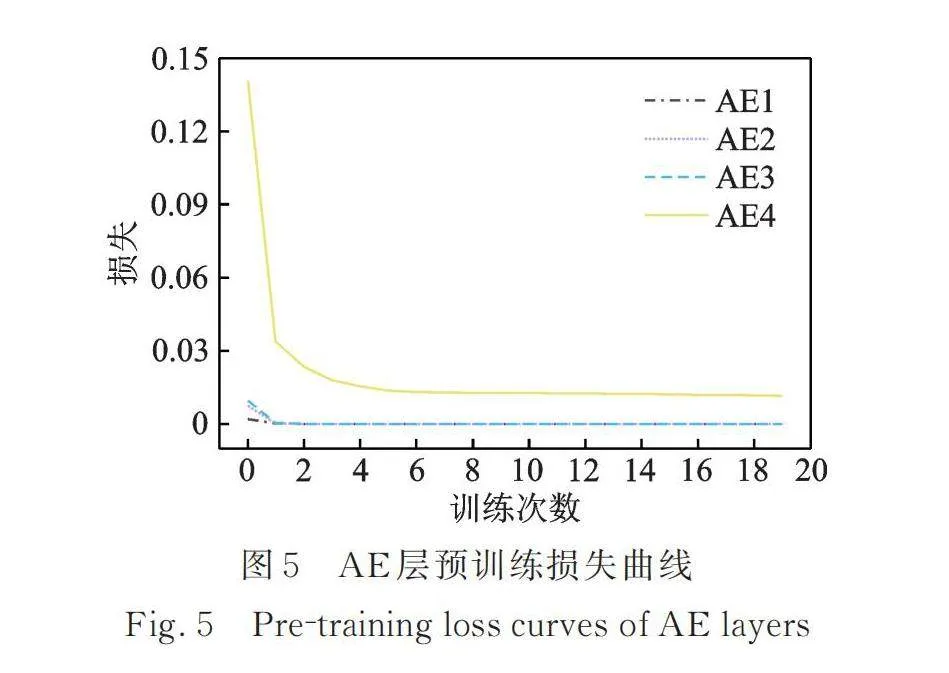
4个AE层预训练的损失曲线如图5所示。每个AE层的训练损失在开始阶段即大幅下降，第5轮后基本趋于稳定，接近于0，说明隐藏层的特征压缩和学习主要在预训练前期完成。

图6（a）为SAE网络的微调结果，蓝色曲线表示训练集，黄色曲线表示验证集，它们的损失函数和准确率曲线在整个训练过程中基本保持一致，说明SAE网络能对训练集以外的样本进行准确分类。此外，随着训练次数的增加，损失值逐渐趋近于0，而准确率达到了97.8%，说明网络良好学习了对训练数据的压缩、特征提取和分类。图6（b）和（c）分别为训练集和验证集的损伤特征在三维空间中的分布，特征由SAE最后1个隐藏层的3个神经元输出，3个神经元数值依次对应X，Y，Z的坐标值，可见19种工况的特征得到了很好的区分，有利于后续的损伤识别。

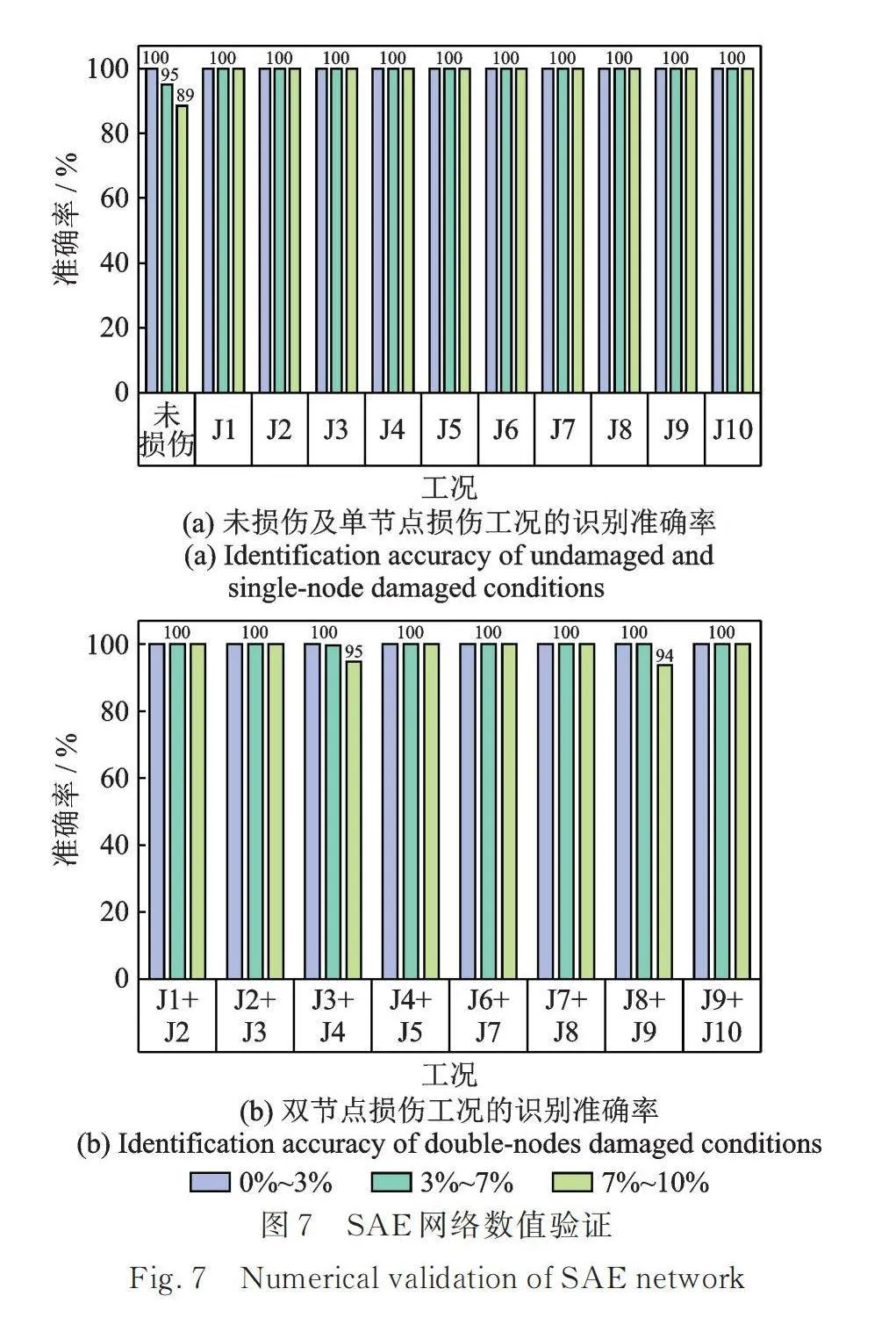
最后，将测试集代入经验证的SAE网络中，得到各工况的损伤识别准确率为99.4%。未损伤、单节点损伤、双节点损伤工况在不同噪声程度下的损伤识别准确率如图7所示。3种工况在0%～3%的噪声程度下都能够进行准确的识别；在3%～7%的噪声程度下，只有未损伤工况出现了个别误判，而单节点损伤工况和双节点损伤工况都能够准确识别；在7%～10%的噪声程度下，未损伤工况依旧能够保证有89%的准确率，双节点损伤工况只有J3+J4和J8+J9损伤时出现了个别误判，而单节点损伤工况的准确率仍高达100%。

4.4 试验数据验证

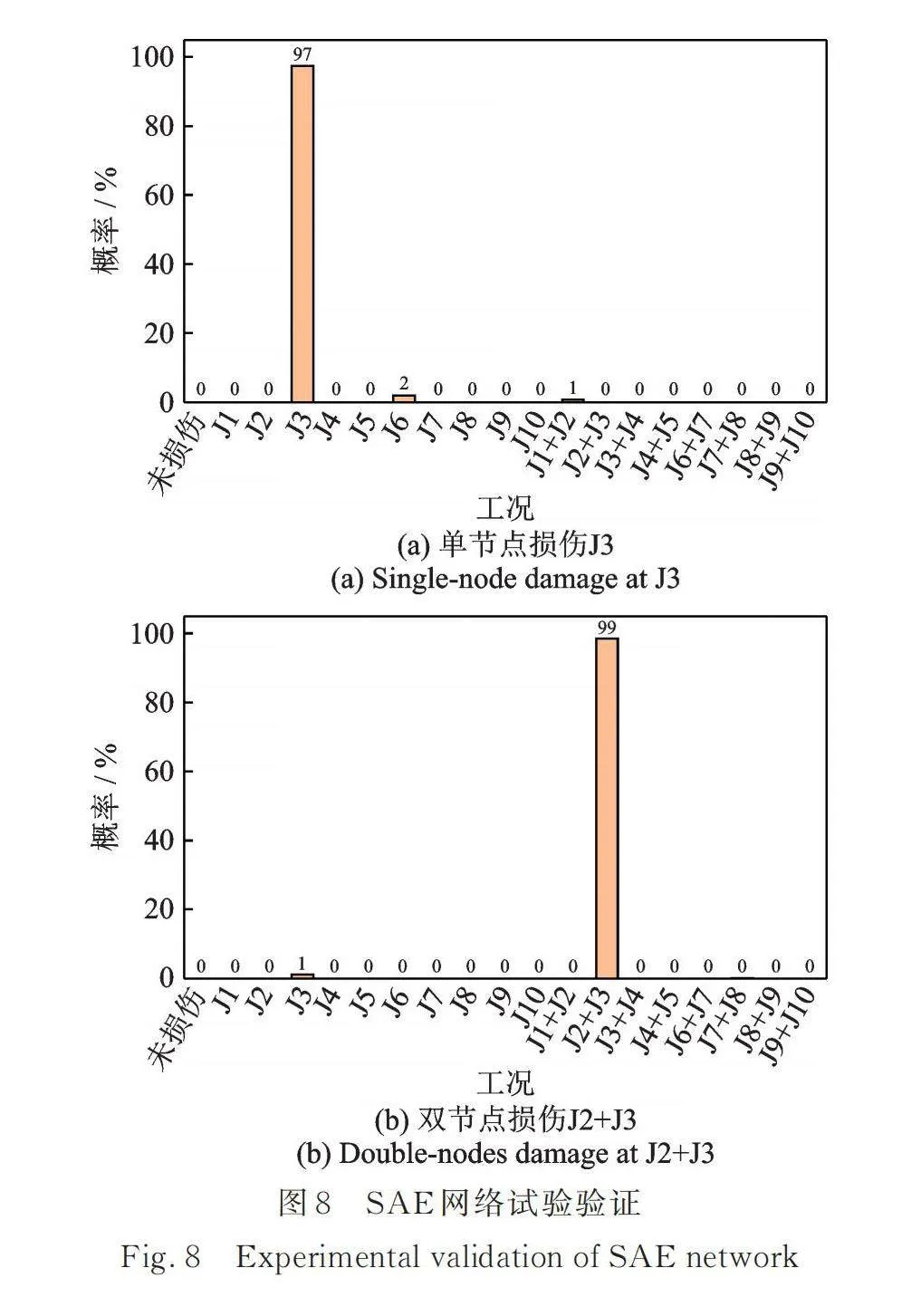
试验框架通过松开节点处螺丝来模拟损伤（图3），共测试了单节点损伤（J3）和双节点损伤（J2+J3）2种工况，并将实测传递比数据输入SAE网络，损伤预测结果如图8所示。图中纵坐标表示识别结果属于某工况的概率。由图可见，所提方法能够准确识别出J3节点处的损伤，以及J2+J3节点处的双损伤，识别概率均接近100%。

4.5 BP神经网络对比

BP 神经网络属于传统浅层人工神经网络，在结构损伤识别中已有较为深入的研究。本文同样基于TensorFlow平台搭建用于该框架损伤识别的BP神经网络，采用与SAE网络相同的样本集。BP网络隐藏层神经元个数为3，激活函数为Sigmoid函数，采用梯度下降优化算法，训练批次大小为100，学习率为0.01，训练次数为5000。

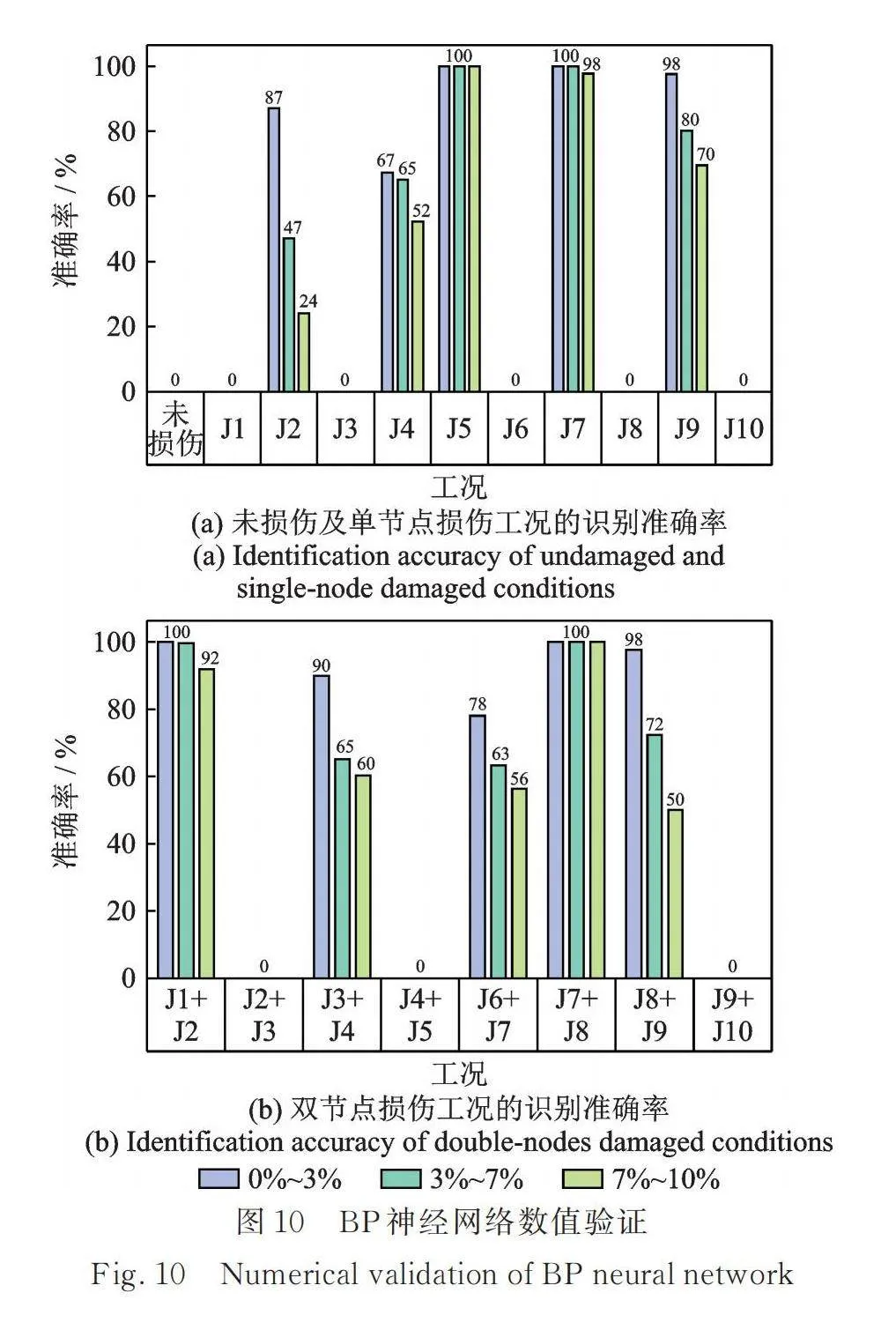
BP网络训练和验证结果如图9所示。图9（a）显示训练集和验证集的损失曲线最后都趋近于1.5，准确率仅在40%左右，反映了BP网络难以对高维响应信号进行压缩、特征提取和分类。图9（b）和（c）分别为训练集和验证集的损伤特征在三维空间中的分布，特征由BP网络隐藏层的3个神经元输出，3个神经元数值依次对应X，Y，Z的坐标值，可见19种工况的特征只有少部分获得区分。此外，将测试集输入网络，得到的损伤识别准确率为40%（图10），明显不如SAE网络的训练结果。值得一提的是，BP网络在不同噪声程度下的损伤识别准确率也比较低，尤其是添加了7%～10%的噪声后的抗噪性较差。最后，将试验测得的J3单节点损伤和J2+J3双节点损伤的传递比值代入BP网络，损伤预测结果如图11所示，发现两种损伤工况下均出现了误判。

5 结 论

为便于土木工程实践应用，本文提出一种结合传递比函数和栈式自编码器的结构损伤识别方法，实现对结构动力响应数据的高效压缩、特征提取和分类，并通过一榀试验框架验证了方法的可行性。研究结果表明：

（1）混合学习机制下的带分类层SAE网络可以有效进行数据压缩、特征提取和分类，无监督模式下的逐层学习有助于后续有监督学习的迭代收敛，实现准确的特征分类。

（2） 预训练和微调相结合的方式，有利于避免网络出现过拟合问题，可以获取合适的权重和偏置。

（3）SAE网络的损伤识别效果优于传统浅层神经网络，抗噪声能力更强。

最后，在试验框架损伤定位的基础上，将来可继续拓展带分类层SAE网络在损伤程度估计及实际工程结构上的应用，充分挖掘深度学习算法在求解土木结构损伤识别问题上的潜力。

参考文献：

［1］李惠， 鲍跃全， 李顺龙， 等. 结构健康监测数据科学与工程［M］. 北京： 科学出版社， 2016.

［2］Ren W X， Lin Y Q， Fang S E. Structural damage detection based on stochastic subspace identification and statistical pattern recognition： Ⅰ. theory［J］. Smart Materials and Structures， 2011， 20（11）： 115009.

［3］Taghipour R， Nashta M R， Bozorgnasab M， et al. A new index for damage identification in beam structures based on modal parameters［J］. Archive of Mechanical Engineering， 2021， 68（4）： 375-394.

［4］Das S， Saha P， Patro S K. Vibration-based damage detection techniques used for health monitoring of structures： a review［J］. Journal of Civil Structural Health Monitoring， 2016， 6（3）： 477-507.

［5］Fang Y L， Su P R， Shao J Y， et al. Substructure damage identification based on model updating of frequency response function［J］. International Journal of Structural Stability and Dynamics， 2021， 21（12）： 2150171.

［6］Yan W J， Zhao M Y， Sun Q， et al. Transmissibility-based system identification for structural health monitoring： fundamentals， approaches， and applications［J］. Mechanical Systems and Signal Processing， 2019， 117： 453-482.

［7］He X， Tang H. Experimental validation of structural damage identification using vibration transmissibility［C］//Structural Health Monitoring 2015： System Reliability for Verification and Implementation. California， 2015： 335-342.

［8］Johnson T J， Adams D E. Transmissibility as a differential indicator of structural damage［J］. Journal of Vibration and Acoustics， 2002， 124（4）： 634-641.

［9］Cheng L L， Cigada A. An analytical perspective about structural damage identification based on transmissibility function［J］. Structural Health Monitoring， 2020，19（1）： 142-155.

［10］Schallhorn C， Rahmatalla S. Crack detection and health monitoring of highway steel-girder bridges［J］. Structural Health Monitoring， 2015， 14（3）： 281-299.

［11］Schmidhuber J. Deep learning in neural networks： an overview［J］. Neural Networks， 2015， 61： 85-117.

［12］Zhang X D， Zhang Z G， Li X F， et al. Damage identification in cable-stayed bridge based on modal analysis and neural networks［C］//AIP Conference Proceedings. Colorado， 2007： 1435-1442.

［13］Wu H， Liu Y L， Wang J W. Review of text classification methods on deep learning［J］. Computers， Materials and Continua， 2020， 63（3）： 1309-1321.

［14］LeCun Y， Bengio Y， Hinton G. Deep learning［J］. Nature， 2015， 521（7553）： 436-444.

［15］Bao Y Q， Tang Z Y， Li H， et al. Computer vision and deep learning‑based data anomaly detection method for structural health monitoring［J］. Structural Health Monitoring， 2019， 18（2）： 401-421.

［16］Ni F T， Zhang J， Noori M N. Deep learning for data anomaly detection and data compression of a long-span suspension bridge［J］. Computer-Aided Civil and Infrastructure Engineering， 2020， 35（7）： 685-700.

［17］Jiang K J， Han Q， Du X L. Lost data neural semantic recovery framework for structural health monitoring based on deep learning［J］. Computer-Aided Civil and Infrastructure Engineering， 2022， 37（9）： 1160-1187.

［18］Meruane V. Model updating using antiresonant frequencies identified from transmissibility functions［J］. Journal of Sound and Vibration， 2013， 332（4）： 807-820.

［19］傅志方， 华宏星. 模态分析理论与应用［M］. 上海：上海交通大学出版社， 2000.

［20］Bengio Y， Lamblin P， Popovici D， et al. Greedy layer-wise training of deep networks［C］//Advances in Neural Information Processing Systems. Vancouver， 2007： 153-160.

［21］黄文坚， 唐源. Tensorflow实战［M］. 北京： 电子工业出版社， 2017.

Huang Wenjan， Tang Yuan. Actual Combat of TensorFlow［M］. Beijing： Publishing House of Electronics Industry， 2017.

［22］伊恩·古德费洛， 约书亚·本吉奥， 亚伦·库维尔. 深度学习［M］. 赵申剑， 黎或君， 符天凡， 等译. 北京：人民邮电出版社， 2021.

［23］Zhao H Z， Liu F X， Li L Y， et al. A novel softplus linear unit for deep convolutional neural networks［J］. Applied Intelligence， 2018， 48（7）： 1707-1720.

［24］Huyan J， Ma T， Li W， et al. Pixelwise asphalt concrete pavement crack detection via deep learning-based semantic segmentation method［J］. Structural Control and Health Monitoring， 2022， 29（8）： e2974.

［25］方开泰， 刘民千， 覃红， 等. 均匀试验设计的理论和应用［M］. 北京： 科学出版社， 2019.

［26］Saxe A M， McClelland J L， Ganguli S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks［C］//2nd International Conference on Learning Representation. 2014.

Structural damage identification incorporating transmissibility functions with stacked auto-encoders

FANG Sheng-en1，2， LIU Yang1， ZHANG Xiao-hua1

（1.School of Civil Engineering， Fuzhou University， Fuzhou 350108， China； 2.National & Local Joint Engineering Research Center for Seismic and Disaster Informatization of Civil Engineering， Fuzhou University， Fuzhou 350108， China）

Abstract： The key to damage pattern recognition lies in digging and classifying damage features from the response data of civil structures. To this end， a stack auto-encoder network with several auto-encoder hidden layers and a Softmax classification layer is built for analyzing frame structures. A hybrid learning mechanism is adopted to combining unsupervised and supervised learning strategies. Finite element analysis is used to generate the transmissibility function samples corresponding to different scenarios of a frame structure. The transmissibility samples are then divided into training， validation， and test sets. The parameters of the auto-encoder hidden layers， such as the weights and bias， are determined by a pre-training strategy in order to avoid the phenomenon of network over fitting. A fine-tuning step is employed to adjust the pre-trained network parameters， and the network hyper parameters are further adjusted based on the validation set. The measured transmissibility data are input into the network to evaluate the damage of the frame structure. The analysis results show that the proposed method can effectively extract and classify the damage features. Both the single and double damage scenarios at the frame joints were identified with higher accuracy and better anti-noise ability than the traditional shallow neural network.

Key words： damage identification；stacked auto-encoder；hybrid learning mechanism；transmissibility functions；frame structure

作者简介： 方圣恩（1980―），男，博士，教授，博士生导师。E-mail：shengen.fang@fzu.edu.cn。