基于MVMD‑SSI和Single‑Pass聚类的高层结构动力特性自动跟踪

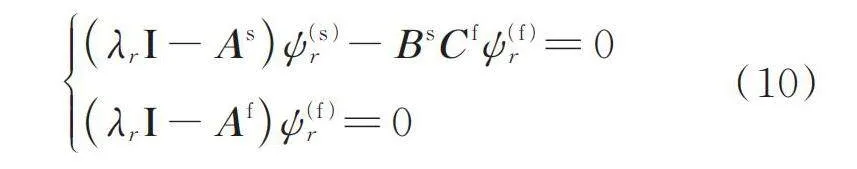
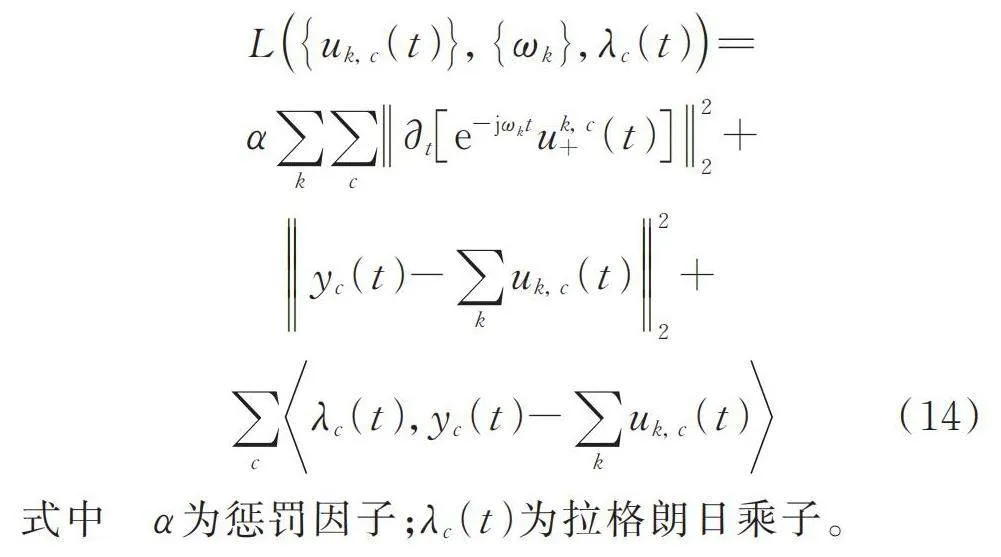
摘要： 随机子空间辨识算法（SSI）在识别高层结构动力特性过程中产生虚假模态，干扰了动力特性的自动跟踪。本文通过状态空间模型证明非白噪声是产生虚假模态的原因之一，并进一步针对非白噪声激励提出了基于多元变分模态分解（MVMD）的信号重构方法，剔除由于非白噪声引起的虚假模态；通过Single‑Pass聚类算法剔除离散虚假极点，消除其他虚假模态。将上述算法应用于超高层结构的现场实测数据，实现了动力特性的长期自动识别与跟踪。

关键词： 高层结构； 随机子空间法； 多元变分模态分解； 动力特性； 自动跟踪

中图分类号： TU973.2+3； TU311.3 文献标志码： A 文章编号： 1004-4523（2024）09-1451-09

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.001

引 言

中国超高层结构多分布在东南沿海城市，而沿海城市台风频发，高层结构舒适度问题引起学者的关注。He等［1］报道了“海马”台风作用下深圳平安大厦118层结构加速度接近0.08 m/s2。吴杰等［2］关注2018年“安比”台风作用下上海中心的振幅和动力特性，发现117层最大振幅仅为0.0080 m/s2。谢壮宁等［3］记录了2011年至2015年4次主要台风下的加速度数据，发现深圳京基100大厦瞬时峰值加速度为0.123 m/s2。Hu等［4］发现当“山竹”台风正面登陆深圳时，京基100大厦96层楼面及顶部钢架的瞬时加速度极值接近规范限值。在赛格大厦5.18有感振动事件中，胡卫华等［5］发现赛格大厦在5月20日再次振动时，结构69层楼面最大加速度为0.055 m/s2，尽管这一值小于国家规范限值，但结构有感振动会引起人员不适和恐慌。

动力特性自动跟踪有助于深入理解并解决超高层结构舒适度问题，也有助于进行结构状态评估。近年来，高层结构的动力特性自动识别与跟踪技术日益受到关注。Bagchi等［6］基于频域分解法识别了某高层建筑在运营状态下的动力参数。Aguilar等［7］进一步将运营模态参数识别技术应用到高层建筑的健康状态评估中。这些技术尚不能做到高层建筑在服役状态下的自动参数识别，从而无法实现结构舒适度和健康状态的准确评估。

阻碍模态参数自动识别的主要因素是非白噪声输入引起的虚假模态的干扰。针对该问题，Zhang等［8］结合了快速密度峰值聚类算法与协方差驱动的随机子空间识别方法，消除了斜拉桥实测数据识别的虚假模态；茅建校等［9］将模态验证标准向量（MVC）作为每个模态点的特征向量， 结合主成分分析、k均值聚类分析和层次聚类算法等实现对苏通大桥的模态自动跟踪；胡异丁等［10］针对非白噪声激励导致的虚假模态问题，提出了延时随机子空间方法。Teng等［11］提出了基于密度聚类的虚假模态提出算法，实现了桥梁物理模态的长期跟踪，发现了模态参数长期围绕着基准值波动的性质。

目前超高层结构动力特性自动跟踪研究与应用存在如下两个问题：首先，目前的研究相对缺乏对虚假模态产生的机理分析，较难完全消除虚假模态的干扰。其次，高层结构与桥梁结构模态参数特点存在较大差异，基于桥梁结构模态参数特性开发的虚假模态消除算法在高层结构上的应用存在一定局限性。针对以上两个问题，本文首先尝试探寻非白噪声激励是虚假模态产生的原因之一，提出了基于多元变分模态分解的信号重构方法，实现信号中非白噪声的消除。然后，采用Single‑Pass聚类算法进一步消除稳态图中的离散虚假极点，准确识别结构模态。将上述算法应用于高层结构现场实测信号，成功实现了动力特性的长期自动跟踪。

1 白噪声与非白噪声激励的随机子空间识别算法

1.1 白噪声激励的随机子空间识别算法

随机子空间识别算法（Stochastic Subspace Identification， SSI）假设环境激励为白噪声，并且目标结构为一个线性时不变的物理系统，在此基础上将目标结构简化为连续时间随机状态空间模型。考虑监测过程中环境噪声和测量噪声的影响，离散的时间随机状态空间模型为［12］：

（1）

式中 A和C分别表示结构的状态矩阵和观测矩阵；和分别表示结构的状态向量和响应向量；和分别表示过程噪声和测量噪声，k = 0， 1， 2， … ， N-1，N表示离散的计算时刻。

在基于实测数据和随机子空间识别算法进行系统模态参数识别的过程中，虚假模态的干扰是影响模态参数跟踪的主要难题。虚假模态产生的原因包括非白噪声输入、非线性因素、阻尼效应、阶次冗余、噪声干扰影响等，这些影响在稳定图中表现为集中出现的稳定轴或者零散分布的极点。为了消除虚假模态干扰，目前主要采用稳定图法对识别的模态进行判定，稳定图中不同系统阶次下的物理模态会组成明显的稳定轴，通过稳定性判断理论上可以识别模态是否为虚假模态［12］。然而，当输入激励为非白噪声时，非白噪声激励作用于系统，也会形成由极点构成的稳定轴，引入虚假模态。目前基于稳定图的虚假模态消除方法难以有效消除由非白噪声激励导致的虚假模态。接下来针对非白噪声激励的情况进行讨论。

1.2 非白噪声激励的随机子空间识别算法

在工程结构服役过程中，实际的外部环境激励较为复杂，可能包含一些显著的频率成分，从而使得环境输入并非理想的白噪声信号，在频谱上呈现出一条并非完美的水平直线，这样的外部环境激励被视为非白噪声激励。

为了区分不同的状态空间模型，本文将白噪声激励表示为，非白噪声激励表示为，非白噪声信号可以看作是由白噪声信号通过某一线性时变的动力系统而获得的。在构建新的系统状态空间模型过程中，可以将外部环境激励视为平稳白噪声信号经过一个线性时变的预处理滤波器产生非白噪声激励，即是的一种特殊情况。

根据状态空间方程原理，非白噪声环境激励下的扩展状态空间模型（如图1所示）可以表示为［13‑16］：

（2）

式中 分别为非白噪声激励下的状态、输入、观测和直馈矩阵；为非白噪声环境激励下的状态向量。

在图1所示的扩展状态空间模型中，假定非白噪声环境激励是白噪声激励通过某预处理滤波器产生的，如下式所示：

（3）

式中 ，，，为扩展状态空间模型中预处理滤波器的状态、输入、观测和直馈矩阵，为对应的状态向量。

结合式（2）和式（3），建立外部激励为理想白噪声激励，经过预处理滤波器后产生非白噪声激励的离散时间扩展状态空间模型为：

（4）

式中

（5）

（6）

（7）

（8）

（9）

为具有时变持性的观测向量。噪声项和维持不变。可以看出，离散时间扩展状态空间模型可以严格满足随机子空间方法所要求的基于白噪声环境激励假定的离散时间随机状态空间模型。由于基于状态空间方程的模态参数识别方法主要通过对系统状态矩阵求取特征值和特征向量以获取系统模态参数，因此需要计算特征多项式，展开可以得到：

（10）

式中 表示单位矩阵；为扩展模型状态矩阵的第阶特征值，对应的第阶特征向量为：

（11）

状态矩阵和不可能具有相同的非零特征值，且状态矩阵的特征值中既包含状态矩阵的特征值也包含状态矩阵的特征值。与此同时，对于状态矩阵的特征值，在状态矩阵中对应的特征向量中的，即预处理滤波器不会影响到对原始结构系统模态参数的提取。

由此可见，非白噪声环境激励并没有改变原始结构系统模态参数的提取结果，而是在状态空间模型中完整地保留了它们。然而，非白噪声环境激励会在状态空间模型中通过产生特征值以及其对应的特征向量的方式，在模态参数识别结果中混入虚假模态，从而干扰对原始结构系统模态参数的识别。上述论证说明了通过状态空间方程识别模态参数的可行性以及状态空间方程本身无法区分系统固有模态和虚假模态的局限性，因此需要采取有效手段加以区分，去除虚假模态对动力特性自动跟踪的干扰。

2 虚假模态消除算法

2.1 多元变分模态分解

为了削弱非白噪声环境激励对结构动力响应的影响，抑制虚假模态的产生，本文引入多元变分模态分解（Multivariate Variational Mode Decomposition， MVMD） ［16］对采样信号进行重构。MVMD是一种非递归的、自适应的信号分解方法，抗噪性能优良，能够有效抑制端点效应、有效避免模态混叠，适用于多通道信号的分解，并且具备坚实的数学理论基础，是信号处理和噪声抑制的有效手段［17］。

MVMD将单个模态分量信号定义为有限带宽调幅调频（AM‑FM）的内涵模态分量函数（Intrinsic Mode Function， IMF）。针对多元振荡信号，单个模态分量信号的实数域可以用矢量的形式表达：

（12）

式中 为信道c中单个模态分量的信号；和分别为信道c中单个模态分量随时间变化的幅值函数和相位函数；C为采样信号的信道总数量。包含了同一模态分量在各个采样信道中的实数域信号函数，符合结构动力学对单个模态动力响应时程函数的定义。

为了获得每个模态分量的信号数据，MVMD引入变分概念，将信号分解转变为求解当所有模态分量的带宽之和最小时各模态分量的信号数据的问题，即求解变分问题的最优解，并且要求所获得的模态分量能够精确地重构原始信号。借助Hilbert变换和Frobenius范数，构建变分约束模型以及目标函数：

（13）

式中 为第k个模态分量的中心频率；为第k个模态分量中第c个信道的解析信号；为第k个模态分量中第c个信道的实信号；为第c个信道总响应信号。

为了求解变分约束模型的最优解，MVMD采用拉格朗日乘子法，利用多个线性约束条件，构造增广的拉格朗日函数：

（14）

式中 为惩罚因子；为拉格朗日乘子。

通过求解式（12）即可将信号分解为多个满足式（10）定义的IMF，原响应信号与分解后信号之间的关系为：

（15）

式中 为原采样信号；为不满足IMF定义的残差噪声。根据各IMF的中心频率等特征，选择其中反映结构模态响应的IMF组合即可实现结构动力响应信号的重构，从而削弱非白噪声环境激励对结构动力响应的影响，抑制虚假模态的产生。

多元变分模态分解可以有效消除非白噪音激励导致的虚假模态，但在系统识别过程中仍存在非线性因素、阻尼效应、阶次冗余、噪声干扰影响等，这些影响在稳定图中表现为零散分布的极点。下文尝试采用聚类算法消除此类虚假模态对动力特性自动跟踪的干扰。

2.2 基于聚类算法的虚假模态消除

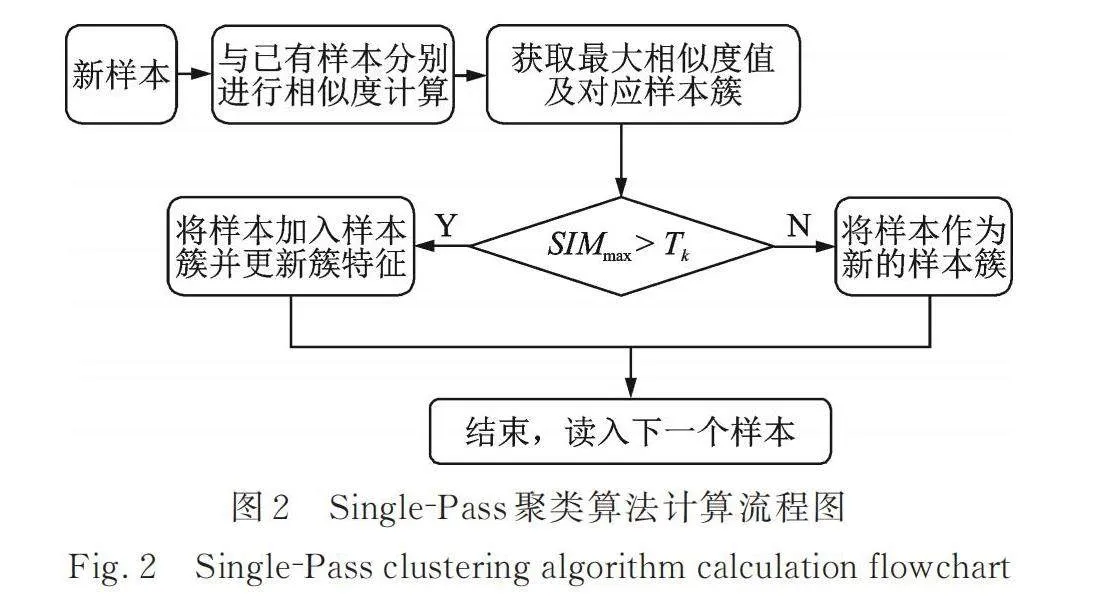
Single‑Pass聚类算法是一种增量聚类算法（Incremental Clustering Algorithm），常常被用于针对网络文本数据的聚类［18］。该聚类方法是流式数据聚类的经典方法，对于依次到达的数据流，该方法按输入顺序每次处理一个数据，依据当前数据与已有聚类簇的匹配度大小，将该数据聚类进已有的聚类簇或者创建一个新的聚类簇，实现流式数据的增量和动态聚类。聚类样本集中的每个样本只需要经过该算法计算一次。

根据稳定图中虚假模态的分布特性，设计了如图2所示的Single‑Pass聚类算法。

该算法的具体步骤如下：

（1）依次从目标样本集S = ｛s1， s2， …， sn｝中导入新的样本数据si，如果是第一个样本s1，则以该样本数据作为种子创建第一个样本簇；

（2）用新样本si的数据与已建立的样本簇之间分别进行相似度SIM计算；

（3）获取其中最大的相似度值SIMmax以及对应的样本簇Ck；

（4）将最大相似度值SIMmax与对应的样本簇Ck的簇特征阈值Tk进行比较，如果SIMmax大于Tk则将新样本si聚类进样本簇Ck并更新样本簇特征阈值Tk，否则将新样本si作为种子创建新的样本簇；

（5）流程结束，导入下一个样本si+1；

（6）所有样本聚类完成后，通过设置最小样本簇规模，滤除样本数小于最小样本簇规模的样本簇，即噪声点和孤立点；

（7）样本集S聚类完成。

3 虚假模态消除算法的验证

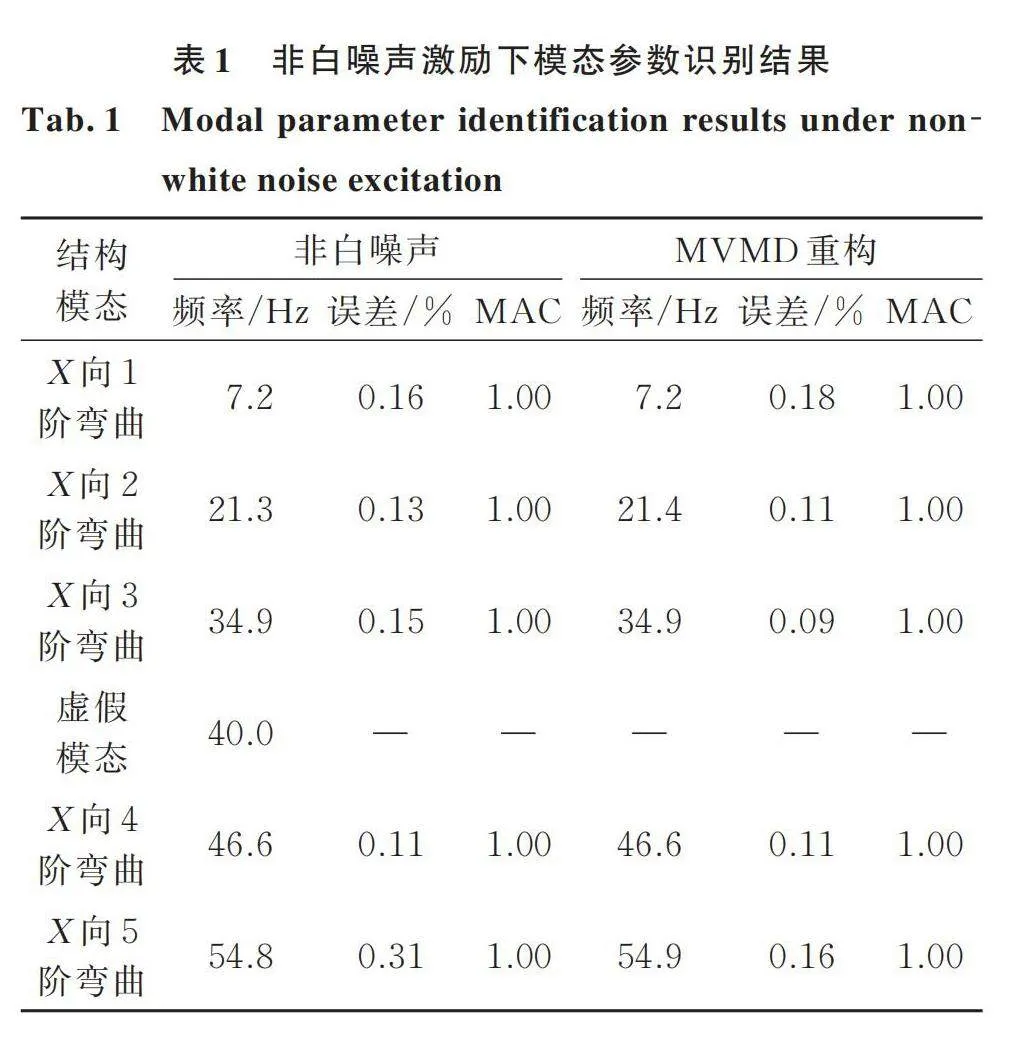
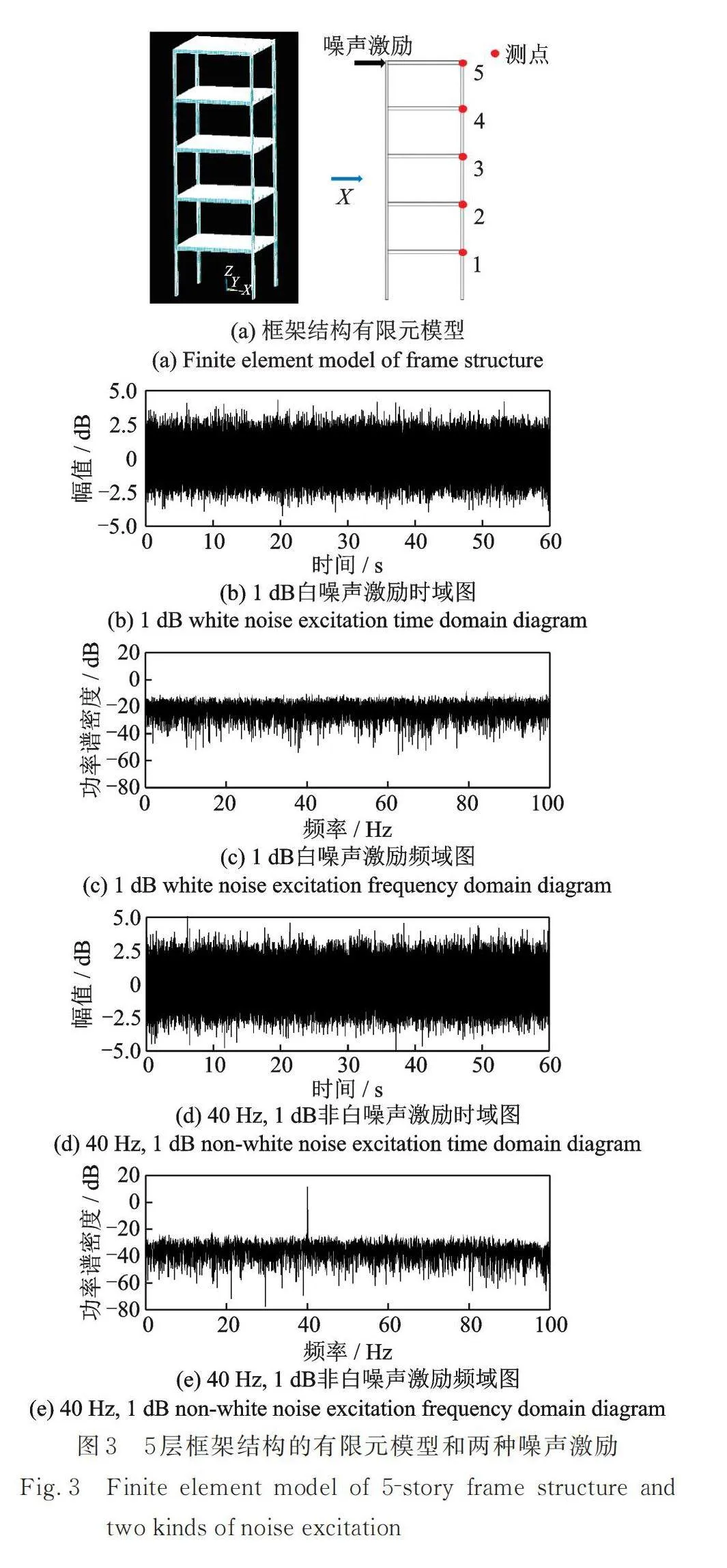
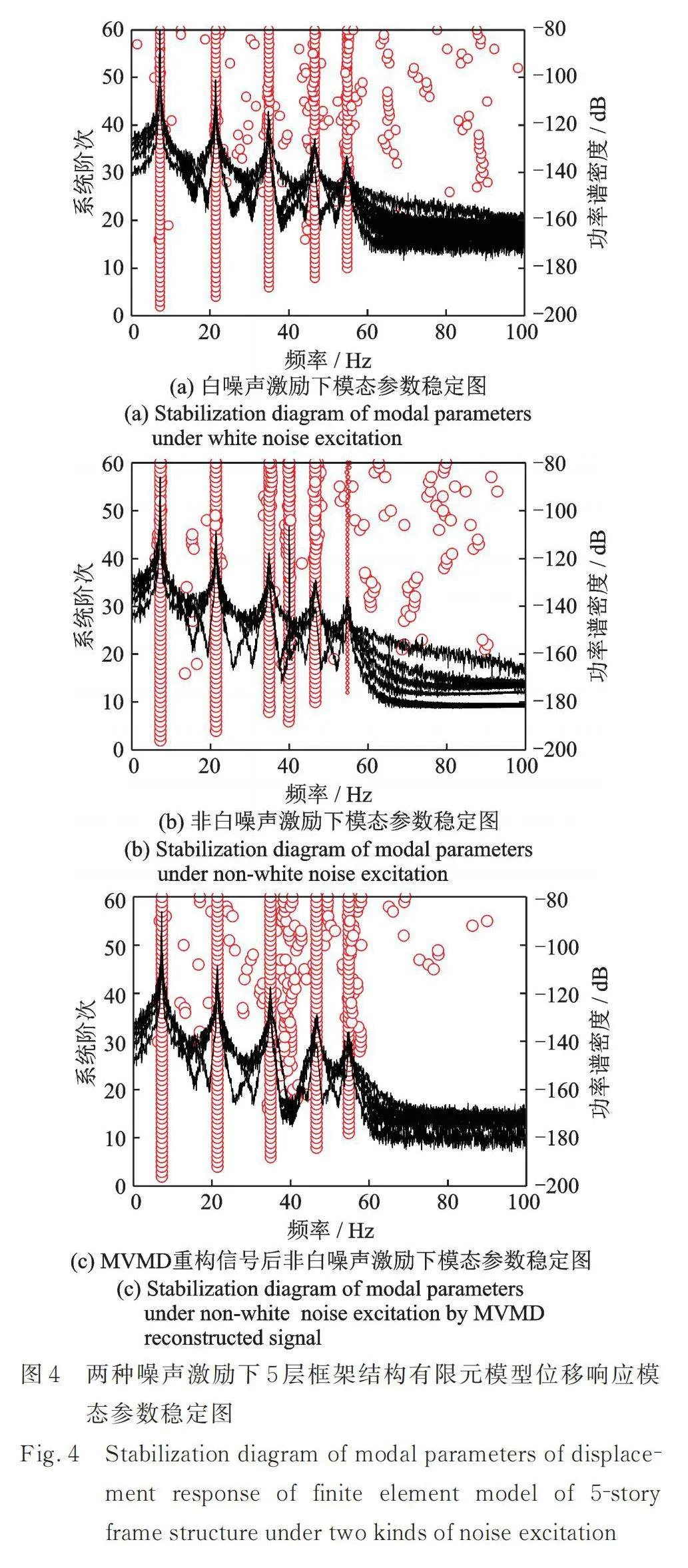
为了验证第2节所述方法的可行性，本文以一个5层框架结构的有限元模型作为数值仿真对象，该模型高1.8 m，长、宽皆为0.46 m。分别采用1 dB的白噪声激励和40 Hz，1 dB的非白噪声激励对模型进行X方向瞬态分析，并提取模型每层的位移响应信号。结构模型以及瞬态分析实验示意图如图3（a）所示；实验采用1 dB的白噪声激励的时域图和频域图分别如图3（b）和图3（c）所示；40 Hz，1 dB的非白噪声激励的时域图和频域图分别如图3（d）和图3（e）所示。通过随机子空间算法分析模型位移响应信号，获得模型分别在白噪声激励和非白噪声激励的各阶次模态参数稳定图，结果如图4（a）和图4（b）所示。

对比两种工况下的稳定图可以清晰地看到，在40 Hz非白噪声激励下模型位移响应中含有明显的40 Hz信号。该信号不是结构的固有模态响应信号，但是会作为虚假模态混在模态参数识别结果中，其在稳定图上表现出来的特点与结构的固有模态相同，无法将其从模态参数识别结果中分辨出来。于是采用MVMD方法对初始响应信号预先进行信号重构，然后再进行模态参数识别。通过MVMD处理后在非白噪声激励下5层框架结构有限元模型位移响应模态参数稳定图及识别结果分别如图4（c）与表1所示。

表1 非白噪声激励下模态参数识别结果

由图4（c）可以看出MVMD重构的信号既完整保留了结构模态响应，又消除了非白噪声激励产生的40 Hz虚假模态。该有限元模拟实验验证了采用多元变分模态分解方法抑制非白噪声产生的虚假模态的可行性。表1给出了非白噪声激励和MVDM重构后的频率识别误差，可以看出，频率识别精度最大可提升0.15%。

为了对比Single‑Pass聚类算法的有效性，在输出响应中加入5 dB的噪声。应用Single‑Pass前、后的稳定图如图5所示。

对比图5（a）和图5（b）可以看出，零散的虚假极点被有效消除。

4 高层结构动力特性自动跟踪

深圳市某大厦坐落于深圳市福田区繁华地段，结构的建筑物屋面标高为291.6 m，含顶部钢结构桅杆标高为353 m。结构共有76层，其中地下4层，地上72层，1～10层为裙楼， 72层屋顶部设有直升机停机坪。主体结构采用规整的正方形切角八边形平面，建筑与架构紧密结合，使用钢管混凝土架构。

该结构在2021年5月18日发生异常振动后，作者第一时间在主体结构的19，34，49，63和70层分别安装了自行研制的分布式同步采集系统，获取结构24 h同步响应数据。

每个楼层包含一套北斗授时无线传输分布式同步长期在线监测设备，每层布置4个测点，每个测点包含2个水平加速度传感器，共8个水平向加速度传感器。

该系统24 h在线获取高层结构的响应，每10 min产生一组响应数据，采样频率为50 Hz，通过北斗卫星授时系统对所有测点进行对时获取同步数据。结构监测系统布置情况如图6所示，为了避免再次发生异常振动，其顶部钢结构桅杆目前已被拆除。

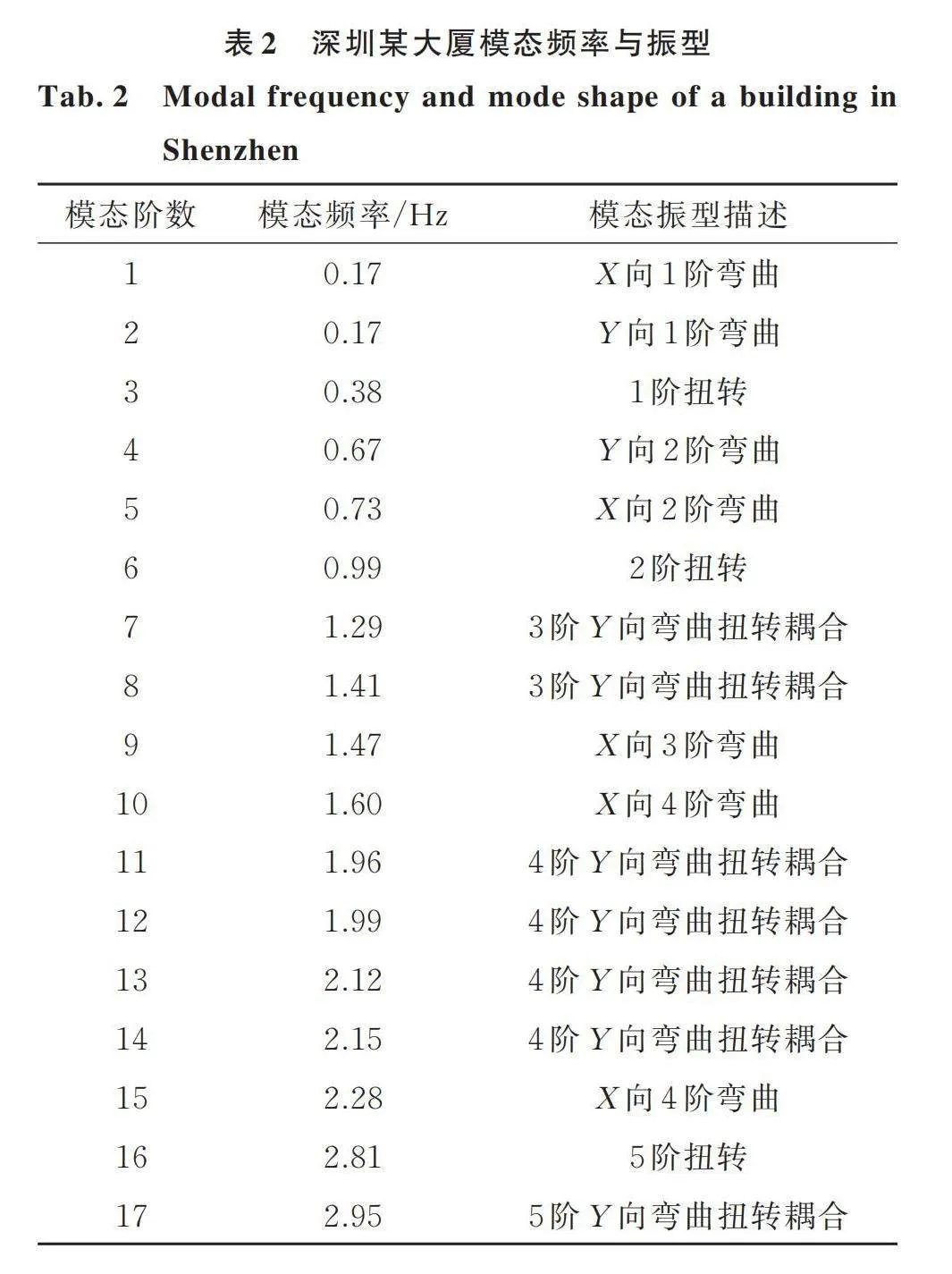
通过MVMD‑SSI方法计算监测系统采集的大厦加速度响应数据，获得大厦模态频率与振型如表2所示。

在对深圳市某大厦的监测过程中，存在着多种非白噪声环境激励，这些环境激励不可避免地在随机子空间方法模态参数识别过程中产生虚假模态。

在深圳市某大厦的结构健康监+Fbz0agNzhvKPGrWzz8mRg==测系统中获得非白噪声环境激励作用下的加速度采样信号如图7（a）所示，该例为大厦70层Y方向加速度采样信号。采用SSI方法分析图7（a）中的加速度采样信号，获得模态参数稳定图如图7（b）所示。

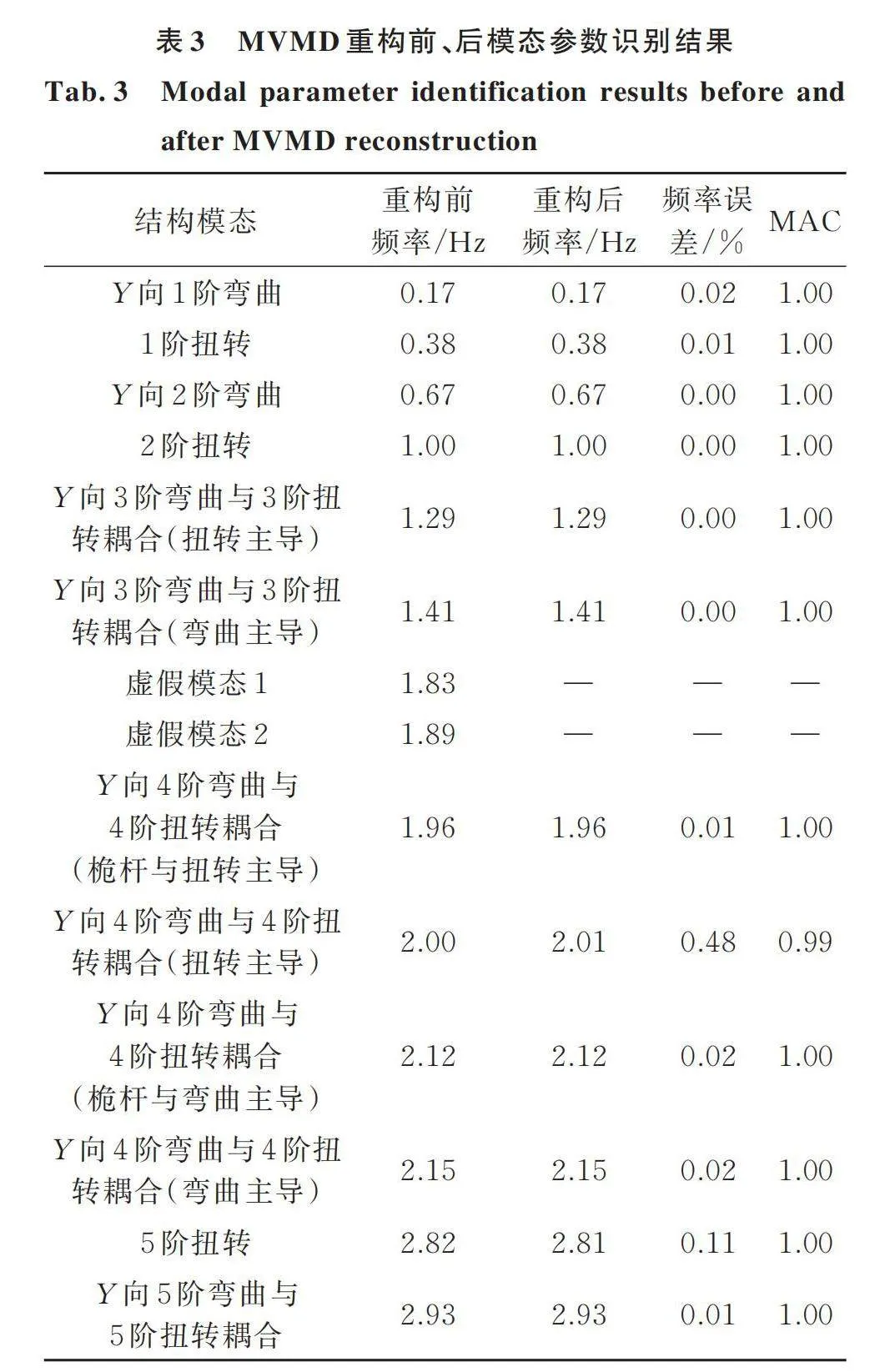
在图7（b）中的1.83和1.89 Hz频率附近出现了两列清晰的稳定轴，且在功率谱密度上有明显的能量峰。然而该高层结构本身并不存在对应频率的模态，因此这两个稳定轴是由非白噪声环境激励产生的虚假模态。

于是本文采用多元变分模态分解方法对该加速度响应信号进行信号重构，得到重构后的加速度响应信号如图7（c）所示。再次采用随机子空间方法分析MVMD重构后的加速度信号，获得模态参数稳定图如图7（d）所示。在图7（d）中1.83和1.89 Hz频率附近两列清晰的稳定轴已经消失，同时结构固有模态的稳定轴也变得更加清晰，具体的结构模态参数识别结果如表3所示。从表3的计算结果可以看出MVMD重构消除了虚假模态，同时完整地保留了大厦结构固有模态。

综合图7和表3可知，采用MVMD方法对结构采样信号进行信号重构能够有效抑制非白噪声环境激励产生的虚假模态，并且完整保留了结构模态响应。

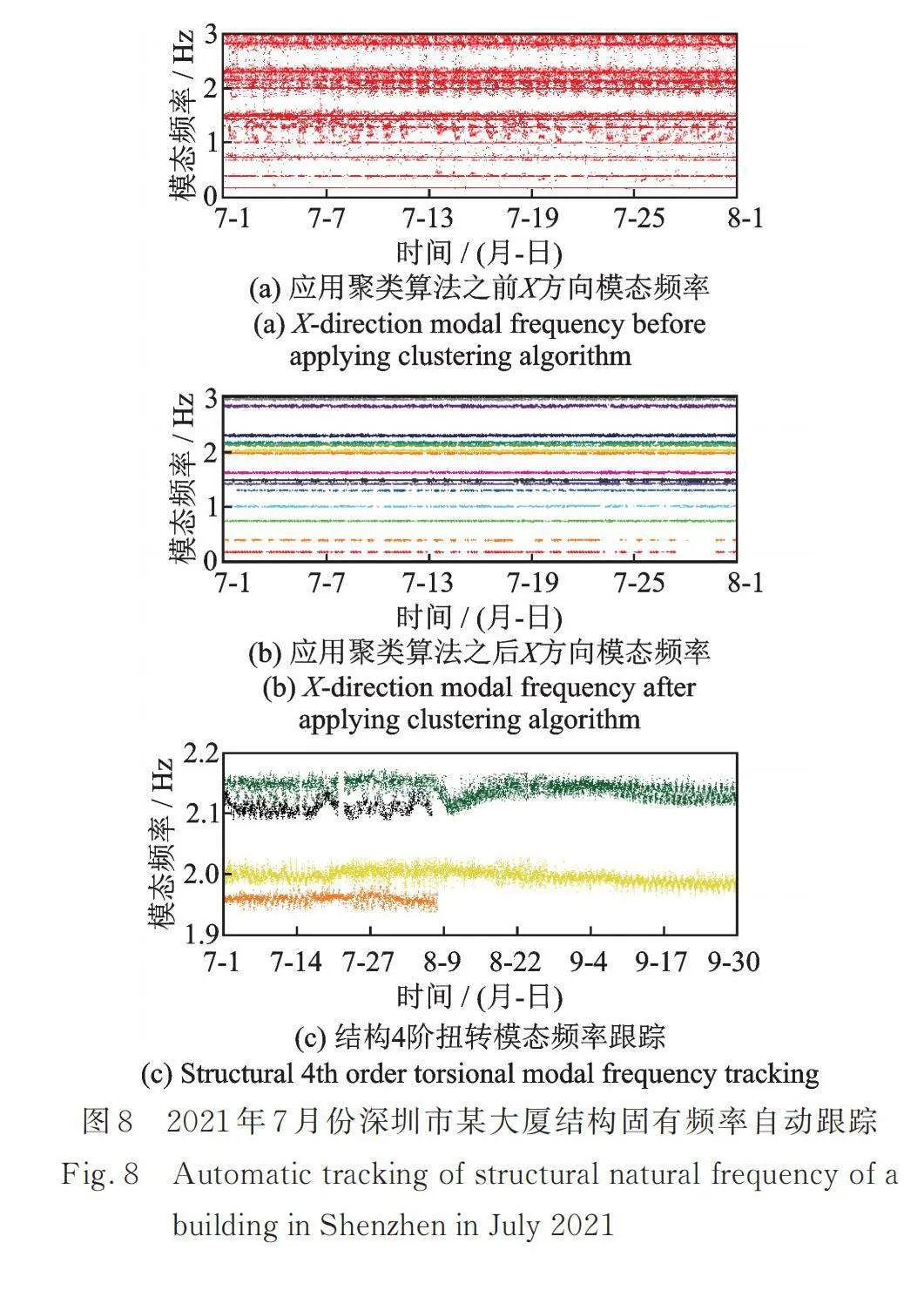
本文采用MVMD‑SSI方法，结合Single‑Pass聚类算法实现计算程序的自动化运行，分析深圳某大厦2021年7月份的加速度响应监测数据，跟踪结构各阶次模态频率在2021年7月份的变化情况，结果如图8所示。对比图8（a）和图8（b）可以发现，应用聚类算法后所有的虚假模态均被消除。由图8（c）可以看出桅杆拆除后的模态频率变化情况。

5 结 论

为了实现对高层结构动力特性的自动跟踪，本文提出了MVMD算法和Single‑Pass聚类算法相结合的结构动力特性自动跟踪方法。本文利用MVMD算法剔除由于非白噪声导致的虚假模态，通过Single‑Pass聚类算法剔除了其他因素导致的离散虚假极点，实现了虚假模态的有效消除，实现了动力特性的自动跟踪。

基于5层框架结构仿真模型和深圳市某大厦动力特性识别验证了MVMD‑SSI方法的可行性与Single‑Pass聚类算法在虚假模态消除上的有效性。将算法应用于深圳市某大厦的监测数据中，实现了结构频率的自动跟踪。本文所提方法可进一步推广应用于对高层结构动力特性变化规律乃至机理的研究。

参考文献：

［1］He Y H， Han X L， Li Q S， et al. Monitoring of wind effects on 600 m high Ping‑An Finance Center during Typhoon Haim［J］. Engineering Structures， 2018， 167： 308‑326.

［2］吴杰， 徐洪俊， 张其林.良态风和台风下的上海中心大厦动力参数分析［J］. 同济大学学报（自然科学版）， 2019， 47（8）：1100‑1105.

Wu Jie， Xu Hongjun， Zhang Qilin. Dynamic analysis of parameters of Shanghai Tower in normal wind and typhoon［J］. Journal of Tongji University（Natural Science）， 2019， 47（8）： 1100‑1105.

［3］谢壮宁， 徐安， 魏琏， 等. 深圳京基100风致响应实测研究［J］. 建筑结构学报， 2016， 37（6）： 93‑100.

Xie Zhuangning，Xu An，Wei Lian， et al. Study on full‑scale measurements of wind‑induced response of the Shenzhen Kingkey 100 Tower［J］. Journal of Building Structures， 2016， 37（6）： 93‑100.

［4］Hu W H， Xu Z M， Bian X H， et al. Operational modal analysis and continuous dynamic monitoring of high‑rise building based on wireless distributed synchronized data acquisition system［J］. Structural Control and Health Monitoring， 2022， 29（11）： 1‑31.

［5］胡卫华， 唐德徽， 李俊燕， 等.基于分布式同步采集的赛格大厦结构动力学参数识别［J］. 建筑结构学报， 2022，43（10）：76‑84.

Hu Weihua， Tang Dehui， Li Junyan， et al. Structural dynamic parameter identification of Saige building based on distributed synchronous acquisition method［J］. Journal of Building Structures， 2022，43（10）：76‑84.

［6］Bagchi S， Sabamehr A， Roy T B， et al. System identification of Concordia University EV building by operational modal analysis［C］∥Proceedings of 30th International Conference on Adaptive Structures and Technologies. Montreal， Canada： 2019.

［7］Aguilar R ， Solís M ， Chácara C ， et al. Structural evaluation of an earthen building from operational modal analysis［C］∥Proceedings of the 32nd IMAC Conference on Structural Dynamics. Orlando， USA， 2014： 71‑79.

［8］Zhang X L， Zhou W S， Huang Y， et al. Automatic identification of structural modal parameters based on density peaks clustering algorithm［J］. Structural Control and Health Monitoring， 2022， 29（12）： 1‑19.

［9］茅建校， 桂桂， 王浩， 等. 大跨度斜拉桥模态参数长期追踪及其变异性分析［J］. 振动工程学报， 2024， 37（1）： 52‑59.

Mao Jianxiao，Gui Gui，Wang Hao，et al. Long‑term tracking and variability analysis of modal parameters of a long‑span cable‑stayed bridge［J］. Journal of Vibration Engineering， 2024， 37（1）： 52‑59.

［10］胡异丁， 李丹， 任伟新， 等. 基于延时随机子空间方法的非白噪声环境激励结构模态参数识别［J］. 振动与冲击， 2015， 34（8）： 71‑76.

Hu Yiding， Li Dan， Ren Weixin， et al. Modal parameter identification of structures under non‑white noise ambient excitations using delay‑index‑based stochastic subspace method［J］. Journal of Vibration and Shock， 2015， 34（8）： 71‑76.

［11］Teng J， Tang D H， Zhang X， et al. Automated modal analysis for tracking structural change during construction and operation phases［J］. Sensors， 2019， 19（4）： 927.

［12］Peeters B. System identification and damage detection in civil engineering［D］. Brussels： Katholieke Unversiteit Leuven， 2000.

［13］Maybeck P S. Srochastic Models Estimation and Control［M］. New York： Academic Press， 1979.

［14］Pridham B A. State space modeling and identification of stochastic linear structural system［D］. Hamilton： McMaster University， 2004.

［15］李丹. 非白噪声环境激励下的结构模态参数识别［D］. 长沙：中南大学， 2012.

Li Dan. Structural modal parameter identification under non‑white ambient vibration［D］. Changsha： Central South University， 2012.

［16］Rehman N U， Aftab H. Multivariate Variational Mode Decomposition［J］. IEEE Transactions on Signal Processing， 2019， 67（23）： 6039‑6052.

［17］赵峰， 王雅娴， 王英， 等. 基于改进MVMD‑SOBI算法的直驱风电机组多通道次同步振荡模态辨识［J］. 高电压技术， 2022， 48（4）： 1365‑1374.

Zhao Feng， Wang Yaxian， Wang Ying， et al. Multi-channel sub‑synchronous oscillation mode identification of direct-drive wind turbines based on improved MVMD and SOBI Algorithms［J］. High Voltage Engineering， 2022， 48（4）： 1365‑1374.

［18］李天怡， 应文豪. 基于改进Single‑Pass算法的新闻话题演化跟踪算法［J］. 电脑知识与技术， 2021， 17（10）： 26‑29.

Li Tianyi， Ying Wenhao. News topic evolution tracking algorithm based on improved Single‑Pass algorithm［J］. Computer Knowledge and Technology， 2021， 17（10）： 26‑29.

Automatic tracking of dynamic characteristics of high‑rise structures based on MVMD‑SSI and Single‑Pass clustering method

HU Wei‑hua1，2， ZHANG Zhen1， TANG De‑hui1， LU Wei1，2， TENG Jun1，2

（1.College of Civil and Environmental Engineering， Harbin Institute of Technology （Shenzhen）， Shenzhen 518056， China； 2.Guangdong Provincial Key Laboratory of Intelligent and Resilient Structures for Civil Engineering， Shenzhen 518056， China）

Abstract： Stochastic subspace identification （SSI） generates spurious modes in the process of identifying the dynamic characteristics of high‑rise structures， which interferes with the automatic tracking of dynamic characteristics. This article has proved that the non‑white noise excitation is one of the causes of spurious modes， and further proposed a signal reconstruction method based on multivariate variational mode decomposition （MVMD） for non‑white noise excitation， which removes the influence of non‑white noise excitation in signals and eliminates spurious modes. A Single‑Pass clustering algorithm is proposed to eliminate discrete spurious poles. The above algorithm has been applied to on‑site monitoring data of super high‑rise structures， achieving long‑term automatic identification and tracking of dynamic characteristics.

Key words： high‑rise structures； stochastic subspace identification；multivariate variational modal decomposition；dynamic performance；automatic tracking

作者简介： 胡卫华（1978—），男，博士，副教授。 E‑mail： huweihua@hit.edu.cn。

通讯作者： 滕 军（1962—），男，博士，教授。电话：（0755）26033806； E‑mail： tengj@hit.edu.cn。