拓展思维 提升素养
2024-10-10徐丽


摘要:在课堂教学中培养、发展和拓展学生的数学思维,就是教会学生用数学的观点去思考和解决问题,从而发展和提高数学核心素养.文章研究者结合“实际问题与一元一次方程(1)”的教学,阐述如何拓展思维、提升素养深度.
关键词:数学思维;一元一次方程;实际问题
数学学科从本质上来说是一门“教思维”的学科,培养、发展和拓展学生的数学思维,就是教会学生用数学的观点去思考和解决问题,从而发展和提高数学核心素养.对于一节课而言,问题情境的创设是着力点,可以启发学生的数学思考,引领学生经历思维探究的过程,从而有效拓展数学思维.
下面,以“实际问题与一元一次方程(1)”的教学为例,从学生的思维起点着手,深度剖析教学环节,以问题探究过程呈现学生的思维历程,培养学生的抽象思维、类比思维、有序思维及创新思维,提高数学核心素养[1].
环节1情境导入,兴趣盎然
背景:“新学期,新气象”.为了给每个同学营造一个良好的学习环境和锻炼的机会,全校准备开展一次大扫除活动.若按照以往的分工方法,初一(1)班是将全班分成2个小组,甲组26人打扫包干区,乙组22人打扫教室.但这次由于教室需要深度清洁,因此乙组的人数需是甲组的2倍,那么该如何分配?
学生独立思考.
师:同学们,你们觉得应该如何表示甲组和乙组的人数及其关系呢?
生1:我觉得可以用x表示甲组的人数,那么乙组的人数就是2x.
师:很好,这是一个很好的代数表达方式.那么,根据题意我们能得到关于x的什么代数式呢?
生2:利用重新分配前后的总人数相等,可以得到一个关于x的等式.
师:这个想法很好,谁愿意分享一下你的成果?
生3:我认为如果甲组现在有x人,乙组就是2x人,那么可以得到x+2x=26+22这个等式,解得x=16,所以甲组是16人、乙组是32人.
师:有什么要补充的吗?这是最终答案吗?
生3:哦,这个不是最终答案,这是分配后的人数,题目问的是怎么分配,答案应该是将甲组的10人分配到乙组.
师:很好!这是最终答案.通过刚才的讨论,可以看出这是一个一元一次方程的应用问题.今天我们就来学习如何建立并求解这类问题.
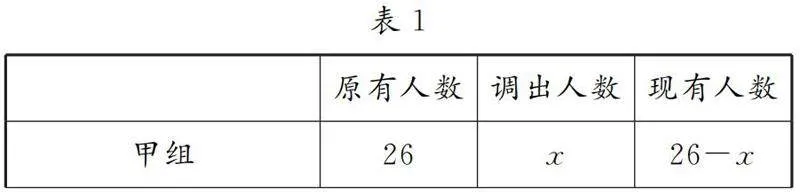
接下来结合图1讲解这类应用题的求解过程,并重点指出:设未知数和找等量关系是列方程的突破点,未知数的设法不同或等量关系不同,所列的方程就可能不同.尽管方程不同,但都可以通过解方程得到实际问题的最终结果.
评析:教学中我们需激发学生的好奇心、求知欲,促使学生积极主动地参与到数学探究中,自主自发地探寻解决问题的途径.这里,教师结合现实生活创设的问题情境极好地激起了学生的学习动机,让学生在简单的数量关系探寻中体会成功的快乐,从而切实感知到“方程这个有效模型是对现实世界数量关系的刻画”,为后续的思维活化做足准备.
环节2渐深探究,有效生成
继续以设置的背景来引导学生思考.
教师追问1:仔细审题,看看你还可以怎么设未知数或列出不同的方程.
学生思考并讨论,但没有新结果.
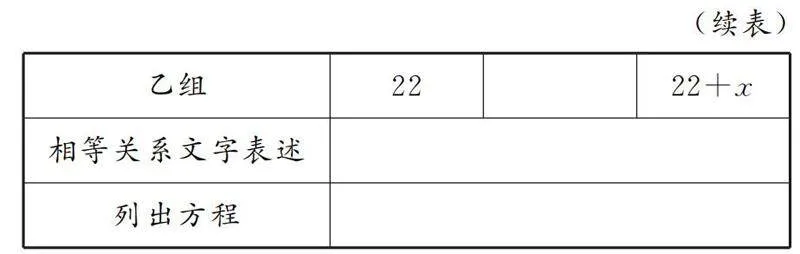
教师追问2:刚才我们通过间接设法来转化问题求解,现在若设从甲组调出x人去乙组,你能把表1填写完整吗?
生1:相等关系可以是“现乙组人数=现甲组人数的2倍”.
生4:我可以列方程为22+x=2(26-x).
评析:大量研究表明数学思维常常无法主动发生,这就需要教师为学生的数学思考提供素材,使学生在引导性材料下深度思考,有效生成.这里,教师适时追问,为学生提供渐深探究的素材和自主探究的时空,让学生在自主解题的过程中感受设元的多样性.
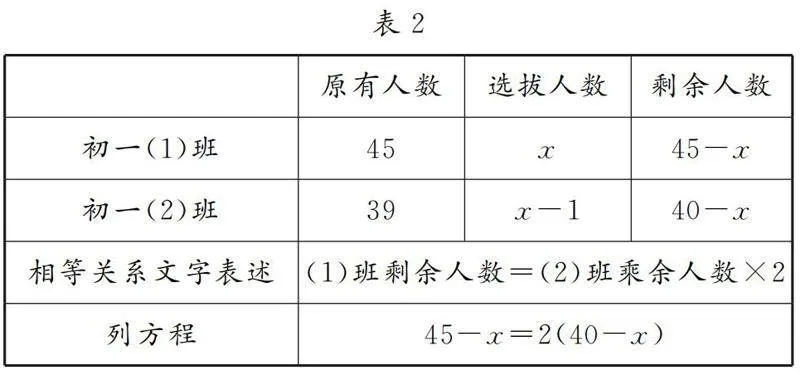
问题背景:某初中初一年级(1)班有45人,(2)班有39人.近期学校打算排一个合唱节目,打算从(1)班和(2)班选拔部分学生参加排练.若(1)班比(2)班多选拔了1人,则(1)班剩余人数刚好是(2)班剩余人数的2倍,(1)班选拔了多少人?(2)班呢?
师:你得到了哪些数量关系?还有没有隐藏的数量关系?怎样用代数表达式表示这些数量关系?
生5:(1)班选拔人数=(2)班选拔人数+1.
生6:(1)班剩余人数=(2)班剩余人数×2.
师(追问):还有吗?谁还发现了其他数量关系?
生2:(1)班选拔的人数+剩余人数=45.
生7:(2)班选拔的人数+剩余人数=39.
师:显然,这一题的数量关系更加复杂了,有没有好方法可以帮助我们厘清这些数量关系?
有了前面的探究经验,学生很快提出“设未知数,制表格”的策略,生成表2与表3.
评析:这个问题也是人员调配问题,只是数量关系越发复杂起来,尽管学生可以轻松找到解题的策略,但找出等量关系是需要深入思考的.有了前面列表的经验,学生很快就能完成数量关系的建立,在构建方程的基础上凝练思维.
环节3课堂练习,拓展认知
问题设计:初一(1)班负责打扫实验楼的有27人,负责打扫包干区的有19人.由于打扫任务繁重,现从外班调20人加入打扫,使得打扫实验楼的人数是打扫包干区人数的2倍,那么往实验楼、包干区各调了多少人?
师:请各位同学先独立思考并解答问题.
学生思考并解答.
师:请各自小组成员互相讨论自己的解决方法和答案.
学生开始分组讨论并展示讨论结果.讨论结束后,教师总结问题的解答过程和结果,并重点强调建模的重要性和解题方法的灵活性,确保学生理解调配人数的具体过程和数学模型的建立,帮助学生巩固相关概念.
评析:课堂练习活动的主要目的在于有效突破本节课的重点和难点,帮助学生切实掌握本节课的关键点,从而让教学目标落到实处.这里,教师以一个变式问题引导学生深度探究,一方面为了检测学生的学习成果,另一方面则是为了让学生完整体验解决问题的全过程,以达到深化理解和发展思维的目的.
环节4课堂小结,升华认识
教师提出问题,让学生分组讨论并整理用一元一次方程解决实际问题的步骤.
…………
评析:教学中的课堂小结看似简单,实则不可忽视.巧妙而适当的小结可以帮助学生厘清知识结构,形成更加清晰的思路,进而构建属于自己的知识结构体系.这里,教师又一次引领学生共同构建知识框架,从而培养学生的抽象能力和反思能力.
总之,数学课堂教学的目的不仅在于知识技能的获取,还在于数学思维的开发与锻炼,我们唯有做到着眼整体、深入钻研、合理安排、巧妙设计、充分让学,才能最大限度地开发学生的创新思维、抽象思维等.只有这样,我们的教学才能达到应有的高度,学生才能在习得知识技能的同时拓展思维、提升素养.
参考文献:
[1]郭靖.浅谈小学数学教学中学生创新能力的培养[J].学周刊,2017(3):157-158.
