巧用几何画板，促进互动生成

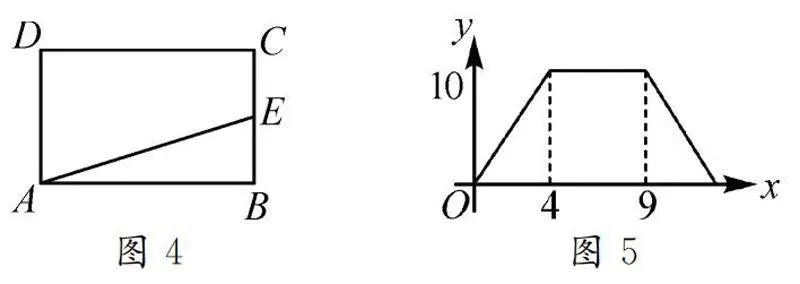
摘要：几何画板是一种绘制图形和动画展示的软件，在数学教学中的应用非常广泛.借助几何画板学生能够直观地感受图形的变化，从而形成更加清晰的认识，构建准确的解题思路.本文中对利用几何画板体验学习活动、构建解题思路、促成互动交流进行探讨，以提升学生的思维能力.

关键词：几何画板;活动体验;问题探究

数学学习以发展学生的核心素养为目标，因此数学学习不能仅仅依靠机械记忆、被动接受、重复练习的学习方式，而需要在自主探究和操作实践中不断提升自己的认知，深化知识理解[1].几何画板能够动态展示图形的变化，使抽象的图形变得更加具体，为学生自主探究、合作学习提供更加直观的学习资源.本文中以几何画板在教学中的使用为例，谈一谈运用几何画板加强师生互动、生成课堂智慧的教学策略，与各位仁交流.

1 注重活动体验，探究概念性质

数学活动是学生在实践操作中进行观察、分析、思考、探究的过程，通过数学活动的体验，学生在实践中发现问题，体会知识的生成和发展过程.数学概念和性质具有抽象性和概括性的特征，几何画板的运用，为学生体验数学活动提供了更加丰富的资源和便利的条件，使抽象的数学概念变得更加具体、直观，强化了学生的体验.

案例1运用几何画板探究旋转概念

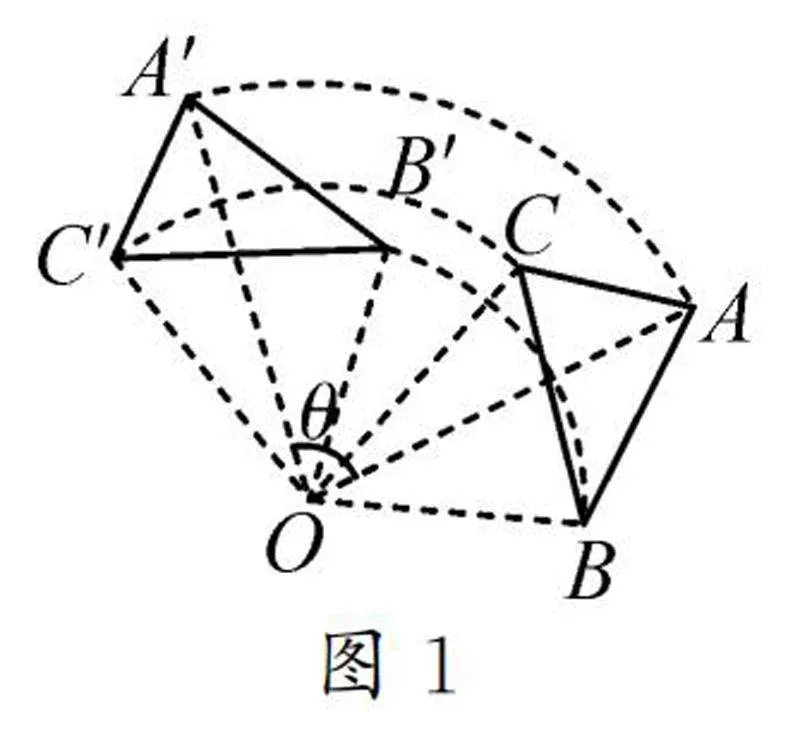
例1如图1，打开几何画板，建立参数θ，将△ABC绕点O旋转θ角度之后形成的△A′B′C′画出来，标上旋转的中心点O.

问题1根据刚才的作图过程，请你说一说什么是旋转.

生1：旋转是指在一个平面内，一个图形围绕固定的点进行一定角度的旋转，从而改变原来图形位置的过程.

师：很好！在旋转的概念中，旋转围绕的固定点称作旋转中心，旋转的角度称作旋转角.原图中的点A在旋转之后形成点A′，这两个点称作对应点，如点B和B′、点C和C′都称为对应点.请大家运用几何画板分别测量出点A和A′、点B和B′、点C和C′到旋转中心的距离，并将测量的结果记录下来.

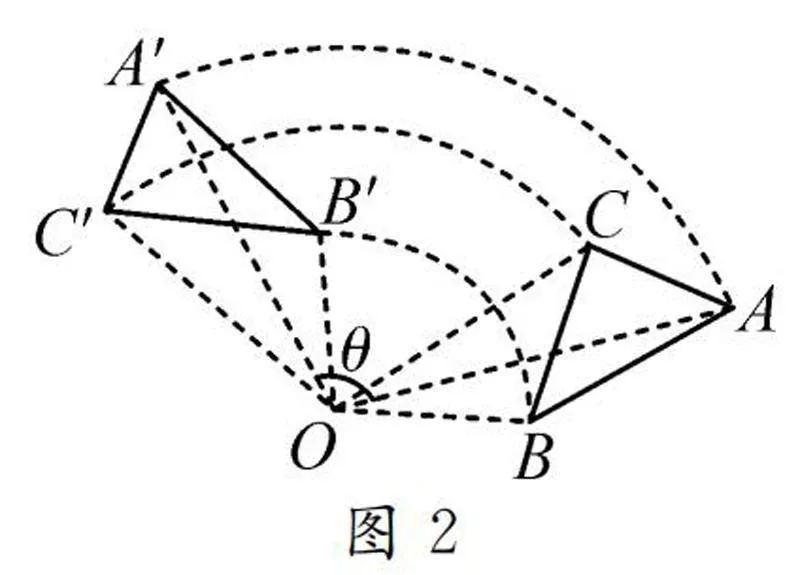
生2：图1中，OA=OA′=8.07 cm，OB=OB′=5.18 cm，OC=OC′=5.96 cm；图2中，OA=OA′=10.65 cm，OB=OB′=5.18 cm，OC=OC′=8.37 cm.我们可以看到无论三角形的形状和大小如何变化，对应点到旋转中心的距离都是相等的.

师：非常好！这就是旋转的第一个性质，即对应点到旋转中心的距离相等.

师：下面我们研究对应点与旋转中心的连线形成的∠AOA′，∠BOB′，∠COC′之间的关系，请大家将度量的结果记录下来.

生2：经过测量，图1中∠AOA′=∠BOB′=∠COC′=80°，图2中∠AOA′=∠BOB′=∠COC′=100°.我们发现虽然三角形的大小和形状不同，旋转的角度也不同，但是对应点与旋转中心的连线形成的角度始终相等.

师：由此我们可以得到旋转的第二个性质，即旋转对应点与旋转中心的连线形成的角相等.

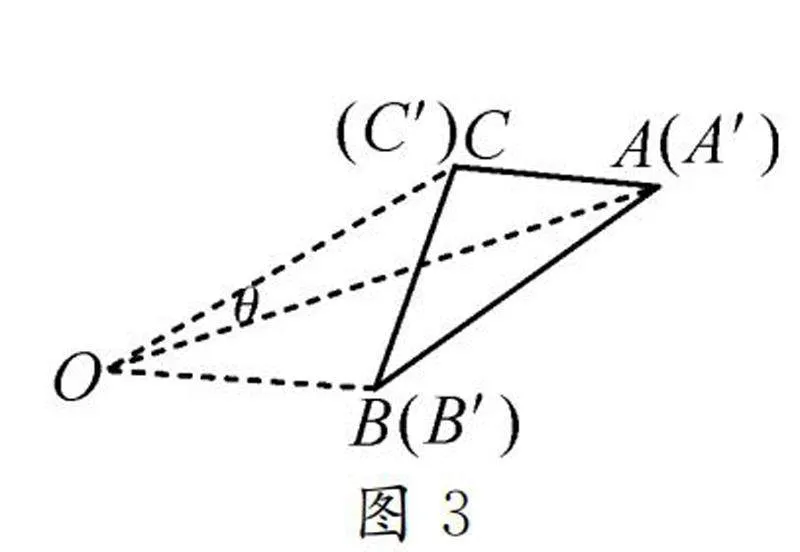
问题2当我们改变旋转角度θ，使得θ=360°，如图3，这时△ABC和△A′B′C′完全重合，因此两个三角形全等，请大家通过几何画板度量进行证明，并归纳旋转的第三个性质.

生3：经过度量可以得到图3中AB=A′B′，AC=A′C′，BC=B′C′.因此，旋转的第三个性质是三角形在旋转后形成的三角形与原图形全等.

2 理清解题思路，感悟数学思想

数学思想是对具体数学问题进行的高度概括和提炼，体现了数学的本质和规律.掌握数学思想方法是学习数学的目标，通过数学学习学生能够学会运用数学的眼光观察问题，并在不同情境中主动进行知识迁移，提升解决数学问题的能力.在教学活动中运用几何画板引导学生进行合作探究，从而理清解题思路，并形成更高层次的抽象与概括，发展学生的思维品质.

案例2运用几何画板教学一次函数

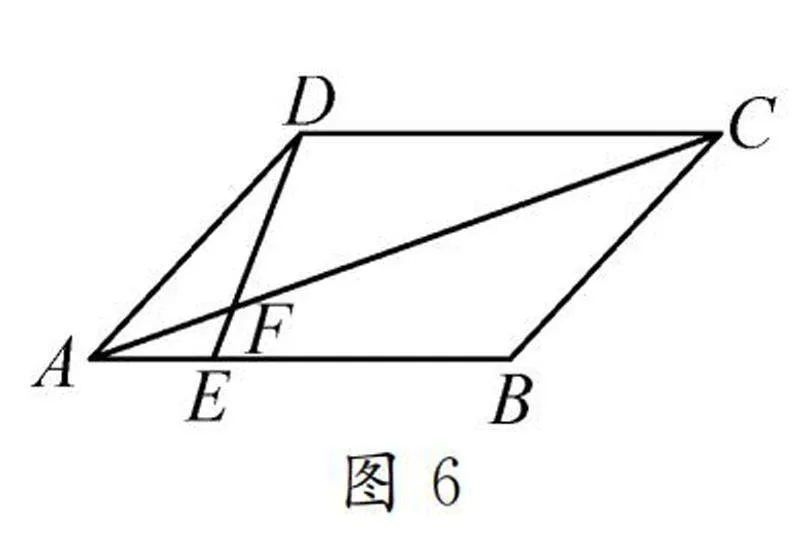
例2如图4，在矩形ABCD中，动点E沿BCDA的方向运动，直到点A处停止运动，设点E的运动路程和△ABE的面积分别为x和y，假设y关于x的函数图象如图5所示，判断下列哪个说法是不正确的.

（1）当x的值为2时，y的值为5.

（2）矩形ABCD的面积等于20.

（3）当x的值为6时，y的值为10.

（4）当y的值为15/2时，x的值为10.

解析：点E在矩形的三条边上运动，要判断以上结论是否正确，需要运用函数图象进行解析.

第一种情况：当0≤x≤4时，对应图5函数图象中的第一段，此时，点E在矩形的BC边上运动.利用几何画板拖动点E可知，△ABE的面积随着点E的运动路程BE的增大而增大，当点E到达点C时，x的值等于BC，△ABE的面积最大.根据函数图象可以知道，y随着x的增大而增大，当x的值为4时，BC的值最大，等于4.因此，当0≤x≤4时，一次函数的解析式为y=5/2x；当x等于2时，代入可得y的值为5，因此，（1）是正确的.

第二种情况：当4＜x≤9时，对应函数图象的第二段，这时点E在矩形CD边上运动.根据图象可知，y的值不变，即△ABE的面积不变，当点E运动到到D点时，x=BC+CD=9，则DC=5.

根据BC，DC的值分别为4和5，可以知道矩形ABCD的面积为20.

当4＜x≤9时，一次函数的解析式为y=10.当x的值为6时，y的值为10.

因此，（2）（3）是正确的.

第三种情况：当9＜x≤13时，点E在AD边上运动.利用几何画板拖动点E可以发现，△ABE的面积随着点E的运动路程x的增大而缩小，当点E与点A重合时，x的值为BC，CD，DA的和，等于13，此时△ABE的面积最小.根据函数图象可知，y随着x的增大而减小，并且x等于13时，y的值最小，点E到点A时停止运动.

当9＜x≤13时，函数的解析式y=5/2（13－x）=－5/2x+65/2.结合函数图象可以知道，当0≤x≤4和9＜x≤13时，两段函数的函数值都有等于15/2时，即y的值等于15/2.当y的值等于15/2，由5/2x=15/2或者－5/2x+65/2=15/2，可以解得x的值为3或者10，因此，（4）是错误的.

3 激发多维互动，生成课堂智慧

课堂教学是师生交流、生生交流的互动过程，有效的互动交流能够活跃课堂气氛，点燃思维火花，生成课堂智慧.几何画板的应用为师生互动交流创设了更加广阔的空间，提供了解决问题的多种途径，从而发展学生思维的灵活性.

案例3运用几何画板探究平行四边形中的相似问题

例3如图6，平行四边形ABCD中，AB上有一点E，AE/EB=1/2，DE与AC相交于点F，求AF∶FC的值.

（1）层层设问，深入挖掘

追问1：若△AEF的面积等于3，求△DCF的面积.

追问2：若△AEF的面积等于6，求△ABC的面积.

（2）变式练习，深化问题

变式训练如图7，平行四边形ABCD中，AB的中点为E，DE与AC相交于点F.

问题1：求EF/DF的值.

问题2：若△AEF的面积为4，求△DCF的面积.

问题3：若△ADF的面积为9，求△DCF的面积.

问题4：如图8，过点B作BH与DE平行，BH与AC相交于点G，与DC交于点H，若AC的值为12，求FC的长度.

参考文献：

[1]史宁中.数学基本思想18讲[M].北京：北京师范大学出版社，2011.