挖题根寻变式

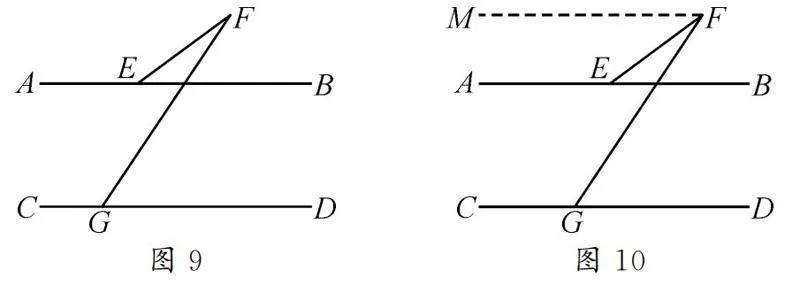
摘要：教师在课堂教学中一定不能就题讲题，可适当根据题目的特点进行变式教学，这是新课改实行一段时间后初中数学教师形成的普遍认识.本文中以折线截平行线中角的关系为例，一方面探讨教师在课堂实践中开展变式教学时需遵循的原则及方法，另一方面探究如何从题根出发实现变式.

关键词：题根；变式；折线；平行线

在平行线这一部分内容中，学生时常会遇见折线截平行线的问题，且这类问题的变式特别多.从学生的解决情况来看，教师应对学生加强这方面的训练.笔者建议使用变式教学法，以不断激发学生的数学思维.为此，本文中以折线截平行线为例，对如何变式及解题进行研究与分析.

1 变式教学法与变式

变式教学法是一种以变式为主的教学方法，是教师不就题讲题、不断拓展学生思维的重要体现.这需要教师不断挖题根，然后在题根的基础上进行变式.

从心理学的角度来看，变式就是将感性的材料通过不同的材料和方法重新进行组织，从而让学生对概念、方法等产生更深刻的理解[1].在初中数学中，题目的变化形式非常多，可从情境出发，也可从思维出发，还可从知识点出发，总之本质不变而形式与方法多变.另外，在变式时应遵循一定的原则，如导向性原则、启发性原则、探究性原则和创新性原则.

首先，导向性原则.教学是一种双向活动，主要参与者是学生和教师，二者围绕着教学目标开展活动[2].变式是作用于师生活动的方法，对教学目标的完成具有导向性作用，所以，变式需遵循导向性原则.

其次，启发性原则.教学是教师不断启发学生思维的过程.因此，教师在开展变式教学时，一定要精心设计问题情境，让问题不断启发学生的思维，从而帮助学生分析和解决问题.

最后，创新性原则.变式虽然是将题根进行变化，但每个变式都不同于题根，是一种创新.不仅如此，题根在变，解题方法也在变，所以变式也是方法的创新.

2 题根及解法示例

为了说明变式在课堂教学中的实践，本文中以折线截平行线为例，并将题根示例如下：

如图1，AB∥CD，试确定∠DGF，∠EFG，∠FEB之间的数量关系，并说明理由.

分析：由于三个角∠DGF，∠EFG，∠FEB无法构造在一个三角形中，因此应充分发挥AB∥CD这个重要条件的作用.此时，可作两种辅助线.一是过点F作AB的平行线，二是连接EG.

解析：如图2，过点F作AB的平行线FM.因为AB∥CD，FM∥AB，所以AB∥CD∥FM.由平行线的性质，可得∠BEF+∠EFM=180°，∠MFG+∠DGF=180°.而∠EFG=∠EFM+∠MFG，所以∠DGF+∠EFG+∠FEB=360°.

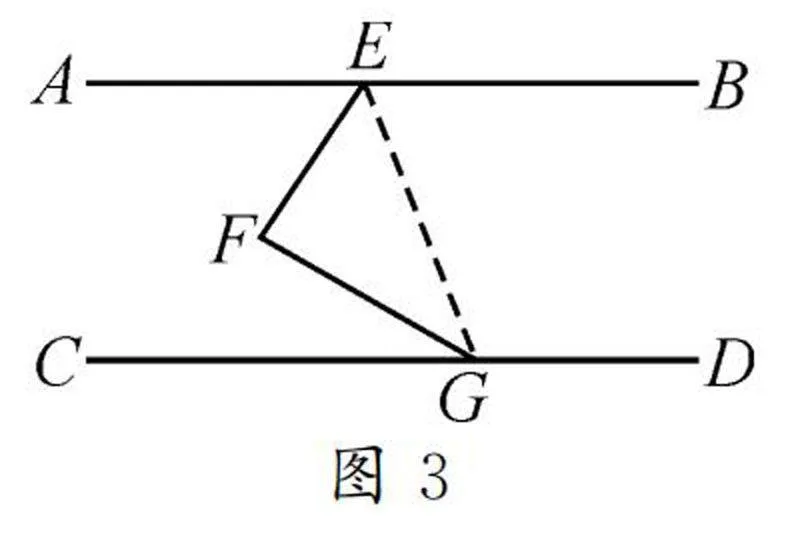
如图3所示，连接EG.因为AB∥CD，所以∠BEG+∠DGE=180°.因为△EFG内角和是180°，∠BEG+∠FEG=∠FEB，∠EGD+∠EGF=∠DGF，所以∠DGF+∠EFG+∠FEB=360°.

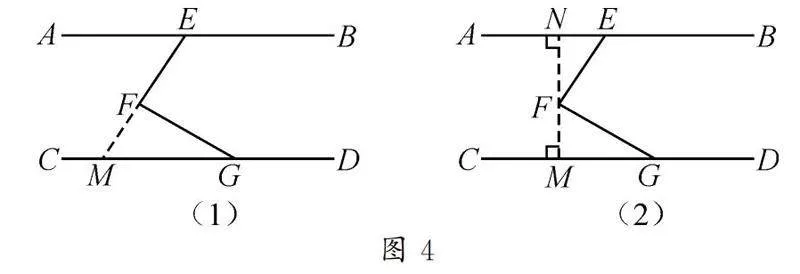
受图1、图2两种作辅助线的方法及两种不同解题思路的启发，本题还可作如图4所示的辅助线，同样可得到“∠DGF+∠EFG+∠FEB=360°”的结果.

3 根题挖掘

通过分析后发现，上述问题的题根是“给出平行线和折线的位置关系求角之间的数量关系”.于是，在这个题根基础上，就给出了两个对象，即两条互相平行的直线和一条折线，同时给出了一个问题，即求三个角之间的数量关系，考查了平行线的性质、判定等知识.同时，从图2、图3两种不同的解法也可看出，解决这类问题可构造平行线，也可构造三角形.甚至，由此拓展出来的图4对应的两种不同解法中，每种方法都综合了前两种方法，同样可达到解题的目的.

由此可得到变式思路，即题根变化、解法变化.首先，变化题根可改变折线的方向，还可将折线的位置由两平行线中间改为外面.其次，在解法上要求学生尽量一题多解.

4 变式呈现及解析

（1）折线在中间且向右

如图5所示，AB∥CD，试确定∠DGF，∠EFG，∠FEB之间的数量关系，并说明理由.

解析：如图6，过点F作AB的平行线，那么AB∥CD∥MF.由平行线的性质，可得∠BEF=∠EFM，∠MFG=∠DGF.而∠EFG=∠EFM+∠MFG，所以∠EFG=∠BEF+∠DGF.

（2）折线在外面且向左

如图7所示，AB∥CD，试确定∠DGF，∠EFG，∠FEB之间的数量关系，并说明理由.

解析：如图8，过点F作AB的平行线，那么AB∥CD∥MF.由平行线的性质，可得∠BEF+∠EFM=180°，∠MFG+∠DGF=180°.而∠EFG=∠MFG-∠EFM，所以∠EFG=∠BEF-∠DGF.

（3）折线在外面且向右

如图9所示，AB∥CD，试确定∠DGF，∠EFG，∠FEB之间的数量关系，并说明理由.

解析：如图10，过点F作AB的平行线.那么AB∥CD∥MF.由平行线的性质，可得∠BEF=∠EFM，∠MFG=∠DGF.而∠EFG=∠MFG-∠EFM，所以∠EFG=∠DGF-∠BEF.

5 反思与总结

课堂是师生不断互动的舞台，所以变式也应该体现出师生互动的过程.为此，笔者认为教师在进行变式或开展变式教学时，应注意以下几个方面：

首先，课堂活动中的变式教学是师生的双向活动，教师在变式时一定要围绕着教学目标进行，应考虑变式是否能帮助教师达到教学目标，是否能帮助学生弥补不足等.

其次，变式教学是为了更加激发学生的思维，让学生得到更深刻的启发.因此，在课堂实践过程中，可让更多的学生参与到变式讨论中.同时在学生讨论的过程，教师可收集相关意见，为接下来的变式提供内驱基础.

最后，变式就是创新，这种创新是否体现在题目改变或解法改变上，都需要教师深刻思考.例如，本文中的三种变式虽然图形发生了改变，但题目没有发生改变，方法也没有发生改变.因此，笔者建议教师应和学生一起就本文中的变式进行更深入的探讨或研究.

综上所述，变式不应局限于条件改变、要求改变，而应深入到解法改变等.只有这样，变式教学发挥的作用才会愈加明显，学生的思维才会被更有效、更彻底地激发，对学生的发展才会更有利.

参考文献：

[1]何珊.变式教学在初中数学“图形与几何”教学中的应用研究——以平行线为例[J].数学学习与研究，2022（16）：146-148.

[2]莘义成.数学试卷评讲课教学策略——以“相交线与平行线”试卷评讲课为例[J].中小学数学（初中版），2020（10）：56-59.