活用“割补法” 转化有思想

摘要：在华师大版九年级数学教材第27章“圆”中，有许多非常基础且是中考命题热点的知识，求圆中不规则图形的面积便是其中之一.本文中从学生提出的一道疑难问题出发，先分析该题的解题思路，挖掘其中蕴含的转化思想，然后以转化思想为指导探究圆中不规则图形面积的求法，旨在一方面为教师课堂教学提供更多有效素材，另一方面间接帮助学生克服这一障碍.

关键词：圆；不规则图形；面积；转化思想

在讲完“27.3圆中的计算问题”后，有位学生进行“弧长及扇形面积计算”的自主练习时，遇到了下面这道题，一时思路受阻，于是找到笔者，希望能得到一些指点.

如图1所示，已知圆形纸片的半径是2 cm，现将其沿着AB，BC翻折，并使得AB和BC正好都经过圆心O，那么，图中阴影部分的面积是（）.

A.2/3π cm² B.π cm²

C.4/3π cm² D.5/3π cm²

细观此题阴影部分的图形，不难发现该图形具有明显的对称美感.尤其该图与少先队员胸前佩戴的红领巾极其相似，瞬间将数学与实际生活联系起来.但在认真思考之后，发现要想求出阴影部分的面积并非易事，因为它是不规则图形.

1 思路探究

根据以往解决问题的经验，当几何问题中出现了不规则图形，通常采用转化思想来解决.根据转化思想，需要把不规则图形转化为若干个规则图形，然后通过各规则图形间面积的和或差求出不规则图形的面积.于是笔者引导学生进行如下观察：

图2观察一：A，B，C是圆上的三个点，它们到圆心O的距离有什么关系？（生：相等.）联系到圆中半径是非常重要的线段，所以不妨先将这三个点分别与圆心O连接，如图2.

观察二：连接OA，OB，OC后，你还有什么发现？（生：出现了三角形和弓形.）不难发现连接OB后，将下方柳叶状阴影部分分成了两个全等的弓形，而它们的面积之和正好与上方扇形AOC空白部分面积相等.

观察三：最初的阴影部分图形有怎样的变化呢？（生：此时图1中不规则的阴影部分的面积就转化为了规则图形扇形AOC的面积.）根据扇形面积公式，⊙O的半径已知，但圆心角∠AOC的大小未知.笔者引导学生思考如何求出∠AOC的大小，因为这已经成为了解决本题的关键.

观察四：笔者提醒学生结合条件并观察图形，思考∠AOC和∠ABC的关系、∠ABO与∠ABC的关系如何？（生：∠AOC=2∠ABC，∠ABC=2∠ABO，所以∠AOC=4∠ABO.）此时过O点作AB的垂线后，就可根据折叠性质及垂径定理得到∠AOC的大小.所以，还需如图3所示过点O作AB的垂线，垂足为D.至此，本题的解决思路探究结束.

2 解题及总结

2.1 解题

经过上述的探究，本题的解决思路已然形成，其解题过程如下：

图3解：连接OA，OB，OC，过点O作AB的垂线，垂足为D，如图3.根据折叠性质，易得OD=1/2OA.

∵OD⊥AB，且OD=1/2OA，

∴∠DAO=30°.

∴∠AOD=60°.

∵OA=OB，

∴∠BOD=60°.

∴∠AOB=120°.

同理，可得∠BOC=120°.

∴∠AOC=120°.

∴S=S=1205π522/360.

∴S=4/3π（cm²）.

故选答案：C.

2.2 总结

从解题过程来看，思路探究成功以后，解题过程其实非常简单，主要应用了以下几个知识点：

（1）利用了折叠性质.图形的折叠在初中几何问题中也非常常见，根据折叠前后图形的对称性，只需找到图中对应的角及对应的边，就可以将边、角进行转化[1].

（2）利用了垂径定理.垂径定理是解决与圆有关的计算或证明题的重要理论基础.本题借助垂径定理得到∠AOD=∠BOD.

（3）利用了直角三角形30°角的性质.由OD⊥AB且OD=1/2OA证得∠DAO=30°，逆用了直角三角形30°角的性质，是本题求扇形圆心角度数的关键.

（4）利用了扇形面积公式.扇形面积公式中最关键的两大因素是圆心角和半径，本题已知半径，而圆心角尚未可知.所以，通过逆用直角三角形30°角的性质解决了这一难题.

除此之外，本题解决思路中最值得反思与总结之处在于“割补法”和转化思想的运用.

在遇到不规则的图形时，常将其中某个部分的位置变动，或将图形进行分割、拼补，从而将不规则图形转化为规则图形来计算，这就是“割补法”，体现了转化思想[2].转化思想在初中数学问题中的运用非常普遍，主要是将未知转化为已知，将特殊转化为一般或将一般转化为特殊，进而将难度较大的问题转化为难度较小的问题[3].

例如，本题将不规则的“系红领巾”图形转化为规则的扇形，降低了解决问题的难度，同时又让学生体验了转化思想的魅力.

3 巩固与拓展

事实上，求扇形面积是“27.3圆中的计算问题”中非常典型的问题，学生会遇到许多求不规则阴影图形面积的问题，其解决方法都是利用“割补法”进行转化.如下面的两道题：

题1如图4所示，扇形AOB和扇形COD的圆心角共用顶点O，且它们的圆心角均为90°.连接AC和BD，如果OA=3，OC=1，试求图中阴影部分的面积.

图4图5

解题关键：本题易知△AOC和△BOD是全等三角形.如果将△AOC绕着点O顺时针旋转90°就得到了△BOD.于是，就形成了图5.接下来，只需求出图5中阴影部分的面积即可.

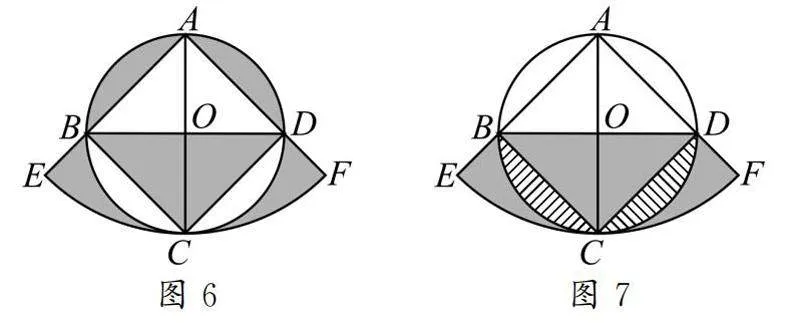
题2如图6所示，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，AC长为半径画圆弧，交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积为（）.

A.4π－8 B.4π－4

C.8π－4D.8π－8

图6图7

解题关键：首先观察图形，虽然阴影部分比较分散，但是可将直径BD以上的两个弓形阴影部分“补”到下方空白处，正好与下方已有阴影部分构成一个完整的图形，如图7.

4 结语

综上所述，“割补法”在解决几何图形的面积问题中发挥了重要作用.不仅如此，它体现出的转化思想也是数学素养中非常重要的内容.所以，利用“割补法”不仅可以灵活解决问题，而且能培养学生的思维，让他们在掌握转化思想之余，能不断提升数学素养.

参考文献：

[1]刘家良.求含圆弧的不规则图形的面积[J].初中生必读，2020（11）：28-29.

[2]李汉平.美丽的阴影部分图形——探究《圆》中阴影部分面积的求法[J].数学学习与研究，2016（6）：149.

[3]朱文文.如何求圆中阴影部分的面积[J].语数外学习：初中版，2020（11）：23-25.