妙用辅助圆，巧解数学中考题

摘要：当前课程的深化改革对初中数学提出了更高的要求，本文中主要以妙用辅助圆，巧解数学中考题为重点进行阐述，首先分析了问题背景和初中数学妙用辅助圆的意义，其次从结合圆定义构建辅助圆、结合圆性质转化实际问题、引入辅助圆解决有关角度和引入辅助圆求有关线段最值问题等几个方面深入说明并探讨.

关键词：初中数学；数学教学；辅助圆；圆的性质；巧解中考题

针对初中数学解题过程而言，很多数学题采用常规的思路都无法得出正确答案，需要通过分析和利用圆的特征，结合题目内容构建辅助圆才能获取正确答案.通过这样的解题方式能够进一步拓展学生的数学解题思路.圆作为几何中的一种特殊图形，具有一定的数学魅力，很多数学题目从表面观察似乎和圆没有太多的关系，但引入辅助圆之后能够将复杂的问题简单化，为学生带来一种流畅清晰的学习美感.

1 初中数学妙用辅助圆意义

很多初中数学题目都与“圆”这一知识有关，其中一些问题看似和圆之间毫无关系，但从题目条件出发需要构造辅助圆，能够起到化隐为显的作用[1].纵观初中学生解决问题中所遇到的困难原因，首先是解题信心不足.因为通过辅助圆解决的中考问题，这种数学题型和纯粹的计算问题存在一定的区别，对学生的数学能力有更高的要求；同时，通过辅助圆涉及到的中考题内容，有文字、图形等不同方式，其中隐藏大量的数量关系，很多初中学生在面对文字的描述内容时，都会感觉无从下手并且十分茫然.因此，学生在面对中考数学问题时，需要正确分析题中的信息，将其中的干扰语句清晰梳理出来，便于题意的直接判断，这样才能发挥出辅助圆对解决中考题的真正价值.其次，是阅读能力不足.中考题其中一个特点就是利用文字进行描述，其中会涉及到很多科学性语言，对学生自身的阅读理解水平有一定的要求.一些初中学生在面对需要利用辅助圆解决问题的中考题时，不能理解甚至不懂得其中专业词语的正确含义，不能结合文字画出正确的辅助圆顺利解决问题，这样就会造成一些对数学知识掌握不牢固的学生难以顺利完成问题解决.最后，是学生普遍建模能力较差.中考数学问题中，很多都是通过数据、文字语言进行表达，有时还会涉及到多种变量关系，对学生的建模能力有一定的要求，要学生通过数学语言理解中考题，分析数学语言之间的关系.但对于一些数学能力较差的初中生而言，很难在阅读题目中将数学知识进行全面性分析，难以发现问题解决的突破口，无法通过辅助圆完成数学模型的构建.

圆作为初中数学的重要组成部分，具有十分特殊的性质，可以辅助学生解决多种数学问题.如对于求线段长度、角度、最值问题，以及取点个数问题的解决，都发挥着搭桥铺路的作用.对于利用辅助圆求线段长度问题，主要是通过有共同端点的几条线段相等，将这一端点作为圆心，等线段长作为圆的半径，实现辅助圆的构建，再充分利用圆自身的特点解决问题.针对利用辅助圆求角度问题，求角度是中考不可缺少的一个考点，有些问题难度挺大，根据已知条件常常将公共顶点作为一个定点，作三角形的外接圆，通过等角和辅助圆之间的关系实现CKfh1e9l2jnJPCgl9Zvobg==对数学问题的解决.针对辅助圆求线段最值问题，这是初中几何中常见的等角求最值问题，要引导学生发现运动中的不变量，通过构造辅助圆，再利用三角形三边关系，可轻松得出问题的正确答案[2].

2 妙用辅助圆巧解数学中考题策略

2.1 结合圆的定义，构建辅助圆

如果初中生可以掌握画辅助圆的本质，那么解决数学问题就会比较简单.圆是初中数学的重要知识，但学生采用单一的常规方式完成问题解决存在一定的难度，也会浪费更多的时间，不利于学生在解题中积极性的建立.针对这一问题，通过引导学生构建辅助圆，能够将问题变得更加简单，加深学生对知识内容的理解.对于圆来说，描述性定义就是其中的一种，能够为学生构建辅助圆提供全面性支持.圆的描述性定义内涵，是将线段绕一个端点在平面内旋转一周，另一个端点所形成的图形叫做圆.对于定义中的旋转，在中考题中出现“旋转”变化，就可构造一个以旋转中心为圆心的辅助圆，进一步将问题适当转化，方便学生更加深入地完成探究[3].

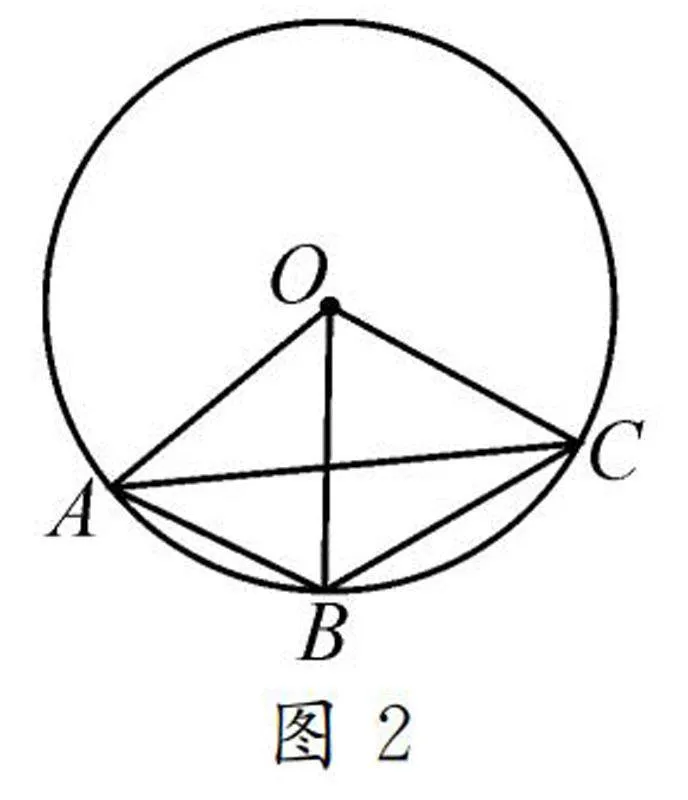
例1如图1，已知OA=OB=OC，∠AOB=50°，求∠ACB的度数.

常规思路：由OA=OB=OC，图中有三个等腰三角形，利用两底角相等，易求得∠OAB=∠OBA=65°，再设元或引进参量，利用三角形内角和定理得到一个数量关系，列方程求解，具体解法如下.

解法一：∵OA=OB，∠AOB=50°，

∴∠OAB=∠OBA=65°.

设AC与OB交于点D，∠ACB=x，∠OAC=y，

∴∠CAB=∠OAB－∠OAC=65°－y.

∵OA=OC，

∴∠OCA=∠OAC=y.

又OB=OC，

∴∠OBC=∠OCB=x+y.

∴在△BOC中，∠BOC=180°－2（x+y）.

∵∠CAB+∠OBA=∠BOC+∠OCA，

∴65°－y+65°=180°－2（x+y）+y.

∴x=25°， 即∠ACB=25°.

按上面方法求解此题，学生会有一定难度.我们如果以点O为圆心，OA为半径构造辅助圆，再利用圆的性质求解，就会把复杂问题简单化.

解法二：∵OA=OB=OC，

∴A，B，C三点在以点O为圆心，OA长为半径的⊙O上（如图2）.

∵AB=AB，

∴∠ACB= 1/2∠AOB.

∴∠ACB=1/2×50°=25°.

对比以上两种解答过程，可以发现根据圆的定义构造辅助圆解题比用常规方法简便很多，同时也印证了让学生掌握这种方法的必要性.

2.2 结合圆的性质，转化实际问题

对于圆的性质而言，主要在于圆周角、弧、弦等之间关系的转化，当遇到角、线段问题时，可以引入辅助圆，借助圆的性质可以更好地解决问题.其中，圆周角“动而不变”这一性质又能充分体现出在中考数学题中的价值[4].圆的性质中“一条弧所对的圆周角等于它所对的圆心角的一半”这一内容，同一条弧所对应的圆周角有无数个，虽然这些角的顶点位置发生变化但其角度不变，这就是“动而不变”性质，可引导学生从这一性质入手解决数学问题.

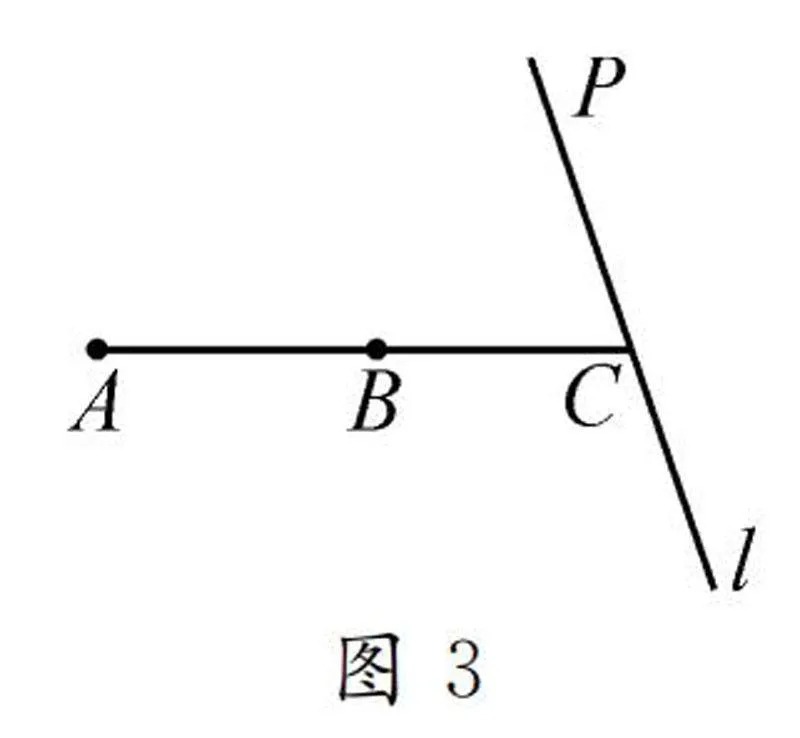
例2如图3，B是线段AC的中点，过点C的直线l和AC之间成60°的角，在直线l上取一点P，使得∠APB=30°，问满足这样条件的点P有多少个？

针对这一问题进行分析，主要求满足条件的点P的个数，需要以AB为边作一个等边三角形OAB，得到OA=OB=AB=BC，此时∠ABO=∠ACP=60°，OB∥l，然后以点O为圆心，OA为半径构造⊙O，当点O在AB上方时，如图4，⊙O与l有2个交点P，P，满足∠APB=1/2∠AOB=1/2×60°=30°.当点O在AB下方时，如图5，l与⊙O相离，没有符合条件的点P.所以符合条件的点P只有两个.

2.3 引入辅助圆，解决有关角度问题

对于初中几何，有时求角的大小也是一个难点，通常将一个顶点作为定点，进一步通过三角形完成外接圆的构建，把握好等角和辅助圆之间的关系，要求学生能够灵活综合运用圆的性质，即根据同圆或等圆中相等的圆周角所对的弧相等、所对的弦相等，构造辅助圆.这类题目隐蔽性较强，学生不易想到，对思维的要求较高.

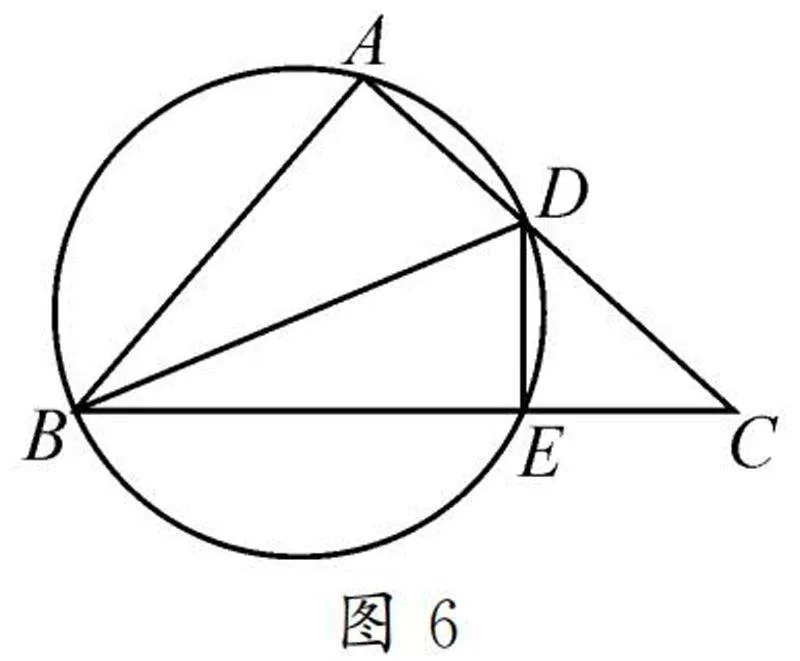
例3已知在△ABC中，AB=AC，∠ABC的平分线BD交AC边于点D，且BD+AD=BC，求∠A的度数.

对于此题，要引导学生分析已知条件，由BD平分∠ABC，得∠ABD=∠DBC.

联想到若作△ABD的外接圆，如图6，就可推出AD=DE.

由∠ABC+∠ADE=180°，∠EDC+∠ADE=180°，得到∠ABC=∠EDC.而∠ABC=∠C，所以∠EDC=∠C，于是DE=CE.

所以DE=CE=AD.

又因为BD+AD=BC，而BE+CE=BC，于是BD=BE.

设∠ABD=∠DBC=x，则∠BED=∠BDE=180°－x/2，∠ABC=∠C=2x，∠A=180°－4x.

由圆的内接四边形对角互补，得∠A+∠BED=180°，则

180°－4x+180°－x/2=180°.

解得x=20°，所以∠A=100°.

通过引入辅助圆，强化学生逻辑思维的有效提升，实现学生在知识和能力方面的共同进步，提高数学素养.

2.4 引入辅助圆，求有关线段最值问题

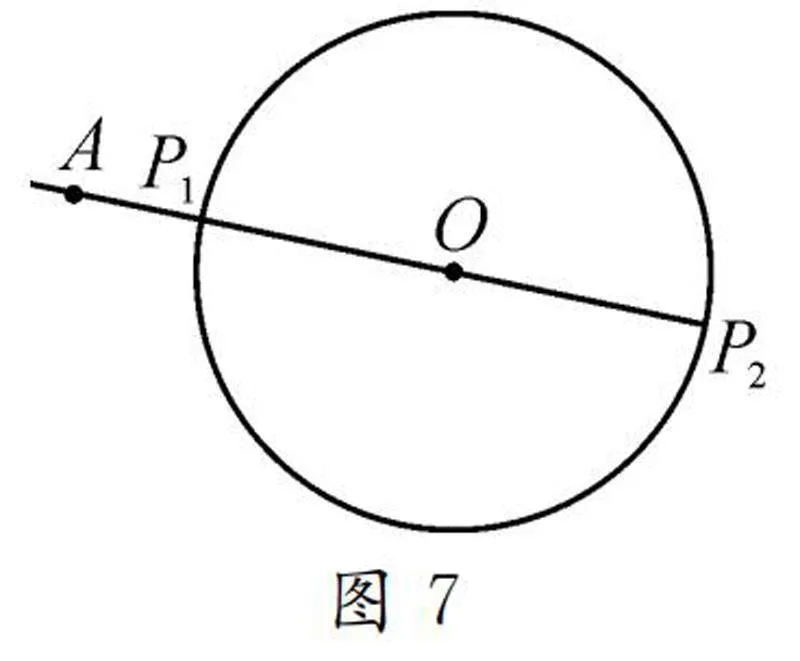
在中考几何解题中，求线段最值问题始终是个难点，学生对这类问题感到困惑，特别有一类求线段最值问题需要构造辅助圆来解决，很多学生无从下手.关于圆的性质，还要让学生掌握一个与圆有关的最值结论：连接圆外一个定点与圆上的各动点的所有线段中，过圆心UFsMeBvlXNWmFDULkK1fjQ==时线段取得最小值和最大值.

如图7中，A为圆O外一定点，P为圆O上的动点，我们可以作直线AO，使其与圆O有两个交点P，P，此时AP1为最小值，AP2为最大值，利用这个基本知识，可以解决某些最值问题.

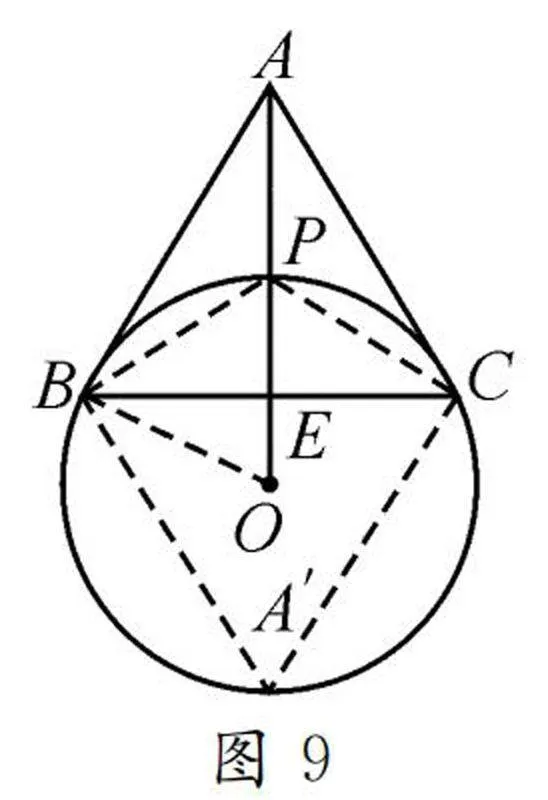
例4如图8所示，△ABC为等边三角形，AB=2，若点P为△ABC内一动点，且满足∠ABP=∠BCP，求线段AP的最小值.

此题已知条件较少，看上去较简单，但难倒了很多学生.分析后发现，∠ABP+∠PBC=60°，又∠ABP=∠BCP，可得∠BCP+∠PBC=60°.由内角和定理，可得∠BPC=120°.

我们会发现P虽然是动点，但∠BPC的度数保持不变，引导学生想到圆的一个性质：同弧或等弧所对的圆周角相等，也就是说角的顶点位置变了，但角度不变.所以点P运动的轨迹是一段弧，因此会很自然地想到构造一个辅助圆，可以在BC下方作等边三角形A′BC，然后作它的外接圆（如图9）.根据∠A′=60°，利用圆的性质，可得∠BPC=120°.

因为点P在△ABC内，所以我们只要选取弦BC上方的一段弧就行了，点P在弦BC上方的那段弧运动时，都能满足∠BPC=120°.当A，P，O三点不共线时，因为三角形的两边之差小于第三边，就有AP>OA-OP；当A，P，O三点共线时，AP=OA-OP，此时AP取得最小值[5].再利用等边三角形的性质和锐角三角函数知识即可求得，可以连接OB，OA=2/cos 30°=4/33，OP=OB=1/2OA=2/33，所以AP=OA-OP=2/33，即线段AP的最小值为233.

此题是几何中常见的等角求线段最值问题，学生要想到构造辅助圆，要善于发现运动中的不变量，挖掘有关信息，寻求解题思路，积累解题经验，以提高严谨的数学思维能力.

近年来，各省中考数学加强了对圆相关知识的考查，题型也比较创新和灵活.其中构造辅助圆常常出现在中考数学试卷中，是一种能够快捷且灵活地解决问题的方法，它可以将问题中的条件进行简单化呈现.只有引导学生通过圆的性质、定理之间内在的关系，加强结论和条件之间的关联性，从不同角度完成对问题的分析，这样才能促使学生在问题解决中取得更好的效果，实现学习效率和质量的有效提升，为学生今后的高中数学学习奠定坚实基础.

参考文献：

[1]刘怀权.“构造辅助圆”在初中数学解题中的应用[J].数理天地（初中版），2022（12）：21-22.

[2]张海营.巧构辅助圆：道是无“圆”却有“圆”[J].广东教育（综合版），2022（5）：47-48.

[3]林明新.巧作辅助线——辅助圆解决初中几何中的面积最值问题[J].数理天地（初中版），2022（7）：62-63.

[4]束浩东.有“圆”千里来相会[J].中学生数学，2022（6）：34-37.

[5]叶玉霞.探究点运动形成的路径问题构造辅助圆解决问题[J].理科考试研究，2021，28（22）：11-15.