探究式教学在数学教学中的应用

摘要：探究式教学是在“以生为本”的基础上，践行“立德树人”教育理念的一种教学方式.文章以“二次函数的认识”教学为例，分别从“旧知回顾，思维热身”“创设情境，引发探究”“练习训练，辨析概念”“应用概念，完善认知”“课堂总结，拓展延伸”五个环节展开探究式教学，并谈一些思考.

关键词：探究式教学；思维；探究

探究式教学是指学生积极参与课堂教学活动，主动探究教学内容，发展创新意识与实践能力的一种教学方式.这种教学方式更注重“探究”过程，学生通过独立思考或合作探究完成学习任务，这是一种化被动为主动的学习模式，学生在思维、情感等方面都体现出“主动性”[1].

1 教学过程

1.1 旧知回顾，思维热身

师：请大家回顾一次函数、反比例函数的定义与一般形式，说说它们和整式之间是否存在什么联系.当初学习一次函数的基本流程是什么？

生1：一次函数的解析式中y=kx+b（k≠0）等号右边为关于x的一次整式，即一次二项式或一次单项式.

师：着重强调“k≠0”这个条件的理由是什么？

生2：当k=0时，函数y=kx+b就是y=b（非一次函数）的情况，此为常函数.

设计意图：在旧知回顾的基础上创设学生感兴趣的情境，能有效激发学生的探究欲，达到让学生的思维热身的作用，为进一步进入探索状态、构建新的概念奠定基础.

1.2 创设情境，引发探究

探究1生活中常见这样一种现象：将一颗石子扔进水里，水面会呈现出不断向外扩展的波纹，这些波纹构成一系列同心圆，分别说说此过程中的常量与变量，变量间存在怎样的联系等.

生3：波纹所形成的圆的周长C和圆的半径R之间的关系为C=2πR.

师：周长是否为半径的一次函数？判断依据是什么？

生4：结合函数及一次函数的定义可确定周长是半径的一次函数.

师：还有其他发现吗？

学生分别提出：①水波纹形成的圆的面积S和圆的半径R间的关系为S=πR²；②石子掉入水中的深度h与掉落时间t之间的关系为h=1/2at²；③石子掉入水中所形成的声音会随着时间的延长而变小，但无法用函数关系式表达，应该也是一种函数关系.

探究2若张伯准备用16 m长的篱笆筑成一个长方形的家禽饲养场，其中有哪些是变量，哪些是常量，各个量之间存在怎样的联系？你是如何判断的？

生5：该情境中，篱笆的长度16 m固定不变，是常量，而长方形的长与宽（x与y）是变量，同时长方形的面积S也为变量，其中存在的关系为x+y=8，y=8－x（0＜x＜8），S=x（8－x）（0＜x＜8）.

变式1张伯准备用16 m长的篱笆围成一个家禽饲养场，其中有一面靠墙（墙壁足够长），若围成的长方形中与墙面垂直的边长是x m，请写出饲养场面积S和x之间的关系式.

结论：S=x（16－2x）=－2x²+16x（0＜x＜8）.

变式2用一段16 m长的篱笆靠10 m长的墙围成一个长方形的家禽饲养场，所围成饲养场的面积S与长x（单位： m）之间存在怎样的关系？并判断是否为函数、一次函数或反比例函数.

结论：S=x（16－2x）=－2x²+16x（3≤x＜8）.

设计意图：课堂中好的问题不仅能激趣启思，还能开阔视野，挖掘学生的潜能，让学生由表及里地理解问题本质，形成思辨能力.

探究3若想为一面长、宽之比为2∶1的镜子镶上边框，已知镜面价格为120元/m²，边框价格为30元/m，工费为45元/次.假设镜面的宽度是x（单位：m），所需花费的总费用y与x间是怎样的函数关系？

学生自主探究，过程如下：①镜面需要120×2x²=240x²（元）；②边框需要30×6x=180x（元）；③总费用y=240x²+180x+45（元）.

类比一次函数的概念，学生将几个未接触的函数罗列在一起，通过其中存在的共同点推断出二次函数的概念.通过以上探究，发现S=πR²，h=1/2at²，y=240x²+180x+45等，都属于二次函数的范畴.继续与一次函数的一般形式类比，学生不仅自主写出二次函数的一般形式y=ax²+bx+c，还确定了a，b，c是常数，且a≠0的条件，其中x，y分别为自变量与因变量，y为x的函数.

师：对于二次函数的定义，还有什么特别值得关注的地方吗？

生6：a一定不能为0，若为0，那么函数的最高次项就不是二次项了.

师：不错，现在大家来观察S==－2x²+16x（0＜x＜8）与S=－2x²+16x（3≤x＜8），它们的表达式完全一样，能否确定它们为相同的函数？

设计意图：以情境的方式引导学生对问题进行引申、发散，不仅能夯实学生对函数概念的理解，还为接下来探索二次函数图象的性质奠定基础.利用“自变量取值范围对函数的影响”，进一步提升数学思维能力，培养学生的创新意识.

1.3 练习训练，辨析概念

（1）如果y=kxk+1为关于x的二次函数，则k的值是多少？

（2）如果y=（k+1）x|k|+1为关于x的二次函数，则k的值是多少？

（3）如果y=kx|k|+1+2x²+3x为关于x的二次函数，则k的值是多少？

设计意图：练习训练意在进一步帮助学生夯实对二次函数定义的理解，起到辨析定义的作用.学生的思维随着问题难度的增加而深入，新知的应用能力也在问题的解决中得以有效提升，这也是发展学生数学思维的过程.

1.4 应用概念，完善认知

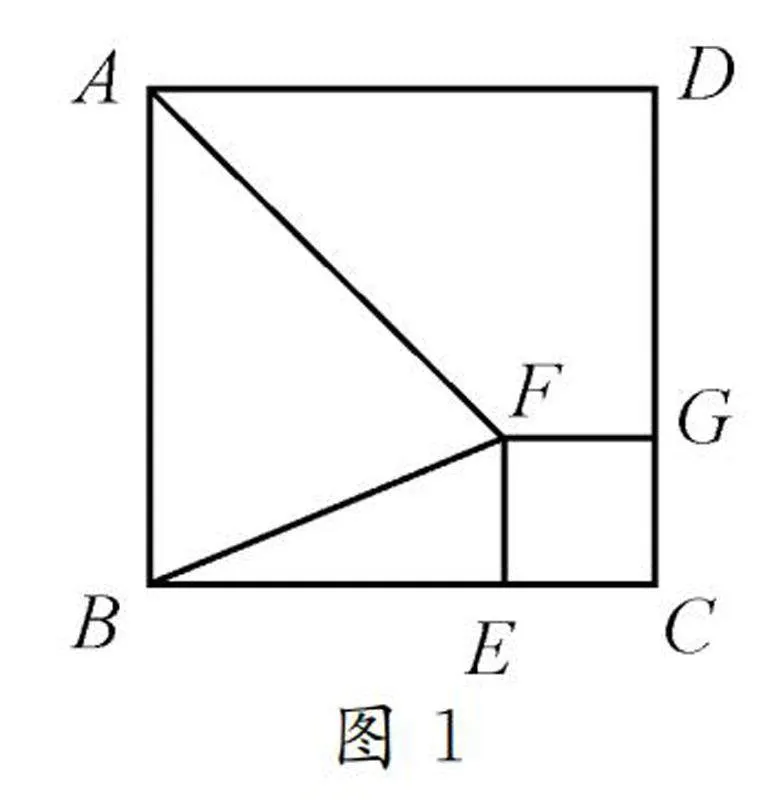
图1如图1，已知正方形ABCD的边长为10，E为BC边上的一个动点，将EC作为边长，在正方形ABCD的内部作一个新的正方形EFGC，点G位于边CD上，分别连接FA，FB，当点E在BC边上运动时，此时图中变量间存在怎样的函数关系？

设计意图：此例为概念的实际应用问题，意在完善学生的认知结构，让学生学会灵活应用所学知识来解决实际问题，凸显合作交流在探究式教学中的重要意义，进一步提升学力.

1.5 课堂总结，拓展延伸

师：回顾本节课的教学，我们探究了哪些内容？分别用什么方法进行探究的？掌握了二次函数的概念之后，接下来还需要掌握与之相关的哪些知识呢？

学生总结回顾本节课的学习历程、探究过程等，提出二次函数等号右侧为二次整式，且当y=0时，其一般形式就变成了ax²+bx+c=0，此为大家熟悉的一元二次方程；当y≥0或y≤0时，y=ax²+bx+c可转化为ax²+bx+c≥0或ax²+bx+c≤0.

类比一次函数与反比例函数的教学研究套路，接下来应探索二次函数的图象、性质以及应用等.

2 教学思考

2.1 突出学生主体性

新课标强调学生是课堂的主人，探究式学习以学生的自主探究与合作学习为主，整个教学过程都需将学生放在主体地位.本节课中，不论是对情境的探究，还是知识的应用，抑或最终的总结，都在“以生为本”的基础上实施.这不仅体现了学生的主人翁意识，还从真正意义上起到育人的作用，为促进学生的终身可持续性发展奠定基础.

2.2 创设合理的探究情境

对于初中阶段的学生而言，他们的数学观、价值观已经初步建立，对事物也具有一定的独立思考能力.教师在探究情境的选择上需结合学生的认知发展规律，创设学生感兴趣的情境来调动学生的探索欲，为教学营造良好的氛围[2].

如本节课的三个探究情境都是基于学生的认知基础而创设的，每个情境看似平常，却又能成功激发学生的探索欲，但又不会出现情境大于问题喧宾夺主的情况.在这三个情境的引导下，学生的思维由浅入深一步步进入二次函数定义的探究中，不仅成功揭露了概念的内涵与外延，还为发展解题能力夯实了知识与技能基础.

2.3 提出高质量的探究问题

数学教学实则是解决问题的过程，随着一个个问题的突破，知识本质与结构也逐渐暴露在学生面前.因此课堂中的每一个问题都要经过深思熟虑，切忌想到哪儿问到哪儿，而应有节奏、有目的地设计高质量的探究问题，让学生的思维在问题的驱动下逐渐深入，最终形成完整的知识结构[3].

参考文献：

[1]郝乐，马乾凯，郝一凡，等.数学教育与逻辑思维能力的培养[J].数学教育学报，2013（6）：9-11.

[2]郑毓信.数学教育视角下的“核心素养”[J].数学教育学报，2016，25（3）：1-5.

[3]王志刚.高中数学新授课中“问题导入”的若干探究[J].教学月刊·中学版（教学参考），2018（10）：37-40.