初中数学课堂教学生成性资源开发和利用

摘要：本文中以“角的平分线的性质”为例，陈述了利用往届数学课堂的生成性资源进行教学设计，通过设计情境引导学生经历角的平分线的性质和角的平分线的尺规作图方法的再生成过程.

关键词：生成性资源；初中数学；课堂教学

《义务教育数学课程标准（2011年版）》在实施建议部分提出：“生成性资源是在教学过程中动态生成的，如师生交互及生生交流过程中产生的新情境、新问题、新思路、新方法、新结果等.合理地利用生成性资源有利于提高教学的有效性.”[1]生成性资源主要是指初中数学课堂教学中生成的课程资源，它是依托数学课堂教学过程，通过师生之间、生生之间的交互产生的.生成性资源是动态的，有教师预设中的生成，也有超出预料范围之外的生成[2].下文以“角的平分线的性质”第1课为例进行说明.

1 利用资源，前置避错

学生的学习错误是一种生成性资源.教学中教师应把握数学学习错误的规律，揭示数学学习错误的成因，适当加工数学学习错误，挖掘数学学习错误的资源性价值[3].课本以文字叙述的形式给出了角的平分线的性质：角的平分线上的点到角的两边的距离相等.证明该性质时，需要分清其题设和结论.往届学生学习错误记录表明：部分学生把“距离”放在结论中，部分学生忽略“点到直线的距离”中隐含着“垂直”的条件，还有部分学生漏了“点在（角平分）线上”，这都导致了符号化的过程出现障碍.为帮助学生顺利跨越该障碍，实施以下教学环节：

1.1 复习巩固，激活记忆

设置课前复习，积累“点到直线的距离隐含垂直的位置关系”的经验，激活长时记忆，促其生成表象，达成前置避错.图1

填空如图1，点O到直线l的距离是线段____的长度.

教师个别提问后板书：“点O到直线l的距离可表示为OP⊥l于点P”强调距离隐含着垂直，点到直线的距离的符号语言中必须交待垂足.

1.2 目测实验，强调题设

问题1分组实验：

学号为奇数的学生做实验A，学号为偶数的学生做实验B.实验结束后，学生交流由实验所得的猜想，再用几何画板验证猜想.

实验A如图2，OC平分∠AOB，点P在OC上，PD⊥AO，PE⊥OB，垂足分别为D，E，点F与G在OB上.

目测：四条线段PD，PE，PF，PG中，____=____.

实验B如图3，OC平分∠AOB，点P，M，N分别在OC，OK，OL上，分别过点M，P，N作OA，OB的垂线段.

目测：三组共端点的垂线段中，两条线段的长度相等的是____.

猜想：____.

目测实验后，学生顺利得出猜想.在此过程中，通过实验A强调“到两边的距离”，通过实验B强调“点在角平分线上”.在学生完成猜想后，标记三个条件：“角平分线”“点在角平分线上”“到两边的距离”，如图4：

往届课堂教学的生成性资源是当下课堂教学的重要资源，值得教师们深入分析其成因，并充分发挥其资源性价值.

2 观察操作，自主生成

多尔（WILLIAME.DOLL）认为，学生应该从“做中学”，生成知识，转化经验，生成不可预知的因素，碰撞出创造的火花，新的知识就这样产生了.课堂“活”起来，学习才是有生命力的[4].笔者让学生经历目测感知→操作体会→归纳猜想→推理证明，实现知识的再生成过程.

2.1 目测感知

目测实验让学生在处理视觉刺激和语言刺激的过程中，自发地猜想出角的平分线的性质，并用提出猜想的学生姓氏命名（如：雷氏猜想），让学生体会成功的同时，明确猜想的三个条件.

2.2 操作体会

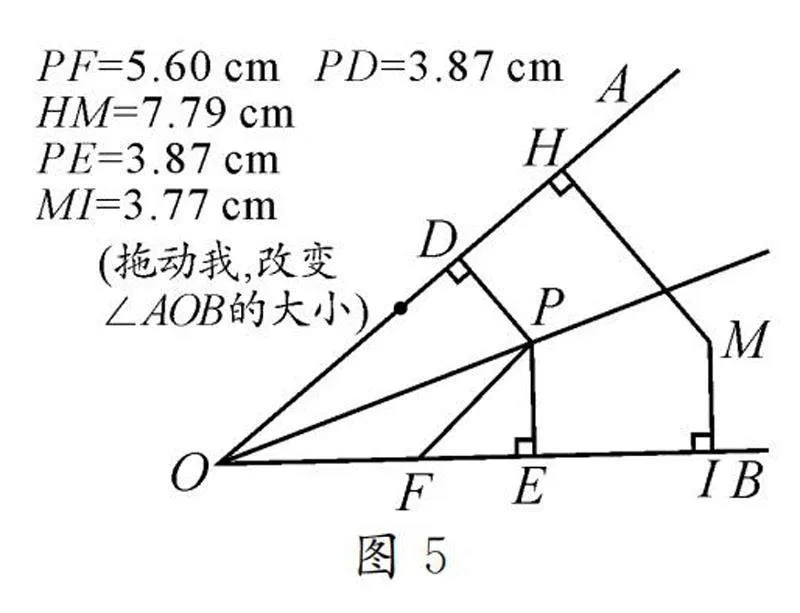
图5为了能更深入地理解命题的内涵，让学生经历几何画板操作实验（如图5），并回答：①你拖动了哪个点？②你观察了哪些数据？③实验后你得到了怎样的结论？

设计意图：让学生通过操作实验，进一步领悟猜想的内涵.改变点M的位置，观察HM和IM的大小变化，进一步强化“点在角的平分线上”的条件.改变点F的位置，观察PF和PD的大小关系，进一步强化“点到角的两边的距离”的条件.改变点P的位置，观察PE和PD的大小关系，让学生体会命题对于角平分线上任意一点都成立.拖动点D，改变∠AOB的大小，让学生领悟命题对任意大小的角都成立.

2.3 推理证明

追问1：经历实验验证，猜想一定成立吗？为什么？

当时，所有学生表示不成立.但是说不出为什么.还有一位李同学举手回答“一定成立”并口头证明了命题.在学习三角形内角和定理的过程中，积累了一定的从实验几何走向论证几何的数学活动经验.这说明学生还没真正领悟证明的必要性.学生的回答得到肯定后，教师再讲述证明的必要性，带领学生从实验几何走向论证几何.

追问2：角的平分线的性质中，题设和结论分别是什么？点到直线的距离隐含着什么条件？

用符号语言写出已知和求证，让李同学再陈述一次证明过程，教师板书，把用全等三角形证明线段（或角）相等的思路称为“李氏思路”.学生经历观察、归纳、猜想、实验验证、推理论证过程，体会研究几何问题的基本思路.

2.4 类比迁移

“用‘李氏思路’还可以找到角平分线的尺规作图方法.”如图6，已知∠AOB，请用尽可能多的方法作出∠AOB的角平分线.（要求用尺规作图.）

设计意图：引导学生借用“李氏思路”，迁移生成作角平分线的尺规作图方法.

学生展示学习成果，如图6、图7.

追问1：方法可行吗？（要求学生口头证明作图方法，养成有理有据的推理习惯，提高推理能力，培养实事求是的科学精神.）

追问2：哪种方法更简便？（利用类比，引导学生自主生成优化策略，体现数学的简练之美.）

3 体验成功，自主内化

课堂总结时，学生骄傲地回答：“这节课我们学习了雷氏性质、李氏思路和角的平分线的尺规作图方法.”用学生的姓氏命名定理和通性通法，激发学生的学习积极性，诱发学生自主内化.

让学生经历数学观察、数学思考、数学表达、概括归纳、迁移运用等学习过程，体会数学是认识、理解与表达现实世界的工具、方法和语言，增强认识现实世界、解决现实问题的能力，树立学好数学的自信心，养成良好的学习习惯[5].

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012：67-71.

[2]雷珮瑛.知惑教学［M］.广州：华南理工大学出版社，2021：6.

[3]雷珮瑛.知惑教学［M］.广州：华南理工大学出版社，2021：7-8.

[4]罗祖兵.生成性教学的基本理念及其实践诉求［J］.高等教育研究，2006（8）：47-53.

[5]中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：87.