经历基本活动体验 参悟宏观解题智慧

摘要：以试题讲评课为例，给出教学设计的基本结构，通过经历基本活动体验，参悟宏观解题智慧，从解题的“术”中感悟数学学习的“道”，培养学生面对问题时的良好心态.

关键词：数学;基本活动经验;宏观解题智慧;重“术”;悟“道”

考试，是教学评价的主体形式，它是教学过程的一个重要组成部分.考试评价的目的是全面了解学生的学习过程和现状，及时调整教学内容和教学节奏，更好地改进以后的教学，从而促进学生的发展.但怎样讲、讲什么才能取得良好的教学效果，常常众说纷纭.纵观目前的试题讲评课，依然大量存在缺乏二次加工处理，就题讲题、不加选择的现象，使很多良好的教学资源白白浪费.

我们知道，试题讲评具有诊断、纠错、示范、引领、鼓励、提升的作用.每次检测都是学习过程中的加油站，能起到提示和唤醒的作用.《义务教育数学课程标准（2022年版）》指出：“评价结果要关注学生已有的学业水平与提升空间，为后续的教学提供参考.教师要分析、反思教学过程中影响学生能力发展和素质提高的原因，寻求改善教学的对策.”［1］

试题讲评要重视解题方法的分析，即“重术”，这是体验，是学生认识问题、获得方法的直接经历；同时，更要引导学生跳出繁杂的题海，而看到习题之间的联系和规律性，即“悟道”.这样才能更好地发挥试题的指向性功能，帮助教师在课堂中落实解题教学的内涵，提升学生的数学核心素养.

最近，笔者在全市范围内执教了一节市级公开课“杜集区九年级数学质量评价试题讲评”.以下是笔者的课堂流程和教学思考，现与读者分享解题教学中的“术”与“道”.

1 教学过程

1.1 统计归纳，以学定教

设计意图：试题统计归纳是为了更好地关注学生已有的学业水平与提升空间，了解存在的问题，以使课堂教学有的放矢，为内容的选择提供有效的参考.

如何能让学生在面对难题时不产生畏惧情绪，我们要从学生的考试心理入手，为他们创造一个熟悉的情境，唤醒他们潜在的知识储备，从而有效地解决问题.这就需要教师对试题进行进一步的改造与加工，直逼知识内核，营造解题的最近发展区.

常言道：选择比努力更重要.因此，把本节课的教学重点就定为掌握计算线段长的一般方法，形成解题策略.

1.2 两重境界，依术启智

1.2.1 勾股定理的双重境界

（1）直接应用：利用勾股定理列方程求各边长.

例1已知直角三角形的斜边是6，两条直角边的比是1∶2，求两条直角边的长.

设计说明：从学生熟知的直角三角形入手，引导学生关注图形的形成过程，发现几何模型，体会方程结构在几何计算中的重要作用.“低起点”就是在接近学生认知最近发展区的地方开始探索之旅，增强他们解题的自信心.

（2）创造性应用：题中没有直角三角形，需要我们添加辅助线后构造直角三角形，然后再利用勾股定理.

例2如图1，在△BEF中，BE=BF=5，EF=2，求tan∠EBF.

分析1：如图2所示，过点E作EQ⊥BF，垂足为Q.在Rt△EBQ和Rt△EFQ中，设BQ=x，分别利用勾股定理把EQ2表示出来，从而列出方程，求出x，进而可以求出EQ，即可求出tan∠EBF.

分析2：在求出BQ之后，也可以先求cos∠EBF，再求出tan∠EBF.

设计说明：为了唤醒学生原有的认知模型，笔者结合试题在例1的基础上设计了例2，它没有现成的直角三角形，需要利用化归思想通过添加辅助线，从而转化为直角三角形的模型.它们都是从学生反馈的试题中的问题提炼出来的数学模型.几何模型的建立以及方程结构的唤醒，将有利于把几何问题转化为代数问题来解决.“小步子”就是在学生学有所获的基础上，及时前行，形成解题的节奏感，感受解题带来的心灵愉悦.

1.2.2 相似三角形的双重境界

（1）直接应用：利用相似三角形的性质，得到比例线段，然后列方程求线段长.

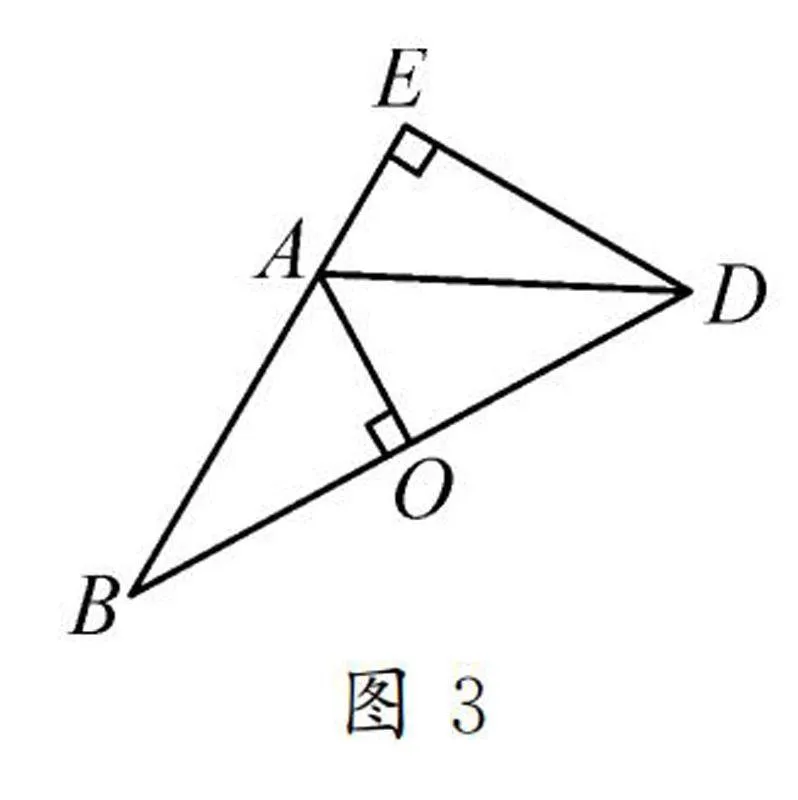
例3如图3，在△BDE中，∠BED=90°，点A是线段BE上的一点，AO⊥BD，垂足是O，AB=AD=5，OA=3，求DE的长.

分析1：由△BAO∽△BDE可以求出DE.

分析2：在Rt△AOB中，可以求出sin B，同理，在Rt△DEB中，可以得到sin B的另一种表达形式，它们显然是相等的，从而求出DE.

分析3：根据条件，可以利用BD，AO的长求出△ABD的面积，也可以利用AB，DE的长表示出△ABD的面积，显然这两种计算的结果是相同的.

分析4：设AE=x，在Rt△ADE中，可以利用勾股定理把DE2表示出来；同理，在Rt△BDE中，可以利用勾股定理把DE2表示出来.显然这两种表示的结果是相同的.求出AE后，就可以利用勾股定理求出DE.

设计说明：本题意在现有图形的基础上，引导学生通过自主学习、合作交流，发现相似三角形模型，体会比例线段这种结构在几何计算中的重要作用.同时，引导学生借助于直角三角形的特殊性质，发现线段计算中利用勾股定理和三角函数所反映出的边角关系，来完成线段计算的任务.

（2）创造性应用：题中没有我们需要的相似三角形，这时就要先添加辅助线再构造相似三角形，然后利用比例线段列方程求解.

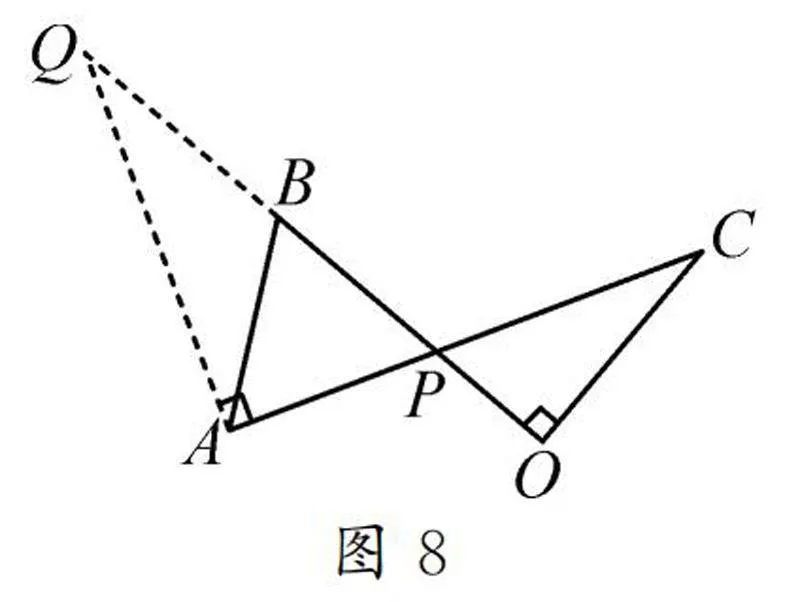
例4如图4，已知线段AC与OB相交于点P，AB=BP=6，OP=4，OC=8.∠COP=90°，求AP的长.

分析：显然，图中没有相似三角形，无法建立起线段之间的数量关系，这时我们就需要添加辅助线来构造相似三角形.

方法1：如图5，过点B作BQ⊥AP，垂足为Q，则Q是AP的中点，△BPQ∽△CPO，从而求出PQ（也可以用三角函数代换）.

方法2：如图6所示，过点A作AQ⊥BP，垂足为Q.

易知△APQ∽△CPO，所以PQ／AQ=OP／OC=4／8=1／2.

设PQ=x，则AQ=2x，BQ=6-x，AP=5x.

在Rt△ABQ中，利用勾股定理就可列出方程求出x.

（也可以用三角函数代换.）

方法3：如图7，延长PO至点Q，使OQ=OP，连接CQ，则

△APB∽△CPQ，

从而得到AP／CP=BP／PQ.

而CP的长先由勾股定理求得，即可求AP的长.

方法4：如图8，过点A作AQ⊥AC，交OB的延长线于点Q.

易证BQ=BA.

由△PAQ∽△POC，可以求出AP.

（也可以用三角函数代换.）

设计说明：这里的例3、例4也都是从试题中提炼出数学模型.借助于这些模型，不仅为破解难题做准备，同时通过这些模型所隐含的解题方法，熟悉解决这类问题的一般策略，即归纳出解题中的“术”.上课时，教师不要“一言堂”式地“单向输出”，要通过师生互动、生生互动，由学生自主发现这些方法.

1.3 学以致用，真题显现

通过知识回顾，熟悉求线段长常见的基本模型及其基本方法，这时再让学生重新审视试题中出现的原题，以获得成功的体验.

设计说明：在数学学习的道路上，学生的兴趣来自于学习带来的成功感.上海市闸北八中刘京海校长曾提出“成功是成功之母”的“成功教育”理念.如果学生在学习过程中，品尝到的尽是失败的苦涩，那么他还有什么动力坚持不懈？本课所选的四道例题都不是试题中的原题，但却是解决试题的“必经之路”，是教师依据试题中出现的模型以及思维方法精心设计的“原创习题”.在学习这四道题之后，破解试题中难题的绊脚石都已攻克，这时再看曾经的拦路虎，就会产生一种柳暗花明、一览众山小的感觉，提升解题的自信心，品尝解题成功的喜悦.

纵观上述四个例题的各种解法，都是利用勾股定理和相似三角形的性质，通过添加辅助线构造解题需要的图形，然后在不断求线段长度的道路上，求出我们所需要的线段长度.

因此，计算线段长的常用解决方法可分为以下两种类型：

第一类：以构造相似三角形为载体，利用比例线段求解.

第二类：以构造直角三角形为载体，利用勾股定理或三角函数求解.

1.4 盘点收获，自我成长

（1）通过本课学习，你学会整理试卷的一般方法了吗？

①按知识点（如勾股定理、相似三角形、二次函数等）分类，整理出与重要概念相关的一般方法.

②按问题（如计算线段长、证明线段相等、求最值等）分类，整理出解决这类问题的一般方法.

③按题型（如选择题、填空题、作图题等）分类，整理出解决各种题型的一般方法.

（2）通过学习，你能总结出求线段长的一般路径吗？

1.5 学以致用，反思提高

（1）以做过的一套模拟试卷为例，把错题按知识点进行分类整理.

（2）结合今天所学，总结出计算线段长的一般规律.

设计说明：试题讲评课的作业不能仅仅满足于订正试题，更要引导学生总结经验教训，归纳提升学习收获，注重知识的整体性和系统性，注重学生学习能力的培养，提高学生的反思意识，这样才能使学生既见树木，又见森林.

2 教学反思

著名数学教育家波利亚说：“掌握数学就意味着善于解题.”罗增儒教授说：“数学学习中发生数学的地方都毫无例外地充满着数学解题活动.”数学学习的最终归宿就是利用数学知识去解决问题.由于问题的多样性和不确定性，使我们很容易跌入题海的泥潭难以自拔.如何才能让学生跳出题海，以“出世”的心态“入世”呢？

高效的试题讲评有利于更好地实现“教学评一体化”，以评定教，以评促学，真正做到目标明确，有的放矢.这就是说数学学习不能只满足于问题解决的“术”，更要从问题解决中提炼出高于具体方法的“道”.

2.1 “有”中生成

前一个“有”是指“看得见”，即解决问题时要发现题目中显性的文字信息和图形信息，包括条件和结论.而“生成”是指“生长、拓展”，即把显性信息通过推理转换得到进一步有价值的隐性信息，要用运动、发展、变化的观点看问题，不能“只见树木，不见森林”，要充分挖掘，做到举一反三.

2.2 “无”中生有

这里的“无”是指“看不见”，即题中没有直接给出有价值的文字信息和图形信息，但这时的“看不见”并不是简单的没有和不存在，而是需要我们辩证地看待“无”，提炼出隐藏在背后的有价值的文字或图形信息.这里的“有”是指“做得出”，即在隐性信息的基础上，通过联系、加工、提炼和创造，发现已知和未知之间的潜在关系，构造适当的数学模型，找出解决问题的方案.当然，还需步步谨慎，最后达到“算的对”的结果.

由此可得，解决数学问题的一般流程（如图9）：

看得（不）见想得到做得出算得对

在“看得（不）见”“想得到”“做得出”“算的对”这四个思维层次中，“看得（不）见”是认知起点，“想得到”是思维关键，“做得出”是统筹能力，“算的对”是最终归宿.

2.3 数学之道

数学学习的终极目标不是学生的分数，而是学生身心的发展.中共中央办公厅、国务院办公厅印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》明确指出，落实“双减”学校责无旁贷.古人说：上人用道，中人用术，下人用力.在茫茫题海中，要切实减轻学生的负担，教师必须为学生点燃学习征途中的指路明灯.显然，“有”“无”的解题观是一种在具体解题之上的“高观点”，是一种哲学视野下的解题观，它不仅适合某一类题，更适合解决所有的数学问题.它是在学生踏遍千山万水之后，内心抽象形成的一种素养、一种境界、一种自信，这种心态是自然的、平和的、通透的.

大道至简，明数学之道，就是要“教会学生思考”，“关注学生的感受”，引导学生通过体验数学的思维过程，从具体方法中概括出一般原理［2］.在学生经历的一次次头脑风暴后，让深度学习真正发生，使试题讲评课给学生带来身心的“豁然开朗”，从“术”的认知上升为“道”的格局.

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[2]章建跃.章建跃数学教育随想录：下卷[M].杭州：浙江教育出版社，2017.