核心素养背景下初中数学深度学习教学策略

摘要：基于如何在核心素养背景下加强学生初中数学的深度学习，本文中从认识深度学习的内涵入手，结合时下出现的一些课堂教学问题进行反思，着手从拓展问题情境、注意提问预设、巧用模型手段、加强团队研究、增强实践操作、采用数形结合等六个方面进行策略研究，重在激发学生主动学习的兴趣，全面引导学生进行深度学习.

关键词：初中数学；核心素养；深度学习；教学策略

1 核心素养背景下课堂教学中存在的问题

1.1 互助学习的习惯缺失，大环境学习欲望较差

随着当前经济的发展，人们走出“农门”，追求经济利益的形势之下，留守儿童也逐渐增多，同时也造成了“5+2=0”的痛心现象，针对学生学习习惯的培养已经逐渐被忽视，同时，家校联合的情况也逐渐减少，造成了学生在成长过程中的学习环境越来越差，家长与孩子的沟通也逐渐减少，学校与家长的交流也显得苍白无力.

1.2 课堂教学的方法单一，学生学习兴趣难激发

很多学校的教师趋于老龄化，凭借多年的教学经验进行教学的教师颇多，教学方法也比较单一，甚至一本一支粉笔的现状仍然存在，灌输形式的教学方式及其简单的信息化技术运用也不能给课堂添彩，导致课堂越来越没有足够的吸引力让学生喜欢上数学，又加上课本中所体现的很多文本资源已经远远脱离了现代学生的认知环境，学生感觉陌生，甚至茫然，从而导致课堂枯燥无味，难以激发学生的学习兴趣.

1.3 教学过程的评价肤浅，激励不到位

现代教学过程中虽然提出了很多种开展数学教学的形式，但是在评价方面仍然做得不够，一些简单的“不错”“挺好”“优良中差”等评价形式，已经不能从本质上促进学生的内在驱动力，这些比较肤浅的评价也让孩子们熟视无睹，难以激活学生对学习的欲望与内心需求.

2 核心素养背景下数学深度学习教学策略

2.1 拓展问题情境，用好链接策略

问题情境往往呈现给学生的是一些生活中的真实问题，如果能引导学生在这些问题情境之下积极开展创造性的分析，并在解答过程中较快地生成解题的思路，将现有的情境与相关的课程目标内容相结合，再通过积极拓展，将情境问题进一步延伸链接，可以让学生在研究的过程中把“学习内容”转化为“驱动任务”，从而实现深度学习.

例如，在学习“平面的镶嵌”内容时，教师播放荷兰艺术家埃舍尔的艺术作品的视频，让学生思考埃舍尔艺术作品的图案所具有的共同特征，感受艺术作品中蕴含着一定的数学图形变换知识，欣赏图形的镶嵌美.同时，引导学生观察图片并思考它们是由哪些几何图形组成的？教师再通过动感图形的演示，帮助学生理解平面镶嵌的条件，引导学生尝试分析镶嵌的原理，并能归纳出平面图形的镶嵌规律.接着，再播放北京故宫石子路镶嵌的视频，拓展学生的知识面，开阔学生的视野，激发学生对数学学习的兴趣，感悟生活中图形的镶嵌美，进一步理解图形镶嵌的本质特点.

2.2 注意提问预设，体现外显策略

千变万化的数学课堂之上面对几十个学生，教学过程中可能发现的事件也难以预测，但是作为教师，应该对课堂上可能出现的问题，及时进行预设，做到“心中有设，处之有案”，方可把控动态课堂.对于“预设”，我们可以从所出现的“概念”“性质”“条件”甚至容易出现的关键点入手，只有这样，才能将学生闪现的问题抓住，及时进行深度思考，从而突破常规深入研究.

例如，在教学“成比例线段”相关内容时，在讲述“成比例线段”概念的过程中，学生提出疑问：四条线段成比例，这里已经说明了是a，b，c，d它们之间的关系是a与b的比等于c与d的比，如果我们不明确指出是哪两个线段的比，如3，5，8和x四个数字成比例，那我们又该怎么求解x呢？是不是可以直接写出3∶5=8∶x呢？面对学生提出的条件改变，问题变得复杂起来.结合新问题引导学生自己思考，同时也加强对问题的深度研究，汇总不同学生的想法，答案逐渐浮出水面：x可能比3小，或者在3和5之间，或者在5和8之间，也可能比8大，分四种情况进行讨论，发现答案有三种.当问题得到解决，我们可以再度引导学生思考处理此类问题的方法与思路，从而加强对数学问题中常见“错点”的深度研究.

2.3 巧用模型手段，增强互动策略

随着人们对数学的思考研究，模型思想也随之深深地映入我们的眼帘之中，特别是这种思想所体现出来的数学与外部世界的联系方式，让学生体验到数学和生活之间的内在关系，应用性极强.因此我们在问题研究过程中，要注意巧用模型，更好地增强学生的互动性，便于促使他们进行深度学习.

例如，在教学“轴对称”探究“将军饮马问题”时，抽象出数学模型：直线l同旁有两个定点A，B，在直线l上存在点P，使得PA+PB的值最小.我们可以将其简称为“两点一线”模型.

结合模型，我们再深入研究，如P是∠MON内的一点，分别在OM，ON上作点A，B，使得△PAB周长最小，变成为“一点两线”模型，如图1.再激发学生的想象力，拓展研究，便会形成“两点两线”模型、“三动点”模型、“两定点一定长”模型等.如此机巧的互动研究，不但能够激发学生兴趣，更能让学生感知、思维，全面参与其中.

2.4 加强团队研究，突出合作策略

初中阶段，学生的自制力还比较弱，但在解题过程中进行团队研究有利于充分发挥每一个成员的优势，通过任务分工，对目标进行分解，强化了学生各自的责任，将各自的任务目标融合在一起，加强了互助合作的关系，更最大化地让学生之间的信息沟通起来，展示合作之后的最佳成果.同时，在合作研究过程中，能更好地引导学生进行深度思考，将自身作用发挥到极致.

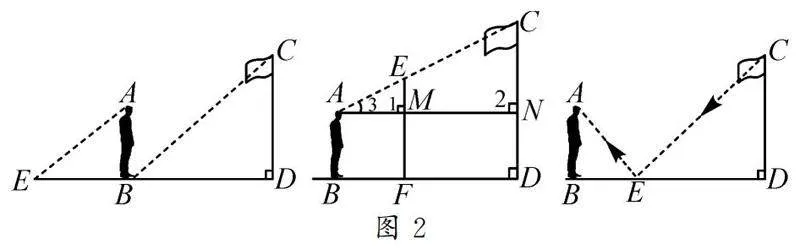
例如，在教学“利用三角形相似测高”相关内容时，我们为了测量旗杆的高度，结合三角形相似知识运用多种方法解题，如图2，以分组合作的方式开展活动并进行全班交流，进一步积累数学活动经验.首先对班级学生进行分组，然后按总规划师、测量师、设计师、计算师、书记员等角色进行分工，再结合具体的方法测量计算，通过任务要求的设置，培养积极的进取精神，从而让学生在合作研究中熟练把握测高的方法，促进学生的深度学习研究.

2.5 增强实践操作，落实研究策略

在数学教学过程中，有些简单的问题单纯靠讲解有时难以让学生明白其中的道理，如果此时结合问题特点进行实践操作，说一定会取得意想不到的效果.

例如在教学“三角形的外角和定理”时，如何引导学生准确理解定理成为教学重点，笔者结合学校的四边形水池、八角花坛设计实际活动方案，让学生分组训练，围绕着水池或花坛每到一个拐弯处行走方向就顺着一个方向转一个角度，并做好记录，看回到原来位置后一共转了多少度？通过实际操作，学生就很容易把握这样的问题了.如此的设计，不仅调动了学生的学习兴趣，更激发了学生创新研究的能力.

2.6 采用数形结合，培养优化策略

在解决数学问题的过程中，如果能有效地将数与形有机地结合起来，能较快抓住解题规律和突破问题的切入口，可以更好地激发学生的数学思维，从而更好地进行数学多元构建，促进对问题的深度研究.

例如，在教学“整式的乘法”相关内容时，将抽象的乘法公式转化为图形来研究，利用图3中边长分别为a，b的正方形，以及长为a、宽为b的长方形卡片若干张，拼成图4中的正方形和图5中的长方形.通过图形的变化，激发学生学习的兴趣，从而能更好地灵活把握和运用公式.在此基础上，利用上述方法拓展研究面积关系，为下文因式分解的学习奠基，如画出面积为2a2+5ab+2b2的长方形，此多项式可以转化为哪些多项式的乘积，围成的图形又如何表示其周长，等等.“以形释数”，利用数形结合思想证明代数问题，也是进行深度学习的敲门砖.

深度学习，不但在改进课堂教学过程中有着重要的意义，对学生和学校的发展也有着深远意义.这就需要我们在初中教学过程中，真正落实深度学习的各个策略，让深度学习积极推进课堂及学校的创新发展，从而更好地落实学生核心素养的培养.