铁精矿监控样品研制

摘要：铁精矿是赤泥选铁后产品，铁精矿全铁含量是铁精矿品质等级判断的重要指标。本文就铁精矿监控样品的研制方法展开说明，包括样品的处理、均匀性试验、定值、不确定度评定和稳定性评价。铁精矿全铁监控样品应用于粉末压片制备样品方式下的X射线荧光光谱分析方法，监控分析方法的过程可靠。

关键词：铁精矿；监控样品；定值

赤泥是铝土矿生产氧化铝过程中所产生的强碱性一般工业固体废弃物。目前，生产1t氧化铝产生1.5～2.0t赤泥。赤泥的大量堆积所引发的环境问题较严重，甚至会危及动植物的生存［1］。赤泥中铁含量在30%左右，是赤泥资源化利用的重要手段，并且具有很好的经济价值。赤泥选铁工艺中，为有效控制工艺流程，需要对流程中的产物进行分析，指导生产工艺有序开展。工厂实验室对选铁工艺过程样品分析，通常采用X射线荧光光谱法，分析速度快，结果可靠。此方法的样品制备方法主要有压片法和熔片法，压片法制作简单、耗时少、实验成本低。铁精矿监控样品与待测样品具有非常接近的成分，可以克服基体效应和矿物效应，减少误差。同时可以监控X射线荧光仪，掌握标准曲线的漂移程度，把握恰当的标准化操作时机，从而保持仪器正常工作状态。

1实验部分

1.1样品的采集和制备

（1）样品的采集。为了克服样品成分不一样导致的矿物效应及元素效应等基体效应，首选工厂内部立盘铁精矿库样品；为了从源头保证样品均匀性，采用单点采集方式；采集量为实验室十年的使用量。

（2）样品的制备。将铁精矿样品用烧开的去离子水浸泡，并不时搅拌，浸泡24小时，洗去浮游物和附碱，用pH试纸检验，满足洁净无附碱状态。将清洗后铁精矿样品置于在110℃烘箱中平铺充分干燥。用研磨机对处理后样品进行研磨。出料用125μm标准筛筛分，筛上物继续研磨，直至全部通过125μm标准筛，得到基础样品。将基础样品充分混合后进行均匀性初检，均匀性初检合格，则分装；若不合格，则继续混合，直至满足要求。将均匀性初检合格样品平均分装于塑料封口袋中，并进行编号，每袋质量约为0.1kg，密封保存于专用柜内。

1.2均匀性初检

（1）初检区域划分。将混样完毕样品装入一个大盆中，平整样品表面，在其表面上绘制五角星图形，将样品表面分成11个区域，在每个区域采用从上至下的方式各取一个样品，采用X射线荧光光谱法测定，进行成分分析。

（2）均匀性初检数据的判断。根据GB/T6730.65—2009的要求，对于给出实验室间允许差的测定方法，可计算出有限次测量的标准偏差（S）后，与实验室间允许差Δ相比较判断。当1.5S0.5Δ时，认为偏析检验合格；当15S＞0.5Δ时，认为偏析检验不合格。即：3SΔ，样品均匀性合格；3S＞Δ，样品均匀性不合格。

均匀性初检数据如下，结果表明均匀性初检合格。

1.3均匀性检验

（1）抽样。从分装的样品中随机抽样15个，对从每个样品中抽取的15个样品分别重新编号为1#～15#并进行匀性检验，每袋（小单元）测量三次，按照如下顺序进行测定：

第一次：135791113152468101214

第二次：151413121110987654321

第三次：246810121413579111315

试样压片后在X射线荧光光谱仪上测定成分元素的荧光强度，用方差分析法进行均匀性检验。

（2）均匀性检验数据统计和判断。采用方差分析法进行均匀性检验。

计算总平均值：

x==∑mi=1xim

计算组间偏差平方和：

Q1=∑mi=1n（xi-x=）2（式中Q1=MSamong）

计算组内偏差平方和：

Q2=∑mi=1∑nj=1（xij-xi）2（式中Q2=MSwithin）

计算自由度：

γ1=m-1；γ2=m（n-1）

计算统计量：

F=Q1/γ1Q2/γ2

根据所取显著性水平α和自由度γ1，γ2从F检验临界值表查得Fα，比较F和Fα进行判断：

若F＜Fα，则认为组内和组间无明显差异，样品是均匀的。若FFα，则怀疑各组间有系统误差，即样品间存在一定差异，但实际使用并不受影响。此时计算不均匀性方差，并将其计入特性量标准值扩展不确定度中：

S12=1nQ1γ1-Q2γ2

若F〉Fα，则认为样品不均匀。

（3）均匀性检验结果。均匀性检验数据和结果如下：

从均匀性检验数据看，所研制铁精矿监控样品均匀性检验F值均满足了F＜F0.05（2.04）的要求，组内与组间无明显差异，因此铁精矿监控样品是均匀的。

表中：RSD—相对标准偏差（kps的百分比），F—统计量，S12—不均匀性方差（kps）。

2定值

通过有资质的能力验证符合实验室进行化学分析方法定值，并进行正态分布检验，可疑值检验后，抽样进行实验室间比对。

2.1正态分布检验

用夏皮罗威尔克（ShapiroWilk）法检验全部数据是否符合正态分布，统计量计算公式如下：

W=∑hK=1αKXn+1-K-XK2∑nk=1XK-X-2

式中：K取值1～h，对于测量次数n是偶数时，h=n2；对于测定次数是奇数时h=（n-1）2。系数αK是与n和K有关的特定值。

当W＞W（n，P）时，则接受测定数据为正态分布。W（n，p）是与测定次数及置信概率有关的数值。

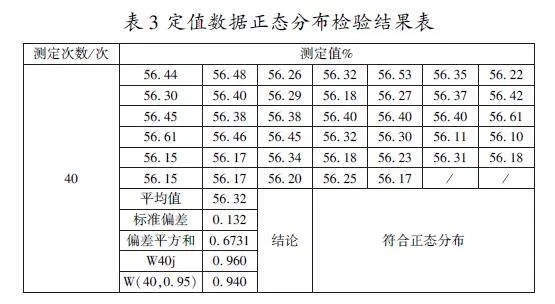
正态分布检验结果表明，定值数据均呈正态分布。

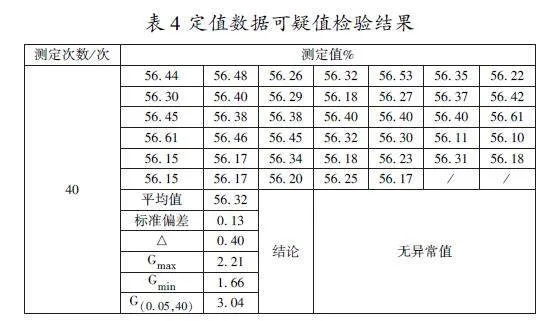
2.2可疑值检验

再用格拉布斯（Grubbs）法检验所有数据是否存在可疑值，从数理统计上剔除可疑值。如某测定值xi，有残差νi=xi-x-。当νi＞λ（α，n）s时，则xi应被剔除。λ（α，n）是与测量次数及给定的显著性水平α有关的数值。

2.3实验室间比对

随机抽取4个样品，送检有资质和能力验证符合的实验室进行比对，从比对结果看，分析结果都在允许差内，说明分析过程可靠。

3标准值的确定与不确定度的评估

（1）A类不确定度。对标准样品的特性量进行测定时，由一家实验室测定40次，的测定平均值为X-i，当测定数据服从正态分布，计算算术平均值，计算算术平均值x-

计算得x-=1n∑ni=1xi=56.32

单次试验标准差S

sxi=∑ni=1xi-x-2n-1=0.13

（2）B类不确定度。通过对测定影响因素的分析，估计出B类不确定度，记为SB。

（3）不均匀性引起的不确定度。不均匀性产生的标准偏差为：S1=1nQ1γ1-Q2γ2

式中，Q1为组间偏差平方和：Q1=∑mi=1nxi-x=2

Q2为组内偏差平方和：Q2=∑mi=1∑nj=1xij-xi2

ν1、ν2为自由度：γ1=m-1，γ2=mn-1；m为单元数，n为每个单元的测定次数。

（4）稳定性引起的不确定度。类似于不均匀性引起的不确定度，稳定性引起的不确定度为：

ST=1nQ1γ1-Q2γ2

（5）扩展不确定度U：

U=kSxi2+SB2+Sl2+ST2

式中k为由置信概率和自由度决定的包含因子，k一般取2～3（本实验k=2）。对于定值实验室已经能力验证并采用标准方法分析的固体金属样品，通常结果的B类不确定度SB和稳定性不确定度ST可忽略；均匀性检验结果表明本系列标准样品是均匀的，所以不均匀性引起的不确定度Sl亦可忽略。则：

U=kSxi2（k=2）

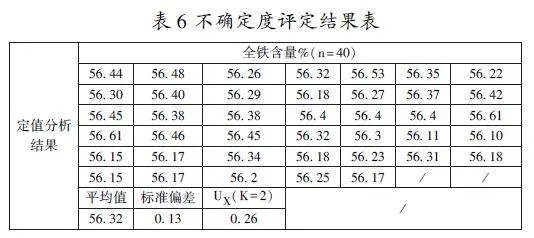
不确定度评估结果如下：

因此，本系列标准样品研制过程的不确定度只包括定值过程产生的不确定度，定值结果为：标准值±扩展不确定度。

定值结果：铁精矿监控样品TJK；全铁含量为：56.32%，K=2时，U=0.26%。

4稳定性检验

用GB/T6730.65—2009三氯化钛还原重铬酸钾滴定法进行稳定性检验，保持与定值时操作及实验条件的一致，精密度和准确度满足要求。从分装成最小包装单元的样品中随机抽取样品，抽取的样品单元的分布对于总体样品有足够的代表性。在每个时间点，都不少于2个独立单元。

监控样品稳定性监测采用以下方式判断：

xCRM-xmeasku2CRM+u2meas

式中：xCRM——CRM的特性值；xmeas——测量的观测值；umeas——测量不确定度；uCRM——标准样品证书上标准值的标准不确定度；k——置信概率95％时一个适当的包含因子（本实验k=2）。

若满足上式，则表明检验对象是足够稳定的，其稳定性可得到证实。实际上，只要测定结果最大的偏差的绝对值满足上式要求，其他测定结果的偏差的绝对值自然就能满足，证明每次测定结果都符合要求，从而表明样品是稳定性的。因此，判断式为：

xCRM-xmeasmaxku2CRM+u2meas

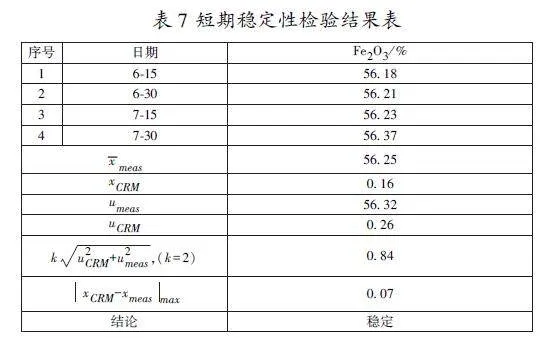
短期稳定性检验。在2个月周期内进行了短期稳定性检验，分4个时间点每次随机抽取2个最小单元进行测定，短期稳定性检验结果如下，结果表明样品稳定。

结语

研制的铁精矿监控样品定值结果全铁含量56.32%，置信度95%的扩展不确定度为0.26%。可用于实验室内部X射线荧光光谱分析质量控制，可以节约实验室成本支出，保证仪器的稳定和分析数据的准确，为赤泥资源化利用的重要计量保障。

参考文献：

［1］陈吉忠，马幸，梁婉.赤泥资源化利用最新研究进展及展望［J］.中国资源综合利用，2023（3）：105110.

［2］韩尚云，姚延伟，骆虹伟.拜耳法赤泥脱碱技术与综合利用的研究现状［J］.科技和产业，2021（7）：204207.

［3］李艳军，张浩，韩跃新，等.赤泥资源化回收利用研究进展［J］.金属矿山，2021（4）：119.

作者简介：赵飞辉（1984—），女，汉族，广西桂林人，本科，工程师，研究方向：分析化学。