适用于任意阶数的BOC信号无模糊度捕获算法

摘 要：针对二进制偏移载波（binary offset carrier， BOC）调制信号在捕获过程中的模糊度问题，提出了一种基于自相关函数加减互补的BOC（m，n）信号无模糊度捕获算法。根据副载波脉冲周期延拓的特性，通过拆分副载波，进而分离自相关函数，将关于码相位对称的第一个子相关函数和最后一个子相关函数做加减法运算后求差值，最后通过取模求和运算将旁峰完全消除。理论和仿真实验结果表明，该算法的适应性良好，适用于任意阶数的BOC调制信号，并且可以完全消除旁峰，保留窄相关峰特性。相比于SCPC、ASPeCT和BPSK-Like三种传统BOC信号无模糊度捕获算法，该算法的载噪比性能有约1.5～4.5dBHz提高。

关键词：二进制偏移载波调制；信号捕获；自相关函数；无模糊度；分离重构

DOI：10.15938/j.jhust.2024.03.011

中图分类号： TN967.1

文献标志码： A

文章编号： 1007-2683（2024）03-0090-09

An Unambiguous Acquisition Algorithm for BOC Signal with Arbitrary Order

SHU Yi1， HU Hui1， XIE Hongqun2， FU Yufei3

（1.School of Information and Software Engineering， East China Jiaotong University， Nanchang 330013， China;

2.Innovation Academy for Microsatellites of Chinese Academy of Sciences，University of Chinese Academy of Sciences，

Shanghai 201304， China;

3.School of Advanced Technology， Xi’an Jiaotong-liverpool University， Suzhou 215123， China）

Abstract：Aiming at the ambiguity problem in the acquisition process of BOC （binary offset carrier） modulated signal， an unambiguous acquisition algorithm of BOC（m，n） signal based on auto-correlation addition and subtraction complementary is proposed. According to the characteristics of subcarrier pulse periodic extension， the purpose of separating the autocorrelation function is achieved by splitting the subcarriers. The first and last sub-correlation functions with respect to code phase symmetry are added and subtracted to calculate the difference， and finally the side peaks are completely eliminated by modulo summation operation. The theoretical and simulation results show that the algorithm has good adaptability， is suitable for BOC modulation signals with arbitrary order， and can completely eliminate side peaks while retaining the narrow correlation peak characteristics. Compared with SCPC， ASPeCT and BPSK-Like three traditional BOC signal unambiguous acquisition algorithms， the proposed algorithm has an increase in SNR performance of about 1.5～4.5dBHz.

Keywords：binary offset carrier modulation; signal acquisition; auto-correlation function; unambiguous; separation and reconstruction

0 引 言

基于全球卫星导航系统发展迅速，各国自主的卫星导航系统由军用渐渐转向民用，服务不同领域不同需求的各个用户。伴随着卫星数量的增多，卫星导航系统建设初期使用的BPSK（binary phase shift keying，二进制相移键控）技术在兼容性、定位精度、频谱利用率等方面的局限性暴露出来，已无法满足用户的需求。为了消除这些局限性，同时进一步提高导航信号的可用性，提出了二进制偏移载波（BOC，binary offset carrier）调制［1］，并将其作为导航信号的主要调制方式。BOC调制采用方波对伪随机码进行预先调制，使得信号的频谱分布在主载波中心频率的附近，降低了公共频带间的相互干扰［2］，充分利用了频谱资源，且其能量更集中在高频段，有效带宽更大，具有更好的抗噪声性能。但是BOC信号以其调制复杂度为代价，不仅带来了BOC信号的窄带特性，还带来自相关函数（autocorrelation function， ACF）的旁峰。这种多峰性容易导致捕获过程中信号的误捕和漏捕［3-4］，且相关主峰越窄，旁峰越接近主峰。

与传统BPSK调制信号相比，BOC调制信号的能量向频谱边缘搬移，避免了各卫星信号之间的相互干扰，随着调制阶数的增高相关峰会变得更窄、频谱能量也会更加靠近频带边缘，提高了信号抗噪声能力和定位精度，但是在相关峰主峰变窄的同时也产生了边锋，存在接收机误捕和漏捕的模糊度问题。针对这一问题，本文设计一种分离重构思想应用于BOC信号捕获中，该方法不但能完全消除边锋，还适用于任意类型BOC信号捕获，对于新一代卫星信号（GPS L5）捕获有一定的参考意义。这篇文章针对新型卫星信号调制方式存在的问题，研究其原理，提出了一种无模糊度算法，模拟仿真新型卫星调制信号，进行实验，结果表明此算法可以解决捕获过程中的模糊度问题。

针对BOC信号多峰性在捕获过程中带来的模糊度问题，国内外主要专家提出以下几种技术方法：①BPSK-Like法，即非相干边带类捕获方法［5-6］，这种方法的核心思想是通过增加滤波器，来达到滤除旁锋的目的。这种方法可以滤除一定的旁峰，但其缺点极其突出，首先滤波器的引入造成了能量损失，其次该算法需要滤波器，使得硬件复杂度大大增高，而且没有保留BOC信号的特窄相关特性。②自相关边锋消除［7］ （autocorrelation side-peak cancellation technique， ASPeCT）技术，该方法通过调整传统BOC信号自相关函数和BOC信号与伪随机码序列的互相关函数两个相关峰的系数后再相减，进而达到消除边锋的目的。但是两个相关函数的旁锋只是相似，并不完全一样，所以无法完全消除边锋。而且该算法只适用于BOC（n，n）类信号，存在一定局限性。③副载波相位消除法［8-9］（subcarrier phase cancellation， SCPC），该方法将BOC码与QBOC码的互相关函数平方与BOC的自相关函数平方相加，以达到消除边锋的目的，但该算法没有保留BOC信号捕获高精度性能优势。

针对上述算法中存在的未保留窄相关特性、未完全去除捕获模糊度等问题，国内外专家提出了BOC信号捕获的分离重构思想。该思想的核心在于拆分副载波、伪随机码或者相关函数等，得到特定的子相关函数，再根据特定的子相关函数之间的特性，设计重组规则，将其进行组合重构，构造出一个无模糊度的相关峰。文［10-12］利用本地信号与接收信号的互相关函数的非线性组合构建无模糊的合成相关函数，解决BOC信号旁峰带来的模糊度问题。文［13-15］根据BOC子相关函数的特性，通过将不同子相关函数进行相加、相乘等线性方法重构变换获得边峰消除能力。文［16］提出了一种分离重构的捕获算法，基于信号中码片延拓关系进行分离后，根据对称性重构出一个无模糊单峰，该种方法适用于任意阶数BOC信号，且保留了BOC信号窄相关特性，但随着调制阶数的增大，该方法算法运算量将远高于传统算法。文［17］对四路自相关和互相关函数的I，Q支路相关信号进行非点积运算，构造非线性的无模糊捕获的判决合成函数，但该方法需要四路相关器，大大提高了接收机设计的复杂度，增加了硬件资源消耗。文［18］提出的CSSPeCT法根据BOC单元相关函数的特性，通过与移位半个码片取反后的新函数相乘，最终实现消除边峰的能力，但该方法仅适用于调制阶数中m=n的情况。文［19］提出了一种移位相乘法，通过移位相乘构造出一个无模糊度的新相关函数，达到消除旁峰的效果，但该方法并未完全消去旁峰，且实现复杂。

考虑到目前算法存在的一些问题，本文提出了一种基于自相关函数加减互补的无模糊度算法。

1 算法分析

1.1 BOC调制信号模型分析

BOC调制信号是在传统BPSK调制信号基础上将副载波与伪随机码序列相乘进行二次调制，

一般表示为BOC（m，n）。其中m为副载波频率fsc与基准频率f0的比值，n为伪随机码片频率fc与基准频率f0的比值，f0=1.023MHz，m和n的值一般是正整数或正整数加上0.5，k=2m/n是BOC信号的调制阶数，表明一个伪随机码片内的半个周期副载波数目，k与BOC信号的性质密切相关。

BOC（m，n）信号的自相关函数（ACF）可以通过BOC信号与经副载波预调制的PRN（pseudo random noise）码序列之间的相关运算获得。BOC（1，1）信号的自相关函数的模型如下：

RBOC（1，1）（τ）=Λ（τ）－12Λ（τ+12）+Λ（τ－12）（1）

式中：RBOC（1，1）（τ）为自相关函数；τ为码片延迟；aΛ（τ/d）表示高度为a，宽度为d，中心在x=0处的三角函数。图1为BPSK、BOC（1，1）和BOC（3，2）自相关函数MATLAB仿真的结果比较。

由图1可见，BPSK调制信号的自相关函数只存在主峰，而BOC调制信号的自相关函数除了主峰还存在多个旁峰，BOC（1，1）主峰宽度只有BPSK的一半，BOC（3，2）则为1/3。由BOC（1，1），BOC（3，2）可以看出，随着调制阶数的增加，主峰变窄的同时也产生了更多的旁锋，旁锋的峰值越接近主峰，使得捕获更容易造成误捕，并且零点数量的增加，漏捕的风险也进一步提升。

1.2 分离重构原理

1.2.1 相关函数的分解

当本地的伪随机码和本地副载波保持严格同步时，BOC（m，n）信号的每个伪随机码片由k个副载波脉冲调制，且一个伪随机码片内调制的k个副载波脉冲之间存在周期延拓关系。假如以第一个副载波脉冲为基准，后面的k－1个副载波脉冲都是由这个基准脉冲时延不同矩形脉冲宽度得到的，符号与基准脉冲相同或相反。因此可以将每个伪随机码片内调制的第一个副载波脉冲分解出来，构成新的子副载波SCF（t），SCF（t）也称作基准子副载波；则每个伪随机码片内的第N个副载波脉冲分解出来构成新的子副载波SCN（t），子副载波可以看作是基准子副载波SCF（t）延迟N－1个副载波脉冲宽度，符号随着N的奇偶而变化，由此就实现了将一个完整的副载波拆分成k个子副载波单元。

假设在每个伪随机码片，完整的副载波为SC（t），可表示为

SC（t）=∑k－1i=0（－1）isc（t－iTsc）（2）

与CSSPeCT法和其他传统捕获算法不同，本文算法是根据不同调制阶数的副载波延拓特性进行拆分，因此本算法适用于任意调制阶数。其中由基准脉冲生成的子副载波单元，如式（3）所示：

SCN（t）=（－1）N－1SCF（t－（N－1）Tsc）

N=2，3，4，…，k（3）

每个伪随机码片内所调制的第k个副载波脉冲构成的子副载波定义为SCL（t），如式（4）所示：

SCL（t）=（－1）k－1SCF（t－（k－1）Tsc）（4）

其中Tsc为一个副载波脉冲的宽度。以BOC（2，1）信号为例，图2为本地完整副载波的分解结果。

由图2可见，SC（t）为BOC（2，1）信号的副载波，SC0/F（t）、SC1（t）、SC2（t）和SC3/L（t）为本地副载波分解的子载波单元。

按照分离原理，将副载波按调制阶数，拆分为各路子副载波单元后，

伪随机码经由基准子副载波SCF（t）调制，生成的BOC信号可以看作基准子BOC信号，表示为BOCF（t）。那么一个BOC（m，n）信号可由BOCF（t）及其周期延拓相加构成，表示为BOC（t），BOCL（t）也可以看作是BOCF（t）延迟k－1个副载波脉冲得到。BOCF（t），BOC（t），BOCL（t）可表示为：

BOCF=∑∞－∞CiPTsc（t－iTC）（5）

BOC（t）=∑k－1N=0（－1）NBOCF（t－NTsc）（6）

BOCL（t）=（－1）k－1BOCF（t－（k－1）Tsc）（7）

假设BOCF（t）与BOC（t）做相关运算，BOC（m，n）信号的自相关函数R（τ）可以表示为RF（τ）和RF（τ）每延迟k－1副载波脉冲后的累加，如式（8）所示：

R（τ）=∑k－1N=0RF（τ－NTsc）（8）

由于BOCL（t）是BOCF（t）延迟k－1个副载波脉冲得到，假设RL（τ）是BOC（t）和BOCL（t）做相关运算得到的，那么RL（τ）就是上式（8）的最后一项，表示为式（9）：

RL（τ）=（－1）k－1RF（τ－（k－1）Tsc）（9）

当输入信号为BOC（2，1）时，调制阶数k=4，对应的自相关及其子相关函数的分离结果如下图3所示.

如图3所示，R（τ）为BOC（2，1）信号自相关函数，R0/F（τ）、R1（τ）、R2（τ）和R3/L（τ）是本地伪随机码分别经由本地分解副载波SC0/F（t）、SC1（t）、SC2（t）

和SC3/L（t）调制后与BOC（2，1）信号进行相关运算得到的相关函数。由图3可知R0/F（τ）和R3/L（τ）关于τ=400码相位对称，因此利用这两路子相关函数，将其通过移位、相加减、取绝对值等运算，可以构造无模糊度的相关峰。

1.2.2 相关函数的重构

按照上述BOC（m，n）信号自相关函数分离策略，将调制阶数为k的BOC信号自相关函数拆分为k份后，再根据重构策略，将拆分的子相关函数重构，即可得到无模糊度的检测量。当输入信号为BOC（2，1）时，对应的子相关函数的重构原理如图4所示。

如图4所示，从上至下依次为RF+L（τ）、RF－L（τ）、Rrecon（τ）和R（τ）。根据分离后RF（τ）和RL（τ）是关于τ=400码相位对称的这一特点，将RF（τ）和RL（τ）相加后取绝对值，得到RF+L（τ），如下式（10）所示：

RF+L（τ）=|RF（τ）+RL（τ）|（10）

再将RF（τ）和RL（τ）相减后取绝对值得到RF－L（τ），如式（11）所示：

RF－L（τ）=|RF（τ）－RL（τ）|（11）

然后将RF+L（τ）与RF－L（τ）相减得到Rrecon（τ），如式（12）所示：

Rrecon（τ）=RF+L（τ）－RF－L（τ）（12）

最后将Rrecon（τ）取模相加得到无模糊度的检测量R（τ），如式（13）所示：

R（τ）=|Rrecon（τ）|+Rrecon（τ）（13）

综上所述，对于k为任意值，即任意调制阶数的BOC（m，n）信号都有同样的结论，即经过分离副载波和组合子相关函数，

重构一个新的无模糊度的相关函数，具体过程如下：

1）根据副载波脉冲周期延拓的特性，分解本地完整的副载波，得到基准子副载波SCF（t）和基准子副载波延迟N－1个副载波脉冲宽度得到的子副载波SCN（t）。

2）伪随机码经由基准子副载波SCF（t）调制，生成基准子BOC信号BOCF（t）及其周期延拓BOCL（t）。

3）将子BOC信号与BOC信号做相关，生成k个子相关函数Rj（τ）。

4）将自相关函数R（τ）中的第一项子相关函数RF（τ）和最后一项子相关函数RL（τ）进行相加减后分别取绝对值得到两个结果RF+L和RF－L。

5）将RF+L与RF－L相减得到Rrecon（τ），最后将Rrecon（τ）取模相加得到无模糊度的检测量R（τ）。

1.3 加减互补捕获算法

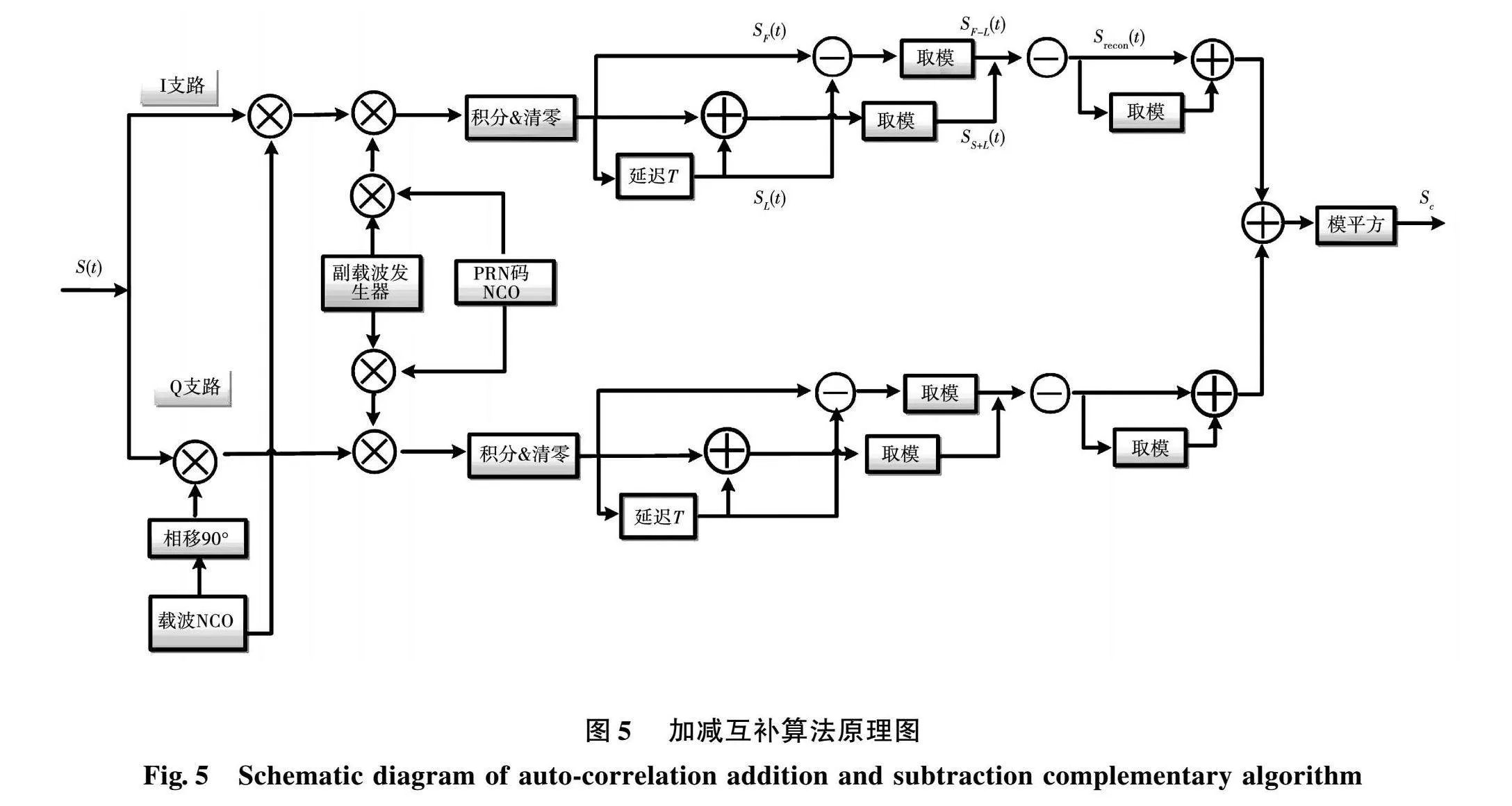
根据上述结论，提出了加减互补捕获算法，原理框图如图5所示。这里选择I支路进行分析，首先将接收的中频BOC（m，n）信号记为S（t），分为I、Q两路分别与本地两个相位正交的载波混频得到同相、正交两路信号；同时，将按调制阶数拆分后的子副载波随伪随机码调制，生成基带子BOC信号，与载波剥离后的接收BOC信号进行相关运算，得到BOC子相关函数；关于τ=400码相位对称的第一个子相关结果和最后一个子相关结果经积分处理后输出为SF（t）和SL（t）；然后将SF（t）和SL（t）相加和相减分别取模得到SF+L（t）和SF－L（t）；然后将SF+L（t）与SF－L（t）相减得到srecon（t）；最后采用非相干的方法，对相减结果进行重构，将相减结果srecon（t）和取绝对值结果|srecon（t）|相加，取包络检测，得到最终的检测量Sc（t）。

接收的BOC信号可表示为

S（t）=PSC（t－τ）D（t－τ）SC（t－τ）×

cos（2π（fIF+fD）t）+n（t）（14）

式中：PS为输入信号功率；C（t）为伪随机码序列；D（t）为导航数据；SC（t）为副载波；τ为输入信号的码相位延迟；fIF为输入中频信号的频率；fD为输入信号的多普勒频率；n（t）为噪声项。

根据式（3）～（9），将本地完整副载波分离，进而将自相关函数分离，得到关于τ=400码相位对称的第一项子相关函数RF和和最后一项子相关函数RL。

由于导航电文D（t）为一个常数，此处不考虑导航数据位的跳变。数据经积分处理并求模后的输出为

S—F=PSRF（Δτ）TSsinc（πΔfDTS）×

［cos（πΔfDTS）+sin（πΔfDTS）］+NF（15）

S—L=PSRL（Δτ）TSsinc（πΔfDTS）×

［cos（πΔfDTS）+sin（πΔfDTS）］+NL（16）

简记为

S—F=SF（Δτ，ΔfD）+NF（17）

S—L=SL（Δτ，ΔfD）+NL（18）

式中：RF（Δτ）表示第一路子相关函数，RL（Δτ）表示最后一路子相关函数，SF和SL分别为S—F和S—L中的信号部分，Δτ为码相位误差，ΔfD表示多普勒误差，NF和NL为服从N（0，σ2）的高斯噪声。

根据式（10）～（11），将S—F和S—L进行相加减，则有：

SF+L=|［SF（Δτ，ΔfD）+NF］+［SL（Δτ，ΔfD）+NL］|（19）

SF-L=|［SF（Δτ，ΔfD）+NF］－［SL（Δτ，ΔfD）+NL］|（20）

根据式（12）～（13），按重构规则，将SF+L和SF－L进行相减，再将得到的结果与相减结果的模值相加，此处对重构后相关函数作近似处理，则有：

Srecon=SF+L－SF－L（21）

S1=|Srecon|+Srecon≈2Srecon（22）

经过M段数据的非相干累加，得到最终检测量Sc，如下式（23）所示：

Sc=2∑Ml=1（|Srecon|2）=2∑Ml=1（（|SF+L－SF－L|）2）（23）

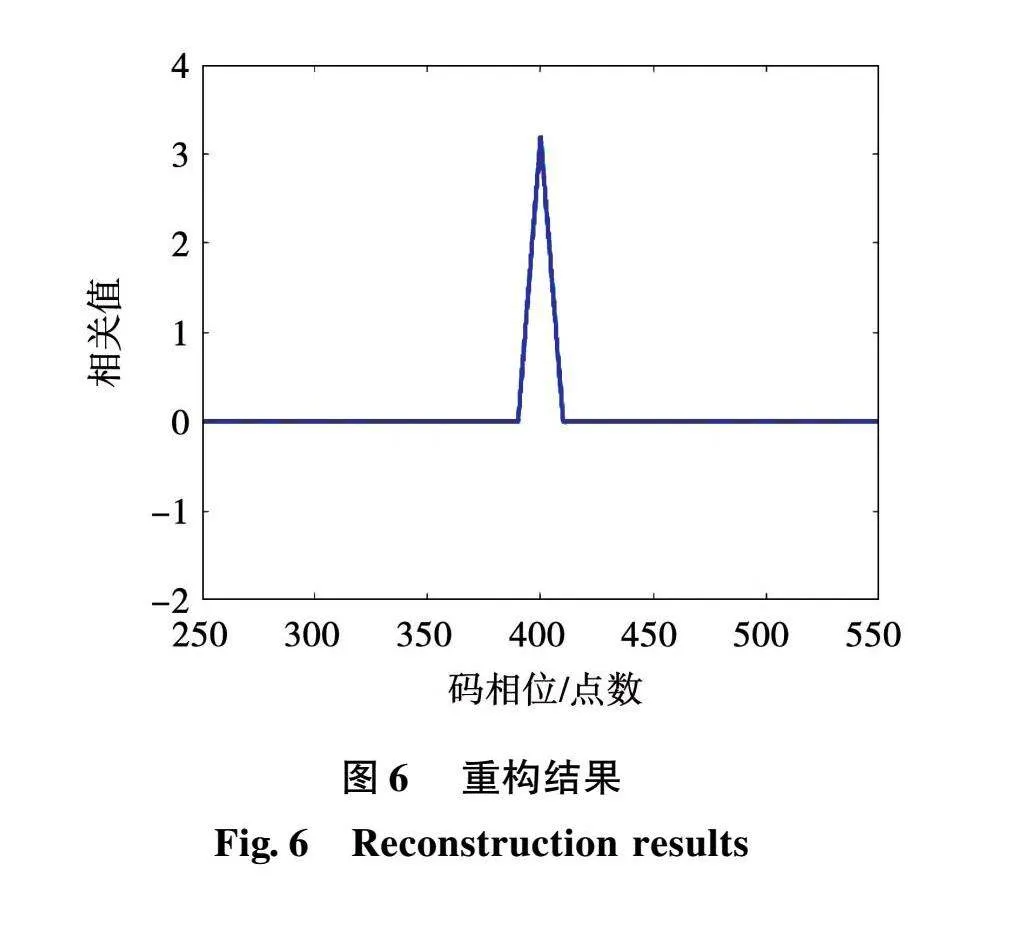
其中噪声NF和NL为不相关的高斯白噪声，其均值为0，方差为σ2。以BOC（2，1）信号为例，码相位延迟为τ=400，重构后得到的相关峰如图6所示。

2 检测统计量分析

2.1 统计检测量分析

将式（23）化简为：

S=2∑Ml=1（|Srecon|2）=2∑Mj=1（（|SF+L|－|SF－L|）2）=

8∑Mj=1（|SL（Δτ，ΔfD）|2j）+

16∑Mj=1（|SL（Δτ，ΔfD）|jNL）+8∑Mj=1（NL）2j（24）

将式（24）整理得到纯信号项如下式（25）所示：

A=8∑Mj=1（|SL（Δτ，ΔfD）|2j）（25）

纯噪声项如下式（26）所示：

v=8∑Mj=1（NL）2j（26）

交叉项如下式（27）所示：

H=16∑Mj=1（|SL（Δτ，ΔfD）|jNL）（27）

其中：NL为高斯白噪声；v服从正态乘积分布；v的概率密度函数如下式（28）所示：

P（v）=K0（|v|/σ2）πσ2（28）

∫∞0tμKv（t）dt=2μ－1Γμ+v+12Γμ－v+12（JRjNll7+o+ON4Xz3+dW2GQ==29）

其中：K（·）为第二类n阶的Bessel函数；Γ（·）为Gamma函数，则v的方差如式（30）所示：

D/dGlCm/MuIU3ESrclRgng==

P（v）=K0（|v|/σ2）πσ2（30）

根据中心极限定理，纯噪声项v服从高斯分布，其方差如式（31）所示：

σ2v=64Mσ4（31）

交叉项为加权常数后的高斯噪声，因此H的方差如式（32）所示：

σ2H=D（H）=16PST2S|RL（Δτ）|2l（32）

最终检测量S中的交叉项方差如式（33）所示：

σ2HS=∑Ml=0［16PST2S|RL（Δτ）|2l］（33）

综上，S为高斯分布，其均值和方差如式（34）、（35）所示：

ms=E（S）=16MP2ST2S|RL（Δτ）|2l（34）

σ2S=D（S）=64Mσ4+∑Ml=0［16PST2S|RL（Δτ）|2l］（35）

当检测量输出中不存在信号仅存在噪声时，Sc遵循瑞利分布［20］，其均值和方差如式（36）、（37）所示：

E（S）=0（36）

D（S）=64Mσ4（37）

检测量输出的概率密度函数如式（38）所示：

P（S）=S（64Mσ4）2exp－S22（64Mσ4）2（38）

虚警概率如式（39）所示：

Pfa（S）=∫+∞Vtp（S）dS（39）

根据Neyman-Pearson准则，可求出检测量输出中不存在信号仅存在噪声时本文算法的检测门限值Vt。

当检测量输出中存在信号加噪声时，Sc遵守莱斯分布［21］，其均值和方差如式（40）、（41）所示：

E（S）=16MP2ST2S|RL（Δτ）|2l（40）

D（S）=64Mσ4+∑Ml=0［16PST2S|RL（Δτ）|2l］（41）

检测量输出的概率密度函数如式（42）所示：

P（S）=Sσ2exp－S2+a22σ2I0aSσ2（42）

式中：a2/σ2为信噪比，I0（x）表示第一类零阶修正Bessel函数，则检测概率如式（43）所示：

Pfb（S）=∫+∞Vtp（S）dS（43）

同理可得检测量输出中存在信号加噪声时本文算法的检测门限值Vt。

2.2 检测性能分析

图7为本文加减互补法、移位相乘法、CSSPeCT法、BPSK-LIKE法、SCPC法、ASPeCT法捕获的检测概率随载噪比的变化情况。信号捕获仿真实验条件设置为：输入信号为BOC（2，1），相干积分时间为1ms，虚警概率为Pf=0.01。捕获判定的依据为不同载噪比条件下，最大峰值出现的位置与码相位偏移位置的误差在±1/4个码片内［22］。

从图7可以看出，在相同载噪比条件下，加减互补法性能与移位相乘法相差不大，捕获概率最高，性能最佳。当检测概率Pd=90%时，本文改进算法在载噪比约38.3dBHz时可达到相应的检测性能，分别优于SCPC法、CSSPeCT法、ASPeCT法和BPSK-LIKE法1.7dBHz、2.45dBHz、2.5dBHz和4.5dBHz，提高了捕获性能。

3 实验结果与分析

基于Matlab平台对加减互补算法进行捕获仿真实验，设采样率fS=81.84MHz，码长为2046个码片，输入信号的中频fIF=4.092MHz，相干积分时间T=1ms，多普勒频移fD=3000Hz，搜索的多普勒频率范围为［－10kHz，10kHz］，搜索步长为500Hz，码相位延迟τ=401。

3.1 三维捕获结果分析

以BOC（2，1）信号为例，对其进行捕获仿真实验，加减互补法的三维捕获结果如图8所示。

由三维捕获结果可以看出，捕获得到检测峰所在的码相位为τ=401，多普勒频移为fD=3000Hz，即捕获实验搜索到的检测峰参数与预设参数相同，验证了本文算法可以实现稳定无模糊度捕获BOC信号。

3.2 二维捕获结果分析

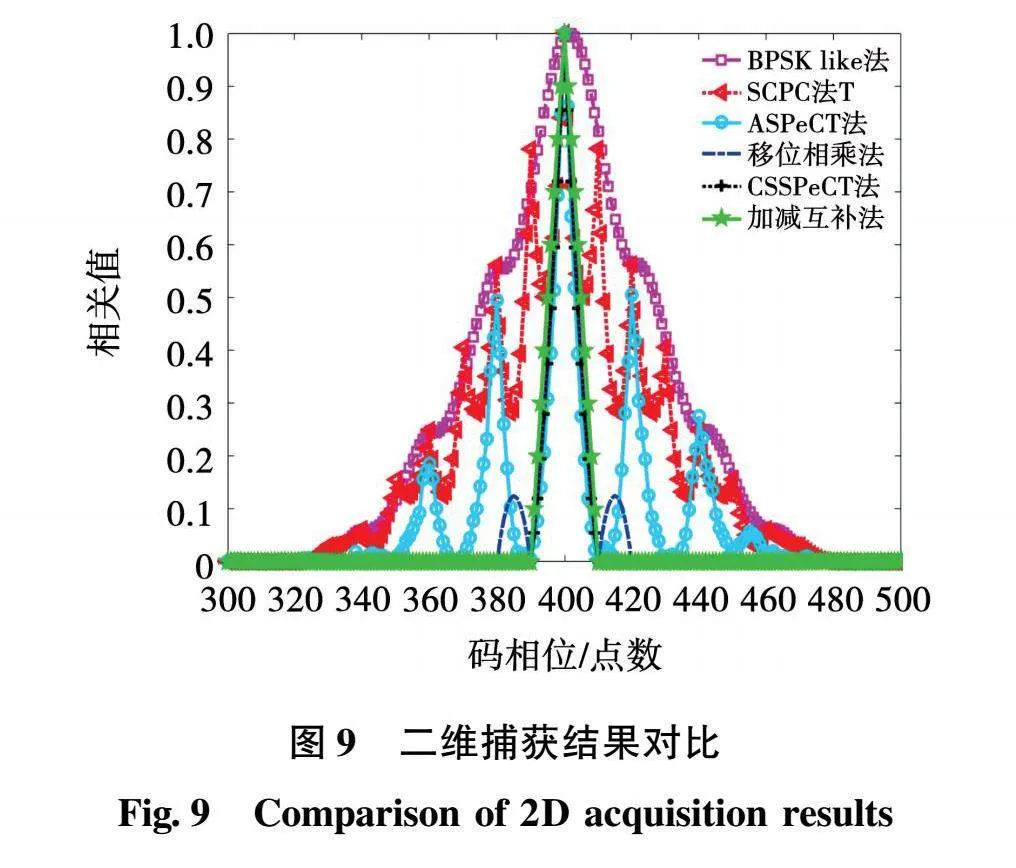
加减互补法、移位相乘法、CSSPeCT法、BPSK-LIKE法、SCPC法、ASPeCT法相关峰跨度对比结果如图9所示。从结果图可以明显看出，SCPC法和BPSK-Like法解决了捕获模糊度的问题，但其主峰变宽，

失去了BOC信号的性能优势，降低了捕获精度。而ASPeCT法没有解决捕获模糊度，虽然主峰跨度小，但是其捕获信号存在较高的峰峰比，旁峰检测量的值约为0.5624。在降低捕获门限的情况下，误捕的概率将大大增加，不能达到去模糊度的目的，且随着调制阶数的增大，ASPeCT法中的旁峰检测量越来越高，无法实现BOC信号无模糊度捕获。移位相乘法虽然保留了窄相关峰，但仍然存在两个旁峰。CSSPeCT法在保留窄相关峰的同时，完全解决了捕获模糊的问题，但是仅适用于调制阶数中m=n的情况。本文算法在保留了窄相关峰的同时，能够完全消除旁锋，适用于任意调制阶数的正余弦副载波相位BOC（m，n）信号，且本文算法随着调制阶数增大，主峰宽度会越窄。

4 结 论

根据现有算法无法完全消除BOC信号相关峰模糊度的问题，本文研究了自相关函数的性质，对子相关函数进行加减重构，提出了一种基于自相关函数的加减互补算法。结果表明加减互补法能在保留BOC信号窄带特性的同时，达到消除旁峰，实现无模糊度捕获的目的，且适用于任意调制阶数的BOC调制信号，具有很好的适用性，对于BOC（m，n）调制信号捕获的研究有一定的参考意义，对我国北斗三代卫星B1C信号的接收有很好的参考意义。

下一步工作将针对算法复杂度方面对本文算法进行优化改进，提出一种快速算法来解决加减互补法实现复杂的问题。

参 考 文 献：

［1］ BETZ J W. Binary Offset Carrier Modulations for Radionavigation［J］. Navigation： Journal of the Institute of Navigation， 2001， 48（4）：227.

［2］ 刘瀛翔，谢郁辰，唐小妹.基于多相分解的BOC信号高效捕获算法［J］.电子学报，2023，51（1）：1.

LIU Yingxiang， XIE Yuchen， TANG Xiaomei. An Efficient BOC Signal Acquisition Method Based on Polyphase Decomposition［J］. Acta Electronica Sinica， 2023，51（1）：1.

［3］ JI Yuanfa， SONG Sisi， SUN Xi yan， et al. A Novel Unambiguous Acquisition Algorithm Based on Segmentation Reconstruction for BOC （n，n） Signal［J］. IEICE Transactions on Communications advpub.0， 2022： 2022EBP3042.

［4］ HAN Q， ZHU K， HU C， et al. BOC Signal Acquisition Algorithm Based on Similar Enfoldment［J］. International Journal of Aerospace Engineering， 2020（4）：1.

［5］ FISHMAN P， BETZ J W. Predicting Performance of Direct Acquisition for the M-code Signal［C］//Anaheim： Proceedings of the 2000 National Technical Meeting of The Institute of Navigation， 2000：574.

［6］ BURIAN A， LOHAN E S， RENFORS M. BPSK-like Methods for Hybrid-Search Acquisition of Galileo Signals［C］//Istanbul： 2006th IEEE International Conference on Communications， 2006：5211.

［7］ JULIEN， OLIVIER， et al. ASPeCT： Unambiguous Sine-BOC （n， n） Acquisition/tracking Technique for Navigation Applications［C］//Fredericton： IEEE Transactions on Aerospace and Electronic Systems， 2007：150.

［8］ LIU Z， XU B， TANG X. Multipath Mitigating Technique for BOC （kn， n） Signal in GNSS［C］//Nanjing： 2015 International Conference on Wireless Commun-ications & Signal Processing （WCSP）， 2015： 1.

［9］ WANG H J， JI Y F， SHI H L， et al. The Performance Analysis of Unambiguous Acquisition Methods for BOC（m，n） Modulated Signals［C］//Wuhan： 2011 7th International Conference on Wireless Communications， Networking and Mobile Computing， 2011： 1.

［10］沈锋，徐广辉，冯海玉.基于合成相关函数的sin-BOC/MBOC无模糊捕获方法［J］.系统工程与电子技术，2015，37（9）：1980.

SHEN Feng， XU Guanghui， FENG Yuhai. Synthesized Correlation Function Based Unambiguous Acquisition Technique for Sin-BOC/ MBOC Modulated Signals［J］. Systems Engineering and Electronics， 2015，37（9）：1980.

［11］张鑫鑫， 程亚文， 郭承军， 等.一种新的BOC（1，1）信号无模糊度捕获算法［C］//上海：中国卫星导航学术年会， 2017： 1.

ZHANG Xinxin， CHENG Yawen， GUO Chengjun， et al. A Novel Blur-less Acquisition Algorithm for BOC（1，1）［C］// Shanghai： China Satellite Navigation Academic Annual Meeting， 2017： 1.

［12］张天骐，江晓磊，赵军桃， 等.二进制偏移载波及其衍生信号的通用无模糊捕获算法［J］.电子与信息学报，2017，39（2）：451.

ZHANG Tianqi， JIANG Xiaolei， ZHAO Juntao， et al. Unambiguous General Acquisition for Binary Offset Carrier and Its Derivative Signals［J］. Journal of Electronics & Information Technology， 2017，39（2）：451.

［13］张洪伦，巴晓辉，陈杰， 等.适用于BOC（m，n）信号的无模糊捕获技术［J］.航空学报，2017，38（4）：222.

ZHANG Honglun， BA Xiaohui， CHEN Jie， et al. The Unambiguous Acquisition Technology for BOC（m，n） Signals［J］. Acta Aeronautica et Astronautica Sinica， 2017， 38（4）：222.

［14］SHIM D S， JEON J S. An Unambiguous Delay-And-Multiply Acquisition Scheme for GPS L1C Signals［J］. Sensors （Basel， Switzerland）， 2018， 18（6）：1739.

［15］SUN Xiyan， ZHOU Qing， JI Yuanfa， et al. An Unambiguous Acquisition Algorithm for BOC（n，n） Signal Based on Sub-correlation Combination［J］. Wireless Personal Communications， 2019， 106： 1609.

［16］胡辉，李林，雷明东， 等. 一种新的二进制偏移载波调制信号无模糊度捕获算法［J］. 中国惯性技术学报， 2014， 22（6）：763.

HU Hui， LI Lin， LEI Mingdong， et al. New Unambiguous Acquisition Algorithm for Binary Offset Carrier Modulated Signal［J］. Journal of Chinese Inertial Technology， 2014，22（6）：763.

［17］黄新明，张鹏程，侯林源， 等.一种基于边峰消除的BOC信号无模糊捕获方法： CN202111133567.2［P］.2023.

HUANG Xinming， ZHANG Pengcheng， HOU Lingyuan， et al. An Unambiguous Acquisition Method of BOC Signal Based on Edge Peak Elimination： CN202111133567.2［P］.2023.

［18］孙希延，郝放，纪元法， 等.基于相关移位BOC（n，n）无模糊度捕获算法［J］.北京理工大学学报，2020，40（3）：298.

SUNXiyan， HAO Fang， JI Yuanfa， et al. An Unambiguous Acquisition Algorithm Based on Correlation Shift for BOC（n， n）［J］. Transactions of Beijing Institute of Technology， 2020， 40（3）：298.

［19］李明，胡辉，郭萌， 等.基于互相关移位相乘BOC（m，n）无模糊捕获算法［J］.航空学报，2022，43（8）：621.

LI Ming， HU Hui， GUO Meng， et al. Unambiguous Acquisition Algorithm Based on Cross-correlation Function Shift Multiplication for BOC（m，n）［J］. Acta Aeronautica et Astronautica Sinica，2022，43（8）：621.

［20］M. K. Arti. Product of Squared-SR Random Variables： Application to Sate-llite Communication［J］. IEEE Tran-sactions on Aerospace and Electronic S-ystems， 2020， 56（1）：486.

［21］杨再秀，杨俊武，郑晓冬， 等. 现代GNSS信号捕获性能评估理论与应用［J］.中国科学：物理学 力学 天文学， 2021， 51（1）： 187.

YANG Zaixiu， YANG Junwu， ZHENG Xiaodong， et al. Theoretical Assessment and Application of Modern GNSS Signals Acquisition Performance［J］. Scientia Sinica （Physica， Mechanica & Astronomica）， 2021， 51（1）： 187.

［22］陈柯勋，张雪英，邱伟.一种改进的GNSS接收机完好性监测算法［J］.哈尔滨理工大学学报，2021，26（3）：103.

CHEN Kexun， ZHANG Xueying， QIU Wei. An Improved Integrity Monitoring Algorithm for GNSS Receiver［J］. Journal of Harbin University of Science and Technology， 2021，26（3）：103.

（编辑：温泽宇）