二维波动方程的高阶精度紧致显式差分格式及稳定性分析

摘 要：针对具有初边值问题的二维波动方程，提出了一种数值求解该方程的高阶紧致显式有限差分格式。首先，根据相关文献对导数的离散近似，得到周期边界条件下的六阶紧致差分格式。其次，在空间方向上，边界节点导数项利用原方程代入的方法进行计算，而内部节点的导数项利用六阶紧致差分公式近似，使空间精度达到六阶。同时，在时间方向上，利用泰勒级数展开公式、原方程代入以及中心差分公式推导出时间层的二阶精度差分格式，为了将整体上的时间精度由二阶提高至四阶，采用外推算法实现时间层的高阶近似。再次，再利用傅里叶分析法对该格式的稳定性进行分析，得到在此精度下的稳定性条件，即|a|λ∈［0，1276］。最后，通过数值实验验证了所提出的HOCE（6，4）格式的高效性和准确性。

关键词：波动方程；中心差分；紧致差分；外推算法；稳定性

DOI：10.15938/j.jhust.2024.03.017

中图分类号： O241

文献标志码： A

文章编号： 1007-2683（2024）03-0141-08

High Order Compact Explicit Difference Schemes and

Stability Analysis for Two-dimensional Wave Equations

SUN Yang1， SONG Linlin1， AI Xiaohui2

（1.School of Science， Harbin University of Science and Technology， Harbin 150080， China；

2.School of Science， Northeast Forestry University， Harbin 150040， China）

Abstract：In this paper， a high-order compact explicit finite difference scheme is proposed to numerically solve two-dimensional wave equations with initial boundary value problems. First of all， according to the discrete approximation of derivatives in the existing literature， a sixth-order compact difference scheme with periodic boundary conditions is obtained. Then， in the spatial direction， the derivative term of the boundary node is calculated by substituting the original equation， and the derivative term of the internal node is approximated by the sixth order compact difference formula， so that the spatial accuracy can reach the sixth order. For the time direction， the second-order accuracy difference scheme of the time layer is derived by using the Taylor series expansion formula， the original equation substitution and the central difference formula. In order to improve the overall time accuracy from the second order to the fourth order， the Richardson extrapolation method is used to realize the high-order approximation of the time layer. Furthermore the stability of the scheme is analyzed by Fourier analysis method and the stability condition is |a|λ∈［0，1276］. Finally， the efficiency and accuracy of the proposed HOCE（6，4） scheme are verified by numerical experiments.

Keywords：wave equation; central difference; compact finite difference; Richardson extrapolation; stability

0 引 言

波动方程作为一类重要的描述波动现象的双曲型偏微分方程，一直以来受到人们的广泛关注。其在弹性力学、流体力学、电磁学及气象学等诸多自然科学领域都有着较为深入的研究与应用［1］。众所周知，实际问题具有高度的复杂性，求解偏微分方程的解析解有时较为困难。因此，对于偏微分方程数值解法的研究具有重要意义。

目前，数值求解方法主要有：有限差分法、有限元法、有限体积法以及谱方法等。其中以离散点的差商近似导数作为研究手段的有限差分法具有形式简单、易于编程实现和计算精度高等优点，是求解偏微分方程的有效方法［2］。有限差分法的产生时间较早，其数学理论也已经较为成熟，常见的分析差分法稳定性的方法主要有Von Neumann方法、矩阵分析方法和能量分析方法［3-4］。

低精度的差分离散格式虽然计算相对稳定，但是由于其较低的计算精度和分辨率，往往导致数值计算失真，因此众多的计算数学工作者专注于高精度、高分辨率的计算格式研究。研究表明，高精度格式较低精度格式可以有效地减小对步长的限制，即使所使用的网格为粗网格，也能够获得低精度格式在较细网格上的计算精度，即在计算域内利用比较少的网格点就可以获得较高的计算精度，从而提高计算效率。此外，有研究表明，高精度的数值方法可以有效抑制数值色散。然而，随着计算精度的提高，高精度格式可能会出现数值不稳定。因此，发展波动方程的高精度（高于二阶精度）且稳定性好的差分格式是重要且具有实际意义的研究课题［5-6］。

近年来，较多学者对波动方程进行了大量的研究，并提出了很多精确有效的方法。其中，文［7］针对一维波动方程，应用Runge-Kutta方法，提出了一种具有严格的稳定性条件的的二阶精度的显式格式。在文［8-10］中利用Richardson外推法，将时间二阶精度提高至四阶，但需要计算细网格的二阶精度解进一步得到粗网格上的四阶精度解，从而降低计算效率。综上，许多学者在解决此类问题时，使用的方法在时间或空间上精度较低［11-12］。对于多维问题，高精度差分格式因其较小的数值耗散等优点有着广泛的应用，但是也存在明显的问题：即在处理边界条件问题上存在不足，所需精度越高节点就越多，导致处理边界时计算区域两端会出现所谓“冒点”的情况，从而增加边界处理难度，同时破坏了系数矩阵的对称性、增加了计算时间，导致高精度格式的计算效率有所下降。如果采用隐式方法，由于有限差分算子的有理函数将替代差分算子，进而每个时间步都要解决三对角系统，使计算量增加。常用的解决方法是交替方向隐（alternating direction implicit， ADI）格式和局部一维（local one-dimension， LOD）格式［13-14］。ADI格式是将高维问题转化为一维问题进行计算，从而减少计算量。在引入ADI格式用于求解双曲型方程后，有很多学者将其推广到二维非线性双曲方程，在文［15］中有详细介绍。但是，ADI格式对计算区域有限制条件。LOD格式相比ADI格式解决了这一问题。在文［16］中，讨论了基于Richardson外推的时间和空间四阶LOD格式。在文［17］中提出包含LOD的三层隐式格式。然而，以上提出的这些方法都是非紧致的，或者只有在特殊条件下才能使用。为了解决这些问题，一些学者致力于各种紧致的高阶差分格式的研究与应用。高阶紧致差分格式是利用不同节点处空间导数值的线性组合等于不同节点处函数的线性组合进行差分，然后根据不同的精度要求，通过待定系数法得到这些组合系数。近年来，相关数值实验可以证明，相比非紧致和低阶方法，高阶紧致差分格式要求的计算节点相对较少、边界处理相对简单且在一定程度上具有更好的分辨率，并且能够证明紧致格式的截断误差通常比非紧致格式的截断误差在同阶格式下小四到六倍［18-19］。

本文针对二维波动方程，应用有限差分思想，构造一种高阶精度紧致显C2g2dZTCI14Ktlqq0X8bPA==式有限差分格式。由于本文格式是显式的，因此不需要任何迭代过程，能够有效的缩短计算时间。以往数值结果表明，紧致格式优于相应的同阶显式格式。因此，本文格式是将常见的二阶或四阶空间精度提高到六阶，时间方向上利用Richardson外推，将时间精度由二阶提高至四阶的高阶紧致显式差分格式。然后利用Fourier分析法分析该格式的稳定性。为了方便起见，将本文的空间六阶、时间四阶计算格式简写为HOCE（6，4）格式。为验证其计算效率和高精度特性，本文在数值实验中选择了其它两种计算格式：空间四阶、时间二阶（简称：HOCE（4，2））格式［21］和空间六阶、时间二阶（简称：HOCE（6，2））格式，并且与本文HOCE（6，4）格式的计算结果进行比较分析，从而验证了本文格式的高精度特性以及在计算效率方面的较强优势。

1 问题描述

对于如下二维波动方程的初边值问题

2ut2=a2（2ux2+2uy2）+f（x，y，t）

（x，y，t）∈D×（0，T］

u（x，y，0）=φ（x，y）

u（x，y，0）t=ψ（x，y）

u（0，y，t）=g0（y，t），u（1，y，t）=g1（y，t）

u（x，0，t）=h0（x，t），u（x，1，t）=h1（x，t）（1）

由于进行数值求解，需要增加的周期边界条件如下：

u（x+1，y，t）=－u（x，y，t）

u（x，y+1，t）=－u（x，y，t）（2）

式中：u（x，y，t）是未知函数；D=［0，1］×［0，1］；f（x，y，t）、φ（x，y）、ψ（x，y）、g0（y，t）、g1（y，t）、h0（x，t）、h1（x，t）均为已知函数，且充分光滑；a为波动系数。

在计算区域内，进行等距网格剖分，h是空间步长，τ是时间步长，（xi，yj，tn）是网格节点，其中，xi=ih，yj=jh，tn=nτ，i，j=0，1，…，N，n=0，1，…，M，用uni，j近似表示（xi，yj，tn）的近似值。

2 HOCE（6，4）格式

首先，根据文［18-19］中的二阶导数的离散，可以得到如下公式

αu″j－1+u″j+αu″j+1=

a1uj+1－2uj+uj－1h2+a2uj+2－2uj+uj－24h2（3）

式中α，a1，a2为自由参数，且决定格式的精度，在这里可取

a1=43（1－α），a2=13（10α－1）。

当α=211时，即a1=1211， a2=311，此时式（3）即为六阶精度。在周期边界条件下，将上述参数α，a1，a2代入式（3），可得如下的六阶精度格式

211u″j－1+u″j+211u″j+1=

1211uj+1－2uj+uj－1h2+311uj+2－2uj+uj－24h2

即

8u″j－1+44u″j+8u″j+1=

3uj+2+48uj+1－102uj+3uj－2+48uj－1h2（4）

当参数α=110，a1=1210，a2=0时，式（3）为四阶精度，即

u″j－1+10u″j+u″j+1=12uj+1－2uj+uj－1h2（5）

2.1 计算（2ux2）ni，j和（2uy2）ni，j的值

空间内部节点利用六阶紧致差分格式，则有

8（2ux2）ni+1，j+44（2ux2）ni，j+8（2ux2）ni-1，j=

3uni+2，j+48uni+1，j－102uni，j+3uni－2，j+48uni－1，jh2（6）

式中i=2，3，…，N－2，j=0，1，…，N。

8（2uy2ni，j+1+44（2uy2）ni，j+8（2uy2ni，j－1=

3uni，j+2+48uni，j+1－102uni，j+3uni，j－2+48uni，j－1h2（7）

式中：j=2，3，…，N－2；i=0，1，…，N。

对空间边界点进行处理，由式（1）和式（2）可得

（2ux2）n0，j=1a2（2ut2-f）n0，j-（2uy2）n0，j=

1a2（2g0t2-f）n0，j－（2g0y2n0，j（8）

式中j=0，1，…，N。

（2ux2nN，j=1a2（2ut2-f）nN，j－（2uy2nN，j=

1a2（2g1t2-f）nN，j－（2g1y2nN，j（9）

式中j=0，1，…，N。

（2uy2）n0，j=1a2（2ut2-f）ni，0-（2uy2）ni，0=

1a2（2h0t2-f）ni，0－（2h0y2ni，0（10）

式中i=0，1，…，N。

（2uy2）ni，N=1a2（2ut2-f）ni，N-（2uy2）ni，N=

1a2（2h1t2-f）ni，N－（2h1y2ni，N（11）

式中i=0，1，…，N。

2.2 第一个时间层的离散

利用Taylor公式展开得到

u1i，j=u0i，j+τ（ut）0i，j+τ22（2ut2）0i，j+O（τ3）=

u0i，j+τ（ut0i，j+τ22（2ut2）0i，j+O（τ3）（12）

利用式（1），对上式右端项进行整理可得

（2ut2）0i，j=a2［（2ux20i，j+（2uy2）0i，j］+f0i，j=

a2［（φxx）i，j+（φyy）i，j］+f0i，j（13）

将式（13）代入式（12），化简并舍去截断误差项得

u1i，j=φ（xi，yj）+τψ（xi，yj）+

τ22［a2φxx（xi，yj）+a2φyy（xi，yj）+f（xi，yj，0）］（14）

2.3 其他时间层

利用中心差分格式近似时间的二阶导数，并利用Taylor公式展开，可得

un+1i，j－2uni，j+un－1i，jτ2=a2［（2ux2）ni，j+（2uy2）ni，j］+

fni，j+o（τ2）（15）

对式（15）化简整理，并舍去截断误差项得到

un+1i，j=2uni，j－un－1i，j+a2τ2［（2ux2）ni，j+（2uy2）ni，j］+fni，j（16）

式（16）即为空间六阶精度，时间二阶精度HOCE/kyzO3GOmU/AWuTjHnRhFQ==（6，2）的显式紧致差分格式，该格式的截断误差为

O（h6+τ2h2+τ2）。

2.4 时间层的外推解

式（16）的格式在空间上为六阶精度，但时间精度仅具有二阶，考虑采用如下的Richardson外推法将时间精度提高到四阶

uni，j（τ，h）=（4u2ni，j（τ/2，h）－uni，j（τ，h））/3（17）

其中：式（17）左端项uni，j（τ，h）为所求的四阶精度解，右端项uni，j（τ，h）为格式（16）在时间步长为τ时的解，u2ni，j（τ/2，h）为时间步长取τ/2时的解。

3 稳定性分析

利用Fourier方法分析格式稳定性。这里，假设f精确无误差，且令uni，j=ξnei（σ1xi+σ2yj），（uxx）ni，j=ηnei（σ1xi+σ2yj），（uyy）ni，j=γnei（σ1xi+σ2yj），式中ξ、η、γ为振幅，σ1、σ2为波数，i=－1为虚数单位。

引理1［20］ 实系数二次方程λ2－bλ－c=0的根按模不大于1的充要条件为|b|≤1－c≤2。

由已知条件

uni+1，j=ξnei（σ1xi+1+σ2yj）=

ξnei［σ1（xi+h）+σ2yj］=ξnei（σ1xi+σ2yj）eiσ1h

同理

uni－1，j=ξnei（σ1xi+σ2yj）e－iσ1h

uni+2，j=ξnei（σ1xi+σ2yj）e2iσ1h，uni－2，j=ξnei（σ1xi+σ2yj）e－2iσ1h

uni，j+1=ξnei（σ1xi+σ2yj）eiσ2h，uni，j－1=ξnei（σ1xi+σ2yj）e－iσ2h

uni，j+2=ξnei（σ1xi+σ2yj）eiσ2h，uni，j－2=ξnei（σ1xi+σ2yj）e－iσ2h

且可得到

（uxx）ni+1，j，（uxx）ni-1，j，（uxx）ni+2，j，（uxx）ni-2，j

（uyy）ni，j+1，（uyy）ni，j-1，（uyy）ni，j+2，（uyy）ni，j-2

则将上式代入式（6）化简整理得

ηnei（σ1xi+σ2yj）［16cosσ1h+44］=

12h2ξnei（σ1xi+σ2yj）（cosσ1h－1）（cosσ1h+9）（18）

即

ηn=3h2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11ξn（19）

同理，式（7）化简为

γnei（σ1xi+σ2yj）［16cosσ2h+44］=

12h2ξnei（σ1xi+σ2yj）（cosσ2h－1）（cosσ2h+9）（20）

即

γn=3h2（cosσ2h－1）（cosσ2h+9）4cosσ2h+11ξn（21）

下面进行稳定性分析，令vn+1ij=unij，f≡0，式（16）的矩阵形式如下

un+1ijvn+1ij=2－110un+1ijvnij+

a2τ2000（uxx）nij+（uyy）nij（vxx）nij+（vyy）nij（22）

令Unij=（unij，vnij）T，Unij=ξnei（σ1h+σ2h），并代入式（22），化简为

ξn+1=2－110ξn+a2τ2000（ηn+γn）（23）

将式（19）与式（21）代入式（23），记λ=τh，r=aλ，令

C=2+3r2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11+

（cosσ2h－1）（cosσ2h+9）4cosσ2h+11（24）

可得该格式的误差增长矩阵为

D=C－110

则对应的特征方程是

μ2－2+3r2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11+

（cosσ2h－1）（cosσ2h+9）4cosσ2h+11μ+1=0（24）

由引理1可知，在上述方程式（24）中，

b=2+3r2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11+

（cosσ2h－1）（cosσ2h+9）4cosσ2h+11

c=－1，则该格式稳定的充要条件为

2+3r2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11+

（cosσ2h－1）（cosσ2h+9）4cosσ2h+11≤2（25）

式（25）等价为以下两个不等式

3r2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11+

（cosσ2h－1）（cosσ2h+9）4cosσ2h+11≤0（26）

－4≤3r2（cosσ1h－1）（cosσ1h+9）4cosσ1h+11+

（cosσ2h－1）（cosσ2h+9）4cosσ2h+11（27）

对于式（26），不等式恒成立。

对于式（27），化简为r2≤43A，式中

A=（1－cosσ1h）（cosσ1h+9）4cosσ1h+11+

（1－cosσ2h）（cosσ2h+9）4cosσ2h+11

令α=1－cosσ1h，β=cosσ2h+9，则

A=α（10－α）15－4α+β（10－β）15－4β

且α∈［0，2］，β∈［0，2］，经过特殊取值可发现，当α=β=2时，有

r2≤724

则该格式的稳定性条件为

|a|λ∈［0，1276］

4 数值算例

为验证本文格式的高精度和高分辨率特性，选择比较HOCE（4，2）格式［21］，HOCE（6，2）格式与本文格式。考虑以下方程的初边值问题，计算了不同空间步长的不同时刻的L∞和L2范数误差以及计算时间。其中L∞和L2范数误差的定义如下：

L∞-error=maxi，j|uni，j－u（xi，yj，tn）|

L2-error=h2∑i，j［uni，j－u（xi，yj，tn）］2

算例1［21］

2ut2=2ux2+2uy2

u（0，y，t）=0，u（1，y，t）=0

u（x，0，t）=0，u（x，1，t）=0

u（x，y，0）=sin（πx）sin（πy）

u（x，y，0）t=0（28）

其精确解为u（x，y，t）=sin（πx）sin（πy）cos（2πt）。

通过比较HOCE（4，2）格式和HOCE（6，2）格式及本文格式的计算结果。即当h=1/10，1/20，…，1/320时，计算了τ=0.0002时在第100个时间步上，不同空间步长的范数误差。其中，表1为L∞范数误差，表2为L2范数误差。由表1和表2可知，当空间步长不断减小时，L2和L∞范数误差也相应减小，并且本文的计算结果优于HOCE（4，2）和HOCE（6，2）的格式。表3为通过数值算例进一步说明本文所提出的HOCE（6，4）格式在计算时间方面具有高效性。对于不同的h，由于格式的计算复杂度不同，HOCE（6，4）格式计算时间较其它两种格式有一定的增加。然而，若我们加密网格，在空间步长为h2时，由计算结果能够看出HOCE（6，4）格式相比其它格式的计算时间无明显差别，而计算误差大为减少，从而充分体现了本文HOCE（6，4）格式的高精度的优点。

算例2［21］

2ut2=2ux2+2uy2

u（0，y，t）=0，u（1，y，t）=0

u（x，0，t）=0，u（x，1，t）=0

u（x，y，0）=0

u（x，y，0）t=2πsin（πx）sin（πy）（29）

其精确解为

u（x，y，t）=sin（2πt）sin（πx）sin（πy）

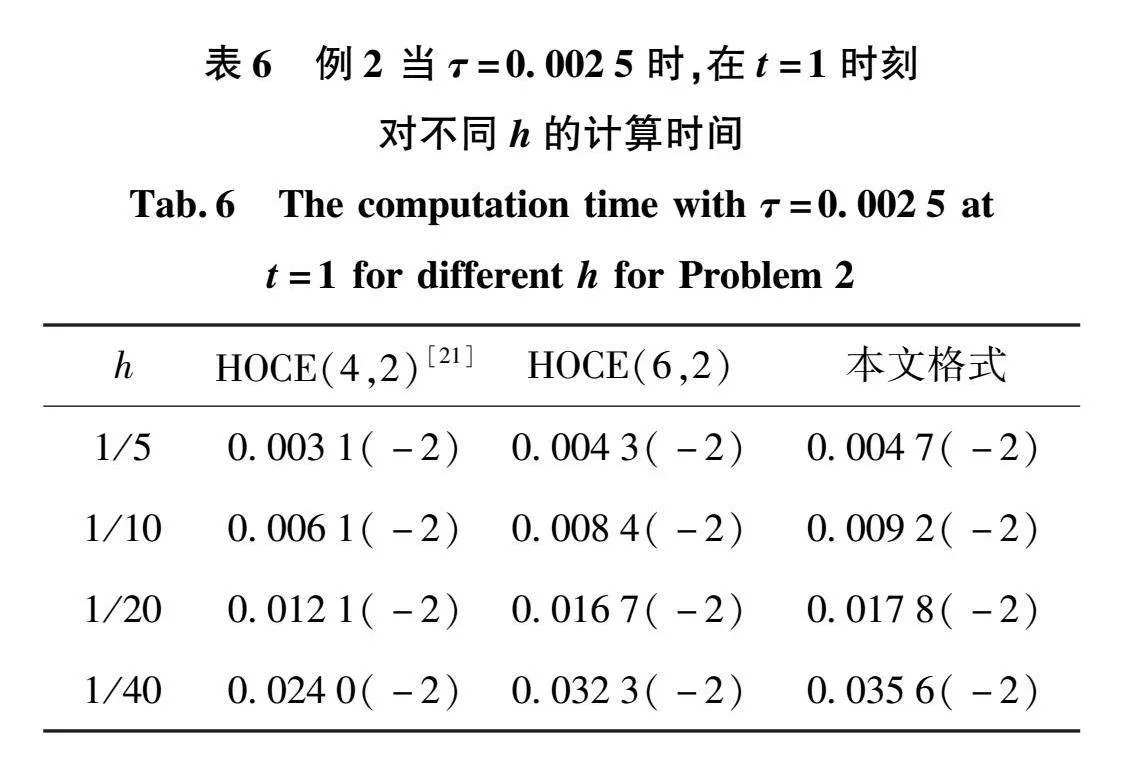
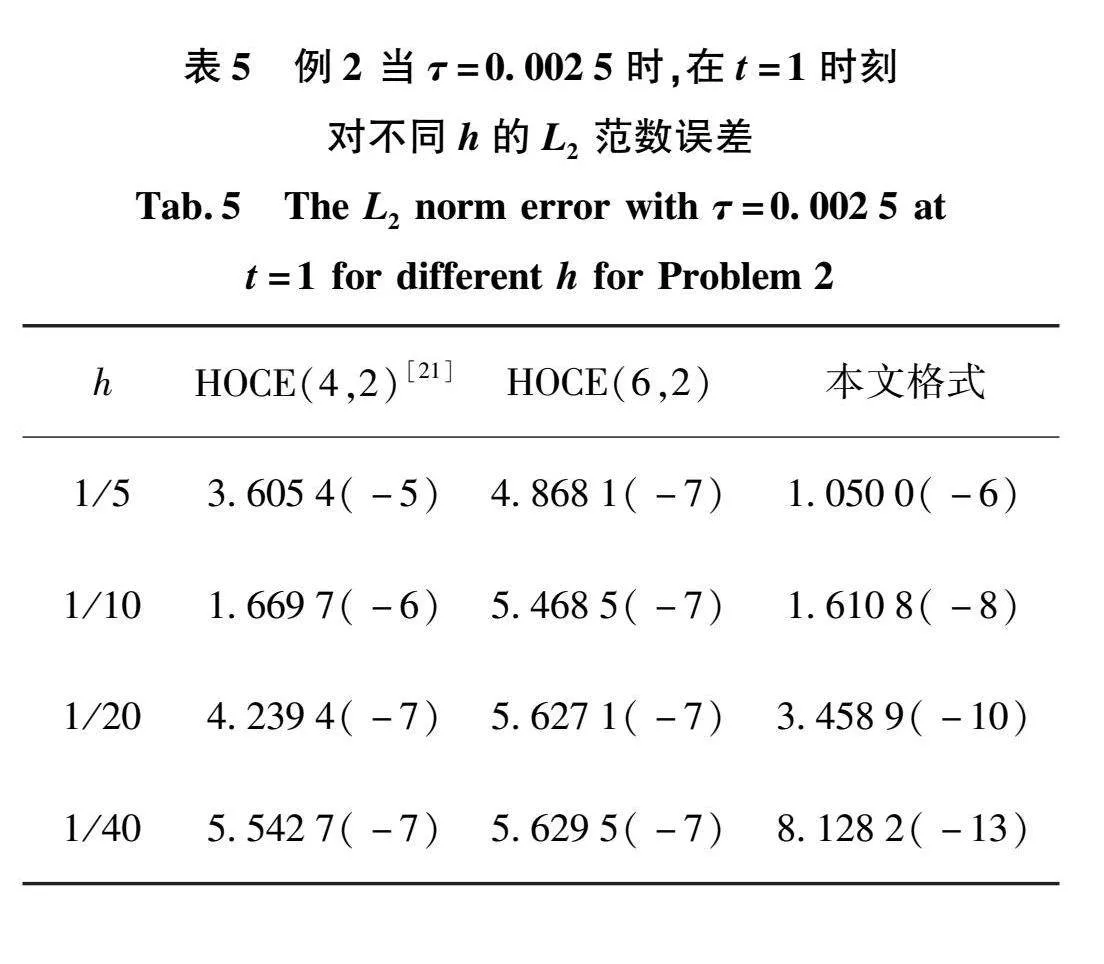
表4和表5给出了本文HOCE（6，4）、本文HOCE（6，2）以及文［21］中的HOCE（4，2）格式的计算结果。计算了τ=0.0025，在t=1时，不同空间步长的范数误差。即，L∞+范数误差和L2范数误差。可知，当空间步长不断减小时，范数误差也相应减小，并且本文的计算结果相对较好。由表6可以得到，本文格式的计算相对简单。

5 结 论

本文针对二维波动方程，利用六阶紧致格式计算二阶导数。由于紧致格式具有基架少，分辨率高等诸多优点，因此特别适用于波动方程等偏微分方程的高精度计算。时间方向上利用Richardson外推，将时间二阶提高到四阶精度。利用Fourier分析法求出了该格式的稳定区域为|a|λ∈［0，1276］。数值实验方面，为验证本文HOCE（6，4）格式的有效性和高分辨率特性，与HOCE（6，2）格式和HOCE（4，2）格式的计算结果进行比较分析。结果表明，不论计算精度还是计算时间方面，本文的HOCE（6，4）格式都具有很高的计算精度和计算效率。HOCE（6，4）格式在计算时间上较HOCE（6，2）格式并没有明显增加，但是在相同时间和空间步长的条件下，本文的HOCE（6，4）格式的计算误差远远小于HOCE（6，2）格式和HOCE（4，2）格式，而且从计算结果可以看出：在粗网格下，本文的HOCE（6，4）格式的数值误差要优于空间步长减半的HOCE（4，2）格式的数值误差。这充分验证了高阶精度能够显著提高差分格式的计算效率，因此可以说本文对计算格式的改进是成功的。

下一步作者考虑将HOCE（6，4）格式推广到三维波动方程以及其它偏微分方程的数值计算当中，可以预见将会有更多较好的成果呈现。

参 考 文 献：

［1］ 张天德， 孙传灼. 关于波动方程的差分格式［J］. 山东工业大学学报， 1995（3）： 283.

ZHANG Tiande， SUN Chuanzhuo. On The Difference Scheme of Wave Equation［J］. Journal of Shandong University of Technology， 1995（3）： 283.

［2］ 王希， 张爽， 胡劲松. 求解广义BBM-KdV方程的守恒型有限差分方法［J］. 哈尔滨理工大学学报， 2022， 27（4）： 147.

WANG Xi， ZHANG Shuang， HU Jinsong. Conservative Finite Difference Method for Solving Generalized BBM-KdV Equation. Journal of Harbin University of Science and Technology ， 2022， 27（4）： 147.

［3］ 冉茂华. 几类分数阶偏微分方程的有限差分方法［D］. 武汉. 华中科技大学， 2016.

［4］ 姜蕴芝， 葛永斌. 求解波动方程的2种显式高精度紧致差分格式［J］. 四川师范大学学报：自然科学版， 2017， 40（2）： 177.

JIANG Yunzhi， GE Yongbin. Two Kinds of Explicit High Order Compact Difference Schemes for Solving Wave Equations［J］. Journal of Sichuan Normal University： Natural Science， 2017， 40（2）： 177.

［5］ HOU Baihui， DONG Liang. The Conservative Time High-Order AVF Compact Finite Difference Schemes for Two-Dimensional Variable Coefficient Acoustic Wave Equations［J］. Journal of Scientific Computing， 2019， 80（2）： 1279.

［6］ BRITT S， TURKEL E， TSYNKOV S. A High Order Compact Time/Space Finite Difference Scheme for The Wave Equation with Variable Speed of Sound［J］. Journal of Scientific Computing， 2018， 76（2）： 777.

［7］ 陈山. 求解波动方程的龙格—库塔型方法及其地震波传播模拟［D］. 北京. 清华大学， 2010.

［8］ HE Dongdong.An Unconditionally Stable Spatial Sixth-Order CCD-ADI Method for The Two-Dimensional Linear Telegraph Equation［J］. Numerical Algorithms， 2016， 72（4）： 1103.

［9］ MA Yuezhen， LI Xiangang， GE Y B.A High-accuracy Alternating Direction Implicit Method for Solving the Two-dimensional Wave Equation［J］. Journal of Sichuan Normal University： Natural Science， 2010， 33（2）： 179.

［10］魏剑英. 求解二维热传导方程的高精度紧致差分方法［J］. 西南师范大学学报：自然科学版， 2013， 38（12）： 5.

WEI Jianying.On a High-Order Compact Difference Method for Solving the Two-Dimensional Heat Equation［J］. Journal of Southwest University： Natural Science， 2013，38（12）： 5.

［11］YANG Dinghui， WANG Nan， CHEN Shan， at all. An Explicit Method Based on The Implicit Runge-Kutta Algorithm for Solving Wave Equations［J］. Bulletin of the Seismological Society of America， 2009， 99（6）： 3340.

［12］DAS S， LIAO Wenyuan， GUPTA A. An Efficient Fourth-Order Low Dispersive Finite Difference Scheme for A 2-D Acoustic Wave Equation［J］. Journal of Computational and Applied Mathematics， 2014， 258： 151.

［13］LI Jichun， CHEN Yitung， LIU Guoqing. High-Order Compact ADI Methods for Parabolic Equations［J］. Computers & Mathematics with Applications， 2006， 52（8/9）： 1343.

［14］MONHANTY R K. An Unconditionally Stable Finite Difference Formula for A Linear Second Order One Space Dimensional Hyperbolic Equation with Variable Coefficients［J］. Applied Mathematics and Computation， 2004， 165（1）： 229.

［15］WU Fengyan， CHENG Xiujun， LI Dongfang， et al. A Two-Level Linearized Compact ADI Scheme for Two-Dimensional Nonlinear Reaction-Diffusion Equations［J］. Computers & Mathematics with Applications， 2018： 2835.

［16］LIAO Wenyuan. On The Dispersion， Stability and Accuracy of A Compact Higher-Order Finite Difference Scheme for 3D Acoustic Wave Equation［J］. Journal of Computational and Applied Mathematics， 2014， 270： 571.

［17］ZHANG Wensheng， LI Tong， CHUNG E T. A New High Accuracy Locally One-Dimensional Scheme for The Wave Equation［J］. Journal of Computational and Applied Mathematics， 2011， 236（6）： 1343.

［18］GE Yongbin， CAI Zhiquan. High-order Compact Difference Schemes and Adaptive Method for Singular Degenerate Diffusion-Reaction Equations［J］. Chinese Journal of Computational Physics， 2017， 34（3）： 309.

［19］SAADANTMANDI A， DEHGHAN M. NumericalSolution of The One-Dimensional Wave Equation with An Integral Condition［J］. Numerical Methods for Partial Differential Equations， 2010， 23（2）： 282.

［20］BIAZAR J， GHAZVINI H.Homotopy Perturbation Method for Solving Hyperbolic Partial Differential Equations［J］. Computers & Mathematics with Applications， 2008， 56（2）： 453.

［21］姜蕴芝. 求解波动方程的高精度紧致显式差分格式［D］.银川：宁夏大学， 2016.

（编辑：温泽宇）