特征融合的卷积神经网络材料性质预测模型

摘 要：针对目前大多数机器学习模型预测材料性质时需要大量的先验知识以及特征向量筛选困难的问题，基于电子轨道矩阵和元素周期表法两种描述符，通过特征融合的方式，设计了一种卷积神经网络模型OPCNN（Orbital of electron and Periodic table CNN）。实验数据表明，OPCNN与其他预测模型相比，在带隙、生成热以及形成能数据集上都有着更好的性能，平均绝对误差分别为0.26eV、0.037KJ/mol和0.073eV/atom，且R2都达到了91%以上。OPCNN在保证了预测准确性的同时对先验知识的要求更低，只需要元素周期表中的信息即可预测材料性质，特征融合的思想可以让特征设计更加灵活，有利于新材料体系快速和准确的预测。

关键词：神经网络；描述符；预测；元素周期表；电子轨道

DOI：10.15938/j.jhust.2024.03.014

中图分类号： TP399

文献标志码： A

文章编号： 1007-2683（2024）03-0116-09

Prediction Model of Material Properties Based on

Feature Fusion and Convolutional Neural Network

SHI Jingchen， LIU Feining， WANG Wenjie， ZHAO Rui

（College of Mathematics and Computer， Jilin Normal University， Siping 136000， China）

Abstract：Aiming at the problem that most machine learning models need a lot of prior knowledge and manual selection of feature vectors in the prediction of material properties， a convolutional neural network model OPCNN （Orbital of Electron and Periodic table CNN） is established by feature fusion based on two descriptors， electronic orbit matrix and periodic table method. The experimental data show that compared with other prediction models， OPCNN has better performance on the bandgap， heat of formation and formation energy datasets， with the mean absolute error of 0.26eV， 0.037KJ/mol and 0.073eV/atom， respectively， and the R2 is more than 91%. OPCNN has lower requirements for prior knowledge while ensuring the accuracy of prediction. It only needs the information in the periodic table to predict the material properties. The idea of feature fusion can make feature design more flexible， which is conducive to the rapid and accurate prediction of new material systems.

Keywords：neural networks; descriptor; prediction; periodic table of elements; electron orbital

0 引 言

随着人工智能的发展，机器学习（ML）成为实验、理论和建模的重要工具［1-4］，并在材料科学领域内得到了广泛的应用，如带隙预测［5-6］、形成能预测［7-8］、材料表面性质预测［9-10］、微观结构识别［11-12］等。其中，描述符的设计是ML模型设计和训练的关键问题，针对不同的需求，会有着不同的描述符设计。通常情况下，将材料的结构和属性映射到特定长度的向量上，在有了一组合适的描述符后，传统的ML算法即使在很小的数据集上也能表现的很好。然而，在材料研究的特定工作中，最佳描述符是不容易获取的，需要通过实验和试错来选择。构建合适的描述符需要深入了解内在机理以及大量的先验知识，具有很大的挑战性。Hwang等［13］提出了“阳离子指纹”（包括元素属性和电子能带结构信息的一维描述符）作为全连接神经网络的输入，预测了氧化玻璃材料具有特定粘度所需的温度。Saidi等［14］以分子的尺寸、卤化物带、第一电离能和电子亲和能、带隙、生成能和AX前驱体的体积，以及ABX3的晶格常数和八面体角作为卷积神经网络（CNN）模型的输入，来预测ABX3型的金属卤化物钙钛矿的带隙。Li等［15］以Magpie描述符作为输入，预测ABX3型钙钛矿的形成能。最近还有研究将材料处理为具有原子性质编码的晶体图［16-18］。尽管方法不同，但它们在预测晶体或分子的性质（如形成能和弹性模量）方面都表现出良好的性能。

然而，手工构建的描述符通常难以解释选择特征的原因，只是因为这些特征构建的数据集在参与ML模型训练后能够获得比较好的性能。元素周期表中包含了丰富的物理化学知识，原子半径、化合价、价电子密度等性质在元素周期表中呈周期性变化。为了简化特征工程的工作，并使它更容易让人理解，原子表法（atom table represent）［19］、元素周期表法（periodic table represent， PTR）［20-21］被提出。但原子表法仅用到了元素周期表中的原子序数信息，对周期表中元素性质成周期性变化的规律以及电子轨道信息等特征难以学习到。本文提出了一种材料性质预测模型，以应用原子表法的ATCNN［19］作为基线模型，基于元素周期表法以及简化的轨道场矩阵［22］（电子轨道矩阵）构建了卷积神经网络模型（OPCNN），用来预测材料的带隙、生成热、形成能等性质。在OPCNN中，不需要其他的先验知识，如原子和物理属性，可以直接通过CNN强大的特征提取能力来读取并融合元素周期表和轨道矩阵的信息，然后由模型来分析提取描述符。作为几乎不需要特征工程的模型，使用元素周期表法的神经网络模型（简称PTR）与ATCNN设计思想相似，都表现出不错的材料性质预测能力，并且元素周期表法也是OPCNN模型的一种特征输入方法，所以这二者被选为了基准模型进行对照研究。测试表明，OPCNN模型融合两种输入特征为神经网络提供了更多的有效信息，并且比基准模型有着更高的准确度。

1 描述符与卷积神经网络结构设计

1.1 数据来源

带隙、生成热和形成能都是材料的基础性质，其中带隙和形成能的预测结果在ATCNN模型上已存在具体数据，在此基础上又增加了生成热数据进行验证。

带隙的样本集来自于Zeng等［19］提供的实验数据，包含了3896个绝缘体化合物，但其使用的原子表法包含的特征信息较为单一，在准确度方面仍有提升空间；生成热的数据集源自于OQMD（open quantum materials database）［23］，其中包括一元、二元、三元化合物共9590种样本；形成能的数据来自于文［19］，源数据同样取自OQMD，包含5886种化合物样本。本文中所涉及的数据集都会随机从中取出80%作为训练数据，并将剩余的20%作为测试数据，其中训练集用来学习，给神经网络模型提供先验知识，而测试集不参与任何的训练。所有数据在经过归一化处理后，构建以元素周期表和电子轨道矩阵同时作为描述符的数据集。

1.2 基于特征融合的描述符设计

OPCNN模型的描述符采用了特征融合的方法，把电子轨道矩阵描述符和元素周期表描述符同时作为神经网络模型的输入。

由于轨道场矩阵［22］需要一定的元素性质，而这些性质从元素周期表中无法获取。所以构建了基于电子轨道的矩阵，利用化学元素的外层电子轨道排布表示原子，并以向量的形式进行编码，例如向量D={s1， s2， p1， p2，…， p6， d1， d2，…d10， f1， f2，…， f14}长度为32，对应表示原子的每一个轨道。向量中的值初始化为0，然后根据元素在化合物中所占比例和其对应电子排布为向量进行赋值。如图1（a）所示，以PbI2为例，Pb原子和I原子的外层电子层排布分别为6s26p2和5s25p5，Pb原子所对应向量的s2， p2的位置（下标从0开始），即向量的DPb（1）和DPb（3）被赋值为0.33，I原子所对应向量的s2，p5的位置，即向量的DI（1）和DI（6） 被赋值为0.67，在得到化合物中每种元素所对应的向量Dk后，电子轨道矩阵的计算如公式（1）所示：

Ok=∑nk-1i=1DTkDi×10（1）

其中：k为所研究的某一化合物；nk为化合物中的元素数；

DTk为该化合物的化学式首元素的向量转置；Di为化合物中除首元素外的其他元素向量。同样以PbI2为例，使用Pb的向量转置与I元素的向量进行矩阵相乘后再乘以10（10只是一个数值放大系数），得到图1（b）中的轨道矩阵（图中空白部分的值为0）。当化学式中含有3个或以上的元素数（n≥3）时，首元素向量的转置将分别乘以其余元素向量，然后相加。由于我们只专注于从元素周期表中获得的信息，所以并未考虑其他因素。

元素周期表具有丰富的物理化学知识，许多物理化学性质在周期表中呈现出周期性变化。根据元素周期表的排列形式，可以将它映射为9行18列的二维矩阵M，如图2所示。黄色部分为元素周期表中已存在元素的对应位置，白色部分表示此位置在元素周期表中为空白，绿色部分表示待研究的化合物中所有化学元素对应的位置及其赋值。元素周期表特征的建立首先会初始化矩阵M中所有单元为0，然后根据目标化合物中包含的元素来决定矩阵M中填充数据的坐标（与元素周期表的位置一致），该坐标位置依据元素在化合物中所占的比例来赋值。Feng等［21］将元素周期表法与随机打乱的周期表分别作为模型的输入进行了对比实验，证明了PTR设计的有效性。本文在此基础上，又对所有输入数据进行了归一化处理，经过对比发现二者并无明显差别。以PbI2为例，首先以0初始化矩阵M中所有储存单元，Pb和I的坐标位置分别为M（6，14）和M（5，17），按照化学式中Pb和I的元素占比，M（6，14）和M（5，17）中分别赋值0.33和0.67，如图2中的绿色方块。我们只需要有化学式以及所要预测的目标性质即可建立数据集。

1.3 卷积神经网络OPCNN结构设计

神经网络的结构决定了最终的预测结果和执行效率，本文设计的模型采用卷积神经网络，基本结构如图3所示。由于输入数据包含两个特征类别，所以网络前半部分的卷积由两个分支组成，分别对应元素周期表法和轨道矩阵。元素周期表法的输入是9×18×1的特征图，首先对其进行0填充操作，得到11×18×1的特征图，然后进行卷积核大小为3×3，步长为1×1的卷积（此次卷积并不进行填充操作），池化大小为2×2，步长为1×2，从而保证输出8×8大小的特征图。轨道矩阵输入特征图为32×32×1，所以在两次3×3的卷积和步长为2×2的池化后就可以得到大小8×8的特征图。当两个分支的特征图大小一致时，在第3个维度进行合并操作。之后再进行卷积和下采样后将提取到的特征图打平，经过两个全连接层得到预测结果的输出。

带隙和形成能的预测模型与上述的神经网络结构一致，但在生成热的预测任务中，我们有着充分的数据，所以在神经网络中添加了一种新的嵌入模块SE（squeeze and excitation）［24］（如图3中虚线红色部分）来提高网络的性能。SE模块是一种注意力机制，它会将特征图池化为与其通道数一致的一维向量，并在通过简单的全连接操作后为每一个特征图的通道增加权重，并且SE模块参与神经网络的梯度下降过程，会随着网络参数的更新而更新。在数据充分且网络中某一部分特征图的通道数较多时，可以加入SE模块来为通道附加权重并以此来提高网络性能。

2 OPCNN材料性质预测的结果分析

2.1 带隙预测

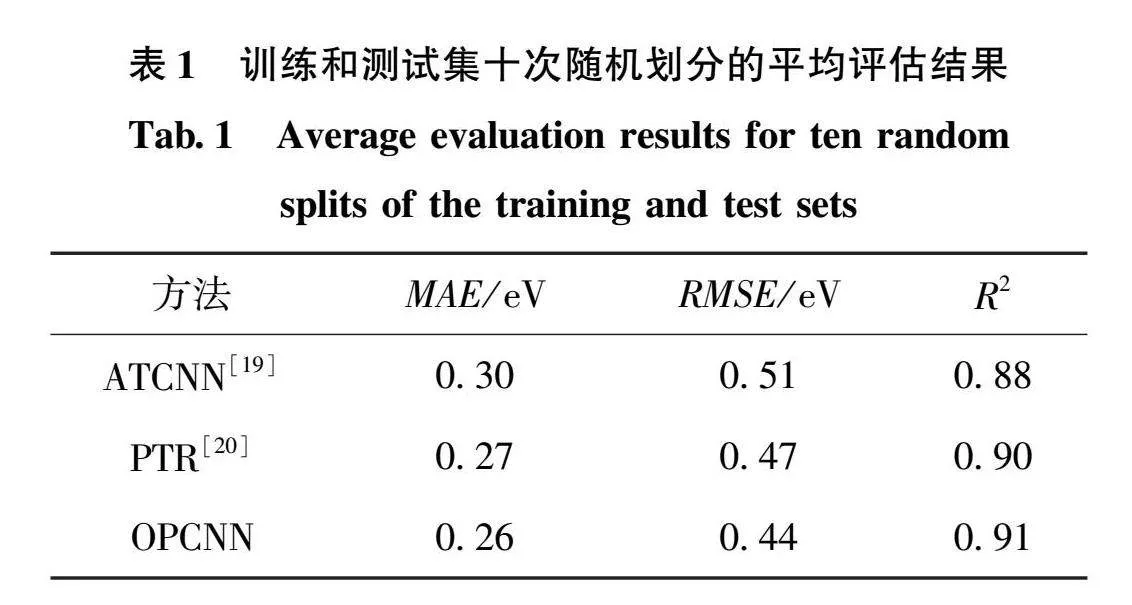
带隙预测在材料信息学中是机器学习较为常见的任务，但过去的方法往往涉及较为复杂的特征工程，还没有形成统一且性能较好的特征设计规范。本文设计的预测模型不涉及任何复杂的特征工程，只基于元素周期表中的信息即可构建数据集。我们选择了包含3896个绝缘体化合物带隙的数据集，但由于数据集的样本数较少，不同的训练集和测试集的划分会对结果产生一定影响。所以进行了10次随机划分，同时建立了10个相同的OPCNN模型分别训练，然后对测试集评估并取平均值。首先，如表1所示，采用原子表法的ATCNN由于只有化合物的元素序列信息，对绝缘体的带隙预测效果相对来说最差，MAE、RMSE、R2的值分别为0.30eV、0.51eV、0.88，而PTR方法中除了元素序列信息，还有元素的周期性规律以及完整的元素周期表结构，其表现比ATCNN更好，MAE减小到了0.27eV，RMSE为0.47eV，R2为0.90。OPCNN方法在PTR方法的基础上又添加了电子轨道信息，其性能得到了进一步的提升，其MAE、RMSE、R2分别为0.26eV、0.44eV、0.91。

绝缘体的带隙预测在测试集上的预测结果和真实值的误差如图4所示。横轴为实验得到的真实带隙值，纵轴为神经网络模型的预测值，数据点的分布越接近红线说明预测的结果越为精准。可以看到ATCNN与PTR相比，PTR中的散点值更加收敛于红线，这表明，PTR比ATCNN的预测值更加接近实验值。而OPCNN模型不仅收敛的更好，同时在较大带隙的预测上也更接近实验值，这是因为OPCNN模型的特征输入不仅包括了元素周期表中的原子排布信息，更提供了与带隙直接相关的价电子轨道信息。带隙预测的实验结果表明，ATCNN的方法仅以原子序数信息建立描述符，简化了神经网络的输入，虽然模型复杂度更小，但带来了更多的误差。使用电子轨道矩阵和元素周期表作为输入的方式只为神经网络模型增加了较小的计算量，却带来了更加准确的带隙值预测。

为了进一步证明特征融合的有效性，在绝缘体数据集中添加了2458种金属化合物，构建了一个同时拥有绝缘体和金属化合物的数据集，其中绝缘体是有带隙值的，而金属带隙值为0。我们的目标是让OPCNN对其进行二分类，即识别出绝缘体和金属。模型结构只需要将图3中OPCNN的最后一层输出改为两个神经元作为最后的输出，分别对应着绝缘体和金属。利用修改后的OPCNN模型对混合数据进行学习，并与ATCNN的预测结果做了对比，分类器将正样本识别为正样本的概率为p1，将负样本识别为正样本的概率为p2，AUC就表示了p1>p2的概率。图5（a）、图5（b）分别为ATCNN和OPCNN的ROC曲线图，OPCNN的ROC曲线下的面积（AUC）为0.98，而ATCNN的AUC为0.96，说明OPCNN的分类能力也优于ATCNN。图5（c）、图5（d）分别为分类结果的混淆矩阵，深色部分为正确分类的结果，浅色部分为错误分类的结果。可以看出，OPCNN无论是在识别半导体还是金属方面都比ATCNN更加准确，且OPCNN将准确率从ATCNN的90.58%提升到了94.39%。

2.2 生成热预测

作为材料性质预测模型，OPCNN也可以应用到其他实验数据，如生成热和形成能，由于生成热数据量比较大，所以我们在OPCNN中添加了基于注意力机制的SE模块。在两种输入特征经过卷积达到相同尺度后进行了在通道维度上的合并，由于融合后的特征在第三维度上有着较大的值，即有很多的通道数，这正适合使用SE模块为每一个通道进行权重赋值，使得对最终结果影响较大的通道有着更大的权重。测试集的测试结果如表2所示，OPCNN模型在测试集上的MAE和RMSE分别为0.037kJ/mol和0.057kJ/mol，且R2评分为0.994。从表2可以看出，在MAE和RMSE的评估标准上OPCNN优于使用原子表法的ATCNN （MAE和RSMSE分别为0.048kJ/mol和0.074kJ/mol）以及仅使用PTR作为输入的网络模型（MAE和RMSE分别为0.039kJ/mol和0.060kJ/mol）。这三种性能较优的模型在R2上差别不大，但MAE能够更加真实的反应真实值和预测值之间的误差。由于MAE在更新梯度时，无论误差大小，都是一样的，所以并不能仅仅依据MAE来评判模型的好坏。RMSE则可以反应真实值与预测值之间的差的平方根期望值。这两种评估标准从另一方面展现出了OPCNN的性能。

OPCNN显然优于其他两种方法，并且从MAE的减小比例上，OPCNN比ATCNN优化了23%。而且可以从测试集的预测结果图中看出三者的明显差异如图6所示。使用原子表法的ATCNN有着相对较差的拟合度，而使用PTR的CNN与ATCNN相比，在接近于零的数据上拟合度更好。OPCNN则在继承了元素周期表法的优点的同时，元素电子轨道信息的输入使得所有测试数据更加收敛。这表明元素周期表加上电子轨道矩阵的特征融合方法使得OPCNN得到了更多的特征信息，从而产生了更好的学习结果。

2.3 形成能预测

对于形成能的预测，OPCNN在测试集中的预测结果与实验值有着很好的一致性。MAE和R2分别为0.073eV/atom和0.99，而DFT计算相对于实验测量的MAE为0.81～0.136eV/atom［23］，这说明OPCNN已经超越了DFT计算的精度。形成能数据集的预测结果上，OPCNN模型与原子表法的ATCNN（MAE为0.078eV/atom）有着相似的效果，但其性能要远远优于使用相同数据集的其他形成能预测模型ElemNet［25］（MAE约为0.15eV/atom），

这是由于不同的网络结构而导致的结果。ElemNet是全连接网络，它将元素之间的关系看作是等价的，需要大量的数据来学习元素间的唯一关系。而ATCNN在加入了卷积层后，产生了更复杂的映射，在简化了神经网络结构的同时，得到了令人满意的性能上的提升。OPCNN在ATCNN的基础上改变了网络的输入，提供了更多的信息被网络模型学习。另外，虽然OPCNN的网络参数比ATCNN要略多一些，但并未产生过拟合现象，这表明尽管在此形成能的数据集上OPCNN只带来了微量的提升，在数据集较大的情况下，相信会有着更强的适应性和学习能力。

3 机理研究

为进一步研究OPCNN模型优于ATCNN模型的原因，从测试集中寻找了不同带隙值区间（0～5eV）的化合物进行对比，如表3所示。两种模型的预测值与真实值都比较接近，但在对具有较大带隙值化合物进行预测时，OPCNN仍保持了较好的准确度，这与图4散点图对比中得到的信息一致。接下来，基于这5种化合物，对于神经网络的可解释性进行了研究。

对比ATCNN和OPCNN模型的结构，发现两种模型都存在若干卷积层，并且经过最后一次卷积层后产生的特征图在大小和通道数上较为相似。另外，该特征图是卷积得到的结果，并在池化和打平后用于全连接层，其中包含的信息从很大程度上决定了模型预测的误差。所以，基于表3中的化合物，对该特征图进行了可视化研究。

如图7所示，图中方格代表了特征图的一个通道（共32个通道），方块颜色越深其在特征图中的值越大。总体上看，不同的化合物在ATCNN和OPCNN的特征图中都得到了体现，并且随着化合物带隙值的增大，ATCNN和OPCNN特征图的表达在可视化结果中都存在着更靠近底部的趋势。但是，相较于ATCNN，在OPCNN的可视化结果中，蓝色方块更多，且颜色更深，包含了更多信息，表达也更加充分。以Ba3In2P4O16 和Na3ClMoO4两种具有较大带隙的化合物为例，ATCNN虽然预测的结果相差较大，但对于二者的可视化结果较为相似，甚至深色方块的位置都近乎一致，而OPCNN对于二者的预测尽管只相差了0.28eV，但其从可视化结果中可以看出二者还是存在着很多的不同之处。这里可视化的特征图可以视为全连接层的描述符，当描述符包含的信息越多，对于后续的预测工作也会更加有利，这也是设计OPCNN结构，使其能同时接收两种输入特征的原因。

4 结 论

本文提出了一种适用于材料性质预测的基于神经网络模型的特征融合方法，并利用此方法构建了神经网络模型OPCNN，在带隙、生成热和形成能的预测上MAE分别为0.26eV、0.037kJ/mol和0.073eV/atom，R2分别为0.91、0.99和0.99。

OPCNN以元素周期表和电子轨道矩阵同时作为输入特征，在之后的特征融合过程中不仅统一了特征图的大小，还完成了相应的特征提取和数据分析任务。不同数据集的实验对比结果以及CNN卷积层的可视化研究表明，相较于单一使用原子表或元素周期表作为神经网络输入的方式，OPCNN在未提高特征工程复杂度（仅需要样本化学式和标签）的情况下得到了更加具体的元素电子轨道信息，其输入的特征信息更加丰富，通用性更强，可以进行多种属性和性质的预测，并不只局限于本文中测试的带隙能、生成热以及形成能。这意味着在做具体的材料研究时，面对广阔的材料空间，OPCNN可以作为一个高效的材料筛选工具，为进一步的材料计算提供有意义指导，从而缩短新材料的开发周期。

此外，本文提出的特征融合思想以及神经网络模型的搭建方式还可以应用在其他方面，在未来数据充足的工作中，可以利用此思想设计更多的融合方式，比如前文中提到的一维描述符阳离子指纹或Magpie描述符等，通过设计网络结构来和PTR进行融合；或者在微观图像识别的任务中，加入一些元素自身的特性共同作为输入可能会带来令人更加满意的结果。

参 考 文 献：

［1］ 孟良， 许同乐， 马金英， 等. 基于 LMD 形态滤波的 LS-SVM 方法研究［J］. 哈尔滨理工大学学报， 2022， 27（1）： 92.

MENG Liang， XU Tongle， MA Jinying， et al.There Search of LS-SVM Based on LMD Morphology Filter［J］.Journal of Harbin University of Science and Technology， 2022， 27（1）： 92.

［2］ 池明赫， 夏若淳， 罗青林， 等.油纸绝缘典型缺陷局放特性及缺陷类型识别［J］. 电机与控制学报， 2022， 26（2）：121.

CHI Minghe， XIA Ruochun， LUO Qinglin， et al. Partial Discharge Characteristics and Defect Type Identification of Typical Defects in Oil-pressboard insulation［J］. Electric Machines and Control， 2022， 26（2）：121.

［3］ 宋昊昕， 尤号田， 刘遥， 等.基于深度学习的无人机多光谱图像柑橘树冠分割［J］. 森林工程， 2023， 39（3）：140.

SONG Haoxin， YOU Haotian， LIU Yao， et al. Deep Learning-based Segmentation of Citrus Tree Canopy from UAV Multispectral Images［J］. Forest Engineering， 2023， 39（3）：140.

［4］ 赵京鹤， 修大元， 王金龙， 等. 绝缘纸板典型缺陷局放特征的CNN识别［J］.哈尔滨理工大学学报， 2022， 27（5）： 79.

ZHAO Jinghe，XIU Dayuan，WANG Jinlong， et al. PD Recognition for Typical Cardboard Insulation Defect with CNN［J］. Journal of Harbin University of Science and Technology， 2022， 27（5）： 79.

［5］ ZHANG Y， XU W， LIU G， et al. Bandgap Prediction of Two-Dimensional Materials using Machine Learning［J］. Plos One， 2021， 16（8）： e0255637.

［6］ GOK E C， YILDIRIM M O， HARIS M P U， et al. Predicting Perovskite Bandgap and Solar Cell Performance with Machine Learning［J］. Solar RRL， 2022， 6（2）： 2100927.

［7］ FAN Z， SUN Z， WANG A， et al. Machine Learning Regression Model for Predicting the Formation Energy of Nonlinear Optical Crystals［J］. Advanced Theory and Simulations， 2023， 6（3）： 2200883.

［8］ ZHANG J， LIU X， BI S， et al. Robust Data-Driven Approach for Predicting the Configurational Energy of High Entropy Alloys［J］. Materials & Design， 2020， 185： 108247.

［9］ 张家有， 宋万万， 白玉珍， 等.基于逐步回归分析法的表面粗糙度预测［J］. 金刚石与磨料磨程， 2021， 41（6）：63.

ZHANG Jiayou，SONG Wanwan， BAI Yvzhen， et al. Surface Roughness Prediction Based on Stepwise Regression Analysis［J］. Diamond & Abrasives Engineering， 2021， 41（6）：63.

［10］张昆， 田业冰， 丛建臣， 等.基于动态惯性权重粒子群算法的磨削低能耗加工方法［J］. 金刚石与磨料磨具工程， 2021， 41（1）：71.

ZHANG Kun， Tian Yebing， Cong Jianchen， et al. Reduce Grinding Energy Consumption by Modified Particle Swarm Optimization Base on Dynamic Inertia Weigh［J］. Diamond & Abrasives Engineering， 2021， 41（1）：71.

［11］GUDA A A， GUDA S A， MARTINI A， et al. Understanding X-ray Absorption Spectra by Means of Descriptors and Machine Learning Algorithms［J］. NPJ Computational Materials， 2021， 7（1）： 1.

［12］HORWATH J P， ZAKHAROV D N， MGRET R， et al. Understanding Important Features of Deep Learning Models for Segmentation of High-Resolution Transmission Electron Microscopy Images［J］. NPJ Computational Materials， 2020， 6（1）： 1.

［13］HWANG J， TANAKA Y， ISHINO S， et al. Prediction of Viscosity Behavior in Oxide Glass Materials using Cation Fingerprints with Artificial Neural Networks［J］. Science and Technology of Advanced Materials， 2020， 21（1）： 492.

［14］SAIDI W A， SHADID W， CASTELLI I E. Machine-Learning Structural and Electronic Properties of Metal Halide Perovskites using a Hierarchical Convolutional Neural Network［J］. NPJ Computational Materials， 2020， 6（1）： 1.

［15］LI X， DAN Y， DONG R， et al. Computational Screening of New Perovskite Materials using Transfer Learning and Deep Learning［J］. Applied Sciences， 2019， 9（24）： 5510.

［16］SUN Y， HU W. Novel Machine Learning Framework for Thermal Conductivity Prediction by Crystal Graph Convolution Embedded Ensemble［J］. SmartMat， 2022， 3（3）： 474.

［17］WANG B， FAN Q， YUE Y. Study of Crystal Properties Based on Attention Mechanism and Crystal Graph Convolutional Neural Network［J］. Journal of Physics： Condensed Matter， 2022， 34（19）： 195901.

［18］KARAMAD M， MAGAR R， SHI Y， et al. Orbital Graph Convolutional Neural Network for Material Property Prediction［J］. Physical Review Materials， 2020， 4（9）： 093801.

［19］ZENG S， ZHAO Y， LI G， et al. Atom Table Convolutional Neural Networks for an Accurate Prediction of Compounds Properties［J］. NPJ Computational Materials， 2019， 5（1）： 1.

［20］ZHENG X， ZHENG P， ZHANG R Z. Machine Learning Material Properties from the Periodic Table using Convolutional Neural Networks［J］. Chemical science， 2018， 9（44）： 8426.

［21］FENG S， FU H， ZHOU H， et al. A General and Transferable Deep Learning Framework for Predicting Phase Formation in Materials［J］. NPJ Computational Materials， 2021， 7（1）： 1.

［22］PHAM T L， KINO H， TERAKURA K， et al. Machine Learning Reveals Orbital Interaction in Materials［J］. Science and Technology of Advanced Materials， 2017， 18（1）： 756.

［23］KIRKLIN S， SAAL J E， MEREDIG B， et al. The Open Quantum Materials Database （OQMD）： Assessing the Accuracy of DFT Formation Energies［J］. NPJ Computational Materials， 2015， 1（1）： 1.

［24］HU J， SHEN L， SUN G. Squeeze-And-Excitation Networks［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018： 7132.

［25］JHA D， WARD L， PAUL A， et al. Elemnet： Deep Learning the Chemistry of Materials from only Elemental Composition［J］. Scientific Reports， 2018， 8（1）： 1.

（编辑：温泽宇）