一类永磁同步电机混沌运动的GWO-RBFNN双参协同智能优化控制

摘 要：针对永磁同步电机（permanent magnet synchronous motor，PMSM）混沌控制问题，提出了一种基于GWO-RBFNN的双参协同智能优化控制方法。从控制器能够自动搜索预期运动状态的角度出发，选择Poincaré截面上两点间距离作为控制器输入，并考虑到系统参数对系统动力学行为的耦合影响作用，基于径向基函数神经网络（radial basis function neural network，RBFNN）设计了双参协同控制器；采用灰狼优化算法（grey wolf optimization，GWO）优化选择控制器参数，以实现最佳的控制器性能；通过对PMSM系统中两个可控参数进行微幅扰动调整，将系统从混沌状态控制到预期的运动状态。研究结果表明，相较于基于GWO-RBFNN的单参数智能优化控制方法，基于GWO-RBFNN的双参协同智能优化控制方法具有更优的性能。虽然两种方法均能实现混沌运动控制，但相较而言，基于GWO-RBFNN的双参协同智能优化控制方法控制速度更快，超调量更小。

关键词：永磁同步电机；混沌运动；双参协同控制；灰狼算法；径向基函数神经网络

DOI：10.15938/j.jhust.2024.03.004

中图分类号： TP183

文献标志码： A

文章编号： 1007-2683（2024）03-0028-09

GWO-RBFNN Dual-parameter Collaborative Intelligent Optimal Control of

Chaotic Motion of a Class of Permanent Magnet Synchronous Motor

LI Ningzhou， QIU Sixuan， WEI Xiaojuan， LI Xiaoqi， LI Gaosong

（School of Rail Transportation， Shanghai Institute of Technology， Shanghai 201418， China）

Abstract：Aiming at the chaos control of permanent magnet synchronous motor， a dual-parameter collaborative intelligent optimal control method based on GWO-RBFNN was proposed. Starting from the perspective that the controller can automatically search for the expected motion state， the distance between two points on the Poincaré cross section is selected as the controller input. And considering the coupling effect of system parameters on the dynamic behavior of the system， a dual-parameter cooperative controller is designed based on radial basis function neural network （RBFNN）; Grey Wolf Optimization （GWO） algorithm is used to optimize and select controller parameters to achieve the best controller performance; The system is controlled from a chaotic state to the expected motion state by adjusting the two controllable parameters in the PMSM system with minor disturbances. The results show that compared with the single-parameter intelligent optimization control method based on GWO-RBFNN， the dual-parameter collaborative intelligent optimal control method based on GWO-RBFNN has better performance. Although both methods can achieve chaotic motion control， the control speed of the dual-parameter collaborative intelligent optimization control method based on GWO-RBFNN is faster and overshoot is smaller.

Keywords：permanent magnet synchronous motor; chaotic motion; dual-parameter cooperative control; grey wolf optimization;radial basis function neural network

0 引 言

永磁同步电机损耗小，功率因数高，效能高，在工业领域中得到广泛运用［1-3］。但其是一个典型的非线性、多变量耦合系统，在特定参数下会引起电机表现出混沌行为［4-6］，降低PMSM系统的运行质量。为消除电机中的混沌现象，许多研究人员相继提出了相应的控制方法［7-12］。

既有的PMSM系统混沌控制方法有PID控制［13］、模糊控制［14］等。李洋洋等［15］设计了一种基于LMI算法的动态滑模补偿混沌控制器，在滑模函数当中增加补偿算法设置，利用LMI算法计算滑模控制律中待求矩阵的最优解，以实现混沌控制。Abolfazl等［16］提出了一种基于鲁棒自适应的滑模控制方法，在控制方案的设计中考虑到了PMSM系统模型中参数不确定性，采用自适应方法估计不确定项、扰动项和非线性项的上界，有效实现了PMSM系统的混沌控制。虽然PMSM系统混沌控制研究，取得了一定的研究成果，但滑模控制抖振问题的存在影响了控制效果。谢东燊等［17］提出了一种解耦自适应滑模混沌控制方法，增设了自适应系统，相比于普通滑模控制器，在不依赖系统参数的情况下，可以更好的实现PMSM系统的混沌控制，且抑制了抖振现象。此外，控制器参数组合的优劣程度，也会影响混沌控制效果。近年来，研究者们针对PMSM混沌控制器的参数优化问题进行了相应探索和研究。黄俊豪等［18］通过建立PMLSM混沌模型，利用BPNN拟合滑模控制器参数，并经由PSO算法优化，确定最优控制参数，进而实现PMSM系统混沌控制。Zhang等［19］提出一种基于状态反馈的模糊自适应非线性混沌控制方法，利用模糊逻辑来近似逼近PMSM系统的非线性项和干扰，同时，利用布谷鸟算法优化控制律，仿真结果表明，所提方法对PMSM系统混沌的快速抑制具有有效性。

虽然研究者们关于PMSM系统混沌控制问题取得了相应研究成果，但是，目前将智能优化算法与RBFNN相结合进行PMSM系统混沌控制的相应研究仍然鲜见，还需要进一步探索和深入；同时，对于PMSM系统双参协同智能优化混沌控制方法暂时还没有公开文献报道。

既有的PMSM系统混沌控制方法，主要是针对系统的一个可控参数进行相应的控制，实现系统混沌的抑制。但是PMSM系统混沌现象的产生本身是一个多参数耦合作用的结果。据此，为了更好的实现PMSM系统的混沌运动控制，本文提出了一种基于GWO-RBFNN的永磁同步电机混沌运动双参协同智能优化控制方法：基于RBFNN设计控制器，采用GWO算法优化控制器的参数（控制器的三类参数（Ci、σi、wi）对应于灰狼的位置矢量），选择Poincaré截面上两点间距离构建优化控制器参数所需的目标函数。在用GWO算法对控制器的参数进行全局优化的同时，利用RBFNN对PMSM系统的可控参数进行微幅调整，从而实现混沌控制。

1 系统动力学特性分析

1.1 PMSM系统模型

永磁同步电机在d-q坐标系下的状态方程（以定子d、q轴电流id、iq及转子角速度ω为状态变量）如式（1）所示［20］：

diddt=（ud－R1id+ωLqiq）/Ld

diqdt=（uq－R1iq+ωLdid－ωψf）/Lq

dωdt=［npψfiq+np（Ld－Lq）idiq－TL－βω］/J（1）

式中：id和iq为定子d、q轴电流；ud和uq为定子d、q轴电压；Ld和Lq为定子d、q轴电感；ω为转子角速度；Ψf是转子磁极磁链；TL是负载转矩；J、β分别为转动惯量和黏滞阻尼系数；R1为定子绕组电阻；np为极对数。

令t=τt～，I=λI～，对式（1）进行时间尺度变换和线性仿射变换，其中I=［id iq ω］T，I～=［i～d i～q ω～］T，b=Lq/Ld，k=β/npτψf，τ=Lq/R1，λ=λd000λq000λω=bk000k0001/τ，得到无量纲化的状态方程为

di～ddt=u～d－bi～d+ω～i～q

di～qdt=－i～q+u～q－ω～i～d+γω～

dω～dt=σ（i～q－ω～）－T～L（2）

式中：γ=ψf/kLq，σ=βτ/J，u～d=ud/kR1，u～q=uq/kR1，T～=τ2TL/J。

本文主要针对均匀气隙的永磁同步电动机的混沌特性进行研究，即考虑Ld=Lq=L的情况。当u～d=u～q=T～L=0时，令［x1 x2 x3］=［i～d i～q ω～］，式（2）可等效为

1=－x1+x3x2

2=－x2－x1x3+γx3

3=σ（x2－x3）（3）

1.2 PMSM系统动力学分析

PMSM系统在断电瞬间因参数变化而产生的混沌运动主要表现为转速的剧烈振荡，这有可能造成电机转子的损伤从而影响系统性能。因此有必要研究并提出适用的控制策略以抑制PMSM系统的混沌运动。而对该系统动力学特性的分析则是实现有效混沌控制的基础。

本文主要研究PMSM系统在气隙均匀的环境下，突然断电瞬间的动力学特性。

1.2.1 分岔图

分岔图是分析PMSM系统动力学情况的一种有效手段，它能够描述PMSM系统随分岔参数改变的工作状态。

PMSM系统的参数γ和σ的变化都会引起系统工作状态的改变。图1所示为随γ/σ变化，PMSM系统的分岔图。其中，图1（a）反映了γ变化时系统的分岔情况，图1（b）反映了σ变化时系统的分岔情况。以图1（a）所示γ变化时PMSM系统的工作状态为例：当系统参数取σ=5.46，γ从0变化到160时系统会出现分岔现象；γ<1时，PMSM系统具有一个稳定的零平衡点；γ>1时，零平衡点不再稳定。γ∈［1，21）时，分离出两个稳定的平衡点，系统的稳定状态取决于初始状态值的选择。当选择不同的初始状态值时，系统会稳定到不同的状态。随着γ的增大，两个非零平衡点会逐渐失去稳定性。当γ∈［21，71.6）的范围内时，γ不断变化的过程中，引发系统的Hopf分岔现象，随着γ参数的继续变化，系统将进入一种复杂的、似乎毫无规律的状态，即混沌状态。当γ∈［71.6，83）范围内时，系统进入周期轨状态；之后，系统再次进入混沌状态。γ≥96后系统再次回到周期轨。

1.2.2 LYAPUNOV指数

Lyapunov指数谱是来判定非线性动力学系统是否稳定的重要指数。它是一种用于度量非线性动力学系统中相邻两条相轨线平均收敛程度的指标。在吸引域内，任意选择一个点作为一条轨迹的起始点，通过模拟或者解析计算，得到从该起始点开始的轨迹。同时，在该起始点周围选择另一个点作为另一条轨迹的起始点，得到另一条轨迹的演化轨迹。如果轨道在初期轨迹非常相似，每次迭代所产生的距离变化将呈指数型增长，如果初始时刻的距离为d0，经过一次迭代后将变为

d0=d1exp（λ1）（4）

通过数值模拟得图2所示PMSM系统的Lyapunov指数谱图。其中，图2（a）反映了γ变化时系统指数的变化情况，图2（b）反映了σ变化时系统指数的变化情况。图2中，黑色曲线是最大Lyapunov指数的变化曲线。

若PMSM系统的最大Lyapunov指数小于零，那么它将处于稳定的周期运动状态。相反，如果PMSM系统的最大Lyapunov指数大于零，那么它将会转入混沌运动状态。通过数值模拟可得图2，可以得到PMSM系统Lyapunov指数的整体变化趋势。

不同的Lyapunov指数对应于不同的PMSM系统状态，以γ变化时的状态为例：从图2（a）可以看出，γ∈［0，21）时最大Lyapunov指数为负，PMSM系统处于稳定状态；γ∈［21，71.6）时最大Lyapunov指数为正，PMSM系统处于混沌状态；γ∈［71.6，83）时最大Lyapunov指数为零，PMSM系统出现周期轨；而后PMSM系统重新进入混沌状态；当γ≥96后PMSM系统进入周期轨状态。表明了PMSM系统丰富的非线性特性。

1.2.3 POINCARé截面

利用Poincaré截面法可以研究相空间内系统的运动轨迹：在相空间内引入一个截面，这个截面和动力系统的轨道相交，这个截面就是Poincaré截面；交点的变化规律可以反映出系统的动力学演化规律。本文基于时间Poincaré映射建立PMSM系统的Poincaré截面（即通过每隔一个周期时间T来选取Poincaré截面）。

分别取σ=5.46、γ=25，σ=5.46、γ=0.48，绘制PMSM系统的Poincaré截面图，如图3所示。从图3可以看出，当Poincaré截面上有许多密集的点，这些点的分布呈现出无序、成片的特征，此时PMSM系统处于混沌状态；亦或Poincaré截面上呈现单环的状态，这种现象表明PMSM系统处于单周期状态。Poincaré截面图也证实了PMSM系统具有混沌特性。

2 GWO算法

GWO算法是一种基于灰狼群体行为的优化算法，并被应用于解决各种复杂的最优控制问题。在GWO算法中，灰狼群体中的每个个体代表问题的一个解，其实时位置可以被用来评估解的优劣性，并通过模拟灰狼的捕猎行为来更新位置。通过不断地迭代和更新位置，GWO算法可以逐渐找到最优解。GWO算法中包含多个层次的灰狼个体，其中最底层的搜索狼被称为z狼，数量为30只。在搜索过程中，每只搜索狼的位置都会被动态地更新，以更好地逼近最优解。同时，GWO算法还包含三只头狼，分别被称为αw、βw和δw狼，数量各为1只。这些头狼的位置也会被更新，但更新频率较低。当一只搜索狼的解优于某只头狼的解时，它才有可能替代该头狼的位置，成为新的头狼。通过不断地更新头狼和搜索狼的位置。在GWO算法中，每次迭代后总是αw狼对应的最优解，而βw与δw狼代表的则是次优和再次优的解。因此，算法的性能取决于z狼（搜索狼）的更新方式。搜索狼z的位置更新公式如式（5）：

dalfa=|C1Xalfa－Xw|

dbeta=|C2Xbeta－Xw|

ddelta=|C3Xdelta－Xw|

X1=Xalfa－A1dalfa

X2=Xbeta－A2dbeta

X3=Xdelta－A3ddelta

Xw（t+1）=X1+X2+X33（5）

αw、βw和δw狼的位置矢量分别用Xalfa，Xbeta和Xdelta来表示，在每次搜索过程中z狼的位置矢量为Xw，在下一次GWO算法搜索中，z狼的位置矢量被更新为Xw（t+1）。其中，A和C的计算公式如式（6）：

A=2ar1－a

C=2r2（6）

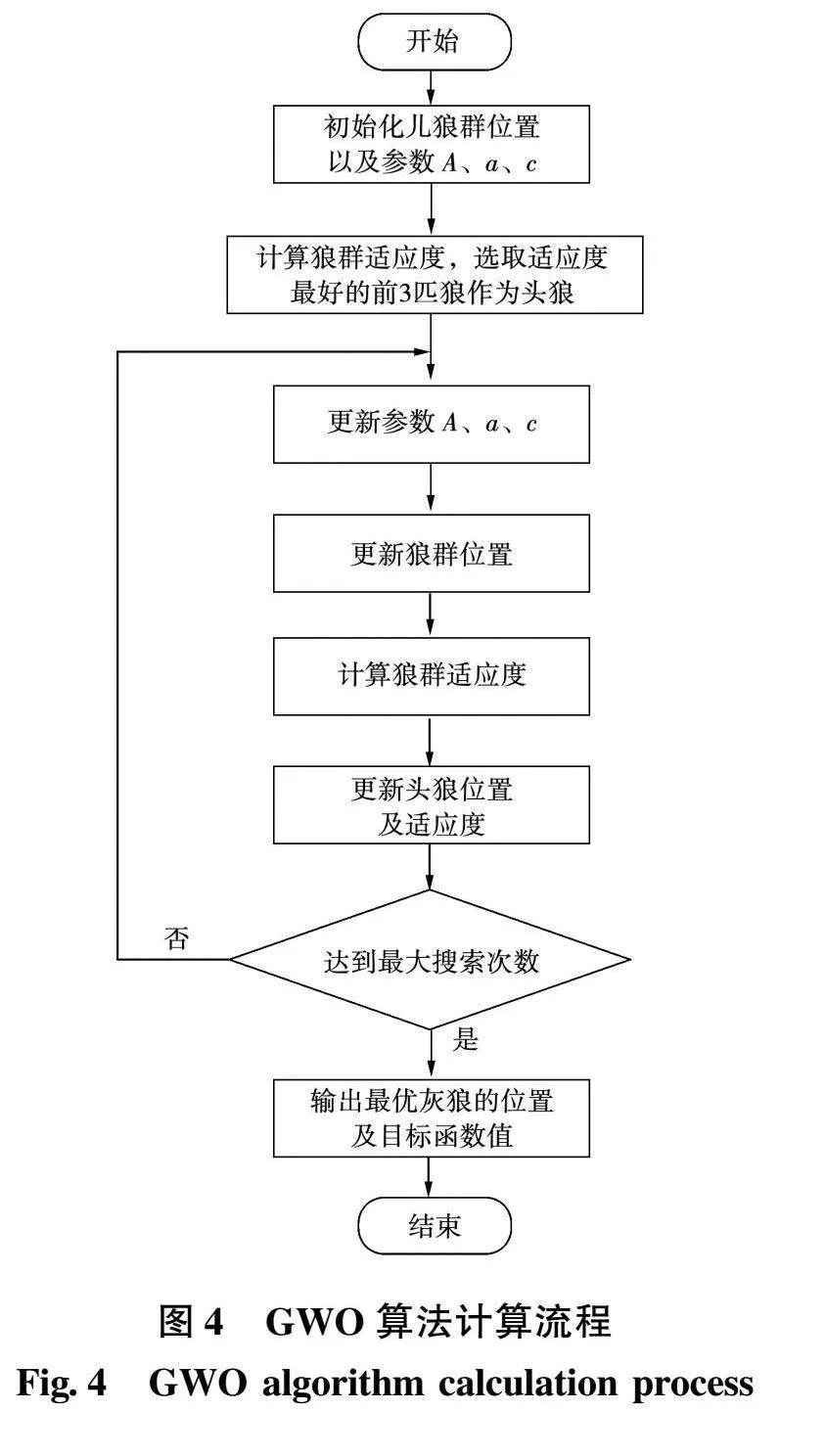
r1、r2的每个元素均是范围为［0，1］的随机值，参数a是一个逐渐减小的向量，其值从2到0随着搜索次数的增加而减小。GWO算法计算流程如图4所示。

为测试GWO算法的搜索性能，特进行测试实验，图5为GWO算法自适应调整示意图，在测试实验中选取狼群目标位置为（0，0），狼群适应度函数为：Fitness=||X||，其中X=［xw，yw］，（xw，yw）表示每次搜索后灰狼的更新位置。图5（a）灰狼位置的快速收敛及图5（b）平均适应度函数值的快速下降，体现了GWO算法搜索最优解的能力。

3 基于GWO-RBFNN的控制策略

3.1 基于RBFNN的双参协同混沌控制器设计

从第一章的仿真分析结果可以看出，PMSM系统在一定的参数条件下会出现混沌行为，而这种混沌振荡行为的出现会破坏PMSM系统的性能，必须加以控制。本文基于RBFNN设计双参协同混沌控制器以消除PMSM系统中有害的混沌现象。使用控制器输出微小的扰动量，施加于PMSM系统的可控参数——γ、σ，通过动态微调，将混沌运动稳定到期望的平衡点。针对式（3）模型，根据非线性系统反馈控制原理可设计控制器为u=［Δγ Δσ］T，则施加了控制的PMSM系统如式（7）所示：

1=－x1+x3x2

2=－x2－x1x3+（γ+Δγ）x3

3=（σ+Δσ）（x2－x3）（7）

图6为基于RBFNN设计的双参协同混沌控制器结构。图6中，RBFNN为三层结构，其中隐层有5个节点，输出层有两个节点；输入层有两个输入：d（k）和d（k-1），它们表示PMSM系统的相轨迹在Poincaré截面上相邻两个投影点之间的距离，即

d（k）=‖X（k）－X（k－1）‖

d（k－1）=‖X（k－1）－X（k－2）‖（8）

X（k）是经过第k次迭代后被控系统测得的状态变量X=［id iq ω］的值。

RBFNN隐层节点数的选取也会影响控制器对混沌运动的控制效果。隐层节点数太少，会导致控制器的非线性映射能力较弱，不能有效学习被控系统的非线性特性；而增加隐层节点虽然能增强控制器的非线性映射能力，但却会增加控制器结构的复杂性，也使得待优化的控制器参数增多，从而加大GWO的搜索难度。因此，在满足控制系统要求的前提下，应尽可能选取紧凑的控制器结构。本文在前期调研和团队研究成果的基础上，经过反复对比试验，确定隐藏层节点数为5。

RBFNN输入层到隐层的激活函数考虑选取高斯径向基函数，即

i（D－Ci）=exp（－‖D－Ci‖22σ2i）（9）

控制器输出量为系统可控参数γ和σ的微幅调整量，即u（k） =［u1（k） u2（k）］T=［Δγ（k） Δσ（k）］T，如式（10）所示：

u1（k）=∑5i=1wii（D，Ci）=

∑5i=1wiexp（－‖D－Ci‖22σ2i）=Δγ

u2（k）=∑5i=1wii（D，Ci）=

∑5i=1wiexp（－‖D－Ci‖22σ2i）=Δσ（10）

为保证控制结果的有效性，考虑设定控制器输出的最大调整量为umax，则有－umax<u<umax。

3.2 基于灰狼优化算法（GWO）的控制器参数优化

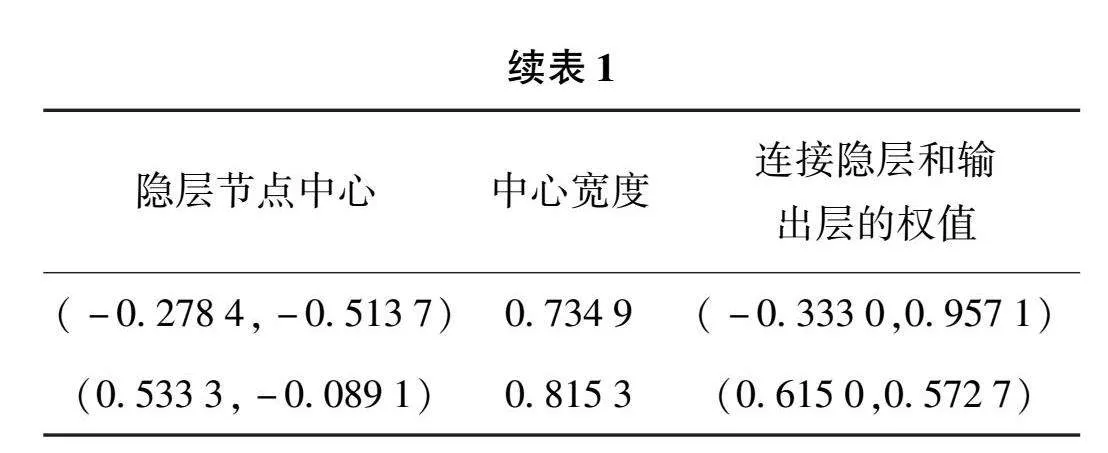
参数的优劣对于控制器的性能至关重要。为了优化控制器的参数（即隐层节点中心Ci、中心宽度σi、连接隐层和输出层的权值wi），采用GWO在控制器的参数空间进行搜索，GWO中灰狼的位置向量对应于控制器的参数向量（该向量的元素为：隐层节点中心Ci、中心宽度σi、连接隐层和输出层的权值wi）。

在本文中，使用相邻两次迭代后相轨迹在Poincaré截面上的投影点间的距离作为搜索预期平衡点的依据。同时考虑在对PMSM系统混沌运动进行控制时所需的最小能量消耗，构建GWO搜索最优控制器参数的目标函数为

Object=log（1γ）（0－‖Xk－Xk－1‖）（11）

使式（11）能够取得最小值是GWO搜索寻优的目标。在这个目标的引导下，GWO中αw狼的位置向量就是相对最优的控制器参数。

4 仿真分析

4.1 系统仿真验证

由第一章可知当γ=25、σ=5.46时系统发生混沌。根据PMSM系统的数学模型的奇点稳定性分析以及中心流定理，对其各个奇点的数学分析可得，奇点P1（0，0，0）是唯一稳定不动点。为了验证基于GWO-RBFNN的双参协同智能优化控制策略的有效性，在MATLAB中进行仿真。

PMSM系统的初始参数选取如下：γ=25、σ=5.46，初值选取x1（0）=14.83、x2（0）=-1.35、x3（0）=0.38。图7所示为未施加控制时系统的状态变化曲线（此时系统产生混沌运动）。

控制策略的仿真验证研究中，将期望控制目标设为平衡点（0，0，0）。GWO算法的搜索次数设置为30。为了更清晰地表现对混沌运动的控制效果，在PMSM系统迭代5000次以后，开始施加控制，并且对基于GWO-RBFNN的双参协同智能优化控制方法与基于GWO-RBFNN的单参智能优化控制方法进行了对比。仿真结果如图8所示。

经GWO算法优化的控制器参数如表1和表2所示。

由图7可见，未施加控制时，PMSM系统处于混沌运动状态，系统响应偏离了平衡点（0，0，0）。

图8施加控制之后，PMSM系统很快脱离了混沌运动状态，系统响应稳定在平衡点（0，0，0）。而且图8也反映出基于GWO-RBFNN的双参协同智能优化控制方法、基于GWO-RBFNN的单参智能优化控制方法都能够使系统自动搜寻并稳定到平衡点。但是通过对比也发现，基于GWO-RBFNN的双参协同智能优化控制方法的控制效果要优于基于GWO-RBFNN的单参智能优化控制方法的控制效果。

根据上述仿真结果可以得知，本文所提出的方法可以有效地控制PMSM系统的混沌行为。

4.2 控制结果分析

仿真结果表明，本文所设计的基于GWO-RBFNN的双参协同智能优化控制方法对于PMSM系统的混沌状态有着良好的控制效果，与基于GWO-RBFNN的单参智能优化控制方法相比，其具有以下两个主要的优点：

1）系统到达期望平衡点的速度更快。对比图8中两种控制方法的控制效果可以发现，基于GWO-RBFNN的双参协同智能优化控制方法的控制速度相较更快，图8（b）、图8（c）中更清楚地反映出了这一点。

2）系统到达期望平衡点前的超调量更小。由图8可见，采用基于GWO-RBFNN的单参智能优化控制方法后，系统到达期望平衡点前有明显的超调量，而采用基于GWO-RBFNN的双参协同智能优化控制方法后，改善了这一点，系统到达期望平衡点前的超调量明显更小。

综上所述，在式（11）所示目标函数的有效引导下，GWO算法成功地搜索到了控制器的相对最优参数，在控制器的作用下，PMSM系统能够快速自动搜索并稳定在平衡点处。

经优化后的双参协同混沌控制器具有良好的学习能力，能够通过学习蕴含在输入/输出数据中的PMSM系统的非线性动态特性，对系统的可控参数实施适宜的调整，最终将PMSM系统的混沌状态控制为稳定的状态。

5 结 论

本文提出了一种基于GWO-RBFNN的永磁同步电机混沌运动双参协同智能优化控制方法。通过仿真结果可知，本文所建立的目标函数可以很好地引导灰狼优化算法搜索到相对最优的控制器参数，提高了控制器的性能，确保控制器可以有效地学习PMSM系统的非线性动态特性。仿真实验结果表明了该控制方法能够有效地控制PMSM系统的混沌状态，并且响应速度快，超调量小，该方法的可行性和有效性得到了验证。

参 考 文 献：

［1］ 吕德刚，姜国威，纪堂龙.永磁同步电机低速域改进高频脉振注入控制［J］.哈尔滨理工大学学报，2022，27（6）：32.

LV Degang，JIANG Guowei，JI Tanglong. Improved High Frequency Pulse Injection Control in Low Speed Domain of Permanent Magnet Synchronous Motor［J］. Journal of Harbin University of Science and Technology， 2022，27（6）：32.

［2］ 朱博，张钰朋，徐攀腾等.实现位置同步的双电机交叉耦合控制策略［J］.哈尔滨理工大学学报，2022，27（5）：114.

ZHU Bo，ZHANG Yupeng，XU Panteng，et al. Dual-motor Cross-coupling Control Strategy for Position Synchronization［J］.Journal of Harbin University of Science and Technology，2022，27（5）：114.

［3］ ZHANG Rongyun，GONG Changfu，SHI Peicheng，et al. Research on Chaos Control of Permanent Magnet Synchronous Motor Based on the Synthetical Sliding Mode Control of Inverse System Decoupling［J］. Journal of Vibration and Control，2020，27（9-10）.

［4］ YANG Li，HUANG Tianmin，DENG Lin，et al. Analysis on Chaotic Mechanism of Direct-Drive Permanent Magnet Synchronous Generators Based on Lyapunov Stability Theory［J］. European Journal of Electrical Engineering，2019，21（6）.

［5］ Vibration and Acoustics. Studies from Anhui Polytechnic University Add New Findings in the Area of Vibration and Acoustics （Research on Chaos Control of Permanent Magnet Synchronous Motor Based on the Synthetical Sliding Mode Control of Inverse System Decoupling）［J］. Journal of Technology & Science，2020.

［6］ ARIF Iqbal，GIRISH Kumar Singh. Chaos Control of Permanent Magnet Synchronous Motor Using Simple Controllers［J］. Transactions of the Institute of Measurement and Control，2019，41（8）.

［7］ Soft Computing.Study Results from Fayoum University Broaden Understanding of Soft Computing （Chaotic Whale Optimizer Variants for Parameters Estimation of the Chaotic Behavior in Permanent Magnet Synchronous Motor）［J］.Computer Weekly News，2019.

［8］ YOUSRI D A， ALLAM Dalia， ETEIBA M B. Chaotic Whale Optimizer Variants for Parameters Estimation of the Chaotic Behavior in Permanent Magnet Synchronous Motor［J］. Applied Soft Computing Journal，2018，74.

［9］ Mathematics-Chaos Research. Reports on Chaos Research from Tianjin Polytechnic University Provide New Insights （Force Analysis and Energy Operation of Chaotic System of Permanent Magnet Synchronous Motor）［J］. Journal of Robotics & Machine Learning，2018.

［10］LI Jun，WANG Libiao，SHI Jing， et al. Chaotic Characteristic Analysis of Brushless DC Motor with Vibration Load Disturbance［J］. Journal of Engineering Science and Technology Review，2018，11（6）.

［11］QI Guoyuan， HU Jianbing. Force Analysis and Energy Operation of Chaotic System of Permanent-Magnet Synchronous Motor［J］. International Journal of Bifurcation and Chaos，2017，27（14）.

［12］ZHENG Kunming， CHEN Haiwei， ZHANG Qiuju， et al. Study the Micro Chaotic Phenomena and Itscontrol of Rigid-flexible Robot［J］. Journal of Mechanical Science and Technology，2022，36（5）.

［13］RAJAGOPAL Karthikeyan，JAHANSHAHI Hadi，JAFARI Sajad，et al.

Coexisting Attractors in a Fractional Order Hydro Turbine Governing System and Fuzzy PID Based Chaos Control［J］. Asian Journal of Control，2020，23（2）.

［14］JIE Z，JIANHUA S，HAI G，et al. Control of PMSM Chaos Using Backstepping-based Adaptive Fuzzy Method in the Presence of Uncertainty and Disturbance［J］. Systems Science & Control Engineering，2021，9（1）.

［15］李洋洋，张懿，戴磊，等.基于LMI算法的永磁同步电机混沌控制［J］.微特电机，2021，49（1）：40.

LI Yangyang，ZHANG Yi，DAI Lei，et al. Chaotic Control of Permanent Magnet Synchronous Motor Based on LMI Algorithm［J］. Micro Motor， 2021，49（1）：40.

［16］ABOLFAZL Karimi， HAMIDREZA Akbari， Somaye Mousavi & Zohre Beheshtipour. Design of an Adaptive Terminal Sliding Mode to Control the PMSM Chaos Phenomenon［J］.Systems Science & Control Engineering，2023，11：1.

［17］谢东燊，杨俊华，熊锋俊，等.永磁直线同步电机解耦自适应滑模混沌控制［J］.计算机仿真，2019，36（5）：263.

XIE Dongshen，YANG Junhua，XIONG Fengjun，et al. Permanent Magnet Linear Synchronous Motor Decouples Adaptive Sliding Mode Chaos Control［J］. Computer Simulation，2019，36（5）：263.

［18］黄俊豪，杨俊华，陈海峰，等.基于PSO优化的永磁直线同步电机混沌滑模控制［J］.计算机仿真，2021，38（11）：215.

HUANG Junhao，YANG Junhua，CHEN Haifeng，et al. Chaotic Sliding Mode Control of Permanent Magnet Linear Synchronous Motor Based on PSO Optimization［J］. Computer Simulation，2021，38（11）：215.

［19］ZHANG Jie， SUN Jianhua， GU Hai. Hesam Poloei & Abolfazl Karami. Control of PMSM Chaos Using Backstepping-based Adaptive Fuzzy Method in the Presence of Uncertainty and Disturbance［J］.Systems Science & Control Engineering，2021，9：1，673.

［20］张波，李忠，毛宗源，等. 一类永磁同步电动机混沌模型与霍夫分叉［J］.中国电机工程学报，2001，21（9）：13.

ZHANG Bo，LI Zhong，MAO Zongyuan，et al. A Class of Permanent Magnet Synchronous Motor Chaosmodel and Hough Bifurcation［J］. Proceedings of the CSEE， 2001，21（9）：13.

（编辑：温泽宇）