竖直面内的圆周运动极值问题分析

竖直面内的圆周运动是高中物理中的一个重要知识点，也是高考物理的常考题型．这类问题通常涉及速度、加速度、向心力、弹力、重力等多个物理量的关系，还涉及临界状态的分析．因此，深入理解并掌握竖直面内圆周运动的极值问题，对于提高物理学科核心素养和考试成绩具有重要意义．

１ 常见类型及深度解析

１.１ 绳模型

绳模型是竖直面内圆周运动中最常见的模型之一．在最高点，由于绳子只能提供拉力，不能提供支持力，因此存在速度的最小值．当速度小于这个最小值时，物体将在达到最高点前做斜抛运动．在最低点，绳子承受的拉力随速度的增大而增大．

在最高点，物体受到重力和绳子拉力的共同作用，这两个力的合力提供向心力．当绳子拉力为零时，重力完全提供向心力，此时速度达到最小值．在最低点，由于速度较大，绳子需要提供的拉力也较大，但绳子本身具有一定的弹性限度，因此在实际情况下，速度过大可能导致绳子断裂．

１.２ 杆模型

杆模型与绳模型类似，但在最高点时，杆既可以提供拉力也可以提供支持力．因此，在最高点速度最小值可以为０．在最低点，杆承受的力随速度的增大而增大，但同样没有理论上的最大值．

杆模型在最高点的受力情况比绳模型复杂．当速度较小时，杆提供支持力;当速度较大时，杆提供拉力．这两种情况下，重力和杆的作用力共同提供向心力．因此，在最高点存在两个临界速度，分别对应最小速度和最大速度．在最低点，由于速度较大，杆需要提供的力也较大，同样受到材料强度等实际因素的限制．

１.３ 轨道模型

轨道模型通常指的是固定在地面上的圆形轨道．在轨道内侧最高点，物体受到重力和轨道的支持力作用．为了保证物体不脱离轨道，轨道的支持力必须大于等于零，因此存在速度的最小值．在最低点，轨道承受的压力随速度的增大而增大，没有理论上的最大值．

轨道模型在最高点的受力情况与绳模型类似，但轨道的支持力始终指向圆心．因此，在最高点只存在一个临界速度，即最小速度．当速度小于这个值时，物体将脱离轨道做斜抛运动．在最低点，由于速度较大，轨道需要承受较大的压力．在实际应用中，轨道的设计需要考虑材料的抗压强度和稳定性等因素．

通过以上总结我们知道，在高中阶段，研究竖直面内的圆周运动极值问题通常只研究两个特殊位置———最低点和最高点．但请注意：以上总结都是理想状态，在具体问题中，到达圆周的最低点和最高点时研究对象的速度并非一定是最大值和最小值．因此，对于这种相对复杂的运动，我们需要对受力有深刻的认知和准确的分析．

２ 实例赏析

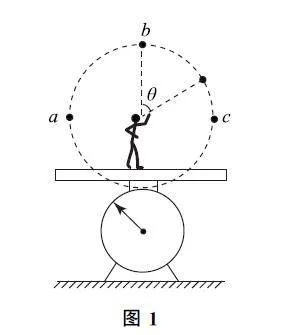
例１ 如图１所示，质量为M 的人站在一台秤上，可认为台秤的示数即人对秤盘的压力;人手中紧握一根长为R 的细线，一个质量为m 的小球系在细线的另一端，小球可绕人手在竖直平面内做顺时针圆周运动．若小球恰好能通过圆轨道最高点b，另知点a、c 是圆轨道水平直径的两个端点，则下列说法正确的是（ ）．

A．小球运动到最高点时，小球的速度为零

B．当小球运动到点b 时，人对秤盘的压力最小，大小为Mg

C．小球在a、b、c 三个位置时，人对秤盘的压力相同

D．小球从c 点运动到最低点的过程中人对秤盘的压力减小

解析

本题属于绳模型，根据题意小球“恰好能通过圆轨道最高点b”可知，小球在最高点存在最小速度，分析受力可知在最高点小球的向心力由自身重力提供．小球运动到最低点时，以人和小球为整体进行受力分析．

因为小球恰好能通过圆轨道最高点，可知在最高点时细绳上的拉力为０，此时小球重力提供向心力，有mg＝mv２b／R ，解得vb＝根号下gR ，故选项A 错误．

在小球运动到最高点时，根据上面分析可知此时细绳上的拉力为０，因此此时台秤的示数为Mg;而在小球从点a 运动到点b 的过程中，细绳上有拉力，受力分析可知台秤示数应小于Mg，所以在小球到达最高点b 时，台秤上的示数并非最小值，选项B错误．

小球在位置a 和c 时，细绳的拉力提供向心力，但由于拉力处于水平方向，对人受力分析可知，竖直方向有FN＝Mg，所以选项C正确．

小球在从点c 运动到最低点的过程中，细绳上的拉力逐渐增大，且拉力与竖直方向的夹角逐渐减小，以人为研究对象进行受力分析可知细绳对人的拉力在竖直方向上的分力逐渐增大，因此台秤的示数也在不断增大，故选项D错误．

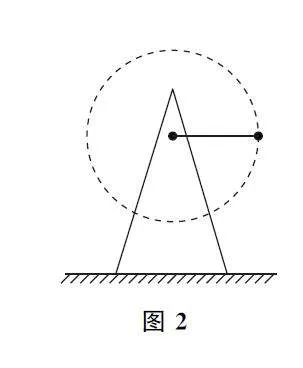
例２ 如图２所示，在水平地面上放置一个质量为M ＝４kg的三角形支架，在支架上部装有一个水平转轴，转轴由电动机驱动．现有一个轻杆安装在转轴上，另一端固定一个质量m ＝１kg的小球，小球与转轴间距离为５cm．电机驱动转轴可带动轻杆和小球在竖直面内做匀速圆周运动，当转轴转速恒为n 时，小球通过最高点时对轻杆的压力为２N，重力加速度g 取１０m··s－２，则（ ）．

A．小球运动到最高点时需要的向心力为１２N

B．小球运动到最高点时，支架对地面的压力为４２N

C．图示中轻杆恰好达到水平位置，此时地面受到的摩擦力为８N，方向水平向右

D．若题中的杆是轻绳，以同样的转速转动，小球无法通过图示的最高点

解析

在最高点，小球的向心力由自身重力和杆的支持力提供．小球运动到图示水平位置时，向心力由杆的拉力提供;杆换成细绳后，能通过最高点且速度最小时的向心力由小球的自身重力提供．知道了以上信息，由牛顿第二定律列式即可求出小球的线速度、绳或杆上的拉力等．

由题意和牛顿第三定律可知，在最高点杆对小球的支持力FN＝２N，在最高点小球所需向心力由自身的重力和杆对其的支持力提供，受力分析可知F＝mg－FN＝１０N－２N＝８N，故选项A 错误．

小球在最高点，杆受到小球的压力为２N，可知支架对地面的压力为F压＝Mg＋FN＝４０N＋２N＝４２N，选项B正确．

轻杆达到图示的水平位置时，设杆对小球的拉力为FT，有FT＝mv２／r ＝F＝８N，根据牛顿第三定律，小球对杆的拉力F′T ＝FT＝８N．以支架为研究对象，由平衡条件可得地面对支架的摩擦力Ff＝F′T ＝８N，方向水平向左，根据牛顿第三定律，可知地面受到的摩擦力为８N，方向水平向右，选项C正确．

由前面分析可知，小球在最高点时有F＝mg－FT＝mv２／r ＝８N，解得在最高点时小球的速度v＝根号下０.４ m·s－１．

换成轻绳后，设小球能达到最高点的最小速度为vmin，此时小球所需向心力由小球自身重力提供，有mg＝mv２min／r ，解得vmin＝根号下０.５ m·s－１＞根号下０.４ m·s－１，所以换成轻绳后，小球以同样的转速无法达到最高点，故选项D正确．

通过以上分析不难看出，解答物体在竖直面内做圆周运动的极值问题只需抓住向心力的来源这一关键，然后运用圆周运动相关规律就能准确解答．

（完）