高中数学中问题链设计的原则与分类

【摘要】高中阶段，正是学生在数学领域进行思维探索、全面发展自己的能力的最好时期，而问题链不仅为学生们搭建了数学学习的框架，也为培养学生高层次的思考创造了条件.结合人教A版数学教材，阐述在高中数学教学中，问题链的设计原则，包括目的性原则、趣味性原则、适度性原则和递进性原则.并依据设计原则，将问题链分为多种类型，以引入型问题链、诊断型问题链和总结型问题链三种类型为例，具体说明问题链设计原则在问题链设计中的实际应用.

【关键词】高中数学；问题链；数学教学

1 引言

在数学中，问题至关重要.哈尔莫斯曾说：“问题是数学的心脏”.众多专家对此进行了深入研究.课堂教育中，以问题为核心，围绕目标设计问题，推动课堂进程很重要.问题间应相互衔接，形成完整问题链.问题链是教师结合教学目标、内容和学生学习情况，巧妙融合数学知识与问题，构建的一系列相互关联的数学问题.国内知名的唐恒钧和张维忠教授，在深入研究问题和问题教学的基础上提出了问题链的概念，这一理念在数学教育界产生了广泛的影响.他们认为，问题链是教师在课前精心准备，在课堂上以多种方式呈现给学生的有序问题序列，它不仅为学生提供了数学学习的基本框架，还为学生发展高级思维能力提供了可能[1].

2 问题链的设计原则

我国教育体系受儒家思想影响，强调启发性教学.但当前课堂问题设计效果欠佳.问题链是新型教学理念，旨在通过系统、有目标的问题，师生共同感受数学抽象与逻辑推理之美.设计问题链需考虑教学目标、内容和学生认知，遵循目的性、趣味性、适度性、递进性等原则.

2.1 目的性原则

教师在设计问题链时，应确保问题服务于教学目标.基于教材，以教学目标为核心，明确教学重难点，并理解每个问题的目的：激发兴趣、培养思考能力或检验知识.问题间应连贯，共同指向核心，逐步解决，直至得出最终答案.整个过程需围绕教学目标，明确思考方向，避免无目的提问，如“是不是？对不对？”等.

比如在研究“函数单调性”时，可以这样设计：请同学们判断以下说法是否正确，并说明原因.（1）f（x）=x2是单调减函数.（2）定义在R上的函数f（x）满足f（1）<f（2），则它在R上是单调增函数.（3）f（x）=x在定义域内是单调函数.每个问题都有背后的目的，围绕教学目标和重难点，强调区间性及任意性，进而凸显出概念的重要性，这种方式比纯粹的文字强调要更有效.

2.2 趣味性原则

趣味性原则要求问题链的设计能够吸引学生注意力.数学问题作为知识与生活的桥梁，教师应以兴趣为导向，创设情景，让学生成为探索者.设计贴近生活的问题链，利用媒体提高参与度.将实际问题转化为数学公式，让学生认识到数学无处不在.设计时需考虑学生能力和兴趣，避免夸张案例.如“排列组合”教学中，可以这样设计：邀请6名同学上台（4男2女）.（1）他们排成一排有多少种排列方式？（2）若女生站一起，有几种排列方式？（3）男生A不能站首位，女生不能站末位，又有几种排列方式？这种设计与生活紧密相连，能调动课堂氛围和促使学生思考.

2.3 适度性原则

在问题链设计中，需依据最近发展区理念，考虑问题的难易程度.中学阶段，学生问答能力和知识储备相对较弱.设计问题链时，要平衡难度与认知水平、实际能力.过易则缺乏思考，过难则影响信心与积极性.

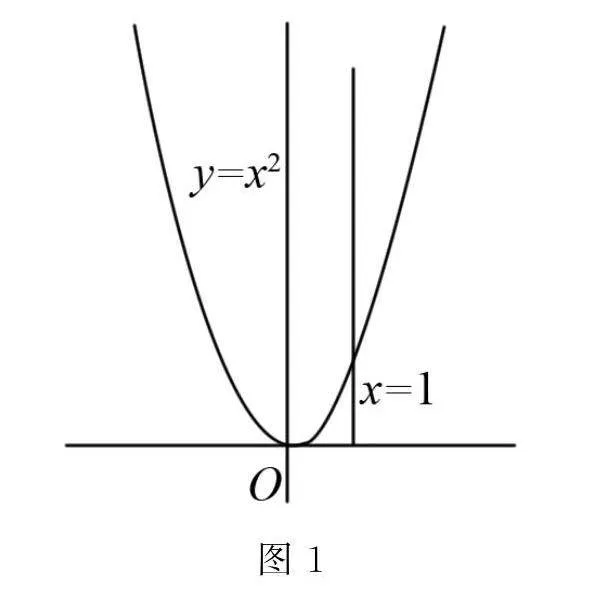
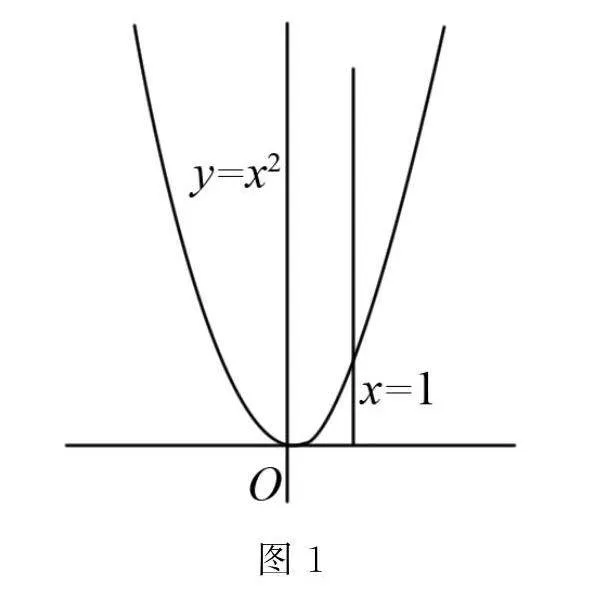
例如 在学习“导数的概念及其意义”时，可以如下设计：（1）请同学们回忆一下，我们是如何定义圆的切线的？（2）大家可以发现圆的切线是根据直线和圆的公共点来定义的，那么它适用于所有曲线吗？（3）我们以y=x2为例，直线x=1与曲线y=x2仅有一个公共点，但它不是曲线的切线，因此不能用公共点的方式来定义，那么我们该如何给y=x2的切线下定义呢？（如图1）先从学生比较熟悉的问题入手，避免他们产生挫N8gNbHqQEl7F6wRBrAf8eQ==败感，接着提出有挑战性的问题，引起他们的认知冲突，也让他们的思维活跃起来，从而自然的引入求曲线切线的课题.

2.4 递进性原则

递进性原则强调在问题链设计中，教师应基于学生认知规律，逐步提出问题以促进其能力发展.数学知识构建从简单到复杂，师生对数学的理解也需由浅入深.设计问题链时，应遵循循序渐进原则，避免急躁.因学生能力各异，教师应调整问题链以适应不同需求.在中学数学教学中，教师应突破传统观念，以充分发挥问题链的指导与启发作用.

例如 在完成“一元函数的导数及其应用”这一章的学习之后，进行练习时可以做如下设计：通过多媒体展示2023年新高考数学Ⅰ卷第19题“已知函数f（x）=a（ex+a）-x，讨论f（x）的单调性”，并询问（1）通过对试题题干的阅读，你能获取那些信息？（函数的定义域、导函数等）（2）我们学习了导数在研究函数中的应用，如何判断f（x）的单调性呢？（判断在某个区间内导函数的正负，即可知道原函数在该区间内的单调性）（3）针对这道题目，其中存在未知量a，应该如何进行单调性的讨论呢？请同学们小组讨论作答，并告知教师答案.通过上述由浅入深的问题，既可以帮助学生掌握导数在研究函数中的应用，感受数学分类讨论的奥妙，也有助于培养学生的班级意识.

3 问题链的类型

课堂中教师提出的问题要符合学生的思维特点，最终目的是让学生更好地学习数学，因此在课前预设好科学合理的问题链，对教学有很大帮助.依据设计原则，并分析课堂实际情况，可以将问题链分为引入型、总结型、诊断型、推广型、探究型、差异型、一题多解型问题链.而本文将以引入型问题链、诊断型问题链和总结型问题链三种类型为例，具体说明问题链设计原则在问题链设计中的实际应用.

3.1 引入型问题链

引入是一堂课最重要的一环，具有承接新旧知识的功能.而顾名思义，引入型问题链的内容可以是对之前所学的知识进行回顾，也可以是通过设置生活中的一些问题情景引入新课.但从实质上讲，引入型问题链是教师通过引入主题，为新内容牵线搭桥，为后续的教学做铺垫，激发学生的认知冲突或兴趣，激发学生的好奇心而精心设置的问题链[2]REF_Ref220＼r＼h.要使学生对概念原理和规律的提出有一个直观的认识，就要求学生建立起属于自己的知识系统，熟练地掌握所学的知识，并通过类比、演绎、归纳等方式揭示新旧知识的联系.引入型问题链多运用生动的案例、丰富多彩的情景、有趣又不乏深度的知识[3]REF_Ref15584＼r＼h.

例如 “基本不等式”这一节课，结合目的性和趣味性原则，可以设计如下问题链进行教学.

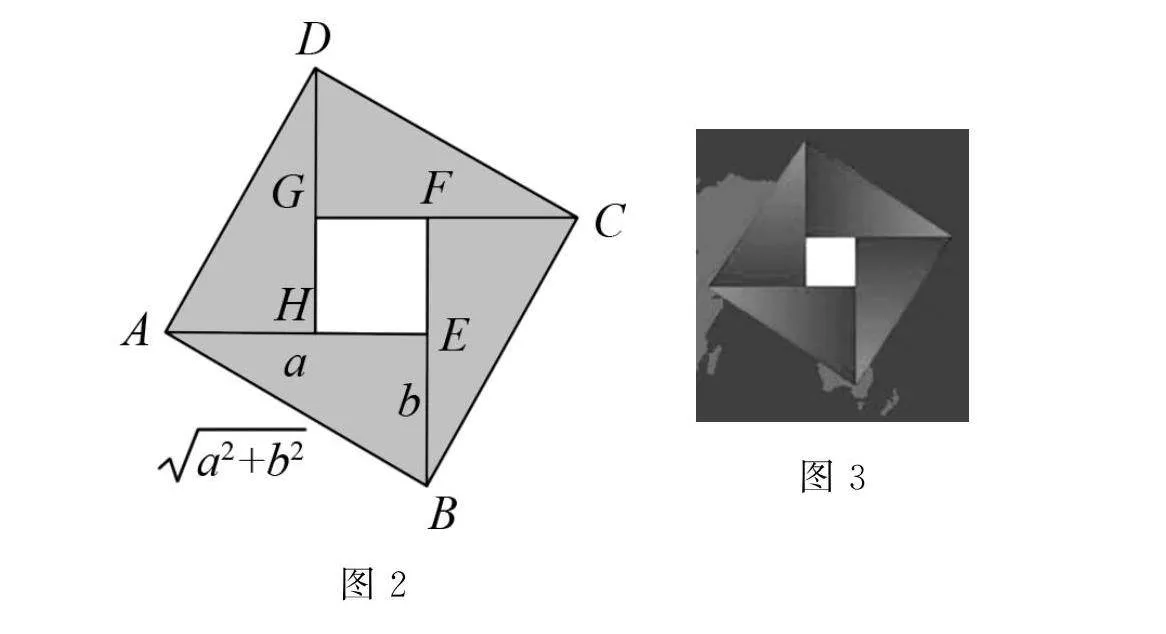
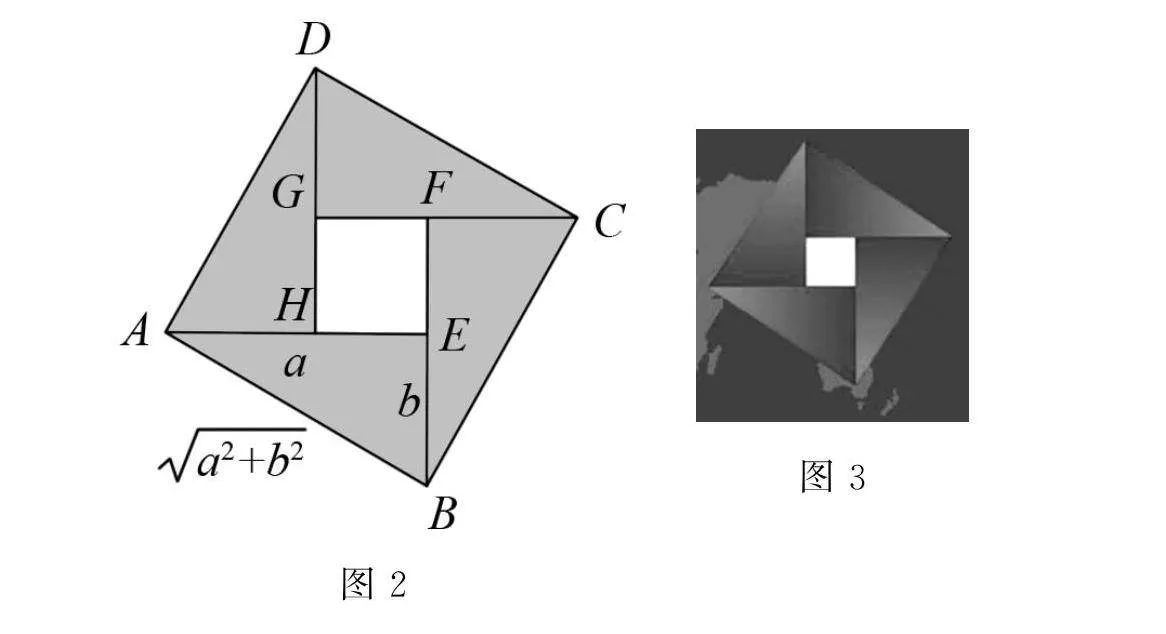
（1）请同学们看一下多媒体所呈现的图形（图2），这是在北京召开的第24届国际数学家大会的会标，其是根据我国古代的赵爽弦图设计的，是不是很像风车呢，我们将图2中的风车抽象成数学模型（图3），即在正方形ABCD中有4个全等的直角三角形，设直角三角形的两条直角边长分别为a，b，那么正方形ABCD的边长为多少？正方形EFGH的边长呢？你能从面积或其他角度入手，在图3中找到“相等”关系吗？

（2）同学们可以在图3中找到“不等”关系吗？（引导学生得到不等式a2+b2≥2ab）

（3）同学们想一想，这种“不等”关系什么时候可以取等号呢？（引导学生发现，当正方形EFGH缩为一个点时，取等号）

（4）用a、b替换a、b，我们可以得出何种不等关系？

教师利用多媒体给学生播放有关视频和第24届国际数学家大会会标并提问.对学生的回答进行总结归纳，并在黑板上展示不等关系的数学表达式.在教师的引导下，学生可以在观察的过程中，归纳出图形中的相等关系以及不等关系.最终可以得到不等式a2+b2≥2ab进而引入新课——基本不等式.

3.2 诊断型问题链

诊断型问题链是围绕教学重点、难点、疑点和易错点设计的问题序列.它鼓励学生犯错并找出原因，保持对数学的好奇与兴趣，防止学生轻视数学，提升课堂参与度.这有助于学生发展数学反思能力，并允许教师基于学生错误进行有针对性的教学改进.简而言之，诊断型问题链使学生在错误中学习和成长.

例如 “等差数列”的课程安排位于“数列的基本概念”后，作为重要的数学模型，其研究方式普遍，并为等比数列学习打下基础.因此，在数列章中地位极为重要.讲授时，可结合适度性原则，设计以下问题链：

小王同学背单词时，他的词汇量只有16个单词，他想要改变这一现状，于是下定决心从下周开始，每周背熟15个新单词，如果他能坚持下去，请问：

（1）小王在两个月后期中考试时能记住多少单词？

（2）按照这样的速度，小王能否达成期末要求的500个单词的词汇量要求？

引导学生以数字的形式，列出小王同学词汇量增加的数列：16，31，46，61，76，91……

列出数列后，学生易发现规律解决第一个问题.但第二个问题学生可能遇阻并出错.针对错误，教师诊断并引导学生思考，使学生保持学习兴趣.通过生活实例引入等差数列，让学生感受数学与生活的紧密联系，认识数学的重要性.设置适当难度问题，激发学生学习兴趣.

3.3 总结型问题链

总结型问题链用于知识点或单元总结，帮助学生回忆所学，构建系统知识结构，反思学习成果.通过整合内容，归纳零散知识，形成知识网络，提升独立思考能力.回顾巩固所学，增强解题成就感，激发学习热情.数学作为研究性学科，需深入研究如何提高教学质量，利用问题链来提升学习能力.

例如 在“数列”这一章节进行复习教学时可以结合递进性原则做如下设计，教师利用多媒体，给学生展示如下总结型问题链.

（1）请同学们回忆一下数列的基本概念.

（2）你能想出生活中有关数列的例子吗？

（3）等差数列和等比数列，分别有什么样的特点？通项公式又是怎样的？怎么求各项的和呢？

总结型问题链是以上面提到的数列总结型问题链为例，结合递进性原则而设置的有序且递进的问题链，不是平行的可以随意作答的问题，因此，教师在引导学生作答的过程中，要根据多媒体给出问题的顺序，逐个击破，让学生们感受数学层层递进的性质.

4 结语

问题链教学法是一种行之有效的方法，它可以提高中学数学课堂的教学效率，提高学生的学习兴趣.问题链是引导学生思考的路标，数学知识以问题链的方式嵌入在教学过程中，能有效地促进教师和学生的共同成长，是教学与学习之间的一座桥梁.通过问题链教学，可以很好地完成新旧知识的传递和能力的提升.问题链能促进教学模式的革新、学习方式的革新、教师主导性和学生主体性的有效发挥.在教学实践中，问题链可以帮助学生更好地理解与掌握知识，培养他们的思维能力，达到预期目标.

参考文献：

[1]唐恒钧，张维忠.数学问题链教学的理论与实践[M].上海：华东师范大学出版社，2021.

[2]王培峰. 基于问题链教学培养高中生化学高阶思维的实践研究[D].山西师范大学，2023.

[3]王露萍.试论化学教学中“问题链”的设计[J].化学教学，2011（03）：6-10.

[4]陈小璐.合理设计“问题链”环环相扣提素养——以“概率中的递推数列”教学设计为例[J].高中数学教与学，2024（11）：1-4+26.

[5]蒋晓清.基于“问题链”的高中数学教学实践——以圆的标准方程为例[J].中学数学，2024（09）：128-129.