留白：让学生的思维向深处漫溯

【摘要】“留白”是书画创作中的一种技法，数学教学与中国书画创作有相通之处，应借鉴书画创作中的留白，给学生一定的思考时间与空间，让学生自由探索，成为学习的主人.教师可在导入新课、探求新知、练习环节中适度留白，以激发学生兴趣，发展学生思维，进而提升学生的核心素养.

【关键词】留白；核心素养；初中数学

“留白”是书画创作中的一种技法，即在书画作品中留出一定空白不着墨迹，旨在给欣赏者以一定的遐想.传统教学中，数学教学更多依赖于教师的讲解，给学生独立思考的时间比较少.数学是思维的体操，没有个人思维的参与，数学教学效果甚微.其实，数学教学与中国书画创作有相通之处，应借鉴书画创作中的留白，给学生一定的思考时间与空间，让学生自由探索，成为学习的主人.这就需要教师在设计留白时，必须深入研读教材，准确把握学情，架设好教师的“讲”与学生的“学”之间的桥梁，它是教学节奏中“张”与“驰”之间的衔接点.需要注意的是，留白并非放任自由，也不可频繁使用，如果留白过多，教学会显得松松垮垮，那么，如何留白才能恰到好处，达到实效呢？

1 留白的理论基础

格式塔心理学派的“完形压强”理论认为，人类通过感官知觉得到的是一个完整的形象，如果遇到了不完美或残缺的图形或事物时，会不自觉产生补缺的想法，以求得内心的平衡.根据上述心理学的理论，教学中设计一定的留白，给学生创造不完满的情境，就会对学生的大脑形成一种刺激，从而激发学生大脑的思维活动，去填补其中的缺憾，促使学生去思考和探究.

建构主义理论认为，学习不能让学生被动地接受知识，而应让学生自主建构.即教学中应以学生为主体，教师为指导，教师与学生要在交流互动中共同推进教学，培养学生自主学习的能力.有了建构主义学习理论，数学教学就有了方法论，要给学生时间与空间，让学生去思考与学习，进而促进学生的个性化发展，这样的课堂是民主的、开放的.

2 留白的路径探寻

2.1 导入新课时留白，激发学生兴趣

课堂导入关系到本节课的起始点与课堂知识的产生.如何把学生的注意点吸引到数学课堂上？教师不能直接将结论告知学生，要以引入知识为时机，给学生设计留白，留下悬念，使学生处于“心求通而未达，口欲言而未能”的状态，进而调动学生的学习兴趣，激起学生的思考.

例如 “一元一次方程”的教学节选

情境 一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶，客车的行驶速度是60千米/小时，卡车的行驶速度是40千米/小时，客车比卡车早2小时经过B地，A、B两地间的路程是多少千米？

学生 当A、B两地间的路程是120千米时，客车需要2小时，卡车需要3小时，客车比卡车早到1小时；当A、B两间的路程是240千米时，客车需要4小时，卡车需要6小时，客车比卡车早到2小时，所以A、B两地间的路程是240千米？

教师 这位同学用列举的方法得到了结果，用方程的方法如何解呢？

学生 设A、B两地间的路程为x千米， 根据题意，得x40－x60=2.

教师 这就是我们本章即将要学习的一元一次方程，如何解这个方程求出x的值呢？

……

通过行程问题中求两地间距离的情境，引出了一元一次方程，但是方程能列出来，如何解这个方程呢？给学生留下了一定的空白，初步感受实际生活中的数量关系可以用一元一次方程来描述，体会一元一次方程的价值，为后期进一步解方程奠定基础.

2.2 探求新知时留白，唤激情

学习是自主建构的过程，在探究知识的过程中完成对知识的理解.然而，学生的认知结构的形成过程是螺旋式上升的.教师在引导过程中要在知识的关键之处留白，要突出数学的本质，使学生在亲历探究中，建立正确的认知.

2.2.1 在提问后留白

思维的建立需要经过一个过程.因此，教师在提出问题后不能急于让学生回答，不要以课堂45分钟时间宝贵为理由，为防止学生的奇思异想打乱教学计划，而不给学生思考的时间，这会在无形中降低教师提出的问题的价值，也不能培养学生的思维能力.在教师提问后，要有所停顿，适当的留白，给学生留下一定的时间和空间，培养学生发现问题、提出问题与解决问题的能力，变教师的精讲为学生的精思，切实提高课堂效率.

例如 在复习“二次函数图象与系数关系”一课中，笔者采用了层层递进，不断深入的方式，引导学生思维走进数学抽象的思维中.已知二次函数y=ax2+bx+c（a≠0）的图象如图1所示.

问题1：如图1所示，如何根据图象在坐标系中的位置求出字母a、b、c的正负号呢？问题2：如图所示，如何根据二次函数图象对称轴的位置求得2a-b的正负号呢？问题3：如图所示，如何得到代数式9a+3b+c，并求出它的正负号呢？问题4：根据上面的研究成果，如何比较c与-3a的大小关系呢？问题5：根据问题4的活动经验，如何比较a+b与am2+bm的大小关系呢？

上面五个问题从旧知到新知，从简单到复杂，逐步把学生的思维引向深入，学生的状态处于主动、自主的状态，思维不断向深处漫溯，教学效果令人满意.

2.2.2 在重难点处留白

影响课堂教学效果的因素着重取决于教师对本节课重难点的把握和突破程度，有不少教师埋怨学生：“我这道题讲了三四遍，并强调这是重要知识，但是你们为什么还要做错呢？”实际上在本节课的重难点之处，不是教师强调这是重难点，学生就一定会掌握的，而适当留白，并适当停顿，设计一些前置性问题，让学生先自主探究，在反思中加深学生对于知识的理解与掌握.

例如 如图2所示，正方形ABCD的边长为5，把它的对角线AC分成n小段，以每一小段为对角线作一个小正方形，那么这n个小正方形的周长之和为多少呢？

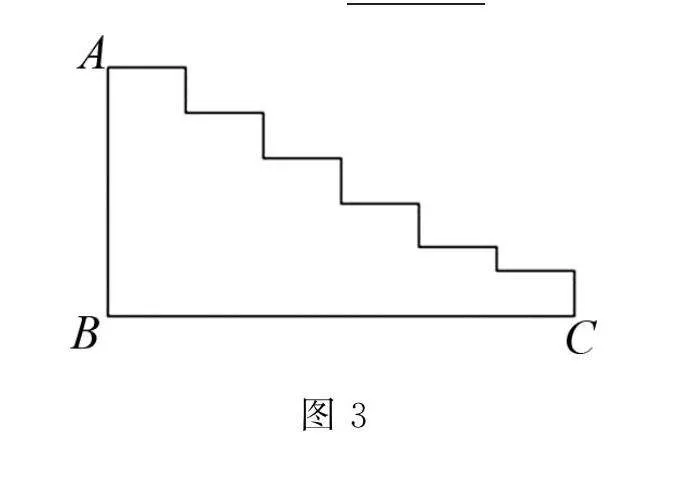
此题考查的是学生能否利用平移解决问题，笔者发现学生对这一问题有困难，为此，笔者提前设置了下面几个前置问题：（1）如图3所示，对于如何求台阶的总长，小红的办法是量出每阶台阶的高度与宽度，然后加起来，小刚的办法是只需量出台阶的高AB和长CD的长，你认为小刚的办法可以吗？（2）如图4在长方形ABCD中，AB=11，BC=5，则图中四个小长方形的周长和为 .

教学中，教师把知识全部掰开喂给学生，就剥夺了学生思考的权力.因此，教师设计一些有思考价值的问题，给学生留下感兴趣的空白，激起学生强烈的认知冲突，点燃学生参与课堂教学的热情，在自主探究中，实现重难点问题的突破.

2.2.3 练习中留白，拓展学生思维

在数学教学中，练习起着巩固新知的重要作用，所以教师要在练习中留白，设计的练习要具有层次性、开放性，给学生更多的探索空间，把学生的思维引向更广阔的天地，它对于拓展学生的思维具有重要作用.

在传统教学中，教师布置作业都是统一的，学生没有拓展的空间.笔者尝试给学生安排了“作业超市”.在作业超市里，有基础题，补差型试题、能力拔高题，学生可以根据自己不同的学习基础，根据对于新知的掌握情况，选择适合自己的作业，一方面提高了学生的选择能力，也开发了学生的潜力，让学生得到最优的发展.

基础性试题：根据当天学习的新知命题，考查知识点为每一个知识点及重点.

补差型试题：对于学习基础不扎实的同学，要布置一些浅显易懂的，让他们也获得成功的快乐，培养这部分学生的自信心.

能力拓展题：对于学有余力的同学，要设计一些有一定难度，且综合性比较强的试题，可以培养学生思维的深刻性与灵活性.

通过基础性试题、补差型试题、拓展型试题，教师可以及时了解学生对于已学知识的掌握情况，并可以根据学生情况调节教学，进而使后期教学更具有针对性，进而提高课堂实效.

3 结语

总之，留白是一种艺术.教学中，教师应在新课导入处，探求新知处、课后练习处进行精心设置留白，以激发学生兴趣，发展学生思维，进而提升学生的核心素养.

参考文献：

[1]陈秀海.幽默引人入胜留白发人深省结语绕梁三日——初中数学课堂教学语言艺术提升研究[J].中学数学，2023（24）：88-89.

[2]徐建国.融创课堂理念下的初中数学课堂留白[J].数学教学通讯，2022（23）：47-48.

[3]杨峰.初中数学课堂留白三策略[J].现代中学生（初中版），2021（06）：5-6.

[4]赵丽.初中数学课堂留白的教学研究[D].重庆：西南大学，2021.