实施“合作学习”，构建高效习题课

【摘要】为打破以往常规“一言一课”的习题课教学模式，本文探究以合作式学习为主的习题课模式，设计知识梳理、真题挑战、变式训练三个环节，层层递进，以点带面，促进课堂的开展.以“平行四边形的性质与判定”为例，通过题组训练、变式训练研究几何图形的性质，引导学生归纳平行四边形的考点策略、基本模型及相关的几何事实.

【关键词】合作学习；初中数学；习题课

习题课作为数学教学的重要组成部分，如何才能使课堂效率最高是值得一线教师深思的问题.目前，习题课教学的现状是，在教师方面，填鸭式的课堂教学重讲授，没有给学生足够的时间进行教学活动，忽略学生的主体性；在学生方面，就题论题，只重解答，缺乏基础知识或思维方法的深度思考，忽略小结与反思.基于以上情况，笔者在习题课教学中实施合作学习，引导学生围绕教师的任务展开合作学习与探究，促使他们在交流、探索中进行思维碰撞，从而获得知识与技能，进而提升多方位的素养能力，如数学交流、合作学习等.

1 合作学习下初中数学高效习题课构建策略

合作学习是种有效的教学方式之一.学生在合作学习中不仅能够获取知识，得到技能的进步，而且能培养数学思维和数学素养，本文从以下几个方面训练学生的合作学习.

1.1 科学高效分组

在分组之前，教师应对学生的数学水平、学习风格和性格特点了如指掌，在组内要将不同类型的学生进行合理搭配，促进组内的互动和互补，在组间尽量确保每个小组的数学水平相当，保证组间的竞争公平性.笔者本次采取以4人为一组（ABBC）的组内设计，避免将水平过高的学生分在同一组，同时明确组员在组内的职责和任务.组织能力强的学生担任组长，表达能力强的学生负责汇报，以充分发挥每个学生的优势，提高习题小组的效率和默契.

1.2 明确任务及要求

初中教师应科学设计小组合作互动内容，围绕习题课中的重点、难点、疑点等开展合作学习与探究，根据具体内容制定合理的小组合作任务，充分发挥任务驱动作用，体现合作意义，让学生的学习行为具有针对性及有效性，引导学生向着共同责任进行分工合作，也能一定程度上避免打击其他学生的学习积极性，激发学生的学习热情，促进组内的合作效率.

1.3 加强教师指导

在实施分组学习的过程中，初中教师需要给予学生必要的指导，例如解题方法的点拨、思路的开拓等，通过适时点拨及指导，能够帮助学生突破合作学习过程中遇到的困惑，顺利推进合作学习全过程.教师还要监督学生的分组学习情况，如果某个小组的进度明显落后于其他小组，则要重新评估学生的学习情况，根据需要适时调整组员角色，确保每个小组都能有效地进行学习.

1.4 合理教学评价

初中数学教师要注意围绕教学目标进行教学评价，制定科学合理的评价竞争机制，评价教学目标是否明确、具体，是否符合学生的实际情况，是否能够通过合作学习达成.还要结合学生的参与度、合作精神、交流能力进行评价，形成质化和量化分析.例如分组是否科学、合理，是否能够充分发挥每个学生的优势，增强合作学习的效果.在评价之后形成教学反思，评价教师对合作学习的反思和改进情况，综合评价学生通过合作学习所取得的学习成果，包括解决问题的能力和数学思维能力的发展，以及学生对合作学习的反馈和建议，不断完善合作学习的教学方法和策略.

2 合作学习下初中数学高效习题课构建实践

平行四边形是初中数学几何领域中的重要内容，而传统习题课讲授模式大多是以题带题，缺乏深入思考与探究.为了更好地落实合作学习在习题课中的应用，本文以“平行四边形的性质与判定”为例，以小组为单位，设计了一节合作式学习的综合型习题课，其具体过程如下：

2.1 教学分析

2.1.1 教材分析

平行四边形是平面内继三角形后又一基本图形，它对学生的逻辑思维能力和推理论证能力要求较高.平行四边形的性质与判定习题课的设计不仅是对三角形、四边形知识的巩固，而且能够为之后的几何综合学习做充分的准备和能力的储备.本课的教学通过对平行四边形的性质与判定知识进行回顾，以典型问题为载体，旨在让学生掌握转化与化归、分类讨论、从特殊到一般等重要数学思想方法.

2.1.2 学情分析

在知识层次上，学生已经掌握了平行四边形的性质与判定内容的相关知识，初步具备了推理能力，并积累了一定的观察、操作等活动经验[1].在思维层次上，学生从直观形象思维逐渐过渡到抽象逻辑思维，具备合作学习中分析、比较、抽象、概括等逻辑思维活动的能力.在心理层次上，抓住学生对合作学习、数学学习感兴趣的特点，通过真题挑战、变式训练，层层递进，给学生创造新问题，充实课堂.通过合作学习、师生小结点评等教学活动，进一步掌握平行四边形的性质与判定，进而升华学生认知.

2.1.3 教学目标

（1）梳理知识要点，构建平行四边形的性质与判定的知识体系；

（2）通过题组训练、变式训练，紧扣数学思想方法，从图形的变化角度研究图形性质，巩固对平行四边形图形特征的认识，培养逻辑推理、几何直观等数学核心素养；

（3）经历平行四边形的性质判定的合作探究过程，积累数学活动经验，体会分类讨论、转化的数学思想，并掌握“一般到特殊、特殊到一般”的解决策略，实现育人价值.

2.1.4 教学重难点

重点 灵活应用平行四边形的性质与判定.

难点 构建知识体系，掌握图形研究的思维方式.

2.2 教学设计

2.2.1 知识梳理

（1）如图1，ABCD中，AB=3，AD=2，∠ABC=120°，

①ABCD的周长是；

②∠ADC=；

③设对角线AC，BD相交于点O，请指出OB的取值范围.

（2）如图1，四边形ABCD中，对角线AC，BD相交于点O.

①当AB∥CD时，再添一个条件：，可以判定四边形ABCD是平行四边形；

②当AB=CD时，再添一个条件：，可以判定四边形ABCD是平行四边形；

③当OA=OC时，再添一个条件：，可以判定四边形ABCD是平行四边形；

④有人提出一个命题：一组对边平行，另一组对边相等时，也能判定四边形是平行四边形，请判定这个命题的真假，如果是真命题，给出证明；如果是假命题，画出反例.

（3）如图1，ABCD中，对角线AC，BD相交于点O，那么△ABC与△ABD面积相等吗？由此你还能得出哪些结论？

教学活动 学生独立完成，限时3分钟.教师公布答案，学生校对，梳理知识.在添加条件时，可能会有多种不同答案.如（2）①添加OA=OC，鼓励学生说出缘由，肯定学生的做法.

设计意图 通过简单的题组问题回顾平行四边形的性质与判定，进而起到梳理知识，归纳常见模型——蝴蝶模型的作用.

2.2.2 真题挑战

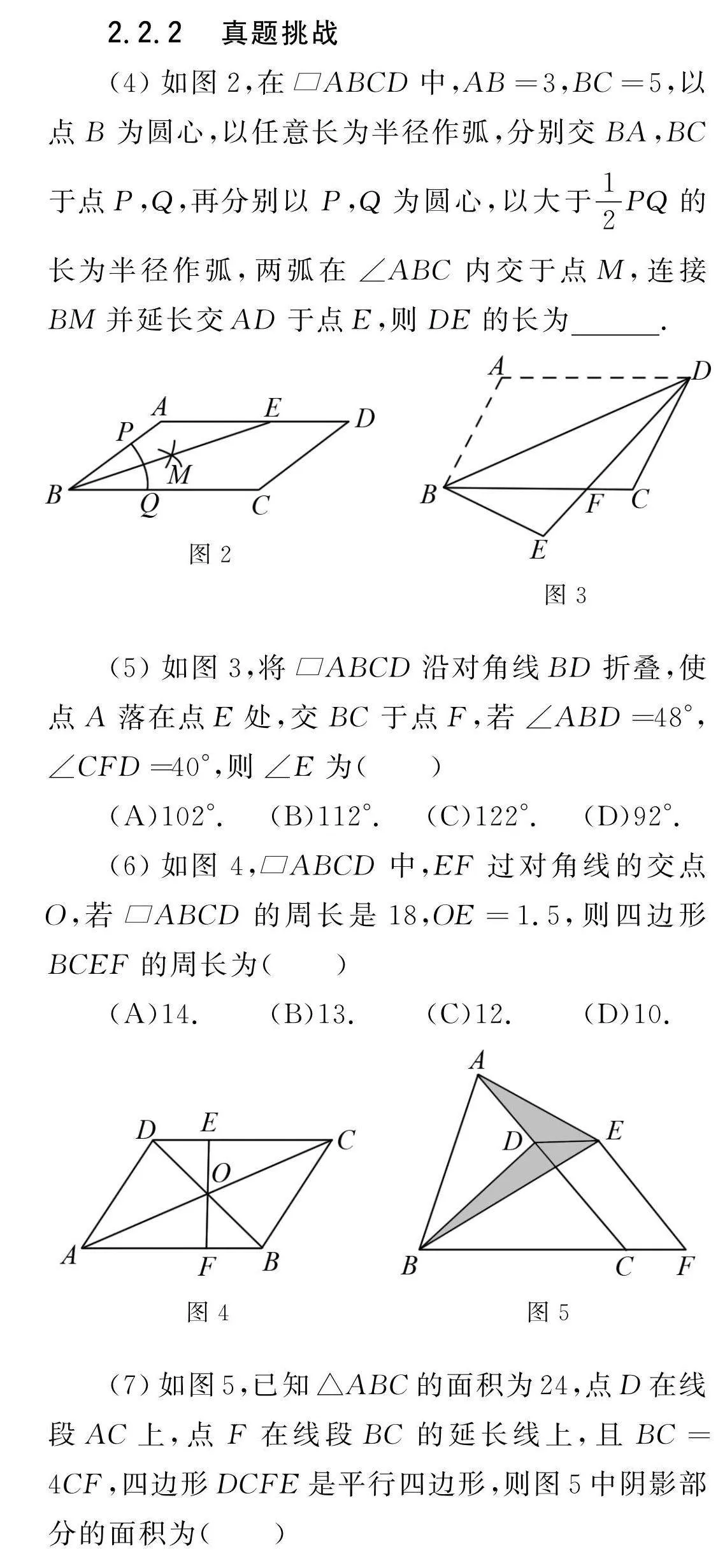
（4）如图2，在ABCD中，AB=3，BC=5，以点B为圆心，以任意长为半径作弧，分别交BA，BC于点P，Q，再分别以P，Q为圆心，以大于12PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为.

（5）如图3，将ABCD沿对角线BD折叠，使点A落在点E处，交BC于点F，若∠ABD=48°，∠CFD=40°，则∠E为（ ）

（A）102°. （B）112°. （C）122°. （D）92°.

（6）如图4，ABCD中，EF过对角线的交点O，若ABCD的周长是18，OE=1.5，则四边形BCEF的周长为（ ）

（A）14. （B）13. （C）12. （D）10.

（7）如图5，已知△ABC的面积为24，点D在线段AC上，点F在线段BC的延长线上，且BC=4CF，四边形DCFE是平行四边形，则图5中阴影部分的面积为（ ）

（A）3. （B）4. （C）6. （D）8.

教学活动 学生先独立完成小组讨论，限时8分钟，最后派学生代表分享成果.学生讲题，教师点评并小结.第（4）题考点涉及角平分线作法及平行四边形性质，引导学生归纳平行+角平分线=等腰三角形；第（5）题考点涉及平行四边形的折叠问题，引导学生根据平行四边形的性质、存在的线段相等、角相等和折叠产生的线段相等、角相等等实现线段、角之间的对应转化；第（6）题考点涉及平行四边形的中心对称性，引导学生归纳平行四边形是中心对称图形，对称中心是对角线的交点，过对称中心的直线将平行四边形分成面积相等的两个部分；第（7）题考点涉及平行线间的距离应用，引导学生归纳平行线间的距离处处相等、同高不同底的两个三角形面积比等于底的比.另外，解第（7）

题时可鼓励学生一题多解，可以将不规则图形的面积转化成规则图形面积计算.

设计意图 从与平行四边形有关的长度、角度、周长、面积计算甄选真题，覆盖的知识面广而精，便于激发学生的好奇心和求知欲.通过学生的独立思考和小组合作，建构知识间的联系，实现知识迁移，进而巩固平行四边形的性质.

2.2.3 变式训练

（8）（深圳龙岗）如图6，在ABCD中，已知点M，N分别是边AD，BC的中点.求证：四边形AMCN为平行四边形.

变式1 如图6，将“点M，N分别是边AB，DC的中点”改为“AM=CN”，结论成立吗？

变式2 如图7，在变式1的基础上，添加条件“分别延长CM，BA交于点E，分别延长AN，DC交于点F”，求证：四边形AECF为平行四边形.

变式3 如图7，在变式2的基础上，连接“ED，BF”，求证：四边形BEDF为平行四边形.

变式4 如图8，在ABCD中，已知AB=6cm，AD=10cm，点M在AD上以每秒1cm的速度从点A向点D运动，点N在CB上以每秒2cm速度从点C出发，在CB间往返运动，点M，N同时出发，当点M到达点D时停止运动，同时点N也停止运动（点M可以与A重合），设运动时间为ts，当t为何值时，以MDNB为顶点的四边形是平行四边形？

教学活动 全体学生完整作答原题，小组成员互相批改；小组成员合理分工，共同完成变式1-4，简写过程；最后整理合作成果并作小组汇报，限时12分钟.在学生展示成果过程中，教师多问：还有没有其他证法？鼓励学生一题多解，并在多解中选择最优做法.如变式3，学生可以由ABCDAE∥CF，AMCNAF∥CE，最后得证.也可以由ABCDOA=OC、OB=OD，AMCNOA=OC、OE=OF，最后由OB=OD、OE=OF得证BEDF（如图8）.变式4，借助几何画板引导学生“化动为静”，要用“静”去理解“动”，在动态问题中判定平行四边形，可根据已知的一个条件，寻找推理另一个条件，另外，引导学生注意进行分类讨论，不要漏解.

设计意图 本环节以常见的基本图形为原型，先是改变点M，N所在的位置，由特殊中点到一般点；然后增加线段，由简单图形变为复杂图形的证明；最后是M，N由定点变为动点，增加证明难度.设计层层递进，符合学生的学习心理.通过小组分工合作，培养学生的合作能力和探究能力，小组成员全员参与，可以让每个学生都得到不同程度的发展.在一题多解的教学过程中，反复再现性质与判定知识，并从不同的角度分析和运用已知条件和判定方法，从而提升学生思维的灵活性、广阔性.

3 教学反思

3.1 从“简单粗暴”到“顶层设计”

本节课是一节以建立知识之间的联系，提高综合应用知识能力的综合型习题课，教师的任务是帮助学生进行顶层设计，而不是以往的题海设计.笔者先以简单的题组训练形式将所学知识进行串联，接着以典型真题为载体将新旧知识进行关联，最后以基础图形为原型将几何图形的方法与套路进行并联.学生通过体验从复杂图形中勾勒出基本图形，从动态问题中抽象出静态问题，不断完善图式，增强几何直观.

3.2 从“以师为主”到“以生为本”

笔者在设计和实施教学时，认识到学生是教育的主体，教育的最终目的是促进学生的全面发展.传统的填鸭式教学方式已经过时，教师不再是单纯的知识传授者，而是成为学生学习的引导者和伙伴，将课堂还给学生，为学生创造良好的学习环境和不同形式的合作学习活动.退一步来讲，容量这么大的课堂只靠教师的讲授是达不到应有的效果的，因此从师本走向生本，建立新型的师生关系，培养学生的自主性和创造性，培养学生的团队意识、合作能力，集思广益，便能将个体的智慧实现最大化，合作学习有利于实现高效数学课堂.

3.3 从“传统教学”到“信息化教学”

为了提高学生的学习积极性和参与度，必须改变过去教师讲得津津有味、学生听得无精打采的讲课风气，创造与时俱进的物质环境、文化环境，向信息化辅助教学转变.因此，在教师、教学内容及学生的基础上增加信息技术手段，这样有利于形成一个合理、协调、有创造性和发展性的学习整体.信息技术化不仅可以调动学生的视觉、听觉，而且可以将抽象的事物具体化.本节课借助一体机平台、利用希沃白板、几何画板等软件辅助教学，这样不仅激发了学生的学习动力，也提高了教学效果和课堂效率.

参考文献：

[1]王礼彬，陆海兵.探究式的初中数学复习课——以“平行四边形专题复习”为例[J].上海中学数学，2018（06）：13-15+22.