三支区间集半概念的代数结构及覆盖粗糙近似算子

摘要： 针对在一个形式背景中以区间集为底集，考虑一个属性集（对象集）拥有的对象集（属性集）和不拥有的对象集（属性集）的知识表述而进行知识提取的问题，采取将区间集概念与三支决策、经典半概念相结合的方法，产生AE-区间集半概念和OE-区间集半概念两种形式的三支区间集半概念，同时发现AE-区间集半概念与OE-区间集半概念的纯双布尔代数结构。进一步深入讨论可知，AE-区间集半概念可分为AE1-区间集半概念与AE2-区间集半概念，利用粗糙集理论分别挖掘与AE1-区间集半概念和AE2-区间集半概念有关的近似算子的结构性质，对偶地可得OE-区间集半概念的相关结果。所得三支区间集半概念拓广了已有的三支决策集分别与区间集概念和半概念相结合的相关成果，成为一个新的知识表述。

关键词： 形式概念分析； 半概念； 三支决策； 区间集概念； 近似算子

中图分类号： TP18

文献标志码： A

文章编号： 1671-6841（2024）06-0084-07

DOI： 10.13705/j.issn.1671-6841.2023123

Algebra Structure and Covering Approximation Operators of

Three-way Interval-set Semiconcepts

MAO Hua1，2 ， NIU Zhenhua1， MA Jingze1， WANG Gang1， ZHANG Zhiming1， YANG Lanzhen1

（1.School of Mathematics and Information Science， Hebei University， Baoding 071002， China;

2.Hebei Key Laboratory of Machine Learning and Computational Intelligence，

Baoding 071002， China）

Abstract： In response to the problem of knowledge extraction in a formal context， which took interval-set as the background set and considered the knowledge expression of the object set （attribute set） owned by an attribute set （object set） and the object set （attribute set） not owned by an attribute set （object set）， the method of combining interval-set concept with three-way decision and classical semiconcept was adopted， resulting in two types of three-way interval-set semiconcept： AE-interval-set semiconcept and OE-interval-set semiconcept. Meanwhile， pure double Boolean algebraic structures were explored for the two new types of interval-set semiconcept， respectively. Further discussion revealed that AE-interval-set semiconcept could be divided into AE1-interval-set semiconcept and AE2-interval-set semiconcept. Rough set theory was applied into mining the constructions and properties relative to approximation operators of AE1-interval-set semiconcept and AE2-interval-set semiconcept， respectively. Dually， the relevant results for OE-interval-set semiconcept were obtained. The obtained three-way interval-set semiconcept generalized the existing results relative to the combination of three-way decision and interval-set or that of three-way decision and semiconcept. Therefore， three-way interval-set semiconcept became a new form to express knowledge.

Key words： formal concept analysis; semiconcept; three-way decision; interval-set concept; approximation opeartor

0 引言

近年来，形式概念分析［1］在数据挖掘、知识发现、粒计算等领域得到广泛应用［2-4］。形式概念（X，A）需满足X*=A且A*=X。由于形式概念的算子条件限制了形式概念分析的发展，因此研究者们减弱了算子的限制条件，半概念成为形式概念分析的重要拓广模型之一。Vormbrock等［5］基于半概念模型提出纯双布尔代数理论。对于区间集概念［6］，其本质思想是将概念中表示外延与内涵的集合推广到区间集，利用区间集反映的不确定信息把形式概念拓广到区间集概念。

Yao［7］在二支决策的基础上提出了三支决策理论，其基本思想是将决策分为接受、拒绝和延迟三种。三支决策思想为很多领域提供了解决问题的新思路［8］。粗糙集是由Pawlak［9］ 提出的一种处理不精确、不确定性数据的数学工具，其理论的核心是一对近似算子。但建立在等价关系上的Pawlak粗糙集模型过于苛刻，限制了粗糙集的应用范围，为此，Yao等［10］提出一种覆盖近似算子。

形式概念分析一经提出，国内外学者分别从概念格的构造、形式概念分析与其他理论的结合等方面进行了研究。例如，Qi等［11］将三支决策与形式概念结合，将对象（属性）集共同拥有的属性（对象）集的运算作为正算子，将对象（属性）集共同不拥有的运算作为负算子，提出三支概念分析理论。Mao等［12］将经典半概念与三支决策结合，提出两种形式的三支半概念。Yao［13］在不完备形式背景下，将三支决策与区间集概念结合，提出三支区间集概念格。Mao［14］将经典半概念与粗糙集结合，提出粗糙半概念。综合上述表述可得，将半概念与区间集结合，并进一步地与三支决策相结合得到三支区间集半概念，是对已有的三支决策、区间集与三支半概念的拓广，是将三者的提纲挈领综合性结果，是一个创新性的结果。因此，本文将区间集概念与三支决策、经典半概念结合，提出两种三支区间集半概念，可以解决只需要考虑属性区间集拥有的对象区间集或对象区间集拥有的属性区间集的问题，并证明它们为纯双布尔代数结构。此外，提出两种三支区间集半概念的粗糙近似算子，可以利用构造的近似算子挖掘潜在知识。

1 预备知识

首先对形式概念分析的基本理论进行简要介绍，接着介绍三支区间集概念与粗糙集的相关知识。经典半概念和三支半概念详细内容见参考文献［2，14，17］，区间集概念详细内容见参考文献［6，18］，双布尔代数详细内容见参考文献［19］，粗糙集详细内容见参考文献［11，12］。

1.1 经典半概念和三支概念

定义1［2］

（1） ≤是集合P上的一个偏序关系。若对于任意的a，b，c∈P，≤满足下列条件，则（P，≤）称为偏序集。

（p1） a≤a（自反性）；

（p2） a≤b且b≤aa=b（反对称性）；

（p3） a≤b且b≤ca≤c（传递性）。

（2） 设（P，≤）是一个偏序集，若对于任意两个元素a，b∈P，存在上确界a∨b和下确界a∧b，则（P，≤）是一个格。

定义2［2］ （1） 形式背景K=（U，V，R）由对象集U、属性集V以及U到V的二元关系R组成。

（2） 若XU且AV，则对应的算子定义如下。

（2.1） 正算子*：P（U）→P（V）和*：P（V）→P（U）定义为

X*=｛v∈Vx∈X，xRv｝;

A*=｛u∈Ua∈A，uRa｝。

（2.2） 负算子*：P（U）→P（V）和*：P（V）→P（U）定义为

X*=｛v∈Vx∈X，xRcv｝;

A*=｛u∈Ua∈A，uRca｝。

定义3［5］ 设XU且AV，

（1） 若X*=A，称（X，A）为∩-半概念；

（2） 若A*=X，称（X，A） 为∪-半概念；

（3） 若X*=A，称（X，A）为N∩-半概念；

（4） 若A*=X，称（X，A）为N∪-半概念。

定义4［12］ 设X，YU且A，BV，

（1） 面向属性的半概念算子（简称AE-半算子）·：P（V）→P（U）×P（U）定义为：A·=（A*，A*）。

（2） 面向对象的半概念算子（简称OE-半算子）·：P（U）→P（V）×P（V）定义为：X·=（X*，X*）。

（3） 若A·=（A*，A*）=（X，Y），则称（（X，Y），A）为面向属性的半概念（简称AE-半概念）。称（X，Y）和A分别为 （（X，Y），A）的外延和内涵。

（4） 若X·=（X*，X*）=（A，B），则称（X，（A，B））为面向对象的半概念（简称OE-半概念）。称X和 （A，B）分别为（X，（A，B））的外延和内涵。

引理1［2］

设K=（U，V，R）是一个形式背景，对于任意的Z，Z1，Z2U（或Z，Z1，Z2V）满足Z1Z2Z*2Z*1。

证明 设Z1，Z2U，由定义3（1）得Z*2Z*1。

1.2 区间集概念

定义5［6］

设M是有限论域，P（M）是集合M的幂集。定义M上的区间集X～

［Xl，Xu］=｛X∈P（M）XlXXu｝。

记IP（M）为M上区间集的全体。

定义6［6，15］ 在形式背景K=（U，V，R）中，若

X～=［Xl，Xu］∈IP（U），A～=

［Al，Au］∈IP（V），则相应的算子定义如下。

（1） 正算子f：IP（U）→IP（V）和g：IP（V）→IP（U）定义为

f（X～）=［X*u，X*l］;

g（A～）=［A*u，A*l］。

（2） 负算子f：IP（U）→IP（V）和g：IP（V）→IP（U）定义为

f（X～）=

［X*u，X*I］;

g（A～）=［A*u，A*l］。

（3） 面向属性的区间集算子（简称AE-区间集算子）：IP（U）→IP（V）×IP（V）和：IP（V）→IP（U）×IP（U）定义为

（X～，Y～）=

f（X～）∩f

（Y～）;A～=

（g（A～），（A～））。

（4） 面向对象的区间集算子（简称OE-区间集算子）：IP（V）→IP（U）×IP（U）和： IP（U）→IP（V）×IP（V）定义为

（A～，

B～

）=g（A～）∩g

（B～）;

X～=（f（A～），

f（A～））。

若A～=（g（A～），

（A～））=（X～，

Y～）且（X～，Y～）=

f（X～）∩f（Y～），

则称（（X～，Y～），A～）

为AE-区间集概念。

1.3 双布尔代数

定义7［16］

双布尔代数F=（E，↓，↑，，，）是一种类型为（2，2，1，1，0，0）的代数结构。对任意的x，y，z∈E，满足以下性质：

（1a）（x∧x）↓y=x∧y;

（1b）（x↑x）↑y=x↑y;

（2a）x∧y=y∧x;

（2b）x↑y=y↑x;

（3a）（x∧y）∧z=x∧（y∧z）;

（3b）（x↑y）↑z=x↑（y↑z）;

（4a）（x∧x）=x;

（4b）（x∧x）=x;

（5a）x∧（x↑y）=x∧x;

（5b）x↑（x∧y）=x↑x;

（6a）x∧（y∨z）=（x∧y）∨（x∧z）;

（6b）x↑（y↓z）=（x↑y）↓（x↑z）;

（7a）x∧（x∨y）=x∧x;

（7b）x↑（x↓y）=x↑x;

（8a）（x∧y）=x∧y;

（8b）（x↑y）=x↑y;

（9a）x∧x=;

（9b）x↑x=;

（10a）=∧;

（10b）=↑;

（11a）=;

（11b）=;

（12）（x∧x）↑（x∧x）=（x↑x）∧（x↑x）;

（13）x∧x=x或x↑x=x。

其中：∨和∧分别定义为x∨y=（x↓y）和

x∧y=（x↑y）。

1.4 粗糙集

定义8［9］ 若G为一个论域D上的二元关系，则称（D，G）是基于关系G上的近似空间。对于任意

XD，X关于这个近似空间的下近似算子和上近似算子分别定义为

GX=∪｛YY∈D/G，YX｝;

GX=∪｛YY∈D/G，Y∩X≠｝。

当GX=GX时，称X是G的可定义集，否则称X是G的粗糙集。

定义9［9］

若G为一个论域D上的二元关系，则称（D，G）是基于关系G上的近似空间。对于任意XD，给定两个算子apr和

apr，当且仅当下列性质成立时，则称apr（X）和apr（X）为（D，G）的上、下近似算子。

（1）apr（X）apr（X）;

（2）apr（X）=apr（X）X是可定义的。

定义10［10］

设D是一个论域，C是D上的一个子集族。若C中的元素都是非空的，并且∪C=D，则称C是D的一个覆盖。

2 AE-区间集半概念

文献［18］将区间集概念与三支决策，提出了两种三支区间集概念——AE-区间集概念和OE-区间集概念。本节将三支区间集概念与半概念结合，提出两种形式的三支区间集半概念——AE-区间集半概念和OE-区间集半概念。因为半概念分为∩-半概念和∪-半概念两种，所以接下来提出的AE-区间集半概念分为AE1-区间集半概念和AE2-区间集半概念两种。

定义11 在形式背景K=（U，V，R）中，设

X～，Y～IP（U），A～IP（V）。若

A～=（g（A～），

（A～））=（X～，Y～），则称

（（X～，Y～），A～）

为AE1-区间集半概念。形式背景K=（U，V，R）中AE1-区间集半概念全体记作ISSAE1（K）。

定义12

在形式背景K=（U，V，R）中，设X～，Y～IP（U），

A～IP（V）。

若（X～，Y～）=f（X～）

∩f（Y～）=A～，则称

（（X～，Y～），A～）

为AE2-区间集半概念。形式背景K=（U，V，R）中AE2-区间集半概念全体记作ISSAE2（K）。

定义13 在形式背景K=（U，V，R）中，设

X～，Y～IP（U），A～IP（V）。

若A～=（g（A～），

（A～））=（X～，Y～）或

（X～，Y～）=f（X～）

∩f（Y～）=

A～，则称（（X～，Y～），

A～）为AE-区间集半概念。形式背景K=（U，V，R）中AE-区间集半概念全体记作ISSAE（K）。

AE-区间集半概念与AE-区间集概念及AE-半概念的关系如下：① 由定义6和定义13可知，AE-区间集概念一定是AE-区间集半概念。② 由定义3和定义13可知，AE-半概念是AE-区间集半概念的一种特殊情况。

下面用一个实例解释AE1-区间集半概念。

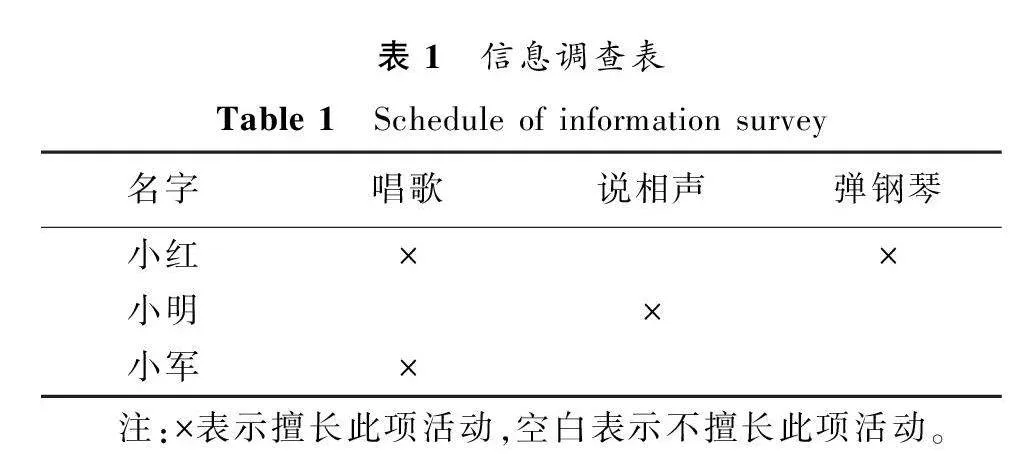
例1 对高中某班三名同学小红、小明、小军进行调查，询问他们是否擅长唱歌、说相声、弹钢琴，调查结果如表1所示。

令1=小红，2=小明，3=小军，a=唱歌，b=说相声，c=弹钢琴。则表1表示的形式背景K1=（U1，V1，R1）如表2所示，其中U1=｛1，2，3｝，V1=｛a，b，c｝。

现在需要挑选一名同学去参加学校举办的歌唱比赛，可首先考虑擅长唱歌的同学，若既擅长唱歌又擅长弹钢琴的同学则更满足挑选的要求。那么可以确定这次班级选拔的属性区间集为A～=［Al，Au］=［a，ac］。根据定义11可得

g（A～）=［1，13］，表示1号同学和3号同学都擅长唱歌，1号同学既擅长唱歌也擅长弹钢琴，更符合歌唱比赛的要求。那么班级可推荐1号同学参加学校举办的歌唱比赛，3号同学可作为班级的替补选手。g（A～）=［2，2］，表示2号同学既不擅长唱歌也不擅长弹钢琴，那么这次活动暂时不推荐2号同学参加。根据定义11可知 （（［1，13］，［2，2］），［a，ac］）为AE1-区间集半概念。

下面给出AE-区间集半概念的纯双布尔代数结构。

在形式背景K=（U，V，R）中，（（X～，Y～），

A～），（（X～1，Y～1），

A～1），（（X～2，

Y～2），A～2）∈ISSAE（K）。定义以下6种运算：

（1） （（X～1，Y～1），

A～1）↓（（X～2，

Y～2），A～2）

=（（X～1，Y～1）∩

（X～2，Y～2），

（（X～1，Y～1）

∩（X～2，Y～2）））;

（2） （（X～1，Y～1），

A～1）↑

（（X～2，Y～2），

A～2）

=（（X～1，Y～1）∪

（X～2，Y～2），

（（X～1，Y～1）∪

（X～2，Y～2）））;

（3）

（（X～，Y～），

A～）=（（X～，

Y～）c，（（X～，

Y～）c））;

（4） （（X～，

Y～），A～）=

（（A～c），A～c）;

（5） =（（［，］，［，］），［V，V］）;

（6） =（（［U，U］，［U，U］），［，］）。

由算子∨和∧的定义可知，

（（X～1，Y～1），

A～1）∨（（X～2，

Y～2），A～2）

=（（A～1∪A～2），

（A～1∪A～2））;

（（X～1，Y～1），

A～1）∧（（X～2，

Y～2），A～2）

=（（A～1∩

A～2），（A～1∩

A～2））。

定理1 在形式背景K中，F=（ISSAE（K），

↓，↑，，，）为纯双布尔代数结构。

证明 需要证明AE-区间集半概念集合在上述定义的6种运算下，满足定义7的所有性质。由于定义7中（ia）和（ib）是相互对偶的（i=1，2，…，11），并且大部分性质的证明过程较简单，在此仅展示定义7中性质（5a）和 （12）的证明过程。

假设

x=（（X～1，Y～1），

A～1），y=（（X～2，

Y～2），A～2）。

（5a）的证明： x∧（x↑y）=（（X～1，Y～1），

A～1）∧

（（A～1∪A～2），

A～1∪A～2）=

（A～1，A～1）=x∧x。

（12）的证明： （x∧x）↑（x∧x）=（A～1，A～1）↑

（A～1，A～1）=

（（A～1，A～1），（x↑x）∧（x↑x））

=（（X～1，Y～1），

（X～1，Y～1））。

当A～1=（X～1，Y～1）时，有

A～1=

（X～1，Y～1）和

（X～1，Y～1）=

A～1成立，故可得

（A～1，

A～1）=（（X～1，

Y～1），

（X～1，Y～1））。

即（x∧x）↑（x∧x）=（x↑x）∧（x↑x）得证。

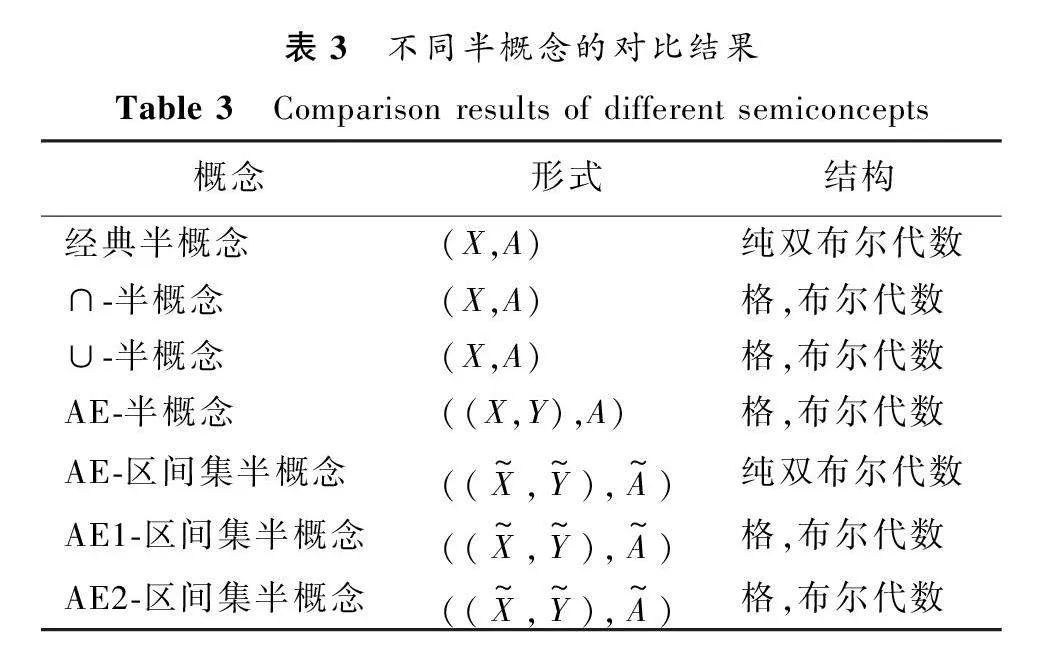
对不同半概念进行了对比，结果见表3。

AE-半概念既考虑了属性拥有的对象，同时也考虑了属性不拥有的对象，而经典半概念只考虑了属性拥有的对象。AE-区间集半概念既考虑属性区间集拥有的对象，同时也考虑了属性区间集不拥有的对象，AE-区间集半概念考虑得更为全面。因此，AE-区间集半概念是经典概念与AE-半概念的拓广。

3 AE-区间集半概念的近似算子

在处理不确定信息时，常常需要借助近似算子来描述这个不确定信息。下面将给出AE-区间集半概念相应的上、下近似算子。

3.1 基于AE1-区间集半概念的近似算子

利用定义11，结合格结构，给出一对上、下近似算子。

定义14［2］

在形式背景K=（U，V，R）中，设（（X～，Y～），

A～）∈ISSAE1（K）， ISSAE1（K）表示AE1-区间集半概念全体，AE1-区间集半概念的一对算子定义为

apr（（X～，Y～），

A～）=∧{（（X～j，

Y～j），A～j）∈

ISSAE1（K）（（X～，

Y～），A～）≤（（X～j，

Y～j），A～j）};

apr（（X～，Y～），

A～）=∨{（（X～i，

Y～i），A～i）∈

ISSAE1（K）（（X～i，Y～i），

A～i）≤（（X～，

Y～），A～）}。

定理2 在形式背景K=（U，V，R）中，由定义14得到AE1-区间集半概念的一对算子具有以下性质：

（1） apr（（X～，Y～），

A～）≤（（X～，

Y～），A～）≤

apr（（X～，Y～），

A～）;

（2） apr（（X～，Y～），

A～）=（（X～，

Y～），A～）=

apr（（X～，Y～），

A～）（（X～，

Y～），A～）∈ISSAE1（K）。

证明

（1） 对任意的A～i，由定义14和二元关系≤得

∪A～iA～，由引理1得

（∪A～i）A～，由定义11得

A～=（X～，Y～）。故得

apr（（X～，Y～），

A～）=

（（∪A～i），∪A～i）≤（（

X～，

Y～），A～）。类似可得

（（X～，Y），A～）≤apr

（（X～，Y～），A～）。

（2） 分成（）和（）两部分来证明。

（）： 对任意的A～i，由定义14 得

（（∪A～i），∪A～i）=

（（X～，Y～），

A～），由定义11得

（∪A～i）=A～=

（X～，Y～），即（（X～，Y），

A～）∈ISSAE1（K）。

（）： 由（（X～，Y），A～）∈ISSAE1（K）得，存在

m使得（（X～m，Y～m），

A～m）=（（X～，Y～），

A～），

由定义14得apr（（X～，

Y～），A～）=

（A～m，

A～m）=

（（X～m，Y～m），

A～m）=（（X～，

Y～），A～）。同理得

apr（（X～，Y～），

A～）=（（X～，Y～），

A～）。

由定义9和定理2可知，定义14给出的一对算子为AE1-区间集半概念的近似算子。

例2（例1续）

若（（X～，Y～），

A～）=（（［1，1］，［2，2］），［a，ac］），

由定义11可知（（［1，1］，［2，2］），［a，ac］）不是AE1-区间集半概念，无明显意义。由定义14求得apr（（［1，1］，［2，2］），［a，ac］）=（（［1，13］，［2，2］），［a，ac］）和apr（（［1，1］，［2，2］），［a，ac］）=（（［1，13］，

［2，2］），［a，ac］）来近似（（［1，1］，［2，2］），［a，ac］），从而获得相关知识，即小红和小军都擅长唱歌，小红既擅长唱歌也擅长弹钢琴，小明既不擅长唱歌也不擅长弹钢琴。

3.2 基于AE2-区间集半概念的近似算子

利用定义12，结合双布尔代数结构，给出一对上、下近似算子。

定义15［2］

在形式背景K=（U，V，R）中，设

（（X～，

Y～），

A～）∈ISSAE2（K），ISSAE2（K）表示AE2-区间集半概念全体，AE2-区间集半概念的一对算子定义为

apr（（X～，Y～），

A～）=↓{（（X～j，

Y～j），A～j）∈

ISSAE2（K）（（X～，

Y～），A～）≤

（（X～j，Y～j），

A～j）};

apr（（X～，Y～），

A～）=↑{（（X～i，

Y～i），A～i）∈

ISSAE2（K）

（（X～i，

Y～i），A～i）≤

（（X～，Y～），

A～）}。

定理3 在形式背景K=（U，V，R）中，设

（（X～，Y），A～）

∈ISSAE2（K），由定义15得到AE2-区间集半概念的一对算子具有以下性质：

（1） apr（（X～，Y～），

A～）≤（（X～，

Y～），A～）≤

apr（（X～，Y～），

A～）;

（2） apr（（X～，Y～），

A～）=（（X～，

Y～），A～）=

apr（（X～，

Y～），A～）

（（X～，Y～），

A～）∈ISSAE2（K）。

定理3的证明过程可参照定理2，本文不再赘述。

4 OE-区间集半概念的相关性质

OE-区间集半概念与AE-区间集半概念为对偶关系，因此下文只对OE-区间集半概念的性质进行简要说明。其证明过程与AE-区间集半概念类似，故省略部分证明过程。首先给出OE-区间集半概念的定义。

定义16

在形式背景K=（U，V，R）中，设X～IP（U），A～，

B～IP（V）。

若X～=（f（X～），

f（X～））=（A～，

B～），则称

（（X～，（A～，

B～））

为OE1-区间集半概念。形式背景K=（U，V，R）中OE1-区间集半概念全体记作ISSOE1（K）。

定义17

在形式背景K=（U，V，R）中，设X～IP（U），A～，

B～IP（V）。

若（A～，B～）=g

（A～）

∩g（B～）=X～，则称

（（X～，（A～，

B～））

为OE2-区间集半概念。形式背景K=（U，V，R）中OE2-区间集半概念全体记作ISSOE2（K）。

定义18

在形式背景K=（U，V，R）中，设

X～IP（U），A～，B～IP（V）。若

X～=（f（X～），

f（X～））=（A～，

B～）或

（A～，B～）=g

（A～）∩g（B～）=

X～，

则称（（X～，

（A～，B～））

为OE-区间集半概念。形式背景K=（U，V，R）中OE-区间集半概念全体记作ISSOE（K）。显然ISSOE（K）=

ISSOE1（K）∪ISSOE2（K）。

接下来给出OE-区间集半概念的纯双布尔代数结构。

在形式背景K=（U，V，R）中，（X～，（A～，

B～）），

（X～1，（A～1，

B～1）），（X～2，

（A～2，B～2））

∈ISSOE（K）。

定义以下6种运算：

（1） （X～1，（A～1，

B～1））↓（X～2，

（A～2，B～2））

=（X～1∩X～2，

（X～1∩X～2）

）;

（2） （X～1，（A～1，

B～1））↑（X～2，

（A～2，B～2））

=（（（A～1，B～1）∩

（A～2，B～2）），

（A～1，B～1）∩

（A～2，B～2））;

（3） （X～，（A～，

B～））=（X～c，

（X～c））;

（4） （（A～，B～），

X～）=（（（A～，

B～）c），（A～，

B～）c）;

（5） =（［，］，（［V，V］，［V，V］））;

（6） =（［U，U］，（［，］，［，］））。

定理4 在形式背景K中，（ISSOE（K），↓，↑，，，，）为纯双布尔代数结构。

下面给出OE1-区间集半概念的近似算子。

定义19 在形式背景K=（U，V，R）中，设

（X～，（A～，

B～））∈ISSOE1（K）， OE1-区间集半概念的一对算子定义为

apr（X～，（A～，

B～））=∧{（X～j，

（A～j，B～j））∈

ISSOE1（K）（X～，（A～，

B～））≤（X～j，

（A～j，B～j））};

apr（X～，（A～，

B～））=∨{（X～i，

（A～i，B～i））∈

ISSOE1（K）（X～i，（

A～i，B～i））≤

（X～，（A～，

B～））}。

定理5 在形式背景K=（U，V，R）中，设

（X～，（A～，

B～））∈ISSOE1（K），由定义19得到OE1-区间集半概念的一对算子具有以下性质：

（1） apr（X～，（A～，

B～））≤（X～，

（A～，B～））≤

apr（X～，（A～，

B～））;

（2） apr（X～，（A～，

B～））=（X～，

（A～，B～））=

apr（X～，（A～，

B～））（X～，

（A～，B～））

∈ISS0E1（K）。

由定义9和定理5可知，定义19给出的算子为OE1-区间集半概念的一对近似算子。

定义20 在形式背景K=（U，V，R）中，设

（X～，（A～，

B～））∈ISSOE2（K），

OE2-区间集半概念的一对算子定义为apr（X～，

（A～，

B～））=↓{（X～j，

（A～j，B～j））∈

ISSOE2（K）

（X～，

（A～，

B～））≤（X～j，

（A～j，B～j））};

apr（X～，（A～，

B～））=↑{（X～i，

（A～i，

B～i））∈

ISSOE2（K）

（X～i，

（A～i，

B～i））≤

（X～，（A～，

B～））}。

定理6 在形式背景K=（U，V，R）中，设

（X～，（A～，

B～））∈ISSOE2（K），由定义20得到OE2-区间集半概念的一对算子具有以下性质：

（1） apr（X～，（A～，

B～））≤（X～，

（A～，B～））≤

apr（X～，

（A～，B～））;

（2） apr（X～，

（A～，

B～））=（X～，

（A～，B～））=

apr（X～，（A～，

B～））（X～，

（A～，B～））

∈ISSOE2（K）。

由定义9和定理6可知，定义20给出的算子为OE2-区间集半概念的一对近似算子。

5 结语

本文将区间集概念与三支决策和经典半概念相结合，提出两种三支区间集半概念，即AE-区间集半概念和OE-区间集半概念，证明了这两种三支区间集半概念具有纯双布尔代数结构。另外，将AE1-区间集半概念和AE2-区间集半概念并称为AE-区间集半概念，将OE1-区间集半概念和OE2-区间集半概念并称为OE-区间集半概念。依据粗糙集理论，得到了AE-区间集半概念的两对近似算子。对偶地，可得到OE-区间集半概念的两对近似算子，为挖掘潜在知识提供了平台。未来的研究工作主要包括在不完备背景下三支区间集半概念格的构造问题以及三支区间集半概念的属性约简问题，如何将三支区间集半概念更加广泛地应用于知识提取、粒计算等领域也是值得关注的问题。

参考文献：

［1］ WILLE R. Restructuring lattice theory： an approach based on hierarchies of concepts［M］∥Ordered Sets. Dordrecht： Springer Press， 1982： 445-470.

［2］ 赵晓倩， 武优西， 王月华， 等. 一种保序序列快速挖掘算法：RSMM［J］. 郑州大学学报（理学版）， 2022， 54（4）： 64-70.

ZHAO X Q， WU Y X， WANG Y H， et al. RSMM： a fast order-preserving sequential pattern mining［J］. Journal of Zhengzhou university （natural science edition）， 2022， 54（4）： 64-70.

［3］ LI J H， MEI C L， WANG J H， et al. Rule-preserved object compression in formal decision contexts using concept lattices［J］. Knowledge-based systems， 2014， 71： 435-445.

［4］ 毛华， 郑博雅， 胥德华， 等. 中智模糊半概念知识提取研究［J］. 郑州大学学报（理学版）， 2023， 55（6）： 84-90.

MAO H， ZHENG B Y， XU D H， et al. Research on knowledge extraction of neutrosophic fuzzy semiconcept［J］. Journal of Zhengzhou university （natural science edition）， 2023， 55（6）： 84-90.

［5］ VORMBROCK B， WILLE R. Semiconcept and protoconcept algebras： the basic theorems［M］∥Formal Concept Analysis. Berlin： Springer Press， 2005： 34-48.

［6］ YAO Y Y. Interval-set algebra for qualitative knowledge representation［C］∥Proceedings of the 5th International Conference on Computing and Information. Piscataway：IEEE Press， 2002： 370-374.

［7］ YAO Y Y. Three-way decision： an interpretation of rules in rough set theory［C］∥International Conference on Rough Sets and Knowledge Technology. Berlin： Springer Press， 2009： 642-649.

［8］ 康凯， 胡军. 基于三支聚类的协同过滤推荐方法［J］. 郑州大学学报（理学版）， 2022， 54（3）： 22-27.

KANG K， HU J. Collaborative filtering recommendation method based on three-way clustering［J］. Journal of Zhengzhou university （natural science edition）， 2022， 54（3）： 22-27.

［9］ 刘晶， 高立超， 孙跃华， 等. 基于知识和数据融合驱动的设备故障诊断方法［J］. 郑州大学学报（理学版）， 2022， 54（2）： 39-46.

LIU J， GAO L C， SUN Y H， et al. Fault diagnosis method for equipment driven by knowledge and data fusion［J］. Journal of Zhengzhou university （natural science edition）， 2022， 54（2）： 39-46.

［8］SHI C J， YAO Y Y. Trilevel multi-criteria decision analysis based on three-way decision［C］∥International Conference on Intelligence Science. Cham： Springer International Publishing， 2021： 115-124.

［9］PAWLAK Z. Rough sets［J］. International journal of computer & information sciences， 1982， 11： 341-356.

［10］YAO Y Y， YAO B X. Covering based rough set approximations［J］. Information sciences， 2012， 200： 91-107.

［11］QI J J， QIAN T， WEI L. The connec0c0cc24d936415da3728d98ac1a61afd7ac2f426ce8702d8846f746f12206acftions between three-way and classical concept lattices［J］. Knowledge-based systems， 2016， 91： 143-151.

［12］MAO H， LIU X Q， WANG G. Two forms of three-way semiconcepts［J］. Journal of intelligent & fuzzy systems， 2021， 40（6）： 10853-10864.

［13］YAO Y Y. Interval sets and three-way concept analysis in incomplete contexts［J］. International journal of machine learning and cybernetics， 2017， 8（1）： 3-20.

［14］MAO H. Approximation operators for semiconcepts［J］. Journal of intelligent & fuzzy systems， 2019， 36（4）： 3333-3343.

［15］刘营营， 米据生， 梁美社， 等. 三支区间集概念格［J］. 山东大学学报（理学版）， 2020， 55（3）： 70-80.

LIU Y Y， MI J S， LIANG M S， et al. Three-way interval-set concept lattice［J］. Journal of Shandong university （natural science）， 2020， 55（3）： 70-80.

［16］WILLE R. Boolean concept logic［M］∥Lecture Notes in Computer Science. Berlin： Springer Press， 2000： 317-331.