基于神经网络架构搜索与特征融合的小样本脉搏波分类方法

摘要： 基于深度学习的脉搏波分类依赖大量有标注数据，现有脉搏波带有疾病标注的数据少、标注方法不统一，导致模型准确率低、泛化能力弱。针对此问题，提出一种基于神经网络架构搜索与特征融合的小样本脉搏波分类方法。首先，在并行的双维度拆分卷积分支与因果空洞卷积分支中进行态射搜索，每次搜索结束，获取超网络分支的子网络作为候选网络进行训练评估。双维度拆分卷积分支提取脉搏波横、纵向维度时空特征，因果空洞卷积分支提取脉搏波节律特征。然后，利用特征融合方法整合分支多尺度特征。最后，依据评估指标得到最佳网络模型完成分类。实验结果表明，所提方法在两个小样本脉搏波数据集上准确率为97.04%和95.96%，F1值为97.04%和95.95%，具有较好分类效果。

关键词： 脉搏波； 小样本； 神经网络架构搜索； 特征融合； 卷积神经网络

中图分类号： TP183

文献标志码： A

文章编号： 1671-6841（2024）06-0054-08

DOI： 10.13705/j.issn.1671-6841.2023025

Small-sample Pulse Wave Classification Based on Neural Architecture

Search and Feature Fusion

XING Yuyang1，2， CHEN Feng3， MAO Xiaobo1，2， SUN Zhixia4， LU Peng1，2，5， QIAO Yunfeng1，2， DOU Yamei1，2

（1.School of Electrical and Information Engineering， Zhengzhou University， Zhengzhou 450001， China;

2.Research Center for Intelligent Science and Engineering Technology of TCM， Zhengzhou 450001， China;

3.Zhengzhou Seventh People′s Hospital， Zhengzhou 450016， China; 4.The Fifth Affiliated Hospital

of Zhengzhou University， Zhengzhou 450052， China; 5.Henan Collaborative Innovation Center for Internet

Based Medical and Health Services， Zhengzhou 450052， China）

Abstract： Classification of pulse wave based on deep learning relied on a large amount of labeled data. However， the existing pulse wave data with disease labels were small and the labeling methods were not uniform， which led to the problems of low accuracy and weak generalization ability of the model. To address this problem， a small-sample pulse wave classification method based on neural architecture search and feature fusion was proposed. Firstly， the morphism search was performed in the parallel super-network branches， the bi-dimensional split convolutional branch and the causal dilated convolutional branch. At the end of each search， the subnetworks in the super-network branches were obtained as candidate networks for training and evaluation. The spatio-temporal features in the horizontal and vertical dimensions of the pulse wave were extracted by the bi-dimensional split convolution branch， and the rhythmic features of the pulse wave were extracted by the causal dilated convolution branch. Then， the branching multiscale features were integrated using the feature fusion method. Finally， the best network model was obtained based on the evaluation index to complete the classification. The experimental results showed that the accuracy of the proposed method on two small sample pulse wave datasets was 97.04% and 95.96%， and the F1 was 97.04% and 95.95%， respectively， which could realize well classification results.

Key words： pulse wave; small sample; neural architecture search; feature fusion; convolutional neural network

0 引言

脉搏波是高度非平稳、非线性、周期性的弱生理信号，蕴含着极其丰富的心血管生理病理信息［1］。

基于脉搏波解决心血管疾病的分类方法主要包括基于先验知识的方法与基于深度学习的方法。

基于先验知识的脉搏波分类方法通常提取脉搏波的时频域特征，利用支持向量机（support vector machine，SVM）［2］、随机森林（random forest，RF）［3］等算法进行分类识别。该类方法特征提取的准确性易受噪声影响，且手工设计特征不足以精准地表达原始脉搏波数据［4］。

基于深度学习的脉搏波分类方法屏蔽了主观特征设计，通过不断训练调整网络连接权重等参数，自动拟合输入与输出之间映射关系。文献［5］采用一维卷积神经网络（one dimensions convolution neural network，1D-CNN）将脉搏波映射到高维空间，提取脉搏波静态特征。文献［6］首先将一维脉搏波信号重组变换为二维数据形式，然后利用二维卷积神经网络（two dimensions convolution neural network，2D-CNN）提取脉搏波空间特征。文献［7-8］将脉搏波视为离散时间序列，采用递归神经网络（recurrent neural network，RNN）与长短时记忆网络（long short-term memory，LSTM）挖掘脉搏波中的时序与节律特征。提取单一特征的方式未能充分利用脉搏波蕴含的多尺度特征，文献［9-10］将CNN与LSTM结合构建多分支网络提取脉搏波多尺度特征。

然而，一方面基于深度学习的脉搏波分类依赖大量有标注数据，现有脉搏波数据集带有疾病标注的数据少、标注方法不统一，影响深度学习模型分类性能。另一方面，仅通过训练调整网络参数提高模型非线性拟合能力，网络结构始终固定不变，而模型知识不仅存在于网络参数中，而且蕴含在网络结构内［11］。

与仅调整网络参数不同，神经网络架构搜索（neural architecture search，NAS）综合考虑调整网络参数与网络结构两方面，在搜索与训练过程优化网络参数与隐层结构，针对特定任务构建高质量网络模型，是提高小样本数据条件下神经网络模型分类性能的新途径。

Wang等［12］采用NAS方法优化网络模型，在小样本数据条件下改善分类效果，并指出模型训练由网络参数与网络结构共同决定，优化网络结构可以降低网络参数拟合的需求，进而减少模型训练所需要的样本数量。

针对脉搏波有标注数据少、标注方法不统一的问题，本文设计一种基于NAS与特征融合的小样本脉搏波分类方法。本文的主要工作总结如下。

1） 设计了一种基于超网络态射的神经网络架构搜索算法，扩展人工设计的网络成为超网络，然后采用网络态射方式进行结构搜索，获取超网络的子网络作为候选网络进行训练评估，最终依据评估指标得到最佳模型结构用于分类。

2） 采用了一个双维度拆分卷积特征提取结构，考虑脉搏波数据属于时序性数据，二维数据形式下横向和纵向维度信息含义不同，将二维卷积核进行分解，在横向和纵向维度提取脉搏波时间与空间特征。

3） 构建了一个双分支特征融合脉搏波分类网络，双维度拆分卷积分支提取脉搏波横向和纵向维度的时空特征；因果空洞卷积分支提取脉搏波随时间变化的节律特征。采用特征融合方法整合网络分支中的多尺度特征完成分类。

4） 在光电容积脉搏波和压力脉搏波数据集上进行分类实验，准确率达到97.04%和95.96%，F1值达到97.04%和95.95%，取得较好的分类效果。

1 方法

1.1 问题描述

NAS核心是一个参数和结构联合损失优化问题。对于一个脉搏波数据集D=｛（xk，yk）｝nk=1，xk为样本序列，yk为对应类别标签。训练集Dtrain、验证集Dval、测试集Dtest是D=｛（xk，yk）｝nk=1的划分，

Dtrain=｛（xk，yk）｝tk=1，

Dval=｛（xk，yk）｝vk=t+1，

Dtest=｛（xk，yk）｝nk=v+1。

学习问题是寻找一系列参数θ满足

y≈f（x;θ）， （x，y）∈Dval，

θ*=argminθ∑（x，y）∈DtrainL（f（x，θ），y），

式中：L为损失函数，计算预测结果与真实标签之间的损失；f表示当前神经网络结构；θ*为f学习的目标参数。

脉搏波分类任务使用交叉熵作为损失函数，计算方法为

loss=-1N∑Ni=1（-∑Mj=1yijlog（pij）），

式中：N为样本数；M为脉搏波类别数量；yij为脉搏波的标签；pij为每个标签对应的预测结果。

基于交叉熵损失函数由Dtrain中样本拟合一个非线性决策函数，并以最小损失值对参数θ优化，然后在Dval上评估模型性能，在Dtest上测试。同时，在搜索空间F中，找到一个网络结构f*∈F满足

f*=argminθ Cost（f（θ*），Dval），

其中：Cost（）为评价度量函数。

1.2 超网络态射搜索

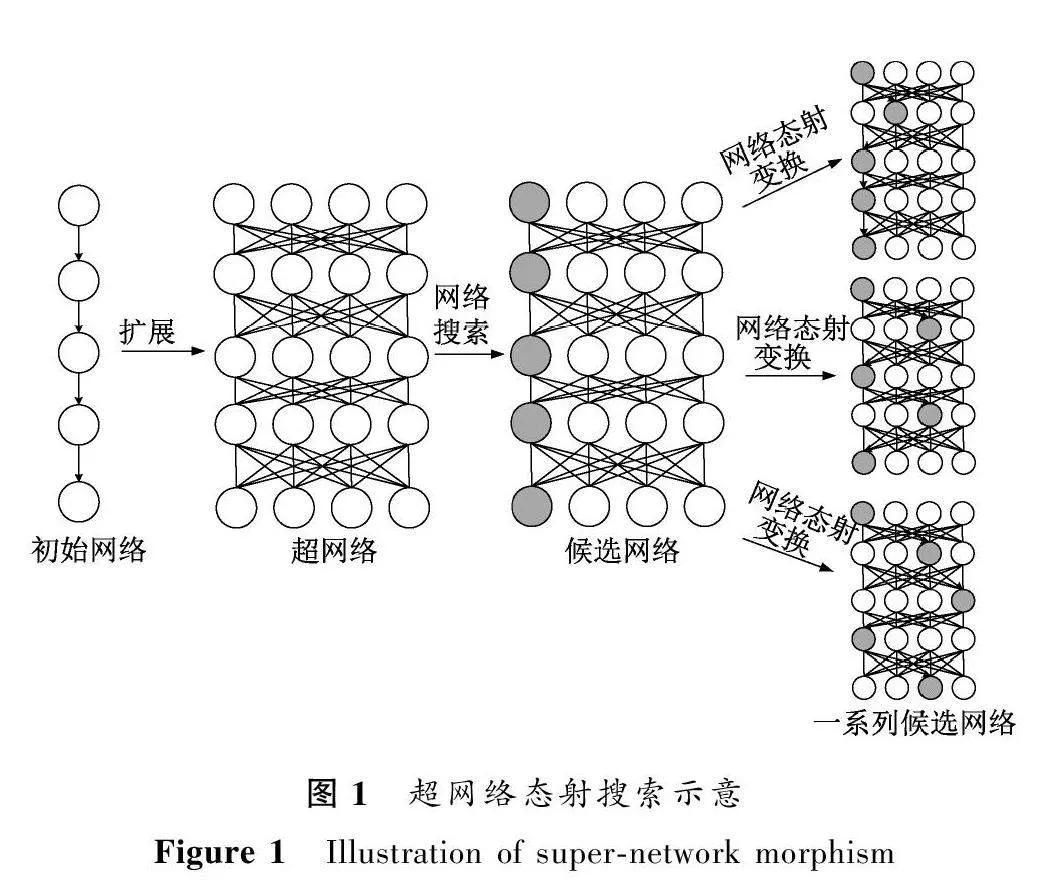
算法1呈现了超网络态射搜索的整个流程，主要由训练阶段3）～6）、搜索阶段8）～25）迭代完成，最终进行择优。以现有人工设计的网络结构作为初始网络，并将其扩展为超网络，然后采用网络态射的方式在预定义的超网络中进行搜索变换。每次搜索结束，获取超网络中子网络作为候选网络进行训练评估，最终依据评估指标得到最佳模型结构，如图1所示。

算法1 超网络态射搜索

输入： Dtrain，Dval，模拟退火温度（T），最低温度（Tlow），温度下降率（Rtd），搜索次数（g），最大搜索次数（G），结构变换函数（M），超网络空间（O）。

输出： 搜索所得最佳网络模型（f*）。

1） 初始化：T=1，g=1，i=1，初始网络f（1）

2） While g≤G do

3） 使用Dtrain训练当前候选网络f（i）

4） 使用Dval 评估f（i）获取评估指标值c（i）

5） 将f（i）与c（i）存入H=｛（f（i），θ（i），c（i））｝与拟搜索网络集合MQ中

6） 根据c（i）对H=｛（f（i），θ（i），c（i））｝排序，得到有序优先序列PQ，根据lowest（c（i））更新cmin

7） While MQ≠ and T>Tlow do

8） 从MQ中弹出一个候选网络f（i）

9） T=T*Rtd

10） 对f（i）进行结构变换得到一系列子代网络｛fj｝：｛fj｝←M（f（i），O）

11） While ｛fj｝≠ do

12） 从｛fj｝中取出一个子代网络fj

13） 计算α（f）=μ（yf）-βσ（yf）

14） if rand（）<exp（cmin－α（fj）T） then

15） 将fj存入MQ

16） else

17） 舍弃fj

18） end if

19） if α（fj）<cmin then

20） cmin=α（fj）， fmin=fj

21） end if

22） end while

23） end while

24） f（i+1）=fmin，g=g+1

25） end while

26） 依据cmin，从PQ中选取出f*

算法1中的9）表示不断更新模拟退火温度T的值，13）表示计算子代网络fj对应的采集函数α（fj）［13］，14）～17）表示利用模拟退火算法与接收函数exp（cmin－α（fj）T） ［13］决定是否将fj存入MQ中，19）～25）表示基于α（fj）对fj评估，若α（fj）值小于cmin，则fj作为下一个候选网络，并对其进行新一轮训练评估，26）表示当达到预设最大搜索次数或对超网络中所有候选网络完成训练评估后，选取cmin对应的最佳网络模型f*。

1.3 双分支特征融合分类网络

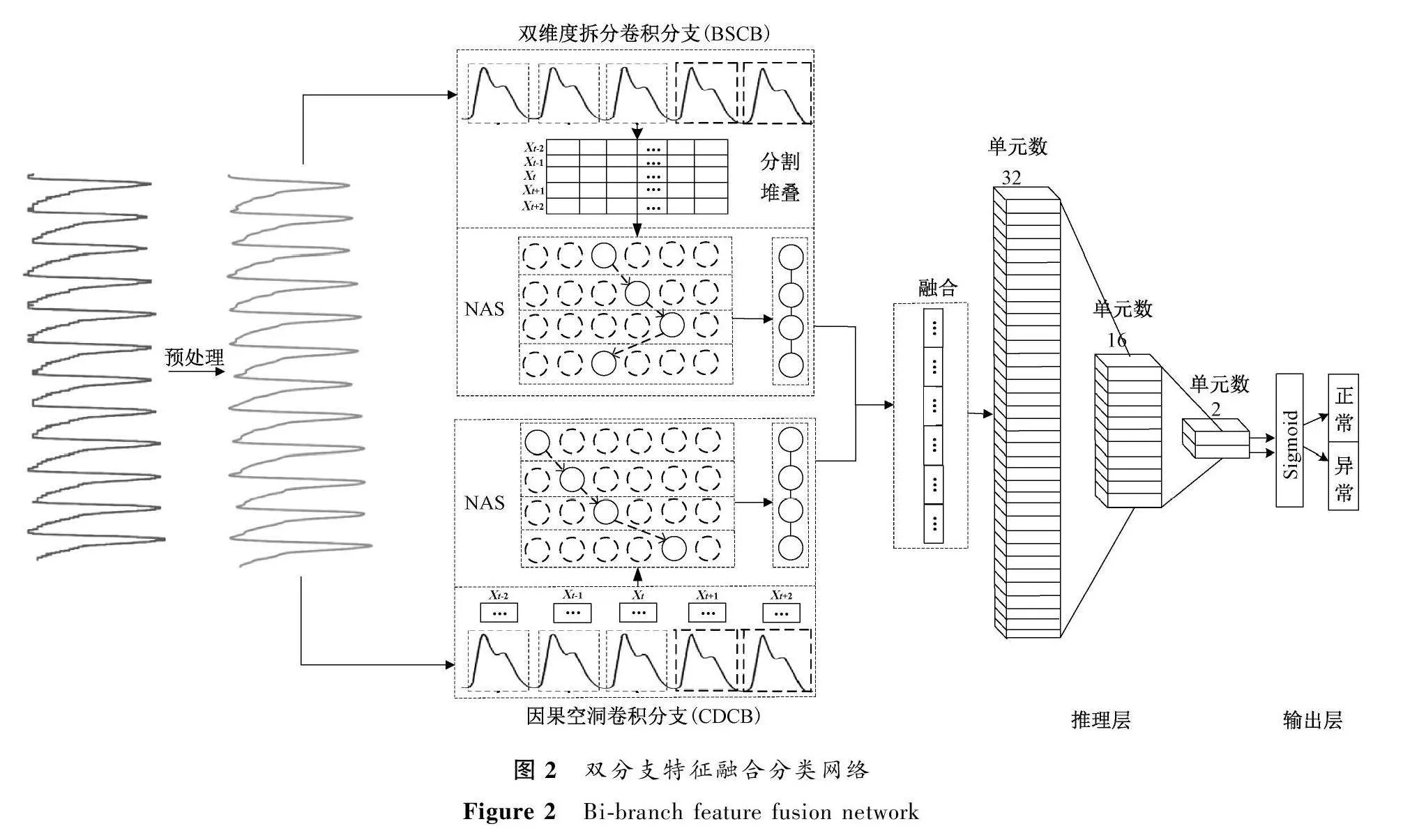
双分支特征融合分类网络整体架构如图2所示，由双维度拆分卷积分支（bi-dimensional split convolutional branch，BSCB）、因果空洞卷积分支（causal dilated convolutional branch，CDCB）以及融合推理层组成。

1.3.1 双维度拆分卷积分支 将基于optimal CNN［6］BSCB作为初始网络。脉搏波数据属于时序性数据，经分割堆叠转换为二维数据，水平和垂直方向信息含义不同，包括空间相对位置变化信息与时序变化信息。

脉搏波数据经过分割堆叠转换二维数据形式，作为BSCB的输入，将对称卷积核进行拆分，使用分解卷积核（1*k和k*1）取代optimal CNN中的对称卷积核（k*k），在横向和纵向维度提取脉搏波的时间与空间特征。

分解卷积层定义为

Yk=f（Yk－1×Wk+bk），

其中：Yk为第k层输出特征向量；f为激活函数；Wk、bk为权重参数与偏差。

池化层用于降低数据维度，定义为

Yi=g（Yi－1），

其中：g为池化函数；Yi为第i层输出特征向量。

1.3.2 因果空洞卷积分支

将基于TEMPO-net［14］前两组单元CDCB作为初始网络。TEMPO-net由因果空洞卷积、一维卷积、平均池化及全连接层构成，用于处理时序生理信号。

因果卷积在时间维度以并行方式处理时序数据，空洞卷积在卷积时进行间隔采样。CDCB将一维脉搏波数据作为输入，采用因果空洞卷积提取随时间变化的节律特征，如图3所示。

因果空洞卷积层定义为

ymt=∑K－1i=0∑Cin－1l=0xlt－di·Wl，mi，

其中：x、y表示输入与输出特征向量；t、m表示输出时间步长与输出通道数；W表示滤波器权重，Cin表示输入通道数；d表示空洞因子；K表示滤波器尺寸；t－di表明方向。

1.3.3 特征融合及推理层

不同特征信息从不同方面描述脉搏波数据。采用并行分支网络结构可以减少模型深度，同时提取与融合脉搏波多尺度特征综合分析。

推理层由全连接层构成，整合网络层中具有类别区分性的局部信息，最后通过Sigmoid层得到预测分类结果作为输出。

FYi=f（FYi－1×Wi+bi），

Y=Sigmoid（FYi－1×Wi+bi），

其中：FYi－1、FYi表示第i层全连接层的输入与输出特征向量；f表示激活函数；Wi、bi表示权重参数与偏差；Y表示0～1之间的输出值。

2 实验设置

2.1 数据集

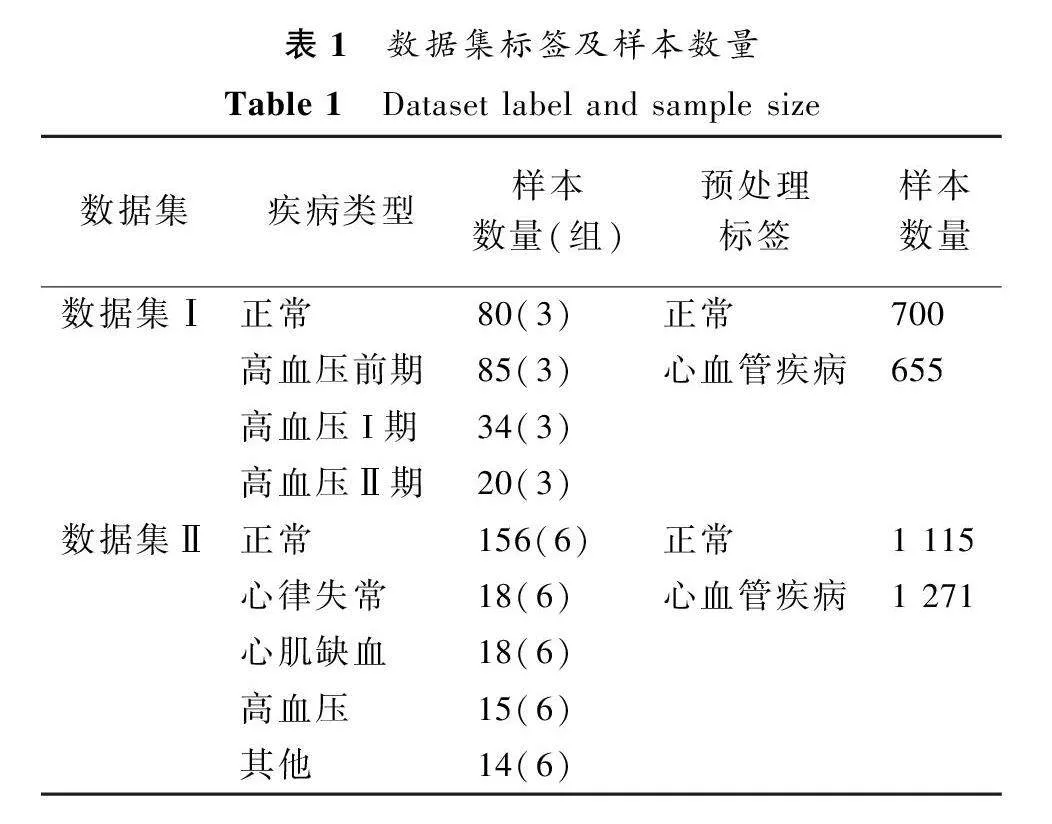
实验所用数据集为光电容积脉搏波数据集和压力脉搏波数据集，数据集的具体信息见表1。

数据集Ⅰ［15］为公开的光电容积脉搏波数据集。收集自桂林人民医院的219名受试者（104名男性和115名女性），提供了正常血压、高血压前期、高血压I期、Ⅱ期四种标签，每种疾病类型均包含三组样本，共包含657条数据，经预处理后分别得到正常与疾病标签样本700条与655条。

数据集Ⅱ为本项目采集的连续无创血压脉搏波数据集，采集地点为郑州大学第五附属医院，每种疾病类型均包含六组样本，一共包含221名年龄在18～83岁之间的受试者6种脉压下的1 326个脉搏波，经预处理后分别得到正常与疾病标签样本1 115条与1 271条。数据集在标准实验条件和规范下收集，实验方案均已获郑州大学第五附属医院药物临床试验伦理委员会批准，并填写知情同意书。采集仪器为ZM-300智能脉搏波采集器，采样频率为200 Hz。

2.2 数据预处理

临床采集的脉搏波信号信噪比低，易受到高频干扰、运动伪影的影响。实验前对临床采集脉搏波进行预处理，得到可训练的脉搏波数据。

脉搏波频率主要分布于低频段。实验采用经验模态分解法［16］自适应提取脉搏波的本征模函数，剔除高频部分，达到去除高频噪声的目的。

实验运用皮尔逊相关系数（Pearson correlation coefficient， PCC）衡量去噪前后信息损失程度，

PCC=∑XY-∑X∑YN（∑X2-（∑X）2N）（∑Y2-（∑Y）2N），

其中：X、Y分别为原始脉搏波及去噪后脉搏波中元素按时间排列组成的集合；N为样本点数。

实验中仅保留滤波后PCC大于0.9的数据，以保证滤波后最大程度保留原始信息。

脉搏波是准周期性波形图，单个周期记录了绝大多数信息。对滤波后的脉搏波进行波峰、波谷检测，取相邻波谷间的波形作为单周期信号进行分割。

脉搏波数据预处理后按照7∶1∶2的比例随机划分为训练集、验证集和测试集。

2.3 搜索空间设置

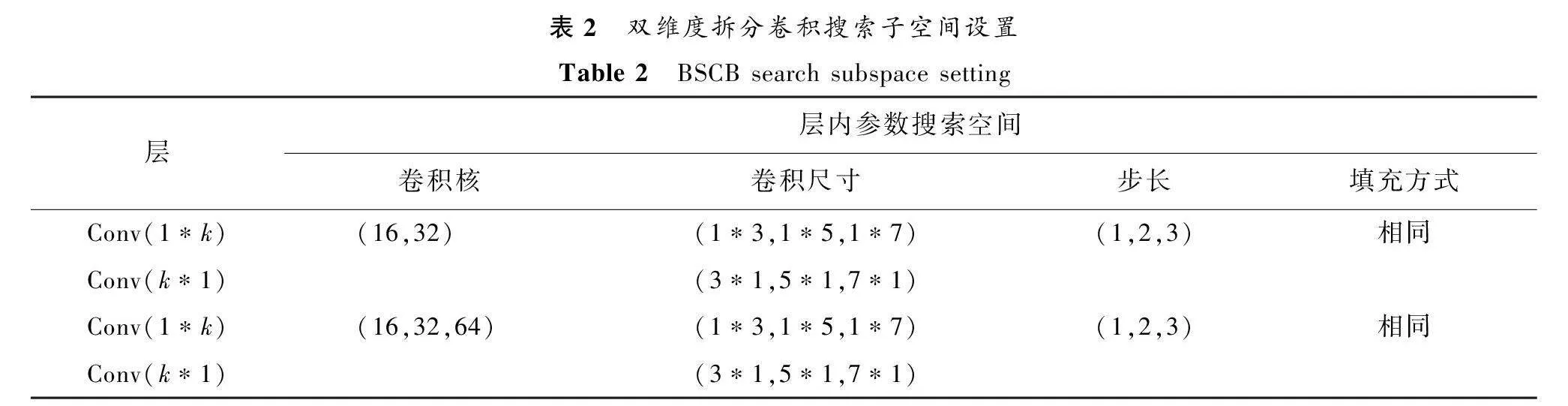
BSCB搜索子空间中卷积操作采用双维度拆分卷积，即采用分解卷积核（1*k与k*1）取代optimal CNN［6］中的对称卷积核（k*k）进行卷积处理，1*k与k*1卷积核的具体搜索空间设置如表2所示。

CDCB搜索子njrrshKucFecMxTTC580zw==空间中卷积操作采用因果空洞卷积，因果空洞卷积的具体搜索空间设置如表3所示。

融合推理层中Dropout取值范围：最小值为0.2，最大值为0.7，步长为0.1。特征融合方式为Concatenate。模型训练时可选择的优化器包括Adam、SGD以及Adam weight decay。学习率的取值包括10-1、10-2、10-3、10-4、10-5。批量值为32，epoch值为100。

2.4 评估指标

准确率（Acc）：整体分类准确率；敏感度（Sen）：异常脉搏波预测结果正确的比例；精确度（Pre）：被分为异常的脉搏波中实际为异常的比例；F1：Sen与Pre的加权调和平均；模型参数量：搜索所得网络模型包含的参数数量。Acc、Sen、Pre与F1的具体计算为

Acc=TP+TNTP+TN+FP+FN，

Sen=TPTP+FN，

Pre=TPTP+FP，

F1=2×Pre×SenPre+Sen，

其中：TP、TN、FP、FN分别表示真阳性、真阴性、假阳性、假阴性。

3 结果与讨论

为验证所提方法的有效性，在两个小样本脉搏波数据集上进行实验。所有实验均在Python（3.8.3）、TensorFlow（2.8.0）、Autokeras（1.0.18）条件下执行。

3.1 不同搜索策略对比

为分析不同搜索策略对脉搏波分类效果的影响，采用贪婪策略（Greedy）、随机策略（Random）、贝叶斯优化策略（Bayesian）与Hyperband策略［17］四种搜索策略进行实验，并选择效果较好的搜索策略应用于后续实验。

实验设置epoch为100，最大搜索次数为100，批量值为32。为避免搜索结果的偶然性，每种搜索策略执行20次实验。

实验结果如图4所示，针对脉搏波数据，采用Hyperband策略进行网络架构搜索，与其他三种搜索策略相比，模型参数量在同一个量级内，分类指标平均值最佳，取得更好的分类效果。此外，由图4可知，采用Hyperband策略执行20次实验所得的指标值波动程度更小，表明采用Hyperband策略搜索结果更稳定。

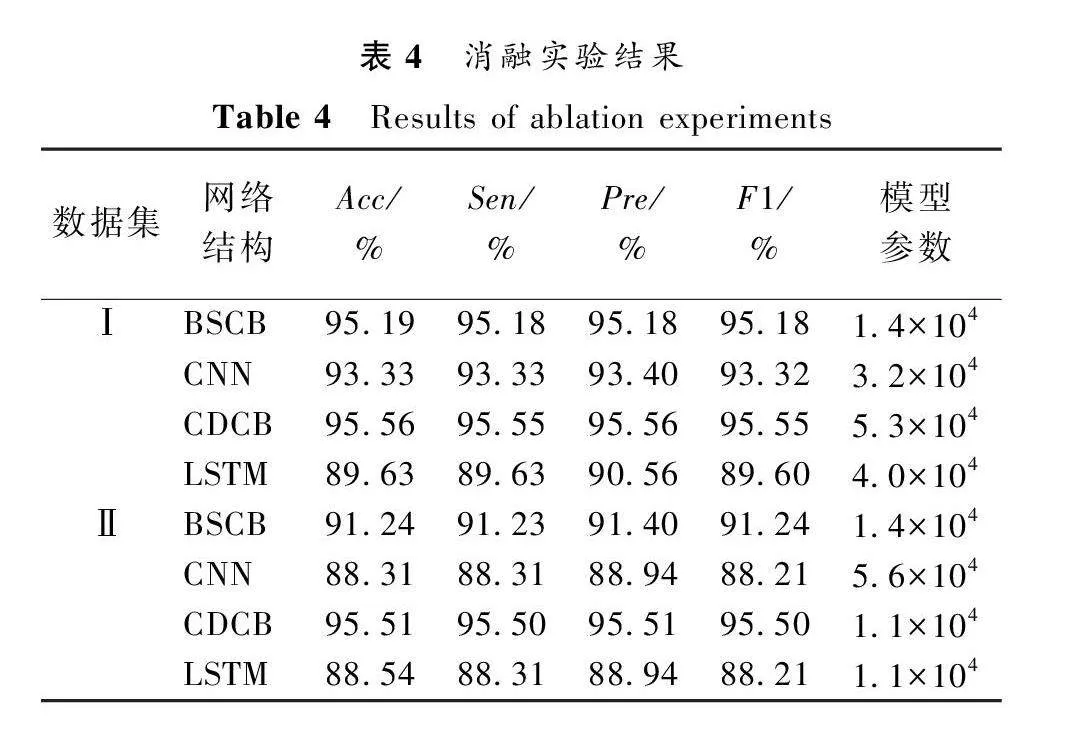
3.2 消融实验

消融实验分析特征融合分支BSCB与CDCB的有效性。实验设置最大搜索次数为100，搜索策略采用Hyperband，实验结果如表4所示。

由实验结果可知，特征融合分支在两个小样本脉搏波数据集上取得较好的分类效果，表明BSCB与CDCB能够有效提取脉搏波特征，有利于提升小样本脉搏波分类效果。此外，与采用均匀卷积的CNN模型相比，BSCB采用拆分卷积，有效降低了模型参数量，适用于小样本数据学习任务；与LSTM模型相比，CDCB分类效果提升明显，能够有效提取脉搏波长时间尺度变化的节律特征。

3.3 不同方法对比

本文方法在数据集Ⅰ上搜索所得最佳模型记为NAS-FF-1，在数据集Ⅱ上搜索所得最佳模型记为NAS-FF-2。NAS-FF-1与NAS-FF-2的区别在于模型内部卷积、池化等操作具有不同的参数值大小。

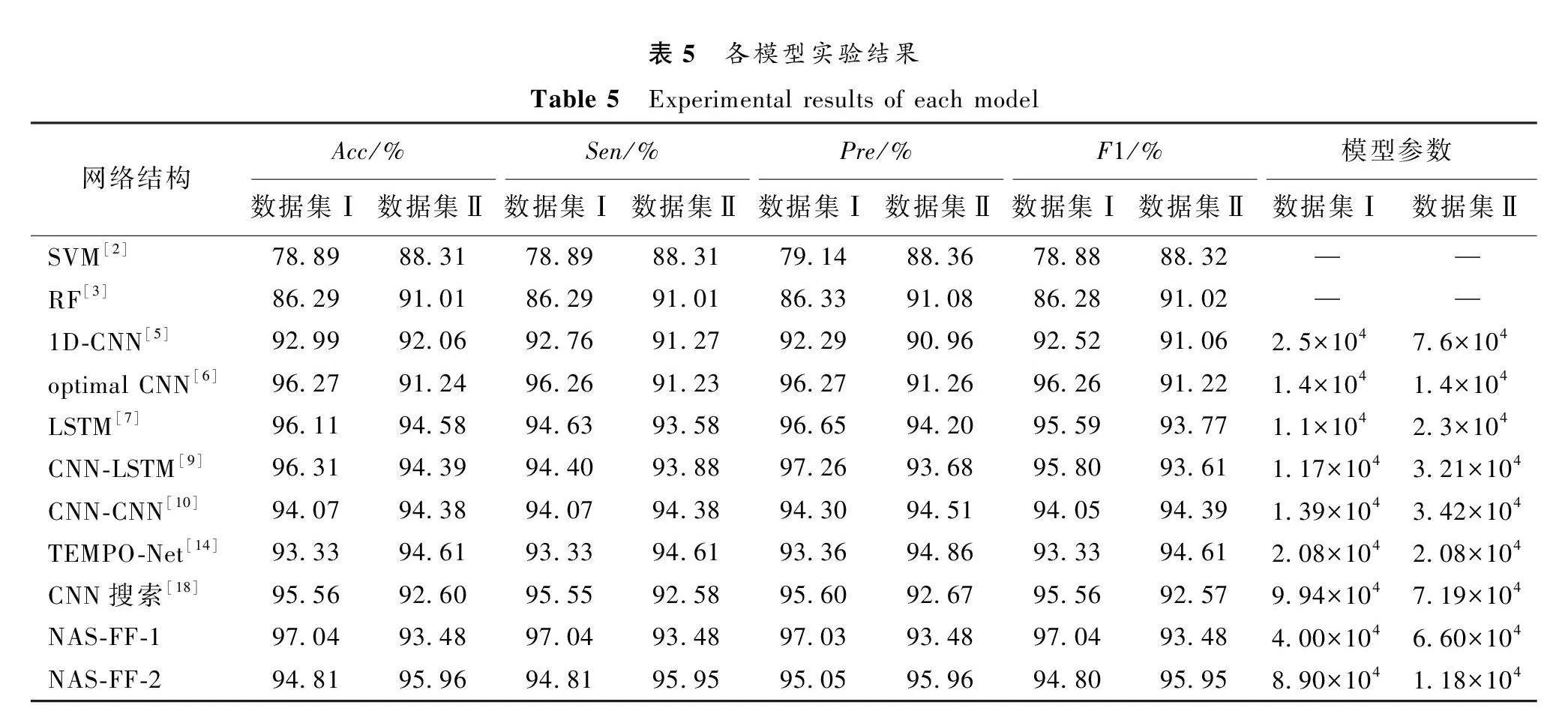
为进一步验证本文方法在两个数据集上搜索所得最佳模型的有效性，与其他脉搏波特征提取方法进行对比实验。对比方法包括：SVM［2］、RF［3］、1D-CNN［5］、optimal CNN［6］、LSTM［7］、CNN-LSTM［9］、CNN-CNN［10］、TEMPO-Net［14］、CNN搜索［18］。实验结果取最后10次结果的平均值，如表5所示。

实验结果表明，本文方法在两个小样本脉搏波数据集上搜索得到的最佳模型取得了较好的分类效果，并且与其他模型相比，模型参数量较小，表明模型能够有效提取脉搏波特征，更好地平衡分类效果与模型参数量，降低了模型过拟合风险，适用于小样本数据学习任务。

NAS-FF-1在两个数据集上Acc相差3.56%，Sen相差3.55%，Pre相差3.56%，F1相差3.56%；NAS-FF-2在两个数据集上Acc相差1.15%，Sen相差1.14%，Pre相差0.91%，F1相差1.15%。实验结果表明，模型在两个小样本脉搏波数据集上的交叉实验取得了较好分类效果，且分类差异较小，模型具有一定的泛化能力。

4 结论

针对脉搏波有标注数据少、标注方法不统一影响模型分类性能的问题，本文设计了一个基于特征融合的NAS方法用于小样本脉搏波分类。首先，扩展两个人工设计的网络结构成为超网络，分别对应两个并行分支：BSCB与CDCB。然后，在预定义的超网络分支中采用NAS方法进行结构变换搜索，获取超网络中子网络作为候选网络进行训练评估，BSCB采用双维度拆分卷积提取二维脉搏波矩阵横向和纵向维度的时间与空间特征，CDCB采用因果空洞卷积提取一维脉搏波向量随时间变化的节律特征，然后采用特征融合方式整合分支特征。最后，依据评估指标获取最佳网络模型完成分类。

在两个小样本脉搏波数据集上进行分类实验，实验结果表明，该方法得到的最佳模型能够有效提取脉搏波特征，在小样本脉搏波条件下取得较好的分类效果。

由于数据量有限，本文只研究所提方法对小样本脉搏波数据的二元分类识别。后续将扩充脉搏波数据量进行多分类实验，并在搜索过程中考虑多目标优化方式。

参考文献：

［1］ SORELLI M， PERRELLA A， BOCCHI L. Detecting vascular age using the analysis of peripheral pulse［J］. IEEE transactions on bio-medical engineering， 2018， 65（12）： 2742-2750.

［2］ DEY J， GAURAV A， TIWARI V N. InstaBP： cuff-less blood pressure monitoring on smartphone using single PPG sensor［C］∥The 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Piscataway： IEEE Press， 2018： 5002-5005.

［3］ KACHUEE M， KIANI M M， MOHAMMADZADE H， et al. Cuffless blood pressure estimation algorithms for continuous health-care monitoring［J］. IEEE transactions on biomedical engineering， 2017， 64（4）： 859-869.

［4］ 逯鹏， 王汉章， 毛晓波， 等. 基于卷积自编码器网络的脉搏波分类模型［J］. 郑州大学学报（工学版）， 2021， 42（5）56-61.

LU P， WANG H Z， MAO X B， et al. Pulse wave classification model based on convolutional autoencoder［J］. Journal of Zhengzhou university （engineering science）， 2021， 42（5）56-61.

［5］ GOH C H， TAN L K， LOVELL N H， et al. Robust PPG motion artifact detection using a 1-D convolution neural network［J］. Computer methods and programs in biomedicine， 2020， 196： 105596.

［6］ LI G Y， WATANABE K， ANZAI H， et al. Pulse-wave-pattern classification with a convolutional neural network［J］. Scientific reports， 2019， 9（1）： 1-11.

［7］ SONG W Z， SUN X Y， HU C H. Cuffless blood prediction with fingertip pulse wave［J］. Journal of physics： conference series， 2020， 1544（1）： 012137.

［8］ GHOSH S， BANERJEE A， RAY N， et al. Using accelerometric and gyroscopic data to improve blood pressure prediction from pulse transit time using recurrent neural network［C］∥The IEEE International Conference on Acoustics， Speech and Signal Processing. Piscataway： IEEE Press， 2018： 935-939.

［9］ HARPER R， SOUTHERN J. End-to-end prediction of emotion from heartbeat data collected by a consumer fitness tracker［C］∥The 8th International Conference on Affective Computing and Intelligent Interaction. Piscataway： IEEE Press， 2019： 1-7.

［10］刘国华， 周文斌. 基于卷积神经网络的脉搏波时频域特征混叠分类［J］. 吉林大学学报（工学版）， 2020， 50（5）： 1818-1825.

LIU G H， ZHOU W B. Pulse wave signal classification algorithm based on time-frequency domain feature aliasing using convolutional neural network［J］. Journal of Jilin university （engineering and technology edition）， 2020， 50（5）： 1818-1825.

［11］LI C L， PENG J F， YUAN L C， et al. Block-wisely supervised neural architecture search with knowledge distillation［C］∥The IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE press， 2020： 1986-1995.

［12］WANG N N， LUO C J， HUANG X， et al. DeepCS： training a deep learning model for cervical spondylosis recognition on small-labeled sensor data［J］. Neurocomputing， 2022， 472： 24-34.

［13］JIN H F， SONG Q Q， HU X. Auto-keras： an efficient neural architecture search system［C］∥Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York： ACM Press， 2019： 1946-1956.

［14］ZANGHIERI M， BENATTI S， BURRELLO A， et al. Robust real-time embedded EMG recognition framework using temporal convolutional networks on a multicore IoT processor［J］. IEEE transactions on biomedical circuits and systems， 2020， 14（2）： 244-256.

［15］LIANG Y B， CHEN Z C， LIU G Y， et al. A new， short-recorded photoplethysmogram dataset for blood pressure monitoring in China［J］. Scientific data， 2018， 5（1）： 1-7.

［16］ABDULHAY E， ALAFEEF M， ALZGHOUL L， et al. Computer-aided autism diagnosis via second-order difference plot area applied to EEG empirical mode decomposition［J］. Neural computing and applications， 2020， 32（15）： 10947-10956.

［17］LI L S， JAMIESON K， DESALVO G， et al. Hyperband： a novel bandit-based approach to hyperparameter optimization［EB/OL］. （2016-10-31）［2022-06-18］. https：∥arxiv.org/abs/1603.06560.

［18］MA J C， HE N， YOON J H， et al. Distinguishing benign and malignant lesions on contrast-enhanced breast cone-beam CT with deep learning neural architecture search［J］. European journal of radiology， 2021， 142： 109878.