预测性维护任务计算卸载与资源分配联合优化

摘要： 针对预测性维护（predictive maintenance，PdM）人工参与资源调配的问题，提出了一种基于改进人工蜂群算法（artificial bee colony，ABC）的计算卸载和资源分配方案。该方法利用遗传算法的进化思想，改进了侦察蜂的搜寻步骤，解决了传统人工蜂群算法容易陷入局部最优解、多样性不足等缺点，能够根据设备故障率生成维护成本最低的资源分配方案。仿真实验结果表明，该算法较其他算法收敛速度更快、收敛质量更高、减少维护成本更明显，能够有效解决PdM场景的计算卸载和资源分配问题。

关键词： 移动边缘计算（MEC）； 预测性维护（PdM）； 任务卸载； 资源分配

中图分类号： TP311

文献标志码： A

文章编号： 1671-6841（2024）06-0039-07

DOI： 10.13705/j.issn.1671-6841.2023016

Task Offloading and Resource Allocation Joint Optimization for

Predictive Maintenance

ZHANG Bo， WANG Chenghao， LI Junfeng

（School of Cyber Science and Engineering， Zhengzhou University， Zhengzhou 450002， China）

Abstract： To address the problem of manual involvement in resource allocation for predictive maintenance （PdM）， a computational offloading and resource allocation scheme based on an improved artificial bee colony（ABC） algorithm was proposed. The method utilized the evolutionary idea of genetic algorithm to improve the searching step of scout bees. The shortcomings of traditional artificial bee colony algorithms such as easy to fall into local optimal solutions and insufficient diversity were solved. The ability to generate the lowest maintenance cost resource allocation plan based on equipment failure rates.The simulation experimental results showed that the algorithm had faster convergence speed， higher convergence quality and more obvious reduction of maintenance cost than other algorithms， and could effectively solve the computational offloading and resource allocation problems of PdM scenarios.

Key words： mobile edge computing（MEC）; predictive maintenance（PdM）; task offloading; resourse allocation

0 引言

设备维护是工业生产中的一项重要组成部分，对成本和设备可靠性有重大的影响，一定程度上影响公司的竞争力。PdM的基本概念是在传感数据的帮助下监测机器的健康状况，以确定机器未来可能出现的退化或故障。PdM通过在必要时进行维护活动，帮助公司优化策略，而不是让设备或组件出现故障后，或在其仍有使用寿命时进行更换。使用PdM可以减少计划内和计划外停机时间，降低维护成本，减少不必要的库存和工作设备上不必要的维护活动［1］。例如，文献［2］系统地概述了基于深度学习（deep learning，DL）的机器健康监测系统，包括四类DL架构：自动编码器、深度信念网络（DBN）、CNN和循环神经网络（RNN），大部分工作针对故障识别和分类。文献［3］提出了一个简单的系统健康管理体系结构，并回顾了自动编码器、CNN和RNN在系统健康管理中的应用。以上大部分PdM的研究都针对提高PdM的准确性以及完整的PdM方法，对于PdM任务的处理或分配的研究还很少。

由于PdM活动会产生大量数据，且有实时性要求，故本地计算以及卸载到云端的办法基本无法满足PdM的需求。移动边缘计算（mobile edge computing，MEC）可以提供强大的通信、存储、网络和通信能力［4-5］。边缘计算是指允许在网络边缘、云服务的下游数据和物联网服务的上游数据上执行计算的使能技术，广泛应用于工业物联网、无人机和车联网［6］。与本地计算相比，边缘计算可以克服终端设备计算能力有限的限制。与将计算卸载到远程云相比，边缘计算可以避免将某些任务卸载到远程云造成的高延迟。如文献［7］考虑了移动设备和MEC服务器之间的带宽限制，以及MEC服务器上的CPU资源有限的情况下，在相应的时延、频谱资源和计算资源的约束下，提出了吞吐量最大化问题。文献［8-9］均设置最大延迟约束，限制时间开销都不得超过最大可容忍延迟，考虑不限制最大可容忍延迟，而是根据延迟时间构建成本函数。

本文目标是在PdM场景下，给出时间软约束，即不具体约束延迟时间的条件下，使维护成本为第一优化目标。采用多个MEC服务器协同计算，利用边缘计算探索高效的资源分配和任务卸载方案，最大限度使得整个PdM的成本最小。考虑任务之间分配资源的数量，给出优先级的定义，并寻找高效的任务卸载和资源分配方案。具体来说，将最终的维护成本作为最终的优化目标，据此制定了一个任务卸载和资源分配问题，并且证明其是NP-hard的。为了解决该问题，本文提出了一种低复杂度的算法，一部分是受进化策略启发的任务卸载算法，结合了人工蜂群算法和遗传算法。另一部分是故障优先资源分配算法，能够在全局搜索更优的任务卸载方案，考虑任务卸载决策与计算资源分配之间的依赖性，使两种算法之间相互作用。

1 系统模型与问题描述

1.1 边缘计算延迟模型

本节详细介绍卸载模型。有多个设备表示为N={N1，N2，…，Ni，…，Nn}，设备在运行过程中会产生PdM需求，产生PdM任务集合T={T1，T2，…，Ti，…，Tn}，在设备的周围部署用K表示的边缘服务器K={K1，K2，…，Ki，…，Kn}。当执行PdM任务时，任务需要向边缘基站卸载，当设备Ni的全部任务Ti结束时，可认为一个PdM的结束。一个边缘服务器可以表示为K={R，F}，其中：R为任务卸载方案；F为资源分配方案，记录分配给边缘服务器上的任务。

每个任务都可以卸载到附近的边缘服务器上，但限制设备Ni一次只能提交一个任务Ki。任意任务Ti可以用5个项目来描述，T={D，c，λ，α，τ}，其中：D是任务T的数据大小；c表示T的处理密度；λ为任务上传时的设备故障率;α为卸载决策变量，即卸载的数据量占任务Ti总数据量的比例。α=0时，任务T局部处理，若α=1，任务T将被完全卸载。此外，大小为αD的数据将被卸载到边缘服务器，（1-α）D的数据将被本地处理。τ为处理结果的数据大小与Ti的数据大小之比［10］。PdM的执行延迟是指从初始子任务开始到最后一个子任务结束的时间。我们采用一种非抢占式的任务调度策略，即只要一个子任务没有完成，它的执行就不会被中断。

本地计算的核心数为g1，β表示为可并行部分，分配给本地计算的每个核心的处理能力为fl。本地将计算（1-α）D比特数据的任务，包括串行部分tls=c（1-β）（1-α）D/fl和可并行部分tlp=cβ（1-α）D/flg1，则本地计算时间可以表达为

tl=tls+tlp=c（1-α）Dfl（1-β+βg1）。（1）

通过以上分析，可以得到αD位数据到边缘的传输延迟。将αD位的数据卸载后，由边缘服务器处理数据。用g2表示分配给边缘处理任务的核数，设fe表示边缘服务器每个核的处理能力（fefl），可串行部分表示为tes=c（1-β）αD/fe，可并行部分表示为tep=cβαD/feg2，边缘计算时间可以表示为

te=tes+tep=cαDfe（1-β+βg2）。（2）

任务Ti的数据可以通过无线通信链路卸载到边缘。对于数据传输速率，用r1表示。根据上述分析，αD位数据卸载到边缘的传输延时表示为

tup=αDr1，（3）

则分配到边缘计算的总耗时为

toff=te+tup。（4）

任务Ti处理完毕后，将结果返回给终端设备。取r2为返回结果过程中的数据传输速率，与卸载数据速率相似。根据上面的分析，τD结果返回的传输延迟可以表示为

tdown=τDr2。（5）

由以上分析可知，处理任务Ti的总延迟是本地计算时间、边缘计算时间、卸载传输延迟和返回结果传输延迟的组合，且边缘计算和本地计算同时进行，则总延迟公式可表示为

td=m864ff261324bfcebe0ff2e478c50f1957b029037fa6d8b1048fbb7a40821ec6fax{tl，te}+tup+tdown。（6）

1.2 维护成本模型

1） 设备故障率模型 我们假设λ为任务在t时刻的故障率，ak为寿命降低因子，bk为故障率增加因子（0<ak<1，0<bk<1）。离散随机变量tk表示从上次实现预测性维护到下一次实现的累计运行时间，设备进行第k次预测性维护后的故障率可表示为分段连续变量［11］，

λk+1（t）=bkλk（t+aktk）。（7）

故障率在初始状态λ1（t）的变化趋势可以通过测试数据得到。故障率的变化随着预测性维护的周期进行，任务的卸载权重会发生变化，任务权重将会影响任务的卸载顺序。

2） 维护成本 当设备发生故障进行维护活动时的成本表示为纠正性更换成本（Cc），我们假设在PdM中涉及的纠正性维修成本为C［1］，

C=Cc（∑Mk=1∫tk0λkdt+∫ε0λM+1dt），（8）

其中：ε表示从上一次PdM活动到计划生产周期P结束的剩余时间。一个预测性维护周期包括维护时间与延迟时间，M表示计划生产周期P中PdM的循环次数，M=P/（td+tp）。

1.3 问题描述

我们提出了延迟软约束的任务计算资源分配问题。给定一组设备N及其产生的任务T，优化问题定义为

min{∑NR，FC}， i∈N。（9）

上述优化问题主要通过调整任务卸载方案R和资源分配方案F，使所有设备的维护成本最小化。公式（10）约束卸载的总计算时间必须小于任务全部在本地的计算时间，

ti（te，te+tl）≤tli，i∈N。（10）

公式（11）限制分配到Ti的计算资源之和不大于边缘服务器的可用总计算能力，

∑ni=1fli≤F，Ti∈T，Ki∈K。（11）

公式（12）、（13）约束每次进行计算的n个预测任务的数据大小不能超过边缘服务器的总存储空间，且边缘服务器处理任务时应缓存任务所需的资源，

∑ni=1（1-α）D≤Γ，Ti∈T，Ki∈K，（12）

∑ni=1（1-α）（1-β）D≤Γ，Ti∈T，Ki∈K。（13）

我们将通过类比多重背包问题（multiple knapsack problem，MKP）证明我们提出的计算卸载和资源调度问题是NP-hard。多重背包问题的一个实例是将一组表示为{x1，…，xn}的n个任务分配给一组表示为{y1，…，yn}的m个不同背包，其中每个任务xi的相关利润vi>0，权重wi>0，背包yi的容量为Wj。MKP是在不超过每个背包容量的情况下，选择m个不相交的物品子集，使所选物品的总利润最大化。本文所提问题类似于多重背包问题，任务xi可以被切分成两部分：卸载计算和本地计算，卸载比率为α。根据需求二次把本地计算的任务卸载到边缘，以获得更大的计算效率。类比于背包问题，可证明此问题是NP-hard。1） 任务T={T1，T2，…，Ti，…，Tn}可以对应多重背包问题中的{x1，…，xn}。2） 权重wi>0可以对应卸载任务中的故障因子λ。3） m个不同背包的{y1，…，yn}类似于边缘可提供的计算资源量。背包容积Wj为计算资源上限。

2 延迟软约束的G2ABC算法

启发式算法在实践中被广泛应用于解决NP-hard问题。文献［12-13］改进贪心思想结合启发式算法来解决NP-hard问题。文献［14］共同研究了边缘服务器布置和应用分配问题，提出了一种基于局部搜索的启发式算法来有效解决该问题。由于容易陷入局部最优解，并不适合解决PdM问题，因此我们用多种启发式算法，利用遗传算法（GA）和人工蜂群算法（ABC）的优点从全局提出了一种基于GA-ABC算法的卸载和资源分配方法（G2ABC）。此算法包括两部分：1） 算法将为每个任务选择计算边缘节点；2） 算法将决定边缘节点的多少资源分配给任务。提出的算法主要关注获得更低的维护成本、更高的资源利用率。

2.1 任务卸载算法

ABC算法是一种能够摆脱局部最小值的优化技术，可以有效地用于模拟蜜蜂觅食行为的多变量、多模态函数 ［15］。在ABC算法中，人工蜜蜂的蜂群包含三组蜜蜂：雇佣蜜蜂、旁观蜂和侦察兵。在跳舞区等待决定选择食物来源的蜜蜂被称为旁观蜂，而前往自己之前访问过食物来源的蜜蜂被称为雇佣蜜蜂，进行随机搜索的蜜蜂被称为侦察蜂。ABC算法多用于调度问题，例如文献［16］利用改进的人工蜂群算法解决无人机航迹规划问题，加快了求解航迹的收敛速度，提高了航迹规划效率和稳定性。

在ABC算法中，食物来源的位置代表了优化问题的一个可能解，食物来源的花蜜量对应于相关解的质量（适应度）。ABC生成随机分布的初始种群P（G=0）的SN解（食物来源位置），其中SN表示种群大小。每个食物来源是一个E维向量，其中E为优化参数个数。初始化后，位置（解）的填充被反复循环，B=1，2，…，Bmax，表示雇佣蜜蜂、旁观蜂和侦察蜂的搜索过程。雇佣蜂或旁观蜂在寻找新的食物来源时，会对记忆中的位置进行修正，并测试新来源的花蜜量（适合度值）［17］。

遗传算法在由基因和适应度函数组成的类染色体数据结构上进行遗传表示，初始化一个解种群，然后依靠生物启发的算子（如突变、交叉和选择）对其进行改进。

利用上述算法优点，提出一个改进ABC算法的任务卸载方案。借鉴遗传算法的思想，对ABC算法中侦察蜂的搜索过程进行改进，其中修改的部分如下。

1） 食物源 食物源表示为FS=<O，Z，C>，其中：O表示任务卸载方案；Z表示资源分配方案；C为PdM过程对应任务卸载和资源分配方案下的总成本。我们将FS的总集合表示为FSA ［18］，目的是为任务T在边缘服务器上找到一个合适的卸载与分配方案，使得C最小化。

2）雇佣蜂阶段 雇佣蜂从周围寻找食物并记录。为了从旧的蜜源获得一个新的蜜源，ABC算法表达为

vij=xij+ij（xij-xkj）。（14）

3） 围观蜂阶段 旁观蜂选择食物源取决于与该食物源相关的概率值pi，计算为

pi=fiti∑SNn=1fitn，（15）

式中：fiti为溶液i被雇佣蜜蜂评价的适应度值，该适应度值与雇佣蜜蜂位置i处食物源的花蜜量成正比；SN为食物源数量，等于雇佣蜜蜂数量（BN）。通过这种方式，雇佣蜂与旁观蜂交换信息。

4） 侦察蜂阶段 在ABC中，当原食物源在预定周期内无法产生更优解时，部分蜂群会转变为侦察蜂去随机寻找新的食物来源。为了避免过快收敛以及陷入局部最优解，我们参考了遗传算法的交叉变异运算，并能在未知方向寻找更好的解，利用遗传算法的变异过程重新寻找蜂源，从而可以更好地搜索解空间。

根据上述描述，G2ABC算法具体步骤如下。

算法1 G2ABC

输入： 食物源的数量SN，维护任务T，边缘节点K。

输出：任务卸载方案O，资源分配方案Z。

1） FSA=0，初始化轮数cycle

2） for i=1：SN

3） 为每一个任务随机分配一个边缘节点K，将卸载方案表示为O

4） 算法5得到初始资源分配方案Z

5） FS=<O，Z，C>

6） FSA=FS

7） end for

8） while j<cycle

9） 调用算法2

10） 调用算法3

11） 调用算法4

12） end while

13） FS=FSbest

算法1说明了G2ABC的细节。在第一行将种群设置为空完成初始化。首先将种群初始化，随后对种群进行初始化。根据算法5得到最初的分配方案。随后进行轮转搜索。

算法2 雇佣蜂算法

输入： 食物源FSA，维护任务T，边缘节点K。

输出： 更新的食物源FS。

1） for FSi∈FSA

2） 随机选择食物源j，FSj∈FSA

3） FSj.O使用算法5更新新的食物源FSj

4） 根据公式（14）得到食物源FSm

5） FSm.O使用算法5更新新的食物源FSm

6） FS=FSm

7） end for

算法2是雇佣蜂详细过程。对于种群中的每个食物源，根据公式（14）搜索，并生成新的食物源。

算法3 围观蜂算法

输入： 食物源FSA，维护任务T，边缘节点K。

输出： 更新的食物源FS。

1） 根据式（15）概率选择FSj，FSj∈FSA

2） 根据公式（14）得到食物源 FSm

3） FSm.O使用算法4更新新的食物源FSm

4） 对比FSm、FSj更新最优食物源FSbest

算法3介绍了围观蜂的过程。旁观蜂和雇佣蜂的过程相似，根据轮盘对赌搜索出最佳食物源，然后更新最优食物源。

算法4 侦察蜂算法

输入： 食物源FSA，维护任务T，边缘节点K。

输出： 更新的食物源FS。

1） forFSi∈FSA

2） if有侦察蜂出现

3） FSi.O使用交叉变异生成新的FSj.O

4） FSm.O使用算法5更新新的食物源FSm

5） end if

6） 更新食物源 FSi=FSm

7） end for

算法4是基于GA优化的侦察蜂算法。当有侦察蜂出现的时候，步骤2）根据交叉变异形成新的食物源跳脱出原有解，防止陷入局部最优。

2.2 资源分配算法

在PdM活动中，生产设备由于磨损而不断退化，故障率不断上升，合格率不断下降。定义卸载返回后的故障率作为辅助变量集Λ，定义中间变量

yi=λi/fli（16）

为故障率和分配资源的比值，可以反映资源分配的质量。算法需要优先对故障率高的任务分配资源，通过调整资源分配方案，使每个任务的中间向量值趋于统一。

算法借鉴了二分搜索的思想，在公式（11）的约束内找到一个资源分配方案，使得最终的设备维护成本最小［12］，具体算法流程如下。

算法5 故障优先资源分配算法

输入： 任务卸载方案O，边缘节点K，维护任务T。

输出： 资源分配方案Z。

1） for Ki∈K

2） 将Ki上的任务定义为Tres

3） for Ti∈Tres

4） 平均分配计算资源，根据式（16）得到集合Λ

5） ymin=min｛Λi｝，ymax=max｛Λi｝

Y=（ymin+ymax）/2

6） while （y-ymin>0）

7） if 分配的计算资源大于总资源

8） ymax=y

9） else if 分配的计算资源小于总资源

10） ymin=y

11） end if

12） y=（ymin+ymax）/2

13） end while

14） 根据式（16）得到重新分配的计算资源

15） end for

16） end for

17） 将得出的资源分配方案赋值给F

18） return F

算法5根据式（16）对任务进行初始资源分配，并且设定了上、下限。利用二分搜索，在设定计算资源范围内找到合适的值，并对任务重新分配资源。

3 仿真验证与分析

首先介绍实验中的设置和比较算法，然后讨论评价结果。

根据文献［19-20］，将边缘服务器的通信范围设置为500m，边缘服务器计算资源设置为1×109 CPU周期/s，本地计算资源设置为1×104 CPU周期/s。为了对比不同算法之间的性能，将任务数设置为20、40、60和80个，计算资源分别设置为1×109、2×109、3×109和4×109 CPU周期/s。

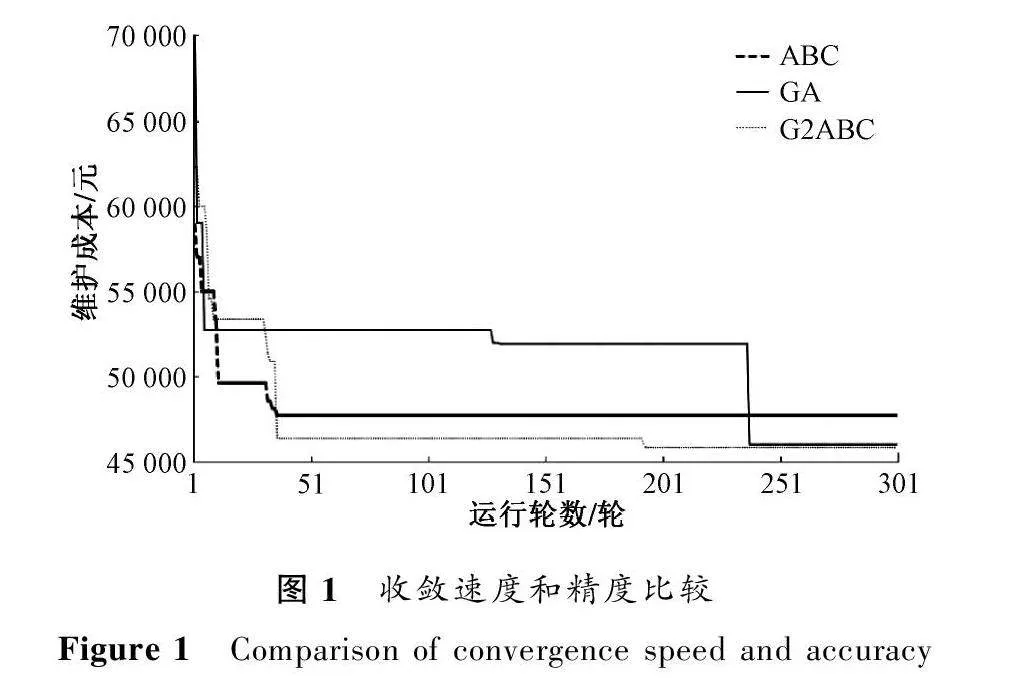
1） 收敛性能。选择基于ABC的任务卸载算法和基于GA的任务卸载算法与G2ABC进行比较。所有的算法都使用统一的资源分配算法。

从图1中我们可以看出G2ABC算法和ABC算法在收敛速度上优于GA算法，且G2ABC算法在进化策略影响下，200次迭代后的维护成本显著小于其他算法。这意味着G2ABC可以快速准确找到任务卸载方案。

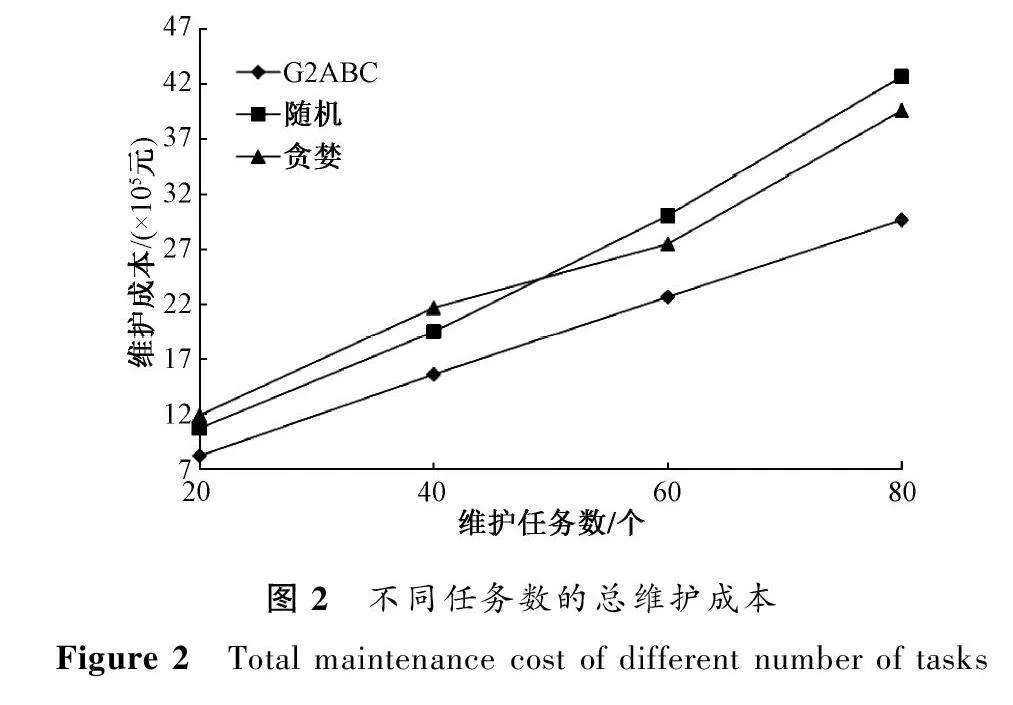
2） 所有任务的总维护成本。为了显示G2ABC算法适用问题，与随机分配算法和贪婪算法进行比较。

图2显示了不同算法在任务数量不同时的维护成本趋势，三种算法的结果都随着任务数的增加而增加。随机算法在任务数40之前的维护成本优于贪婪算法，而随着任务数增加，贪婪算法的维护成本逐渐优于随机算法。对比两种算法，G2ABC可以保持较低的成本损耗，即G2ABC算法可以得到成本相对最小的资源分配方案。

3） 不同计算资源下的对比。为了对比不同算法在不同计算资源下的性能，将维护任务数设置为60。

图3显示了不同算法在边缘服务器计算资源不同时的维护成本趋势，三种算法的结果都随着资源数的增加而减少。由于计算资源的增多，可供任务使用的计算资源增加，计算时间变少，从而维护成本变低。以资源数为3×109 CPU周期/s为例，贪婪算法和随机算法的维护成本值分别为232万元和236万元，本文算法的维护成本为175万元，这说明本文算法在此情况下可得到更少的维护成本。且在不同边缘计算资源数下均有较好的维护成本。

4 结论

在本文中，我们对预测性维护的计算卸载和资源分配问题进行全面的数学建模，并且证明此问题是NP-hard的。为了解决这一问题，本文提出了一种G2ABC算法，算法对延迟时间进行软约束，以减少设备的维护支出为目标，找到合适的任务卸载和资源分配方案。通过实验表明，对比其他算法，我们的方法可以给出一个合适的任务卸载和资源分配方案，减少了预测性维护成本。

参考文献：

［1］ RAN Y Y， ZHOU X， LIN P F， et al. A survey of predictive maintenance： systems， purposes and approaches［EB/OL］. （2019-12-12）［2022-10-16］. https：∥arxiv.org/abs/1912.07383.

［2］ ZHAO R， YAN R Q， CHEN Z H， et al. Deep learning and its applications to machine health monitoring［J］. Mechanical systems and signal processing， 2019， 115： 213-237.

［3］ KHAN S， YAIRI T. A review on the application of deep learning in system health management［J］. Mechanical systems and signal processing， 2018， 107： 241-265.

［4］ TRAN T X， HAJISAMI A， PANDEY P， et al. Collaborative mobile edge computing in 5G networks： new paradigms， scenarios， and challenges［J］. IEEE communications magazine， 2017， 55（4）： 54-61.

［5］ MACH P， BECVAR Z. Mobile edge computing： a survey on architecture and computation offloading［J］. IEEE communications surveys & tutorials， 2017， 19（3）： 1628-1656.

［6］ 田钊， 王超， 贾骏， 等. 基于局部自组网的路况信息可靠共享模型［J］. 郑州大学学报（理学版）， 2022， 54（6）： 82-90.

TIAN Z， WANG C， JIA J， et al. A reliable traffic information sharing model based on local-VANET［J］. Journal of Zhengzhou university （natural science edition）， 2022， 54（6）： 82-90.

［7］ DENG Y Q， CHEN Z G， CHEN X H. Resource allocation for multi-user mobile-edge computing systems with delay constraints［C］∥IEEE Global Communications Conference. Piscataway： IEEE Press， 2021： 1-6.

［8］ AHMED I， YAN S， RAWAT D B， et al. Dynamic resource allocation for IRS assisted energy harvesting systems with statistical delay constraint［J］. IEEE transactions on vehicular technology， 2022， 71（2）： 2158-2163.

［9］ HORIMOTO S， HE F J， OKI E. Delay-aware backup resource allocation with probabilistic protection for network services［C］∥IEEE 22nd International Conference on High Performance Switching and Routing. Piscataway： IEEE Press， 2021： 1-6.

［10］KIANI A， ANSARI N， KHREISHAH A. Hierarchical capacity provisioning for fog computing［J］. IEEE/ACM transactions on networking， 2019， 27（3）： 962-971.

［11］LI D F， HONG P L， XUE K P， et al. Virtual network function placement and resource optimization in NFV and edge computing enabled networks［J］. Computer networks， 2019， 152： 12-24.

［12］DINH T Q， TANG J H， LA Q D， et al. Offloading in mobile edge computing： task allocation and computational frequency scaling［J］. IEEE transactions on communications， 2017， 65（8）： 3571-3584.

［13］LUO Q Y， HU S H， LI C L， et al. Resource scheduling in edge computing： a survey［J］. IEEE communications surveys & tutorials， 2021， 23（4）： 2131-2165.

［14］HE Y H， HAN X， GU C C， et al. Cost-oriented predictive maintenance based on mission reliability state for cyber manufacturing systems［EB/OL］. （2018-01-12） ［2022-12-16］. https：∥doi.org/10.1177/1687814017751467.

［15］刘倩雯. 人工蜂群算法及其在调度问题中的应用研究［D］. 北京： 北京交通大学.

LIU Q W. Artificial bee colony algorithm and its application in scheduling problem［D］. Beijing： Beijing Jiaotong University.

［16］刘琨， 封硕. 面向无人机航迹规划的改进人工蜂群算法［J］. 郑州大学学报（理学版）， 2021， 53（1）： 74-79， 126.

LIU K， FENG S. Improved artificial bee colony algorithm for UAV path planning［J］. Journal of Zhengzhou university （natural science edition）， 2021， 53（1）： 74-79， 126.

［17］KARABOGA D， BASTURK B. A powerful and efficient algorithm for numerical function optimization： artificial bee colony （ABC） algorithm［J］. Journal of global optimization， 2007， 39（3）： 459-471.

［18］ZHOU J Y， ZHANG X L. Fairness-aware task offloading and resource allocation in cooperative mobile-edge computing［J］. IEEE Internet of Things journal， 2022， 9（5）： 3812-3824.

［19］HE Y H， REN J K， YU G D， et al. D2D communications meet mobile edge computing for enhanced computation capacity in cellular networks［J］. IEEE transactions on wireless communications， 2019， 18（3）： 1750-1763.

［20］PARVEZ I， RAHMATI A， GUVENC I， et al. A survey on low latency towards 5G： ran， core network and caching solutions［J］. IEEE communications surveys & tutorials， 2018， 20（4）： 3098-3130.