何时有最大照射宽度

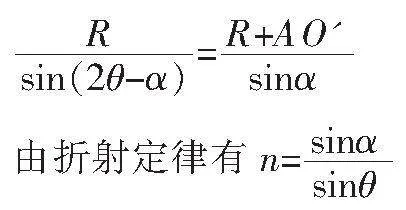
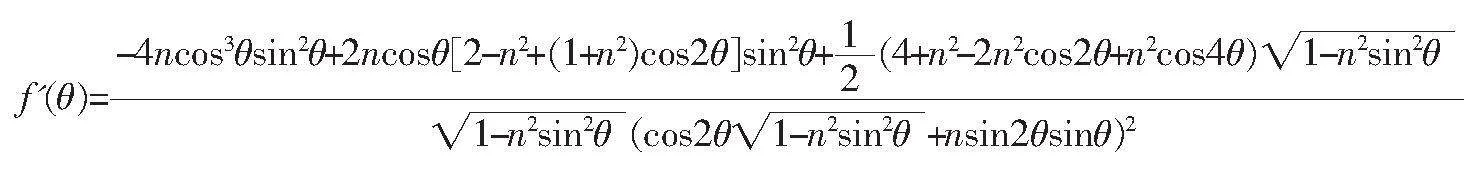
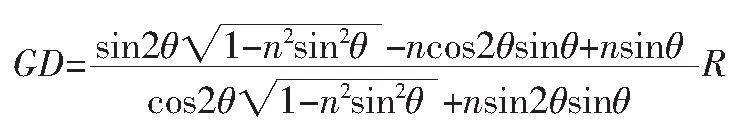
摘 要：通过对一道常见的几何光学题目进行深入分析，指出现有参考答案中的不当之处，并利用数值计算得到正确结果。同时，对此题进行深入分析，得到一般情况下结果的变化趋势，论证该题目命制的“痛点”，提出修改建议。最后，分析了近三年高考物理几何光学试题的命制情况，提出了教学建议。

关键词：几何光学；折射；全反射

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）7-0070-3

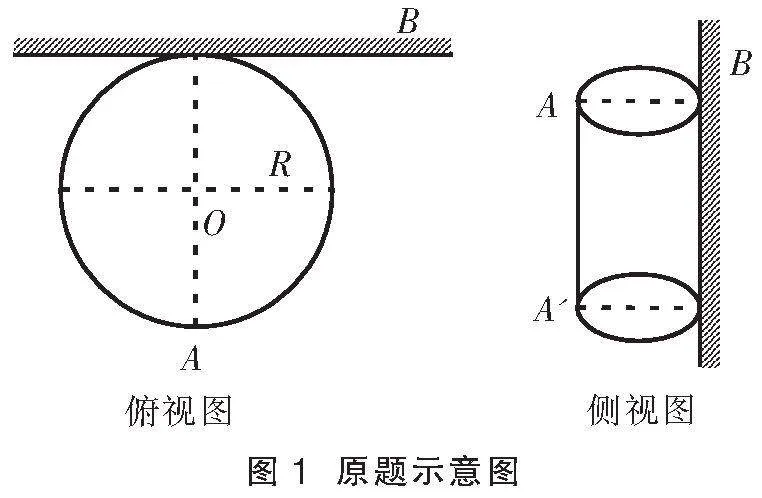
1 原题呈现

（1）灯柱上有光线出射的圆弧面对应的圆心角φ；

（2）背板上有光线照射的宽度d。

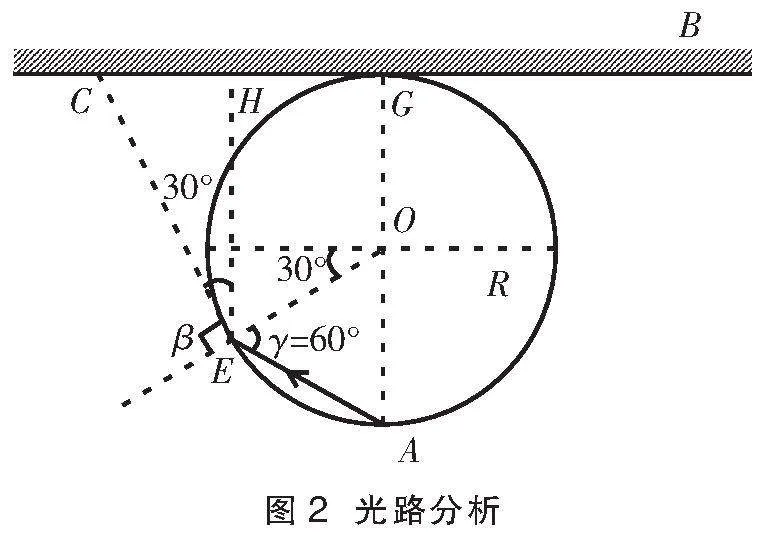
此题现已选编入各种教辅资料，参考答案也基本如出一辙：（1）略；（2）如图2，根据几何关系可知，背板上有光线照射的宽度

d=2（HC+GH）=2（EHtan30°+GH）

得

d=2Rcos30°+2（Rsin30°+R）tan30°

2 提出质疑与解答

按照参考答案理解，背板上有光线照射的宽度d的最大范围的临界位置，即光源发射的入射光线在彩灯壁E点恰好发生全反射时所对应的折射光线CE（该光线实际并不存在）照射在背板上的C点，然后由对称关系求得光线照射的宽度d。学生从定性分析的角度就很容易提出质疑，为什么光线在背板上的最大偏折就在C点？不少教师可能对此不以为然，不加以证明便告知学生这是显而易见的。但事实真的如此吗？现对此题进行深入分析。

对应折射光线为FD，折射角为α。延长DF与GA延长线交于O'点，现对GD的最大值进行讨论。

由几何关系可得

GD=（2R+AO'）tan（2θ-α）

在ΔO'OF中，根据正弦定理，有

可得

令

欲求的GD最值，即求解函数f（θ）的最值，

利用Mathematica对f（θ）求导得

3 对此类题目的几点思考

3.1 对原题的深入分析

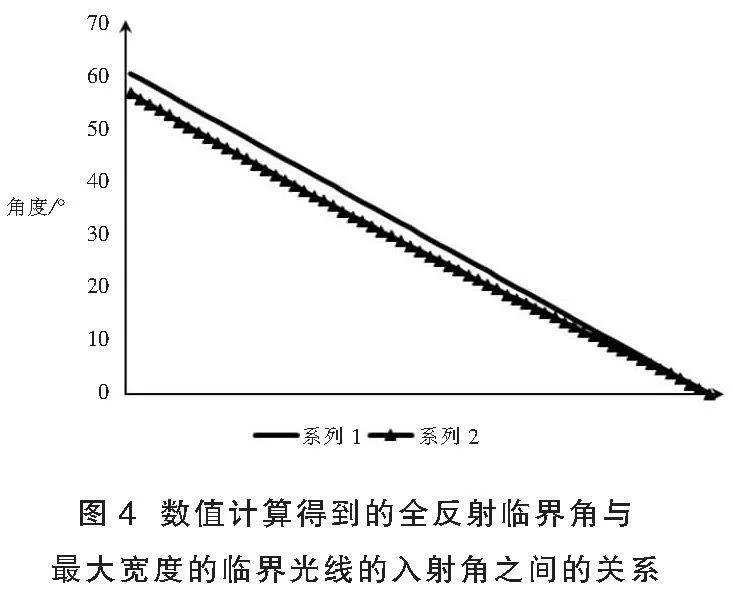
通过数值计算，作出不同折射率的透明灯柱全反射临界角与在背板上有光线照射的最大宽度的临界光线的入射角之间的关系如图4所示，其中系列1表示透明灯柱全反射时的临界角，系列2表示此时背板上有光线照射的最大宽度的临界光线所对应的入射角。由图4可知，随着透明灯柱折射率增大，在背板上有光线照射的最大宽度的临界光线的入射角始终小于临界角，二者之间的差值随着折射率的增大逐渐减小。

最大宽度的临界光线的入射角之间的关系

故而，对于此题而言，即使改变灯柱折射率，背板上有光线照射的宽度d依然难以求解。另外，生活中常见玻璃材料的折射率介于1.40～2.00。因此，在命制此类题目时应尤其注意结合实际，并注意推理论证过程，避免出现科学性错误。

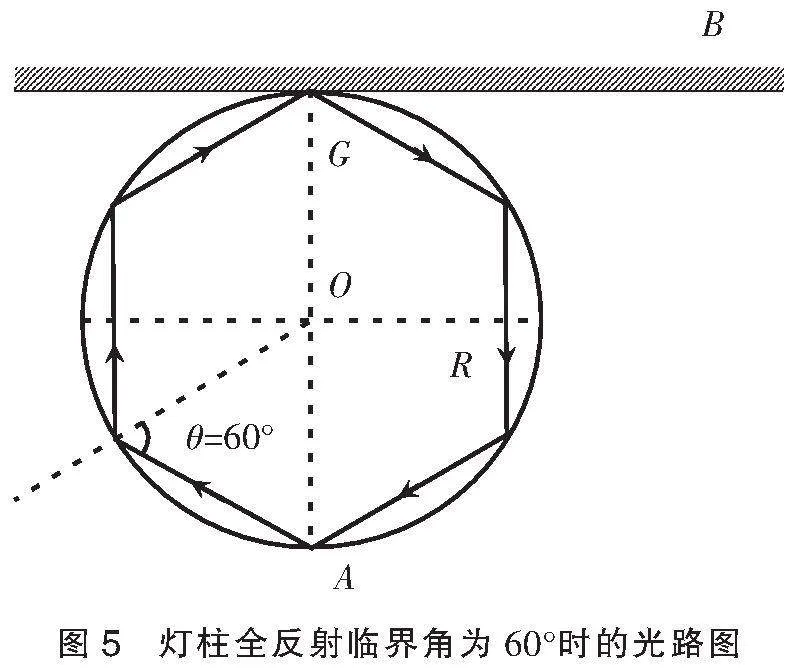
在此，对于模拟试题，第（2）问可进行如下改编：在如俯视图所示圆平面内，从A点发出的光线经多次全反射回到A点的时间最短。对于此问，需要学生进行推理论证：何时从A点发出的光线经多次全反射回到A点的时间最短？回到A点时间最短即光程最短，也就是发生的全反射次数最少。由题意知，灯柱全反射临界角为60°，光路图如图5所示，便能顺利解决。

3.2 高考几何光学题目命制情况与教学建议

3.2.1 高考几何光学考题命制情况

通过对近三年全国部分地区高考物理几何光学题目进行统计与分析发现，关于几何光学考题的具体试题内容情境主要有：仅含折射光路的试题，仅含临界光路的试题，含折射、反射光路的试题以及含两条独立光路的问题等。问题设计主要包括：折射率计算、光传播时间计算、边长度与角度计算等。对于必备知识而言，主要考查光的折射定律、折射率以及全反射。对于关键能力而言，主要考查理解能力与推理论证能力。对于学科素养而言，主要考查物理观念与科学思维。试题主要通过学习探索问题情境体现基础性、综合性与应用性的考查要求。

在处理几何光学问题时，不少学生会反映能算出最终答案，但不知道如何书写过程。这种情况反映出学生的科学思维有待提高。《普通高中物理课程标准（2017年版）》中明确指出，“科学思维”包括模型建构、科学推理、科学论证、质疑创新等要素［1］。学生不会写过程，就是不会科学推理与论证，折射出关键能力中推理论证能力的不足。造成这种情况的原因有多种，其中值得注意的是，教师在平时教学中就应有意识地引导学生进行科学推理与论证。

通过上述分析可知，前文改编后的题目也较好地符合了高考的考查要求。

3.2.2 几何光学教学建议

对于高中阶段的几何光学考题，不少教师和学生均认为此类题目很简单，各种教辅资料也总结出多种处理此类问题的方法，按图索骥，学生也能拿到分数。但纵观近年来高考几何光学问题，不难发现，考题充分体现对学生科学思维的考查，反映学生的推理论证能力。在学生“拿分”与“学科素养”培养之间，作为教师应毫不犹豫地选择并坚持后者。在此，提出两点教学建议供参考。

第一，重视必备知识。必备知识的积累是形成关键能力与学科素养的基础。对于几何光学部分，不能认为学生初中已经学习相关知识就轻视必备知识的学习。不同的学习阶段对知识有不同的理解要求。在高中阶段，学生对知识的理解不应该依然停留在初中阶段的要求。

第二，强化关键能力培养与训练。高考评价体系确立了三个方面的关键能力群［2］：以认识世界为核心的知识获取能力群（理解能力）、以解决实际问题为核心的实践操作能力群（实验探究能力）、涵盖关键思维能力的思维认知能力群（模型建构能力、推理论证能力和创新能力）。对于几何光学问题，高考着重体现在以认识世界为核心的知识获取能力群的基础上，对涵盖关键思维能力的思维认知能力群的考查。学生能力培养并非一蹴而就，作为教师，在教学中必须做好积极示范与引导，应避免此类问题不讲评的现象。对于有争议或有价值的点，即使超出高中阶段学生的知识范围，教师也应做好科学推理与论证。这样，学生不会书写过程的情况将大大减少，同时，更是对学生学科素养的有效培养。

4 结 论

在教学中，我们鼓励学生大胆质疑，作为教师，也应如此。对于大型或权威考试试题，不应盲目信服，要有质疑的精神。但质疑也并非无端猜疑，草木皆兵，在大胆质疑假设的同时，更应该小心求证。故而，教师在教学中就应以培养学生的关键能力、发展学生科学思维、全面提高学生学科素养为教学出发点，做好示范，引导学生实践。唯有这般，学生和教师才都能获得成长。

参考文献：

［1］中华人民共和国教育部.普通高中物理课程标准（2017年版）［S］.北京：人民教育出版社，2018.

［2］教育部考试中心.中国高考评价体系说明［M］.北京：人民教育出版社，2019.