科学思维视域下高效习题课堂设计

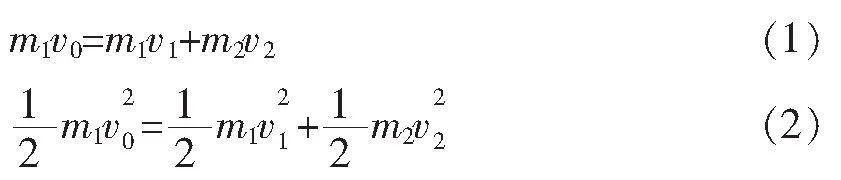
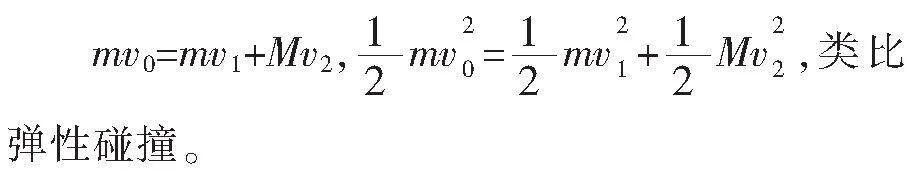
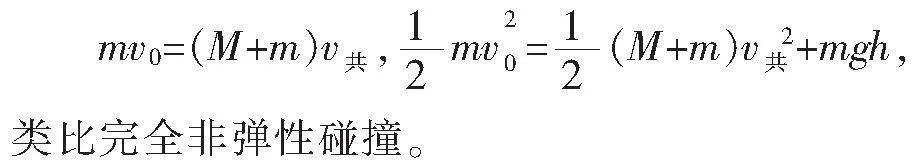
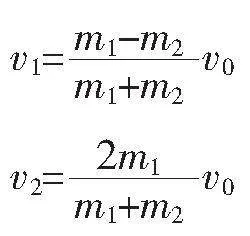
摘 要：基于模型建构，培养学生的逻辑思维能力，针对高三习题课“碰撞模型拓展”进行教学设计。针对“滑块-弹簧”模型，深化对弹性碰撞和完全非弹性碰撞两种特殊情况的理解，并把此方法拓展到其他较复杂模型，使问题得到简化。面对大量不同模型，让学生建立起“模型归一”的思维，尝试在普通的物理课堂中通过课程设计有意识地培养学生的科学思维，从而提高物理课堂效率。

关键词：科学思维；弹性碰撞；完全非弹性碰撞；模型归一

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）7-0038-4

科学思维是物理核心素养的重要方面，是从物理学视角对客观事物的本质属性、内在规律及相互关系的认识方式［1］。在高中物理教学中，训练学生思维，让学生能够用物理的思维方式去认识世界、分析问题是我们教学的重要任务。科学思维包括模型建构、科学推理、科学论证、质疑创新等要素［2］，在物理学中主要体现为求证思维、逻辑思维和证伪思维。其中，求证思维需要发现问题、进行猜想，并论证猜想的正确性；逻辑思维是通过事物的运动规律和发展方式来分析事物间、现象间的本质关系；证伪思维不但要证实物理知识的正确性，还要有质疑其正确性的思想。

逻辑思维对学生学习效率有很大影响，高中物理知识点庞杂，有些问题思维难度较大，如果学生能够建立起科学的逻辑思维，理解知识与知识间、模型与模型间的内在思维联系，建构起完整的知识体系，将会很大程度上提高他们的学习效率。这就需要教师在教学过程中有意识地根据科学思维的要素设计课堂［3］，在平时的教学中对学生进行科学思维方法的渗透。本文以高三一轮复习课堂中习题课“碰撞模型拓展”为例，通过分析不同模型，发现本质联系，让学生建立起“模型归一”的逻辑思维，从而探寻如何帮助学生发展科学思维来设计教学，提高高三习题课堂的复习效率。

1 设计思路

在学生学会分析碰撞基本问题的基础上，对弹性碰撞和完全非弹性碰撞两种特殊情况的结论进行深化，应用模型建构的科学思维将一些较复杂的问题转化为学生所熟悉的上述两种特殊情况，使学生能快速解决一些较难问题。

2 教学过程

2.1 知识回顾

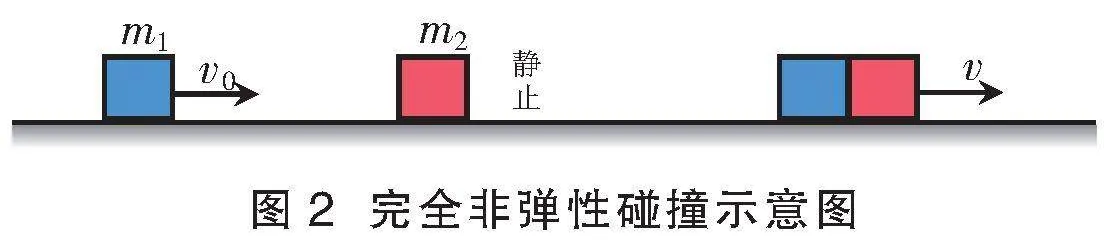
回顾两种特殊的碰撞模型——弹性碰撞（动碰静）（图1）和完全非弹性碰撞（图2），学生上黑板展示方程和结论。

（1）弹性碰撞（动碰静）

由（1）（2）式可得

学生回顾不同质量关系碰撞结论：大碰小一起走，小碰大要反向。

（2）完全非弹性碰撞

m1v0=（m1+m2）v

学生回顾特点：碰后共速，能量损失最大。

2.2 模型分析

通过例题向学生提出问题，分析“滑块-弹簧”模型。

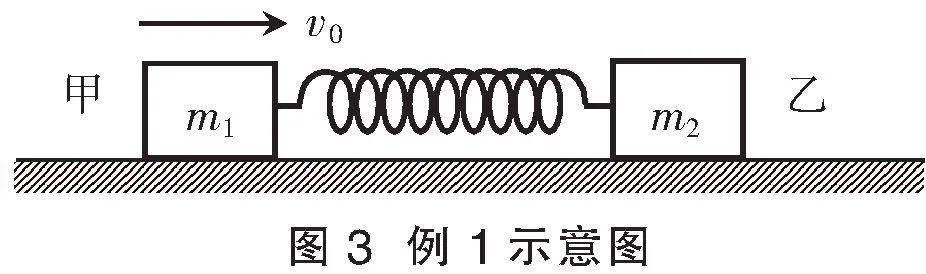
例1 如图3所示，一个轻弹簧的两端与质量分别为m1和m2的两物体甲、乙连接，静止在光滑的水平面上。现在使甲瞬间获得水平向右的TQSEDJT0wN5iOlT7AZV0cLi8AtqK3iNHZ4aQ069BGLk=速度v0=4 m/s，当甲物体的速度减小到1 m/s时，弹簧最短。下列说法中正确的是（ ）

A.此时乙物体的速度大小为1 m/s

B.紧接着甲物体将开始做加速运动

C.甲、乙两物体的质量之比m1∶m2=1∶4

D.当弹簧恢复原长时，乙物体的速度大小为4 m/s

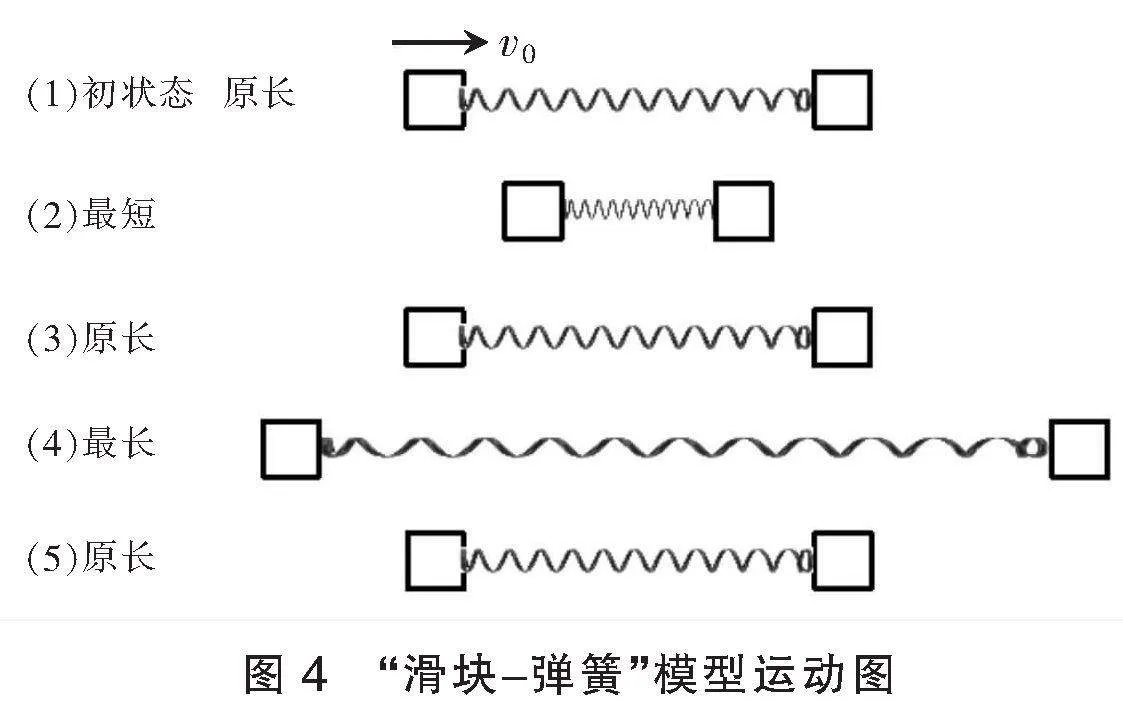
学生阅读题干，小组讨论“滑块-弹簧”模型运动过程（图4）。

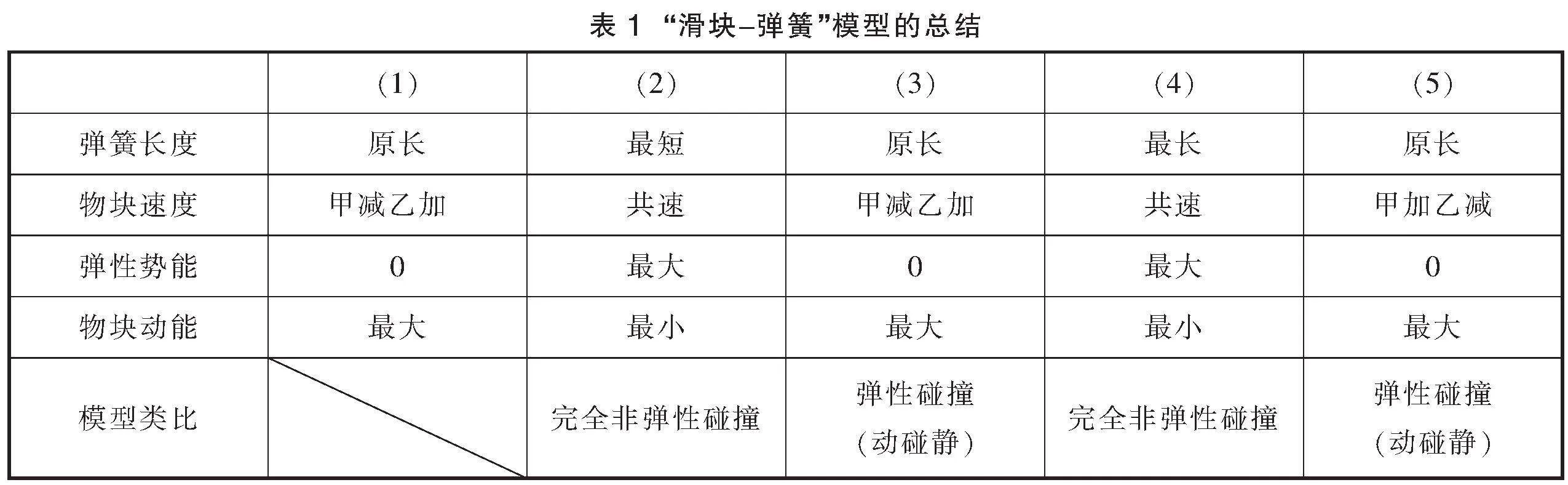
根据图4，学生分组讨论，完成表格内容（表1），并派出代表汇报结论。（假设图4中第3个过程左侧物体速度未减为0）

结论：具有初速度的物体与静止物体通过弹簧相互作用，弹簧最短或最长时可类比完全非弹性碰撞模型进行分析，弹簧恢复原长时可类比非弹性碰撞（动碰静）模型进行分析。

学生再思考，根据上面分析的“滑块-弹簧”模型能不能定性画出两物块的v-t图像呢？学生分组讨论画v-t图像，并找小组展示成果。

2.3 变型分析

通过上面的分析，我们加深了对“滑块-弹簧”模型的理解，对于一些特殊位置可以应用弹性碰撞（动碰静）和完全非弹性碰撞的结论分析，那么还有没有其他情况也可以用同样的方法进行分析呢？下面我们再来分析几种变型。

（1）变型一

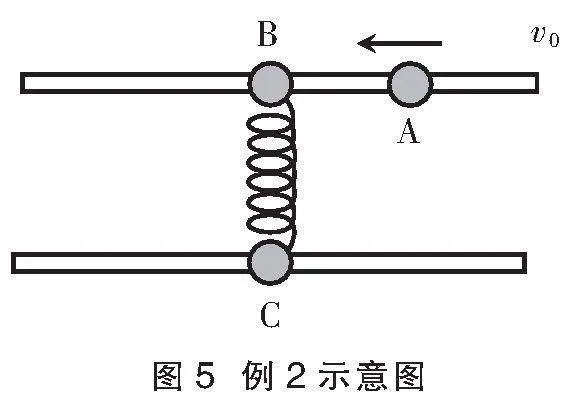
例2 如图5所示，A、B、C三个半径相等的刚性小球穿在两根平行且光滑的足够长的杆上，三个球的质量分别为mA=2 kg、mB=3 kg、mC=2 kg，初状态三个小球均静止，B、C两球之间连着一根轻质弹簧，弹簧处于原长状态。现给A球一个向左的初速度v0=10 m/s，A、B两球碰后A球的速度变为方向向右、大小为2 m/s。下列说法不正确的是（ ）

A.球A和球B间的碰撞是弹性碰撞

B.球A和球B碰后，弹簧恢复到原长时球C的速度大小为9.6 m/s

C.球A和球B碰后，球B的最小速度为1.6 m/s

D.球A和球B碰后，弹簧的最大弹性势能可以达到96 J

带领学生分析：A、B之间碰撞应用动量守恒很容易求出B球速度为8 m/s，通过能量关系可知为弹性碰撞；对B、C之间，B带静止的C运动，类似动碰静，当弹簧最长时B、C共速，类比完全非弹性碰撞可求出最大弹性势能；当弹簧恢复原长时类比弹性碰撞（动带静），代入结论可求出此时B、C的速度，并由mB>mC可知，大带小不反向，所以B的速度并不减为0，此时B的速度即为最小速度；此后，C再带B运动，B开始加速，C减速。

学生再思考，此类解法是不是只适用于有弹簧的系统呢？下面我们再来看一下变型二。

（2）变型二

例3 如图6所示，质量为0.1 kg的小圆环 A穿在光滑的水平直杆上。用长 L=0.8 m的细线拴着质量为0.2 kg的小球 B，B 悬挂在 A 下方并处于静止状态。t=0时刻，小圆环获得沿杆向左的冲量0.6 N·s， g 取10 m/s2。下列说法正确的是（ ）

A.小球 B 做圆周运动

B.小球 B 第一次运动到 A 的正下方时，A 的速度最小

C.从小球 B 开始运动到第一次回到 A 正下方的过程中，细线对 A 一直做负功

D.从小球 B 开始运动到第一次回到A正下方的过程中，合力对 B 的冲量为0.8 N·s

学生思考，小组内交流并汇报成果。此题依然可理解为动带静，开始一段时间在水平方向上A减速、B加速，A、B水平间距逐渐增大，由于绳长不变，则绳与竖直方向夹角逐渐增大，系统重力势能增加，当二者共速时，B至最高点，系统重力势能最大，可类比完全非弹性碰撞分析速度及势能；之后，A继续减速，B继续加速，A、B水平间距减小，当B再次到达A正下方时重力势能全部释放出来为0，则可类比弹性碰撞（动带静）模型分析，另外由于mA<mB，小带大要反向，所以在B第一次回到A正下方之前A的速度已经减为0，之后反向加速，所以A的最小速度为0，并且细线对A做负功使其减速，再做正功使其反向加速。这样应用模型定性分析就可以得到答案，避免了复杂的定量计算。

学生再思考，上面几种模型都是两个物体通过绳或弹簧相互作用，那么有没有不含绳或弹簧的系统依然可以用同样的方法分析呢？下面再看变型三。

（3）变型三：“滑块-斜（曲）面”模型（图7）。

模型分析：

①上升到最大高度：m与M水平共速v，m竖直速度vy=0。

②返回最低点：m与M分离点（弹性正碰）。

由此可见，对于“滑块-斜（曲）面”模型，上述分析方法依然适用。

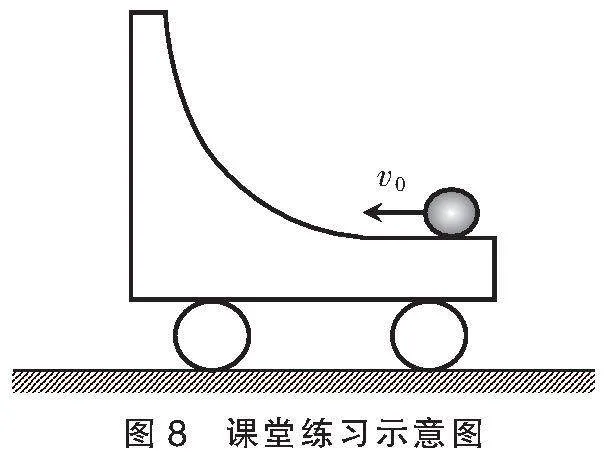
课堂练习：如图8所示，在光滑水平面上停放质量为M=3 kg装有弧形槽的小车。现有一质量为m=1 kg的小球以v0=4 m/s的水平速度沿与切线水平的槽口向小车滑去（不计一切摩擦），到达某一高度后，小球又返回小车右端，则（ ）

A.小球在小车上到达最高点时竖直方向速度大小为1 m/s

B.小球离车后，对地将向左做平抛运动

C.小球离车后，对地将做自由落体运动

D.此过程中小球对车做的功为6 J

3 小 结

本堂课的主要设计思路是基于培养训练学生模型建构的科学思维，通过对“滑块-弹簧”模型的分析，深化弹性碰撞（动碰静）、完全非弹性碰撞两种特殊情况的应用，并把这种模型分析的思维拓展到其他更为复杂的模型，使问题得到简化，提高习题课的效率，让高三学生面对大量复杂的习题时建立起“模型归一”的逻辑思维能力。

参考文献：

［1］中华人民共和国教育部.普通高中物理课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020.

［2］刘洋，蒋炜波，张芳.科学思维视域下物理情境创设的研究综述［J］.中学物理，2023，41（19）：7-12.

［3］刘湘衡.基于学生科学思维培养的高中物理高效课堂建构［J］.新课程研究（中旬），2019（2）：18-19.