基于运动学自动计算系统的运动功能件设计

摘 要：在运动功能件设计时，各项技术指标在设计阶段难以量化计算和评估，累积公差不能精确计算和控制，无法确保设计方案达成设计目标要求。本论文主要论述如何建立运动功能件的运动学自动计算系统，在运动件设计时提前对运动机构进行运动学计算和分析，根据计算结果最优的机构匹配和方案选型。提出了基于运动学自动计算系统辅助的运动功能件设计方法，解决了技术指标在设计阶段难以量化计算和评估的问题。

关键词：运动功能件；运动学自动计算系统；微分迭代算法；系统累积公差；技术指标量化评估

中图分类号：U461 文献标志码：A 文章编号：1005-2550（2024）04-0021-08

Design of Kinematic Function Components Based on Automatic kinematic Calculation System

YA Yong-hou， TANG Jin-xiong， DENG Gui-xin

（ Dongfeng Yanfeng Automotive Cockpit Systems Co.， Ltd.， Wuhan 430056， China）

Abstract： In the design of motion functional parts， it is difficult to quantitatively calculate and evaluate various technical indicators in the design stage， and the cumulative tolerance cannot be accurately calculated and controlled， so as to ensure that the design scheme meets the requirements of the design objectives. This paper mainly discusses how to establish an automatic kinematic calculation system for moving functional parts， carry out kinematic calculation and analysis of the kinematic mechanism in advance during the design of moving parts， and select the optimal mechanism and scheme according to the calculation results. This paper proposes a design method of motion functional components based on the assistance of kinematic automatic calculation system， which solves the problem that it is difficult to quantify and evaluate technical indicators in the design stage.

Key Words： Kinematic Function Components; Automatic Kinematics Calculation System; Differential Iterative Algorithms; System Cumulative Tolerances; Quantitative Evaluation of Technical Indicators

随着汽车座舱产品智能化、自动化的发展，运动功能件在汽车座舱产品中的应用越来越多，目前座舱系统涉及的运动功能件主要包括：中央扶手、手套箱、储物盒、旋转屏幕等各类运动件，以及未来座舱内部可变空间趋势带来的相关运动功能件和机构。为了开发高品质感的功能产品，需要提升用户直接感受的性能指标来实现产品的品质提升，比如操作力误差，操作力衰减率，开启时间误差，操作耐久等指标。难点在于，各项技术指标难以量化计算和评估，以及累积公差如何精确计算和控制。

目前，国内外现有可用于运动功能件性能指标计算的方法中，无论是涵盖范围，计算精度，置信区间都无法达到工程应用的要求，只能作为指导性辅助手段，无法真正实现技术指标在设计阶段进行量化评估的目标。本论文运用基于微分迭代算法的运动力学模拟计算技术，建立运动功能件的运动学自动计算系统，以解决技术指标在设计阶段难以量化计算和评估的问题。

1 建立运动件运动学模型

常用的运动件的运动模型主要有3种：

a）翻转运动；

b）直线运动；

c）特殊轨迹运动。

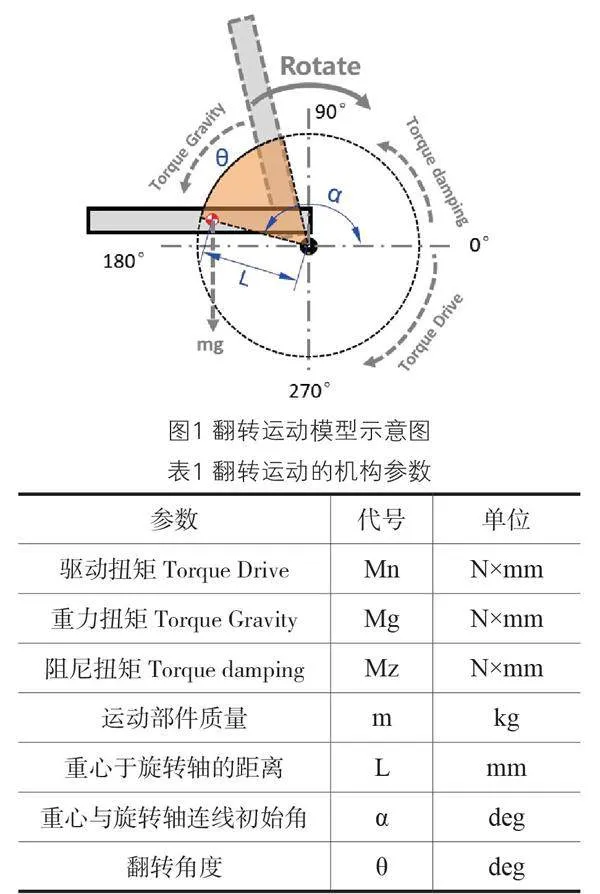
翻转部件的转动惯量J=m×L2；任意位置角加速度：a=ΔM/J；任意位置角速度：ωn=ω0+Δa×Δt。机构参数说明见表 1所示：

以弹簧助力开启翻转扶手为例，在翻转过程中主要受到三种扭矩的综合作用，第一个是扭簧的扭转力矩，作为驱动力使扶手能够克服自身重力向上翻转；第二个扭矩是扶手自身的重力所产生的重力矩；第三个扭矩是阻尼产生的阻尼扭矩，以防止扶手速度过快产生的低品质感；扶手在以上三种合扭矩的作用下产生加速度，从而使扶手发生翻转运动。在翻转过程中，由于扭簧的预紧角在不断的变化，因此弹簧扭矩是不断变化的；同样，随着翻转角度的不断变化，重力的力臂也在不断变化，因此重力矩也是不断变化的；而由于弹簧扭矩和重力矩的不断变化，必然会导致扶手翻转的速度也是不断变化的，而阻尼的扭矩也会随着速度变化而发生变化。因此，扶手在翻转过程中任意时刻的运动姿态都是不断变化的，并不是一个简单的线性运动的过程，无法采用简单的公式进行计算，需要分析任意位置的受力状态，从而推导任意位置的运动状态；

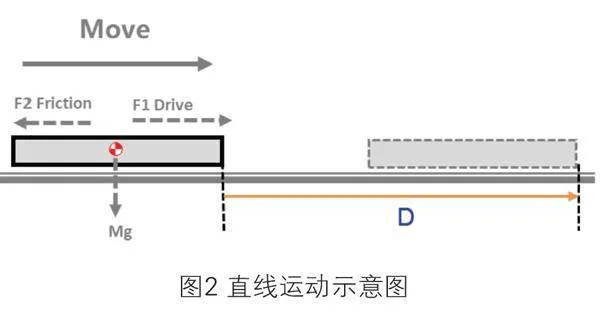
直线运动模型示意图如图 2所示：

部件任意位置加速度：Δa=（Fd- Ff）/m；任意位速度：Vn=V0+Δa×Δt。 运动距离D= V0×Δt+1/2 Δa×Δt²。机构参数说明见表2所示：

2 建立常用机构系列化数据库

由于整个运动过程中，各个因素对于结果的影响是非线性的，无法通过简单的单向运算进行确定，而且对于同一结果需求，输入参数会有多种组合，因此，无法根据结果需求反向计算输入参数，只能通过正向迭代法进行计算，在此条件下，如果每次都需要把所有的参数进行调整，则会耗费大量的工作量，为了减少正向计算的参数调整量，可以通过建立常用机构的标准化数据库，在计算过程中只要选择相应的系列和型号，就可以自动调用该型号的相关参数，可以大大减少工作量；

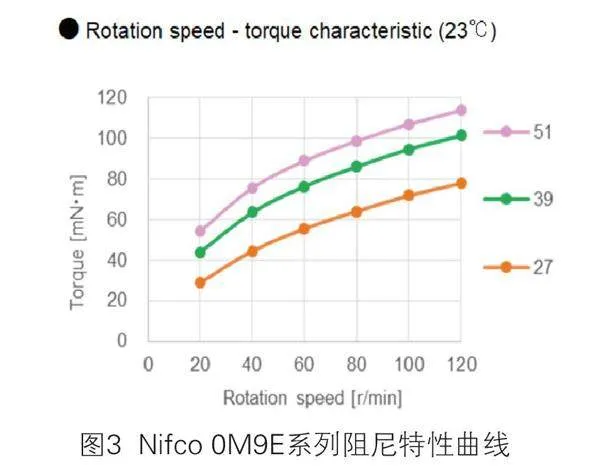
常用的机构部件主要包括扭簧、阻尼等可以作为标准数据库进行管理。例如每一个阻尼型号对应的阻尼-转速特性曲线、阻尼公差、温度特性和耐久特性等参数都已经由试验获得，通过把各种常用系列和型号的产品及其参数做成产品数据库，就可以在计算过程中自动调用，以提高使用方便性。下面以Nifco 0M9E系列阻尼为例对阻尼参数和数据库进行介绍。

2.1 通过试验方法获得阻尼特性参数和曲线

通常阻尼参数特性曲线可以通过试验的方法获得，每种系列的阻尼采样20件以上，并对阻尼不同转速下的扭矩进行测量，对试验数据采集表3所示。

经过方差处理，可以得阻尼扭矩特性公差如表4所示：

以上参数可以制作阻尼特性曲线如图3所示：

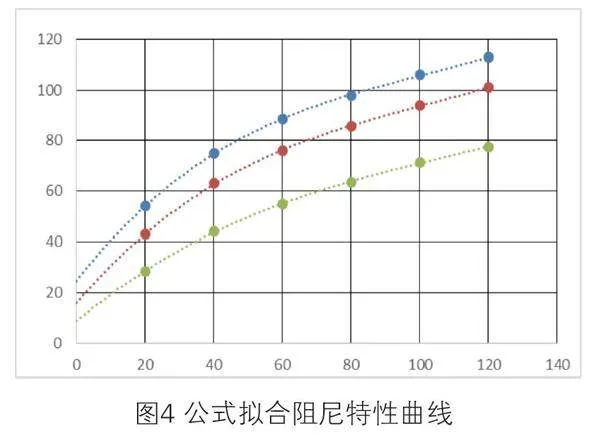
2.2 根据阻尼特性曲线，拟合阻尼扭矩公式和曲线

如图4，就可以通过扭矩公式计算瞬时扭矩Mz=n×I×（X3ω03+X2ω02+X1ω0+C）×（-1）。有了瞬时扭矩计算公式，就可以确定运动部件任意位置的受力状态，从而计算瞬时加速度等参数。其它机构的参数可参照同样的方式进行标准数据库的建立。

3 建立基于微分迭代算法的运动力学模拟计算系统

想要计算部件在任意时刻的运动速度以及运动时间，只能采用微分的方式，对部件整个运动过程进行细致的微分计算，只要确定了部件任意时刻的运动状态，就能计算出其开启时间，速度和加速度的变化等参数，再对整个运动过程进行微分迭代计算，就可以对部件整个运动过程进行模拟计算。以翻转运动为例，任意位置的行程，速度和力矩等因素的计算公式如表5所示。

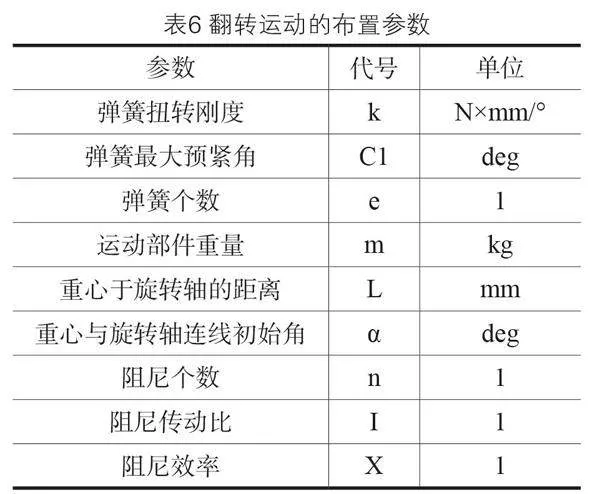
其中，翻转部件的各参数说明如表6。对于常用机构，这些参数可以直接调用步骤2中的常用机构数据库的参数进行自动计算。

4 运动模型选型，布置参数确定

计算系统建立后，在方案设计之前，就可以针对方案所选型的机构先进行模拟运动学计算，以翻转运动扶手开启时间计算为例，通过以下步骤对设计方案进行模拟计算。

4.1 运动机构选型

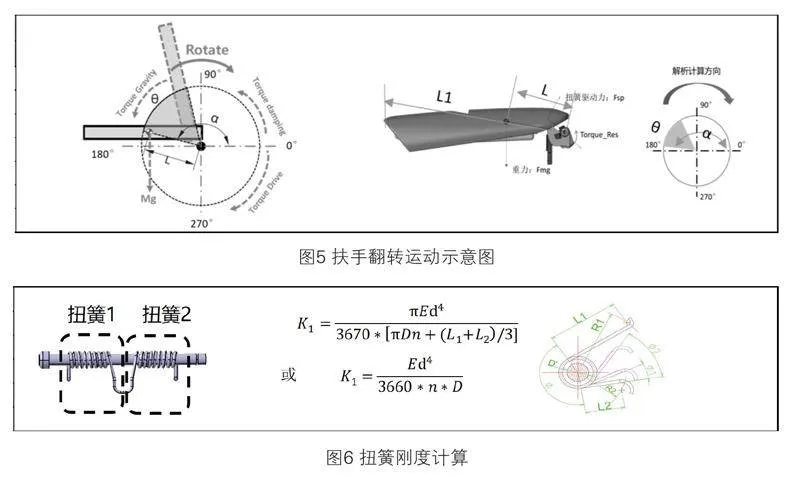
根据扶手的运动特性和布置参数，选定翻转运动运动模型如图5所示。

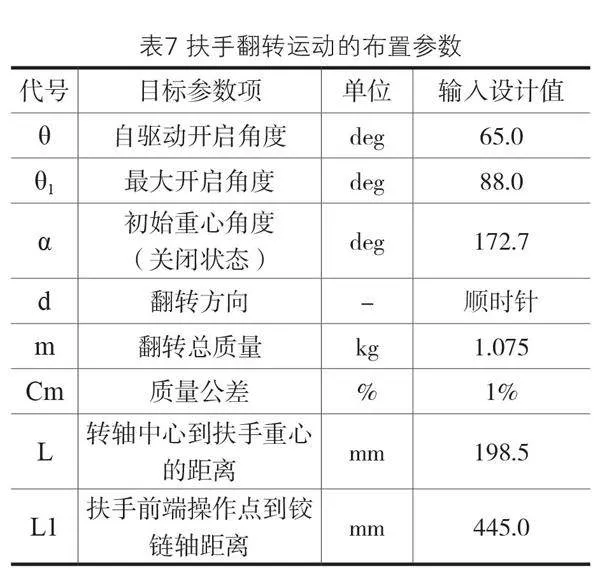
其中扶手各参数如表7所示：

4.2 弹簧选型

根据设计方案构想，选用双扭簧作为翻转驱动力，扭簧刚度计算如图6所示。

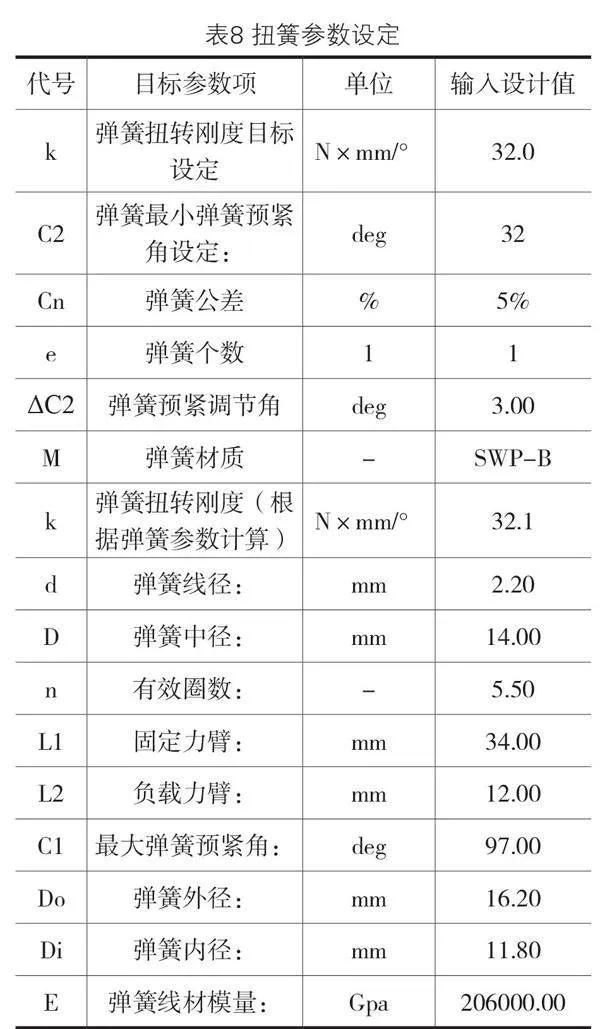
根据设计方案布置，弹簧各参数设定如表8所示。

4.3 阻尼选型

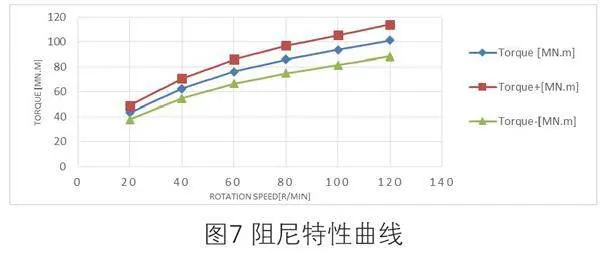
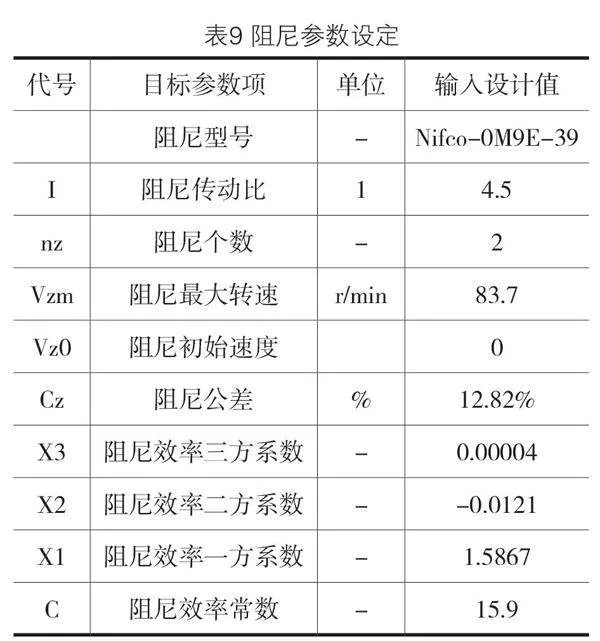
根据设计方案构想，采用齿轮硅油阻尼，输入阻尼传动比和阻尼个数等参数设定如表9所示，由于在前面已经建立常用系列化阻尼数据库，当对阻尼型号进行选型之后，系统会自动调用该型号阻尼的特性参数进行自动计算，无需每个参数一一输入。

同时系统自动生成阻尼特性曲线如图 7所示：

5 计算结果分析，方案迭代计算

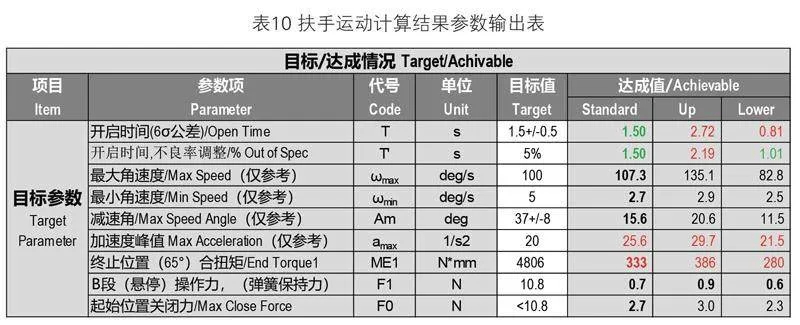
经过以上的设计构想和方案选型之后，系统会自动计算运动结果，自动生成计算报告并输出相关的参数结果如表10所示。

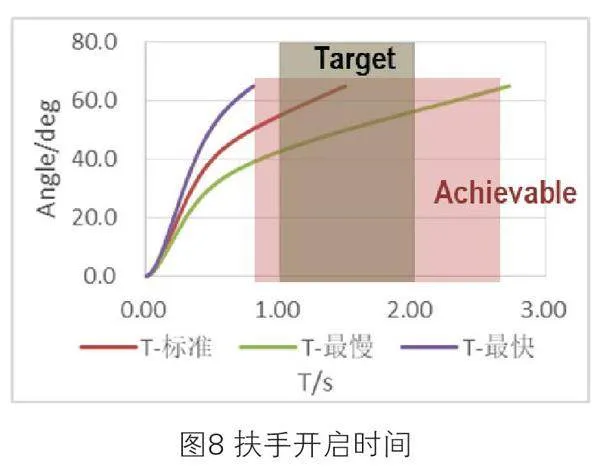
同时，根据目标值的设定，系统会自动生成对应的分析曲线图，如图8所示为扶手开启时间的分析曲线，可以看到目标的开启时间要求为1s-2s，而实际达成值为0.81s-2.72s，没有达成目标要求。

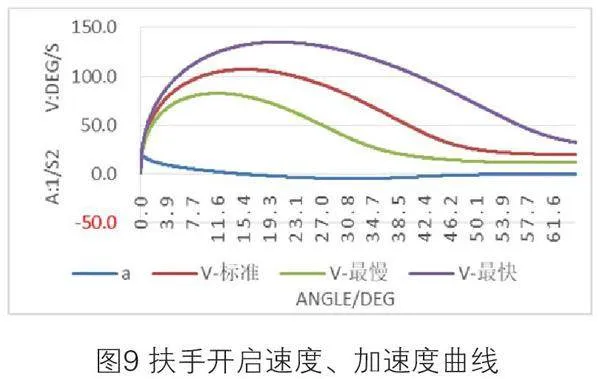
图9为开启过程运动速度曲线。

图10为开启过程扭矩特性曲线，通过对过程运动速度曲线和扭矩特性变化曲线分析，可以了解各因素对扶手翻转运动的影响。

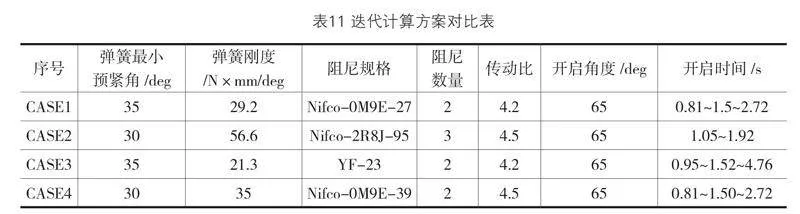
记录该选型方案的计算结果之后，进一步对弹簧、阻尼和其它过程参数进行优化选型和迭代计算，可以计算出一系列的方案组合，对方案组合进行对比分析如表11所示，从而确定最优方案选择，如表10中CASE2可以满足设计要求，可选择CASE2方案组合进行设计。

6 公差分析

在计算某种性能参数时，多影响输入因素下，由于输入参数与输出参数之间并非同一度量，且经过微分后非线性转化，无法采用正态分布的数据公差处理方法来计算输入公差与输出公差的关系。传统方案是通过输入参数的极差值来计算输出参数的公差，根据公差理论，当影响因素大于三个以上，极差值法的置信区间就基本失去了可信度，同时导致计算结果公差带大，标准公差要求相差甚远，但又无法佐证实际的公差能力。因此要解决输入参数与输出参数的累积公差问题，必须采用更科学的方法来实现。

为了验证实际的公差能力，需要引入中间参数，该参数应该具备不同因素的公差采用同一度量表示，输入参数中重量、弹簧力、阻尼力矩都可以转化为旋转扭矩这一中间参数，而且转换过程中均为线性转化；因此可以把输入参数之间的公差转化为合扭矩的累积上下偏差，通过数据正态分布的公差计算方法来推算合扭矩的公差；再通过合扭矩进行微积分计算，就可以计算出输出参数的上下偏差，从而推算输出参数的公差。

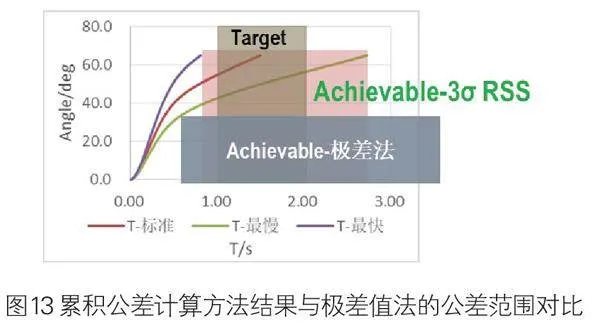
经过计算检验，相对于极差值计算方法，输出参数的公差带可收窄约为40%；其中公差能力按照满足+/-3σ RSS Variation的要求，合格率为99.73%，如图13所示：

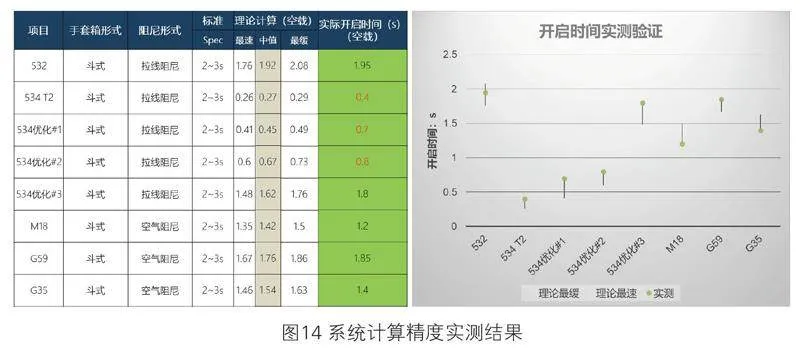
系统间累积公差分析方法的应用，大大提高了系统的计算精度，经过现生产产品实测验证，系统计算能力较为准确，如图14所示，右边这个图黑色的线代表理论计算时间，绿色的点是实测结果，可以看到实测结果基本与理论计算相符合。

7 结论

本论文通过建立对运动功能件运动机构进行力学模型建立，采用微分法对计算过程进行迭代计算，对运动机构运动过程中的时间，速度，加速度以及扭矩特性进行精确模拟，在方案设计之前首先进行力学计算，从而进行精准的机构选型，节省设计时间，规避设计风险。同时，引入中间转化参数，解决了在输入参数与输出参数之间的累积公差问题，相对于极差值法计算的累积公差，大大缩小了公差范围，使得该系统从理论计算层面上升到工程应用层面的转变。

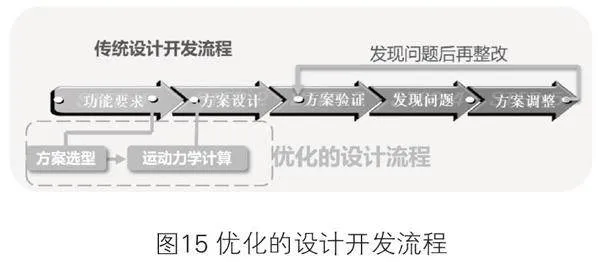
该设计方法在方案设计之前先进行最优方案选择，提升了方案的匹配度，避免由于方案不匹配导致发现问题后来回重新选择方案的重复工作，从而优化了设计开发流程。

参考文献：

[1]黄强编辑.理论力学[Z]. 哈尔滨工业大学理论力学教研室，高等教育出版社，2016.9.

[2]金康宁，谢群丹主编.材料力学[Z].北京大学出版社， 2006. 1.

[3]Bruce Hu.Advanced Tolerance Analysis[R]. 昆明：昆明理工大学，2007：5-3.

[4]茆诗松，程依明，濮晓龙编著.概率论与数理统计教程[M].高等教育出版社，2004.（7）.80～120.

[5]曾五一主编.统计学概论[M].首都经贸大学出版社，2008.（5）.70～110.

专家推荐语

该论文通过自主研究基于微分迭代算法的运动力学模拟计算技术，建立微分迭代自动计算系统，在产品设计阶段对运动功能件的技术指标进行自动计算和分析，解决了各技术指标无法在设计阶段进行量化计算和评估的问题。另一方面，通过巧妙的引入中间参数转化思路，解决不同属性的输入参数之间无法计算累积公差的难题，大大提高了系统的计算精度，建立了部品制程能力与产品制造能力之间的桥梁，使得该系统算法从理论参考层面上升到实际工程应用层面，具备较强的先进性。

论文选题精准，适合汽车智能化、自动化发展的趋势下的运动功能件的开发需求，可提升产品设计开发过程中的指标控制能力，优化了设计开发流程，提高开发效率。论文论点清晰，数据真实，可读性好，具有较强的现实指导意义。