一图三用，让思维之花绽放

［摘 要］在人教版新教材六年级下册的“数学广角”单元中，“鸽巢问题”这一教学内容较旧教材有较大的改动。文章旨在探讨如何通过精心设计的组图来深入挖掘“鸽巢问题”的教学价值，以此促进学生思维能力的发展，并培养他们的核心素养。

［关键词］鸽巢问题；枚举法；平均分法；反证法

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）17-0072-03

数学被视为思维的体操，其教学的一个重要目标是培养学生掌握数学思维方法。挖掘人教版教材中的“数学广角”的教学价值是实现这一目标的有效途径，该部分通过简洁明了的编排和富有趣味性的实例，旨在渗透关键的数学思想方法。

在六年级下册的“数学广角”单元中，“鸽巢问题”这一教学内容较旧教材有很大变化。面对这一变化，教师需要探讨如何有效地开展“鸽巢问题”单元的起始课。这包括如何基于教材内容和学生的学习情况，引导学生进行深度学习，体现“鸽巢问题”的教学价值，并促进学生思维的发展。

一、教材分析

在人教版新旧教材中，“鸽巢问题”都是以例题“把4支铅笔放进3个笔筒中，不管怎么放，总有1个笔筒里至少有2支铅笔。”导入，通过提问的方式帮助学生理解“总有”和“至少”这两个关键词的含义，进而引出枚举和反证两种思维方式，从而让学生可以更好地感知“鸽巢问题”的基本结构和形态，并掌握简单“鸽巢问题”的解题模型。

教材提供了两种解题方法。第一种，枚举法。通过逐一分析一类事件的所有可能情况来得出结论。这种方法旨在让学生通过具体的列举过程，全面概括情况，并深入体验数学的具象性。第二种，反证法。通过对命题进行逻辑论证来证明结论。这是一种形式化的证明方法，教师可以先引导学生用直观的方式大胆提出假设，再细心验证。与枚举法相比，反证法更具抽象性和一般性，能够帮助学生理解更深层次的数学逻辑和证明方法。

二、学情分析

六年级的学生在生活中已经积累了丰富经验，也具有一定的学习能力、动手能力、理解能力，教材中提供的例子与学生的生活紧密相关，这为学生理解和掌握“鸽巢问题”做了良好的铺垫。

然而，当“总有”和“至少”这两个词组合在一起形成“总有……至少……”的表达时，部分学生可能会感到困惑。学生的主要困惑点包括：首先，对于“总有1个笔筒”的表述，学生可能不清楚具体指的是哪个笔筒，以及这个笔筒的具体情况。这是因为“鸽巢问题”中的“不确定性”与学生过去所学的具有“明确指向对象”的思维习惯产生了认知冲突。其次，部分学生可能将“至少”理解为数量上的最少，认为最少的支数就是0支，从而质疑“至少有2支”的说法。这种错误的理解源于将“总有”与“至少”分裂开来，忽略了“至少”的前提。针对这些认知障碍，教师应引导学生对题意进行全面的梳理，确保他们对这两个概念的理解准确无误。

三、教学实践与反思

【教学片段1】初次看图，从“最多”中找“最少”

师（课件出示教材例题，题略）：从题目中你知道要完成什么任务？要证的结论是什么？

生1：题目要求把4支铅笔放进3个笔筒。结论是不管怎么放，总有1个笔筒至少有2支铅笔。

师：你是怎样理解“不管怎么放”“总有”“至少”的意思？

生2：“不管怎么放”的意思就是随意放、顺便放，想怎样放就怎样放。

生3：“总有”就是一定有、肯定有、一定存在。

生4：“至少”就是最少、不少于、最起码。

生5：“至少有2支”就是最少有2支，不能少于2支，也可能是3支或4支。

师：看来大家已经基本理解题目的意思了，你知道为什么总有1个笔筒里至少有2支铅笔吗？眼见为实，下面就请同学们来操作探究，在动手之前请看活动要求。

出示活动要求：

（1）小组合作摆一摆；（只考虑笔筒中铅笔的数量，与笔筒的顺序无关，可以有空笔筒。）

（2）思考一共有几种摆法，把所有的摆法找出来；

（3）用自己喜欢的方式在学习单上记录各种摆法。

（学生4人一组操作，教师巡视）

师：请汇报一下你们的成果。

（教师请一个小组到展台前汇报）

生6：我们小组是用画示意图的方法来表示的，第一种放法是一个笔筒中放4支，其余两个笔筒空着。

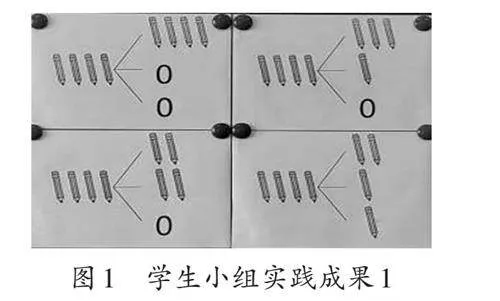
生7：第二种放法是一个笔筒中放3支，另外两个笔筒中有一个笔筒放1支，最后一个笔筒空着；第三种放法是一个笔筒中放2支，另外两个笔筒中有一个笔筒放2支，最后一个笔筒空着；第四种放法是一个笔筒中放2支，另外两个笔筒中有一个笔筒放1支，最后一个笔筒放1支。（如图1所示）

师：请问大家有什么要补充的吗？还有其他的摆法吗？

生8：我们小组是用有序数来表示的，上面的4种摆法分别可以表示为（4，0，0）、（3，1，0）、（2，2，0）、（2，1，1）。（出示图2）

生9：图2显示一共就4种摆法。

师：像这样，从条件出发一一列举所有情况的方法称为“枚举法”。

师：观察图2，为什么总有1个笔筒里至少有2支铅笔？我们来逐一验证。

师：在第一种摆法中，至少有2支铅笔的笔筒有多少个？请把它圈出来。圈出的笔筒里有几支铅笔？

生（齐）：圈出的笔筒1个，它里面有4支铅笔。

师：在第二种摆法中，至少有2支铅笔的笔筒有多少个？请把它圈出来。圈出的笔筒里有几支铅笔？

生（齐）：圈出的笔筒有1个，里面有3支铅笔。

师：在第三种摆法中，至少有2支铅笔的笔筒有多少个？请把它圈出来。圈出的笔筒里有几支铅笔？

生（齐）：圈出的笔筒有2个，里面都是有2支铅笔。

师：在第四种摆法中，至少有2支铅笔的笔筒有多少个？请把它圈出来。圈出的笔筒里有几支铅笔？

生（齐）：圈出的笔筒有1个，里面有2支铅笔。

（学生圈完之后得到图3）

师：根据图示可以知道，符合题目结论“至少有2支铅笔”的那个笔筒在每种摆法中的3个笔筒中铅笔数量都是最多的。因此，“总有一个笔筒”指的是哪个笔筒？

生10：铅笔最多的笔筒。

师：那为什么说至少有2支？

生11：这几个被圈起来的笔筒的铅笔数分别是4、3、2、2、2，其中最少的有2支，也就是至少有2支。

【设计意图：为了帮助学生理解“总有1个笔筒里至少有2支铅笔”的含义，教学有两个关键步骤。一是确定“总有1个笔筒”。教师引导学生在列举出的各种情况中找出铅笔数量不少于2支的笔筒，学生发现这个笔筒在每种摆法中都是铅笔数量最多的，即在验证过程中被圈起来的笔筒。二是理解“至少有2支铅笔”。学生需要确定被圈画的笔筒中铅笔的最少支数。通过观察，学生会发现符合“至少有2支铅笔”的笔筒中，最少的支数确实是2支。通过这种“行为表征→图像表征→符号表征”的三次表征和两次抽象过程，学生能够逐步理解并得到一个基本的数学结论，即最不利情况。这样的教学方法有助于学生从具体到抽象的思维过渡，加深对“鸽巢问题”核心概念的理解，并提高解决问题的能力。】

【教学片段2】二次看图，从“平均分”到“最不利”

师（指着图2）：你认为这4种摆法中，哪种最能说明“总有1个笔筒里至少有2支铅笔”这个结论？它是怎样分的？

生1：第四种摆法（（2，1，1）的摆法）。

师（提供操作材料）：请生1上来演示分法。

生1（边操作边说）：4支铅笔放进3个笔筒里，先在每个笔筒里放1支铅笔，剩下的最后1支铅笔放在任意一个笔筒里。

师：为什么你在每个笔筒中先放1支铅笔呢？

生1：因为将4支铅笔平均分到3个笔筒，每个笔筒就只能分到1支铅笔。

师：这样平均分后，就会使最多的笔筒里的铅笔数量怎样呢？大家可以看图2的4种摆法后回答。

生2：通过对比可以发现，前面三种摆法中都有空的笔筒，这样就会使得最多的笔筒里的铅笔更多，而第四种摆法实际上是先平均分，每个笔筒里都有铅笔，就可以使最多的笔筒里的铅笔尽可能少一点。

师：平均分的分法就是做了一个最坏的打算，也就是考虑到了“最不利情况”。

【设计意图：为了让学生深入理解“鸽巢问题”的核心概念，教学设计聚焦于最具代表性的摆法（2，1，1），并将其定义为“运气最坏的情况”。在这种摆法中，每个笔筒的铅笔数量尽可能均匀，即通过平均分配的方式，使得铅笔最多的笔筒与铅笔最少的笔筒之间的铅笔数量差距最小。这种摆法体现了“最不利情况”，即在所有可能的分配中，确保至少有一个笔筒里至少有2支铅笔。通过分析这种“运气最坏的情况”，学生可以理解，即使在最不利的情况下也能保证“总有1个笔筒里至少有2支铅笔”，那么在其他任何情况下，这一结论必然成立。这种从最不利情况出发的思维方式，有助于学生掌握“鸽巢问题”的独特思维特征，即在解决类似问题时，首先考虑最不利的情况，从而更有效地解决问题。】

[教学片段3]三次看图，从“顺向”到“反向”

师：前面我们研究的是被圈起来的笔筒，现在我们来重点研究其余的笔筒。请大家再次看图2。

师（指着没被圈起来的笔筒）：这个笔筒有几支铅笔？这个笔筒呢？……

生（齐）：0支、1支……

师：这些笔筒里的铅笔数符合“至少有2支”吗？

生（齐）：不符合。

师：没有被圈出来的笔筒里铅笔数最多的一个有几支铅笔？

生1：铅笔数最多的笔筒有1支铅笔。

师：如果每个笔筒中最多放1支铅笔，那么3个笔筒中一共最多放几支？

生（齐）：3支。

师：可是现在有4支铅笔，出现了什么情况？

生2：假设的3支和实际的4支数量上对不上。

师：因此，在有4支铅笔放到3个笔筒的情况下，我们的假设“每个笔筒中最多放1支铅笔”是错误的，这也就从反面证明了“总有1个笔筒里至少有2支铅笔”。

师：我们把这种思考方法称为“反证法”。

【设计意图：人教版新教材介绍“鸽巢问题”的例题1的第二种方法，旨在引导学生运用“假设”这一思路进行推理，以得出结论。假设教材给出的例题结论不成立，即每个笔筒中的铅笔数量都少于2支，那么每个笔筒中最多只能有1支铅笔。这种假设在推理过程中体现了“鸽巢原理”的数学价值与意义。人教版新教材通过“每个笔筒中最多放1支铅笔”的假设条件，引入了“反证法”的概念。与前面两个教学片段的“顺向”思考相比，教学片段3采用了“反向”思考的方法，即从否定的角度出发，对“总有1个笔筒里至少有2支铅笔”的结论进行验证。这种正反两个方向的探究，不仅验证了结论的正确性，而且促进了学生抽象思维和逻辑推理能力的发展。】

四、教学反思

（一）明确方向，直观演示

在教学过程中，教师首先引导学生关注放铅笔数量最多的笔筒，以此明确“总有”的概念。接着，教师引导学生关注笔筒内铅笔的支数，以便理解“至少”的含义。在明确了这两个关键概念后，学生才能够更好地把握“总有”和“至少”的实质。为了帮助学生深入理解，教师可以展示一张包含4种不同摆放方式的组图，让学生借助组图这个“脚手架”从不同角度观察和思考，从而自主领悟“鸽巢问题”这一数学思想。

（二）渗透方法，强化推理

逻辑推理是数学核心素养的主要表现之一，教师在教学中应将“枚举法”和“反证法”结合起来，通过“说理”和“证明”，加强学生逻辑推理能力的培养。“鸽巢问题”本质上是一种针对特定结构的数学或生活问题的求解模型，体现了数学的思想方法。在教学过程中，教师在采用枚举法的同时应融入有序性的思维理念，通过数形结合和符号化手段来展现所有可能的摆法，并辅以反证法等思想方法，以全面而深入地阐述该原理。

（责编 梁桂广）