玩“小”魔术，悟“大”道理

［摘 要］“隔空数数”一课充满着数学与魔术相结合的奇妙魅力，课程设计巧妙运用数学原理设计魔术，既蕴含数学的智慧，又体现魔术的乐趣。数学与魔术的结合，彰显了数学学科特有的魅力，打破了数学被视为“枯燥乏味”的刻板印象。在这样的课程中，教师以有趣的魔术作为探究线索，让学生在尝试破解的过程中学会认真倾听、学会分析，进而发现其中的数学规律，发现数学的美。

［关键词］数学魔术；数学规律；数学模型；数学本质

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）17-0068-04

【课前慎思】

针对学生对“9的倍数特征”的掌握情况，通过魔术的呈现形式激发学生的学习热情和求知欲，让学生在尝试破解的过程中，掌握仔细观察、认真模仿、分析数据、整理信息和分析信息等技能，进而发现其中的数学规律，形成自主探究的能力。通过实验、观察、思考和发现等活动，让学生感受魔术“9的倍数特征”的规律，感受数学与魔术的联系，使数学理念通过具体的活动巧妙体现出来，进而将数学课堂打造成一个知识的游乐场，充分调动学生的学习积极性与探究欲。

【教学目标】

1.让学生经历收集、分析、整理、对比数据，激发学生的好奇心与探究欲望，揭秘数学魔术的原理，从而积累探究经验。

2.通过数学魔术探索规律并作出相关判断，感受数量中“变中不变”的规律。

3.透过数学魔术的表象，找到“变中不变”的规律，发现数学的本质。

【教学重点】

探究任意两位数减去其十位上数字与个位上数字之后，结果一定是9的倍数的原因。

【教学难点】

通过魔术发现数学规律，建构数学模型。

【教具准备】

学习单、任务单、课件、书签。

【课中笃行】

一、创境导入、引发兴趣

（一）课前谈话

师：你们喜欢魔术吗？

生（齐）：喜欢，魔术很神奇。

师：因为魔术神奇、神秘，所以有这么多人喜欢它。你想成为魔术师吗？

生（齐）：想！

师：老师带来了一盒书签，我抽取一部分，再从抽取的书签去掉一部分，你知道还剩多少张吗？

生1：不知道。

生2：可以根据书签的厚度猜一猜。

师：这样能准确知道书签的数量吗？

生（齐）：不能。

（二）课题导入

师：你们不行，老师行，比这还要难的我都能猜出来，你们信不信？

（学生表示疑惑，对教师接下来要说的话充满期待。）

师：下面我们来玩一个数学魔术，魔术的名字叫隔空数数。（板书课题：隔空数数）

【设计意图】9的倍数的特征的概念对小学生来说是抽象和枯燥的，借助数学魔术的形式展开教学，可以吸引学生的注意力，提高他们的学习主观能动性，并激发他们的学习兴趣和探究欲望。

二、体验神奇、探究总结

（一）读一读，明确规则

师：要想成为一个优秀的魔术师，首先要明白魔术步骤，请大家拿出学习单（如图1）读一读。

师：你们了解这个魔术的步骤了吗？

（教师板书：抽数—相加—相减）

师：你们从板书中读出了数学味吗？假如抽取的书签是23张，怎么用数学语言表示呢？

生1：抽出23张，十位的2和个位的3相加得5，再从23里减去5得18。

（教师板书：23，2+3=5，23-5=18）

（二）玩一玩，体验神奇

师：现在我先请两名同学当助手，一名同学操作，另一名同学记录，我来猜。其他同学一起观察，看看能不能破解其中的奥秘。

师：下面开始我们的魔术表演。

第一次表演：

生1操作（抽出了35张书签），生2记录：35，3+5=8，35-8=27。其他学生根据生1和生2完成的步骤告诉教师“第一步抽数完成了”“第二步相加完成了”“第三步相减完成了”。（全班同学参与到魔术的过程中）

师：把书签放到老师手里，倒数三个数——3、2、1，我知道了，剩的是27张。

生（齐）：对了。

生2：老师，您是怎么知道的？

生3：这会不会只是巧合？我要求再来一次！

师：没问题。

第二次表演：

生3操作（抽出了19张书签），生4记录：19，1+9=10，19-10=9。其他学生根据生3和生4完成的步骤，告诉教师魔术的实时节点。

师：把书签放到老师手里，倒数三个数让我们再次见证奇迹——3、2、1，剩的是9张。

生（齐）：太神奇了。

师：惊讶之余，你们有没有思考剩下的书签数可能和什么有关？

生4：可能和9有关，9、18、27都是9的倍数。

【设计意图】数学魔术之所以令人惊叹，原因并非仅仅在于其表现形式的神奇，更在于潜藏于其背后的数学原理。让学生在感受魔术神奇之时，产生自主探究的动力。

三、关联迁移、探究规律

（一）写一写，呈现数据

师：真的是这样的吗？（出示任务单1，如图2所示）

师：你们在任务单1上任意写两位数，并验证你们的猜想。

（组织学生汇报，教师适时板书，如图3所示）

师：看到这些数据，你们有什么想法？

生5：剩下的书签数都是9的倍数。

师：能用数学的眼光去观察、思考和表达问题，正是我们学习数学的目的。

（二）想一想，发掘原理

1.收集数据

师：当有大量数据指向同一特征的时候，可能不是巧合，也许真的有规律存在。

师：为什么是9的倍数呢？我们退回一开始的举例，23，2+3=5，23-5=18。

师：能把这两个算式写成一个综合算式吗？

生1：23-（2+3）=18。

师：还可以怎么写？

生2：23-2-3=18。

生3：23-3-2=18。

师：这3个综合算式，你喜欢哪个？

生4：我喜欢生3的做法，先减去了这个两位数的个位数，后面计算更简便。

师：接下来，我们就用这种方法来研究其中的秘密吧。

师：大家写了这么多两位数，要想把10～99全部罗列出来的话，有多少个两位数？

生5：有90个。

2.整理数据

师：大家写的两位数有十几、五十几、三十几……太乱了，怎么研究呢？

生1：可以整理一下，进行分类。

生2：把十几的分一组，二十几的分一组，三十几的分一组……

师：太好了，我们把这些数据分成了9组。

（教师板书：1□、2□、3□……9□）

3.分析数据

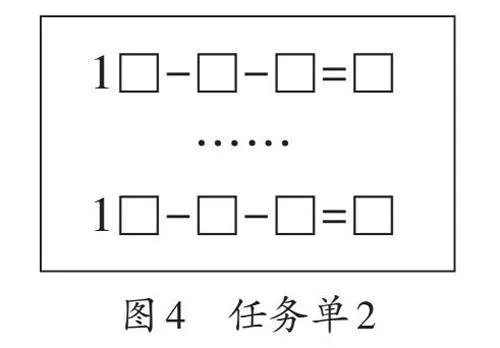
师：我们先从简单的开始研究，从十几开始，10-0-1=9，拿出任务单2，开始吧。（如图4）

师：写好了可以和同桌说一说你的发现。

师：谁来汇报你们交流的结果？

（学生展示交流结果，教师批注如图5所示）

生3：我发现这一组的数先减去个位数就是10，再减十位的1就等于9。

师：十几的这一组算式归纳成了10-1=9，其他组呢？选择你喜欢的一组研究吧。

（学生探究活动，师巡视并收集作品）

生4：我们小组研究的是二十几这组。我发现，二十几先减个位数就是20，20再减十位上的2等于18。

师：这一组算式归纳为20-2=18。

师：三十几的这一组呢？

生5：这一组算式归纳成了30-3=27。

……

（教师课件出示图6）

师：同学们太了不起了，把90个算式归纳成了9个算式。

师：还能再浓缩一点儿，把这9个算式归纳成一个算式吗？

生6：几十减几就等于几个9。

师（板书如图7所示）：你们找出了算式之间的联系，把它们简化成9组算式，又把9组算式提炼出一个模型。给你们点赞！

【设计意图】外表看起来冰冷的数学，其实蕴含着火热的思考，数学思考可以理解为是数学魔术的灵魂。在学生深度参与知识的建构过程中，他们对数学产生了浓厚的兴趣。

四、巩固深化、揭示本质

（一）说一说，表示规律

师：怎么确定最后剩下的书签数是9的几倍呢？

师：为了方便大家说出其中的道理，我们可以用小棒来演示。

师：10-1怎么减？

生1：解开一捆小棒，拿掉1根就是9根。

师：20-2怎么减？

生2：用2捆小棒表示，解开其中一捆小棒，拿掉2根就是18根。

生3：也可以2捆小棒都解开，分别拿掉1根就剩2个9根，就是18根。

师：你们觉得哪种表示方式更简洁明了。

生4：我喜欢生3的方式，一眼就能看出是2个9。

师：30-3呢？40呢？……90呢？

……

师：谁能用一句话说出其中的道理？

生5：几十减几，就是把几捆小棒都打开，每捆分别拿出1根，剩下的还剩几个9。

生6：几十减几等于几个9。

师：那怎么知道剩的书签数量是几个9的呢？

生7：得先知道1个9的标准也就是9张书签有多厚，再看有几个这样的9张书签就知道了。

师：一开始，没有揭秘魔术的时候你们感到惊奇，现在揭开了谜底，你想说什么？

生8：原来魔术就是障眼法，它的背后其实是一个简单的数学规律。

（二）亲身体验

师：现在你会玩这个魔术了吗？

师：现在请两名同学来给我们演示一下这个魔术吧。

师：下课后，同桌间轮流扮演魔术师来表演一次这个魔术吧。

（三）回顾反思

师：回顾我们的研究过程，我们通过“读一读”，读出了数学信息；通过“写一写”，发现了可能有数学规律；通过“想一想”，验证了确实有规律；通过“说一说”，用小棒说出其中的道理。

师：我们透过复杂的表象，找到事物发展的规律，就能发现本质。（板书：透过表象，发现本质）

（四）实践应用

师：我不光会隔空数数，我还会隔空看图呢，你们信吗？（课件出示图8）

师：随便选一个两位数，试一试，算好了就直接盯着最后的所对应的图。

师（出示图9）：又是见证奇迹的时刻——3、2、1，最后计算出来的数对应的是猴子。这时候，你们知道这个魔术的秘密了吗？

【设计意图】教学不仅要引导学生发现规律、验证规律还要让他们学会应用规律，学生经历合理的推测和验证，他们的思维变得更加缜密，从而增强他们的数学学习能力。在面对相似问题时，学生能从现象出发，挖掘背后隐藏的规律，进而进一步培养他们的数学核心素养。

五、全课总结、拓展延伸

师：今天我们玩了一个数学魔术，你有哪些收获呢？

生1：我知道这个魔术的秘密，它就是一个数学问题。

生2：这个看似神奇的魔术，在对它进行分析后，我们发现了它的数学规律。

生3：这个魔术背后的规律就是几十减几就是几个9。

师：这个规律固然重要，但可能第二天你就忘这个魔术，我们要记住的是以后面对新问题，主动地去寻找规律，要保持有一颗探究之心！

师：课下可以根据所学的知识，设计出一个数学魔术，和你的家人一起玩一玩。

【设计意图】数学知识不仅存在于课本中，还内隐于生活中。通过知识的拓展延伸，教师应引导学生面对新问题时，积极探寻，始终保持一颗求知之心，拓宽他们的视野，提升价值观，最终实现育人的目标。

【教学反思】

“隔空数数”是一节好玩的数学魔术课，学生在课堂上展现出了极高的热情和专注度，这主要得益于教师精心的教学设计。在教学中教师抓住“趣”，追求“智”，将一个“小”的数学魔术，玩出了“大”智慧。

一、从“教”数学到“玩”数学

传统的数学课侧重于知识传授，较少关注激发学生兴趣及发掘其自主探究能力。西蒙斯·帕珀特曾说过：“学习是建构，而不是接收。”学生应该成为知识的创造者和建构者，而不仅仅是知识的接收者。在教学“9的倍数特征”时，借助数学魔术的形式展开教学，笔者设计了两次魔术演示的环节。第一次演示让学生体验神奇，第二次演示让学生产生怀疑，引发思考“剩下的书签数可能和什么有关？”激发了学生学习兴趣和探究欲望。接下来，学生迫不及待地进行“写一写”环节，发现剩下的书签数和9有关。在“想一想”环节，教师则引导学生回归知识起点，自主搜集、整理、分析数据，最后归纳出“几十减几就等于9的几倍”。在“说一说”环节，学生阐述这一发现背后的道理。这些探究活动将传统的教师“教数学”转变为学生的创造性“玩数学”。

二、从玩“游戏”到玩“数学”

如果仅仅停留在游戏的“玩”上，就不能亲身体会到数学的“趣”。从“玩游戏”到“玩数学”，需要引导学生跳出游戏的框架，发掘数学之美，体验数学之乐。这节课，从两次魔术表演，完美地升级到数学规律的探究。“写一写”环节，学生发现剩下的书签数是有规律的。“想一想”环节，学生主动去探究这些算式，发现算式中的数之间存在一定的关联，并用数学知识去验证规律。“说一说”环节，借助小棒阐述其中道理。一系列活动让学生领悟到，其实玩的不是游戏而是数学。这场游戏之旅，学生领略了数学的魅力，尽享数学带来的乐趣。

三、从“是什么”到“为什么”

学习数学，不能仅满足于表面认知，了解“是什么”是远远不够的，知其然还要知其所以然。从认识表面现象到深入领悟数学原理，是学生在学习数学过程中不可或缺的环节。当学生掌握了魔术背后的秘密，明白为何结果是9的倍数时，他们尝试运用所学知识来解释“几十减几等于9的几倍”的规律。然而，这一规律对于部分学生而言，仍只是一知半解。因此，教师引导学生乘胜追击，借助小棒图，继续挖掘其背后的深层逻辑。道理越辩越明，逻辑越辩越清，一捆小棒去掉1根就是9根，几十减几就是从几捆小棒分别都去掉1根，每一捆剩下都是9根，所以几十减几就是9的几倍。透过魔术的表象，发现数学的本质，让学生在掌握知识的同时，领略数学魔术的无穷魅力。

【本文系2022年安徽省教育科学研究项目“基于学生立场的小学数学智趣教学实践研究”（课题批准号：JK22091）的研究成果之一。】

（责编 梁桂广）